Analysis of Friction Noise Mechanism in Lead Screw System of Autonomous Vehicle Seats and Dynamic Instability Prediction Based on Deep Neural Network
Abstract
:1. Introduction
Problem Formulation
2. Modeling and Results
2.1. Single Component Modal Analysis and Experiment
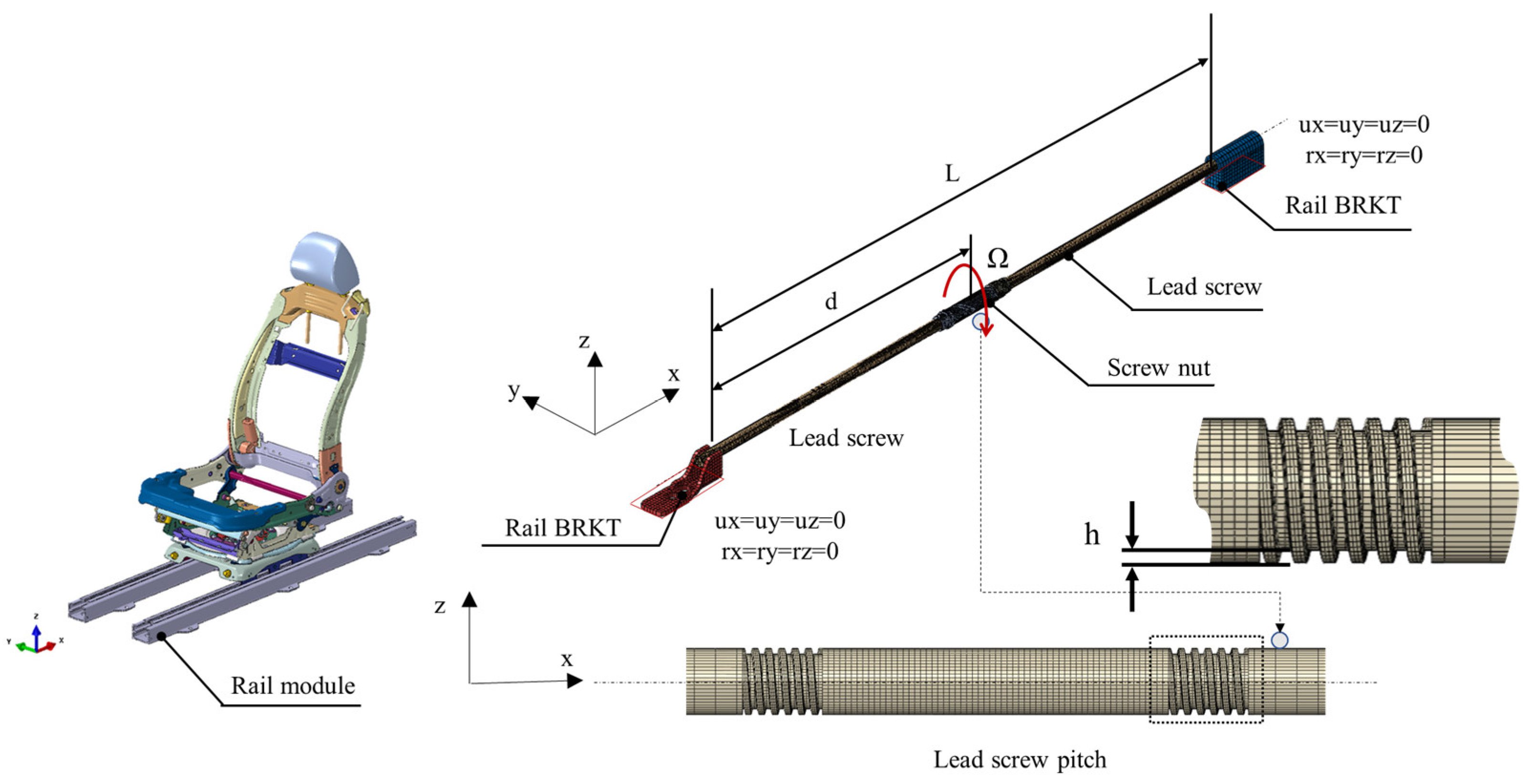
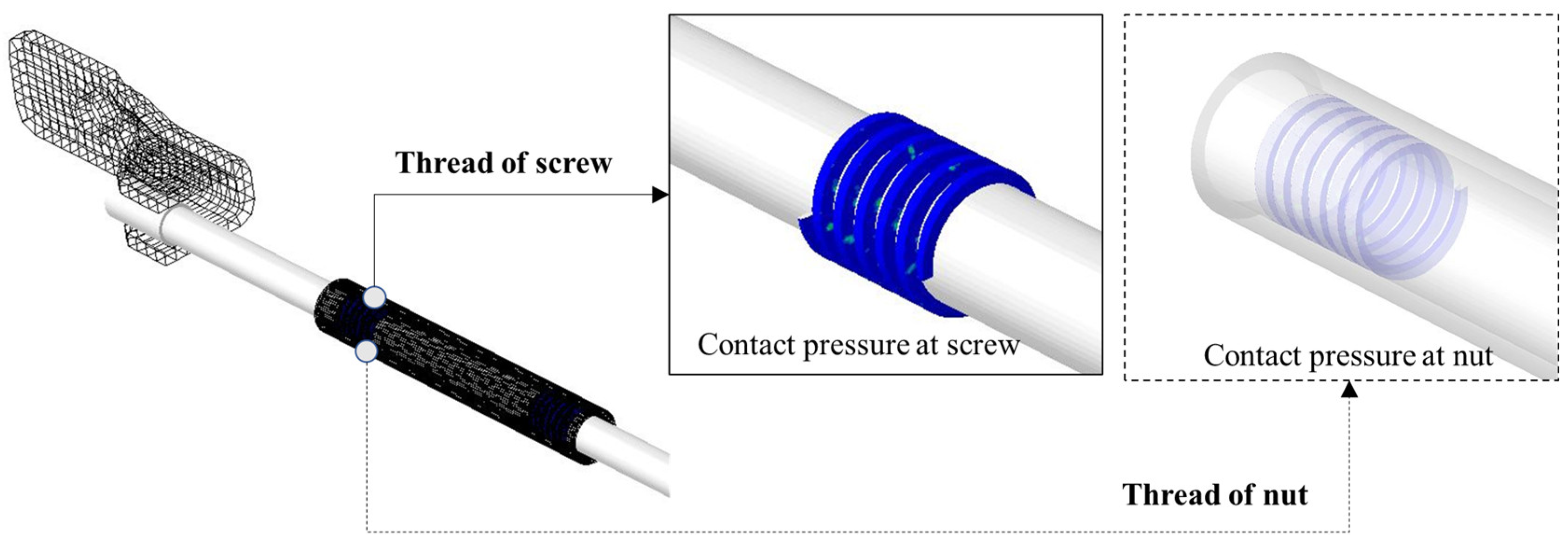
2.2. Finite Element Model
2.3. Method for Complex Eigenvalue Analysis of Finite Element Model
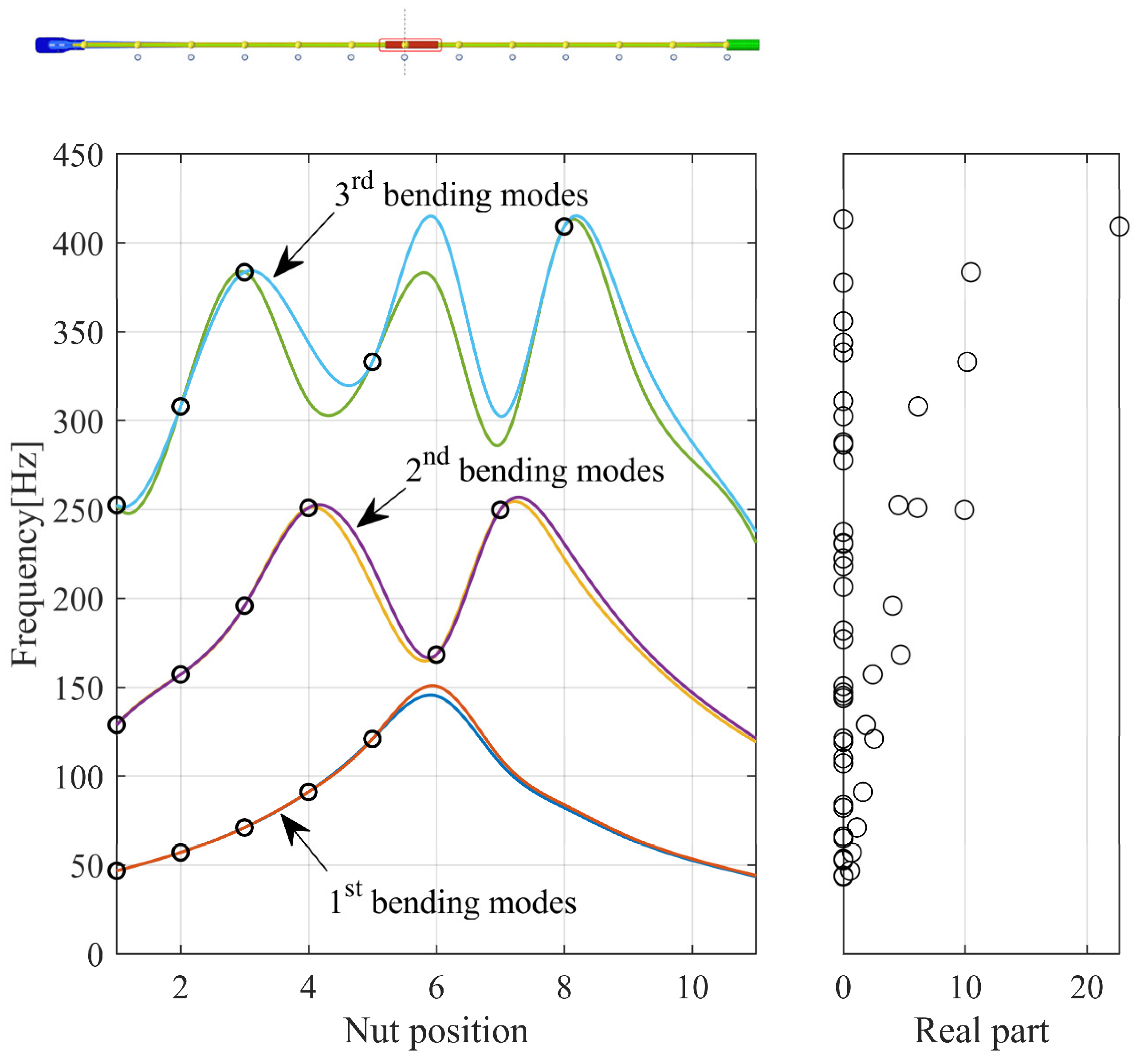
2.4. Results of Complex Eigenvalue Analysis of Finite Element Model
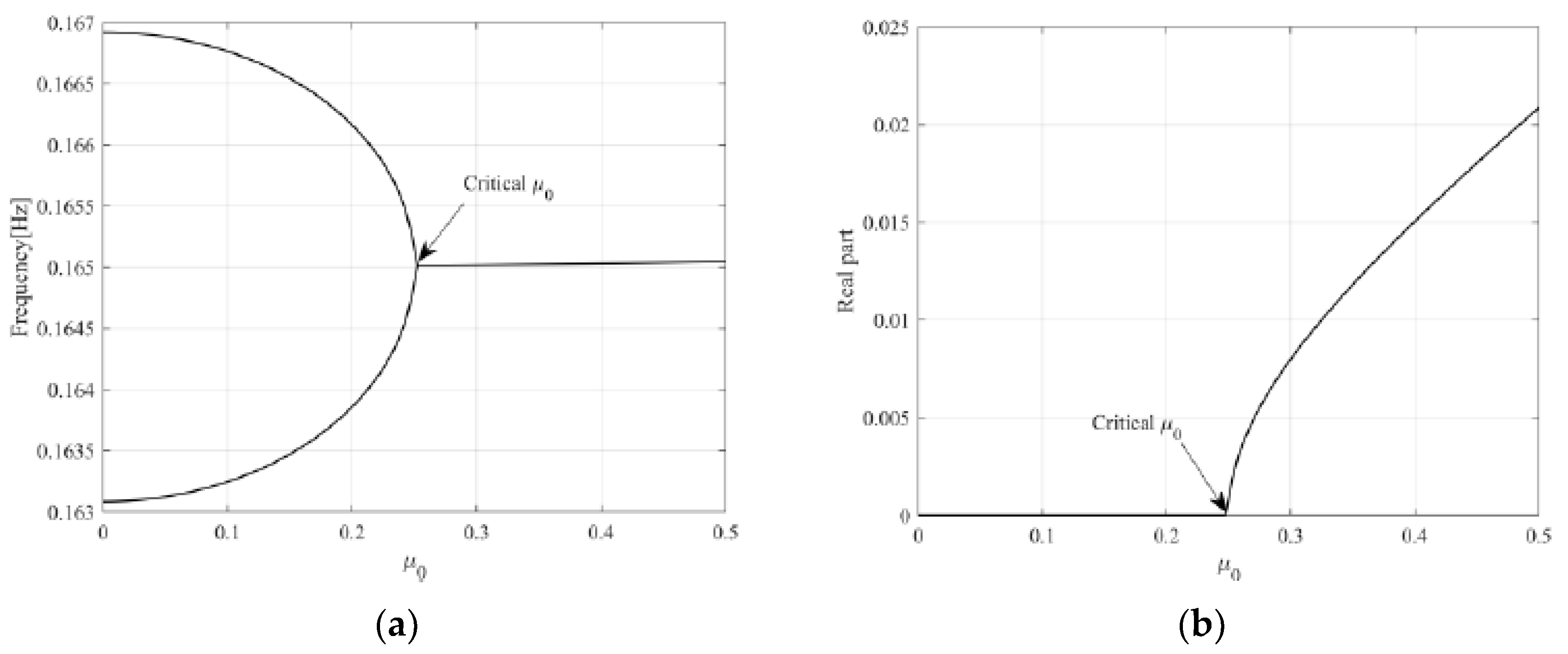
2.5. Lead Screw Squeal Instability Mechanism
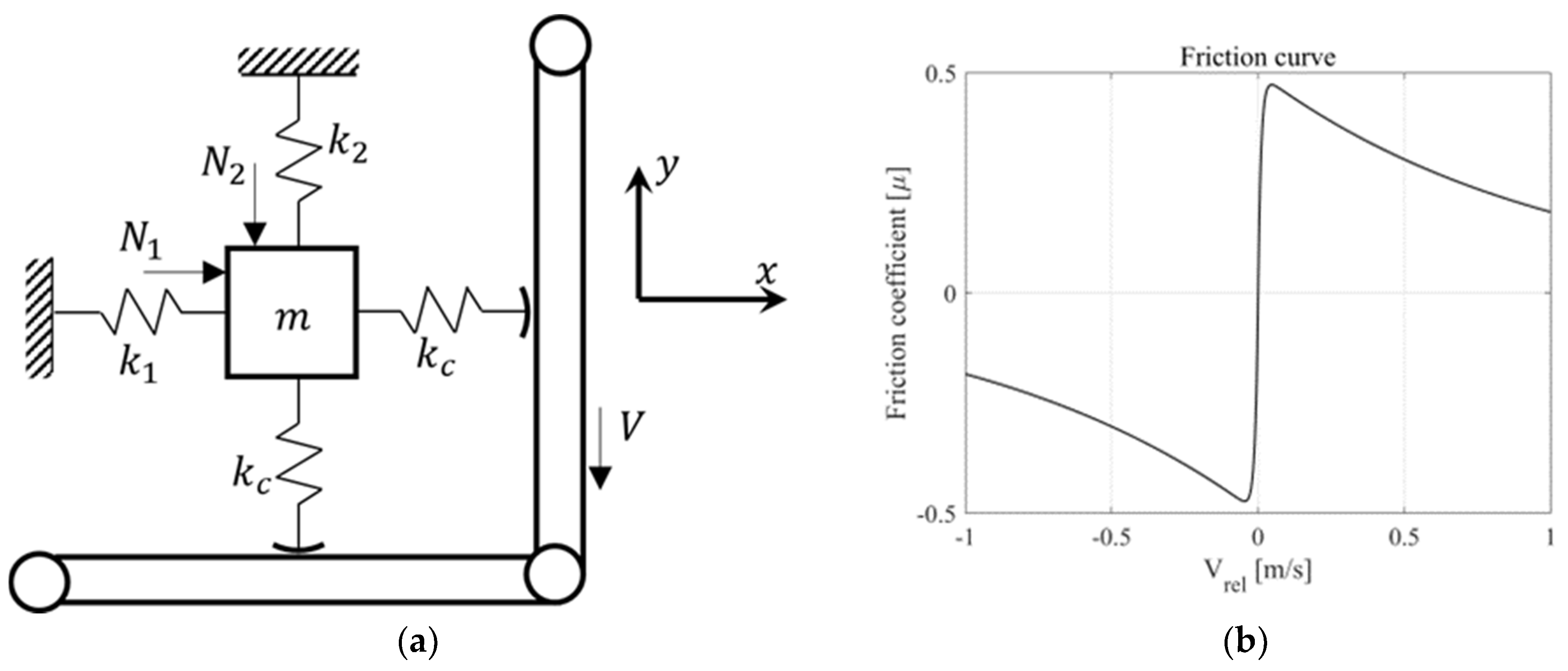
2.5.1. Description of Minimal Model
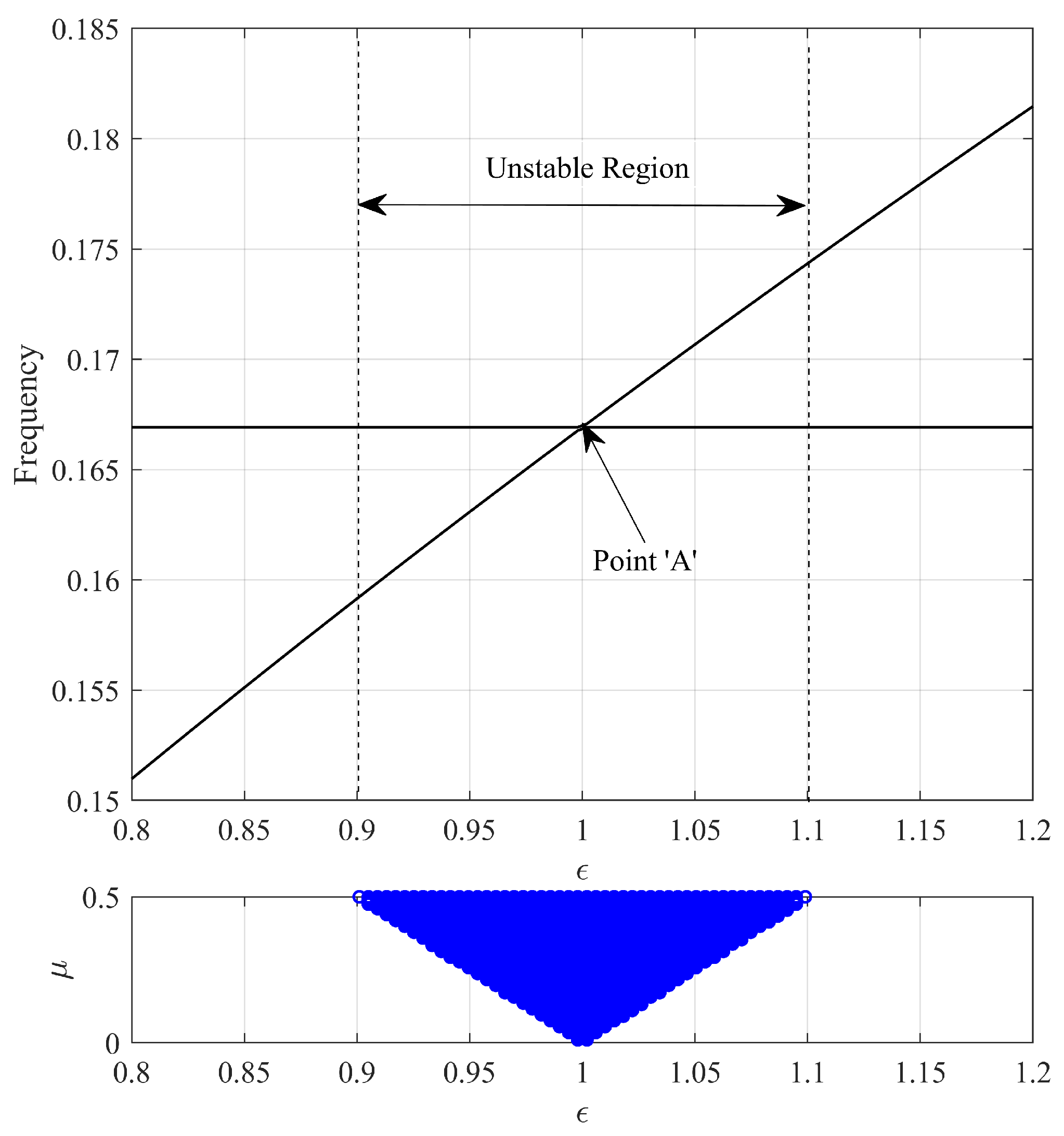
2.5.2. Analysis Results of Degree of Freedom of Minimal Model Mechanism
2.6. Deep Neural Network Based Squeal Instability Estimation
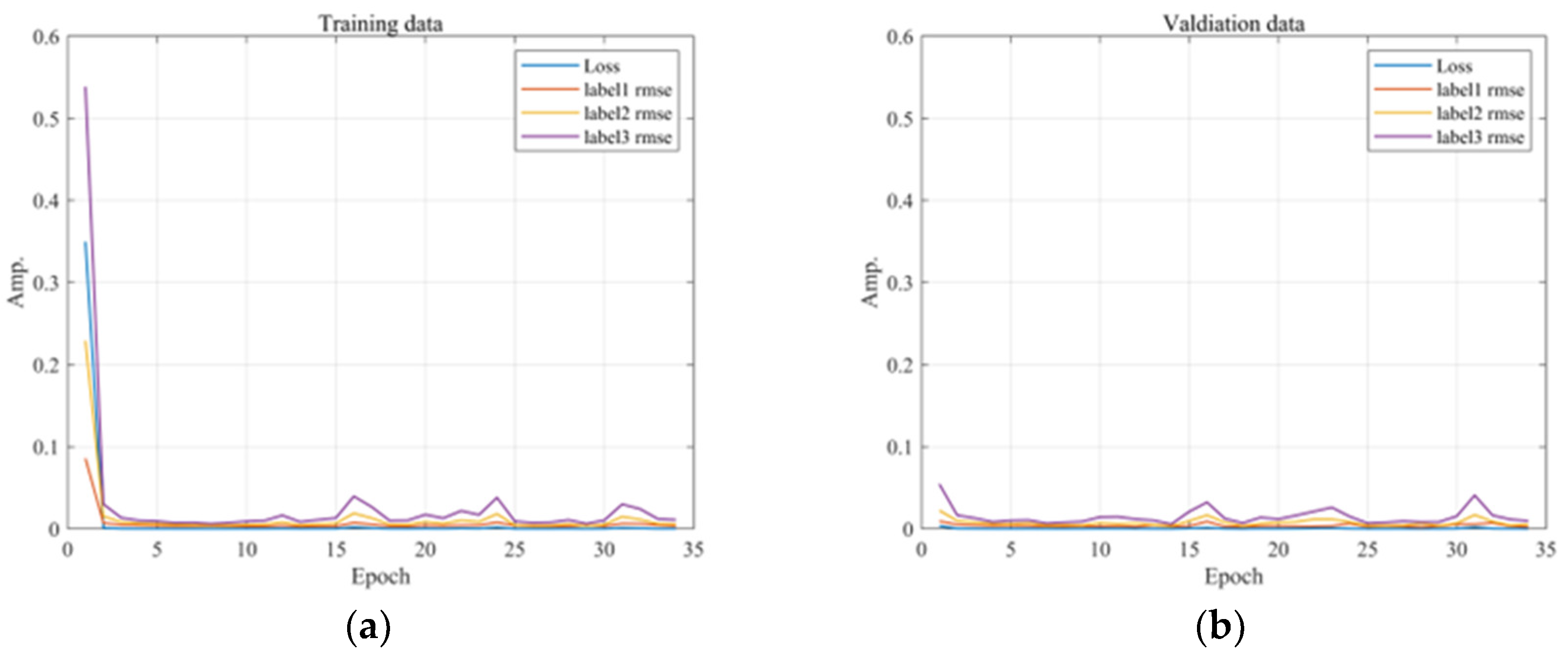
2.6.1. Data Augmentation
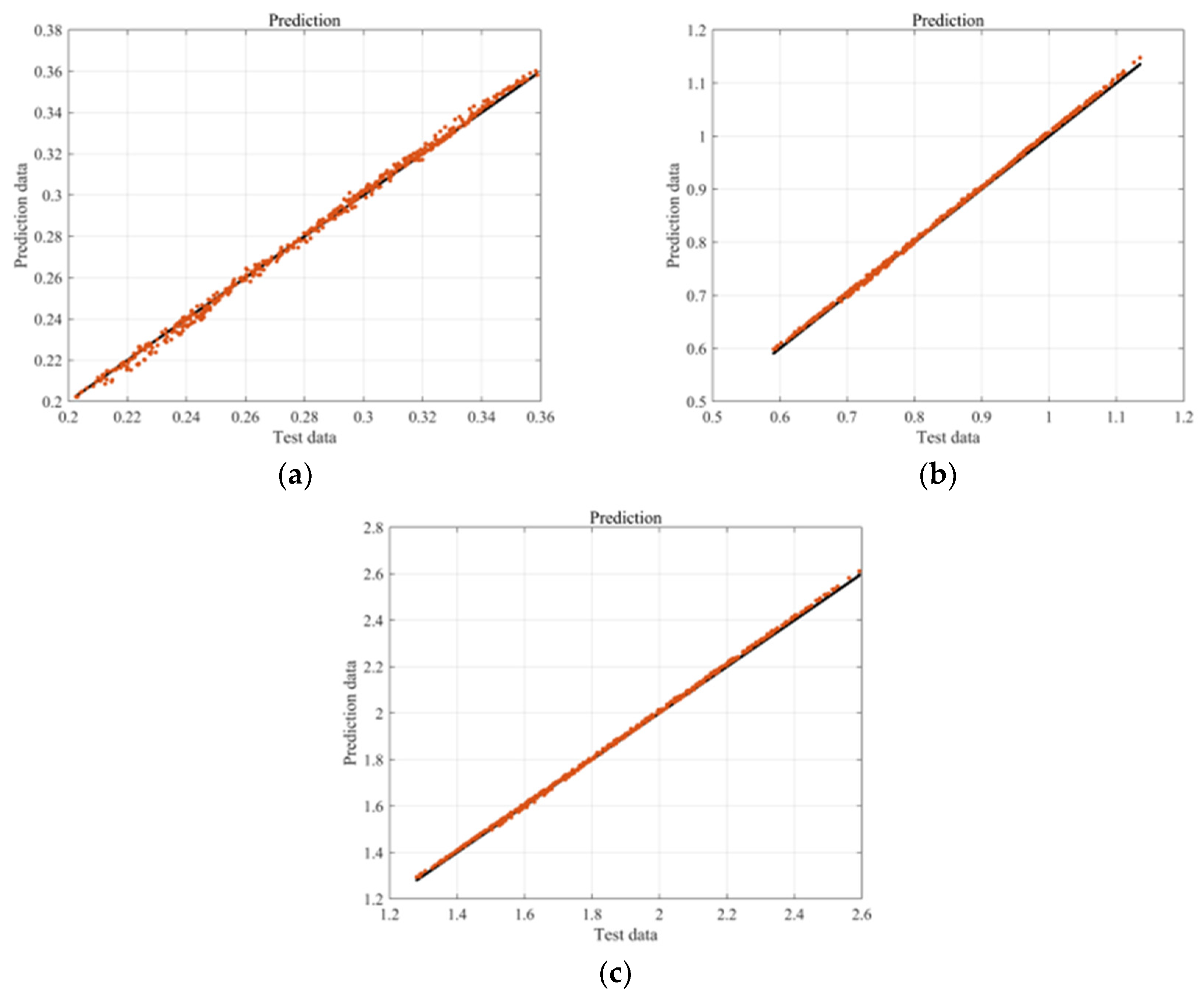
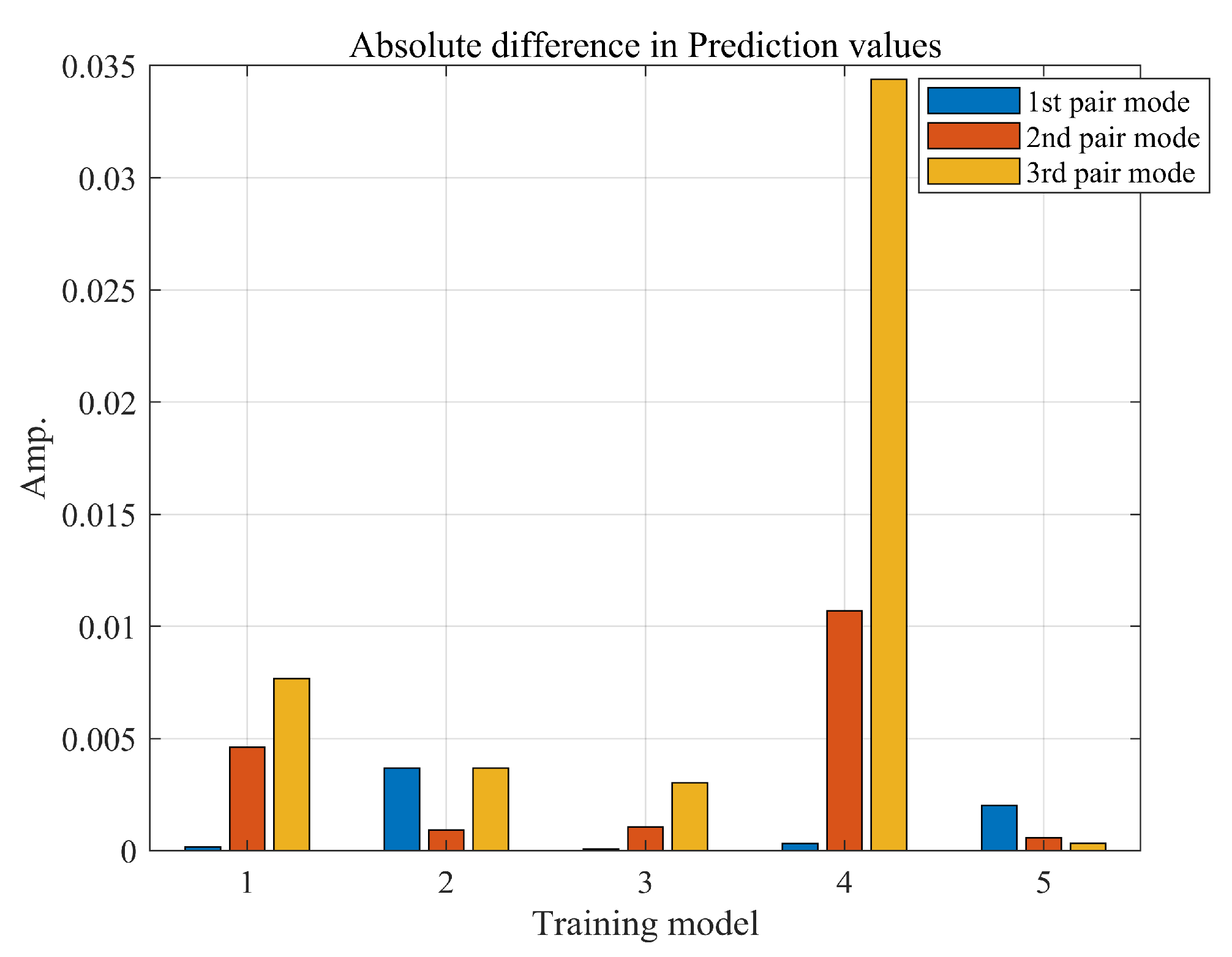
2.6.2. Squeal Noise Prediction Using Deep Learning
3. Discussion and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Papinniemi, A.; Lai, J.C.; Zhao, J.; Loader, L. Brake squeal: A literature review. Appl. Acoust. 2002, 63, 391–400. [Google Scholar] [CrossRef]
- Kang, J. Finite element modelling for the investigation of in-plane modes and damping shims in disc brake squeal. J. Sound Vib. 2012, 331, 2190–2202. [Google Scholar] [CrossRef]
- Nack, W.V. Brake squeal analysis by finite elements. Int. J. Veh. Des. 2000, 23, 263–275. [Google Scholar] [CrossRef]
- Kinkaid, N.M.; O’Reilly, O.M.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2003, 267, 105–166. [Google Scholar] [CrossRef]
- Liu, P.; Zheng, H.; Cai, C.; Wang, Y.Y.; Lu, C.; Ang, K.H.; Liu, G.R. Analysis of disc brake squeal using the complex eigenvalue method. Appl. Acoust. 2007, 68, 603–615. [Google Scholar] [CrossRef]
- Gallina, P. Vibration in screw jack mechanisms: Experimental results. J. Sound Vib. 2005, 282, 1025–1041. [Google Scholar] [CrossRef]
- Gallina, P.; Giovagnoni, M. Design of a screw jack mechanism to avoid self-excited vibrations. J. Dyn. Sys. Meas. Control 2002, 124, 477–480. [Google Scholar] [CrossRef]
- Vahid, O.; Eslaminasab, N.; Golnaraghi, M.F. Friction-induced vibration in lead screw systems: Mathematical modeling and experimental studies. J. Vib. Acoust. 2009, 131, 021003. [Google Scholar] [CrossRef]
- Olofsson, U.; Ekerfors, L. Friction-induced noise in screw-nut transmissions. Wear 1991, 148, 25–37. [Google Scholar] [CrossRef]
- Kang, J.; Seo, K.; Kim, K. Experimental investigation of friction noise in lead screw system under mode-coupling. J. Mech. Sci. Technol. 2015, 29, 5183–5188. [Google Scholar] [CrossRef]
- Nam, J.; Do, H.; Kang, J. Investigation of friction induced vibration in lead screw system using FE model and its experimental validation. Appl. Acoust. 2017, 122, 98–106. [Google Scholar] [CrossRef]
- Bergman, F.; Eriksson, M.; Jacobson, S. The effect of reduced contact area on the occurrence of disc brake squeals for an automotive brake pad. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2000, 214, 561–568. [Google Scholar] [CrossRef]
- Nam, J.; Kang, J. Friction-induced vibration by dust effect. Trans. Korean Soc. Noise Vib. Eng. 2020, 30, 201–210. [Google Scholar] [CrossRef]
- Kang, J. Investigation on friction noise in beam structure under mode-coupling by using analytical finite-element squeal model. Trans. Korean Soc. Mech. Eng. A 2014, 38, 545–550. [Google Scholar] [CrossRef]
- Weiss, C.; Morlock, M.M.; Hoffmann, N.P. Friction induced dynamics of ball joints: Instability and post bifurcation behavior. Eur. J. Mech.-A/Solids 2014, 45, 161–173. [Google Scholar] [CrossRef]
- Wang, D.W.; Mo, J.L.; Ouyang, H.; Chen, G.X.; Zhu, M.H.; Zhou, Z.R. Experimental and numerical studies of friction-induced vibration and noise and the effects of groove-textured surfaces. Mech. Syst. Signal Process. 2014, 46, 191–208. [Google Scholar] [CrossRef]
- Nam, J.; Kang, J. Chaos signal classification and verification using CNN. Trans. Korean Soc. Noise Vib. Eng. 2021, 31, 82–90. [Google Scholar] [CrossRef]
- Revach, G.; Shlezinger, N.; Ni, X.; Escoriza, A.L.; Van Sloun, R.J.; Eldar, Y.C. KalmanNet: Neural network aided Kalman filtering for partially known dynamics. IEEE Trans. Signal Process. 2022, 70, 1532–1547. [Google Scholar] [CrossRef]
- An, D.; Yoo, I.; Lee, S. Improvement of multivariable, nonlinear, and overdispersion modeling with deep learning: A case study on prediction of vehicle fuel consumption rate. Int. J. Highw. Eng. 2017, 19, 1–7. [Google Scholar] [CrossRef]
- Choi, H. Nonlinear adaptive prediction using locally and globally recurrent neural networks. J. Inst. Electron. Eng. Korea 2003, 40, 139–147. [Google Scholar]
- Wang, G.A. perspective on deep imaging. IEEE Access 2016, 4, 8914–8924. [Google Scholar] [CrossRef]
- Park, J.; Choi, E.; Kim, B.; Moon, Y. Comparison of prediction performance of flight status variables using deep learning. In Proceedings of the KSAS 2021 Fall Conference, Jeju, Republic of Korea, 17–19 November 2021; pp. 339–340. [Google Scholar]
- Lee, J.Y.; Moon, H.C.; Kim, S.J.; Kim, J.G. Compression of CNN using local nonlinear quantization in MPEG-NNR. In Proceedings of the Korean Society of Broadcast Engineers Conference, Online, 13–15 July 2020; pp. 662–663. [Google Scholar]
- Kim, D.; Min, K.; Kim, H.; Huh, K. Vehicle sideslip angle estimation using deep ensemble-based adaptive Kalman filter. Mech. Syst. Signal Process 2020, 144, 106862. [Google Scholar] [CrossRef]
- Tork, N.; Amirkhani, A.; Shokouhi, S.B. An adaptive modified neural lateral-longitudinal control system for path following of autonomous vehicles. Eng. Sci. Technol. Int. J. 2021, 24, 126–137. [Google Scholar] [CrossRef]
- Šabanovič, E.; Žuraulis, V.; Prentkovskis, O.; Skrickij, V. Identification of Road-Surface Type Using Deep Neural Networks for Friction Coefficient Estimation. Sensors 2020, 20, 612. [Google Scholar] [CrossRef] [Green Version]
- Nam, J.; Kang, J. Semi-analytical approach for brake squeal of a rail pad. J. Mech. Sci. Technol. 2020, 34, 3147–3153. [Google Scholar] [CrossRef]
- Anutcharee, K.; Kiatfa, T.; Supachai, P.; Nuttapong, L. Study of Brake Pad Shim Modification to Improve Stability against High Frequency Squeal Noise by Finite Element Analysis. Eng. J. 2022, 26, 25–34. [Google Scholar]
- Liu, S.; Silva, U.; Chen, D.; Leslie, A.; Meehan, P. Experimental investigation of wheel squeal noise under mode coupling. In Proceedings of the 12th International Conference on Contact Mechanics and Wear of Rail/Wheel System, Melbourne, VIC, Australia, 4–7 September 2022; pp. 266–267. [Google Scholar]
- Meehan, P.; Leslie, A. On the mechanisms, growth, amplitude and mitigation of brake squeal noise. Mech. Syst. Signal Process. 2021, 152, 107469. [Google Scholar] [CrossRef]
- Kang, J. Tilting effect of automotive seat system on squeak noise. Trans. Korean Soc. Noise Vib. Eng. 2010, 20, 577–582. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, N.; Gaul, L. A sufficient criterion for the onset of sprag-slip oscillations. Arch. Appl. Mech. 2004, 73, 650–660. [Google Scholar] [CrossRef]
- Denny, M. Stick–slip motion: An important example of self-excited oscillation. Eur. J. Phys. 2004, 25, 311. [Google Scholar] [CrossRef]
- Sandwell, D.T. Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data. Geophys. Res. Lett. 1987, 14, 139–142. [Google Scholar] [CrossRef] [Green Version]
- Nam, J.; Kang, J. Comparison of vibration visualization methods for classification of chaos based on CNN. J. Mech. Sci. Technol. 2022, 36, 2749–2757. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on Imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]

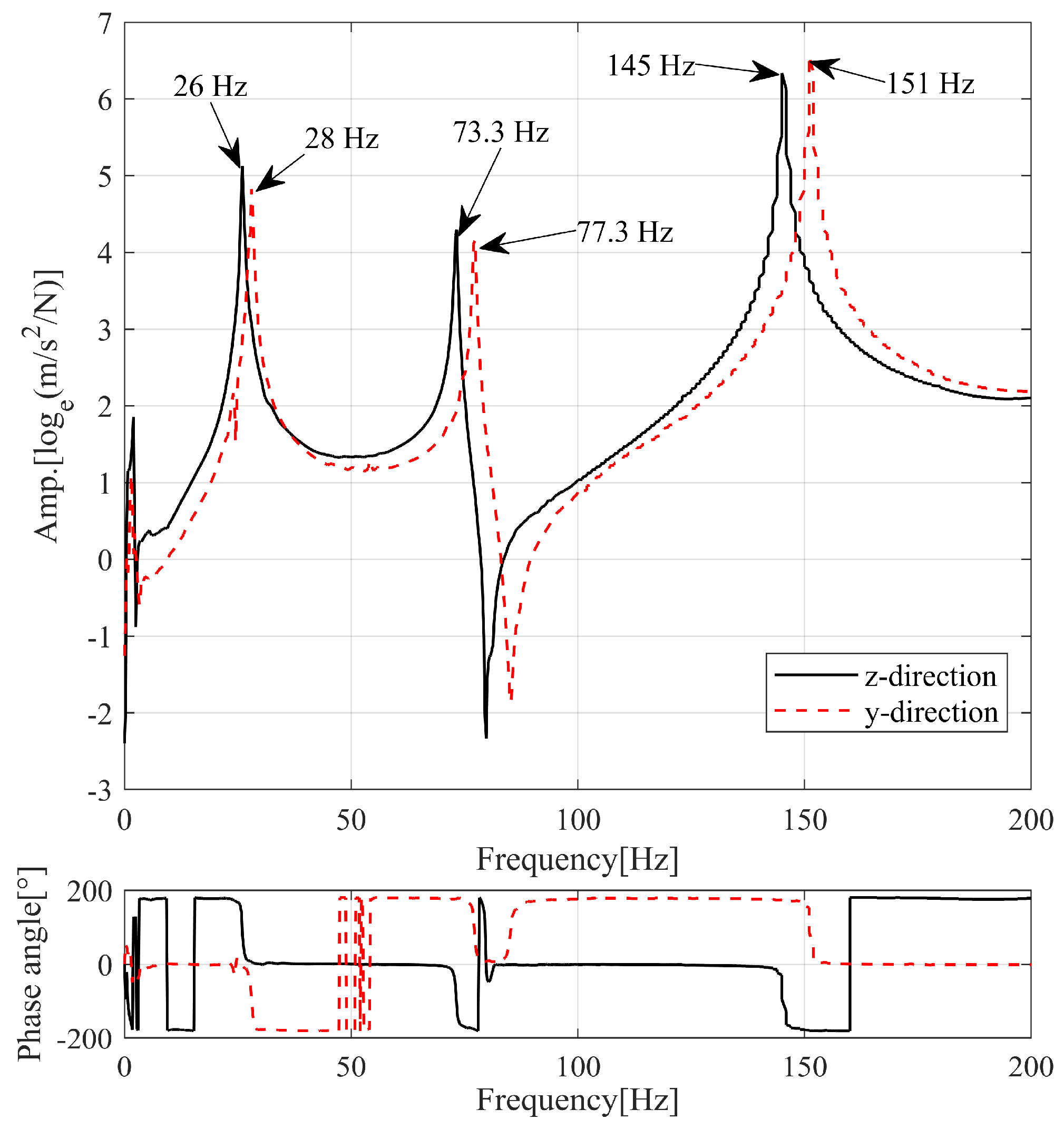
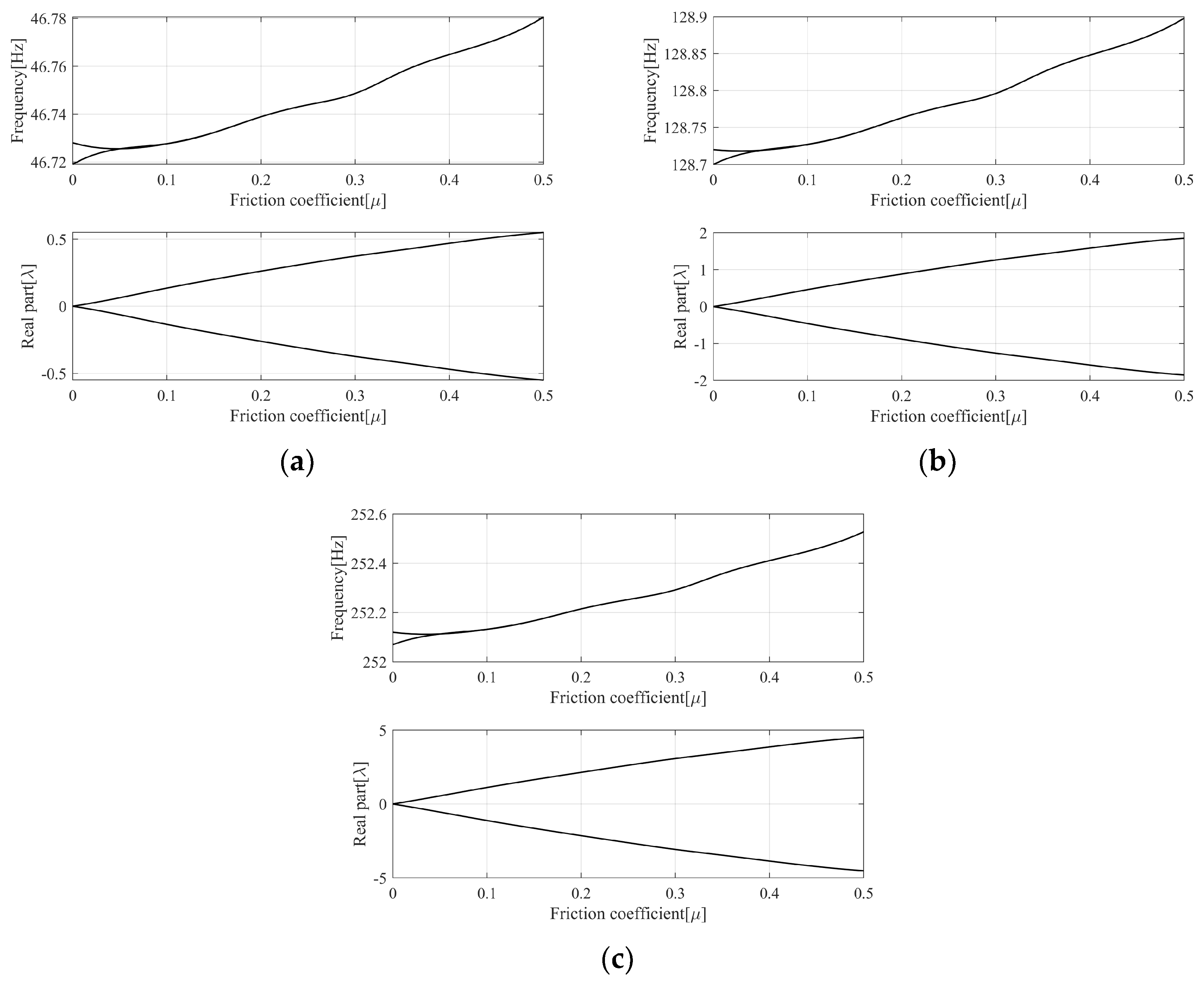

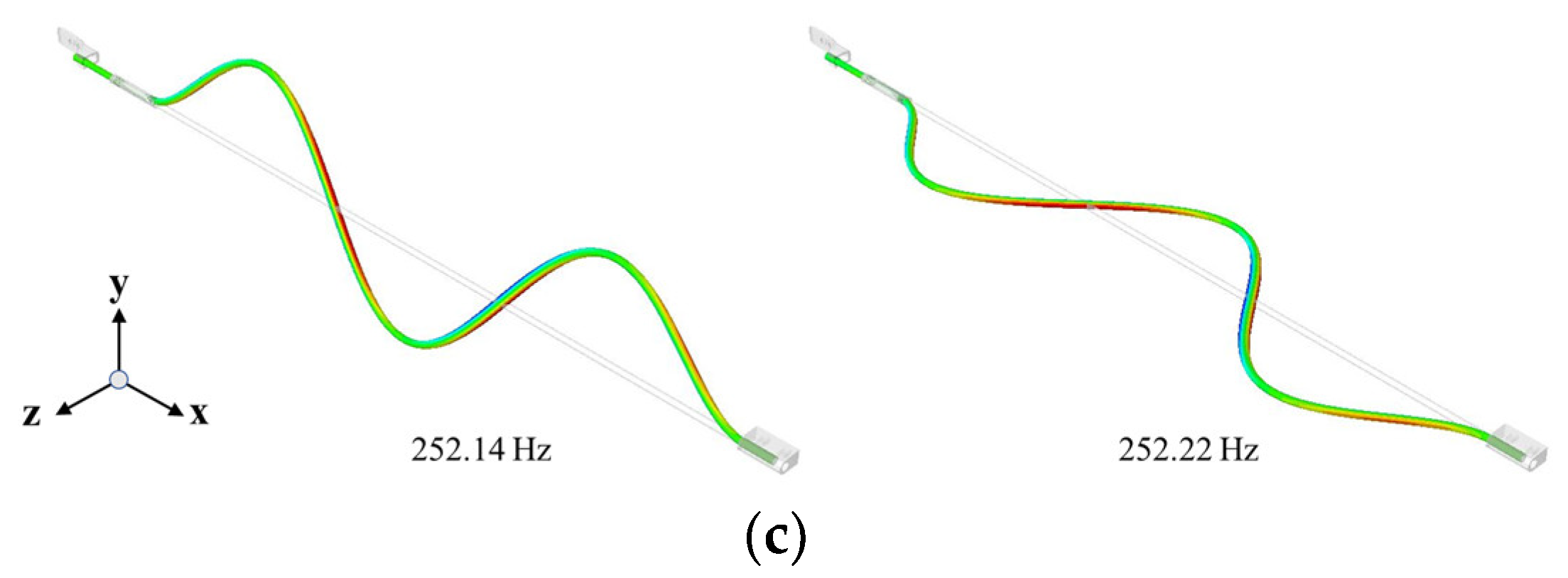


| Simulation [Hz] | Experiment [Hz] | Error [%] | Mode Shape |
|---|---|---|---|
| 25.9 | 26.0 | 0.4 | 1st bending pair |
| 28.4 | 28.0 | 1.4 | |
| 74.2 | 73.3 | 1.2 | 2nd bending pair |
| 79.3 | 77.3 | 2.6 | |
| 147.0 | 145.0 | 1.4 | 3rd bending pair |
| 156.0 | 151.0 | 3.3 |
| Parameter | Symbol | Value |
|---|---|---|
| Translation distance | d | variable |
| Rotational speed | ohm | 28.64 rpm |
| Length of lead screw | L | 996.301 mm |
| Young’s modulus | E | 240 GPa |
| Density | ρ | 7.96 × 109 ton/mm3 |
| Data | Percentage | Number of Samples |
|---|---|---|
| Training | 56% | 1400 |
| Validation | 14% | 350 |
| Testing | 30% | 750 |
| Layer | Output Shape | Param# | Connect to |
|---|---|---|---|
| Input Layer | (None, 2) | 0 | - |
| Dense 1 | (None, 256) | 768 | Input Layer |
| Dense 2 | (None, 128) | 32,896 | Dense 1 |
| Dense 3 | (None, 64) | 8256 | Dense 2 |
| Dense 4 | (None, 32) | 2080 | Dense 3 |
| Y1_output | (None, 1) | 129 | Dense 2 |
| Y2_output | (None, 1) | 65 | Dense 3 |
| Y3_output | (None, 1) | 33 | Dense 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nam, J.; Kim, S.; Ko, D. Analysis of Friction Noise Mechanism in Lead Screw System of Autonomous Vehicle Seats and Dynamic Instability Prediction Based on Deep Neural Network. Sensors 2023, 23, 6169. https://doi.org/10.3390/s23136169
Nam J, Kim S, Ko D. Analysis of Friction Noise Mechanism in Lead Screw System of Autonomous Vehicle Seats and Dynamic Instability Prediction Based on Deep Neural Network. Sensors. 2023; 23(13):6169. https://doi.org/10.3390/s23136169
Chicago/Turabian StyleNam, Jaehyeon, Soul Kim, and Dongshin Ko. 2023. "Analysis of Friction Noise Mechanism in Lead Screw System of Autonomous Vehicle Seats and Dynamic Instability Prediction Based on Deep Neural Network" Sensors 23, no. 13: 6169. https://doi.org/10.3390/s23136169






