A New Technique for Broadband Matching of Open-Ended Rectangular Waveguide Radiator
Abstract
:1. Introduction
- OEG impedance matching over more than an octave bandwidth;
- Achieving −20 dB reflection in the standard waveguide band;
- OEG matching with a series of printed-circuit capacitive elements precisely placed inside a waveguide via a low-dielectric-constant material.
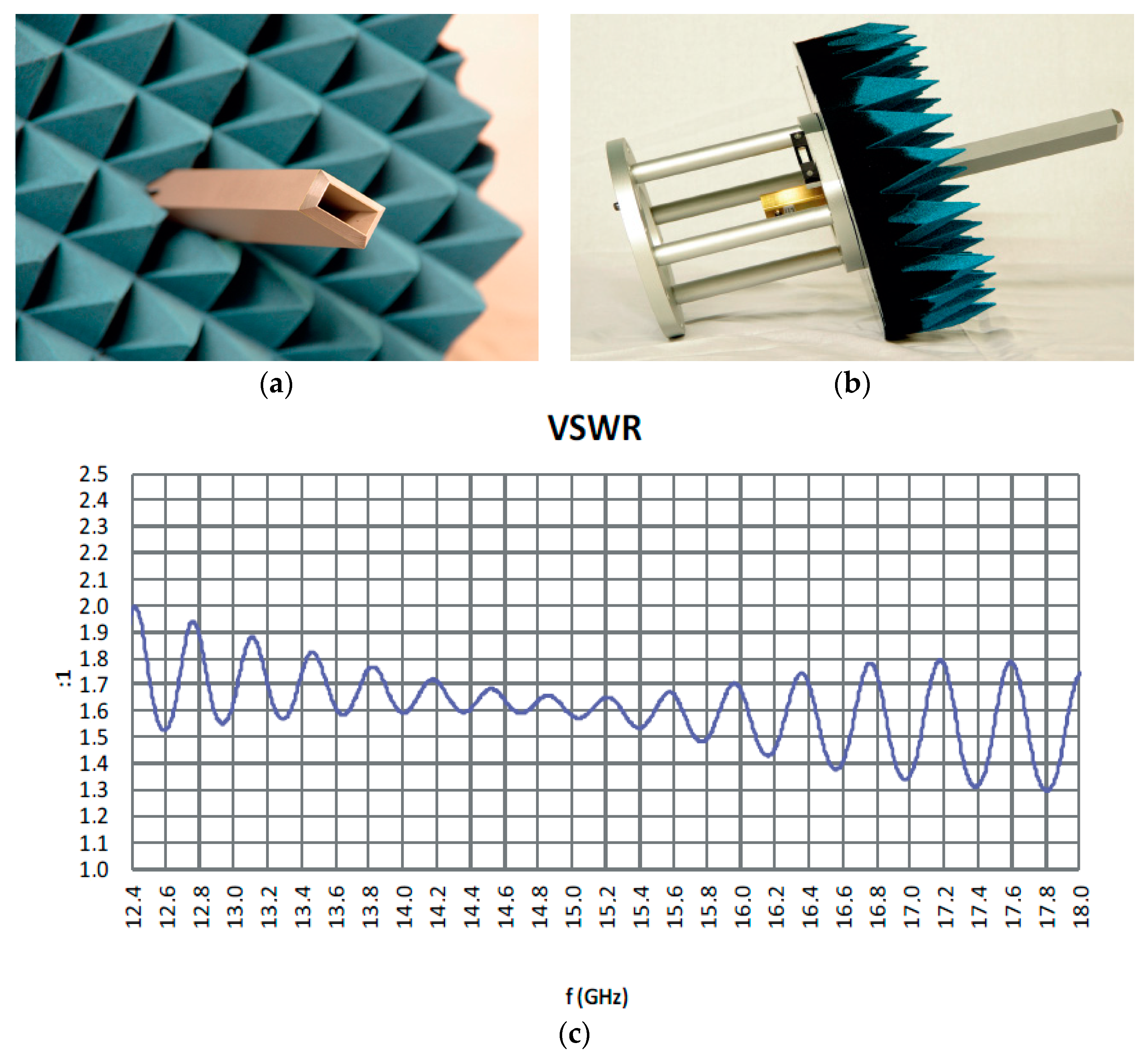
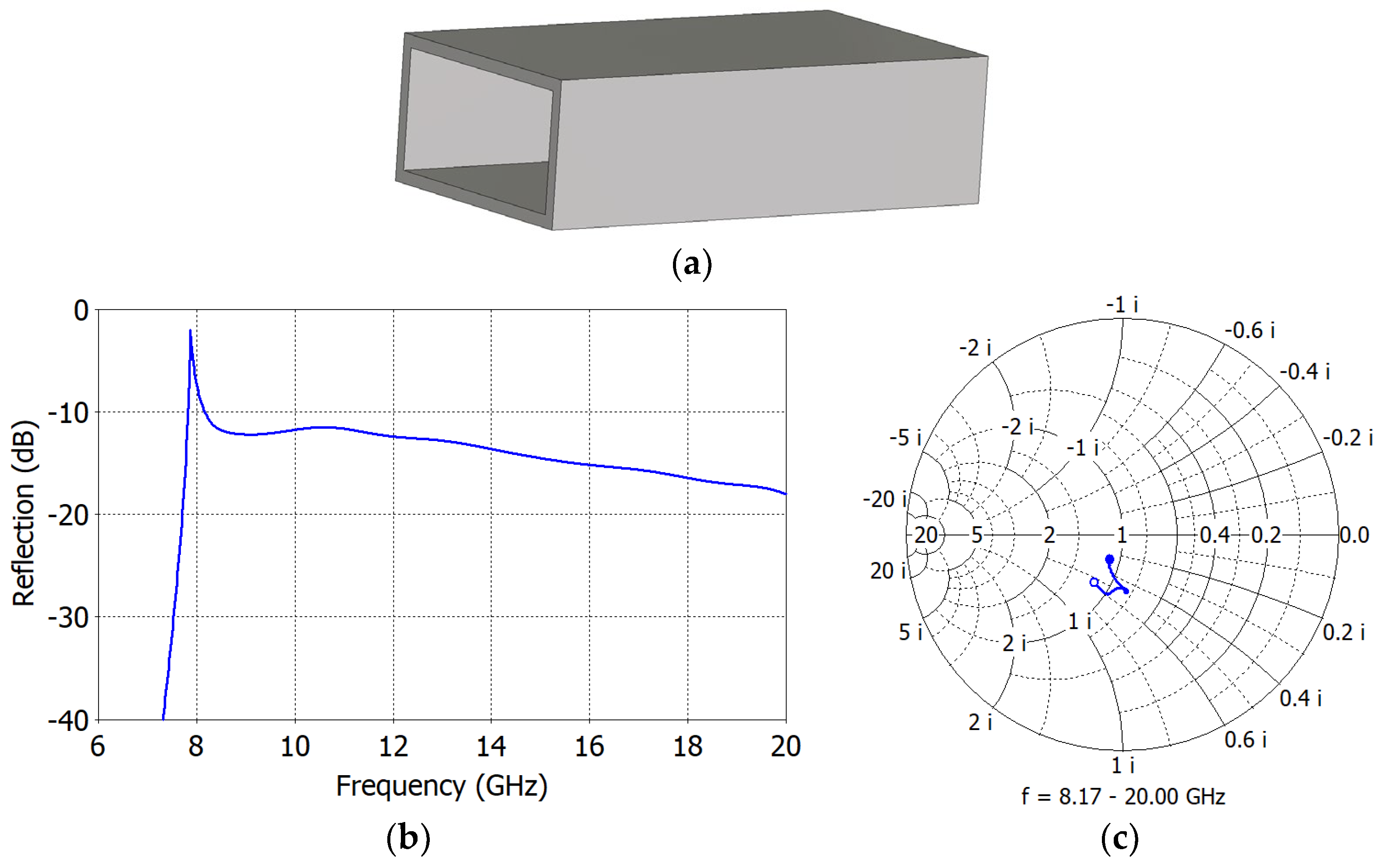
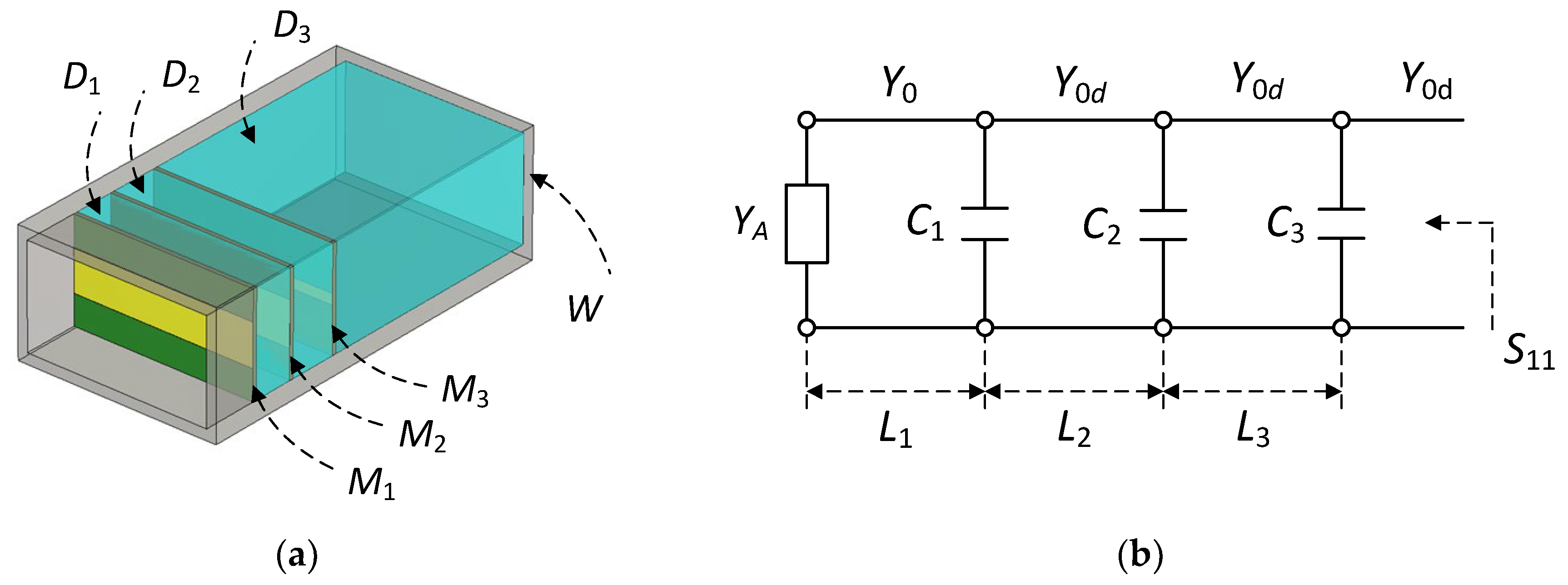
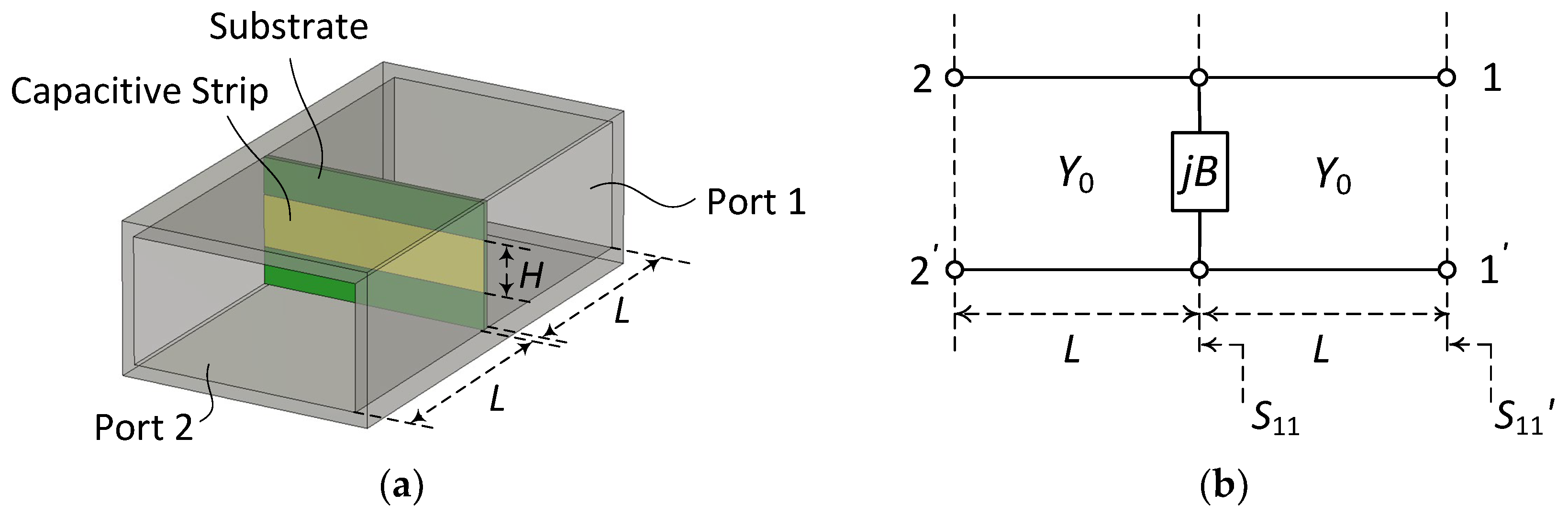
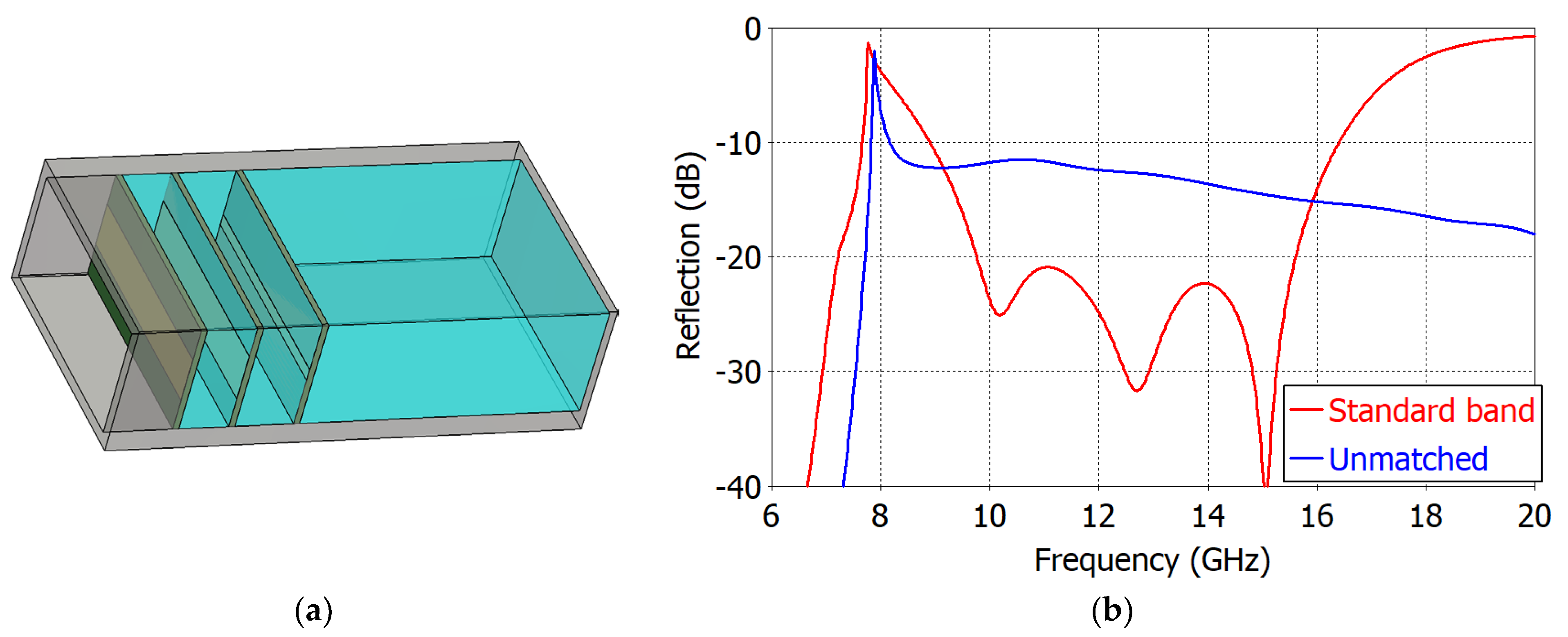
2. Aperture Matching of the Rectangular Waveguide Open End
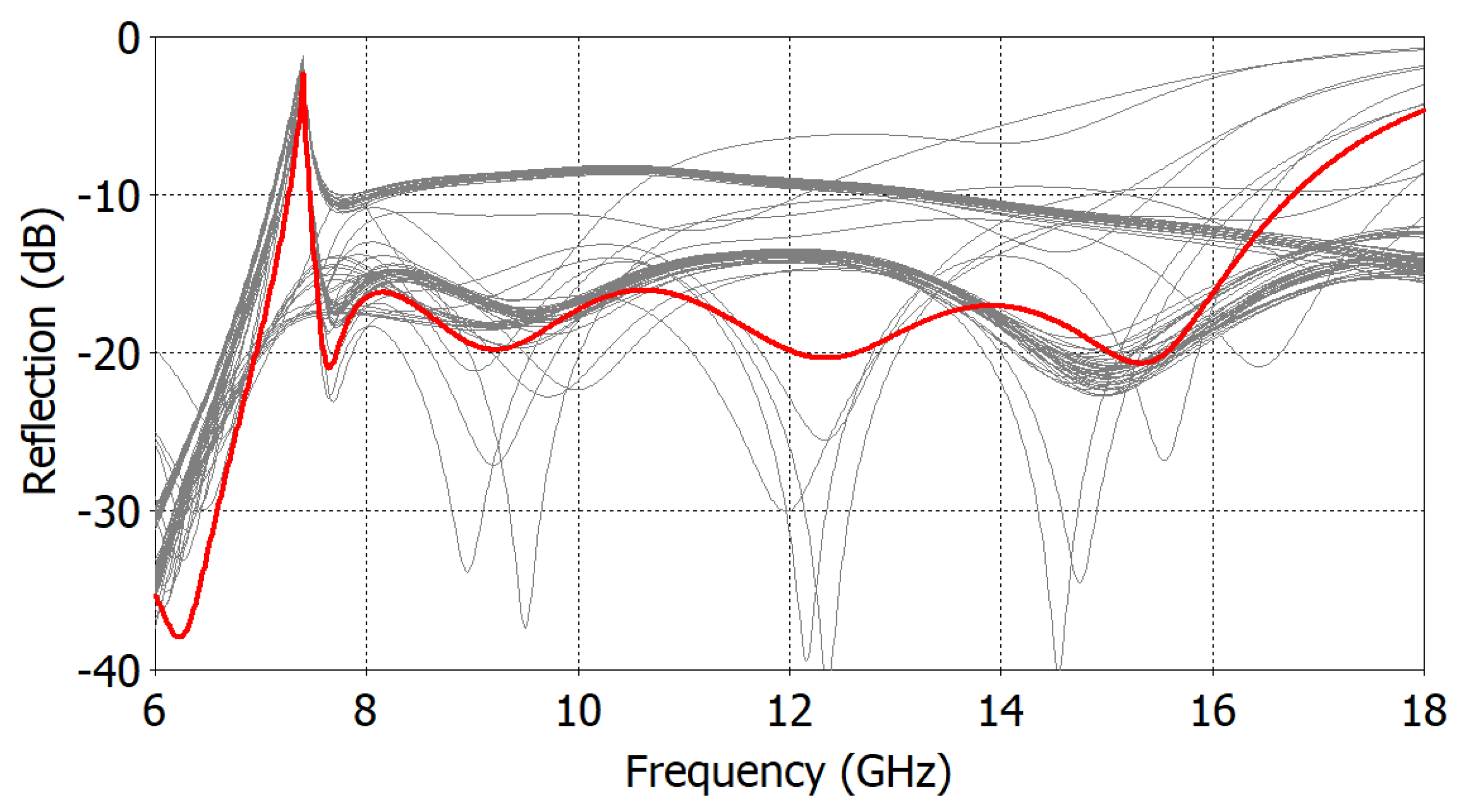
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ramsay, J.-F. Microwave antenna and waveguide techniques before 1900. Proc. IRE 1958, 46, 405–415. [Google Scholar] [CrossRef]
- Barrow, W.-L.; Greene, F.-M. Rectangular hollow-pipe radiators. Proc. IRE 1938, 26, 1498–1519. [Google Scholar] [CrossRef]
- Yaghjian, A. Approximate formulas for the far field and gain of open-ended rectangular waveguide. IEEE Trans. Antennas Propag. 1984, 32, 378–384. [Google Scholar] [CrossRef]
- Paulus, A.; Eibert, T.-F. Fully probe-corrected near-field far-field transformations with unknown probe antennas. IEEE Trans. Antennas Propag. 2023, 71, 5967–5980. [Google Scholar] [CrossRef]
- Sun, B.; Wen, Y.; Wang, Z. Calibration on open-ended rectangular waveguide from 1GHz to 26.5GHz. In Proceedings of the 5th IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications (MAPE), Chengdu, China, 29–31 October 2013. [Google Scholar]
- Wu, D.-I.; Kanda, M. Comparison of theoretical and experimental data for the near field of an open-ended rectangular waveguide. IEEE Trans. Electromag. Compat. 1989, 31, 353–358. [Google Scholar] [CrossRef]
- Selvan, K.-T.; Poddar, D.-R.; Kini, K.-R. Off-axis gain and field in the finite range of an open-ended rectangular waveguide. IEEE Trans. Electromag. Compat. 2001, 43, 685–688. [Google Scholar] [CrossRef]
- Kawalko, S.-F.; Kanda, M. Near-zone gain of open-ended rectangular waveguides. IEEE Trans. Electromag. Compat. 1997, 39, 408–413. [Google Scholar] [CrossRef]
- Kim, J.-H.; Enkhbayar, B.; Bang, J.-H.; Ahn, B.-C.; Cha, E.-J. New formulas for the reflection coefficient of an open-ended rectangular waveguide radiating into air including the effect of wall thickness or flange. Prog. Electromag. Res. M 2010, 12, 143–153. [Google Scholar] [CrossRef]
- Vaccaro, M.; Al Qaseer, M.T.; Zoughi, R. Dielectric characterization of curved structures using flangeless open-ended waveguide measurement. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022. [Google Scholar]
- Chang, C.-W.; Chen, K.-M.; Qian, J. Nondestructive determination of electromagnetic parameters of dielectric materials at X-band frequencies using a waveguide probe system. IEEE Trans. Instrum. Meas. 1997, 46, 1084–1092. [Google Scholar] [CrossRef]
- Ali, M.; Sanyal, S. FDTD analysis of rectangular waveguide in receiving mode as EMI sensors. Prog. Electromag. Res. B 2008, 2, 291–303. [Google Scholar] [CrossRef]
- Li, Q.; Gandhi, O.-P.; Kang, G. An open-ended waveguide system for SAR system validation or probe calibration for frequencies above 3 GHz. Phys. Med. Biol. 2004, 49, 4173. [Google Scholar] [CrossRef] [PubMed]
- Zarifi, D.; Farahbakhsh, A.; Zaman, A.-U.; Kildal, P.-S. A high gain ridge gap waveguide fed slot antenna array for 60 GHz applications. In Proceedings of the 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016. [Google Scholar]
- Fang, Y.; Lu, Z.; Yan, X. Design of an open-ended waveguide array with a plane radome. In Proceedings of the International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2019. [Google Scholar]
- Visser, H.-J. Planar, faceted and curved array antenna research at TNO physics and electronics laboratory. In Proceedings of the Conference on Perspectives on Radio Astronomy: Science with Large Antenna Array, Hague, The Netherlands, 12−14 April 1999. [Google Scholar]
- Ishigami, S.; Wu, I.; Sato, K.-I.; Gotoh, K.; Matsumoto, Y. Calibration of electric-field probe using open-ended waveguides. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Austin, TX, USA, 17–21 August 2009. [Google Scholar]
- Monebi, A.M.; Otgonbat, D.; Ahn, B.-C.; Lee, C.-S.; Ahn, J.-H. Conceptual design of a semi-dual polarized monopulse antenna by computer simulation. Appl. Sci. 2023, 13, 2960. [Google Scholar] [CrossRef]
- Ghasr, M.-T.; Kharkovsky, S.; Zoughi, R.; Austin, R. Comparison of near-field millimeter-wave probes for detecting corrosion precursor pitting under paint. IEEE Trans. Instrum. Meas. 2005, 54, 1497–1504. [Google Scholar] [CrossRef]
- Abou-Khousa, M.-A.; Rahman, M.-S.-U.; Donnell, K.-M.; Qaseer, M.-T.-A. Detection of surface cracks in metals using microwave and millimeter-wave nondestructive testing techniques—A review. IEEE Trans. Instrum. Meas. 2023, 72, 1–18. [Google Scholar] [CrossRef]
- Qaddoumi, N.-N.; Saleh, W.-M.; Abou-Khousa, M. Innovative near-field microwave nondestructive testing of corroded metallic structures utilizing open-ended rectangular waveguide probes. IEEE Trans. Instrum. Meas. 2007, 56, 1961–1966. [Google Scholar] [CrossRef]
- Baskakova, A.; Hoffmann, K. W-Band imaging sensor using a rectangular waveguide structure with choke. IEEE Microw. Wirel. Compon. Lett. 2022, 32, 230–233. [Google Scholar] [CrossRef]
- Leung, K.-W.; So, K.-K. Rectangular waveguide excitation of dielectric resonator antenna. IEEE Trans. Antennas Propag. 2003, 51, 2477–2481. [Google Scholar] [CrossRef]
- Kumar, P.; Masa-Campos, J.-L. Waveguide fed circular microstrip patch antenna for Ku band applications. Microw. Opt. Technol. Lett. 2015, 57, 585–589. [Google Scholar] [CrossRef]
- Yoo, I.; Smith, D.R. Design of conformal array of rectangular waveguide-fed metasurfaces. IEEE Trans. Antennas Propag. 2022, 70, 6060–6065. [Google Scholar] [CrossRef]
- Trinh-Van, S.; Thi, T.N.; Yang, Y.; Lee, K.-Y.; Jung, K.-Y.; Hwang, K.C. High-gain waveguide-fed circularly polarized spidron fractal aperture antenna. Appl. Sci. 2019, 9, 691. [Google Scholar] [CrossRef]
- Gardiol, F.E. Open-ended waveguides: Principles and applications. In Advances in Electronics and Electron Physics; Hawks, P.W., Ed.; Academic Press: New York, NY, USA, 1985; pp. 139–187. [Google Scholar]
- TTI Norte. Open-Ended Rectangular Waveguide Probe (OE-RWP). Available online: https://www.ttinorte.es/wp-content/uploads/2019/08/OE-RWP_Open-Ended-Rectangular-Waveguide.pdf (accessed on 17 October 2023).
- IEEE Antennas and Propagation Society. IEEE Recommended Practice for Near-Field Antenna Measurements; IEEE: New York, NY, USA, 2012; pp. 18–19. [Google Scholar]
- Ivanchenko, I.; Khruslov, M.; Plakhtiy, V.; Popenko, N.; Ronnow, D. X-band aperture antenna with hybrid dielectric inserts. Prog. Electromag. Res. C 2016, 61, 27–35. [Google Scholar] [CrossRef]
- Zhang, L.-J.; Choi, S.-G.; Ahn, B.-C.; Bang, J.-H.; Kim, D.H.; Choi, Y.-T. Simplified feed prime focus reflector antenna. Microw. J. 2016, 59, 395–399. [Google Scholar]
- Schaik, H. The performance of an iris-loaded planar phased-array antenna of rectangular waveguides with an external dielectric sheet. IEEE Trans. Antennas Propag. 1978, 26, 413–419. [Google Scholar] [CrossRef]
- Ghen, C. Octave band waveguide radiators for wide-angle scan phased arrays. In Proceedings of the Antennas and Propagation Society International Symposium, Boulder, CO, USA, 22–24 April 1973. [Google Scholar]
- Ludlow, P.; Fusco, V. Increased bandwidth evanescent open-ended waveguide antenna design using the imaginary smith chart. IEEE Trans. Antennas Propag. 2012, 60, 5423–5428. [Google Scholar] [CrossRef]
- Magill, E.; Wheeler, H. Wide-angle impedance matching of a planar array antenna by a dielectric sheet. IEEE Trans. Antennas Propag. 1966, 14, 49–53. [Google Scholar] [CrossRef]
- Ludlow, P.; Fusco, V. Matching evanescent open-ended waveguide antennas using the imaginary smith chart. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011. [Google Scholar]
- Ludlow, P.; Fusco, V.; Goussetis, G.; Zelenchuk, D.-E. Applying band-pass filter techniques to the design of small-aperture evanescent-mode waveguide antennas. IEEE Trans. Antennas Propag. 2013, 61, 134–142. [Google Scholar] [CrossRef]
- Ludlow, P.; Fusco, V.; Goussetis, G.; Zelenchuk, D.E. Small aperture evanescent-mode waveguide antenna matched using distributed coupled resonators. Electron. Lett. 2013, 49, 580–582. [Google Scholar] [CrossRef]
- Hrabar, S.; Bartolic, J.; Sipus, Z. Waveguide miniaturization using uniaxial negative permeability metamaterial. IEEE Trans. Antennas Propag. 2005, 53, 110–119. [Google Scholar] [CrossRef]
- Samad, M.-A.; Hamid, A.-K. Miniaturization of waveguide antenna using square/circular arrays of SRR. In Proceedings of the 5th International Conference on Electronic Devices, Systems and Applications (ICEDSA), Ras Al Khaimah, United Arab Emirates, 6–8 December 2016. [Google Scholar]
- Ouda, M.; Abutahoun, N. Rectangular waveguide radiator miniaturization using electromagnetic infinity-shaped metamaterial resonator. IUG J. Nat. Eng. Stud. 2013, 21, 69–82. [Google Scholar]
- Yu, B.; Yang, J.; Song, Y.; Wang, Z.; Zhang, T.; Yan, B.; Xu, R. Terahertz metamaterial waveguide with I-shaped resonators for phase and absorption modulation. Photonics 2023, 10, 816. [Google Scholar] [CrossRef]
- Jalali, M.; Sedghi, T.; Shokri, M. A novel metamatarial SRR for waveguide antenna. In Proceedings of the Mediterrannean Microwave Symposium (MMS), Tangiers, Morocco, 15–17 November 2009. [Google Scholar]
- Singhal, D.; Dhwaj, K. Dielectric resonator-based evanescent-mode waveguide filtering antenna. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1413–1417. [Google Scholar] [CrossRef]
- Sánchez-Escuderos, D.; Ruiz-Garnica, J.; Baquero-Escudero, M.; Soto, P.; Boria, V.-E.; Toso, G.; Angeletti, P.; Guglielmi, M. Evanescent-mode ridge-waveguide radiating filters for space applications. IEEE Trans. Antennas Propag. 2019, 67, 6286–6297. [Google Scholar] [CrossRef]
- Mahmud, R.-H.; Salih, I.H.; Shang, X.; Skaik, T.; Wang, Y. A filtering waveguide aperture antenna based on all-resonator structures. Microw. Opt. Technol. Lett. 2023, 65, 2378–2383. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, S.; Tu, H.; Li, Y.; Yu, Y.; Wu, D.-L. Coaxial probe-fed open-ended waveguide antenna based on sand casting process with filtering characteristics and all-in-one structure. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, e22494. [Google Scholar] [CrossRef]
- DuPont Electronics & Industrial. EI 10109 Pyralux TAS. Available online: https://www.dupont.com/electronics-industrial/pyralux-ta-tas.html (accessed on 17 October 2023).
- Isola. I-Tera MT40. Available online: https://www.isola-group.com/pcb-laminates-prepreg/i-tera-mt40-rf-mw/ (accessed on 17 October 2023).
- Marcuvitz, N. Waveguide Handbook; Peter Peregrinus: Stevenage, UK, 1985; pp. 218–221. [Google Scholar]
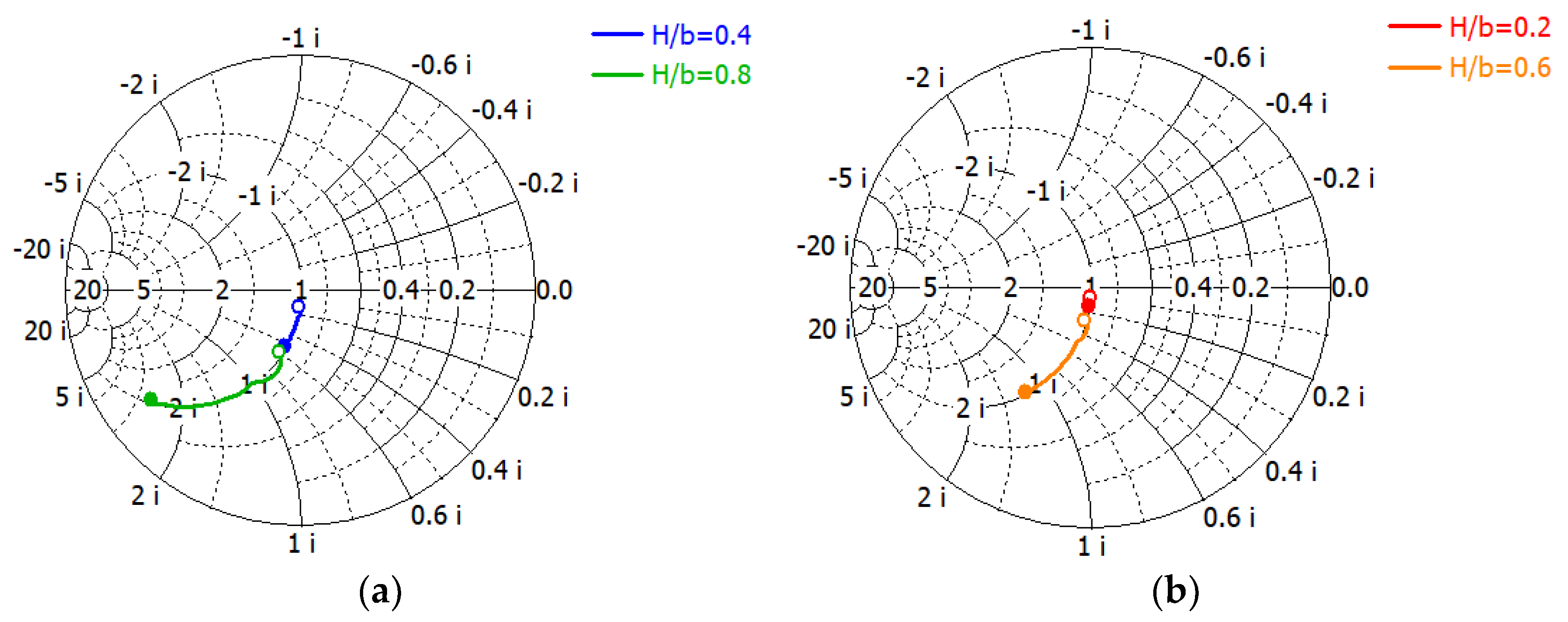




| H/b | Min (B/Y0) | Max (B/Y0) |
|---|---|---|
| 0.2 | 0.082 | 0.162 |
| 0.4 | 0.151 | 0.517 |
| 0.6 | 0.282 | 1.214 |
| 0.8 | 0.593 | 2.651 |
| Parameter | Meaning |
|---|---|
| a, b, t | Waveguide broad-wall width, narrow-wall height and wall thickness |
| εr | Dielectric constant of the material supporting the matching elements and filling the waveguide |
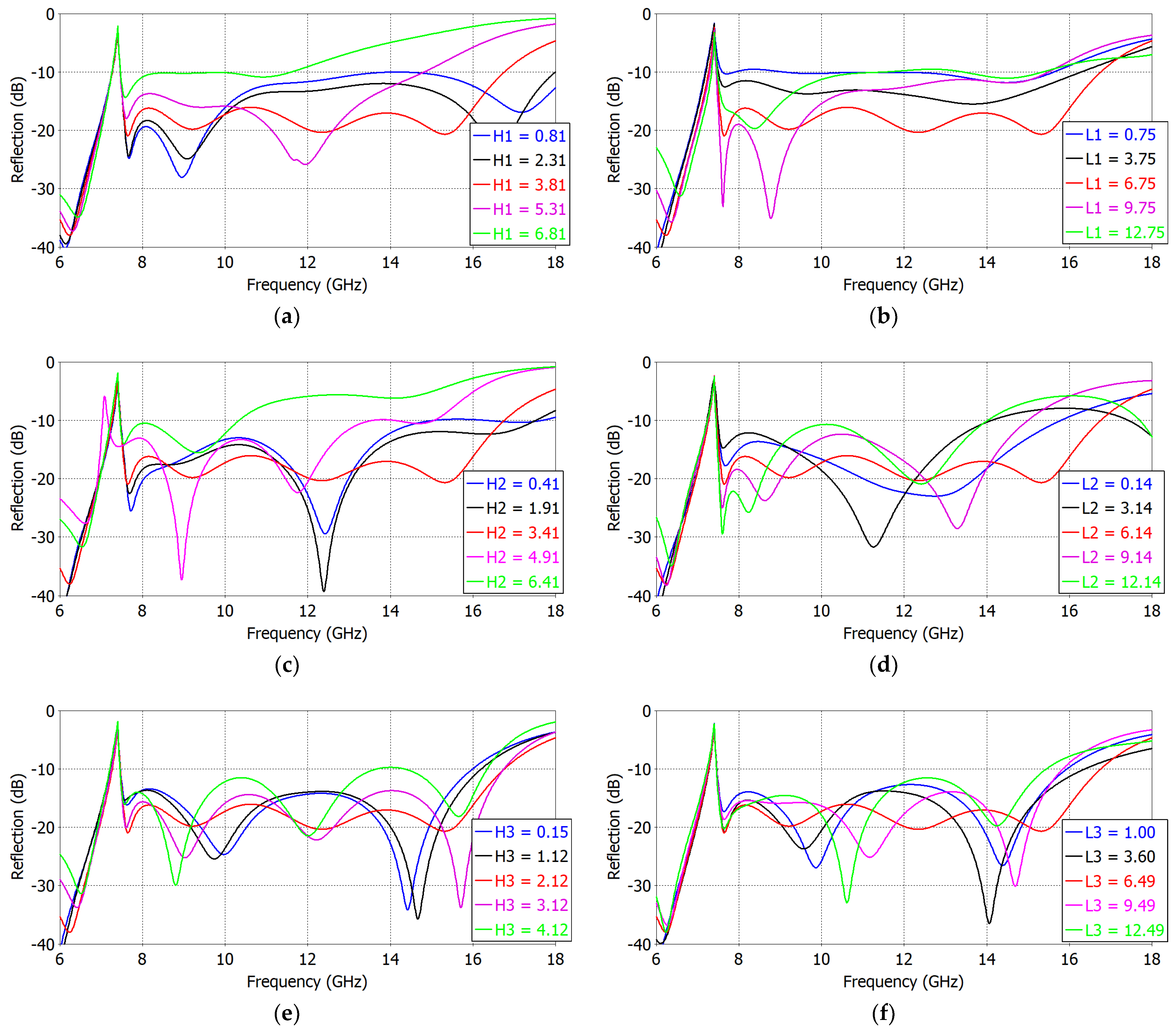
| H1, H2, H3 | Strip width of the capacitive matching elements M1, M2 and M3, respectively |
| L1 | Distance between the matching element M1 and the waveguide aperture |
| L2, L3 | Distances between the matching elements M1 and M2, M2 and M3, respectively |
| P0 | Plane of the aperture |
| P1, P2, P3 | Plane right after the matching elements M1, M2 and M3, respectively |
| Design | εr | H1 | H2 | H3 | L1 | L2 | L3 | Substrate |
|---|---|---|---|---|---|---|---|---|
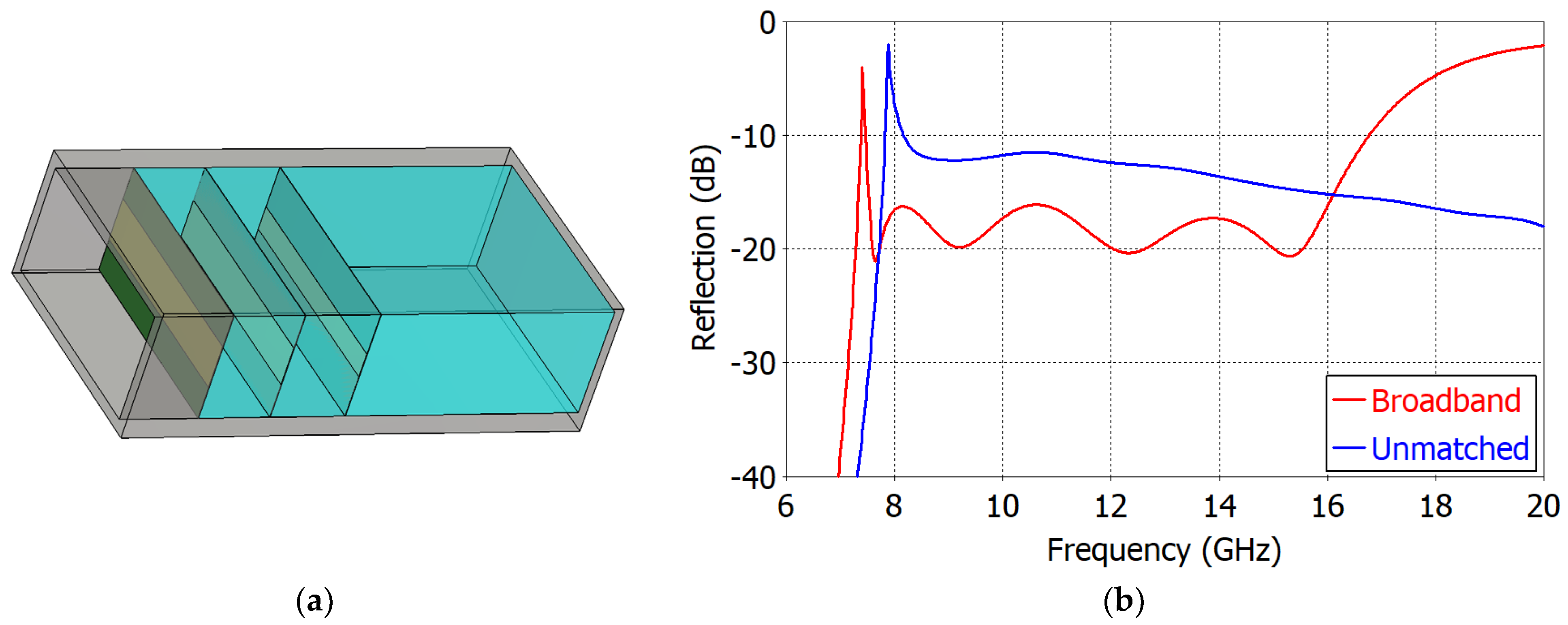
| Broadband | 1.13 | 3.81 | 3.41 | 2.12 | 6.75 | 6.14 | 6.49 | εr = 3.4, tanδ = 0.0045, h = 0.045, t = 0.012 |
| Standard Band | 1.03 | 3.92 | 4.12 | 1.01 | 5.75 | 4.14 | 4.90 | εr = 3.45, tanδ = 0.0031, h = 0.51, t = 0.018 |
| Work | Type | Frequency Range f1−f2 (GHz) | Reflection (dB) | Ratio Bandwidth f2/f1 | Complexity |
|---|---|---|---|---|---|
| [30] | Dielectric plug | 9.5–10.5 | −15 | 1.11 | Low |
| [32] | Inductive iris | 5.4–5.9 | −10 | 1.09 | Low |
| [34] | Dielectric slab | 2.13–2.70 | −10 | 1.27 | Low |
| [37] | Multiple conducting posts | 2.30–2.68 | −10 | 1.17 | Medium |
| [38] | Distributed coupled resonators | 2.00−2.45 | −10 | 1.23 | Medium |
| This Work | Printed capacitive elements | 9.89−15.99 | −20 | 1.62 | Medium |
| 7.53–16.01 | −16 | 2.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, J.-W.; Xu, S.; Altanzaya, E.; Zhang, Q.; Lee, C.-S.; Ahn, B.-C.; Ahn, J.-H.; Choi, S.-G. A New Technique for Broadband Matching of Open-Ended Rectangular Waveguide Radiator. Sensors 2023, 23, 9176. https://doi.org/10.3390/s23229176
Heo J-W, Xu S, Altanzaya E, Zhang Q, Lee C-S, Ahn B-C, Ahn J-H, Choi S-G. A New Technique for Broadband Matching of Open-Ended Rectangular Waveguide Radiator. Sensors. 2023; 23(22):9176. https://doi.org/10.3390/s23229176
Chicago/Turabian StyleHeo, Ji-Won, Songyuan Xu, Erdenesukh Altanzaya, Qiongyue Zhang, Chan-Soo Lee, Bierng-Chearl Ahn, Jae-Hyeong Ahn, and Seong-Gon Choi. 2023. "A New Technique for Broadband Matching of Open-Ended Rectangular Waveguide Radiator" Sensors 23, no. 22: 9176. https://doi.org/10.3390/s23229176
APA StyleHeo, J.-W., Xu, S., Altanzaya, E., Zhang, Q., Lee, C.-S., Ahn, B.-C., Ahn, J.-H., & Choi, S.-G. (2023). A New Technique for Broadband Matching of Open-Ended Rectangular Waveguide Radiator. Sensors, 23(22), 9176. https://doi.org/10.3390/s23229176










