Toward Optimal Irrigation Management at the Plot Level: Evaluation of Commercial Water Potential Sensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Water Potential Sensors: Description and Setup
2.2. Test 1: Sensor Accuracy Evaluation
2.2.1. Soils
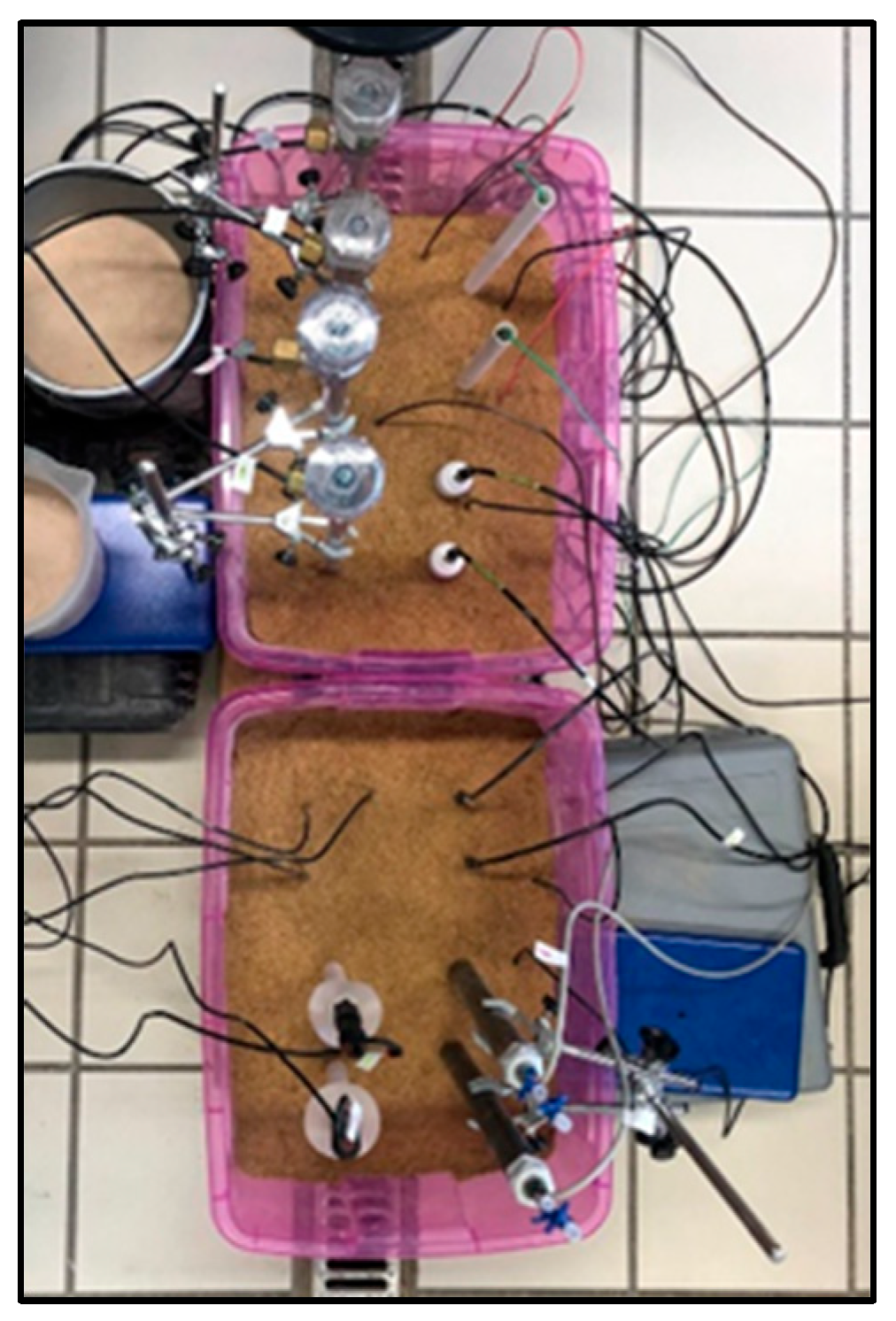
2.2.2. Experimentation
2.3. Test 2: Variability (Repeatability and Reproducibility) in Readings
3. Results and Discussion
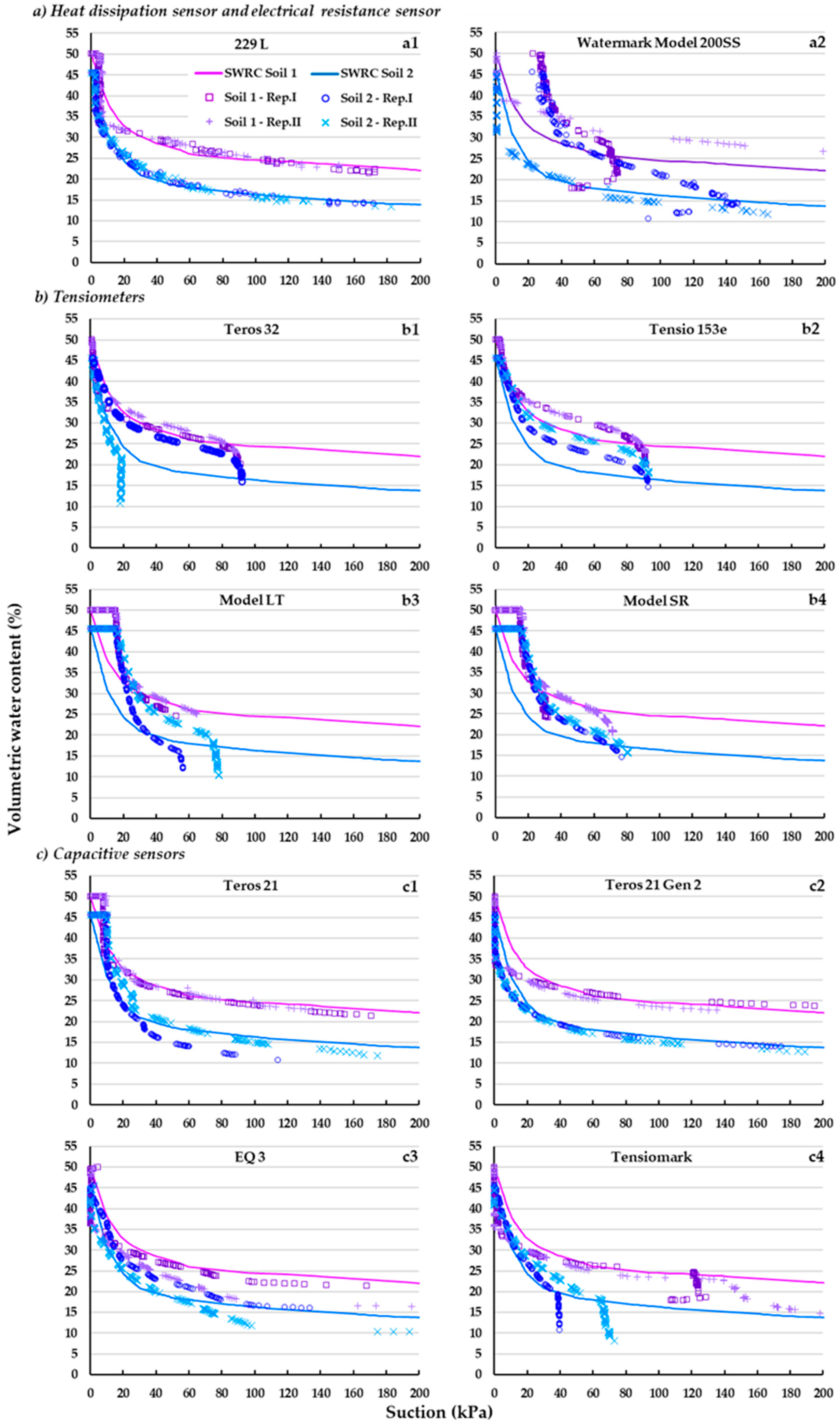
3.1. Description of Water Retention Curves
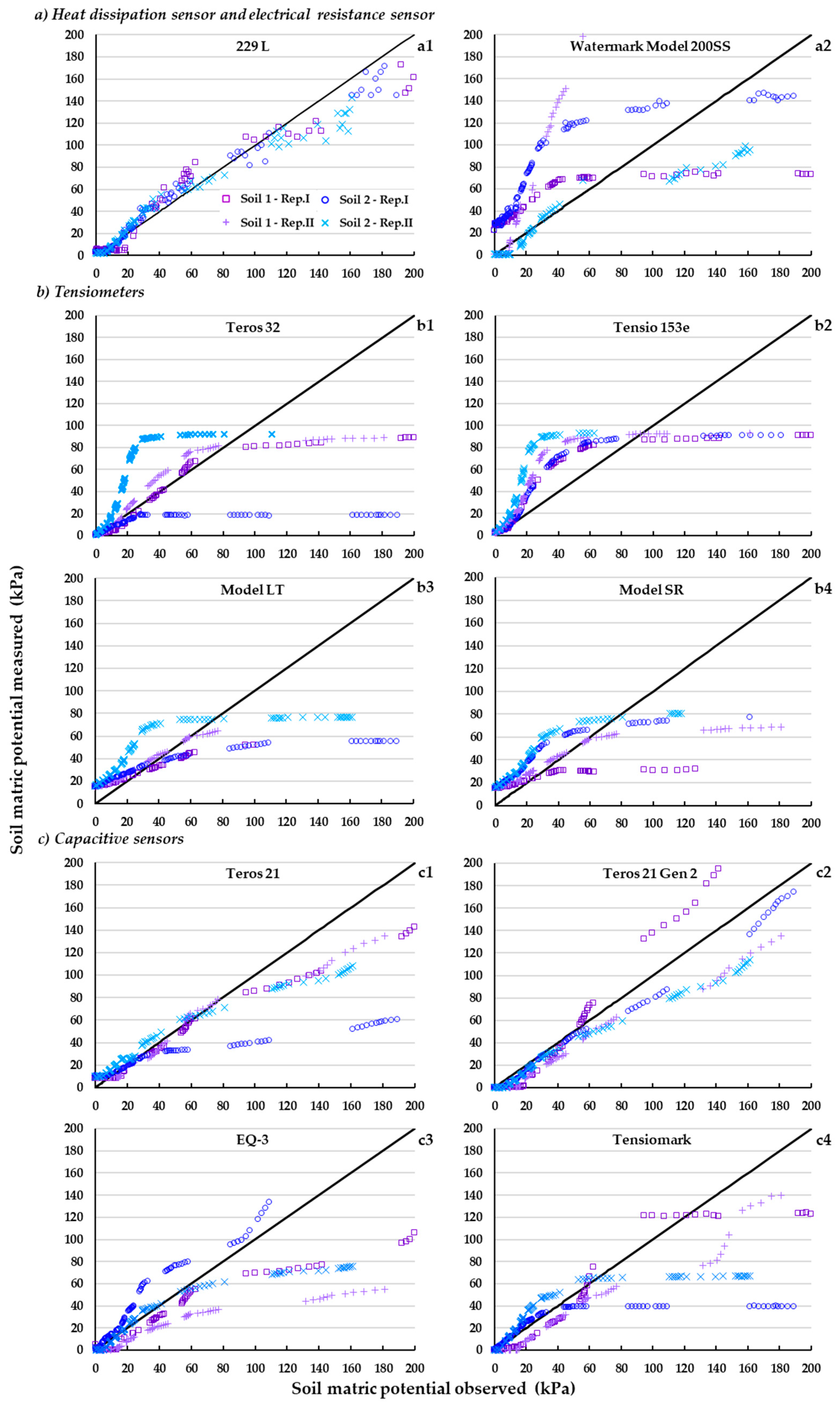
3.2. Observed Suction Values vs. Reference Value
3.3. Statistical Analysis
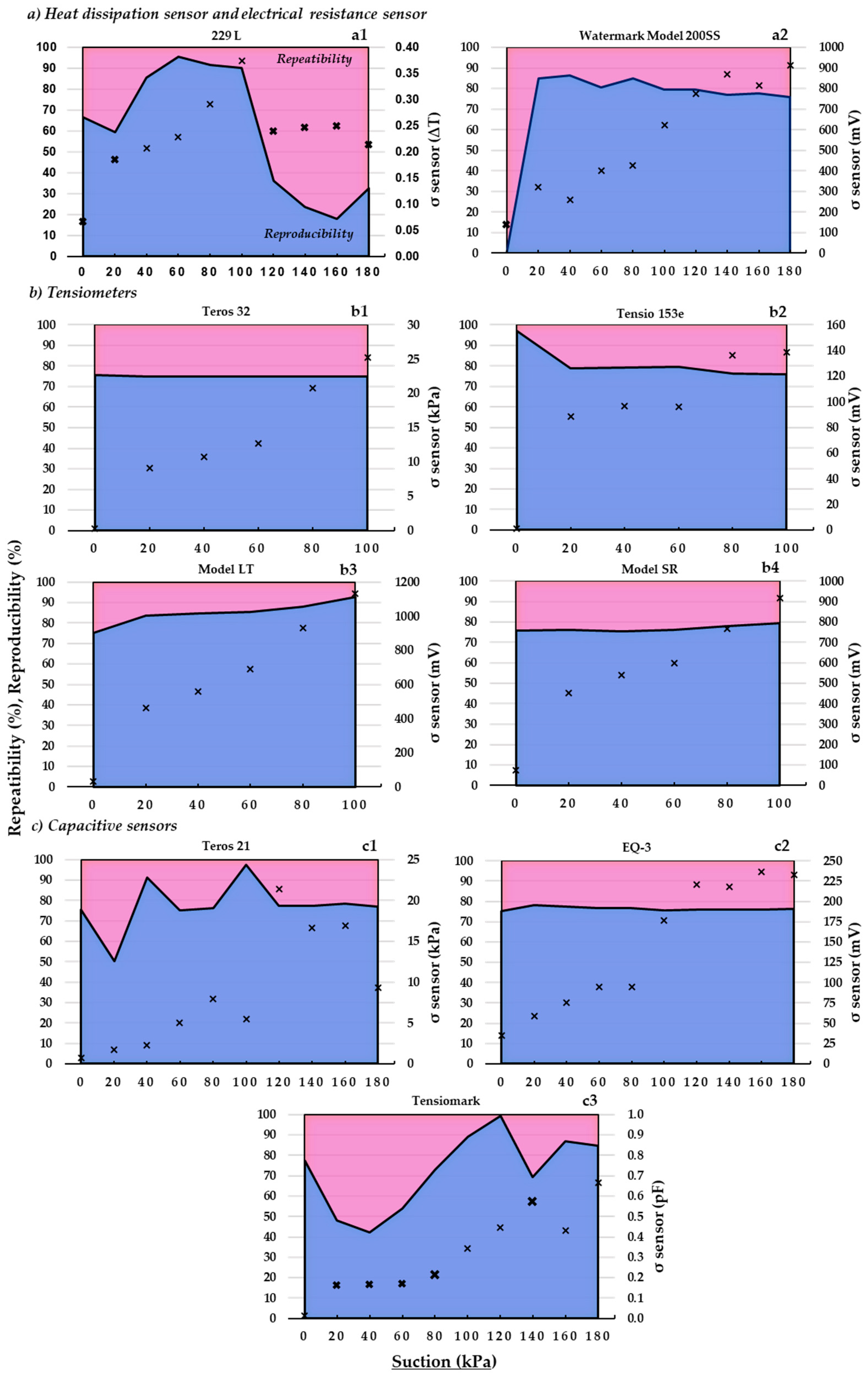
3.4. Repeatability and Reproducibility Indices
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blackmore, S. Precision Farming: An Introduction. Outlook Agric. 1994, 23, 275–280. [Google Scholar] [CrossRef]
- Elijah, O.; Rahman, T.A.; Orikumhi, I.; Leow, C.Y.; Hindia, M.N. An Overview of Internet of Things (IoT) and Data Analytics in Agriculture: Benefits and Challenges. IEEE Internet Things J. 2018, 5, 3758–3773. [Google Scholar] [CrossRef]
- Friha, O.; Ferrag, M.A.; Shu, L.; Maglaras, L.; Wang, X. Internet of Things for the Future of Smart Agriculture: A Comprehensive Survey of Emerging Technologies. IEEE/CAA J. Autom. Sin. 2021, 8, 718–752. [Google Scholar] [CrossRef]
- Fares, A.; Alva, A.K. Evaluation of Capacitance Probes for Optimal Irrigation of Citrus through Soil Moisture Monitoring in an Entisol Profile. Irrig. Sci. 2000, 19, 57–64. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R. Field Devices For Monitoring Soil Water Content; University of Florida George A Smathers Libraries: Gainesville, FL, USA, 2007. [Google Scholar]
- Nolz, R.; Kammerer, G.; Cepuder, P. Calibrating Soil Water Potential Sensors Integrated into a Wireless Monitoring Network. Agric. Water Manag. 2013, 116, 12–20. [Google Scholar] [CrossRef]
- Mzezewa, J.; Gwata, E.T.; van Rensburg, L.D. Yield and Seasonal Water Productivity of Sunflower as Affected by Tillage and Cropping Systems under Dryland Conditions in the Limpopo Province of South Africa. Agric. Water Manag. 2011, 98, 1641–1648. [Google Scholar] [CrossRef]
- Kizito, F.; Campbell, C.S.; Campbell, G.S.; Cobos, D.R.; Teare, B.L.; Carter, B.; Hopmans, J.W. Frequency, Electrical Conductivity and Temperature Analysis of a Low-Cost Capacitance Soil Moisture Sensor. J. Hydrol. 2008, 352, 367–378. [Google Scholar] [CrossRef]
- Hillel, D. Enviromental Soil Physics; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Dane, J.H.; Hopmans, J.W. Water Retention and Storage. In Methods of Soil Analysis. Part 4—Physical Methods; SSSA: Madison, WI, USA, 2002; pp. 671–673. [Google Scholar]
- Klute, A. Water Retention: Laboratory Methods. In Methods of Soil Analysis: Part 1 Physical and Mineralogical Methods; Klute, A., Ed.; ASA and SSSA: Madison, WI, USA, 1986; pp. 635–662. [Google Scholar]
- Jackisch, C.; Germer, K.; Graeff, T.; Andrä, I.; Schulz, K.; Schiedung, M.; Haller-Jans, J.; Schneider, J.; Jaquemotte, J.; Helmer, P.; et al. Soil Moisture and Matric Potential—An Open Field Comparison of Sensor Systems. Earth Syst. Sci. Data 2020, 12, 683–697. [Google Scholar] [CrossRef]
- Bittelli, M. Measuring Soil Water Potential for Water Management in Agriculture: A Review. Sustainability 2010, 2, 1226–1251. [Google Scholar] [CrossRef]
- Susha Lekshmi, S.U.; Singh, D.N.; Shojaei Baghini, M. A Critical Review of Soil Moisture Measurement. Meas. J. Int. Meas. Confed. 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Young, M.H.; Sisson, J. Tensiometry. In Methods of Soil Analysis. Part 4—Physical Methods; Soil Science Society of America, Inc.: Madison, WI, USA, 2002. [Google Scholar]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil Moisture Measurement for Ecological and Hydrological Watershed-Scale Observatories: A Review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Andraski, B.J.; Bilskie, J. 3.2.4 Miscellaneous Methods for Measuring Matric or Water Potential. In Methods of Soil Analysis: Part 4 Physical Methods; Soil Science Society of America, Inc.: Madison, WI, USA, 2002; pp. 643–669. [Google Scholar]
- Campbell, G.S.; Campbell, C.S. Water Content and Potential, Measurement. In Encyclopedia of Soils in the Environment; Hillel, D., Hatfield, J.L., Powlson, D.S., Rosenzweig, C., Scow, K.M., Singer, M.J., Sparks, D.L., Eds.; Amsterdam: Ugstergeist, The Netherlands, 2005; pp. 253–257. ISBN 978-0-12-348530-4. [Google Scholar]
- Centeno, A.; Baeza, P.; Lissarrague, J.R. Relationship between Soil and Plant Water Status in Wine Grapes under Various Water Deficit Regimes. Horttechnology 2010, 20, 585–593. [Google Scholar] [CrossRef]
- METER Group. Teros 32; METER Group: Pullman, WA, USA, 2020. [Google Scholar]
- METER Group. Teros 21 Gen 1; METER Group: Pullman, WA, USA, 2019. [Google Scholar]
- METER Group. Teros 21 GEN 2; METER Group: Pullman, WA, USA, 2019. [Google Scholar]
- EcoTech. Manual for Installation and Use of Tensiomarks; EcoTech: Lancaster, PA, USA, 2014. [Google Scholar]
- METER Environment SDI-12: Everything You Need to Know to Be Successful. Available online: https://publications.metergroup.com/Sales%20and%20Support/METER%20Environment/Website%20Articles/sdi-12-everything-need-know-successful.pdf (accessed on 26 October 2023).
- Delta-T Devis Ltd. User Manual for the EQ3 Equitensiometer; Delta-T Devis Ltd.: Plano, TX, USA, 2014. [Google Scholar]
- Irrometer. IRROMETER Tensiometers Model–SR; Irrometer: Riverside, CA, USA, 2018. [Google Scholar]
- Irrometer. IRROMETER Tensiometers Model–LT; Irrometer: Riverside, CA, USA, 2018. [Google Scholar]
- Tensio 153e—Pressure Transducer Tensiometer. Available online: https://ugt-online.de/en/solutions/tensio-153e-pressure-transducer-tensiometer/ (accessed on 26 October 2023).
- Irrometer. WATERMARK Soil Moisture Sensor—MODEL 200SS; Irrometer: Riverside, CA, USA, 2019. [Google Scholar]
- Campbell Scientific Spain, S.L. 229 Heat Dissipation Matric Water Potential Sensor: Instruction Manual; Campbell Scientific: Barcelona, Spain, 2006. [Google Scholar]
- Reder, A.; Rianna, G.; Pagano, L. Calibration of TDRs and Heat Dissipation Probes in Pyroclastic Soils. Procedia Earth Planet. Sci. 2014, 9, 171–179. [Google Scholar] [CrossRef]
- Dirksen, C. Soil Physics Measurements; Catena Verlag: Reiskirchen, Germany, 1999; ISBN 3923381433. [Google Scholar]
- Gomes de Andrade, J.; Pacheco, J.; Carlesso, R.; Trois, C.; Knies, A.E. Pérdidas de Agua Por Evaporación En Maíz Con Siembra Convencional y Directa Para Diferentes Niveles de Cobertura Muerta. I. Resultados Experimentales. Cienc. Técnicas Agropecu. 2011, 20, 60–64. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principle. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance Evaluation of Hydrological Models: Statistical Significance for Reducing Subjectivity in Goodness-of-Fit Assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison With Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Thompson, R.B.; Gallardo, M.; Valdez, L.C.; Fernández, M.D. Using Plant Water Status to Define Threshold Values for Irrigation Management of Vegetable Crops Using Soil Moisture Sensors. Agric. Water Manag. 2007, 88, 147–158. [Google Scholar] [CrossRef]
- Shock, C.C.; Wang, F.X. Soil Water Tension, a Powerful Measurement for Productivity and Stewardship. HortScience 2011, 46, 178–185. [Google Scholar] [CrossRef]
- Lemay, I.; Caron, J.; Dorais, M.; Pepin, S. Defining Irrigation Set Points Based on Substrate Properties for Variable Irrigation and Constant Matric Potential Devices in Greenhouse Tomato. HortScience 2012, 47, 1141–1152. [Google Scholar] [CrossRef]
- Létourneau, G.; Caron, J.; Anderson, L.; Cormier, J. Matric Potential-Based Irrigation Management of Field-Grown Strawberry: Effects on Yield and Water Use Efficiency. Agric. Water Manag. 2015, 161, 102–113. [Google Scholar] [CrossRef]
- Kloss, S.; Schütze, N.; Schmidhalter, U. Evaluation of Very High Soil-Water Tension Threshold Values in Sensor-Based Deficit Irrigation Systems. J. Irrig. Drain. Eng. 2014, 140, A4014003. [Google Scholar] [CrossRef]
- Contreras, J.I.; Alonso, F.; Cánovas, G.; Baeza, R. Irrigation Management of Greenhouse Zucchini with Different Soil Matric Potential Level. Agronomic and Environmental Effects. Agric. Water Manag. 2017, 183, 26–34. [Google Scholar] [CrossRef]
- Burdick, R.K.; Borror, C.M.; Montgomery, D.C. A Review of Methods for Measurement Systems Capability Analysis. J. Qual. Technol. 2003, 35, 342–354. [Google Scholar] [CrossRef]
- Quaglino, M.; Pagura, J.; Dianda, D.; Lupachini, E. Estudio de Sistemas de Medida Con Ensayos Destructivos. Una Aplicación Sobre Tiempos de Producción. SaberEs 2010, 2, 59–72. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Huisman, J.A.; Weuthen, A.; Vereecken, H.; Bogena, H.R. Sensor-to-Sensor Variability of the ECH2O EC-5, TE, and 5TE Sensors in Dielectric Liquids. Vadose Zone J. 2010, 9, 181–186. [Google Scholar] [CrossRef]
- Tsai, P. Variable Gauge Repeatability and Reproducibility Study Using the Analysis of Variance Method. Qual. Eng. 1988, 1, 107–115. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; von Unold, G.; Mueller, L.; Wieland, R. The Evaporation Method: Extending the Measurement Range of Soil Hydraulic Properties Using the Air-Entry Pressure of the Ceramic Cup. J. Plant Nutr. Soil Sci. 2010, 173, 563–572. [Google Scholar] [CrossRef]
- Aldaz-Lusarreta, A.; Giménez, R.; Campo-Bescós, M.A.; Arregui, L.M.; Virto, I. Effects of Innovative Long-Term Soil and Crop Management on Topsoil Properties of a Mediterranean Soil Based on Detailed Water Retention Curves. Soil 2022, 8, 655–671. [Google Scholar] [CrossRef]
- Llamosa, L.E.; Meza Contreras, L.G.; Botero, M. Estudio de Repetibilidad y Reproducibilidad Utilizando El Método de Promedios y Rangos Para El Aseguramiento de La Calidad de Los Resultados de Calibración de Acuerdo Con La Norma Técnica NTCISO/IEC17025. Sci. Technol. 2007, 1, 455–460. [Google Scholar]
- Montgomery, D.C. Introduction to Statistical Quality Control, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2005. [Google Scholar]
- González-Teruel, J.D.; Torres-Sánchez, R.; Blaya-Ros, P.J.; Toledo-Moreo, A.B.; Jiménez-Buendía, M.; Soto-Valles, F. Design and Calibration of a Low-Cost SDI-12 Soil Moisture Sensor. Sensors 2019, 19, 491. [Google Scholar] [CrossRef]
- Kosugi, K.; Hopmans, J.W.; Dane, J.H. Parametric Models. In Methods of Soil Analysis. Part 4—Physical Methods; Dane, J.H., Clarke Topp, G., Eds.; SSSA: Madison, WI, USA, 2002; pp. 739–757. [Google Scholar]
- Malazian, A.; Hartsough, P.; Kamai, T.; Campbell, G.S.; Cobos, D.R.; Hopmans, J.W. Evaluation of MPS-1 Soil Water Potential Sensor. J. Hydrol. 2011, 402, 126–134. [Google Scholar] [CrossRef]
- Savva, A.P.; Frenken, K. Irrigation Manual Module 4 Crop Water Requirements and Irrigation Scheduling; Water Resources Development and Management Officers FAO Sub-Regional Office for East and Southern Africa: Harare, Zimbabwe, 2002. [Google Scholar]
- Irmak, S.; Haman, D.Z. Performance of the Watermark. Granular Matrix Sensor in Sandy Soils. Appl. Eng. Agric. 2001, 17, 787. [Google Scholar] [CrossRef]



| Soil 1 | Soil 2 | |
|---|---|---|
| Sand (Coarse) (%) | 7.2 | 17.3 |
| Sand (Fine) (%) | 21.8 | 29.3 |
| Silt (%) | 39.4 | 39.4 |
| Clay (%) | 31.7 | 14.0 |
| Texture (USDA) | Clay loam | Loam |
| pH | 8.1 | 7.7 |
| EC (μS-cm)−1 | 176.0 | 484.0 |
| Organic matter content (%) | 2.0 | 1.9 |
| Carbonates (%) | 20.6 | 40.3 |
| CIC (Cmol-Kg−1) | 1.7 | 1.1 |
| Tensiometers | Model SR | 0.59 [0.32–0.79] | 16.40 [10.15–24.81] | +6.9% | |||
| Model LT | 0.75 [0.64–0.87] | 11.93 [8.35–17.74] | +15.85% | ||||
| Teros 32 | 0.84 [0.79–0.90] | 14.39 [8.08–20.50] | −7.3% | ||||
| Tensio 153e | 0.60 [0.06–0.85] | 16.21 [10.38–21.19] | +39.8% | ||||
| Capacitive Sensors | Tensiomark | 0.81 [0.65–0.89] | 0.85 [0.78–0.90] | 11.19 [9.33–14.76] | 20.30 [11.99–28.49] | −32.0% | −29.1% |
| Teros 21 Gen 2 | 0.79 [0.61–0.86] | 0.84 [0.77–0.89] | 11.60 [9.69–14.06] | 17.74 [11.97–23.84] | −26.6% | −19.1% | |
| Teros 21 | 0.95 [0.92–0.96] | 0.90 [0.88–0.94] | 5.73 [4.48–7.74] | 16.18 [8.13–23.89] | No | −13.6% | |
| EQ-3 | 0.61 [0.33–0.81] | 0.51 [0.23–0.74] | 15.84 [10.49–24.46] | 36.10 [19.74–53.01] | −45.7% | +50.7% | |
| Electrical Resistance Sensor | Watermark Model 200SS | −8.47 [−18.09–0.09] | −1.83 [−11.40–0.44] | 83.28 [35.62–18.68] | 85.58 [40.15–20.64] | +197.5% | +134.2% |
| Heat Dissipation Sensor | 229-L | 0.86 [0.76–0.93] | 0.93 [0.88–0.95] | 9.59 [7.01–12.63] | 13.44 [9.57–17.85] | +11.5% | No |
| Suction Ranges | 0–100 kPa | 0–200 kPa | 0–100 kPa | 0–200 kPa | 0–100 kPa | 0–200 kPa | |
| NSE | RMSE | PBIAS | |||||
| Tensiometers | Model SR | 0.42 [−0.49–0.72] | 17.68 [15.85–20.18] | +69.4% | |||
| Model LT | 0.38 [−0.53–0.64] | 18.33 [13.66–23.00] | +50.3% | ||||
| Teros 32 | −1.12 [−10.27–0.74] | 31.32 [15.31–44.02] | +107.2% | ||||
| Tensio 153e | −0.66 [−5.28–0.61] | 27.22 [16.89–37.80] | +98.1% | ||||
| Capacitive Sensors | Tensiomark | 0.67 [0.48–0.89] | 0.38 [0.14–0.68] | 13.36 [6.60–21.68] | 40.12 [19.20–61.11] | No | −32.6% |
| Teros 21 Gen 2 | 0.91 [0.84–0.93] | 0.92 [0.85–0.97] | 7.02 [5.30–9.17] | 14.84 [7.39–23.59] | −25.3% | −23.4% | |
| Teros 21 | 0.68 [0.50–0.91] | 0.60 [0.32–0.88] | 13.18 [5.78–21.94] | 32.19 [14.21–52.13] | No | −23.7% | |
| EQ-3 | 0.78 [0.29–0.93] | −0.01 [−0.84–0.71] | 10.81 [5.83–16.44] | 51.12 [20.98–86.98] | +22.4% | +21.5% | |
| Electrical Resistance Sensor | Watermark Model 200SS | 0.81 [0.18–0.87] | 0.75 [0.68–0.95] | 7.42 [4.96–12.03] | 28.25 [8.18–44.19] | −17.6% | −33.1% |
| Heat Dissipation Sensor | 229-L | 0.96 [0.88–0.98] | 0.956 [0.93–0.98] | 4.77 [3.31–6.33] | 10.48 [6.20–15.82] | +6.4% | No |
| Suction Ranges | 0–100 kPa | 0–200 kPa | 0–100 kPa | 0–200 kPa | 0–100 kPa | 0–200 kPa | |
| NSE | RMSE | PBIAS | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldaz-Lusarreta, A.; Campo-Bescós, M.Á.; Virto, I.; Giménez, R. Toward Optimal Irrigation Management at the Plot Level: Evaluation of Commercial Water Potential Sensors. Sensors 2023, 23, 9255. https://doi.org/10.3390/s23229255
Aldaz-Lusarreta A, Campo-Bescós MÁ, Virto I, Giménez R. Toward Optimal Irrigation Management at the Plot Level: Evaluation of Commercial Water Potential Sensors. Sensors. 2023; 23(22):9255. https://doi.org/10.3390/s23229255
Chicago/Turabian StyleAldaz-Lusarreta, Alaitz, Miguel Ángel Campo-Bescós, Iñigo Virto, and Rafael Giménez. 2023. "Toward Optimal Irrigation Management at the Plot Level: Evaluation of Commercial Water Potential Sensors" Sensors 23, no. 22: 9255. https://doi.org/10.3390/s23229255
APA StyleAldaz-Lusarreta, A., Campo-Bescós, M. Á., Virto, I., & Giménez, R. (2023). Toward Optimal Irrigation Management at the Plot Level: Evaluation of Commercial Water Potential Sensors. Sensors, 23(22), 9255. https://doi.org/10.3390/s23229255








