Automatic Detection of Magnetic Disturbances in Magnetic Inertial Measurement Unit Sensors Based on Recurrent Neural Networks
Abstract
:1. Introduction
2. Background
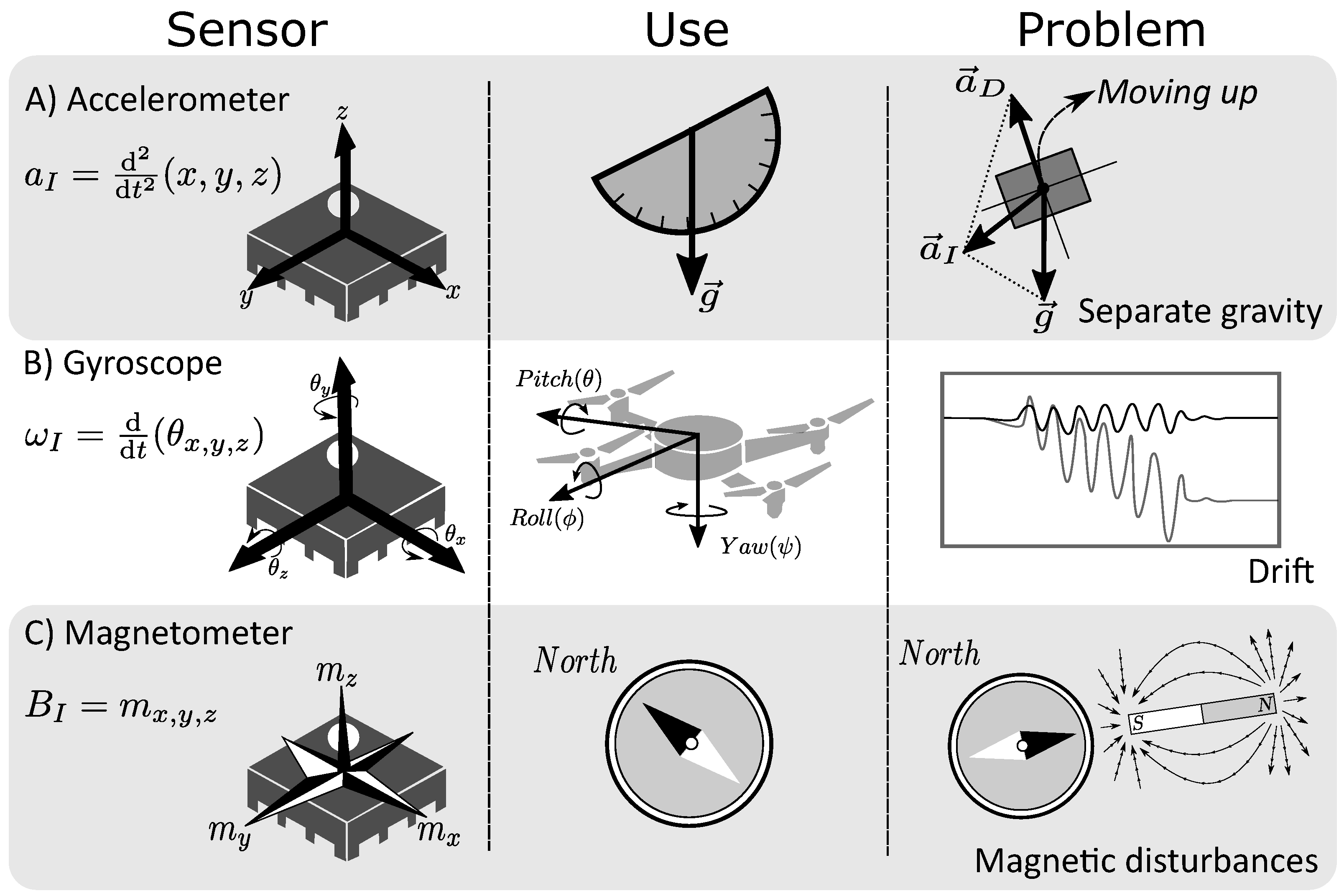
2.1. Basic Principles and Common Issues in MIMU Technology
2.2. Dealing with Magnetic Disturbances
3. Deep Learning Methods
Long Short-Term Memory (LSTM)
4. Materials and Methods
4.1. Sequence-to-Sequence LSTM Model
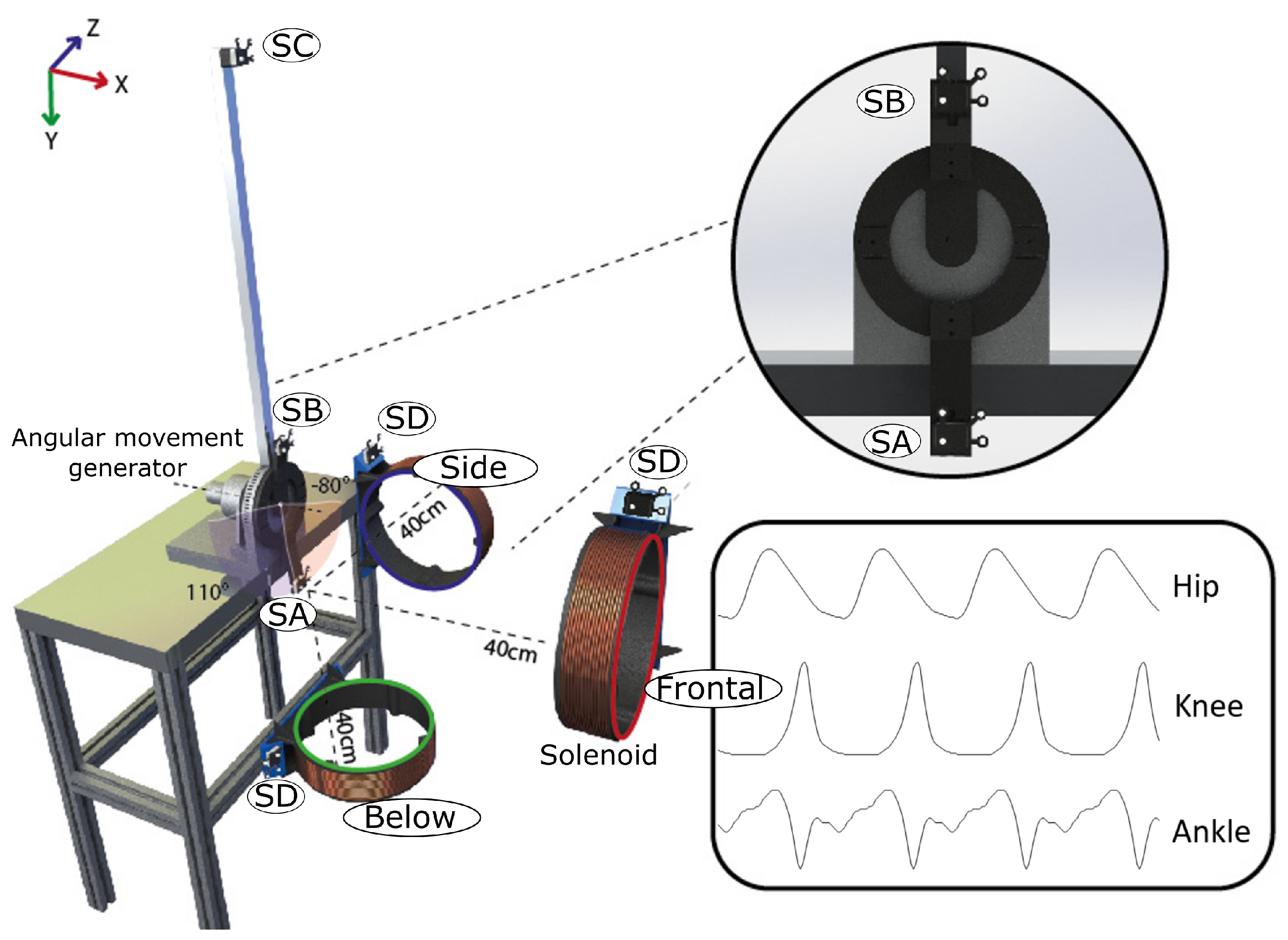
4.2. Experimental Protocol for Data Generation
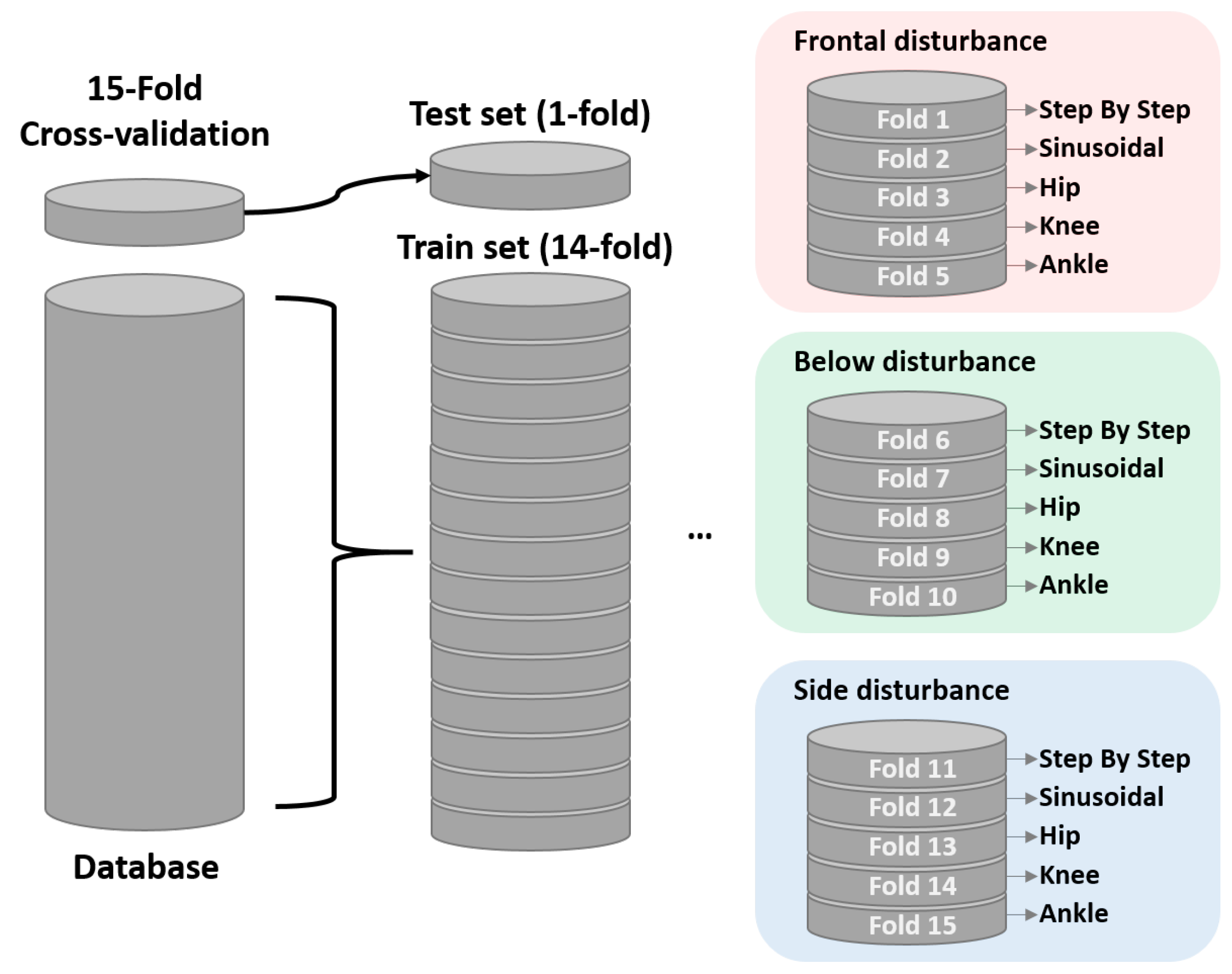
4.3. Experimental Validation
4.4. Performance Analysis
5. Results
5.1. Disturbance Detection Based on Deep Learning
5.2. Comparison with Threshold-Based Methods
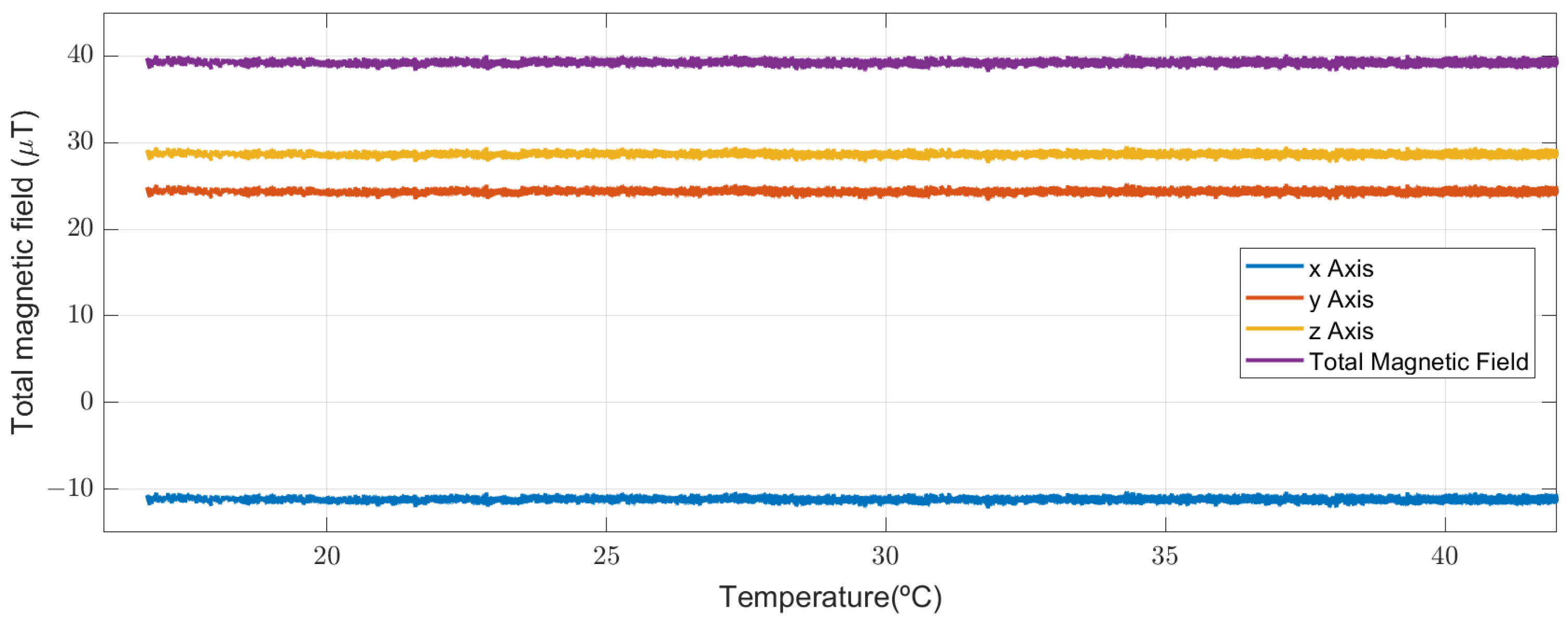
5.3. Magnetic Disturbances Due to Changes in Temperature
6. Discussion
Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, S.; Li, Q. Inertial sensor-based methods in walking speed estimation: A systematic review. Sensors 2012, 12, 6102–6116. [Google Scholar] [CrossRef] [PubMed]
- Tao, W.; Liu, T.; Zheng, R.; Feng, H. Gait Analysis Using Wearable Sensors. Sensors 2012, 12, 2255–2283. [Google Scholar] [CrossRef]
- Bao, S.; Meng, X.; Xiao, W.; Zhang, Z. Fusion of Inertial/Magnetic Sensor Measurements and Map Information for Pedestrian Tracking. Sensors 2017, 17, 340. [Google Scholar] [CrossRef] [PubMed]
- Laudanski, A.; Brouwer, B.; Li, Q. Activity Classification in Persons with Stroke Based on Frequency Features. Med. Eng. Phys. 2015, 37, 180–186. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef]
- Madgwick, S.; Harrison, A.J.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Seel, T.; Raisch, J.; Schauer, T. IMU-based joint angle measurement for gait analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Bachmann, E.R.; Yun, X.; Brumfield, A. Limitations of Attitude Estimnation Algorithms for Inertial Magnetic Sensor Modules. IEEE Robot. Autom. Mag. 2007, 14, 76–87. [Google Scholar] [CrossRef]
- Vries, W.D.; Veeger, H.; Baten, C.; van der Helm, F. Magnetic Distortion in Motion Labs, Implications for Validating Inertial Magnetic Sensors. Gait Posture 2009, 29, 535–541. [Google Scholar] [CrossRef] [PubMed]
- Salehi, S.; Mostofi, N.; Bleser, G. An in-field magnetometer calibration method for IMUs. In Proceedings of the IROS Workshop on Cognitive Assistive Systems: Closing the Action-Perception Loop, Vila Moura, Portugal, 7 October 2012; pp. 39–44. [Google Scholar]
- Harada, T.; Mori, T.; Sato, T. Development of a tiny orientation estimation device to operate under motion and magnetic disturbance. Int. J. Robot. Res. 2007, 26, 547–559. [Google Scholar] [CrossRef]
- Lee, J.; Park, E. Minimum-Order Kalman Filter With Vector Selector for Accurate Estimation of Human Body Orientation. IEEE Trans. Robot. 2009, 25, 1196–1201. [Google Scholar]
- Bleser, G.; Hendeby, G.; Miezal, M. Using egocentric vision to achieve robust inertial body tracking under magnetic disturbances. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 103–109. [Google Scholar]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.M.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef] [PubMed]
- Bonato, P. Wearable sensors/systems and their impact on biomedical engineering. IEEE Eng. Med. Biol. Mag. 2003, 22, 18–20. [Google Scholar] [CrossRef] [PubMed]
- Novak, D.; Rebersek, P.; Rossi, S.D.; Donati, M.; Podobnik, J.; Beravs, T.; Lenzi, T.; Vitiello, N.; Carrozza, M.; Munih, M. Automated detection of gait initiation and termination using wearable sensors. Med. Eng. Phys. 2013, 35, 1713–1720. [Google Scholar] [CrossRef] [PubMed]
- Ikuta, K.; Takahashi, A.; Ikeda, K.; Maruo, S. Fully integrated micro biochemical laboratory using Biochemical IC chips. In Proceedings of the The Sixteenth Annual International Conference on Micro Electro Mechanical Systems, Kyoto, Japan, 19–23 January 2003; pp. 451–454. [Google Scholar]
- Morris, D.; Schazmann, B.; Wu, Y.; Coyle, S.; Brady, S.; Fay, C.; Hayes, J.; Lau, K.; Wallace, G.; Diamond, D. Wearable technology for bio-chemical analysis of body fluids during exercise. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 5741–5744. [Google Scholar]
- Wang, L.; Yang, G.; Huang, J.; Zhang, J.; Yu, L.; Nie, Z.; Cumming, D.R.S. A Wireless Biomedical Signal Interface System-on-Chip for Body Sensor Networks. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 112–117. [Google Scholar] [CrossRef] [PubMed]
- Goršič, M.; Kamnik, R.; Ambrožič, L.; Vitiello, N.; Lefeber, D.; Pasquini, G.; Munih, M. Online Phase Detection Using Wearable Sensors for Walking with a Robotic Prosthesis. Sensors 2014, 14, 2776–2794. [Google Scholar] [CrossRef]
- Ermes, M.; PÄrkkÄ, J.; MÄntyjÄrvi, J.; Korhonen, I. Detection of Daily Activities and Sports With Wearable Sensors in Controlled and Uncontrolled Conditions. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 20–26. [Google Scholar] [CrossRef]
- Šlajpah, S.; Kamnik, R.; Munih, M. Kinematics based sensory fusion for wearable motion assessment in human walking. Comput. Methods Programs Biomed. 2014, 116, 131–144. [Google Scholar] [CrossRef]
- O’Donovan, K.J.; Kamnik, R.; O’Keeffe, D.T.; Lyons, G.M. An inertial and magnetic sensor based technique for joint angle measurement. J. Biomech. 2007, 40, 2604–2611. [Google Scholar] [CrossRef]
- Luinge, H.; Veltink, P. Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Med. Biol. Eng. Comput. 2005, 43, 273–282. [Google Scholar] [CrossRef]
- Caramia, C.; Torricelli, D.; Schmid, M.; Muñoz-Gonzalez, A.; Gonzalez-Vargas, J.; Grandas, F.; Pons, J.L. IMU-Based Classification of Parkinson’s Disease From Gait: A Sensitivity Analysis on Sensor Location and Feature Selection. IEEE J. Biomed. Health Inform. 2018, 22, 1765–1774. [Google Scholar] [CrossRef]
- Taccini, N.; Loriga, G.; Pacelli, M.; Paradiso, R. Wearable monitoring system for chronic cardio-respiratory diseases. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 3690–3693. [Google Scholar]
- Winter, D. Biomechanical motor patterns in normal walking. J. Mot. Behav. 1983, 15, 302–330. [Google Scholar] [CrossRef]
- Whittle, M. Gait Analysis: An Introduction; Butterworth/Heinemann: Oxford, UK, 1996. [Google Scholar]
- Sutherland, D. The evolution of clinical gait analysis: Part II Kinematics. Gait Posture 2002, 16, 159–179. [Google Scholar] [CrossRef] [PubMed]
- Kralj, A.; Jaeger, R.J.; Munih, M. Analysis of standing up and sitting down in humans: Definitions and normative data presentation. J. Biomech. 1990, 23, 1123–1138. [Google Scholar] [CrossRef] [PubMed]
- Kamnik, R.; Bajd, T.; Kralj, A. Functional electrical stimulation and arm supported sit-to-stand transfer after paraplegia: A study of kinetic parameters. Artif. Organs 1999, 23, 413–417. [Google Scholar] [CrossRef] [PubMed]
- Dickstein, R.; Dunsky, A.; Marcovitz, E. Motor imagery for gait rehabilitation in post-stroke hemiparesis. Phys. Ther. 2004, 84, 1167–1177. [Google Scholar] [CrossRef] [PubMed]
- Duschau-Wicke, A.; von Zitzewitz, J.; Caprez, A.; Lunenburger, L.; Riener, R. Path Control: A Method for Patient-Cooperative Robot-Aided Gait Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 38–48. [Google Scholar] [CrossRef] [PubMed]
- Sup, F.; Bohara, A.; Goldfarb, M. Design and control of a powered transfemoral prosthesis. Int. J. Robot. Res. 2008, 27, 263–273. [Google Scholar] [CrossRef] [PubMed]
- Ambrozic, L.; Gorsic, M.; Geeroms, J.; Flynn, L.; Molino Lova, R.; Kamnik, R.; Munih, M.; Vitiello, N. CYBERLEGs: A User-Oriented Robotic Transfemoral Prosthesis with Whole-Body Awareness Control. IEEE Robot. Autom. Mag. 2014, 21, 82–93. [Google Scholar] [CrossRef]
- Moreno, J.C.; de Lima, E.R.; Ruiz, A.F.; Brunetti, F.J.; Pons, J.L. Design and implementation of an inertial measurement unit for control of artificial limbs: Application on leg orthoses. Sens. Actuators B Chem. 2006, 118, 333–337. [Google Scholar] [CrossRef]
- Blaya, J.A.; Herr, H. Adaptive control of a variable-impedance ankle-foot orthosis to assist drop-foot gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 24–31. [Google Scholar] [CrossRef]
- Muller, E.; Schwameder, H. Biomechanical aspects of new techniques in alpine skiing and ski-jumping. J. Sport. Sci. 2003, 21, 679–692. [Google Scholar] [CrossRef] [PubMed]
- Melzi, S.; Borsani, L.P.; Cesana, M. The Virtual Trainer: Supervising Movements Through a Wearable Wireless Sensor Network. In Proceedings of the 2009 6th IEEE Annual Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks Workshops, Rome, Italy, 22–26 June 2009; pp. 1–3. [Google Scholar]
- Cerne, T.; Kamnik, R.; Munih, M. The measurement setup for real-time biomechanical analysis of rowing on an ergometer. Measurement 2011, 44, 1819–1827. [Google Scholar] [CrossRef]
- Aggarwal, P.; Syed, Z.; Niu, X.; El-Sheimy, N. A Standard Testing and Calibration Procedure for Low Cost MEMS Inertial Sensors and Units. J. Navig. 2008, 61, 323–336. [Google Scholar] [CrossRef]
- Mak, M.; Levin, O.; Mizrahi, J.; Hui-Chan, C. Joint torques during sit-to-stand in healthy subjects and people with Parkinson’s disease. Clin. Biomech. 2003, 18, 197–206. [Google Scholar] [CrossRef] [PubMed]
- Campolo, D.; Fabris, M.; Cavallo, G.; Accoto, D.; Keller, F.; Guglielmelli, E. A Novel Procedure for In-field Calibration of Sourceless Inertial/Magnetic Orientation Tracking Wearable Devices. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, Pisa, Italy, 20–22 February 2006; pp. 471–476. [Google Scholar]
- Beravs, T.; Reberšek, P.; Novak, D.; Podobnik, J.; Munih, M. Development and validation of a wearable inertial measurement system for use with lower limb exoskeletons. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 212–217. [Google Scholar]
- Roetenberg, D.; Slycke, P.J.; Veltink, P.H. Ambulatory Position and Orientation Tracking Fusing Magnetic and Inertial Sensing. IEEE Trans. Biomed. Eng. 2007, 54, 883–890. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A. Variable-State-Dimension Kalman-Based Filter for Orientation Determination Using Inertial and Magnetic Sensors. Sensors 2012, 12, 8491–8506. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A. Estimating three-dimensional orientation of human body parts by inertial/magnetic sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef]
- Fernández, S.; Graves, A.; Schmidhuber, J. Sequence Labelling in Structured Domains with Hierarchical Recurrent Neural Networks. In Proceedings of the International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007. [Google Scholar]
- He, T.; Droppo, J. Exploiting LSTM structure in deep neural networks for speech recognition. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 5445–5449. [Google Scholar]
- Sak, H.; Senior, A.W.; Beaufays, F. Long Short-Term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition. arXiv 2014, arXiv:abs/1402.1128. [Google Scholar]
- Qu, Z.; Haghani, P.; Weinstein, E.; Moreno, P. Syllable-based acoustic modeling with CTC-SMBR-LSTM. In Proceedings of the 2017 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Okinawa, Japan, 16–20 December 2017; pp. 173–177. [Google Scholar]
- Altché, F.; de La Fortelle, A. An LSTM network for highway trajectory prediction. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 353–359. [Google Scholar]
- Palangi, H.; Deng, L.; Shen, Y.; Gao, J.; He, X.; Chen, J.; Song, X.; Ward, R. Deep Sentence Embedding Using Long Short-Term Memory Networks: Analysis and Application to Information Retrieval. IEEE/ACM Trans. Audio Speech Lang. Proc. 2016, 24, 694–707. [Google Scholar] [CrossRef]
- Mallinar, N.R.; Rosset, C. Deep Canonically Correlated LSTMs. arXiv 2018, arXiv:1801.05407. [Google Scholar]
- Wu, X.; Huang, S.; Li, M.; Deng, Y. Vector Magnetic Anomaly Detection via an Attention Mechanism Deep-Learning Model. Appl. Sci. 2021, 11, 11533. [Google Scholar] [CrossRef]
- Sun, T.; Wang, X.; Wang, J.; Yang, X.; Meng, T.; Shuai, Y.; Chen, Y. Magnetic anomaly detection of adjacent parallel pipelines using deep learning neural networks. Comput. Geosci. 2022, 159, 104987. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.; Tino, P.; Giles, C. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar]
- Mozer, M.C. Induction of Multiscale Temporal Structure. In Proceedings of the Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1991. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Chen, I.; Caus, A. Human velocity tracking and localization using 3 IMU sensors. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Philippines, 12–15 November 2013; pp. 25–30. [Google Scholar]



| Direction | Signal | Acc (%) | AUC | Sens (%) | Spec (%) | Recall (%) | F Score (%) | |
|---|---|---|---|---|---|---|---|---|
| Fold-1 | Front | Step By Step | 85.97 | 0.834 | 98.66 | 76.89 | 98.66 | 85.49 |
| Fold-2 | Sinusoidal | 92.53 | 0.906 | 99.86 | 87.38 | 99.86 | 91.70 | |
| Fold-3 | Hip | 99.83 | 0.998 | 99.98 | 99.72 | 99.98 | 99.80 | |
| Fold-4 | Knee | 99.93 | 0.996 | 99.98 | 99.90 | 99.98 | 99.92 | |
| Fold-5 | Ankle | 99.88 | 0.997 | 99.98 | 99.81 | 99.98 | 99.86 | |
| Fold-6 | Below | Step By Step | 99.84 | 0.998 | 99.98 | 99.74 | 99.98 | 99.81 |
| Fold-7 | Sinusoidal | 99.86 | 0.999 | 99.98 | 99.77 | 99.98 | 99.84 | |
| Fold-8 | Hip | 99.84 | 0.999 | 99.98 | 99.74 | 99.98 | 99.81 | |
| Fold-9 | Knee | 99.91 | 0.994 | 99.98 | 99.87 | 99.98 | 99.90 | |
| Fold-10 | Ankle | 99.84 | 0.993 | 99.98 | 99.73 | 99.98 | 99.81 | |
| Fold-11 | Side | Step By Step | 99.83 | 0.998 | 99.98 | 99.71 | 99.98 | 99.80 |
| Fold-12 | Sinusoidal | 99.91 | 0.997 | 99.98 | 99.86 | 99.98 | 99.89 | |
| Fold-13 | Hip | 99.87 | 0.996 | 99.98 | 99.78 | 99.98 | 99.85 | |
| Fold-14 | Knee | 99.92 | 0.997 | 99.98 | 99.88 | 99.98 | 99.91 | |
| Fold-15 | Ankle | 99.88 | 0.996 | 99.98 | 99.80 | 99.98 | 99.86 | |
| Average | 98.46 | 0.986 | 99.88 | 97.44 | 99.88 | 98.35 |
| Acc (%) | Sens (%) | Spec (%) | Recall (%) | F-Score (%) | |
|---|---|---|---|---|---|
| Case I | 92.50 ± 10.37 | 98.99 ± 1.91 | 87.64 ± 16.80 | 98.99 ± 1.91 | 92.58 ± 10.50 |
| Case II | 86.99 ± 6.21 | 93.11 ± 12.55 | 81.25 ± 11.51 | 93.11 ± 12.55 | 86.28 ± 7.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belalcazar-Bolaños, E.A.; Torricelli, D.; Pons, J.L. Automatic Detection of Magnetic Disturbances in Magnetic Inertial Measurement Unit Sensors Based on Recurrent Neural Networks. Sensors 2023, 23, 9683. https://doi.org/10.3390/s23249683
Belalcazar-Bolaños EA, Torricelli D, Pons JL. Automatic Detection of Magnetic Disturbances in Magnetic Inertial Measurement Unit Sensors Based on Recurrent Neural Networks. Sensors. 2023; 23(24):9683. https://doi.org/10.3390/s23249683
Chicago/Turabian StyleBelalcazar-Bolaños, Elkyn Alexander, Diego Torricelli, and José L. Pons. 2023. "Automatic Detection of Magnetic Disturbances in Magnetic Inertial Measurement Unit Sensors Based on Recurrent Neural Networks" Sensors 23, no. 24: 9683. https://doi.org/10.3390/s23249683
APA StyleBelalcazar-Bolaños, E. A., Torricelli, D., & Pons, J. L. (2023). Automatic Detection of Magnetic Disturbances in Magnetic Inertial Measurement Unit Sensors Based on Recurrent Neural Networks. Sensors, 23(24), 9683. https://doi.org/10.3390/s23249683





