Vibration-Based Recognition of Wheel–Terrain Interaction for Terramechanics Model Selection and Terrain Parameter Identification for Lugged-Wheel Planetary Rovers
Abstract
:1. Introduction
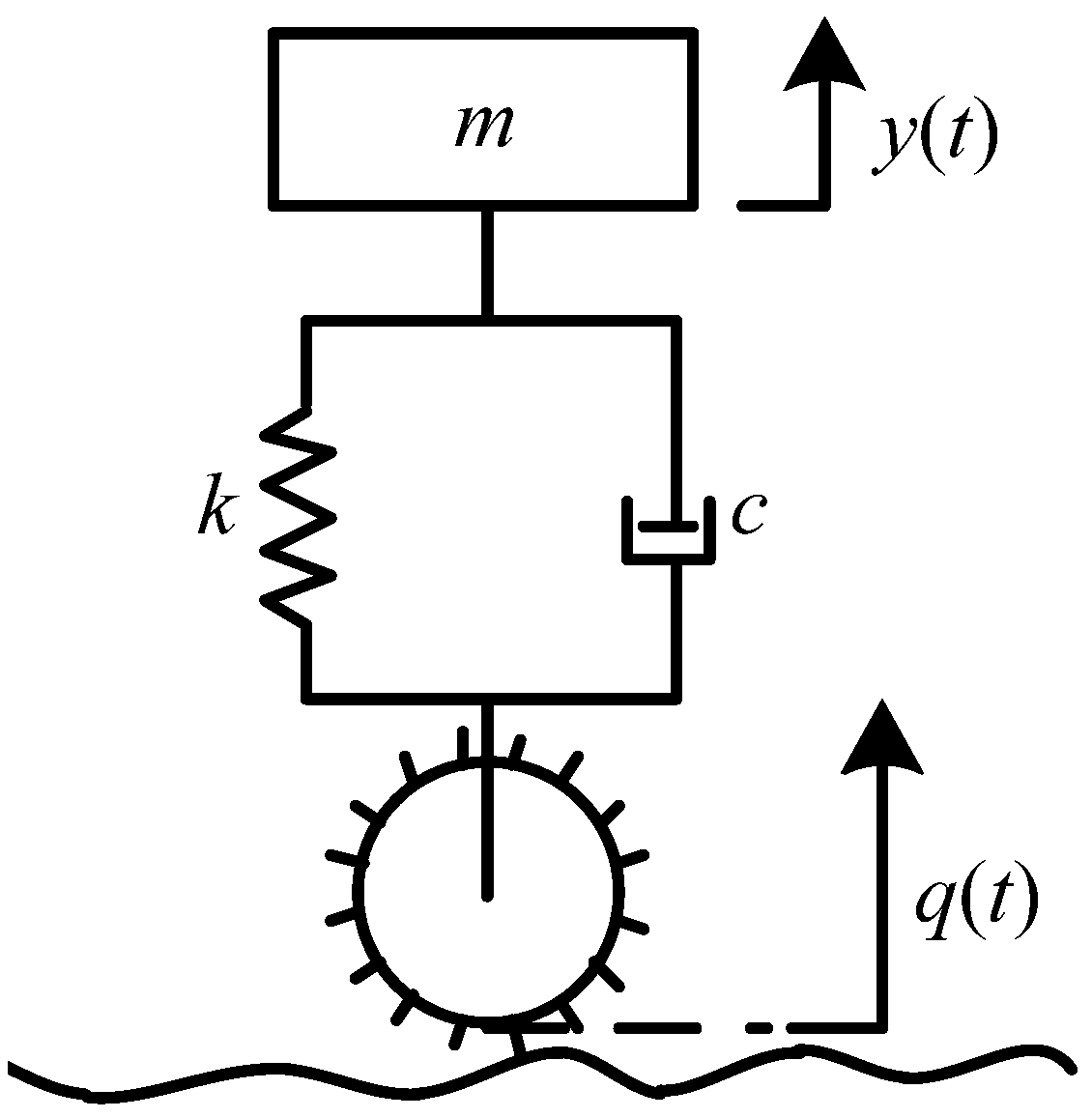
2. Vertical Vibration for Lugged Wheels of Planetary Rovers
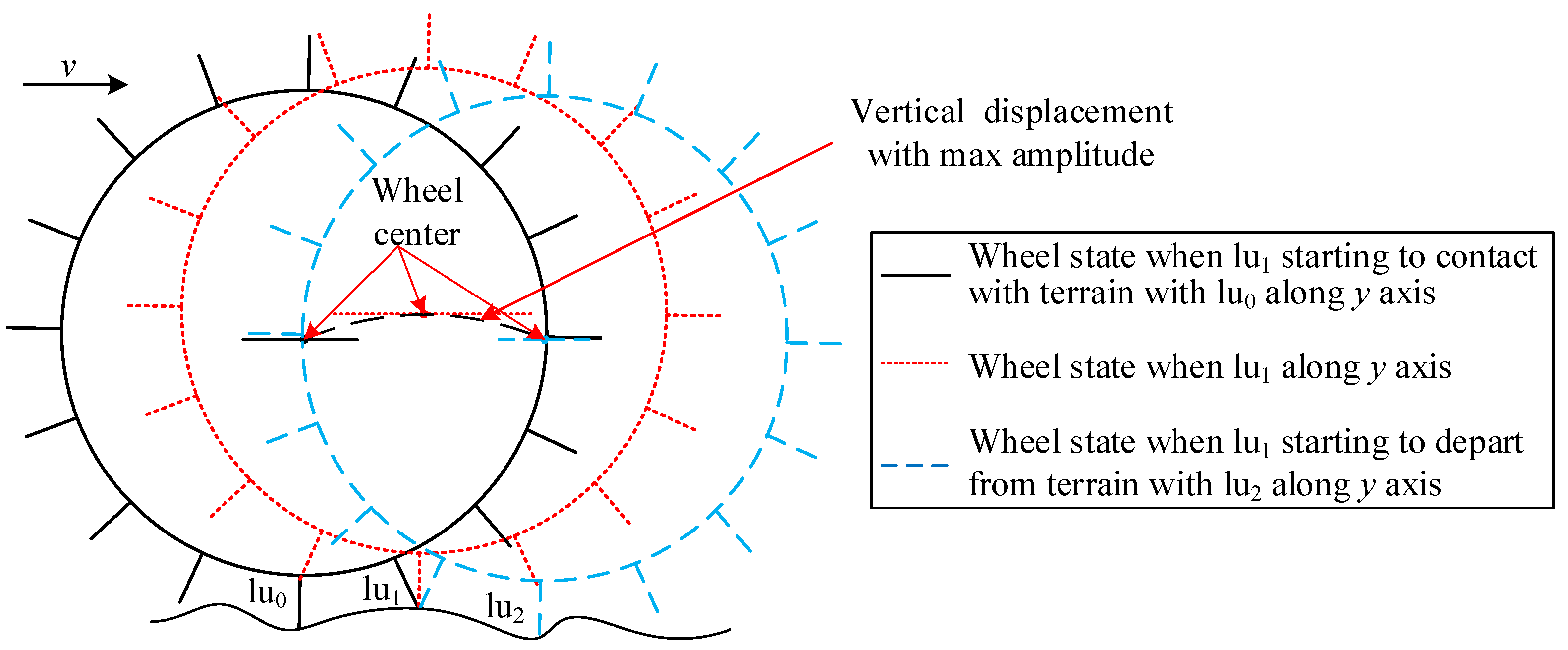
2.1. Vertical Dynamics Model of Wheel Motion
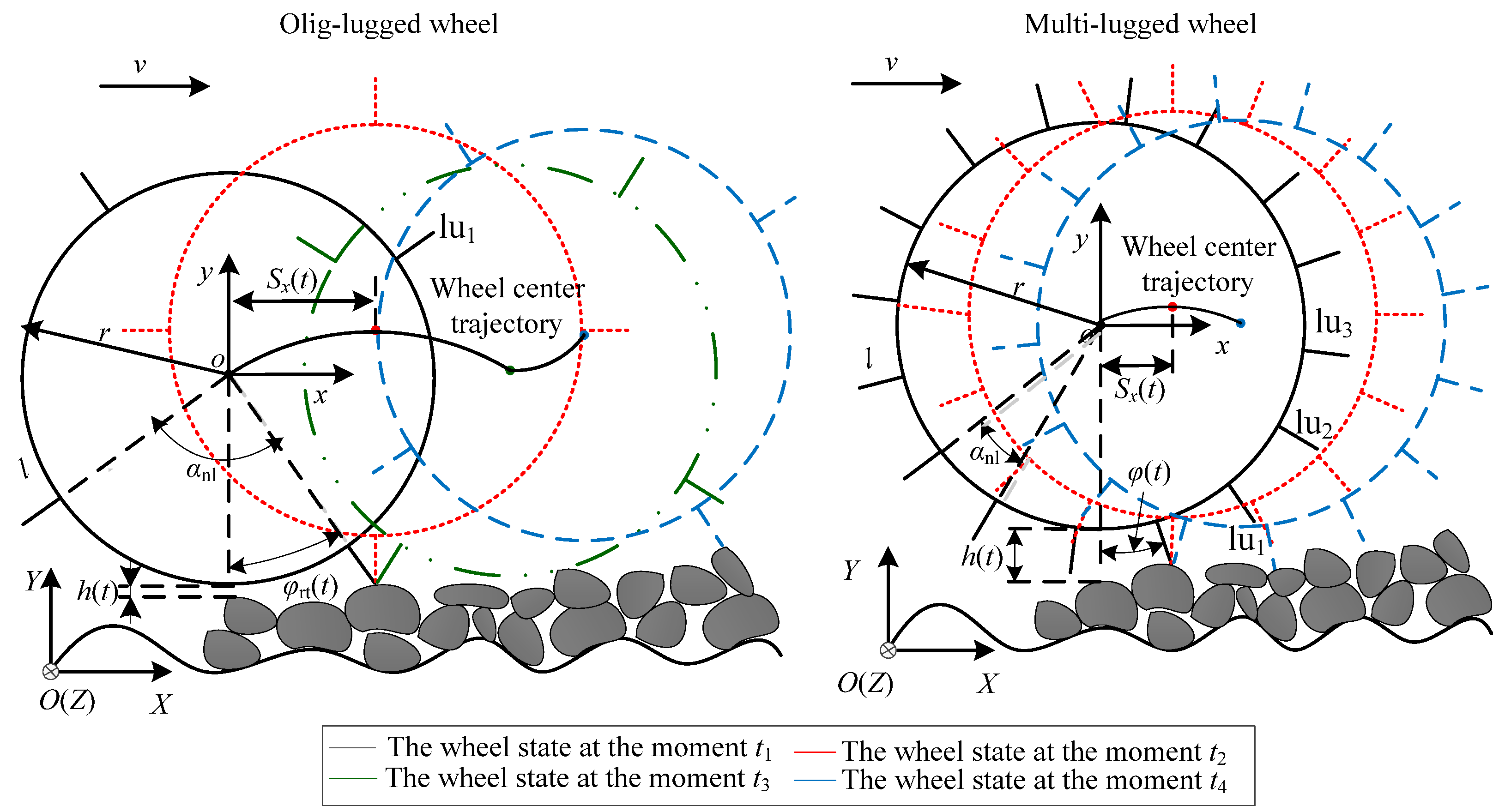
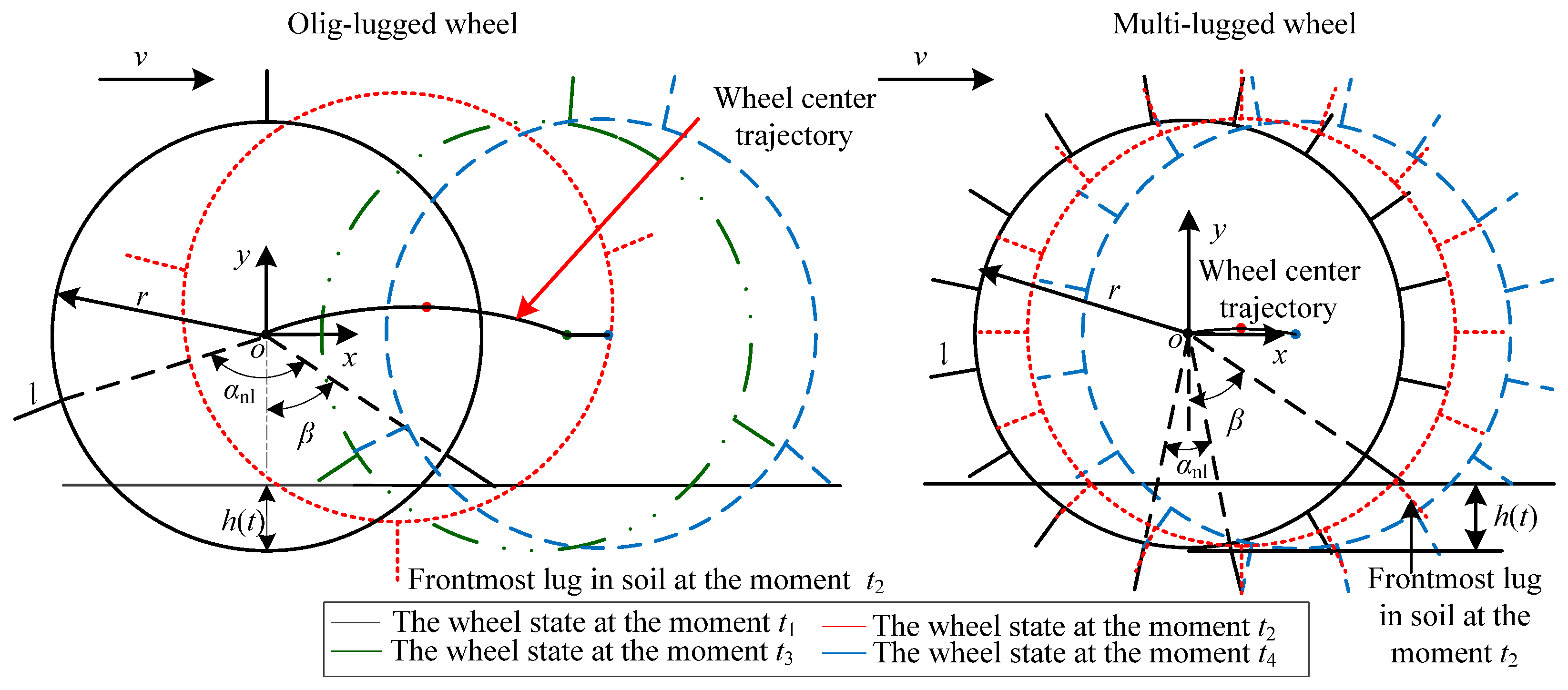
2.2. Vibration Models for Wheels Moving on Different Terrains in Wheels’ Center Plane
2.2.1. Vibration Model of Wheels Moving on Flat Hard Terrain
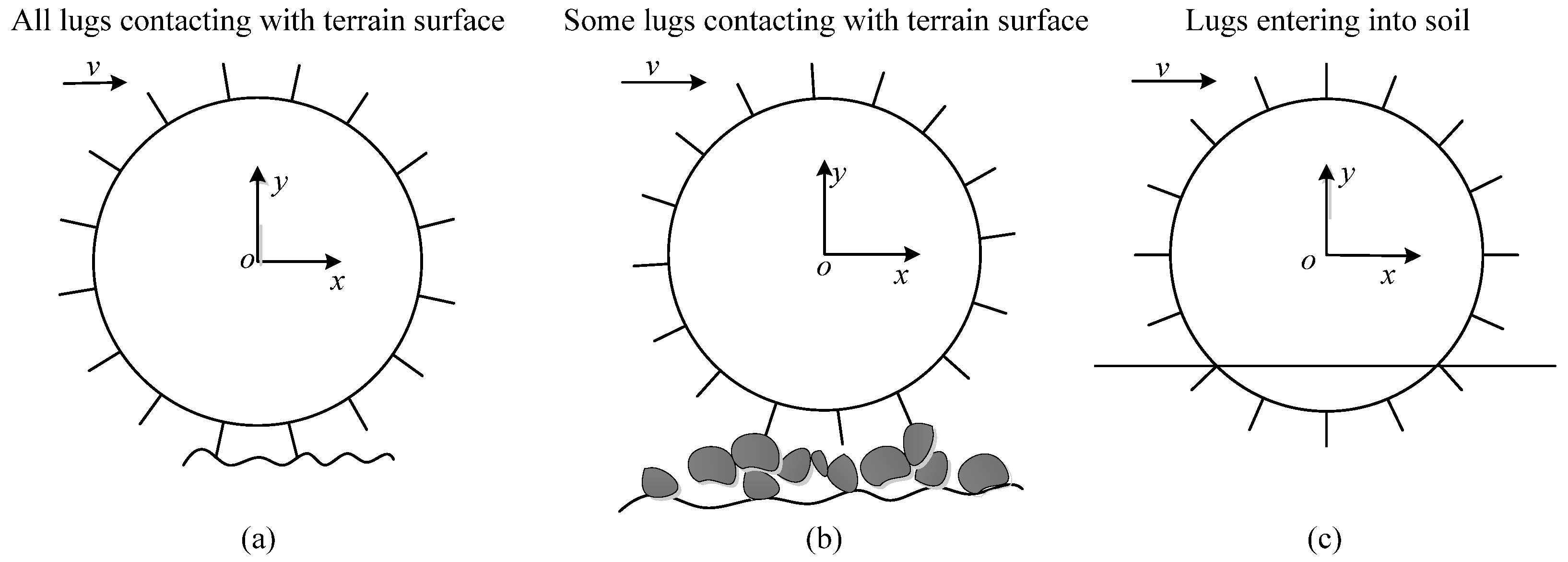
2.2.2. Vibration Model of Wheels with All Lugs Contacting Terrain Surface
2.2.3. Vibration Model of Wheels with Some Lugs Contacting Terrain Surface
2.2.4. Vibration Model of Wheels with Lugs Entering the Soil
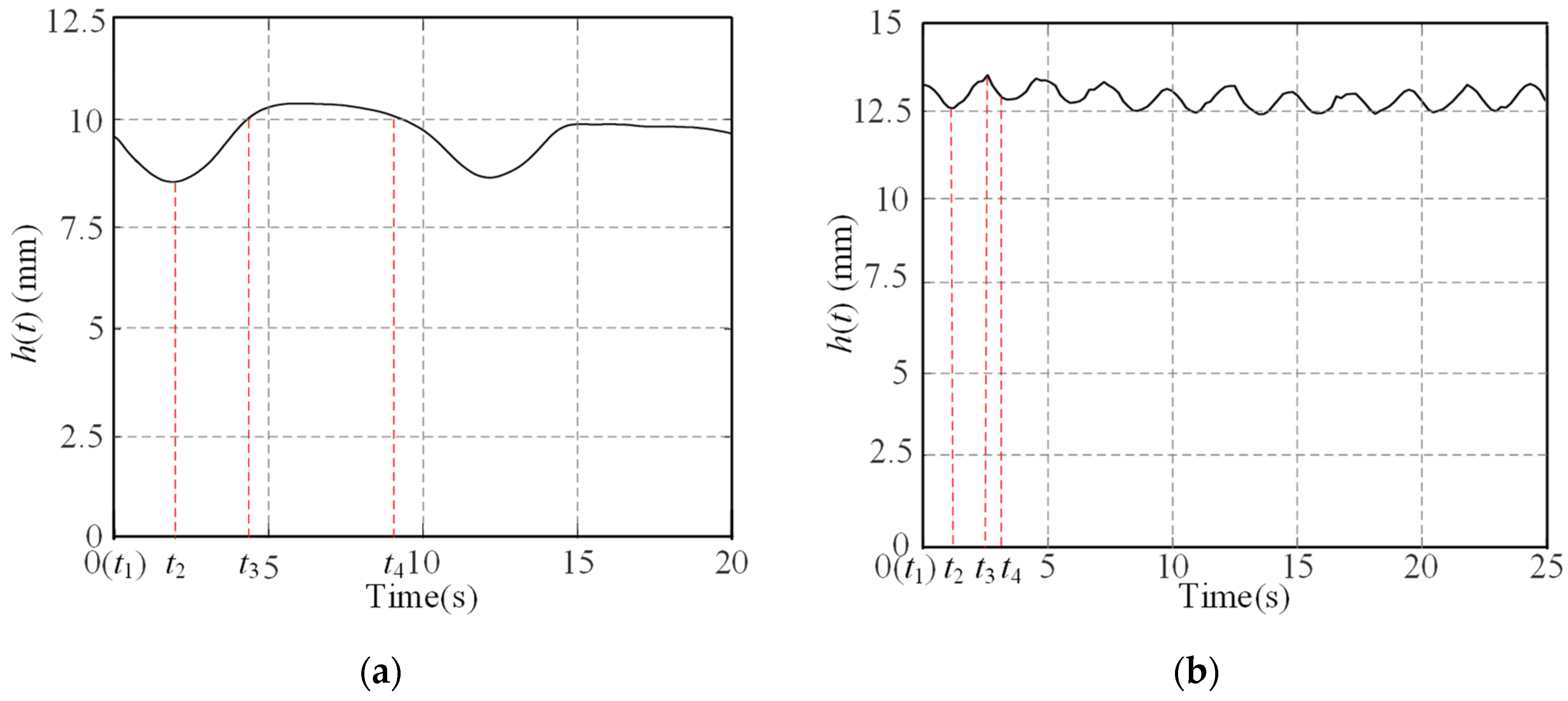
2.3. Simplification of Vibration Outputs for Wheels Traversing Different Terrains
3. Analysis and Extraction of Statistical Vibration Features Independent of the Wheel Velocity
3.1. Extraction of Vibration Features Independent of Wheel Velocity
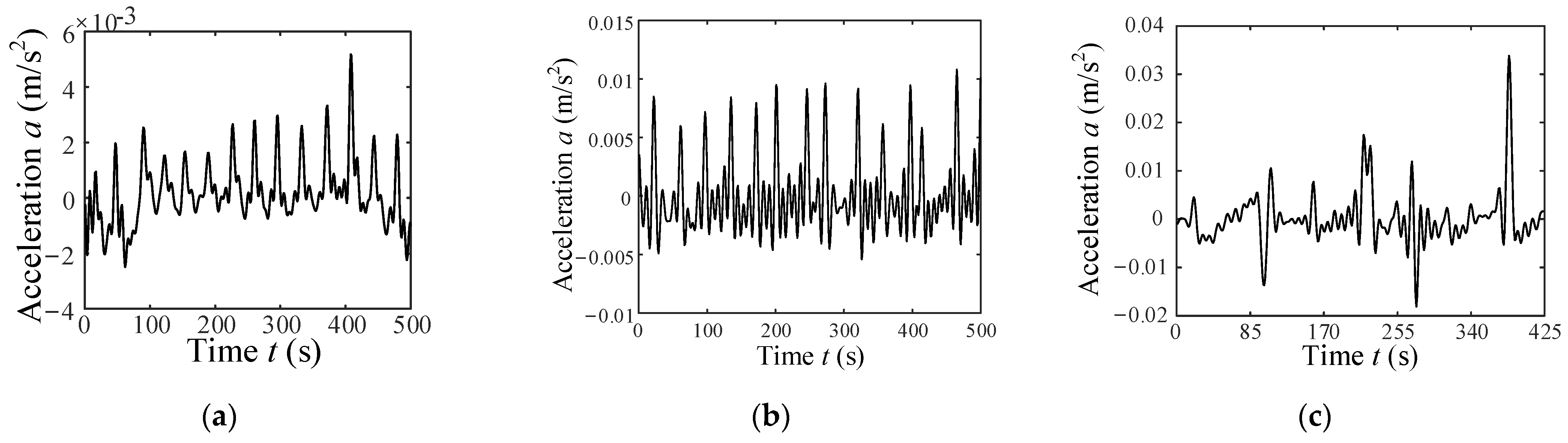
3.2. Analysis of Vibration Features Based on a Single-Wheel Experiment
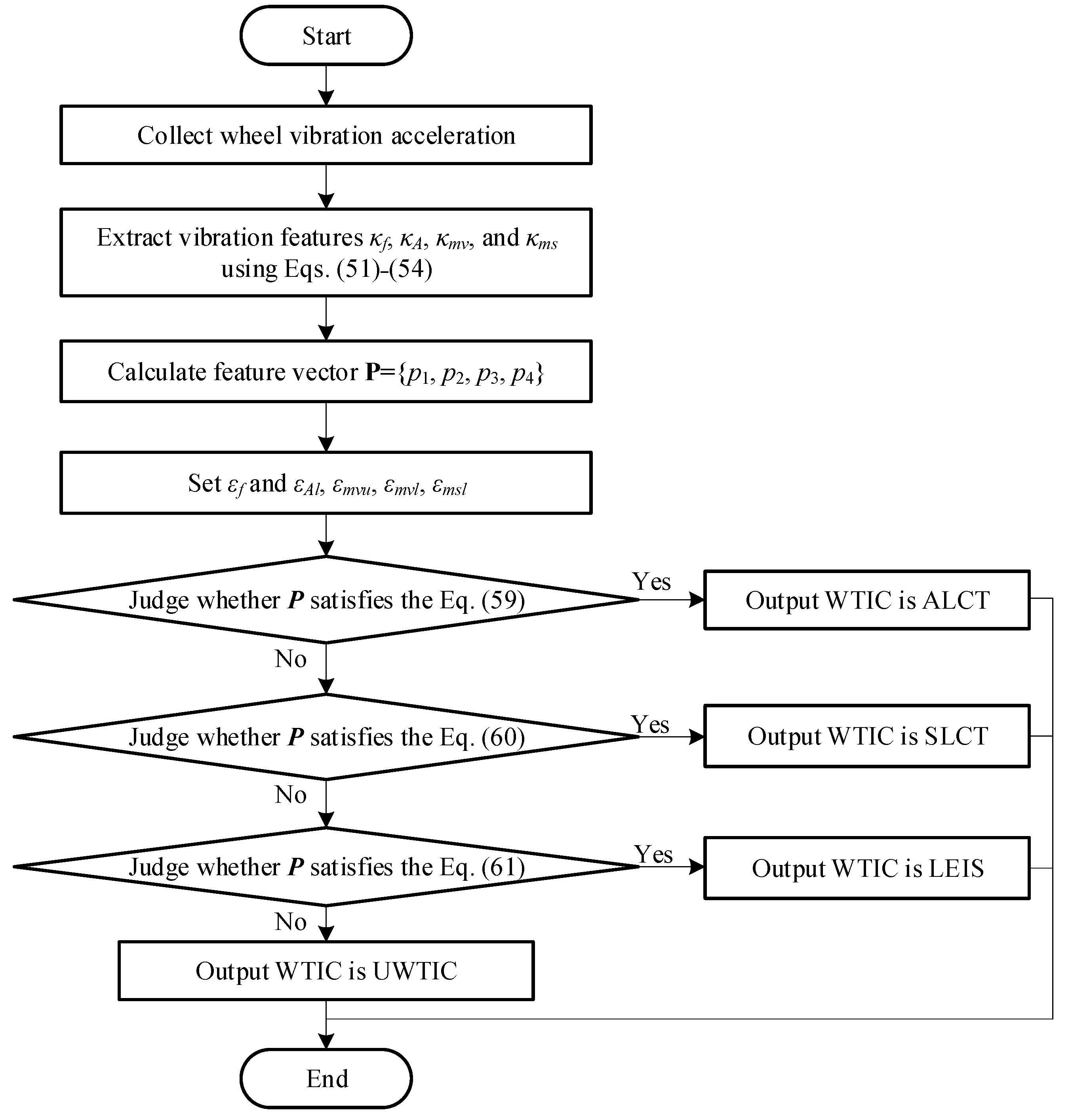
4. Recognition of Wheel–Terrain Interaction Class Based on Speed-Independent Vibration Features
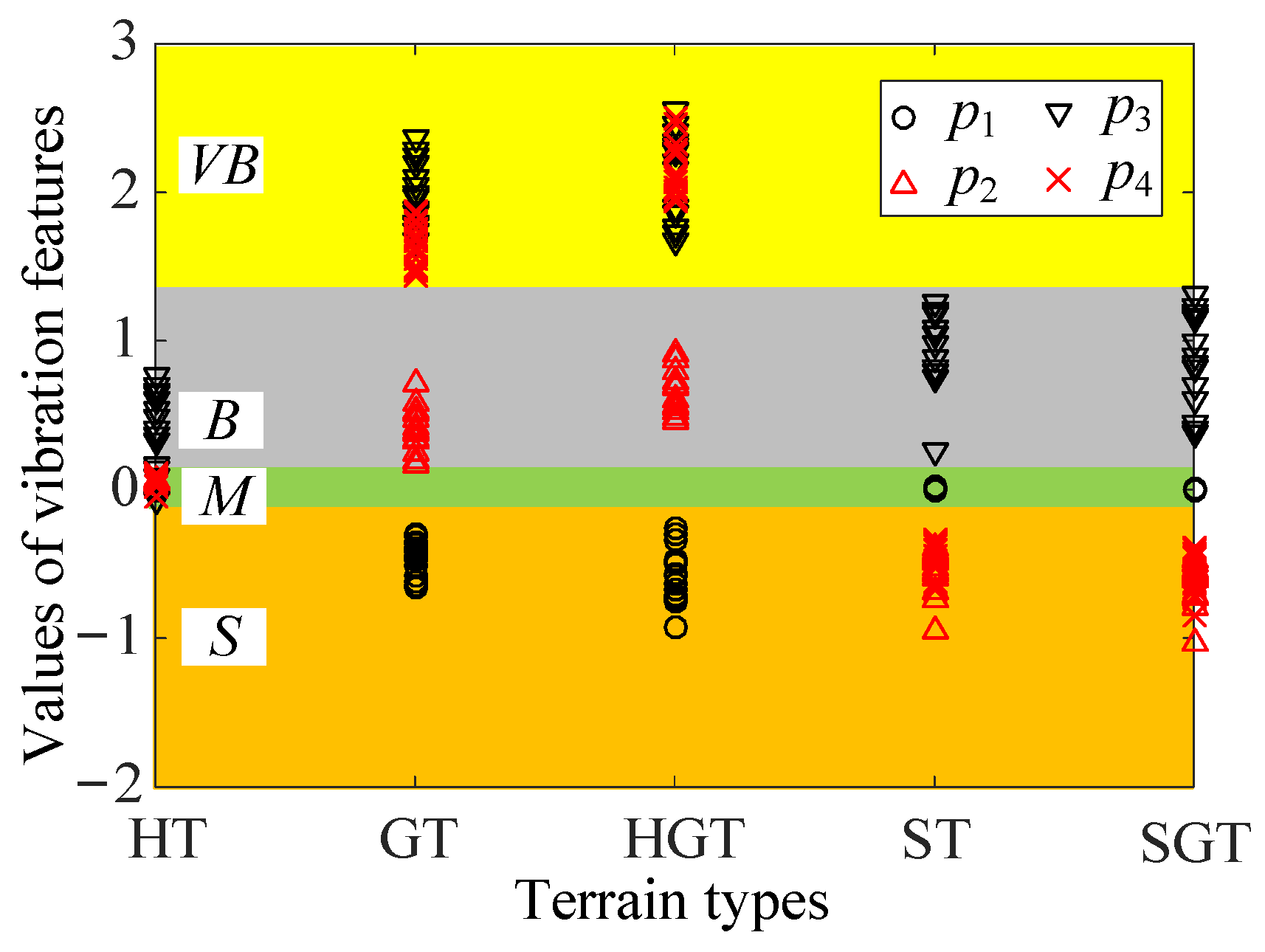
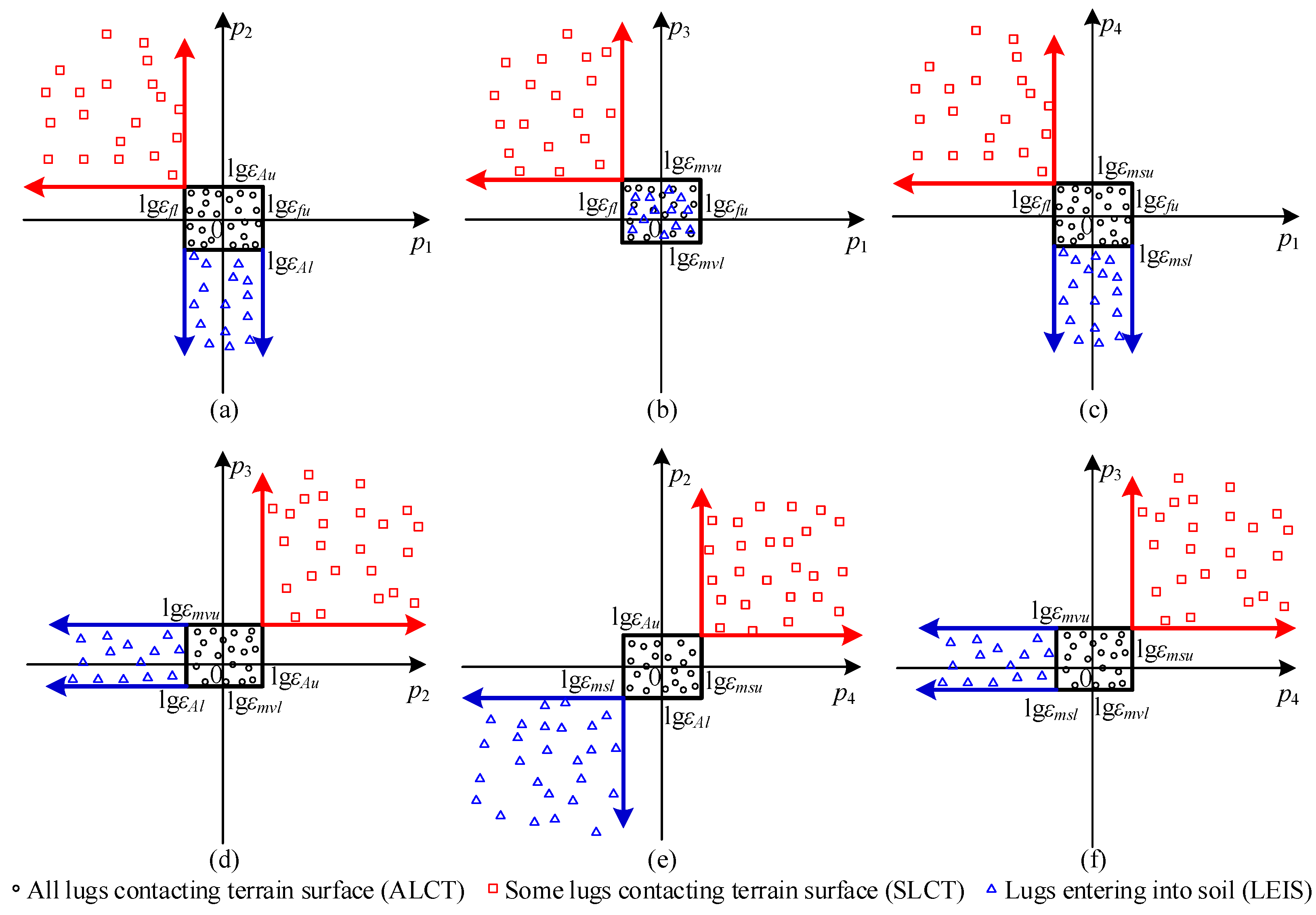
4.1. Analysis of Feature Space of the Four Speed-Independent Features
4.2. Analysis of Feature Vector P for the All Lugs Contacting Terrain Surface within the Vicinity of Zero
4.3. Recognition of Wheel–Terrain Interaction Class Based on Vibration Features
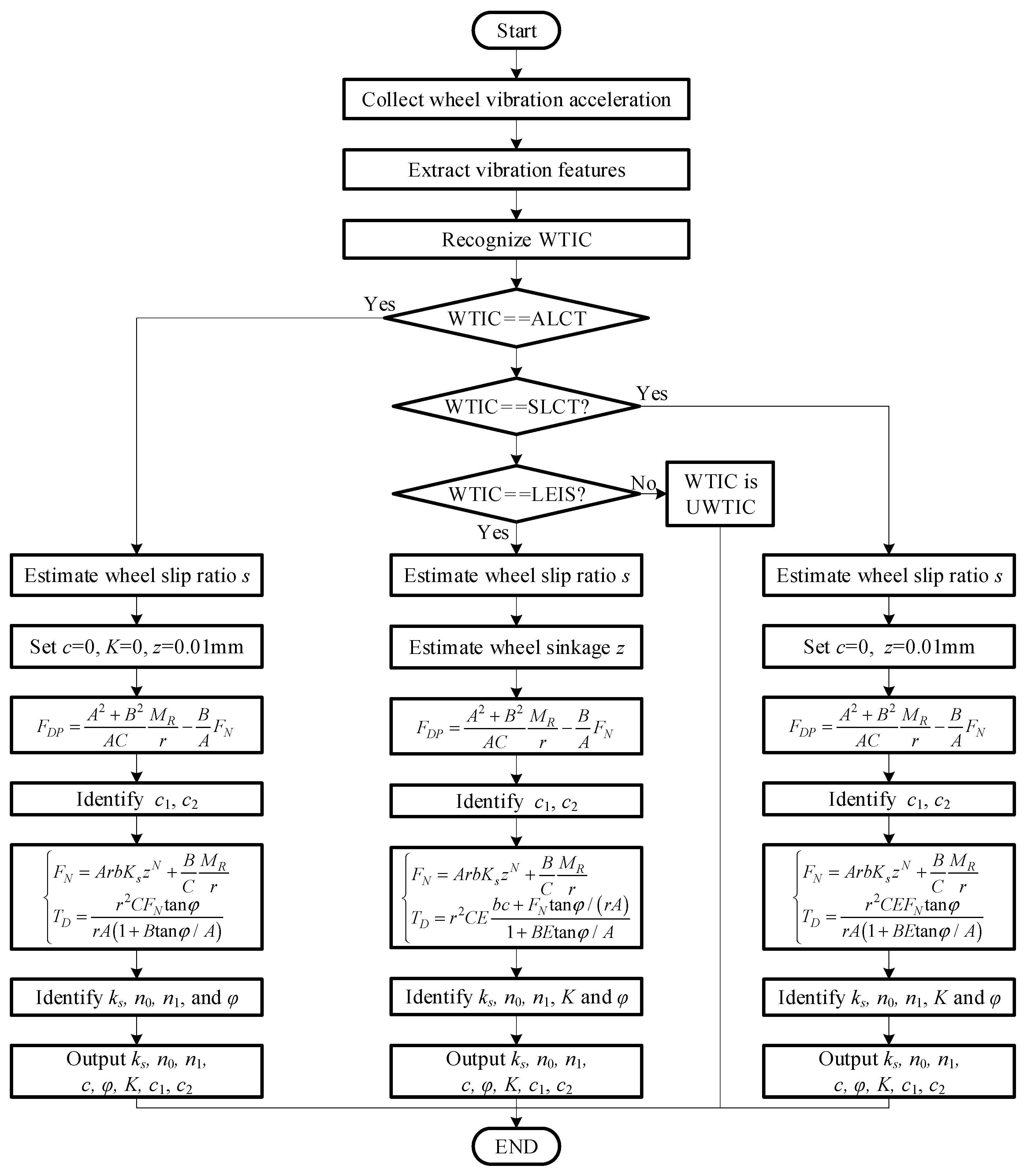
5. Estimation of Terrain Properties Based on the Recognition of Wheel–Terrain Interaction Class
5.1. Switchable Terramechanics Model
5.2. Unified Identification Model for Terrain Parameters
5.3. Identification of Terrain Parameters Based on Terramechanics Model Switching
6. Experiments for Wheel–Terrain Interaction Class Recognition and Terrain Parameter Identification Using a Planetary Rover Prototype
6.1. Introduction of Planetary Rover Prototype and Terrain Environment
6.2. Recognition of Wheel–Terrain Interaction Class for Planetary Rover Prototype
6.3. Terrain Parameter Identification for Planetary Rover Prototype
6.3.1. Introduction of Sinkage Detection for Wheels Moving on Soft Terrain
6.3.2. Introduction of Wheel Slip Ratio Detection
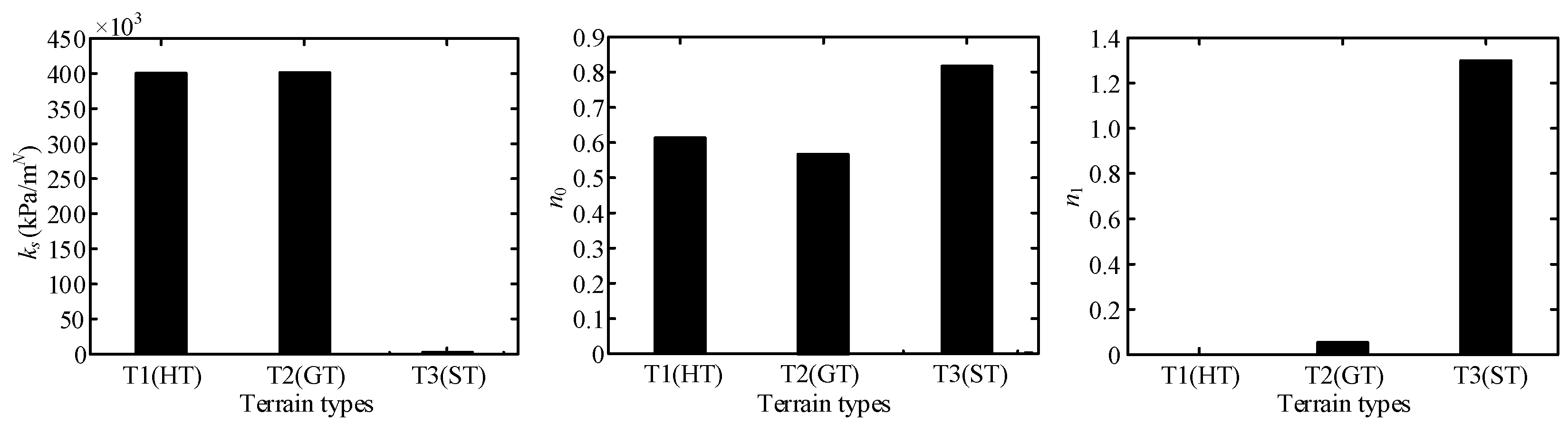
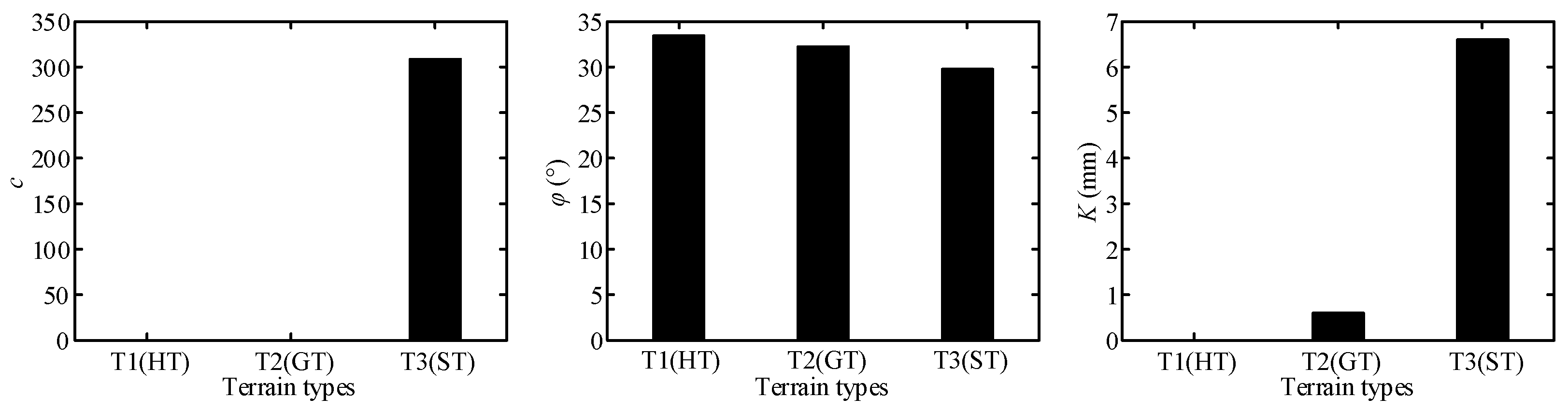
6.3.3. Identification Results of Terrain Parameters for Three Classes of Terrain
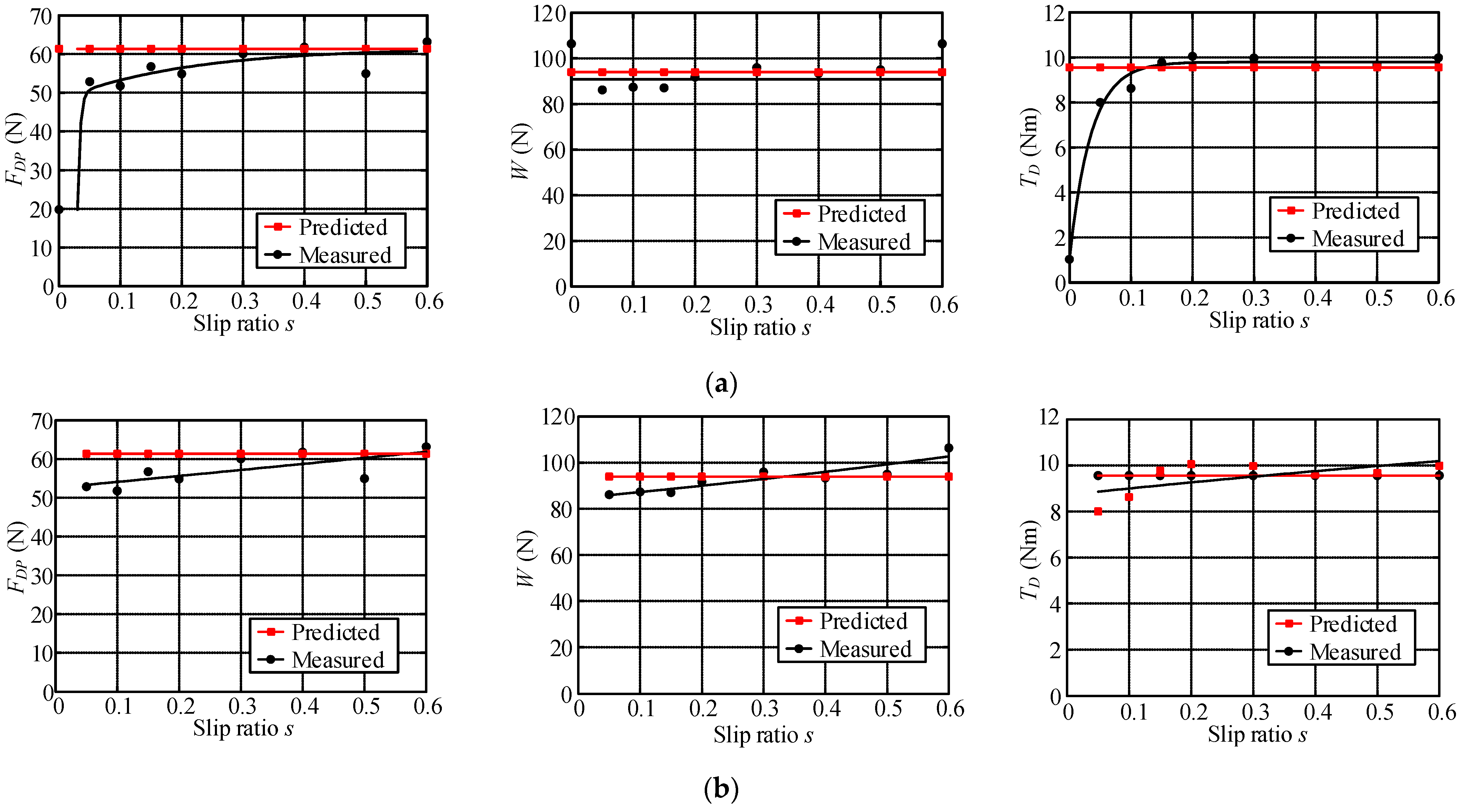
6.3.4. Analysis of Parameter Identification Results of Hard Terrain
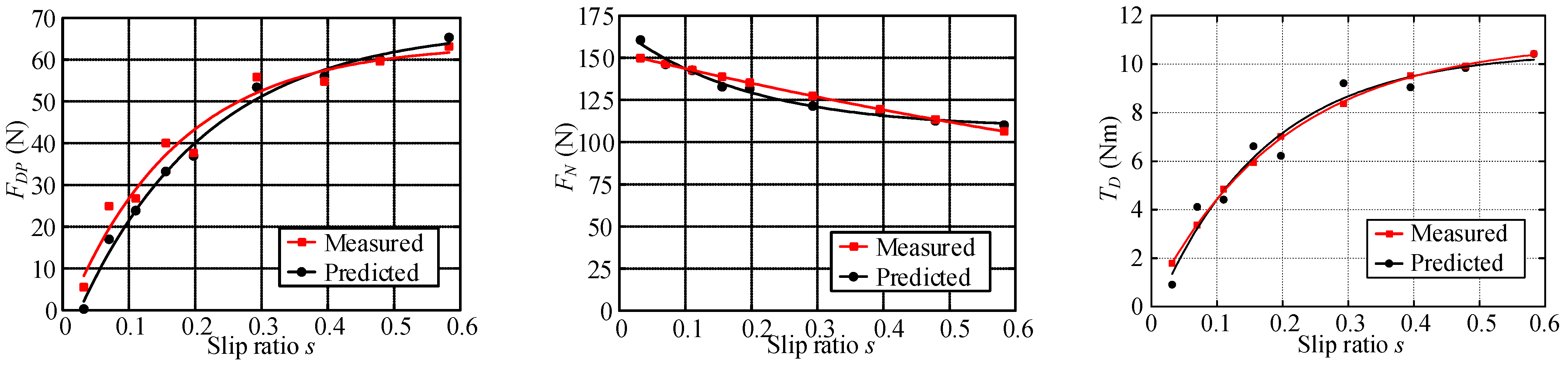
6.3.5. Analysis of Parameter Identification Results of Gravel Terrain
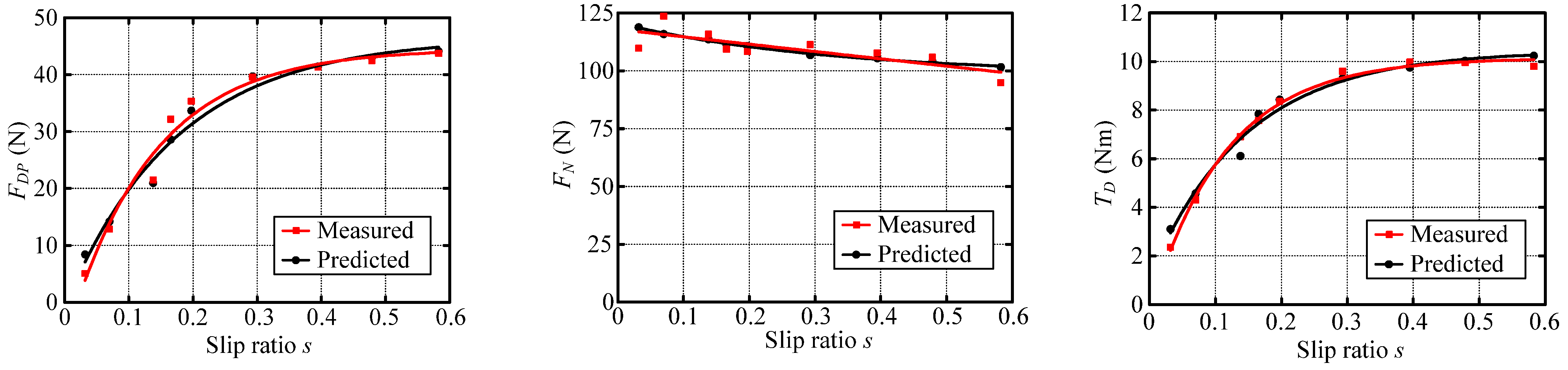
6.3.6. Analysis for Parameter Identification Results of Sandy Terrain
7. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ellery, A. Environment-robot interaction–the basis for mobility in planetary micro-rovers. Robot. Auton. Syst. 2005, 51, 29–39. [Google Scholar] [CrossRef]
- Banerjee, S.; Harrison, J.; Furlong, P.M.; Pavone, M. Adaptive meta-learning for identification of rover-terrain dynamics. arXiv 2020, arXiv:2009.10191. [Google Scholar]
- Ono, M.; Fuchs, T.J.; Steffy, A.; Maimone, M.; Yen, J. Risk-aware planetary rover operation: Autonomous terrain classification and path planning. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Otsu, K.; Ono, M.; Fuchs, T.J.; Baldwin, I.; Kubota, T. Autonomous terrain classification with co- and self-Training approach. IEEE Robot. Autom. Lett. 2016, 1, 814–819. [Google Scholar] [CrossRef]
- Lu, L.; Ordonez, C.; Collins, E.G.J.; Coyle, E.J.; Palejiya, D. Terrain surface classification with a control mode update rule using a 2D laser, stripe-based structured light sensor. Robot. Auton. Syst. 2011, 59, 954–965. [Google Scholar] [CrossRef]
- Huang, G.; Yang, L.; Cai, Y.; Zhang, D.P. Terrain classification-based rover traverse planner with kinematic constraints for Mars exploration. Planet. Space Sci. 2021, 209, 105371. [Google Scholar] [CrossRef]
- Guo, J.L.; Zhang, X.Y.; Dong, Y.P.; Huang, B. Terrain classification using mars raw images based on deep learning algorithms with application to wheeled planetary rovers. J. Terramechanics 2023, 108, 33–38. [Google Scholar] [CrossRef]
- Halatci, I.; Brooks, C.A.; Iagnemma, K. A study of visual and tactile terrain classification and classifier fusion for planetary exploration rovers. Robotica 2008, 26, 767–779. [Google Scholar] [CrossRef]
- Brooks, C.A.; Iagnemma, K. Vibration-based terrain classification for planetary exploration rovers. IEEE Trans. Robot. 2005, 21, 1185–1191. [Google Scholar] [CrossRef]
- Brooks, C.A.; Iagnemma, K. Self-supervised terrain classification for planetary surface exploration rovers. J. Field Robot. 2012, 29, 445–468. [Google Scholar] [CrossRef]
- Vicente, A.; Liu, J.; Yang, G.Z. Surface classification based on vibration on omni-wheel mobile base. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015. [Google Scholar]
- Bai, C.C.; Guo, J.F.; Guo, L.L.; Song, J.L. Deep multi-layer perception based terrain classification for planetary exploration rover. Sensors 2019, 19, 3102. [Google Scholar] [CrossRef] [PubMed]
- Ugenti, A.; Vulpi, F.; Domínguez, R.; Cordes, F.; Milella, A.; Reina, G. On the role of feature and signal selection for terrain learning in planetary exploration robots. J. Field Robot. 2022, 39, 355–370. [Google Scholar] [CrossRef]
- DuPont, E.M.; Moore, C.A.; Roberts, R.G. Terrain classification for mobile robots traveling at various speeds: An eigenspace manifold approach. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008. [Google Scholar]
- Iagnemma, K.; Dubowsky, S. Mobile robot rough-terrain control (RTC) for planetary exploration. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Baltimore, MD, USA, 10–13 September 2000. [Google Scholar]
- Iagnemma, K.; Kang, S.; Shibly, H.; Dubowsky, S. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers. IEEE Trans. Robot. 2004, 20, 921–927. [Google Scholar] [CrossRef]
- Hutangkabodee, S.; Zweiri, Y.H.; Seneviratne, L.D.; Althoefer, K. Soil parameter identification for wheel-soil interaction dynamics and traversability prediction. Int. J. Autom. Comput. 2006, 3, 244–251. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, R.; Yuan, Y.; Yang, H.; Li, J.; Yu, T.; Liu, C.; Wang, J.; Li, S.; Gao, H.; et al. A 2-year locomotive exploration and scientific investigation of the lunar farside by the Yutu-2 rover. Sci. Robot. 2022, 7, eabj6660. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.G.; Ding, L.; Gao, H.B.; Wang, Z.Y.; Lan, Q.N.; Liu, G.J.; Liu, Z.; Li, W.H.; Deng, Z.Q. High-fidelity dynamic modeling and simulation of planetary rovers using single-input-multi-output joints with terrain property map. IEEE Trans. Robot. 2022, 38, 3238–3258. [Google Scholar] [CrossRef]
- Zhou, C. Design and Characteristic Simulation of Automotive Shock Absorbers; Machinery Industry Press: Beijing, China, 2012. [Google Scholar]
- Brooks, C.A.; Iagnemma, K.; Dubowsky, S. Visual wheel sinkage measurement for planetary rover mobility characterization. Auton. Robot. 2006, 21, 55–64. [Google Scholar] [CrossRef]
- Gao, H.B.; Lv, F.T.; Yuan, B.F.; Li, N.; Ding, L.; Li, N.X.; Liu, G.J.; Deng, Z.Q. Sinkage definition and visual detection for planetary rovers wheels on rough terrain based on wheel–soil interaction boundary. Robot. Auton. Syst. 2017, 98, 222–240. [Google Scholar] [CrossRef]
- Lv, F.T.; Gao, H.B.; Li, N.; Ding, L.; Deng, Z.Q.; Liu, G.J. Monocular vision-based estimation of wheel slip ratio for planetary rovers in soft terrain. J. Mech. Eng. 2020, 56, 77–85. [Google Scholar]
- Hutangkabodee, S.; Zweiri, Y.H.; Seneviratne, L.D.; Althoefer, K. Performance prediction of a wheeled vehicle on unknown terrain using identified soil parameters. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]











| Terrain Class | WTIC |
|---|---|
| T1 | all lugs contacting terrain surface (ALCT) |
| T2 | some lugs contacting terrain surface (SLCT) |
| T3 | lugs entering into soil (LEIS) |
| Vibration Features | WTIC | ||
|---|---|---|---|
| ALCT | SLCT | LEIS | |
| p1 = lg(κf) | M | S | M |
| p2 = lg(κA) | M | B | S |
| p3 = lg(κmv) | MB | VB | MB |
| p4 = lg(κms) | M | VB | S |
| Feature vector {p1, p2, p3, p4} | {M, M, MB, M} | {S, B, VB, VB} | {M, S, MB, S} |
| Actual WTIC | Recognized WTIC | |||
|---|---|---|---|---|
| ALCT | SLCT | LEIS | UWTIC | |
| ALCT (wheel–HT interaction) | 58 | 0 | 0 | 2 |
| SLCT (wheel–GT/HGT interaction) | 0 | 118 | 0 | 2 |
| LEIS (wheel–ST/SGT interaction) | 0 | 0 | 116 | 4 |
| WTIC | Terrain Parameters | |
|---|---|---|
| Soil Cohesion c | Shearing Deformation Modulus K | |
| ALCT | 0 | 0 |
| SLCT | 0 | Without setting value |
| LEIS | Without setting value | Without setting value |
| Actual WTIC | Recognized WTIC | |||
|---|---|---|---|---|
| ALCT | SLCT | LEIS | UWTIC | |
| ALCT (wheel–HT interaction) | 133 | 0 | 0 | 11 |
| SLCT (wheel–GT/HGT interaction) | 0 | 134 | 0 | 10 |
| LEIS (wheel–ST/SGT interaction) | 0 | 0 | 144 | 0 |
| Terrain | c1 | c2 | Ks (KPa/mN) | n0 | n1 | c (KPa) | φ (°) | K (mm) |
|---|---|---|---|---|---|---|---|---|
| T1 (HT) | 0.8069 | 0 | 3.9999 × 105 | 0.6104 | 0.000 | 0 | 33.34 | 0 |
| T2 (GT) | 0 | 0 | 4.0053 × 105 | 0.5680 | 0.054 | 0 | 32.17 | 0.6 |
| T3 (ST) | 0.4424 | −0.6379 | 2.4904 × 103 | 0.8169 | 1.296 | 308.6 | 29.67 | 6.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, F.; Li, N.; Gao, H.; Ding, L.; Deng, Z.; Yu, H.; Liu, Z. Vibration-Based Recognition of Wheel–Terrain Interaction for Terramechanics Model Selection and Terrain Parameter Identification for Lugged-Wheel Planetary Rovers. Sensors 2023, 23, 9752. https://doi.org/10.3390/s23249752
Lv F, Li N, Gao H, Ding L, Deng Z, Yu H, Liu Z. Vibration-Based Recognition of Wheel–Terrain Interaction for Terramechanics Model Selection and Terrain Parameter Identification for Lugged-Wheel Planetary Rovers. Sensors. 2023; 23(24):9752. https://doi.org/10.3390/s23249752
Chicago/Turabian StyleLv, Fengtian, Nan Li, Haibo Gao, Liang Ding, Zongquan Deng, Haitao Yu, and Zhen Liu. 2023. "Vibration-Based Recognition of Wheel–Terrain Interaction for Terramechanics Model Selection and Terrain Parameter Identification for Lugged-Wheel Planetary Rovers" Sensors 23, no. 24: 9752. https://doi.org/10.3390/s23249752
APA StyleLv, F., Li, N., Gao, H., Ding, L., Deng, Z., Yu, H., & Liu, Z. (2023). Vibration-Based Recognition of Wheel–Terrain Interaction for Terramechanics Model Selection and Terrain Parameter Identification for Lugged-Wheel Planetary Rovers. Sensors, 23(24), 9752. https://doi.org/10.3390/s23249752








