Differential Sensing with Replicated Plasmonic Gratings Interrogated in the Optical Switch Configuration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
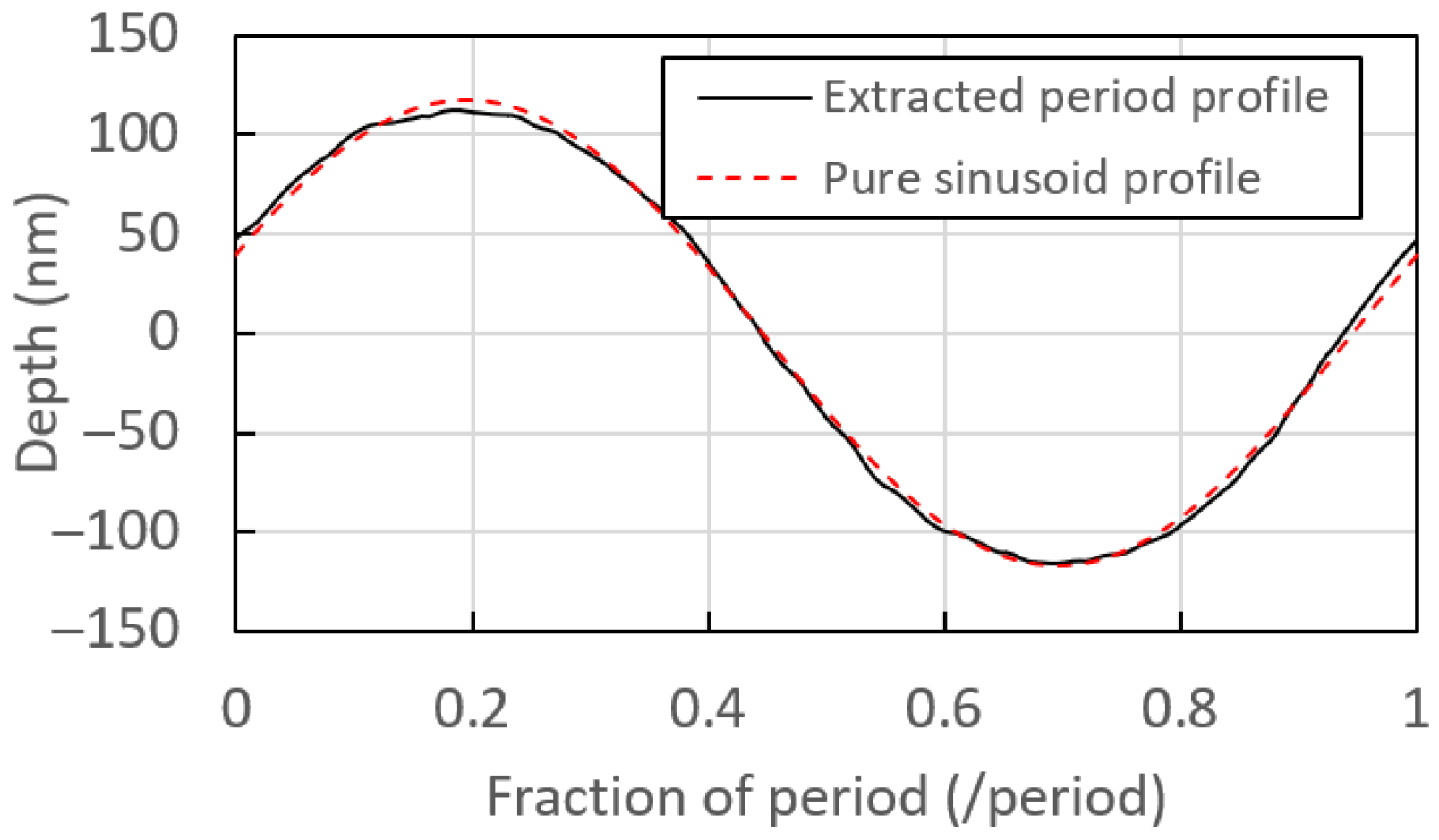
2.2. Production of Grating Masters
2.3. Production of Grating Replicas
2.4. Deposition of Thin Metal Layers
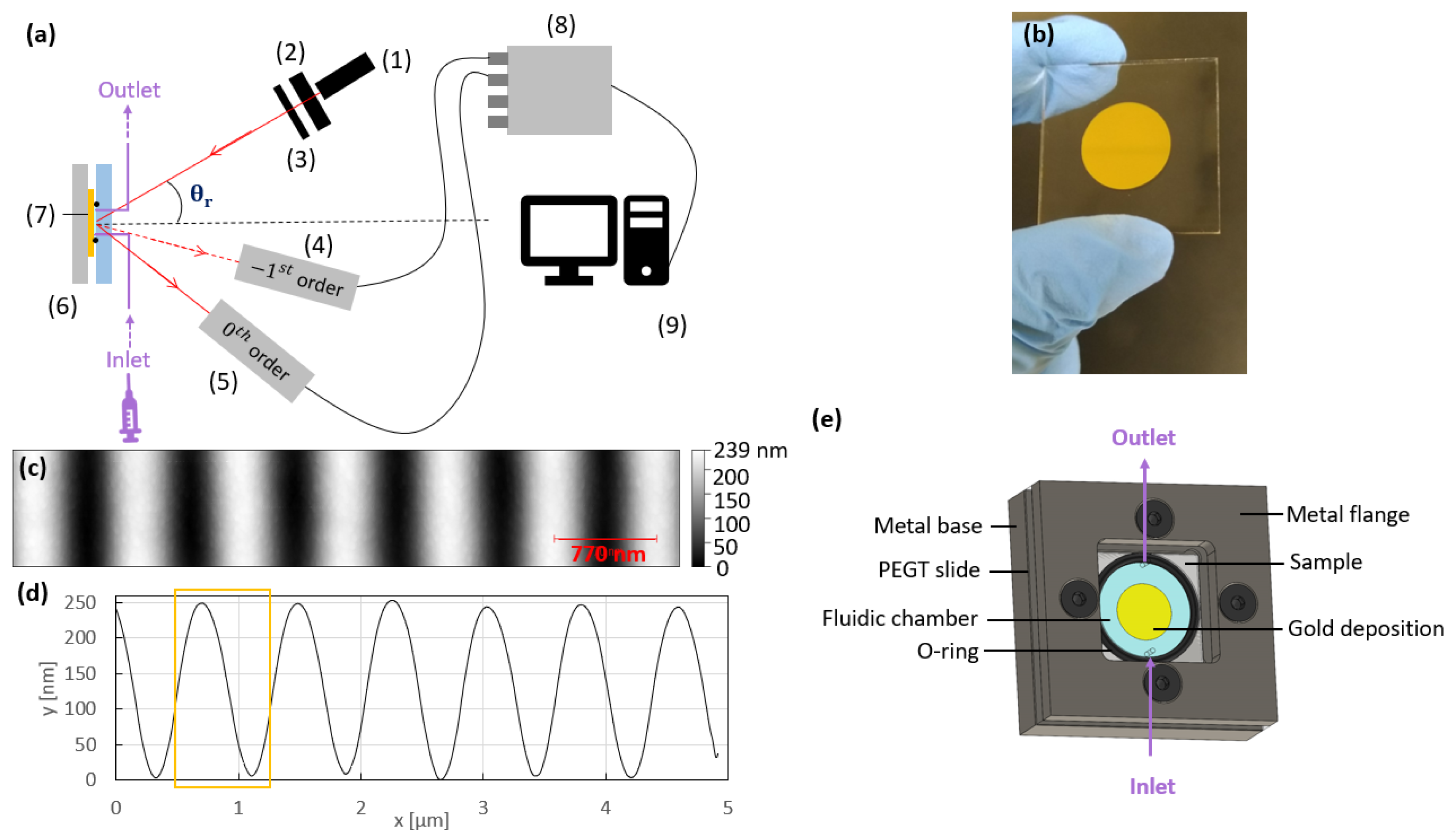
2.5. Sensing Platform
2.6. Interrogation Setup
2.7. Solution Preparation
3. Results and Discussion
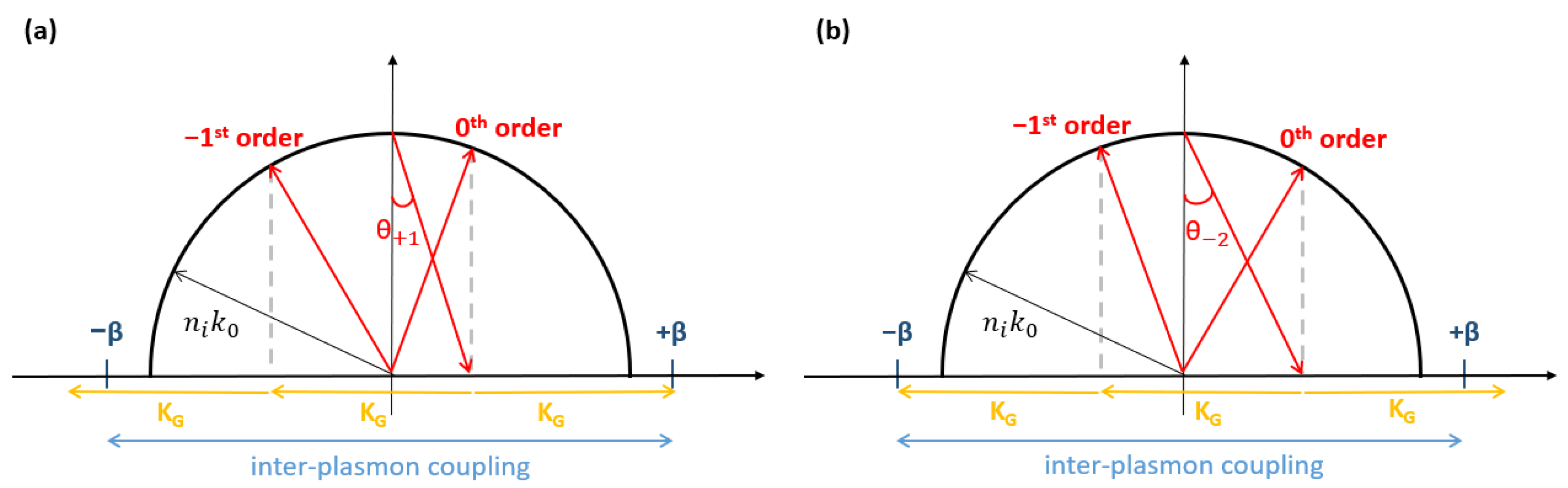
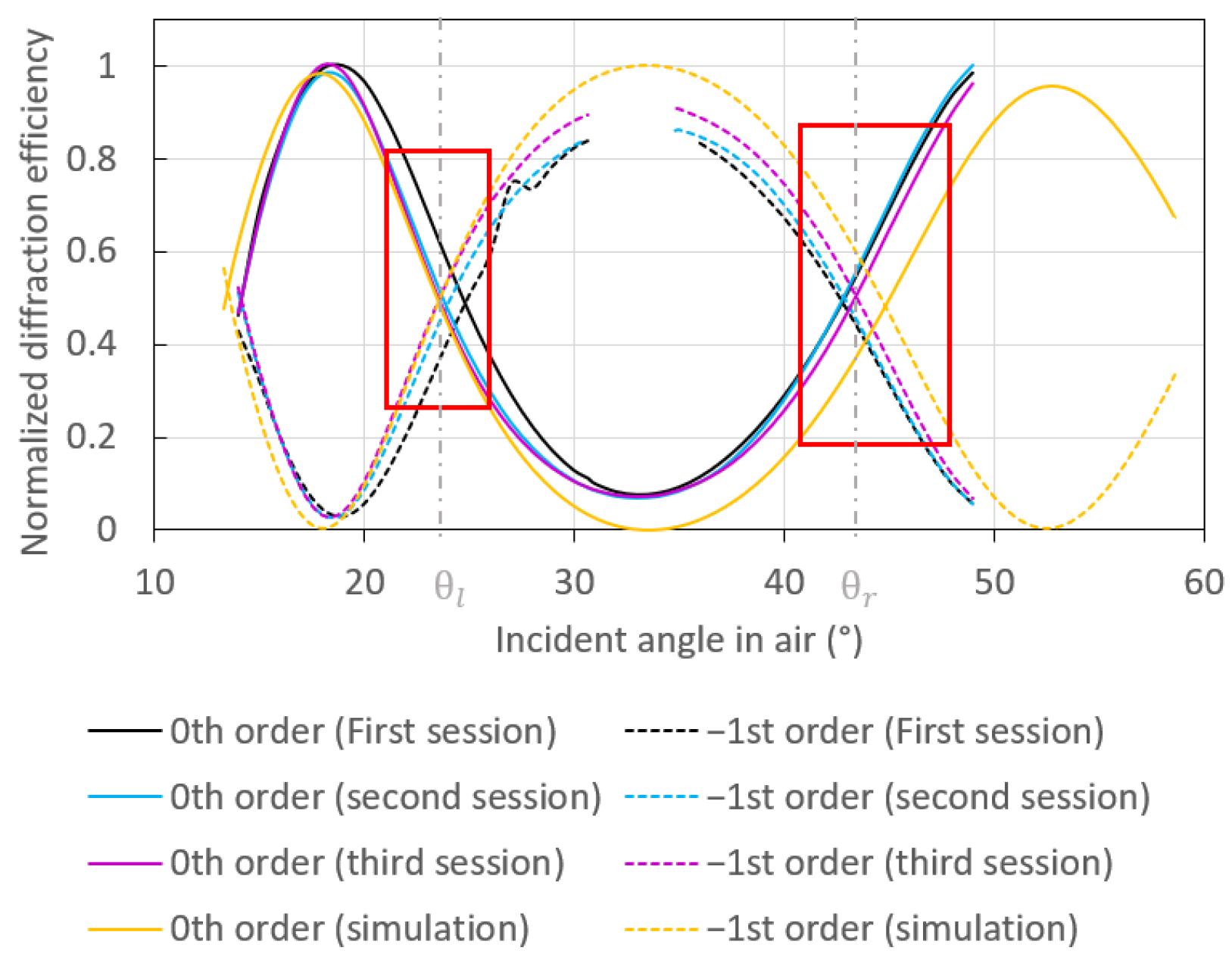
3.1. Theoretical and Experimental Switch Patterns
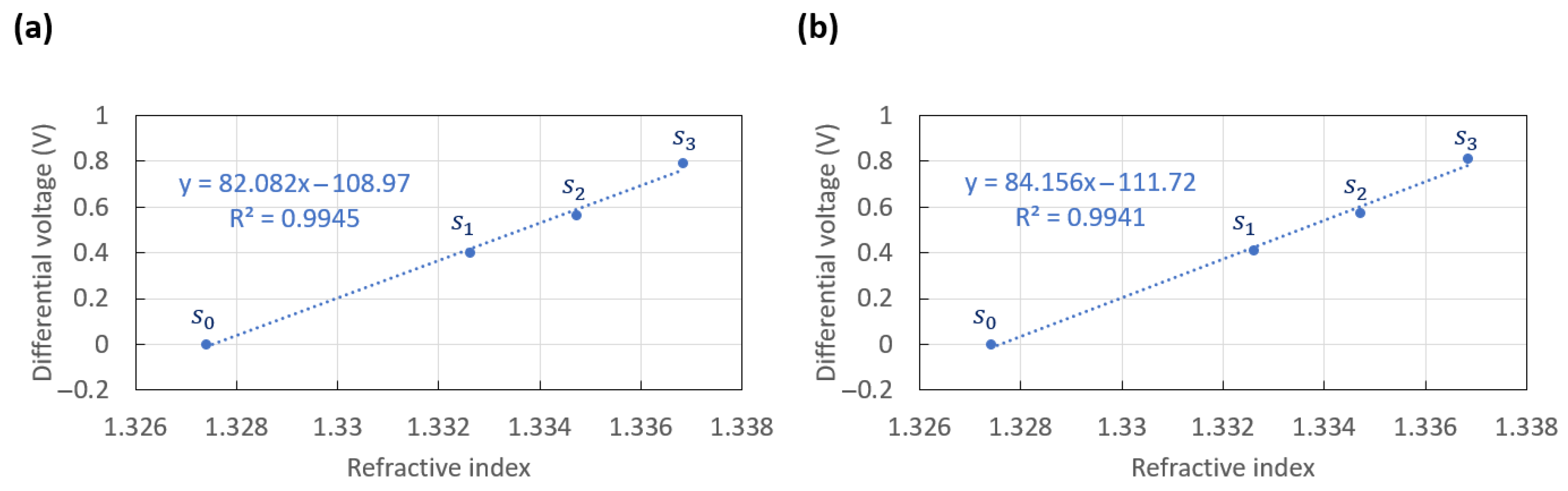
3.2. Sensitivity
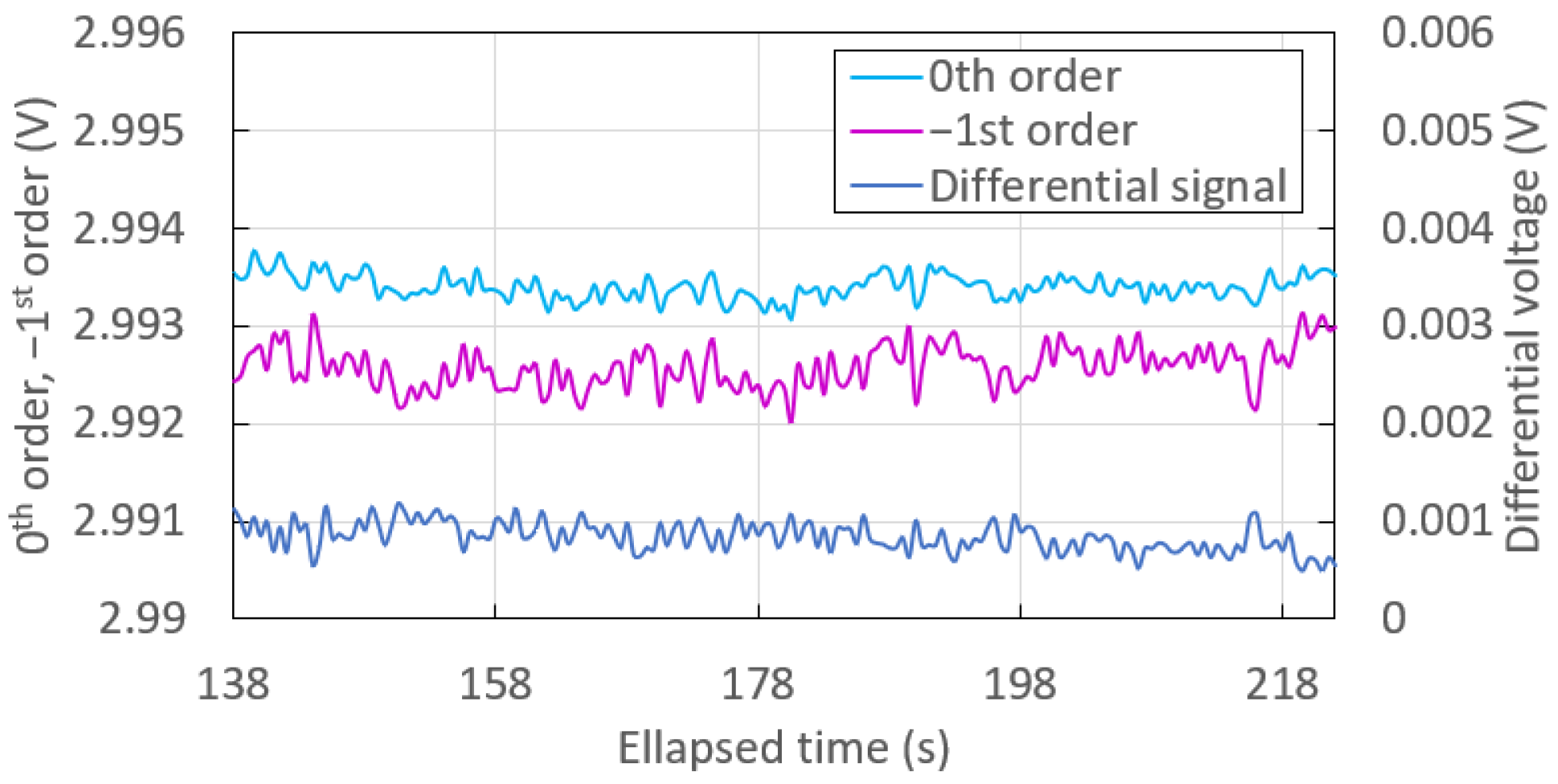
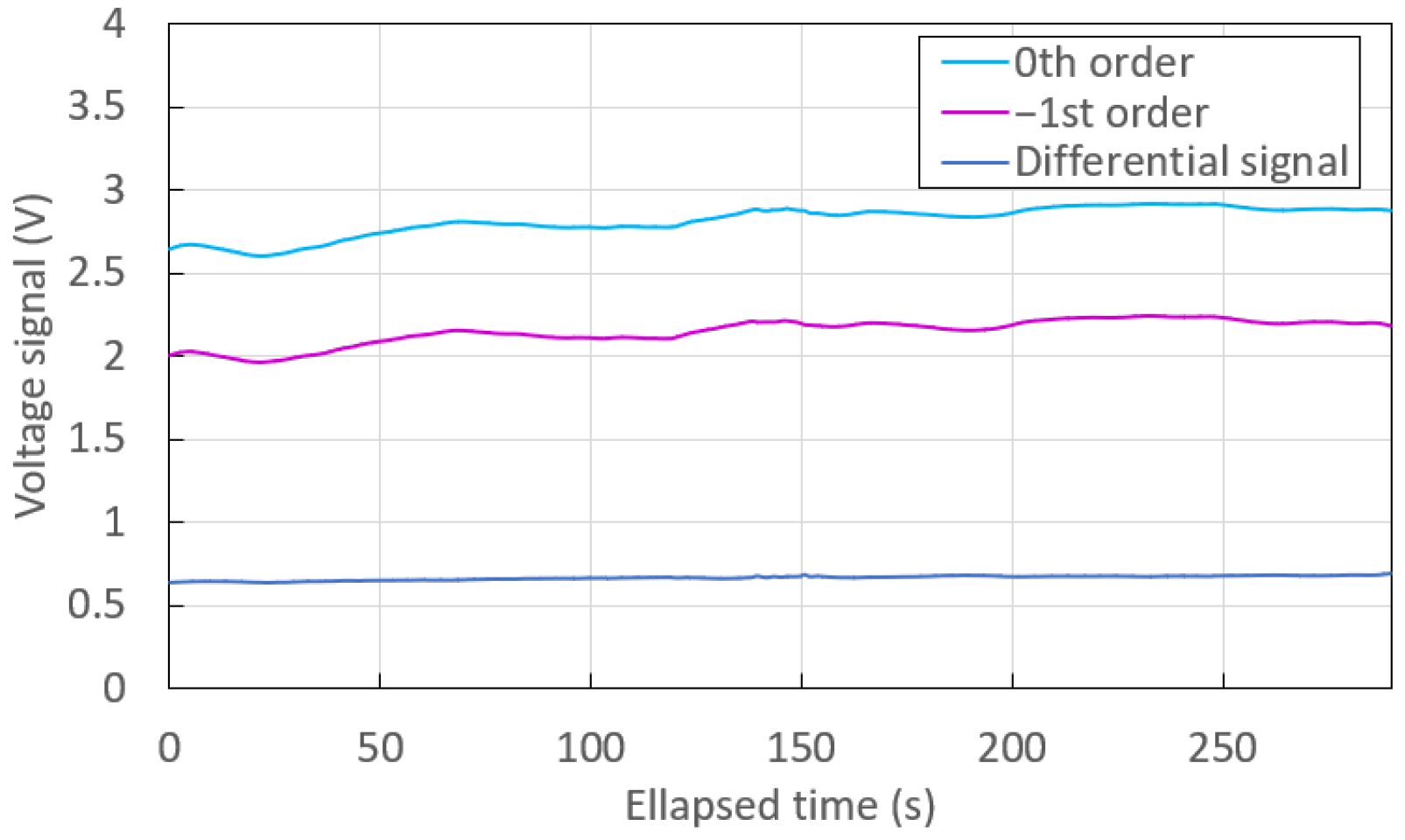
3.3. Noise and Differential Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Mattioli, I.A.; Hassan, A.; Oliveira, O.N., Jr.; Crespilho, F.N. On the challenges for the diagnosis of SARS-CoV-2 based on a review of current methodologies. ACS Sens. 2020, 5, 3655–3677. [Google Scholar] [CrossRef] [PubMed]
- Das, C.M.; Guo, Y.; Kang, L.; Ho, H.P.; Yong, K.T. Investigation of plasmonic detection of human respiratory virus. Adv. Theory Simul. 2020, 3, 2000074. [Google Scholar] [CrossRef] [PubMed]
- Dutta, P.; Su, T.Y.; Fu, A.Y.; Chang, M.C.; Guo, Y.J.; Tsai, I.J.; Wei, P.K.; Chang, Y.S.; Lin, C.Y.; Fan, Y.J. Combining portable solar-powered centrifuge to nanoplasmonic sensing chip with smartphone reader for rheumatoid arthritis detection. Chem. Eng. J. 2022, 434, 133864. [Google Scholar] [CrossRef]
- Kuo, C.W.; Wang, S.H.; Lo, S.C.; Yong, W.H.; Ho, Y.L.; Delaunay, J.J.; Tsai, W.S.; Wei, P.K. Sensitive Oligonucleotide Detection Using Resonant Coupling between Fano Resonance and Image Dipoles of Gold Nanoparticles. ACS Appl. Mater. Interfaces 2022, 14, 14012–14024. [Google Scholar] [CrossRef]
- Li, Z.; Leustean, L.; Inci, F.; Zheng, M.; Demirci, U.; Wang, S. Plasmonic-based platforms for diagnosis of infectious diseases at the point-of-care. Biotechnol. Adv. 2019, 37, 107440. [Google Scholar] [CrossRef]
- Sjahrurachman, A.; Dewi, B.E.; Lischer, K.; Pratami, D.K.; Flamandita, D.; Sahlan, M. Surface plasmon resonance analysis for detecting non-structural protein 1 of dengue virus in Indonesia. Saudi J. Biol. Sci. 2020, 27, 1931–1937. [Google Scholar]
- Wu, Y.; Zeng, X.; Gan, Q. A Compact Surface Plasmon Resonance Biosensor for Sensitive Detection of Exosomal Proteins for Cancer Diagnosis. In Biomedical Engineering Technologies; Springer: Berlin/Heidelberg, Germany, 2022; pp. 3–14. [Google Scholar]
- Nor, S.N.S.; Rasanang, N.S.; Karman, S.; Zaman, W.S.W.K.; Harun, S.W.; Arof, H. A Review: Surface Plasmon Resonance-Based Biosensor for Early Screening of SARS-CoV2 Infection. IEEE Access 2021, 10, 1228–1244. [Google Scholar]
- Meneghello, A.; Sonato, A.; Ruffato, G.; Zacco, G.; Romanato, F. A novel high sensitive surface plasmon resonance Legionella pneumophila sensing platform. Sens. Actuators B Chem. 2017, 250, 351–355. [Google Scholar] [CrossRef]
- Nair, S.; Gomez-Cruz, J.; Manjarrez-Hernandez, Á.; Ascanio, G.; Sabat, R.G.; Escobedo, C. Selective uropathogenic E. coli detection using crossed surface-relief gratings. Sensors 2018, 18, 3634. [Google Scholar] [CrossRef] [Green Version]
- Wong, W.R.; Fan, H.; Adikan, F.R.M.; Berini, P. Multichannel long-range surface plasmon waveguides for parallel biosensing. J. Light. Technol. 2018, 36, 5536–5546. [Google Scholar] [CrossRef]
- Krupin, O.; Wong, W.R.; Adikan, F.R.M.; Berini, P. Detection of small molecules using long-range surface plasmon polariton waveguides. IEEE J. Sel. Top. Quantum Electron. 2016, 23, 103–112. [Google Scholar] [CrossRef]
- Saha, N.; Brunetti, G.; Kumar, A.; Armenise, M.N.; Ciminelli, C. Highly sensitive refractive index sensor based on polymer bragg grating: A case study on extracellular vesicles detection. Biosensors 2022, 12, 415. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, T.; Noureen, S.; Afsheen, S.; Khan, M.Y.; Ijaz, M. Rectangular and sinusoidal Au-grating as plasmonic sensor: A comparative study. Opt. Mater. 2020, 99, 109530. [Google Scholar] [CrossRef]
- Sadeghi, Z.; Shirkani, H. Highly sensitive mid-infrared SPR biosensor for a wide range of biomolecules and biological cells based on graphene-gold grating. Phys. E Low-Dimens. Syst. Nanostructures 2020, 119, 114005. [Google Scholar] [CrossRef]
- Dormeny, A.A.; Sohi, P.A.; Kahrizi, M. Design and simulation of a refractive index sensor based on SPR and LSPR using gold nanostructures. Results Phys. 2020, 16, 102869. [Google Scholar] [CrossRef]
- López-Muñoz, G.A.; Estevez, M.C.; Peláez-Gutierrez, E.C.; Homs-Corbera, A.; García-Hernandez, M.C.; Imbaud, J.I.; Lechuga, L.M. A label-free nanostructured plasmonic biosensor based on Blu-ray discs with integrated microfluidics for sensitive biodetection. Biosens. Bioelectron. 2017, 96, 260–267. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Murray, J.; Haverstick, J.; Tripp, R.A.; Zhao, Y. Silver nanotriangle array based LSPR sensor for rapid coronavirus detection. Sens. Actuators B Chem. 2022, 359, 131604. [Google Scholar] [CrossRef]
- Calandrini, E.; Giovannini, G.; Garoli, D. 3D nanoporous antennas as a platform for high sensitivity IR plasmonic sensing. Opt. Express 2019, 27, 25912–25919. [Google Scholar] [CrossRef] [Green Version]
- Prasad, A.; Choi, J.; Jia, Z.; Park, S.; Gartia, M.R. Nanohole array plasmonic biosensors: Emerging point-of-care applications. Biosens. Bioelectron. 2019, 130, 185–203. [Google Scholar] [CrossRef]
- Šípova, H.; Zhang, S.; Dudley, A.M.; Galas, D.; Wang, K.; Homola, J. Surface plasmon resonance biosensor for rapid label-free detection of microribonucleic acid at subfemtomole level. Anal. Chem. 2010, 82, 10110–10115. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Khan, I.; Zhang, Q.; Liu, X.; Dostalek, J.; Liedberg, B.; Wang, Y. Lipopolysaccharides detection on a grating-coupled surface plasmon resonance smartphone biosensor. Biosens. Bioelectron. 2018, 99, 312–317. [Google Scholar] [CrossRef] [PubMed]
- Tishchenko, A.V.; Parriaux, O. Coupled-Mode Analysis of the Low-Loss Plasmon-Triggered Switching Between the 0th and −1st Orders of a Metal Grating. IEEE Photonics J. 2015, 7, 4800909. [Google Scholar] [CrossRef]
- Parriaux, O. Guided-mode triggered switching between TE orders of a metal-based grating-waveguide. J. Eur. Opt. Soc. Rapid Publ. 2015, 10, 15040. [Google Scholar] [CrossRef] [Green Version]
- Sauvage-Vincent, J.; Jourlin, Y.; Petiton, V.; Tishchenko, A.; Verrier, I.; Parriaux, O. Low-loss plasmon-triggered switching between reflected free-space diffraction orders. Opt. Express 2014, 22, 13314–13321. [Google Scholar] [CrossRef]
- Parriaux, O.; Jourlin, Y. Lossless 0th and- 1st order switching by dual-excitation of grating waveguide mode. J. Opt. 2019, 21, 075603. [Google Scholar] [CrossRef]
- Lasagni, A.F. Laser interference patterning methods: Possibilities for high-throughput fabrication of periodic surface patterns. Adv. Opt. Technol. 2017, 6, 265–275. [Google Scholar] [CrossRef]
- Lyndin, N. MC Grating Software. Available online: https://mcgrating.com/ (accessed on 10 December 2022).
- Pan, S.P.; Liu, T.S.; Tasi, M.C.; Liou, H.C. Grating pitch measurement beyond the diffraction limit with modified laser diffractometry. Jpn. J. Appl. Phys. 2011, 50, 06GJ04. [Google Scholar] [CrossRef] [Green Version]
- Dostálek, J.; Homola, J.; Miler, M. Rich information format surface plasmon resonance biosensor based on array of diffraction gratings. Sens. Actuators B Chem. 2005, 107, 154–161. [Google Scholar] [CrossRef]
- Li, L.; Chandezon, J.; Granet, G.; Plumey, J.P. Rigorous and efficient grating-analysis method made easy for optical engineers. Appl. Opt. 1999, 38, 304–313. [Google Scholar] [CrossRef]
- Bruhier, H.; Verrier, I.; Gueye, T.; Varenne, C.; Ndiaye, A.; Parriaux, O.; Veillas, C.; Reynaud, S.; Brunet, J.; Jourlin, Y. Effect of roughness on surface plasmons propagation along deep and shallow metallic diffraction gratings. Opt. Lett. 2022, 47, 349–352. [Google Scholar] [CrossRef]
- Sarov, Y.; Sainov, S.; Kostic, I.; Sarova, V.; Mitkov, S. Automatic VIS-near IR laser refractometer. Rev. Sci. Instrum. 2004, 75, 3342–3344. [Google Scholar] [CrossRef]
- Krupin, O.; Asiri, H.; Wang, C.; Tait, R.N.; Berini, P. Biosensing using straight long-range surface plasmon waveguides. Opt. Express 2013, 21, 698–709. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.R.; Krupin, O.; Sekaran, S.D.; Mahamd Adikan, F.R.; Berini, P. Serological diagnosis of dengue infection in blood plasma using long-range surface plasmon waveguides. Anal. Chem. 2014, 86, 1735–1743. [Google Scholar] [CrossRef] [PubMed]

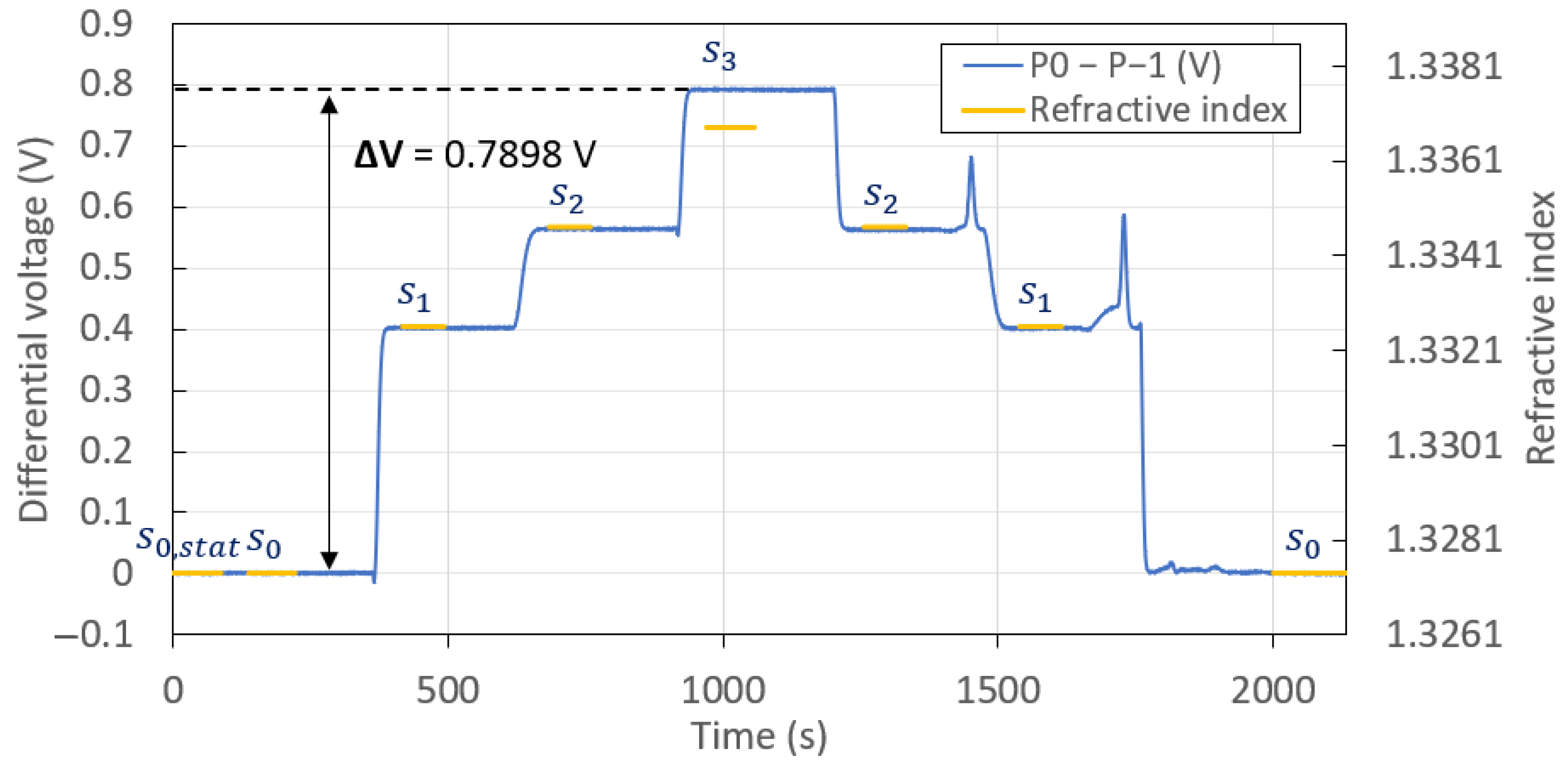
| Solution | RI ( = 1312 nm) | RI ( = 850 nm) | Mean (V) | Standard Deviation (mV) |
|---|---|---|---|---|
| 1.3211 | 1.3274 | 0.00062 | 0.18 | |
| 1.3211 | 1.3274 | 0.00083 | 0.15 | |
| 1.3265 | 1.3326 | 0.40162 | 0.14 | |
| 1.3283 | 1.3347 | 0.56299 | 0.11 | |
| 1.3311 | 1.3368 | 0.79070 | 0.14 | |
| 1.3283 | 1.3347 | 0.56193 | 0.14 | |
| 1.3265 | 1.3326 | 0.40099 | 0.24 | |
| 1.3211 | 1.3274 | 0.00037 | 0.39 |
| Solution | RI ( = 1312 nm) | RI ( = 850 nm) | Mean (V) | Standard Deviation (mV) |
|---|---|---|---|---|
| 1.3211 | 1.3274 | 0.00059 | 0.30 | |
| 1.3211 | 1.3274 | −0.00025 | 0.27 | |
| 1.3265 | 1.3326 | 0.40876 | 0.25 | |
| 1.3283 | 1.3347 | 0.57487 | 0.28 | |
| 1.3311 | 1.3368 | 0.81001 | 0.26 | |
| 1.3283 | 1.3347 | 0.57303 | 0.26 | |
| 1.3265 | 1.3326 | 0.40529 | 0.31 | |
| 1.3211 | 1.3274 | −0.00245 | 0.60 |
| Signal | Mean (V) | Standard Deviation (mV) |
|---|---|---|
| 0th order | 2.99340 | 0.13 |
| st order | 2.99257 | 0.22 |
| Differential | 0.00083 | 0.15 |
| Signal | Mean (V) | Standard Deviation (mV) |
|---|---|---|
| 0th order | 2.81716 | 88.09 |
| st order | 2.14836 | 75.60 |
| Differential | 0.66880 | 13.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laffont, E.; Crespo-Monteiro, N.; Valour, A.; Berini, P.; Jourlin, Y. Differential Sensing with Replicated Plasmonic Gratings Interrogated in the Optical Switch Configuration. Sensors 2023, 23, 1188. https://doi.org/10.3390/s23031188
Laffont E, Crespo-Monteiro N, Valour A, Berini P, Jourlin Y. Differential Sensing with Replicated Plasmonic Gratings Interrogated in the Optical Switch Configuration. Sensors. 2023; 23(3):1188. https://doi.org/10.3390/s23031188
Chicago/Turabian StyleLaffont, Emilie, Nicolas Crespo-Monteiro, Arnaud Valour, Pierre Berini, and Yves Jourlin. 2023. "Differential Sensing with Replicated Plasmonic Gratings Interrogated in the Optical Switch Configuration" Sensors 23, no. 3: 1188. https://doi.org/10.3390/s23031188






