Evaluation of Geometric Data Registration of Small Objects from Non-Invasive Techniques: Applicability to the HBIM Field
Abstract
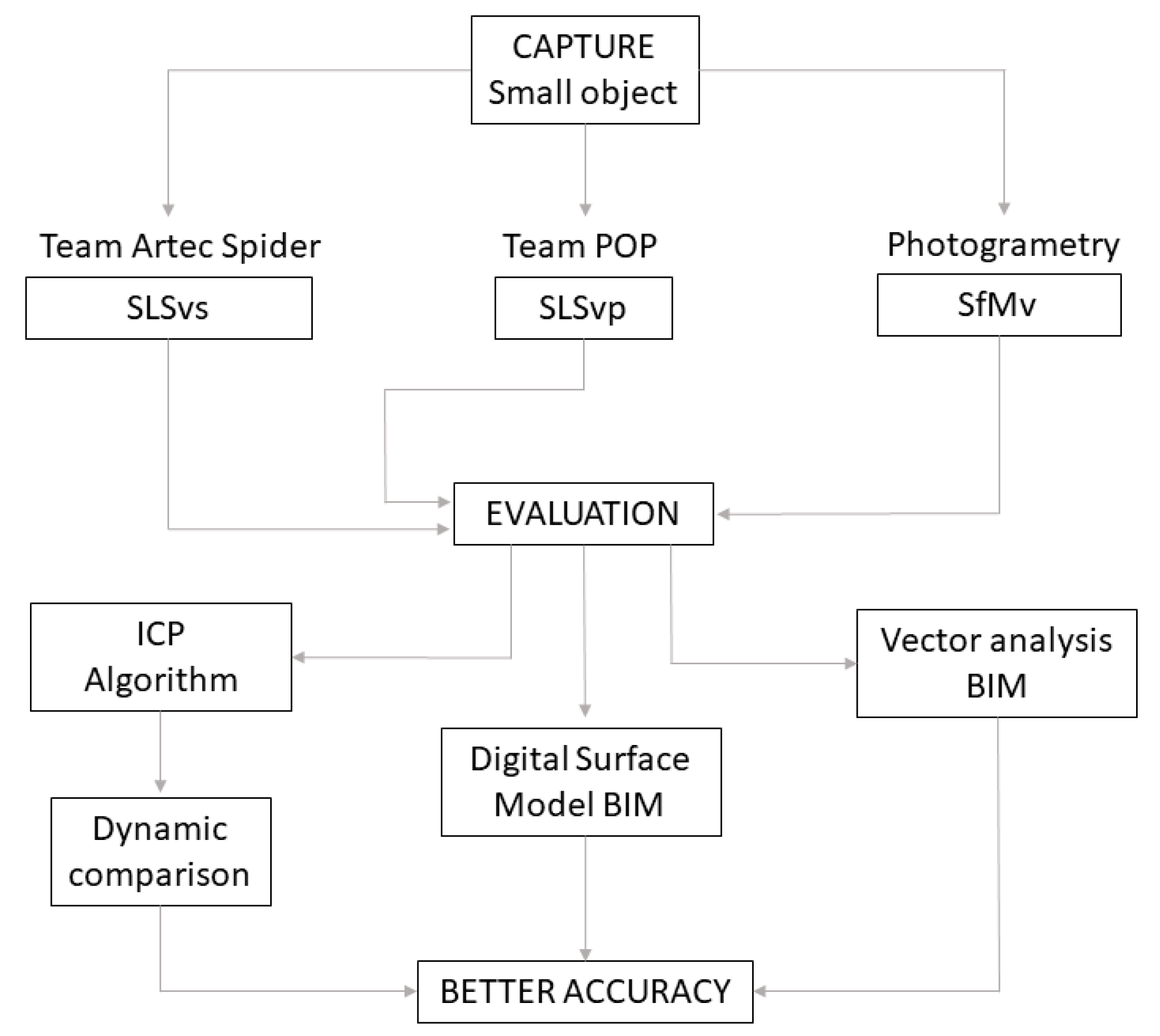
:1. Introduction
2. Case Study
3. Sensor Characteristics and Data Acquisition
3.1. Artec Spider
3.2. Revopoint POP 3D Scanner
3.3. Structure from Motion Survey
4. Experimental Study and Data Analysis
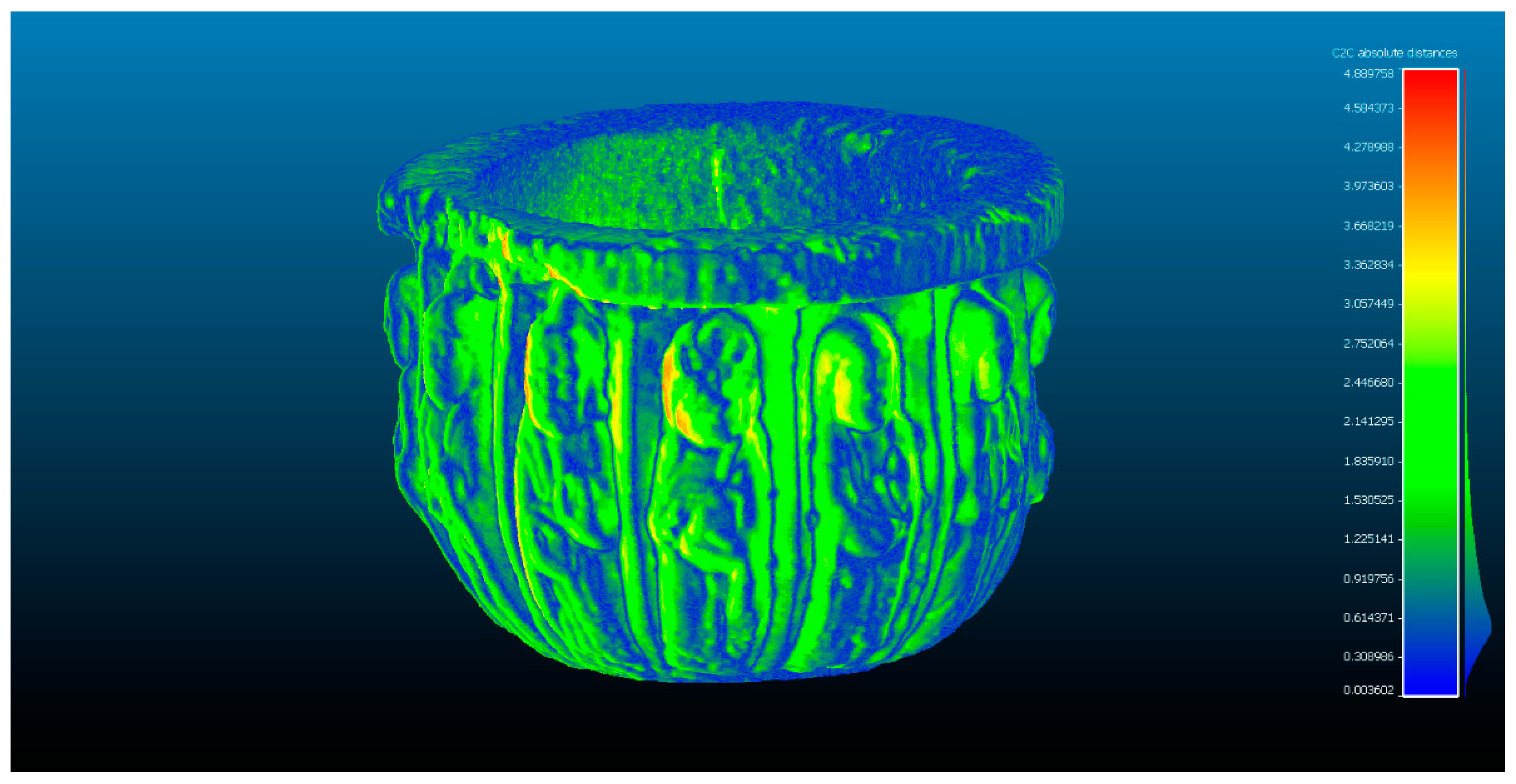
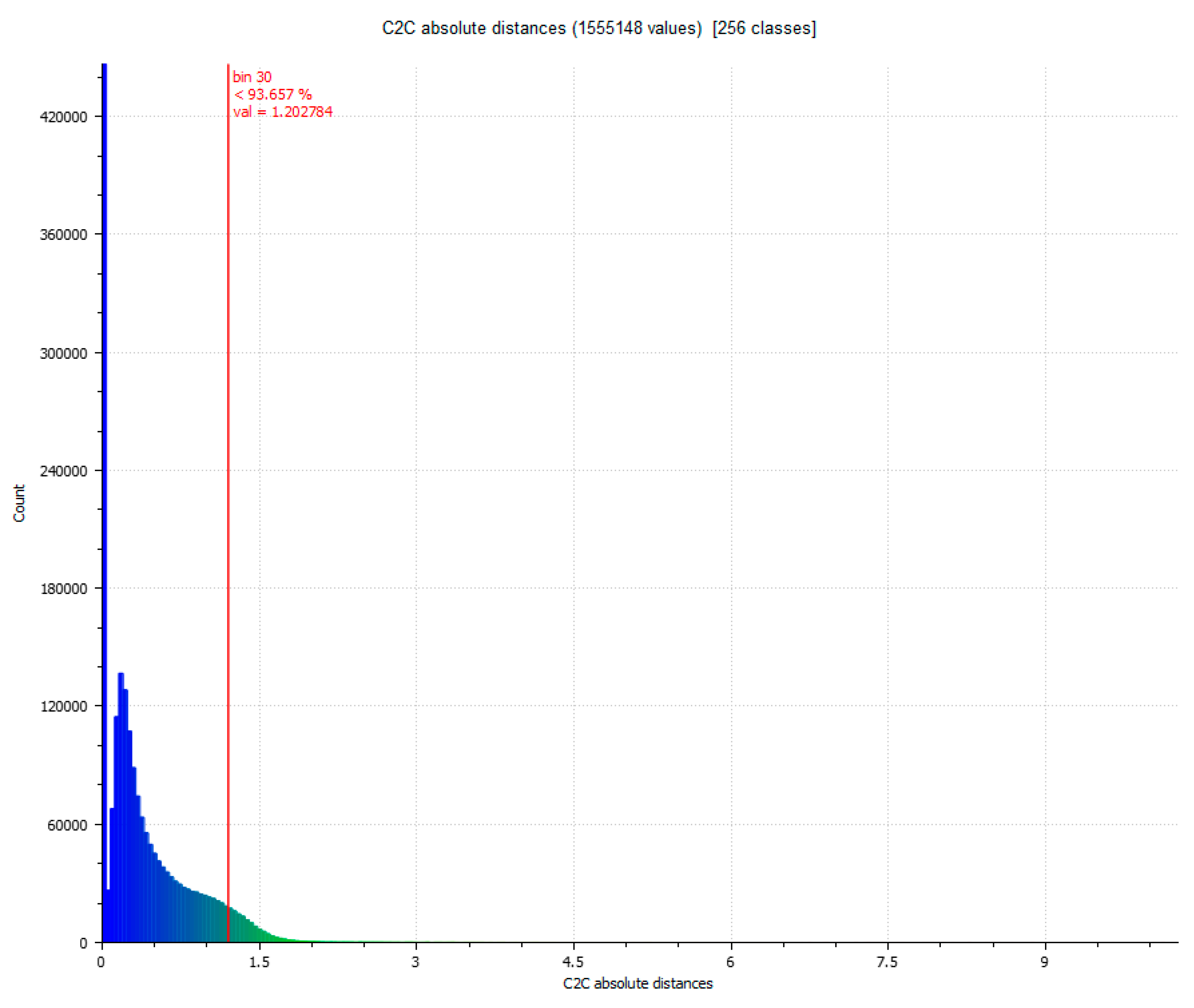
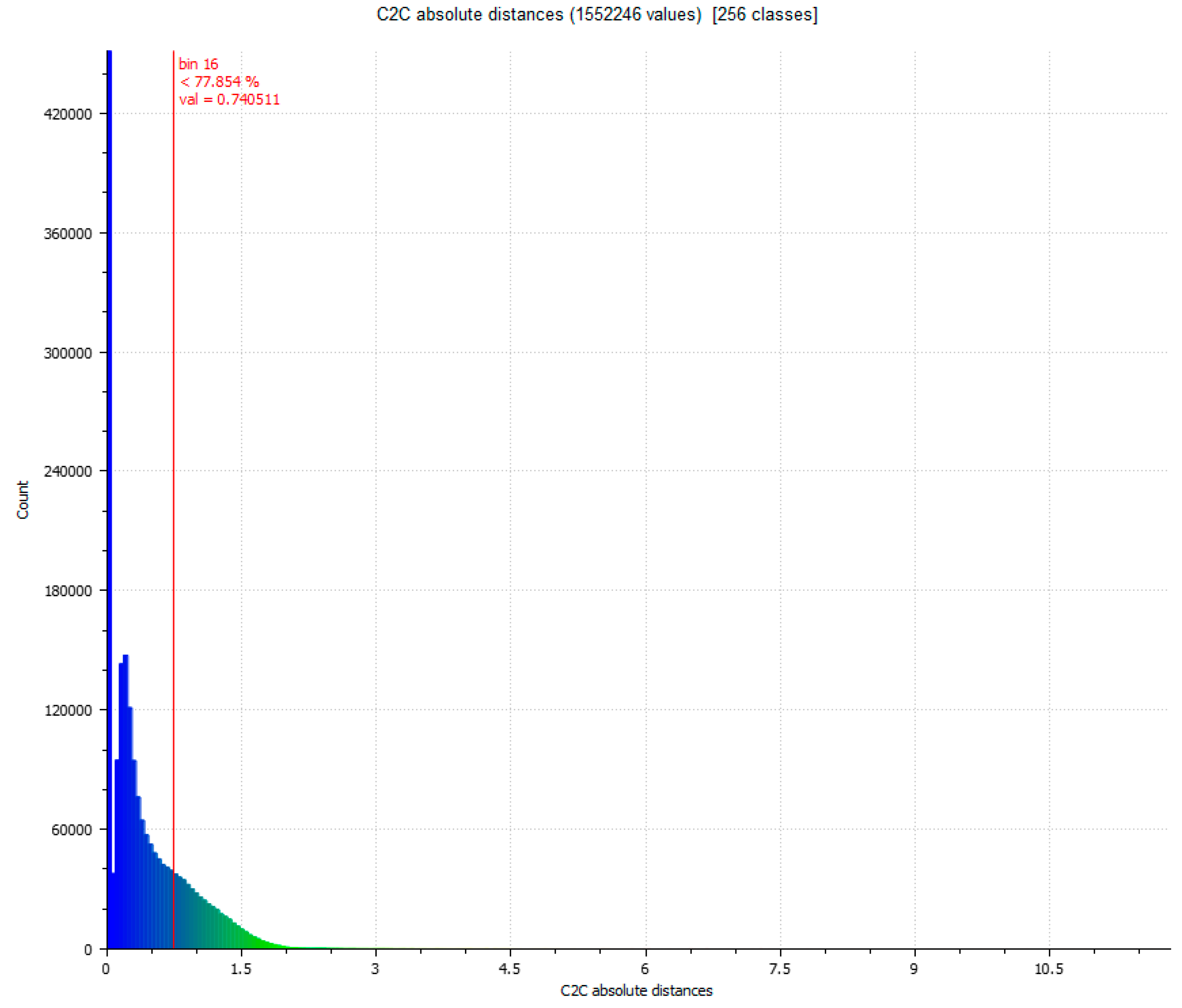
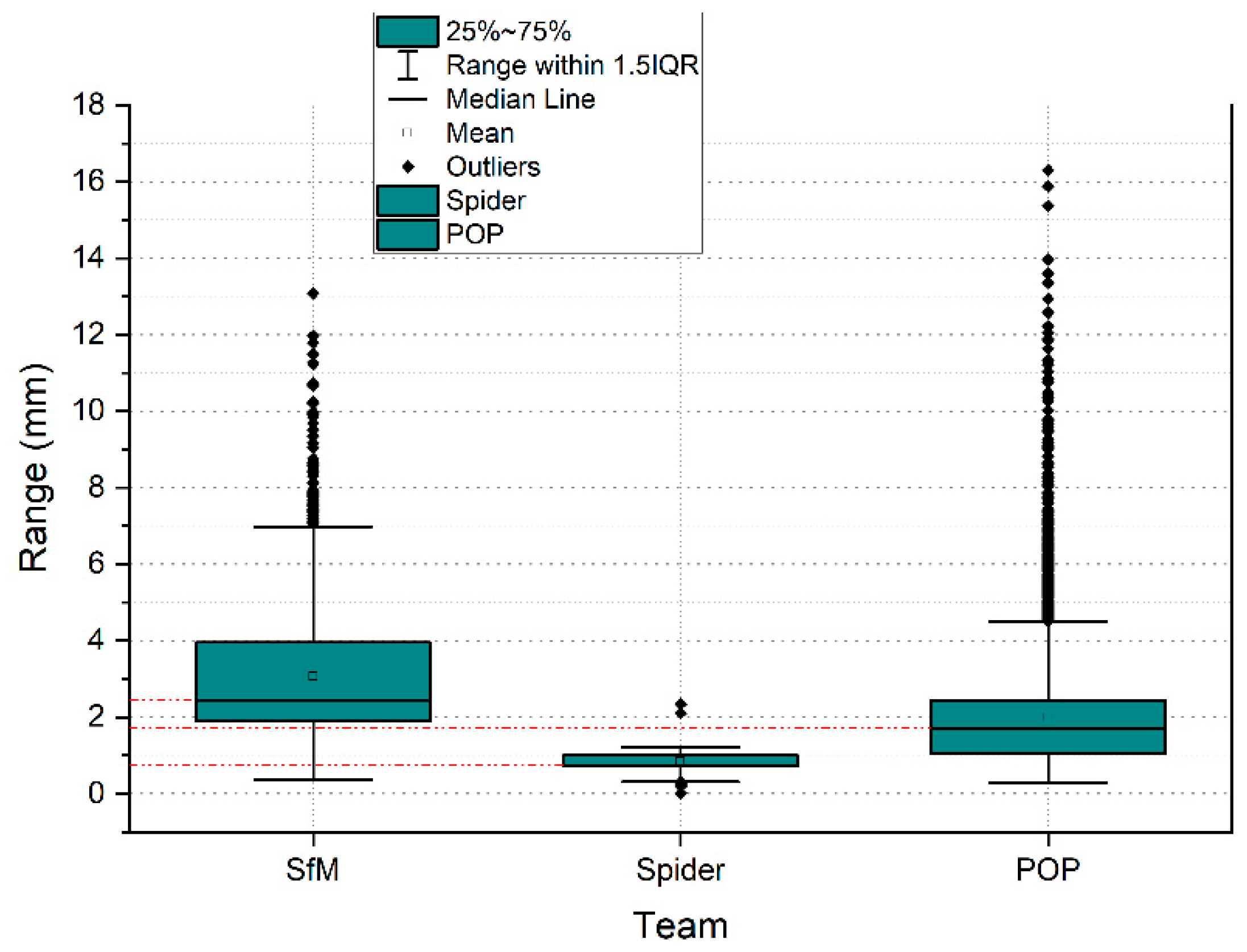
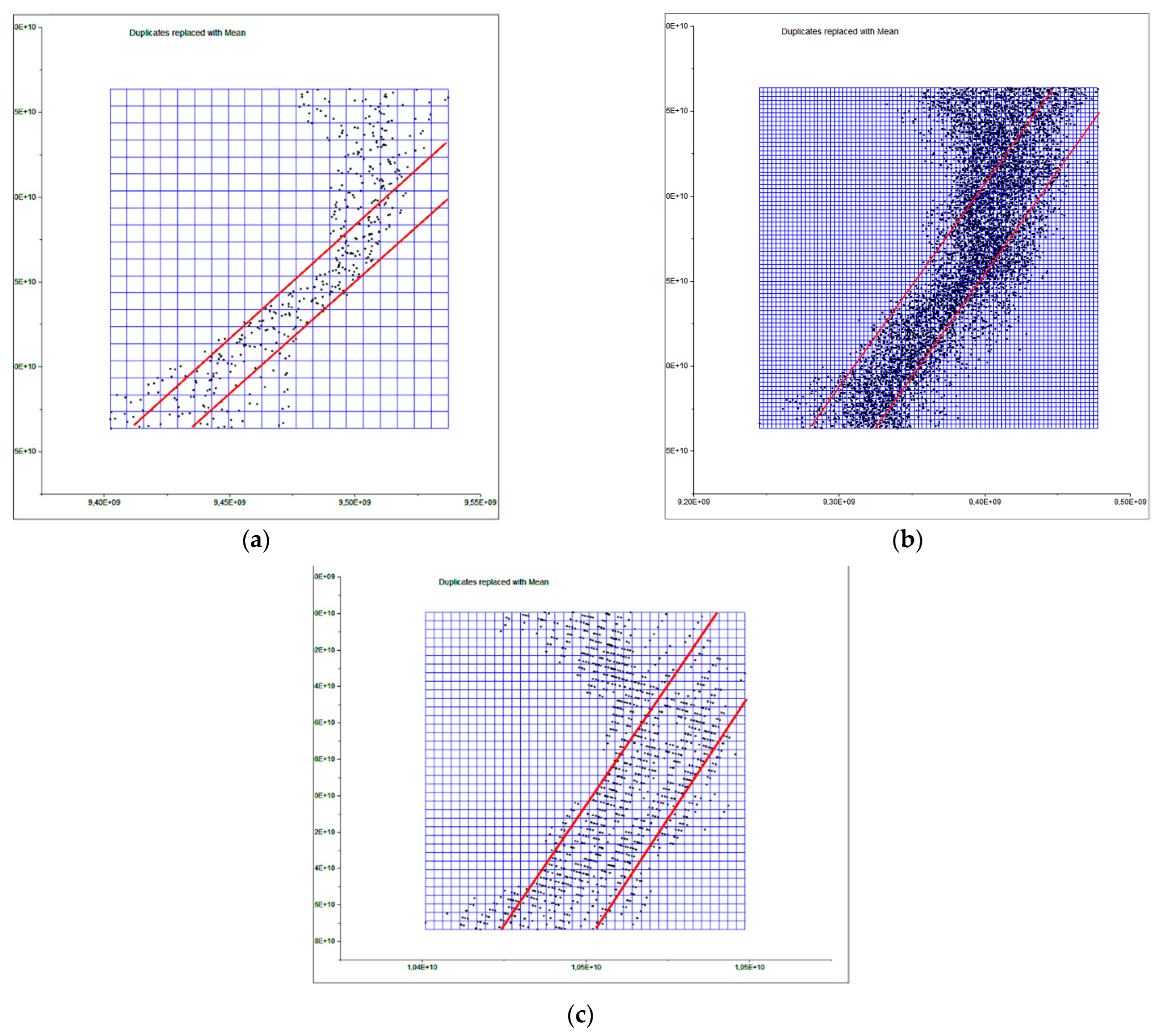
4.1. Point-Cloud Accuracy Using ICP Algorithm
4.2. Validation of the Accuracy of the Equipment through a New Case Study
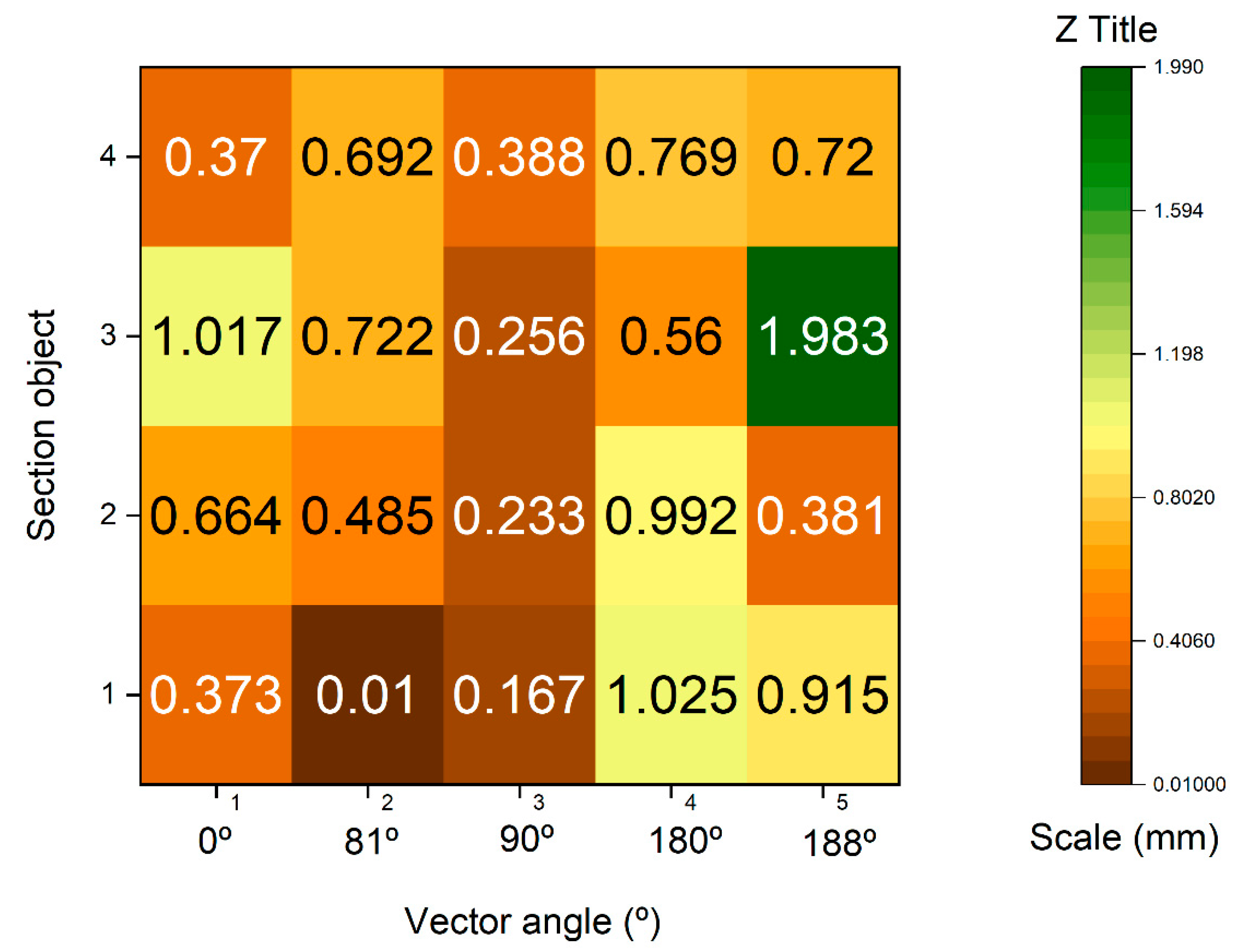
4.3. Spatial Resolution of the Point Cloud of the Systems Used
4.4. Accuracy Analysis between Point Clouds Using BIM Environment
4.5. Bring an Archeological Object to BIM
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vecco, M. A definition of cultural heritage: From the tangible to the intangible. J. Cult. Herit. 2010, 11, 321–324. [Google Scholar] [CrossRef]
- Maiorova, K.; Vorobiov, I.; Boiko, M.; Suponina, V.; Komisarov, O. Implementation of reengineering technology to ensure the predefined geometric accuracy of a light aircraft keel. East.-Eur. J. Enterp. Technol. 2021, 6, 6–12. [Google Scholar] [CrossRef]
- Marić, I.; Šiljeg, A.; Domazetović, F. Precision Assessment of Artec Space Spider 3D Handheld Scanner for Quantifying Tufa Formation Dynamics on Small Limestone Plates (PLs). In Proceedings of the 8th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2022), Athens, Greece, 27–29 April 2022; pp. 67–74. [Google Scholar]
- Vasiljević, I.; Obradović, R.; Ðurić, I.; Popkonstantinović, B.; Budak, I.; Kulić, L.; Milojević, Z. Copyright Protection of 3D Digitized Artistic Sculptures by Adding Unique Local Inconspicuous Errors by Sculptors. Appl. Sci. 2021, 11, 7481. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, W.; Mellado, N.; Grussenmeyer, P.; Li, R.; Chen, Y.; Wan, P.; Zhang, X.; Cai, S. Automated markerless registration of point clouds from TLS and structured light scanner for heritage documentation. J. Cult. Herit. 2019, 35, 16–24. [Google Scholar] [CrossRef]
- Guarnieri, A.; Vettore, A.; Camarda, M.; Domenica, C. Automatic registration of large range datasets with spin-images. J. Cult. Herit. 2011, 12, 476–484. [Google Scholar] [CrossRef]
- Moyano, J.; Nieto-Julián, J.E.; Bienvenido-Huertas, D.; Marín-García, D. Validation of Close-Range Photogrammetry for Architectural and Archaeological Heritage: Analysis of Point Density and 3d Mesh Geometry. Remote Sens. 2020, 12, 3571. [Google Scholar] [CrossRef]
- de la Plata, A.R.M.; Franco, P.A.C.; Franco, J.C.; Bravo, V.G. Protocol Development for Point Clouds, Triangulated Meshes and Parametric Model Acquisition and Integration in an HBIM Workflow for Change Control and Management in a UNESCO’s World Heritage Site. Sensors 2021, 21, 1083. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.-M. Structure-From-Motion Revisited. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Deja, M.; Dobrzyński, M.; Rymkiewicz, M. Application of reverse engineering technology in part design for shipbuilding industry. Pol. Marit. Res. 2019, 26, 126–133. [Google Scholar] [CrossRef]
- Kaleev, A.A.; Kashapov, L.N.; Kashapov, N.F.; Kashapov, R.N. Application of reverse engineering in the medical industry. IOP Conf. Ser. Mater. Sci. Eng. 2017, 240, 012030. [Google Scholar] [CrossRef]
- Redaelli, D.F.; Gonizzi Barsanti, S.; Fraschini, P.; Biffi, E.; Colombo, G.; Redaelli, D.F.; Gonizzi Barsanti, S.; Fraschini, P.; Biffi, E.; Colombo, G. Low-Cost 3d Devices and Laser Scanners Comparison for the Application in Orthopedic Centres. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 953–960. [Google Scholar] [CrossRef] [Green Version]
- Carfagni, M.; Furferi, R.; Governi, L.; Servi, M.; Uccheddu, F.; Volpe, Y.; Mcgreevy, K. Fast and Low Cost Acquisition and Reconstruction System for Human Hand-wrist-arm Anatomy. Procedia Manuf. 2017, 11, 1600–1608. [Google Scholar] [CrossRef]
- Hofmann, B.; Konopka, K.; Fischer, D.C.; Kundt, G.; Martin, H.; Mittlmeier, T. 3D optical scanning as an objective and reliable tool for volumetry of the foot and ankle region. Foot Ankle Surg. 2022, 28, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Achille, C.; Brumana, R.; Fassi, F.; Fregonese, L.; Monti, C.; Taffurelli, L.; Vio, E. Transportable 3D Acquisition Systems for Cultural Heritage. Reverse Engineering and Rapid Prototyping of the Bronze Lions of the Saint Isidoro Chapel in the Basilica of San Marco in Venice. In Proceedings of the IISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information, C.VI, WG VI/4, Sciences, Athens, Greece, 1–6 October 2007; pp. 1–6. [Google Scholar]
- McPherron, S.P.; Gernat, T.; Hublin, J.J. Structured light scanning for high-resolution documentation of in situ archaeological finds. J. Archaeol. Sci. 2009, 36, 19–24. [Google Scholar] [CrossRef]
- Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation. Sensors 2009, 9, 568–601. [Google Scholar] [CrossRef]
- Adamopoulos, E.; Volinia, M.; Girotto, M.; Rinaudo, F. Three-Dimensional Thermal Mapping from IRT Images for Rapid Architectural Heritage NDT. Buildings 2020, 10, 187. [Google Scholar] [CrossRef]
- Adamopoulos, E.; Patrucco, G.; Volinia, M.; Girotto, M.; Rinaudo, F.; Tonolo, F.G.; Spanò, A. 3D Thermal Mapping of Architectural Heritage: Up-To-Date Workflows for the Production of Three-Dimensional Thermographic Models for Built Heritage NDT. In Digital Heritage. Progress in Cultural Heritage: Documentation, Preservation, and Protection; Springer: Berlin/Heidelberg, Germany, 2021; Volume 12642 LNCS, pp. 26–37. [Google Scholar] [CrossRef]
- Ramm, R.; Heinze, M.; Kühmstedt, P.; Christoph, A.; Heist, S.; Notni, G. Portable solution for high-resolution 3D and color texture on-site digitization of cultural heritOkage objects. J. Cult. Herit. 2022, 53, 165–175. [Google Scholar] [CrossRef]
- Badillo, P.D.; Parfenov, V.A.; Kuleshov, D.S. 3D Scanning for Periodical Conservation State Monitoring of Oil Paintings. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering, ElConRus 2022, St. Petersburg, Russia, 25–28 January 2022; pp. 1098–1102. [Google Scholar] [CrossRef]
- Li, R.; Luo, T.; Zha, H. 3D Digitization and Its Applications in Cultural Heritage. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2010; Volume 6436 LNCS, pp. 381–388. [Google Scholar] [CrossRef]
- Reu, J.D.; Plets, G.; Verhoeven, G.; Smedt, P.D.; Bats, M.; Cherretté, B.; Maeyer, W.D.; Deconynck, J.; Herremans, D.; Laloo, P.; et al. Towards a three-dimensional cost-effective registration of the archaeological heritage. J. Archaeol. Sci. 2013, 40, 1108–1121. [Google Scholar] [CrossRef]
- Tsiafakis, D.; Tsirliganis, N.; Pavlidis, G.; Evangelidis, V.; Chamzas, C. Karabournaki-recording the past: The digitization of an archaeological site. In Proceedings of the International Conference on Electronic Imaging & the Visual Arts EVA 2004, Florence, Italy, 29 March–2 April 2004. [Google Scholar]
- Koutsoudis, A.; Chamzas, C. 3D pottery shape matching using depth map images. J. Cult. Herit. 2011, 12, 128–133. [Google Scholar] [CrossRef]
- Zapassky, E.; Finkelstein, I.; Benenson, I. Ancient standards of volume: Negevite Iron Age pottery (Israel) as a case study in 3D modeling. J. Archaeol. Sci. 2006, 33, 1734–1743. [Google Scholar] [CrossRef]
- Molero Alonso, B.; Barba, S.; Álvaro Tordesillas, A. Documentación del patrimonio cultural. Método basado en la fusión de técnicas fotogramétricas y de escaneado óptico de triangulación. EGA. Rev. De Expresión Gráfica Arquit. 2016, 21, 236. [Google Scholar] [CrossRef]
- Kersten, T.P.; Lindstaedt, M.; Starosta, D. Comparative Geometrical Accuracy Investigations of Hand-Held 3d Scanning Systems—AN Update. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 422, 487–494. [Google Scholar] [CrossRef]
- Lachat, E.; Macher, H.; Landes, T.; Grussenmeyer, P. Assessment and Calibration of a RGB-D Camera (Kinect v2 Sensor) Towards a Potential Use for Close-Range 3D Modeling. Remote Sens. 2015, 7, 13070–13097. [Google Scholar] [CrossRef]
- Liu, S.; Huang, W.L.; Gordon, C.; Armand, M. Automated Implant Resizing for Single-Stage Cranioplasty. IEEE Robot. Autom. Lett. 2021, 6, 6624–6631. [Google Scholar] [CrossRef] [PubMed]
- Morena, S.; Barba, S.; Álvaro-Tordesillas, A. Shining 3D EinScan-Pro, application and validation in the field of cultural heritage, from the Chillida-Leku museum to the archaeological museum of Sarno. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 135–142. [Google Scholar] [CrossRef]
- Paul Besl, N.J.; McKay, N.D.; Besi, P.J. Method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 1611, 586–606. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Zhang, H.; Wu, Y. Measuring the 3D shape of high temperature objects using blue sinusoidal structured light. Meas. Sci. Technol. 2015, 26, 125205. [Google Scholar] [CrossRef]
- Wang, P.; Jin, X.; Li, S.; Wang, C.; Zhao, H. Digital Modeling of Slope Micro-geomorphology Based on Artec Eva 3D Scanning Technology. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 052116. [Google Scholar] [CrossRef] [Green Version]
- Park, H.; Lee, D. Comparison between point cloud and mesh models using images from an unmanned aerial vehicle. Measurement 2019, 138, 461–466. [Google Scholar] [CrossRef]
- Bolognesi, C.; Garagnani, S. From a point cloud survey to a mass 3d modelling: Renaissance HBIM in Poggio a Caiano. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2018, XLII-2, 117–123. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer: London, UK, 2010. [Google Scholar]
- Girardeau-Montaut, D. CloudCompare Point Cloud Processing Workshop. Available online: www.cloudcompare.org@CloudCompareGPL (accessed on 28 January 2021).
- Jafari, B.M. Deflection Measurement through 3D Point Cloud Analysis; George Mason University: Fairfax, VA, USA, 2016. [Google Scholar]
- Fuad, N.A.; Yusoff, A.R.; Ismail, Z.; Majid, Z. Comparing the performance of point cloud registration methods for landslide monitoring using mobile laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-4/W9, 11–21. [Google Scholar] [CrossRef]
- Moyano, J.; Gil-Arizón, I.; Nieto-Julián, J.E.; Marín-García, D. Analysis and management of structural deformations through parametric models and HBIM workflow in architectural heritage. J. Build. Eng. 2021, 45, 103274. [Google Scholar] [CrossRef]
- Esposito, G.; Salvini, R.; Matano, F.; Sacchi, M.; Danzi, M.; Somma, R.; Troise, C. Multitemporal monitoring of a coastal landslide through SfM-derived point cloud comparison. Photogramm. Rec. 2017, 32, 459–479. [Google Scholar] [CrossRef]
- Jakovljevic, G.; Govedarica, M.; Alvarez-Taboada, F.; Pajic, V. Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping. Geosciences 2019, 9, 323. [Google Scholar] [CrossRef]
- Valkaniotis, S.; Papathanassiou, G.; Ganas, A. Mapping an earthquake-induced landslide based on UAV imagery; case study of the 2015 Okeanos landslide, Lefkada, Greece. Eng. Geol. 2018, 245, 141–152. [Google Scholar] [CrossRef]
- Sammartano, G.; Spanò, A.; Teppati Losè, L.; Sammartano, G.; Spanò, A.; Teppati Losè, L. A Fusion-Based Workflow for Turning Slam Point Clouds and Fisheye Data Into Texture-Enhanced 3d Models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4217, 295–302. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Remondino, F.; Baltsavias, E.; El-Hakim, S.; Picard, M.; Grammatikopoulos, L. Image-Based 3D Modeling of the Erechteion, Acropolis of Athens. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1083–1092. [Google Scholar] [CrossRef]
- Figueira, W.; Ferrari, R.; Weatherby, E.; Porter, A.; Hawes, S.; Byrne, M. Accuracy and Precision of Habitat Structural Complexity Metrics Derived from Underwater Photogrammetry. Remote Sens. 2015, 7, 16883–16900. [Google Scholar] [CrossRef]
- Antón, D.; Medjdoub, B.; Shrahily, R.; Moyano, J. Accuracy evaluation of the semi-automatic 3D modeling for historical building information models. Int. J. Archit. Herit. 2018, 12, 790–805. [Google Scholar] [CrossRef]
- Arias, P.; Ordóñez, C.; Lorenzo, H.; Herraez, J. Methods for documenting historical agro-industrial buildings: A comparative study and a simple photogrammetric method. J. Cult. Herit. 2006, 7, 350–354. [Google Scholar] [CrossRef]
- Kuçak, R.A.; Erol, S.; Erol, B. An Experimental Study of a New Keypoint Matching Algorithm for Automatic Point Cloud Registration. ISPRS Int. J. Geo-Inf. 2021, 10, 204. [Google Scholar] [CrossRef]
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The ball-pivoting algorithm for surface reconstruction. IEEE Trans. Vis. Comput. Graph. 1999, 5, 349–359. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. In Symposium on Geometry Processing; Polthier, K., Sheffer, A., Eds.; The Eurographics Association: Lisbon, Portugal, 2006; pp. 61–70. [Google Scholar]
- Mill, T.; Alt, A.; Liias, R. Combined 3D building surveying techniques—terrestrial laser scanning (TLS) and total station surveying for BIM data management purposes. J. Civ. Eng. Manag. 2013, 19, S23–S32. [Google Scholar] [CrossRef]
- Moyano, J.; Odriozola, C.P.; Nieto-Julián, J.E.; Vargas, J.M.; Barrera, J.A.; León, J. Bringing BIM to archaeological heritage: Interdisciplinary method/strategy and accuracy applied to a megalithic monument of the Copper Age. J. Cult. Herit. 2020, 45, 303–314. [Google Scholar] [CrossRef]
- Osello, A. The Future of Drawing with BIM for Engineers and Architects; Dario Flaccovio Editore srl: Palermo, Italy, 2012; pp. 1–323. [Google Scholar]
- Moyano, J.; Nieto-Julián, J.E.; Lenin, L.M.; Bruno, S. Operability of Point Cloud Data in an Architectural Heritage Information Model. Int. J. Archit. Herit. 2021, 16, 1–20. [Google Scholar] [CrossRef]
- Mousa, Y.A.; Helmholz, P.; Belton, D.; Bulatov, D. Building detection and regularisation using DSM and imagery information. Photogramm. Rec. 2019, 34, 85–107. [Google Scholar] [CrossRef]
- Chen, S.Y.; Chang, S.F.; Yang, C.W. Generate 3D Triangular Meshes from Spliced Point Clouds with Cloudcompare. In Proceedings of the 3rd IEEE Eurasia Conference on IOT, Communication and Engineering 2021, ECICE 2021, Taiwan, China, 29–31 October 2021; pp. 72–76. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Robert McNeel & Associates Rhinoceros. Available online: https://www.rhino3d.com/ (accessed on 24 January 2020).
- Murphy, M.; McGovern, E.; Pavia, S. Historic building information modelling (HBIM). Struct. Surv. 2009, 27, 311–327. [Google Scholar] [CrossRef]
- Torres, J.C.; Cano, P.; Melero, J.; España, M.; Moreno, J. Aplicaciones de la digitalización 3D del patrimonio. Virtual Archaeol. Rev. 2010, 1, 51. [Google Scholar] [CrossRef]
- U.S. General Services Administration. Guía BIM 03—Imágenes 3D|GSA. Available online: https://www.gsa.gov/real-estate/design-construction/3d4d-building-information-modeling/bim-guides/bim-guide-03-3d-imaging (accessed on 23 February 2022).
- Bonduel, M.; Bassier, M.; Vergauwen, M.; Pauwels, P.; Klein, R. Scan-to-bim output validation: Towards a standardized geometric quality assessment of building information models based on point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 45–52. [Google Scholar] [CrossRef]
- Magazine, L. USIBD’s Version 3 of the Level of Accuracy (LOA) Specification Version 3.0 Publishes Today—LIDAR Magazine. Available online: https://lidarmag.com/2019/08/20/usibds-version-3-of-the-level-of-accuracy-loa-specification-version-3-0-publishes-today/ (accessed on 25 January 2022).
- Peña-Villasenín, S.; Gil-Docampo, M.; Ortiz-Sanz, J. 3-D Modeling of Historic Façades Using SFM Photogrammetry Metric Documentation of Different Building Types of a Historic Center. Int. J. Archit. Herit. 2017, 11, 871–890. [Google Scholar] [CrossRef]
- DigitalEurope Digital Building Transformations for Europe’s Green Renovations: Sustainable Living and Working. Available online: https://www.digitaleurope.org/resources/digital-building-transformations-for-europes-green-renovations-sustainable-living-and-working/ (accessed on 30 August 2021).









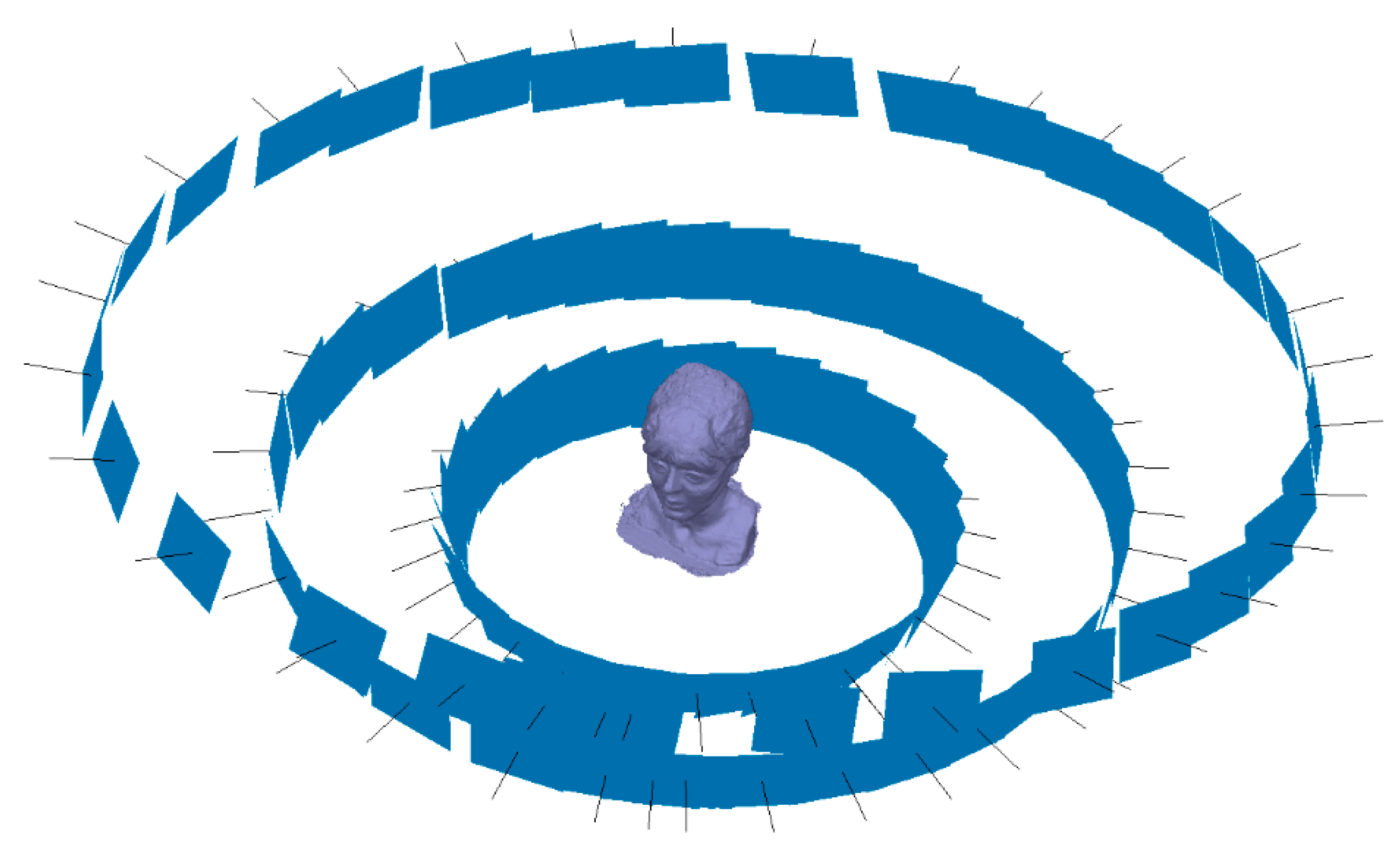










| Panasonic DMC-GF3 | |
|---|---|
| Nº of images | 142 |
| Resolution | 12 MP |
| Distance to the object | ≤0.50 m |
| ISO | 320 |
| Sensor | Live MOS (17.3 × 13 mm) |
| Exposure | 1/60 s f 3.5 |
| Step | Parameter | Selection |
|---|---|---|
| Align cameras | Accuracy | High |
| Generic/Reference preselection | Yes | |
| Key point limit | 40,000 | |
| Tie point limit | 4000 | |
| Adaptive camera model fitting | Yes | |
| Build dense cloud | Quality | High |
| Filtering mode | Moderate | |
| Calculate point colors | Yes | |
| Build mesh | Source data | Dense cloud |
| Quality | Medium | |
| Surface type | Arbitrary |
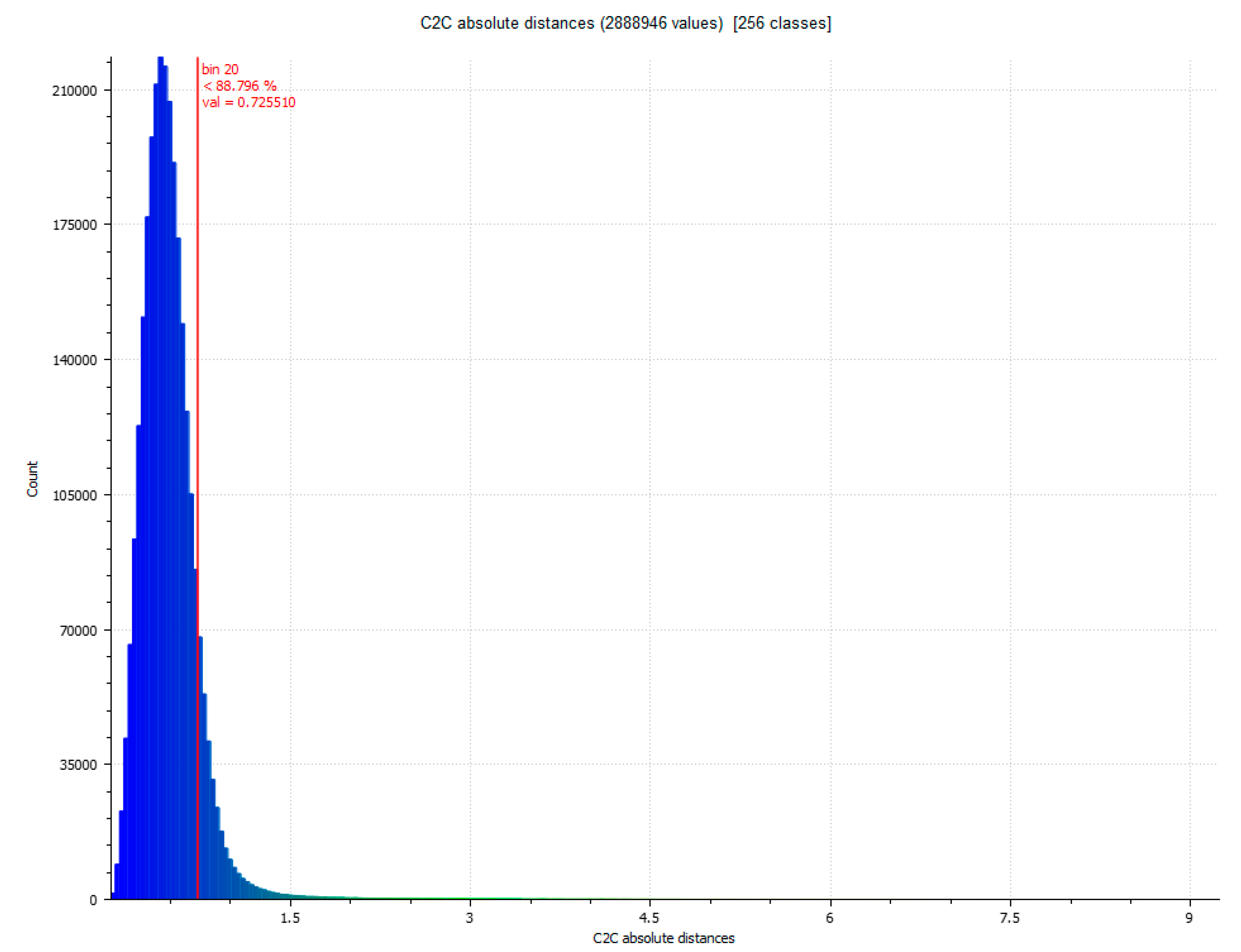
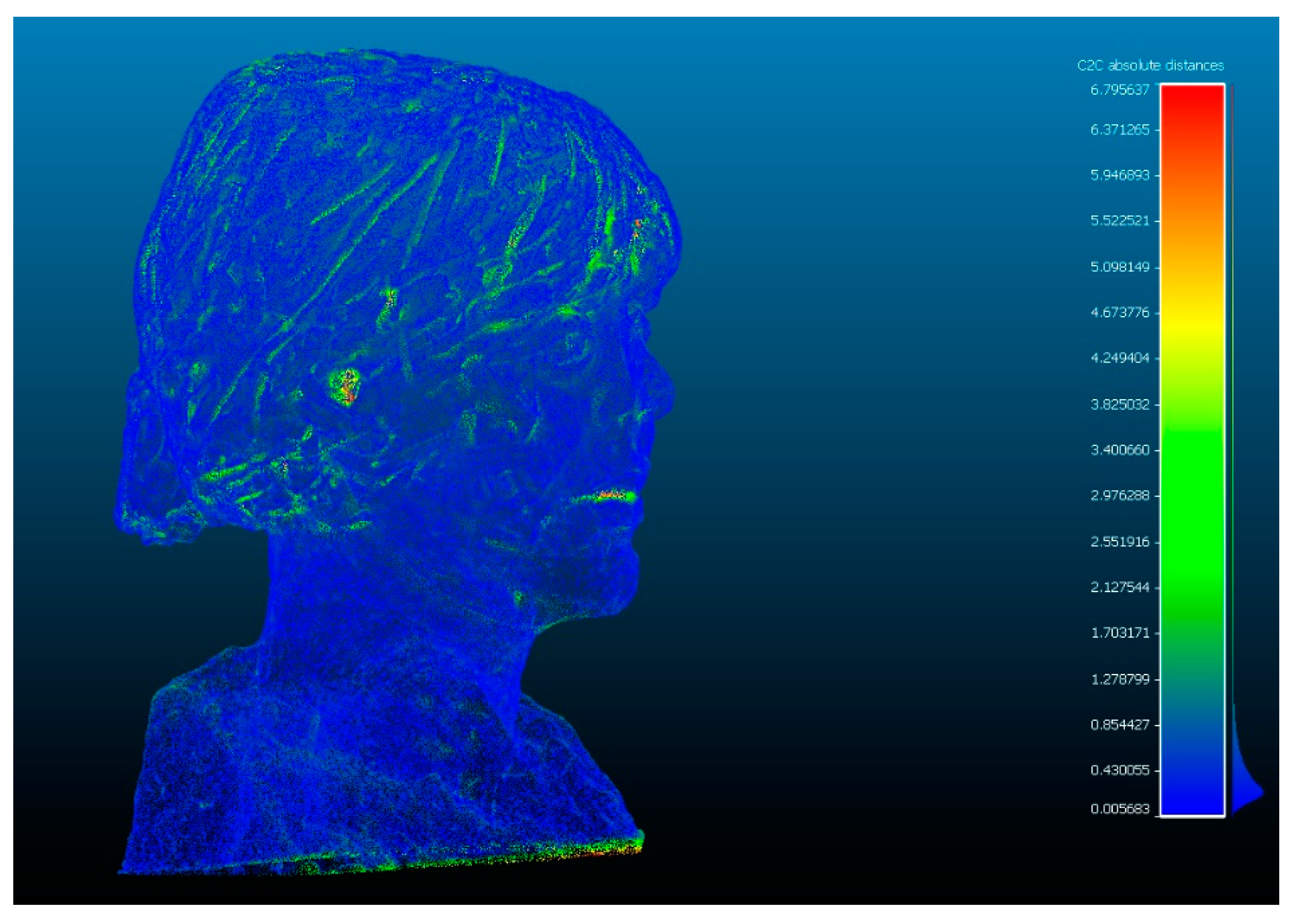
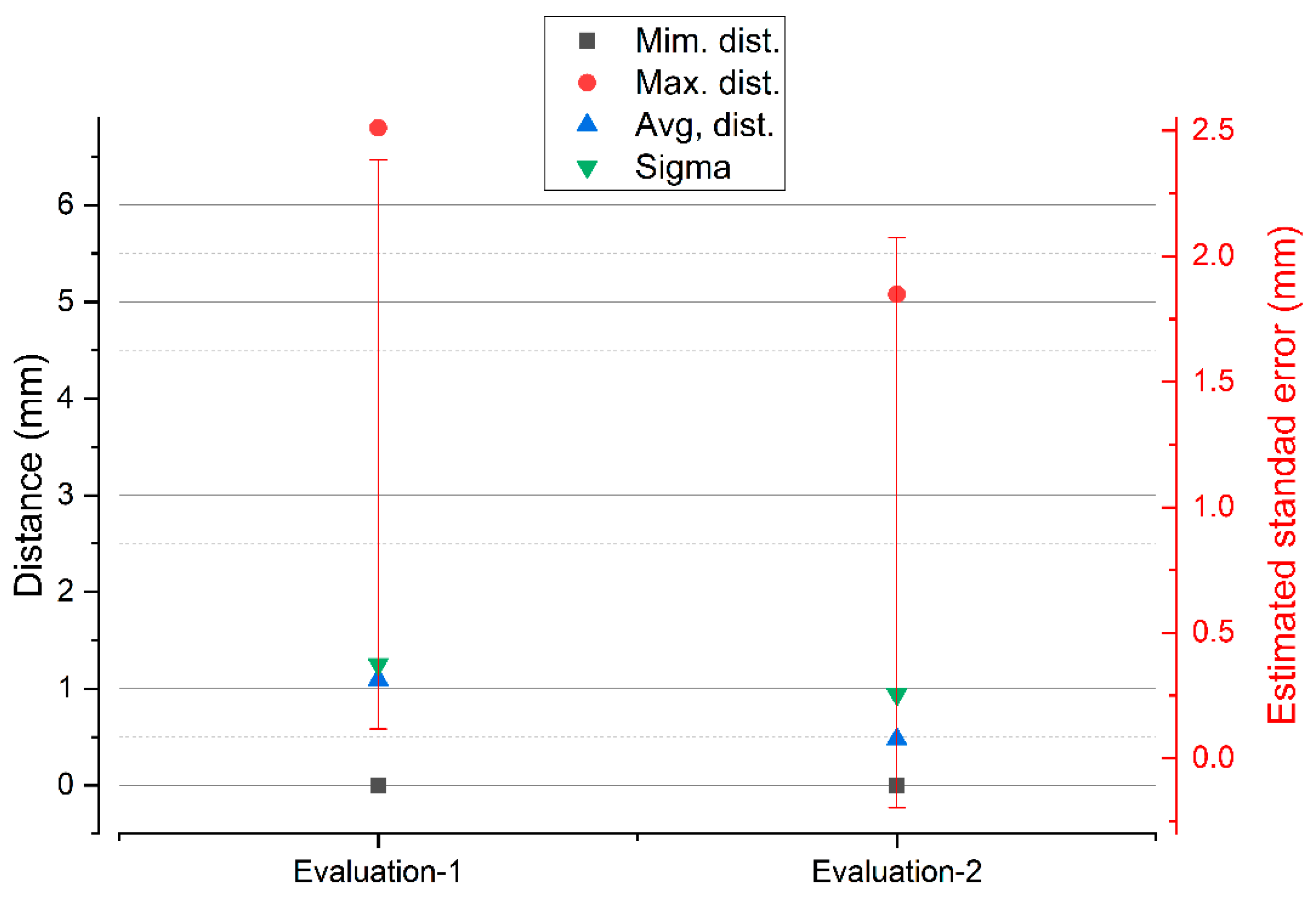
| Comparison between SPIDER and POP | Standard Deviation (σ) (mm) | Min. Distance (mm) | Max. Distance (mm) | Average Distance (mm) | Estimated Standard Error (mm) |
|---|---|---|---|---|---|
| Evaluation 1 | 1.2863 | 0 | 7.1653 | 1.2533 | 1.1352 |
| Evaluation 2 | 1.0338 | 0 | 5.5619 | 0.6260 | 1.1352 |
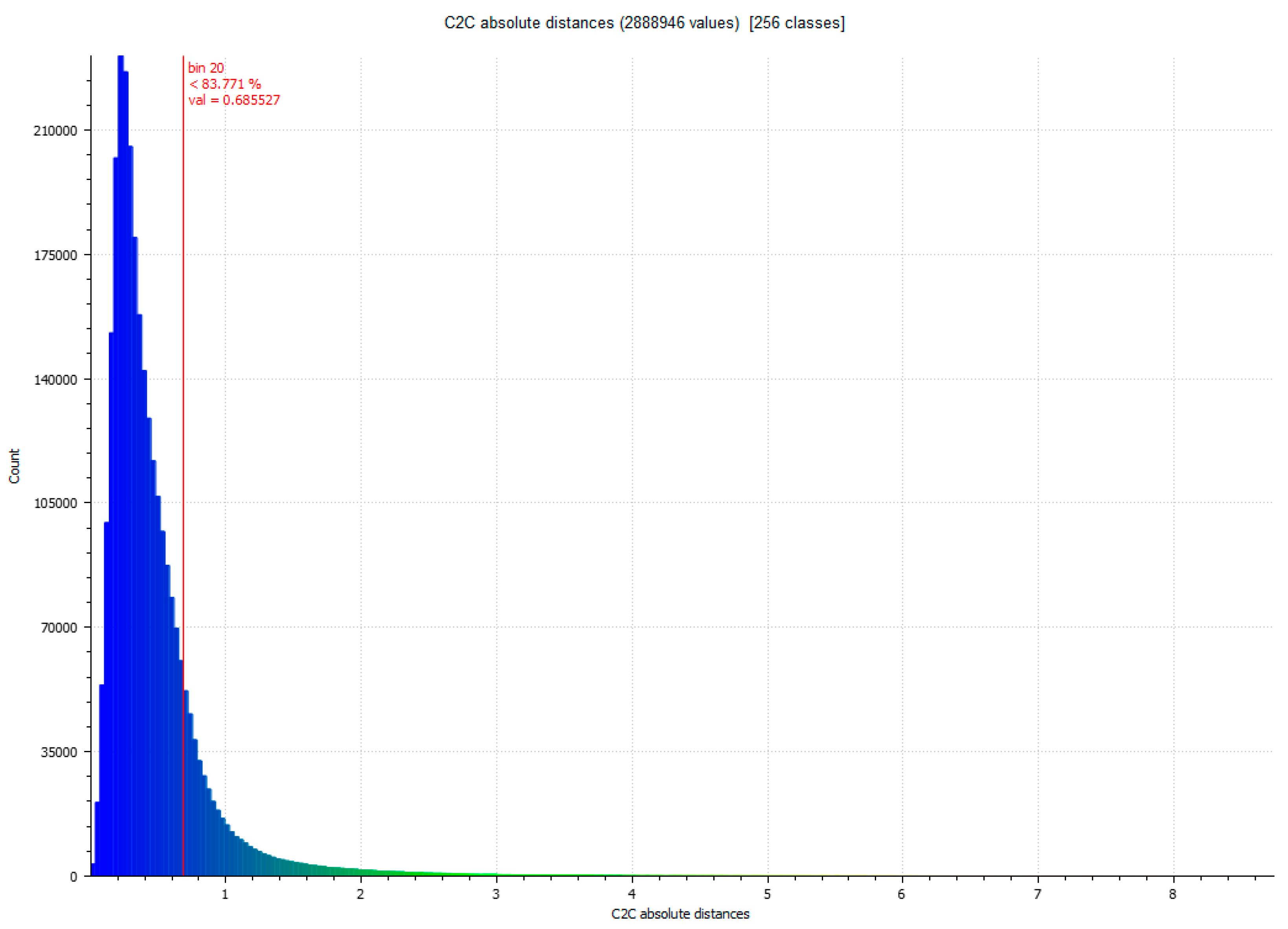
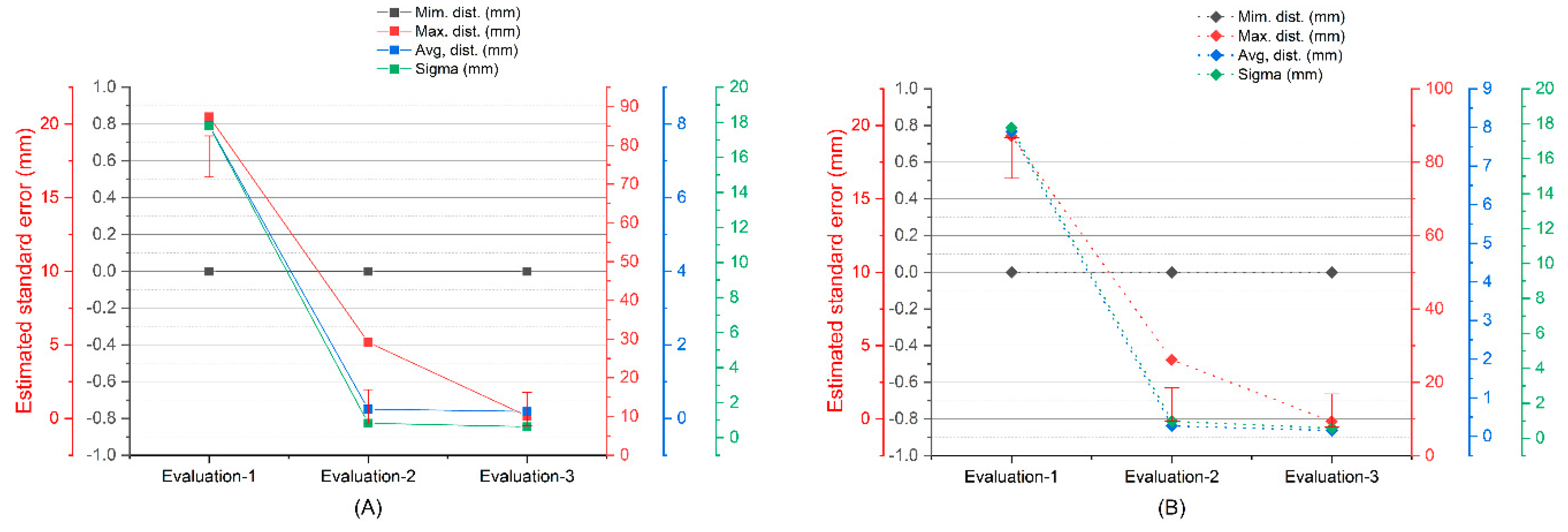
| Comparison between SPIDER and SfM | Standard Deviation (σ) (mm) | Min. Distance (mm) | Max. Distance (mm) | Average Distance (mm) | Estimated Standard Error (mm) |
|---|---|---|---|---|---|
| Evaluation 1 | 1.0269 | 0 | 10.3225 | 0.5361 | 1.1263 |
| Evaluation 2 | 1.0038 | 0 | 9.2875 | 0.5259 | 1.1263 |
| Evaluation 3 | 0.9475 | 0 | 9.2875 | 0.4952 | 1.1263 |
| Comparison between SfM and POP | Standard Deviation (σ) (mm) | Min. Distance (mm) | Max. Distance (mm) | Average Distance (mm) | Estimated Standard Error (mm) |
|---|---|---|---|---|---|
| Automatic alignments with 6 points | |||||
| Evaluation 1 | 17.7964 | 0 | 87.4128 | 7.9585 | 1.4026 |
| Evaluation 2 | 0.8249 | 0 | 29.1707 | 0.2519 | 1.1320 |
| Evaluation 3 | 0.6299 | 0 | 10.1253 | 0.1871 | 1.1320 |
| Best fitting manual | |||||
| Evaluation 1 | 17.7819 | 0 | 87.1341 | 7.8895 | 1.3875 |
| Evaluation 2 | 0.9804 | 0 | 26.1719 | 0.2729 | 1.1305 |
| Evaluation 3 | 0.5731 | 0 | 9.3219 | 0.1535 | 1.1305 |
| Dataset ID | Number of Point | Output File | Scale | Number of Segment Points | Points Density (pto./mm2) | |
|---|---|---|---|---|---|---|
| Artec Spider | VSLVVs | 495.964 | .stl | mm | 1.268 | 2.776 |
| POP 3D | VSLSVP | 2.982.902 | .ply | mm | 6.592 | 18.593 |
| SfM | VSfMV | 1.653.479 | .e57 | m | 2.999 | 7.028 |
| Comparison between | Standard Deviation (σ) (mm) | Min. Distance (mm) | Max. Distance (mm) | Average Distance (mm) | Estimated Standard Error (mm) |
|---|---|---|---|---|---|
| VSfMV and VSLSVP | 0.6183 | 0 | 8.5811 | 0.1480 | 1.2936 |
| VSLVVS and VSLSVP | 0.4830 | 0 | 9.7524 | 0.0901 | 1.3032 |
| VSLVVS and VSfMV | 0.7350 | 0 | 8.2376 | 0.2097 | 1.3025 |
| α Dispersion Angle | Distance between Lines (mm) | |
|---|---|---|
| SLVVS (SPIDER) | 42° | 3.5 |
| SLVVP (POP) | 57° | 9 |
| SfMV (SFM) | 54° | 5 |
| Spider-SFM | Spider-POP | SFM-POP | |
|---|---|---|---|
| Standard deviation (σ) (mm) | 0.9475 | 1.0338 | 0.5731 |
| Spider-SFM | Spider-POP | SFM-POP | |
|---|---|---|---|
| Standard deviation (σ) (mm) | 0.7350 | 0.4830 | 0.6183 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moyano, J.; Cabrera-Revuelta, E.; Nieto-Julián, J.E.; Fernández-Alconchel, M.; Fernández-Valderrama, P. Evaluation of Geometric Data Registration of Small Objects from Non-Invasive Techniques: Applicability to the HBIM Field. Sensors 2023, 23, 1730. https://doi.org/10.3390/s23031730
Moyano J, Cabrera-Revuelta E, Nieto-Julián JE, Fernández-Alconchel M, Fernández-Valderrama P. Evaluation of Geometric Data Registration of Small Objects from Non-Invasive Techniques: Applicability to the HBIM Field. Sensors. 2023; 23(3):1730. https://doi.org/10.3390/s23031730
Chicago/Turabian StyleMoyano, Juan, Elena Cabrera-Revuelta, Juan E. Nieto-Julián, María Fernández-Alconchel, and Pedro Fernández-Valderrama. 2023. "Evaluation of Geometric Data Registration of Small Objects from Non-Invasive Techniques: Applicability to the HBIM Field" Sensors 23, no. 3: 1730. https://doi.org/10.3390/s23031730
APA StyleMoyano, J., Cabrera-Revuelta, E., Nieto-Julián, J. E., Fernández-Alconchel, M., & Fernández-Valderrama, P. (2023). Evaluation of Geometric Data Registration of Small Objects from Non-Invasive Techniques: Applicability to the HBIM Field. Sensors, 23(3), 1730. https://doi.org/10.3390/s23031730








