A Method to Improve Mounting Tolerance of Open-Type Optical Linear Encoder
Abstract
:1. Introduction
2. Methods
2.1. Theoretical Investigation
2.2. Simulations
2.3. Fabrication
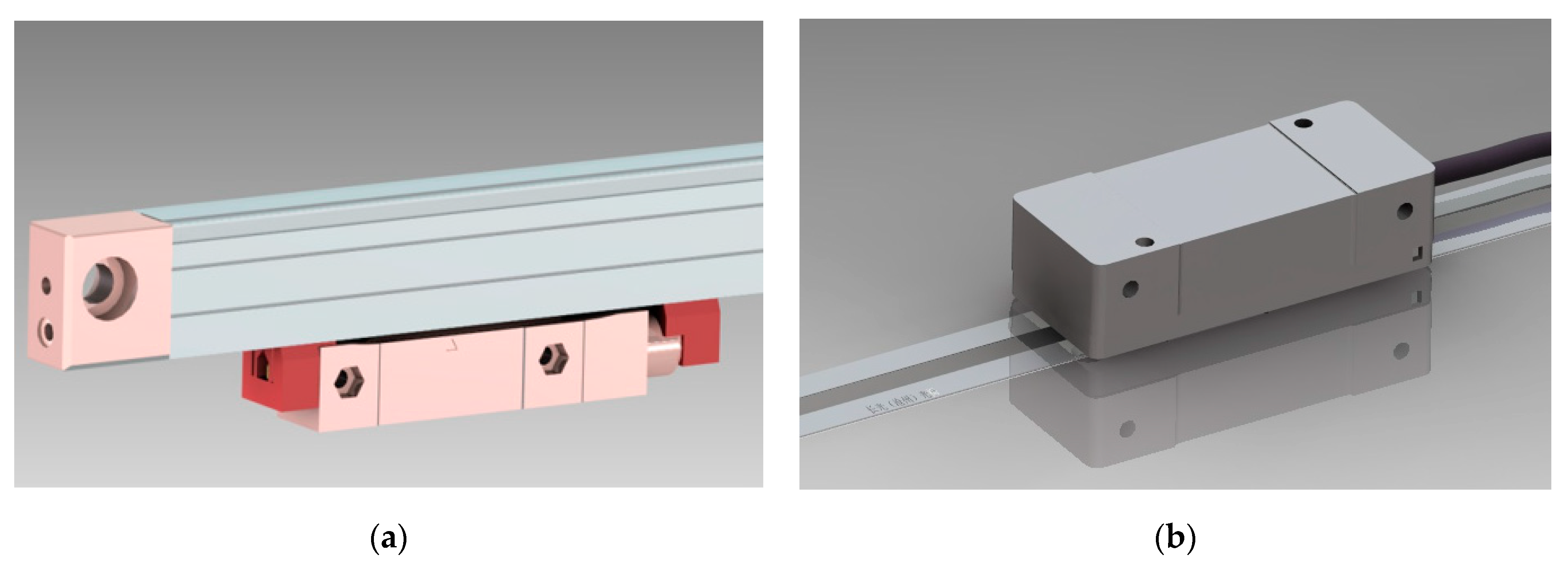
3. Investigation Methodology and Experiment Setup
- Five prototypes of the optical linear encoder’s reading heads with two different types of scanning reticles inside.
- A Zolix TSMV5-1A vertical stage, with a travel range of 5 mm, and a sensitivity of 3 μm to control the mounting distance between the reading head and main scale.
- A reflective stainless-steel tape made by Precizika Meteorology UAB, and the pitch period of the incremental track is 20 μm.
- An oscilloscope from Agilent Technologies to observe the output electrical signals.
4. Experimental Results and Discussion
- The results using reading heads 4–5 indicate that the optical linear encoder with the traditional scanning reticle can only operate at distances of 0.40, 0.45, 0.90, and 0.95 mm. With such rigorous requirements, the mechanical surface for the installment must be perfectly leveled, and a high-precision mounting device must be employed. On the other hand, with the proposed scanning reticle, reading heads 1–3 indicate that the effective mounting distance can range from 0.45 to 1.00 mm. If the instructed mounting distance of the optical linear is set as 0.72 mm, then the mounting tolerance is ±0.275 mm. Such mounting tolerance makes the installation of the optical linear encoder without a high-precision mounting device possible and can reduce errors incurred by incorrect mounting distance.
- The reading heads 1–3 show a similar workable mounting distance range and trend. Nonetheless, there are still deviations at some mounting distances. For instance, at 0.40 mm, the signal amplitude ratio is 0.83, 0.53, and 0.59. This is possibly caused by the slight angle difference in the scanning reticles when fixed onto the reading heads since there was no angle measurement equipment for this experiment. The theoretical model of the light distribution with the angle difference between the scanning reticle and main grating should be developed based on generalized grating imaging for future work. The angle measurement equipment should be built for more precise experiments and investigations.
- The theoretical calculations and Virtual Lab simulations indicate that the light distribution intensities are stable with the proposed scanning reticle, which means that the quality of optical signals should be adequate for the subsequent electronic system to generate sine and cosine waves. As for the traditional scanning reticles, the light distribution intensities were unstable, which suggests that the quality of optical signals is unlikely to be readable by the electronics system during the entire mounting range. The Experimental Results support such assumptions.
- Other characteristics of the optical linear encoders can be improved in the future based on this work. For reading heads 1–3, the signal amplitude ratios were all above 0.6 for the entire range from 0.45 to 1.00 mm, but the deficiency was that they are not uniform, and this could lead to a different quality of the interpolation of the electrical signals. Future work plans will focus on developing an algorithm to compensate for the electrical signals.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Das, S.; Sarkar, T.S. A New Method of Linear Displacement Measurement Utilizing Grayscale Image. Int. J. Electron. Electr. Eng. 2013, 1, 176–181. [Google Scholar] [CrossRef]
- Fleming, A.J. A Review of Nanometer Resolution Position Sensors: Operation and Performance. Sens. Actuators A Phys. 2013, 190, 106–126. [Google Scholar] [CrossRef]
- Calarco, N.; Mombello, L.; Lipovetzky, J.; Lutenberg, A.; Perez Quintián, F. Self-Aligning CMOS Photodetector Sensor for Application on an NDB-Based Optical Encoder. Appl. Opt. 2019, 58, 9172. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Donate, C.; Osornio-Rios, R.A.; Rivera-Guillen, J.R.; Romero-Troncoso, R.d.J. Fused Smart Sensor Network for Multi-Axis Forward Kinematics Estimation in Industrial Robots. Sensors 2011, 11, 4335–4357. [Google Scholar] [CrossRef] [PubMed]
- CerónViveros, M.F.; Rojas Arciniegas, A.J. Development of a Closed-Loop Control System for the Movements of the Extruder and Platform of a FDM 3D Printing System. NIP Digit. Fabr. Conf. 2018, 2018, 176–181. [Google Scholar] [CrossRef]
- Liu, H.; Yu, H.; Jiang, W.; Li, X.; Fan, S.; Lei, B.; Shi, Y.; Yin, L.; Chen, B. An Accelerometer with Integrative Intensity-Modulated Optical Encoder and Patterned Leaf Spring for Low-Frequency Vibration Monitoring. Sens. Actuators A Phys. 2016, 251, 75–83. [Google Scholar] [CrossRef]
- Elhawary, H.; Zivanovic, A.; Rea, M.; Davies, B.L.; Besant, C.; Young, I.; Lamperth, M.U. A Modular Approach to MRI-Compatible Robotics. IEEE Eng. Med. Biol. Mag. 2008, 27, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Coaplen, J.; Tomizuka, M. Precision Positioning of Wafer Scanners. Available online: https://ieeexplore.ieee.org/document/4272324 (accessed on 6 February 2023).
- Xu, X.; Zhao, M.; Lin, J. Detecting Weak Position Fluctuations from Encoder Signal Using Singular Spectrum Analysis. ISA Trans. 2017, 71, 440–447. [Google Scholar] [CrossRef] [PubMed]
- Gurauskis, D.; Kilikevičius, A.; Borodinas, S.; Kasparaitis, A. Analysis of Geometric and Thermal Errors of Linear Encoder for Real-Time Compensation. Sens. Actuators A Phys. 2019, 296, 145–154. [Google Scholar] [CrossRef]
- Lopez, J.; Artes, M. A New Methodology for Vibration Error Compensation of Optical Encoders. Sensors 2012, 12, 4918–4933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Wang, J.; Chen, B.; Xiao, P.; Chen, X.; Cai, N.; Ling, B.W.-K. Absolute Optical Imaging Position Encoder. Measurement 2015, 67, 42–50. [Google Scholar] [CrossRef]
- Cai, N.; Xiao, P.; Ye, Q.; Wang, H.; Chen, X.; Ling, B.W. Improving the Measurement Accuracy of an Absolute Imaging Position Encoder via a New Edge Detection Method. IET Sci. Meas. Technol. 2017, 11, 406–413. [Google Scholar] [CrossRef]
- Sanchez-Brea, L.M.; Morlanes, T. Metrological Errors in Optical Encoders. Meas. Sci. Technol. 2008, 19, 115104. [Google Scholar] [CrossRef]
- Alejandre, I.; Artés, M. Method for the Evaluation of Optical Encoders Performance under Vibration. Precis. Eng. 2007, 31, 114–121. [Google Scholar] [CrossRef]
- Gurauskis, D.; Kilikevičius, A.; Kasparaitis, A. Thermal and Geometric Error Compensation Approach for an Optical Linear Encoder. Sensors 2021, 21, 360. [Google Scholar] [CrossRef] [PubMed]
- Cai, N.; Xie, W.; Peng, H.; Wang, H.; Yang, Z.; Chen, X. A Novel Error Compensation Method for an Absolute Optical Encoder Based on Empirical Mode Decomposition. Mech. Syst. Signal Process. 2017, 88, 81–88. [Google Scholar] [CrossRef]
- López, J.; Artés, M.; Alejandre, I. Analysis of Optical Linear Encoders’ Errors under Vibration at Different Mounting Conditions. Measurement 2011, 44, 1367–1380. [Google Scholar] [CrossRef]
- Torcal-Milla, F.J.; Sanchez-Brea, L.M.; Bernabeu, E. Self-Imaging of Gratings with Rough Strips. J. Opt. Soc. Am. A 2008, 25, 2390. [Google Scholar] [CrossRef] [PubMed]
- Talbot Simulation. Available online: https://www.lighttrans.com/use-cases/application/talbot-effect.html (accessed on 30 November 2022).
- Kao, C.-F.; Lu, M.-H. Optical Encoder Based on the Fractional Talbot Effect. Opt. Commun. 2005, 250, 16–23. [Google Scholar] [CrossRef]


















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Kilikevičius, A.; Yang, F.; Gurauskis, D. A Method to Improve Mounting Tolerance of Open-Type Optical Linear Encoder. Sensors 2023, 23, 1987. https://doi.org/10.3390/s23041987
Lu X, Kilikevičius A, Yang F, Gurauskis D. A Method to Improve Mounting Tolerance of Open-Type Optical Linear Encoder. Sensors. 2023; 23(4):1987. https://doi.org/10.3390/s23041987
Chicago/Turabian StyleLu, Xinji, Artūras Kilikevičius, Fan Yang, and Donatas Gurauskis. 2023. "A Method to Improve Mounting Tolerance of Open-Type Optical Linear Encoder" Sensors 23, no. 4: 1987. https://doi.org/10.3390/s23041987
APA StyleLu, X., Kilikevičius, A., Yang, F., & Gurauskis, D. (2023). A Method to Improve Mounting Tolerance of Open-Type Optical Linear Encoder. Sensors, 23(4), 1987. https://doi.org/10.3390/s23041987







