Preparation of Discontinuous Cu/SiO2 Multilayers—AC Conduction and Determining the Measurement Uncertainty
Abstract
:1. Introduction
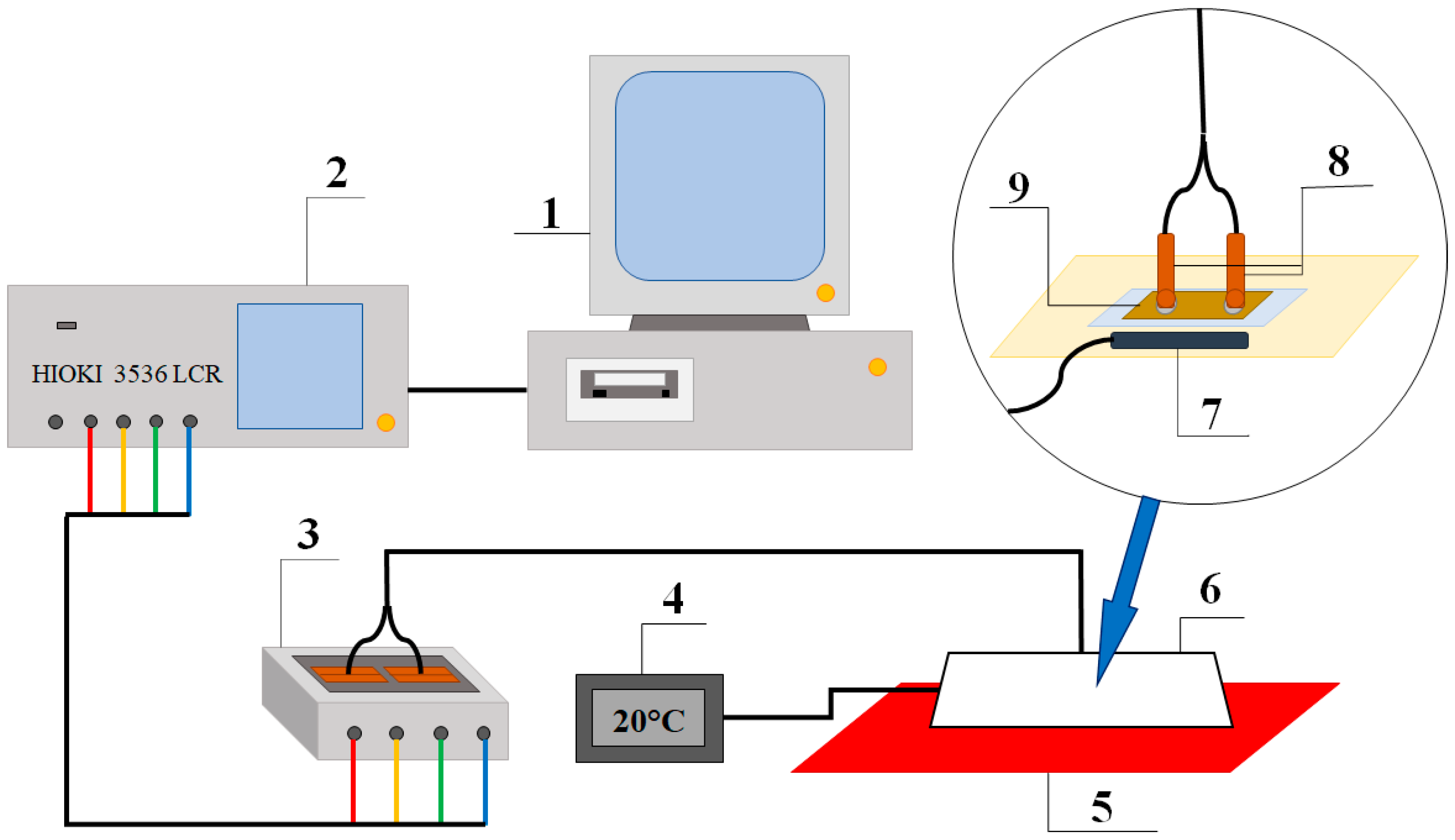
2. Technology of Obtaining Multilayer Nanocomposite Structures and Measurement Method
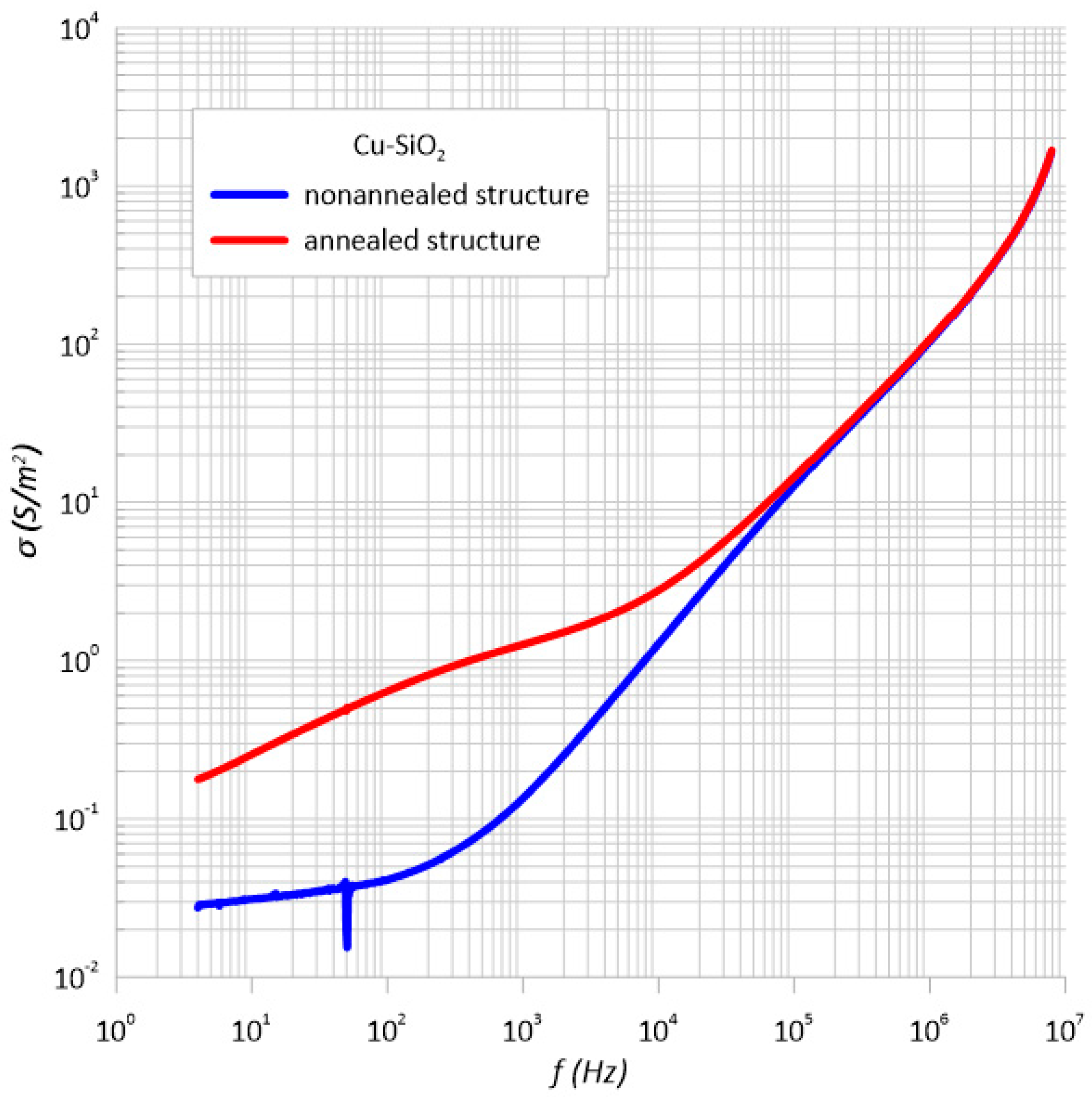
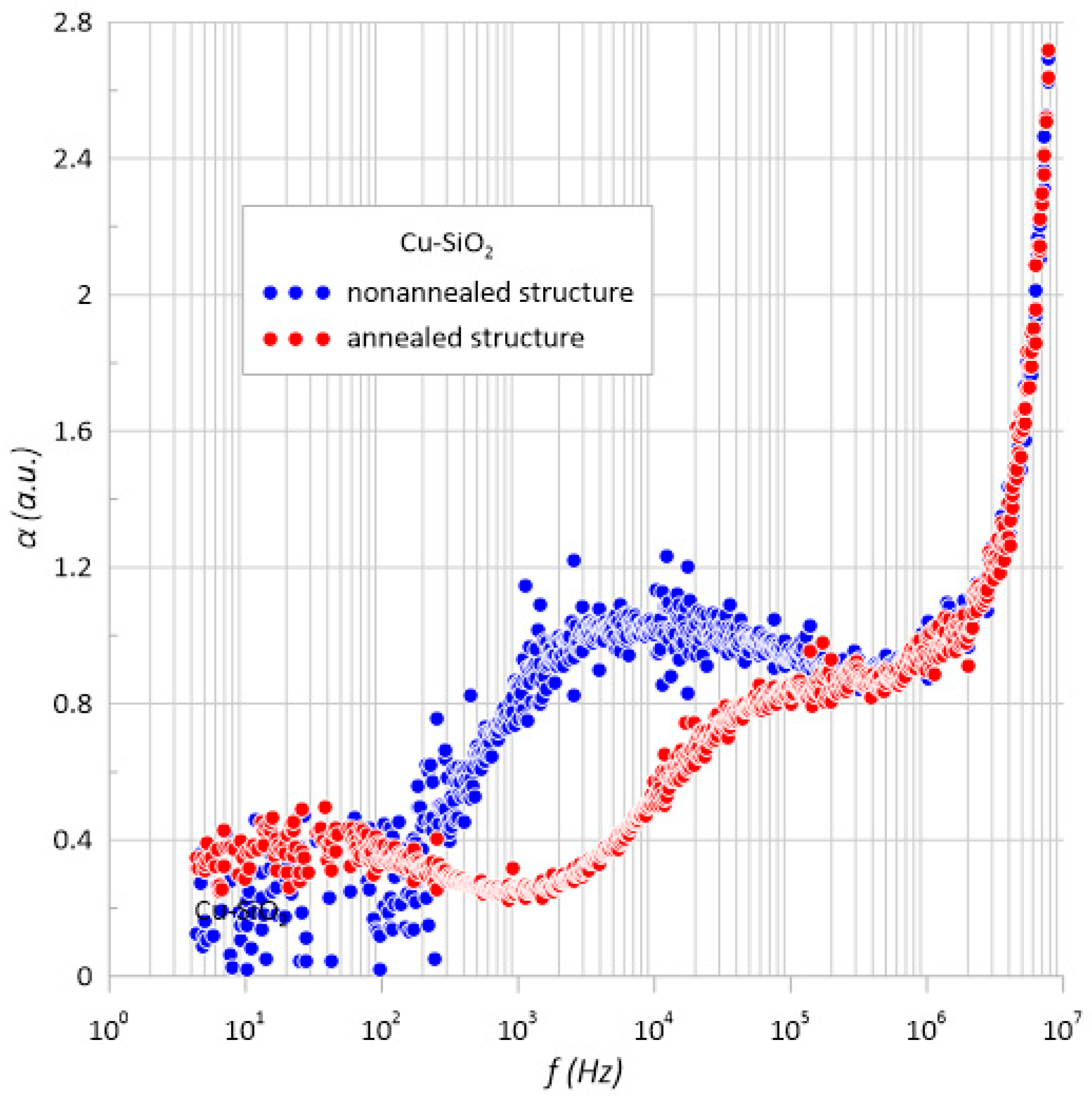
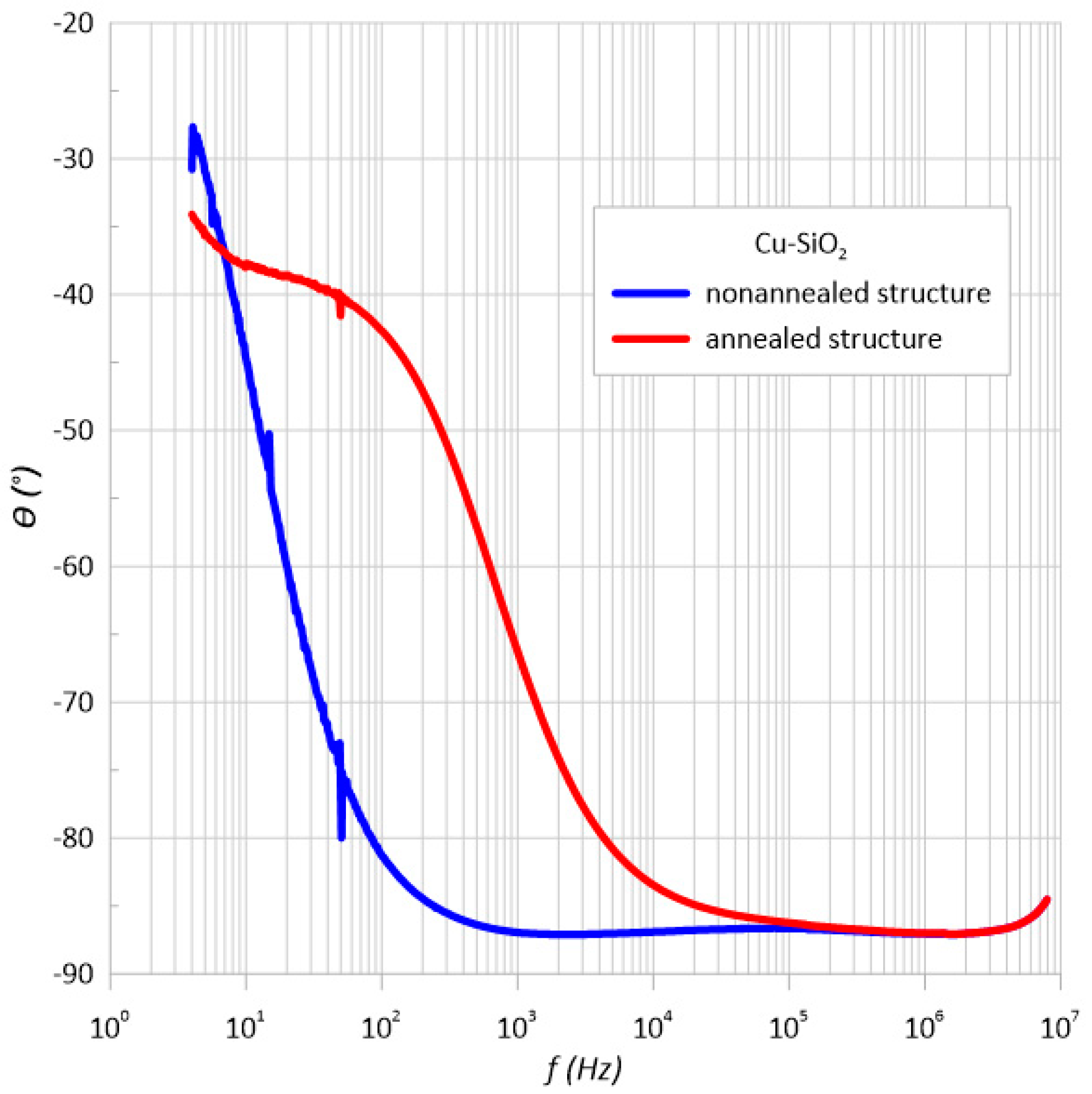
3. Result
3.1. Structural Studies of the Nanocomposite Cu-SiO2
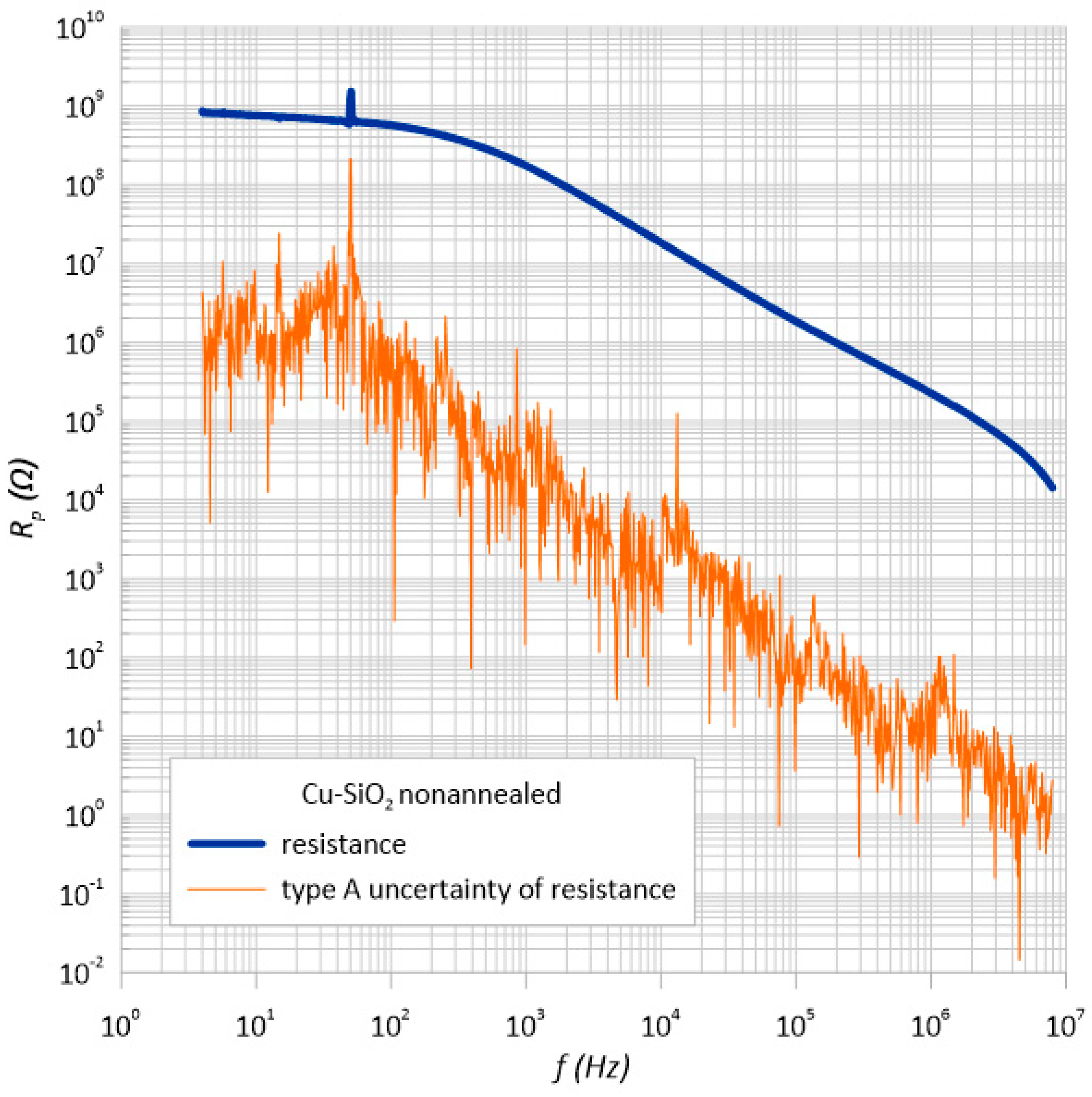
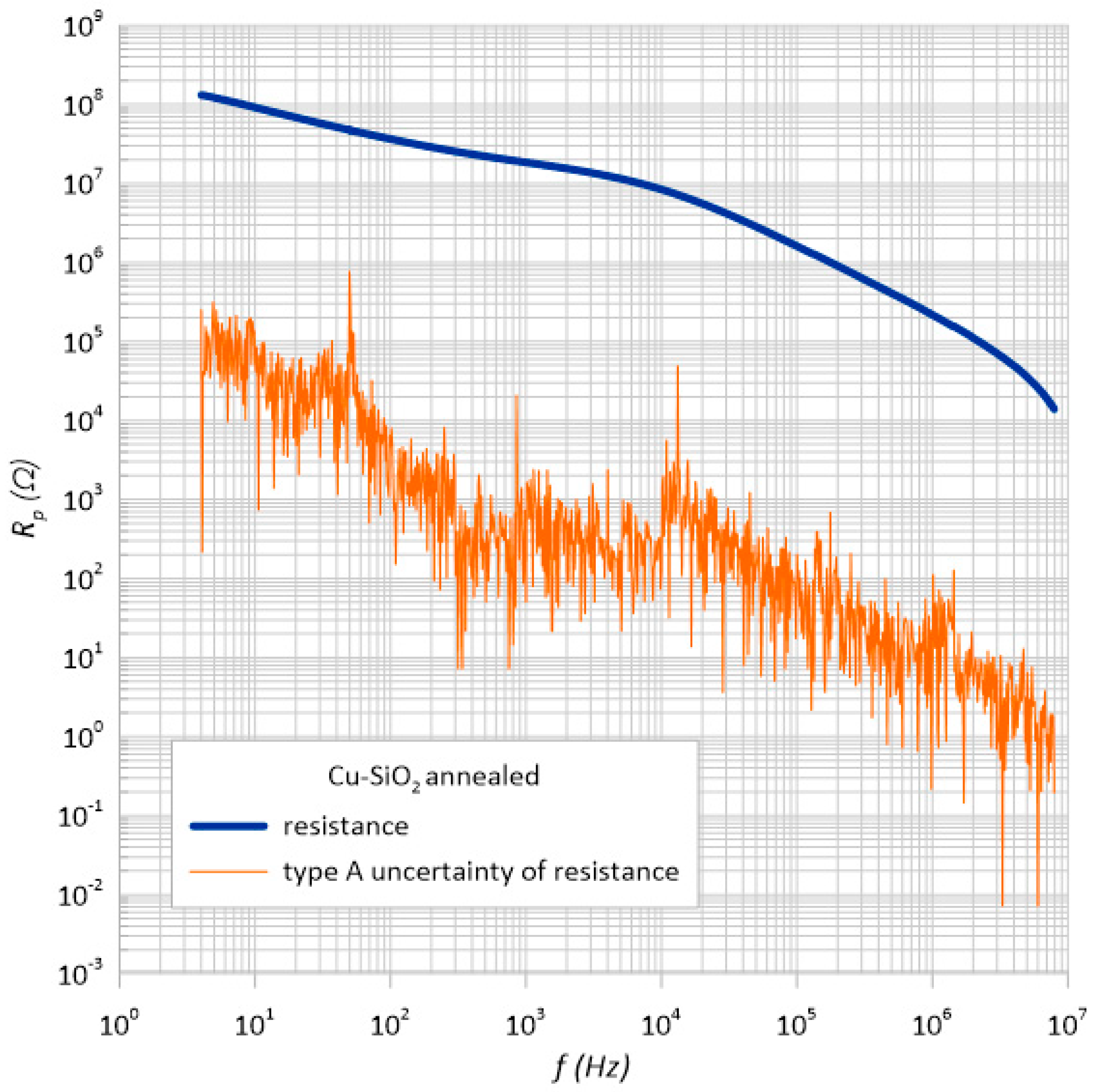
3.2. Standard Uncertainty of Type a Measurements
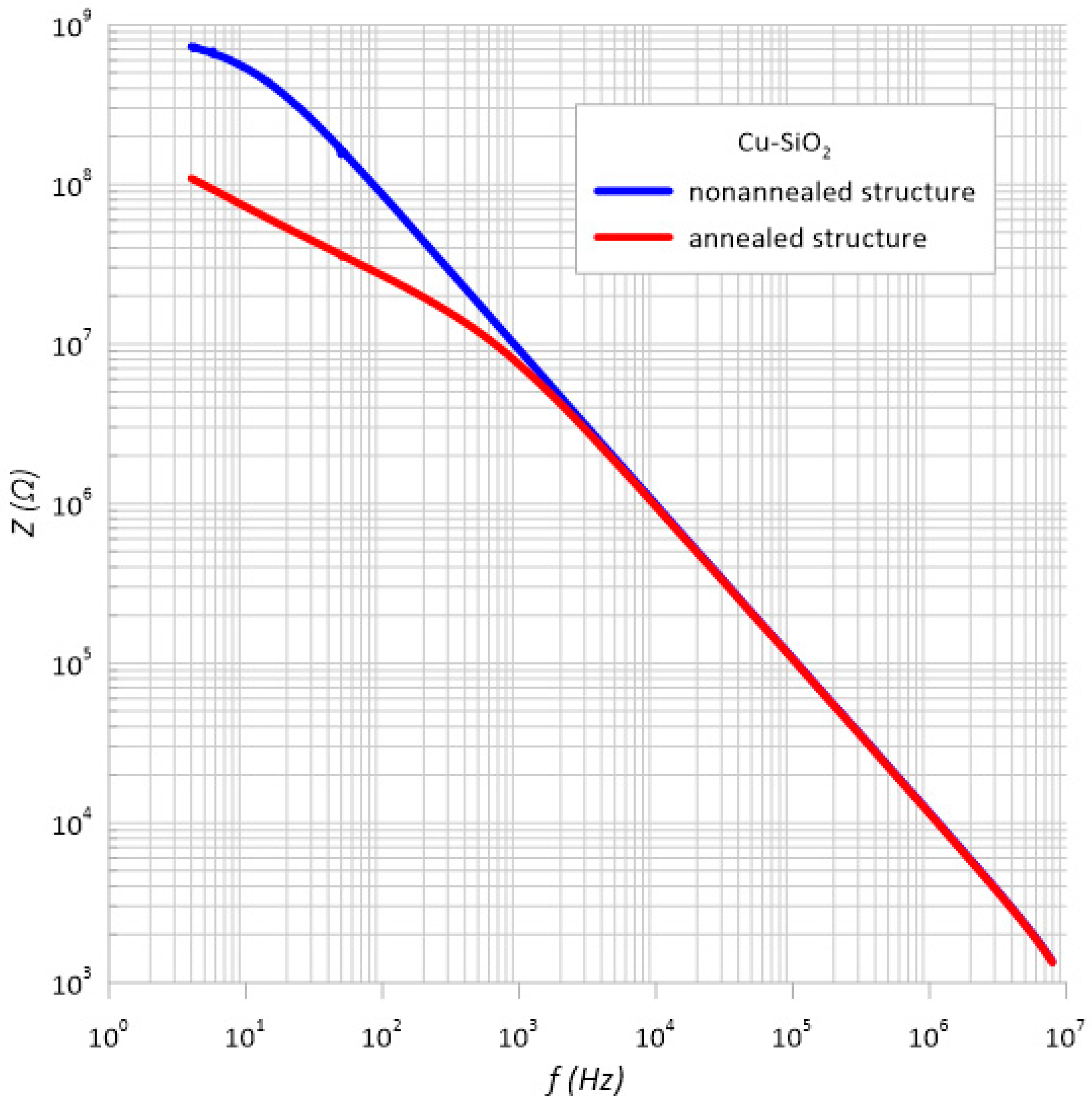
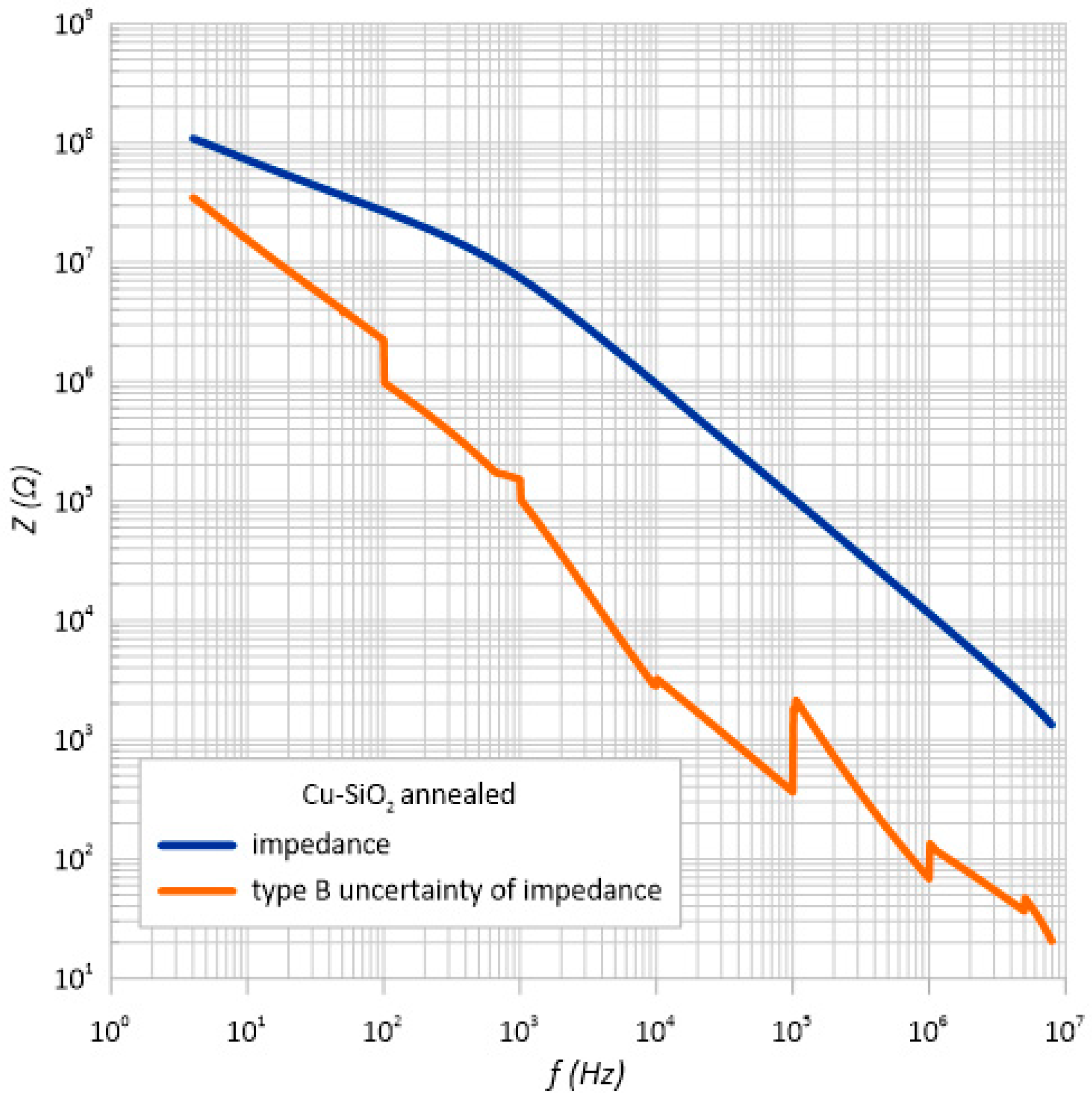
3.3. Standard Uncertainty of Type B Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kołtunowicz, T.N.; Zhukowski, P.; Fedotova, V.V.; Saad, A.M.; Fedotov, A.K. Hopping Conductance in Nanocomposites (Fe0.45Co0.45Zr0.10)x(Al2O3)1−x Manufactured by Ion-Beam Sputtering of Complex Target in Ar+O2 Ambient Gas. Acta Phys. Pol. A 2011, 120, 39–42. [Google Scholar] [CrossRef]
- Koltunowicz, T.N. Inductive type properties of FeCoZr–CaF2 and FeCoZr–PZT nanocomposites. J. Mater. Sci. Mater. Electron. 2015, 26, 6450–6457. [Google Scholar] [CrossRef] [Green Version]
- Myagkov, V.G.; Bykoba, L.E.; Bayukov, O.A.; Zhigalov, V.S.; Tambasov, I.A.; Bondarenko, G.N. Solid state synthesis and characterization of Fe–ZrO2 ferromagnetic nanocomposite thin films. J. Alloys Compd. 2015, 636, 223–228. [Google Scholar] [CrossRef]
- Reithmaier, J.; Petkov, P.; Kulisch, W.; Popov, C. Nanostructured Materials for Advanced Technological Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 447–476. [Google Scholar]
- Dizon, J.R.C.; Chen, Q.; Valino, A.D.; Advincula, R.C. Thermo-mechanical and swelling properties of three-dimensional-printed poly (ethylene glycol) diacrylate/silica nanocomposites. MRS Commun. 2019, 9, 209–217. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Zhukowski, P.; Fedotov, A.K.; Larkin, A.V.; Patryn, A.; Andryevskyy, B.; Saad, A.; Fedotova, J.A.; Fedotov, V.V. Influence of Matrix Type on Negative Capacitance Effect in Nanogranular Composite Films FeCoZr-Insulator. Elektron. Ir Elektrotechnika 2013, 19, 37–40. [Google Scholar] [CrossRef]
- Kusiak-Najman, E.; Morawski, A.W. TiO2/graphene-based nanocomposites for water treatment: A brief overview of charge carrier transfer, antimicrobial and photocatalytic performance. Appl. Catal. B Environ. 2019, 253, 179–186. [Google Scholar] [CrossRef]
- Shklovski, B.I.; Efros, A.I. Electronic Properties of Semiconductors; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Jonscher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectric Press: London, UK, 1983. [Google Scholar]
- Saberi, A.A. Recent advances in percolation theory and its applications. Phys. Re-Ports 2015, 578, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Haghgoo, M.; Ansari, R.; Hassanzadeh-Aghdam, M.K.; Nankali, M. A novel temperature-dependent percolation model for the electrical conductivity and piezoresistive sensitivity of carbon nanotube-filled nanocomposites. Acta Mater. 2022, 230, 117870. [Google Scholar] [CrossRef]
- Melchert, O.; Katzgraber, H.G.; Novotny, M.A. Site- and bondpercolation thresholds in Knn-based lattices: Vulnerability of quantum annealers to random qubit and coupler failures on chimera topologies. Phys. Rev. E 2016, 93, 042128. [Google Scholar] [CrossRef] [Green Version]
- Scullard, C.R.; Jacobsen, J.L. Bond percolation thresholds on Archimedean lattices from critical polynomial roots. Phys. Rev. Res. 2020, 2, 012050. [Google Scholar] [CrossRef] [Green Version]
- Jacobsen, J.L. High-precision percolation thresholds and Potts-model critical manifolds from graph polynomials. J. Phys. A Math. Theor. 2014, 47, 135001. [Google Scholar] [CrossRef]
- Barsukov, Y.; Macdonald, J. Impedance Spectroscopy: Theory, Experiment, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Miyano, K.; Yanagida, M.; Shirai, Y. Impedance Spectroscopy Revisited. Adv. Energy Mater. 2020, 10, 1903097. [Google Scholar] [CrossRef]
- Alzari, V.; Nuvoli, D.; Sanna, V.; Caruso, T.; Marino, S.; Scaramuzza, N. Study of polymeric nanocomposites prepared by inserting graphene and/or Ag, Au and ZnO nanoparticles in a TEGDA polymer matrix, by means of the use of dielectric spectroscopy. Aip Ad-Vances 2016, 6, 035005. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Liu, P.; Cui, X.; Song, Y. Colossal permittivity and dielectric relaxations in Tl + Nb co-doped TiO2 ceramics. Ceram. Int. 2018, 44, 12137–12143. [Google Scholar] [CrossRef]
- Okram, G.S.; Kaurav, N. Size-dependent resistivity and thermopower of nanocrystalline copper. J. Appl. Phys. 2011, 110, 023713. [Google Scholar] [CrossRef]
- Fukuda, H.; Nagakubo, A.; Usami, S.; Ikeda, M.; Imanishi, M.; Yoshimura, M.; Mori, Y.; Adachi, K.; Ogi, H. Determination of the electron trap level in Fe-doped GaN by phonon-assisted conduction phenomenon. Appl. Phys. Express 2022, 15, 071003. [Google Scholar] [CrossRef]
- Pattanayak, M.D.; Biswal, L.; Roy, N. Study of dielectric property, electric modulus and conduction phenomena of Sn-modified Ba0.5Sr0.5TiO3 ceramics. Ferroelectrics 2022, 588, 88–97. [Google Scholar] [CrossRef]
- Lvovich, V.F. Impedance Spectroscopy: Applications to Electrochemical and Dielectric Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Elhosiny Ali, H.; Abdel-Aziz, M.M.; Algarni, H.; Yahia, I.S.; Khairy, Y. Multifunctional Applications of a Novel Ru-Metal Mixed PVAL Flexible Composite for Limiting Absorption and Varistor: Synthesis, Optical, and Electrical Characterization. J. Inorg. Organomet. Polym. Mater. 2021, 31, 1503–1516. [Google Scholar] [CrossRef]
- Kalinin, Y.E.; Sitnikov, A.V.; Stognei, O.V.; Zolotukhin, I.V.; Neretin, P.V. Electrical properties and giant magnetoresistance of the CoFeB-SiO2 amorphous granular composites. Mater. Sci. Eng. 2011, 304–306, 941–945. [Google Scholar] [CrossRef]
- Koltunowicz, T.N.; Zukowski, P.; Bondariev, V.; Fedotova, J.A.; Fedotov, A.K. The effect of annealing on induction like properties of (FeCoZr)x(CaF2)(100−x) nanocomposite films produced by ion-beam sputtering in the vacuum environment. Vacuum 2015, 120, 44–50. [Google Scholar] [CrossRef]
- Bondariev, V. Hoping conductance in nanocomposites (FeCoZr)x(SiO2)(100−x) produced in mixed Ar and O2 atmosphere. In Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10808. [Google Scholar]
- Guangyi, J.; Haitao, D.; Xiaoyu, M.; Chungang, G.; Chaglong, L. Implantation-synthesized Cu/Cu-Zn core/shell nanoparticles in SiO2 and their optical properties. Opt. Mater. Express 2015, 5, 1156–1167. [Google Scholar]
- Makhavikou, M.; Parkhomenko, I.; Vlasukova, L.; Komarov, F.; Milchanin, O.; Mudryi, A.; Zhivulko, V.; Wendler, E.; Togambayeva, A.; Korolik, O. Raman monitoring of ZnSe and ZnSxSe1−x nanocrystals formed in SiO2 by ion implantation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2018, 435, 56–60. [Google Scholar] [CrossRef]
- Kasiuk, J.; Fedotova, J.; Przewoźnik, J.; Kapusta, C.Z.; Sokora, M.; Żukrowski, J.; Grce, A.; Milosavljelić, M. Oxidation controlled phase composition of FeCo(Zr) nanoparticles in CaF2 matrix. Mater. Charact. 2016, 113, 71–81. [Google Scholar] [CrossRef]
- Dippong, T.; Levei, E.A.; Lengauer, C.L.; Daniel, A.; Toloman, D.; Cadar, O. Investigation of thermal, structural, morphological and photocatalytic properties of CuxCo1−xFe2O4 (0 ≤ x ≤ 1) nanoparticles embedded in SiO2 matrix. Mater. Charact. 2020, 163, 110268. [Google Scholar] [CrossRef]
- Yeshchenko, O.A.; Dmitruk, I.M.; Dmytuk, I.M.; Dmytuk, A.M.; Alexeenko, A.A. Influence of annealing conditions on size and optical properties of copper nanoparticles embedded in silica matrix. Mater. Sci. Eng. B 2007, 137, 247–254. [Google Scholar] [CrossRef]
- Saad, A.M.; Fedotov, A.K.; Fedotova, J.A.; Andrievsky, B.V.; Kalinin, Y.E.; Fedotova, V.V.; Malyutina-Bronskaya, V.; Patryn, V.V.; Mazanik, A.V.; Sitnikov, A.V. Characterization of (Co0.45Fe0.45Zr0.10)x(Al2O3)1−x nanocomposite films applicable as spintronic materials. Phys. Status Solidi C 2006, 3, 1283–1290. [Google Scholar] [CrossRef]
- Saad, A.M.; Fedotov, A.K.; Svito, I.A.; Fedotova, J.A.; Andrievsky, B.V.; Kalinin, Y.E.; Patrym, A.A.; Fedotova, A.A.; Malyutina-Bronskaya, V.; Mazanik, A.V.; et al. Impedance and magnetization of CoFeZr nanoclusters embedded into alumina matrix. J. Alloys Compd. 2006, 423, 176–180. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wan, C.; Liu, H.; Li, Z.Q.; Sheng, P.; Lin, J.J. Giant Hall Effect in Nonmagnetic Granular Metal Films. Phys. Rev. Lett. 2001, 86, 5562–5565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.-J.; Li, M.-H.; Huang, J.-C.-A.; Chen, P. Cu/Cu2O nanocomposite films as a p-type modified layer for efficient perovskite solar cells. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Svito, I.; Fedotov, A.K.; Kołtunowicz, T.N.; Zhukowski, P.; Kalinin, Y.; Sitnikov, A.; Czarnacka, K.; Saad, A. Hopping of electron transport in granular Cux(SiO2)1−x nanocomposite films deposited by ion-beam sputtering. J. Alloys Compd. 2014, 615, S371–S374. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, K.; Kumar, A. Trap states induced hopping transport and persistent photoconductivity in WSe2/MoS2 nanocomposite thin films. J. Appl. Phys. 2021, 130, 125308. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Zukowski, P.; Czarnacka, K.; Bondariev, V.; Boiko, O.; Svito, I.A.; Fedotov, A.K. Dielectric properties of nanocomposite (Cu)x(SiO2)(100−x) produced by ion-beam sputtering. J. Alloys Compd. 2015, 652, 444–449. [Google Scholar] [CrossRef]
- Czarnacka, K. Basic measurements of DC properties of nanocomposites (FeCoZr)x(SiOy)(100−x). In Proceedings of the 2018 ELEKTRO, Mikulov, Czech Republic, 21–23 May 2018; pp. 1–4. [Google Scholar]
- Carmi, S.; Havlin, S.; Kirkpatrick, S.; Shavitt, Y.; Shir, E. A model of Internet topology usingk-shell decomposition. Proc. Natl. Acad. Sci. USA 2007, 104, 11150–11154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Q.; Wang, X.; Yang, K.; Deng, J.; Nie, R.; Deng, Q.; Chen, X.; Yang, H.; Xu, K.; Wang, F. The Positive Temperature Coefficient of Resistivity in BiFeO3 Films. Nanomaterials 2022, 12, 892. [Google Scholar] [CrossRef] [PubMed]
- Kołtunowicz, T.N.; Zhukowski, P.; Bondariev, V.; Fedotova, J.A.; Fedotov, A.K. Annealing of (CoFeZr)x(CaF2)100−x nanocomposites produced by the ion-beam sputtering in the Ar and O2 ambient. Acta Phys. Pol. A 2013, 123, 932–934. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Zhukowski, P.; Fedotova, V.V.; Saad, A.M.; Larkin, A.V.; Fedotov, A.K. The features of real part of admittance in the nanocomposites (Fe45Co45Zr10)x(Al2O3)100−x manufactured by the ion-beam sputtering technique with Ar ions. Acta Phys. Pol. A 2011, 120, 35–38. [Google Scholar] [CrossRef]
- Zhukowski, P.; Kołtunowicz, T.N.; Wegierek, P.; Fedotova, J.A.; Fedotov, A.K.; Larkin, A.V. Formation of noncoil-like inductance in nanocomposites (Fe0.45Co0.45Zr0.10)x(Al2O3)1−x manufactured by ion-beam sputtering of complex targets in Ar + O2 atmosphere. Acta Phys. Pol. A 2011, 120, 43–45. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials Clarendon-Press; Oxford University Press: Oxford, NY, USA, 1971. [Google Scholar]
- Imry, Y.; Tinkham, M. Introduction to Mesoscopic Physics; Oxford University Press: Oxford, NY, USA, 1997. [Google Scholar]
- Urbański, M.K. Opracowywanie Danych Doświadczalnych; Wydział Fizyki Politechniki Warszawskiej: Warszawa, Poland, 2014. [Google Scholar]







| Structure before Annealing | ||||||
|---|---|---|---|---|---|---|
| f, Hz | Arithmetic Average, Ω | uA(Rp), Ω | ||||
| 10 | 7.58 × 108 | 7.52 × 108 | 7.5 × 108 | 7.5 × 108 | 7.52 × 108 | 1,594,641 |
| 100 | 5.64 × 108 | 5.7 × 108 | 5.69 × 108 | 5.69 × 108 | 5.68 × 108 | 1,127,854 |
| 1 k | 1.73 × 108 | 1.73 × 108 | 1.73 × 108 | 1.73 × 108 | 1.73 × 108 | 30,671.73 |
| 10 k | 18,278,700 | 18,273,400 | 1,8276,100 | 18,279,400 | 18,276,900 | 519.6152 |
| 100 k | 1,829,310 | 1,829,550 | 1,829,860 | 1,829,340 | 1,829,515 | 59.1784 |
| 1 M | 224,639 | 224,640 | 224,603 | 224,602 | 224,621 | 5.196152 |
| Structure after Annealing | ||||||
| 10 | 91,705,800 | 92,375,600 | 90,983,000 | 92,493,300 | 91,889,425 | 53,007.97159 |
| 100 | 36,464,200 | 36,482,800 | 36,480,600 | 36,494,600 | 36,480,550 | 4719.838 |
| 1 k | 18,457,000 | 18,455,300 | 18,457,800 | 18,458,600 | 18,457,175 | 50.51815 |
| 10 k | 8,393,890 | 8,393,320 | 8,391,870 | 8,394,820 | 8,393,475 | 119.8002 |
| 100 k | 1,606,470 | 1,607,910 | 1,606,910 | 1,607,400 | 1,607,172.5 | 202.7943 |
| 1 M | 217,540 | 217,515 | 217,518 | 217,468 | 217,510.25 | 8.588085 |
| Structure before Annealing | |||||||
|---|---|---|---|---|---|---|---|
| f, Hz | Z1, Ω | Z2, Ω | Z3, Ω | Z4, Ω | Arithmetic Average, Ω | 𝛿 (Z), % | u(Z), Ω |
| 10 | 537,152,000 | 533,324,000 | 533,601,000 | 535,221,000 | 534,824,500 | 268.41225 | 82,880,6215 |
| 100 | 86,135,500 | 86,118,900 | 86,056,600 | 86,122,800 | 86,108,450 | 44.054225 | 21,901,442 |
| 1 k | 9,202,700 | 9,202,420 | 9,203,060 | 9,203,300 | 9,202,870 | 3.159426 | 167,869.1331 |
| 10 k | 984,202 | 984,199 | 984,174 | 984,169 | 984,186 | 3.152558 | 17,913.46671 |
| 100 k | 107,014 | 107,015 | 107,016 | 107,012 | 107,014.25 | 0.50701425 | 313.257264 |
| 1 M | 11,573.5 | 11,573.5 | 11,573.5 | 11,573.5 | 11,573.5 | 1.047205 | 69.9738542 |
| Structure after annealing | |||||||
| 10 | 72,265,400 | 72,673,000 | 71,998,100 | 72,745,500 | 72,420,500 | 37.21025 | 15,558,347.93 |
| 100 | 26,817,300 | 26,827,600 | 26,825,800 | 26,826,400 | 26,824,275 | 14.4121375 | 2,232,008.079 |
| 1 k | 7,434,060 | 7,433,290 | 7,433,320 | 7,434,160 | 7,433,707.5 | 3.5132585 | 150,783.8913 |
| 10 k | 956387 | 956377 | 956383 | 956384 | 956,382.75 | 0.51308518 | 2833.091319 |
| 100 k | 105671 | 105666 | 105669 | 105673 | 105,669.75 | 0.5989433 | 365.4060768 |
| 1 M | 11,393.6 | 11,393.6 | 11,393.6 | 11,393.5 | 11,393.575 | 1.04180725 | 68.53095179 |
| Structure before Annealing | |||||||
|---|---|---|---|---|---|---|---|
| f, Hz | θ1, ° | θ2, ° | θ3, ° | θ4, ° | Arithmetic Average, ° | 𝛿 (θ), ° | uB(θ), ° |
| 10 | −44.872 | −44.827 | −44.621 | −44.477 | −44.6993 | 8.000013 | −2.064573382 |
| 100 | −81.219 | −81.316 | −81.294 | −81.3 | −81.2823 | 8.000024 | −3.754277757 |
| 1 k | −86.949 | −86.951 | −86.952 | −86.952 | −86.951 | 4.000017 | −2.00805606 |
| 10 k | −86.913 | −86.913 | −86.913 | −86.914 | −86.9133 | 0.708691 | −0.355616972 |
| 100 k | −86.646 | −86.647 | −86.647 | −86.646 | −86.6465 | 0.708665 | −0.354512185 |
| 1 M | −87.047 | −87.047 | −87.046 | −87.046 | −87.0465 | 1.326114 | −0.666456111 |
| Structure after annealing | |||||||
| 10 | −38 | −38.121 | −37.69 | −38.141 | −37.988 | 8.000011 | −1.754593062 |
| 100 | −42.656 | −42.663 | −42.664 | −42.686 | −42.6673 | 8.000013 | −1.970719015 |
| 1 k | −66.248 | −66.248 | −66.252 | −66.25 | −66.2495 | 0.600001 | −0.229495504 |
| 10 k | −83.458 | −83.457 | −83.456 | −83.458 | −83.4573 | 0.600002 | −0.289105198 |
| 100 k | −86.228 | −86.232 | −86.23 | −86.231 | −86.2303 | 0.700001 | −0.348495836 |
| 1 M | −38 | −38.121 | −37.69 | −38.141 | −37.988 | 8.000011 | −0.654273402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczyńska, A.; Kociubiński, A.; Kołtunowicz, T.N. Preparation of Discontinuous Cu/SiO2 Multilayers—AC Conduction and Determining the Measurement Uncertainty. Sensors 2023, 23, 2842. https://doi.org/10.3390/s23052842
Wilczyńska A, Kociubiński A, Kołtunowicz TN. Preparation of Discontinuous Cu/SiO2 Multilayers—AC Conduction and Determining the Measurement Uncertainty. Sensors. 2023; 23(5):2842. https://doi.org/10.3390/s23052842
Chicago/Turabian StyleWilczyńska, Aleksandra, Andrzej Kociubiński, and Tomasz N. Kołtunowicz. 2023. "Preparation of Discontinuous Cu/SiO2 Multilayers—AC Conduction and Determining the Measurement Uncertainty" Sensors 23, no. 5: 2842. https://doi.org/10.3390/s23052842
APA StyleWilczyńska, A., Kociubiński, A., & Kołtunowicz, T. N. (2023). Preparation of Discontinuous Cu/SiO2 Multilayers—AC Conduction and Determining the Measurement Uncertainty. Sensors, 23(5), 2842. https://doi.org/10.3390/s23052842









