A Compensation Method for the Geomagnetic Measurement Error of an Underwater Ship-Borne Magnetometer Based on Constrained Total Least Squares
Abstract
:1. Introduction
2. Modeling of the Underwater Vehicle’s Internal Magnetic Field
2.1. Global Geomagnetic Field Calculation
2.2. Calculation of the Internal Magnetic Field of the Rotating Ellipsoidal Shell Model
2.3. Magnetic Dipole Field Calculation
3. Error Model and Compensation Algorithm of the Ship-Borne Magnetometer
3.1. Error Model
3.2. Compensation Algorithm Based on Constrained Total Least Squares
4. Experiment
4.1. Output Simulation of the Magnetometer
4.2. Compensation Simulation of the Magnetometer’s Measurement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Xu, Z.; Wang, X. Research on error of underwater terrain aided navigation based on TERCOM algorithm. J. Nav. Univ. Eng. 2020, 32, 44–49. [Google Scholar]
- Zou, J.; Cai, T. Improved Particle Swarm Optimization screening iterative algorithm in gravity matching navigation. IEEE Sens. J. 2022, 22, 20866–20876. [Google Scholar] [CrossRef]
- Gao, S.; Cai, T.; Fang, K. Gravity-matching algorithm based on K-Nearest neighbor. Sensors 2022, 22, 4454. [Google Scholar] [CrossRef]
- Zhai, H.; Wang, L. The robust residual-based adaptive estimation Kalman filter method for strap-down inertial and geomagnetic tightly integrated navigation system. Rev. Sci. Instruments 2020, 91, 104501. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.; Chen, Q.; Song, C. Improved particle swarm optimization geomagnetic matching algorithm based on simulated annealing. IEEE Access 2020, 8, 226064–226073. [Google Scholar] [CrossRef]
- Li, J. Study on the Characteristics and Compensation Method of Vehicle Interferential Magnetic Field in Geomagnetic Measurement. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Henkel, P. Calibration of Magnetometers with GNSS Receivers and Magnetometer-Aided GNSS Ambiguity Fixing. J. Sens. 2017, 17, 1324. [Google Scholar] [CrossRef]
- Henkel, P.; Berthold, P.; Kiam, J.J. Calibration of Magnetic Field Sensors with Two Mass-Market GNSS Receivers. In Proceedings of the IEEE Workshop on Positioning, Navigation and Communication (WPNC), Dresden, Germany, 12–13 March 2014; p. 5. [Google Scholar]
- Crassidis, J.; Lai, K.-L.; Harman, R. Real-time attitude-independent three-axis magnetometer calibration. J. Guid. Control Dyn. 2005, 28, 115–120. [Google Scholar] [CrossRef]
- Alimi, R.; Fisher, E.; Nahir, K. In Situ Underwater Localization of Magnetic Sensors Using Natural Computing Algorithms. J. Sens. 2023, 23, 1797. [Google Scholar] [CrossRef]
- Su, X.; Ullah, I.; Liu, X.; Choi, D. A Review of Underwater Localization Techniques, Algorithms, and Challenges. J. Sens. 2020, 2020, 6403161. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Bu, R.; Zhang, E. A Novel Cross-Layer Routing Protocol Based on Network Coding for Underwater Sensor Networks. Sensors 2017, 17, 1821. [Google Scholar] [CrossRef]
- Callmer, J.; Skoglund, M.; Gustafsson, F. Silent Localization of Underwater Sensors Using Magnetometers. EURASIP J. Adv. Signal Process. 2010, 2010, 709318. [Google Scholar] [CrossRef]
- Alonso, R.; Shuster, M.D. Complete Linear Attitude-Independent Magnetometer Calibration. J. Astronaut. Sci. 2003, 50, 477–490. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Elkaim, G.H.; Powell, J.D.; Parkinson, B.W. Calibration of Strapdown Magnetometers in Magnetic Field Domain. J. Aerosp. Eng. 2006, 19, 87–102. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Tian, W. Component Calibration of Three-Axis Magnetometer with Two Step method. Chin. J. Sens. Actuators 2018, 31, 1707–1713. [Google Scholar]
- Wang, L.; Yu, L.; Liang, B.; Qiao, N. Truncated total least squares algorithm in restraining random error of geomagnetic navigation magnetometer. J. Chin. Inert. Technol. 2015, 23, 763–768. [Google Scholar]
- Zhang, Q.; Pan, M.; Chen, D.; Pang, H. Scalar Calibration of Tri-Axial Magnetometer with Linearized Parameter Model. Chin. J. Sens. Actuators 2012, 25, 215–219. [Google Scholar]
- Bonnet, S.; Bassompierre, C.; Godin, C.; Lesecq, S.; Barraud, A. Calibration methods for inertial and magnetic sensors. Sens. Actuators A Phys. 2009, 156, 302–311. [Google Scholar] [CrossRef]
- Pang, H.F.; Luo, S.T.; Chen, D.X.; Pan, M.C.; Zhang, Q. Error Calibration of Fluxgate Magnetometers in Arbitrary Attitude Situation. J. Test Meas. Technol. 2011, 25, 371–375. [Google Scholar]
- Wu, Z.; Wu, Y.; Hu, X.; Wu, M. Calibration of Strapdown Three-axis Magnetometer and Measurement Error Compensation of Geomagnetic Field Based on Total Least Squares. Acta Armamentarii 2012, 33, 1202–1209. [Google Scholar]
- Zhang, Y.; Yang, R.; Li, M.; Zuo, J.; Chen, X. Calibration of Vehicular Three-axis Magnetometer via Truncated Total Least Squares Algorithm. Acta Armamentarii 2015, 36, 427–432. [Google Scholar]
- Sun, H.; Yang, B.; Wu, H.; Li, C.; Wang, R. Integrated Compensation Method of Three-axis Magnetometer Based on EKF Algorithm. J. Proj. Rocket. Missiles Guid. 2019, 39, 149–154. [Google Scholar]
- Yang, B.; Wang, R.; Sun, H. Integrated Error Compensation Method for Three-Axis Magnetometer in Geomagnetic Navigation. In Lecture Notes in Electrical Engineering. In Proceedings of the China Satellite Navigation Conference (CSNC) 2020 Proceedings: Volume I. CSNC 2020; Chengdu, China, 22–25 November 2020, Springer: Singapore, 2020; Volume 650, p. 650. [Google Scholar] [CrossRef]
- Cheng, Z. Calibration Method of Magnetometer Based on BP Neural Network. J. Comput. Commun. 2020, 6, 31–41. [Google Scholar]
- Yu, P.; Zhao, X.; Jia, J.; Zhou, S. An improved neural network method for aeromagnetic compensation. Meas. Sci. Technol. 2021, 32, 045106. [Google Scholar] [CrossRef]
- Zhu, X.L.; Chen, S.H. Method on eliminating magnetic interference in shipboard geomagnetic field measurement. Ship Sci. Technol. 2019, 41, 126–129. [Google Scholar]
- Li, T.; Zhang, J.S.; Wang, S.C.; Li, D.Y. Compensation of geomagnetic field measurement error based on damped particle swarm optimization. Chin. J. Sci. Instrum. 2017, 38, 2246–2452. [Google Scholar]
- Zhang, W.; Zhang, G. New Measuring and Calculate Method of Submarine Space Magnetic Field. Ship Electron. Eng. 2010, 4, 170–173. [Google Scholar]
- Zhang, Y.; Mao, S. Modeling Analysis and Application of Submarine Space Magnetic. Ship Electron. Eng. 2018, 38, 136–139. [Google Scholar]
- Lin, C. Single-row Ellipsoid and Magnetic Dipole Mixed Model in Ship Magnetic Field Depth Conversion. Mine Warf. Ship Prot. 1996, 3, 54–58. [Google Scholar]
- Qu, X.; Yang, R.; Shan, Z. Analysis and comparison on magnetic field modeling method of submarine. Ship Sci. Technol. 2011, 33, 7–11. [Google Scholar]
- Alken, P.; Thebault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, G. Ship Magnetic Field Analysis and Calculation; National Defence Industry Press: Beijing, China, 2004. [Google Scholar]
- Yang, L.; Liu, T. Warship Magnetic Field Simulation Technology Based on Magnetic Dipoles. Ship Electron. Eng. 2017, 37, 60–64. [Google Scholar]
- Foster, C.C.; Elkaim, G.H. Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1070–1078. [Google Scholar] [CrossRef]
- Vasconcelos, J.F.; Elkaim, G.; Silvestre, C.; Oliveira, P.; Cardeira, B. Geometric Approach to Strapdown Magnetometer Calibration in Sensor Frame. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1293–1306. [Google Scholar] [CrossRef]
- Bjorck, A. Least squares methods. Handb. Numer. Anal. 1990, 1, 465–652. [Google Scholar]
- Abatzoglou, T.; Mendel, J.; Harada, G. The constrained total least squares technique and its applications to harmonic superresolution. IEEE Trans. Signal Process. 1991, 39, 1070–1087. [Google Scholar] [CrossRef]
- Golub, G.H.; Loan, C.V. An Analysis of the Total Least Squares Problem; Cornell University: Ithaca, NY, USA, 1980. [Google Scholar]
- Huffel, S.V.; Vandewalle, J. The Total Least Squares Problem: Computational Aspects and Analysis; Society for Industrial and Applied Mathematics: University City, PA, USA, 1991. [Google Scholar]
- Wu, Z. Research on Geomagnetic Measurement Error Compensation for Underwater Geomagnetic Navigation. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]






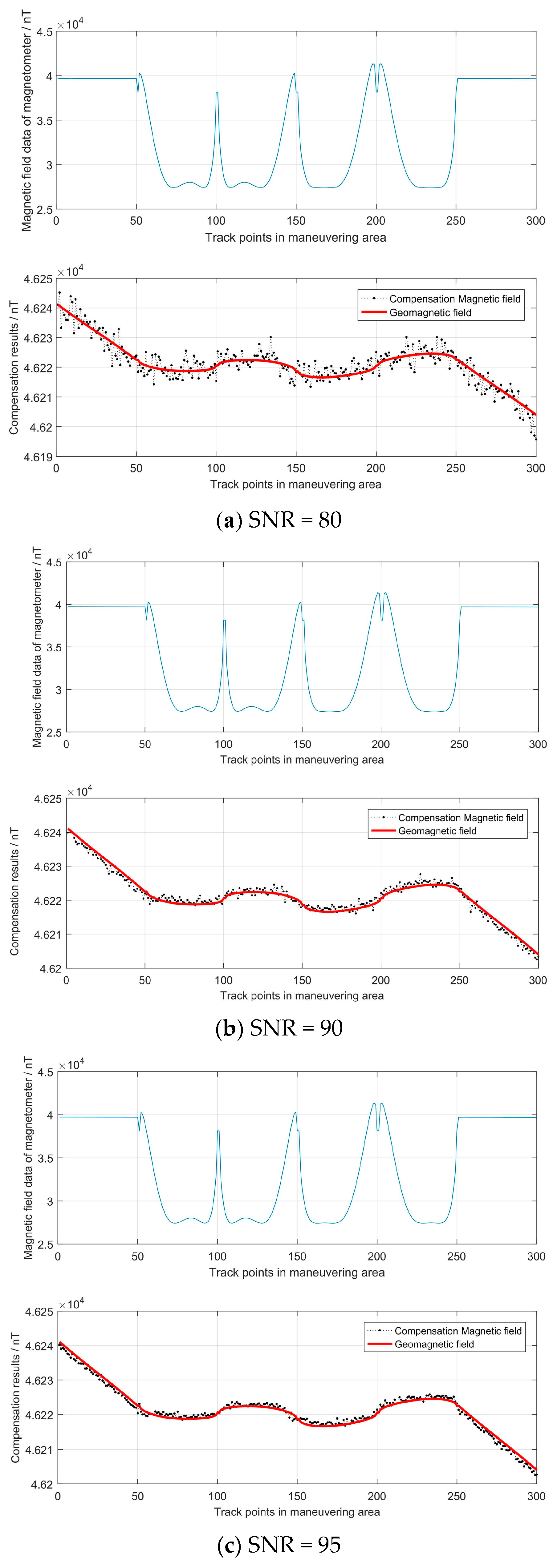
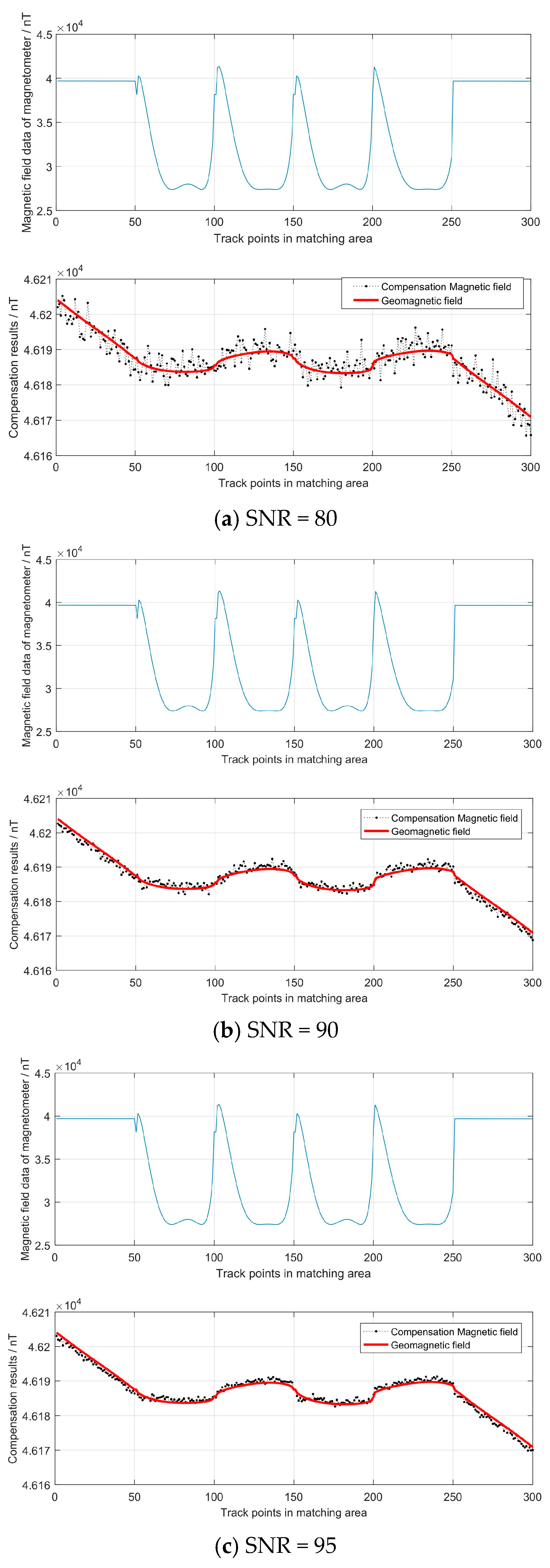
| SNR | P | O | RMSE |
|---|---|---|---|
| 80 | 3.02 | ||
| 90 | 1.86 | ||
| 95 | 1.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Y.; Huang, X.; Chen, Y.; Li, W.; Zha, F. A Compensation Method for the Geomagnetic Measurement Error of an Underwater Ship-Borne Magnetometer Based on Constrained Total Least Squares. Sensors 2024, 24, 3478. https://doi.org/10.3390/s24113478
Tong Y, Huang X, Chen Y, Li W, Zha F. A Compensation Method for the Geomagnetic Measurement Error of an Underwater Ship-Borne Magnetometer Based on Constrained Total Least Squares. Sensors. 2024; 24(11):3478. https://doi.org/10.3390/s24113478
Chicago/Turabian StyleTong, Yude, Xiaoying Huang, Yongbing Chen, Wenkui Li, and Feng Zha. 2024. "A Compensation Method for the Geomagnetic Measurement Error of an Underwater Ship-Borne Magnetometer Based on Constrained Total Least Squares" Sensors 24, no. 11: 3478. https://doi.org/10.3390/s24113478




