Geometric Implications of Photodiode Arrays on Received Power Distribution in Mobile Underwater Optical Wireless Communication
Abstract
1. Introduction
- To provide a thorough review of the existing literature and commercial products of UOWC transmitter and receiver designs, with a focus on mobile UOWCs.
- To devise a model for estimating the received power distribution of diffused line-of-sight mobile optical links that accurately reflects the intensity distribution profiles of LEDs with non-uniform or irregular polar-intensity distributions.
- To conduct a spatial analysis using the above model to investigate the parametric influence of the placement, orientation, and angular spread of PD positioning on array-based receivers for mobile UOWC in different Jerlov seawater types. We assess this for wavelengths within the visible spectrum (400–700 nm), and we compare the results for the overall received power and bit-error rates, employing modulation schemes commonly used for diffused line-of sight optical links. The results highlight the significance of designing dynamically shape-changing receiver arrays.
2. Literature Review
2.1. Transmitters
2.2. Receivers
| Manufacturer | Model | Transmitter Type | Color | Range (m) | Data Rate (max) | Receiver Port Shape | Power Consumption (W) |
|---|---|---|---|---|---|---|---|
| Aquamodem [21] | OP2/OP2L | LED | Cyan | 1 | 80 kbps | Flat | Not available |
| Sonardyne [22] | 8361 Bluecomm 200 | LED | Blue | 150 | 10 Mbps | Dome | Receiver: 10 W Transmitter: 15 W |
| 8361 Bluecomm 200 UV | LED | UV | 75 | 10 Mbps | Dome | Receiver: 10 W Transmitter: 30 W | |
| Hydromea [23] | Luma 100 | LED | Blue | 2 | 115 kbps | Flat, potted | Receiver: 0.5 W Transmitter: 1–2 W |
| Luma 250LP | LED | Blue | 7 | 250 kbps | Flat, potted | Receiver: 0.5 W Transmitter: 2–5 W | |
| Luma 500ER | LED | Blue | 50 | 500 kbps | Flat, potted | Receiver: 1 W Transmitter: 2–5 W | |
| Luma X | LED | Blue | 50 | 10 Mbps | Flat | Receiver: 2 W Transmitter: 2–17 W | |
| Luma X UV | UV LED | UV | 50 | 10 Mbps | Flat | Receiver: 2 W Transmitter: 2–17 W |
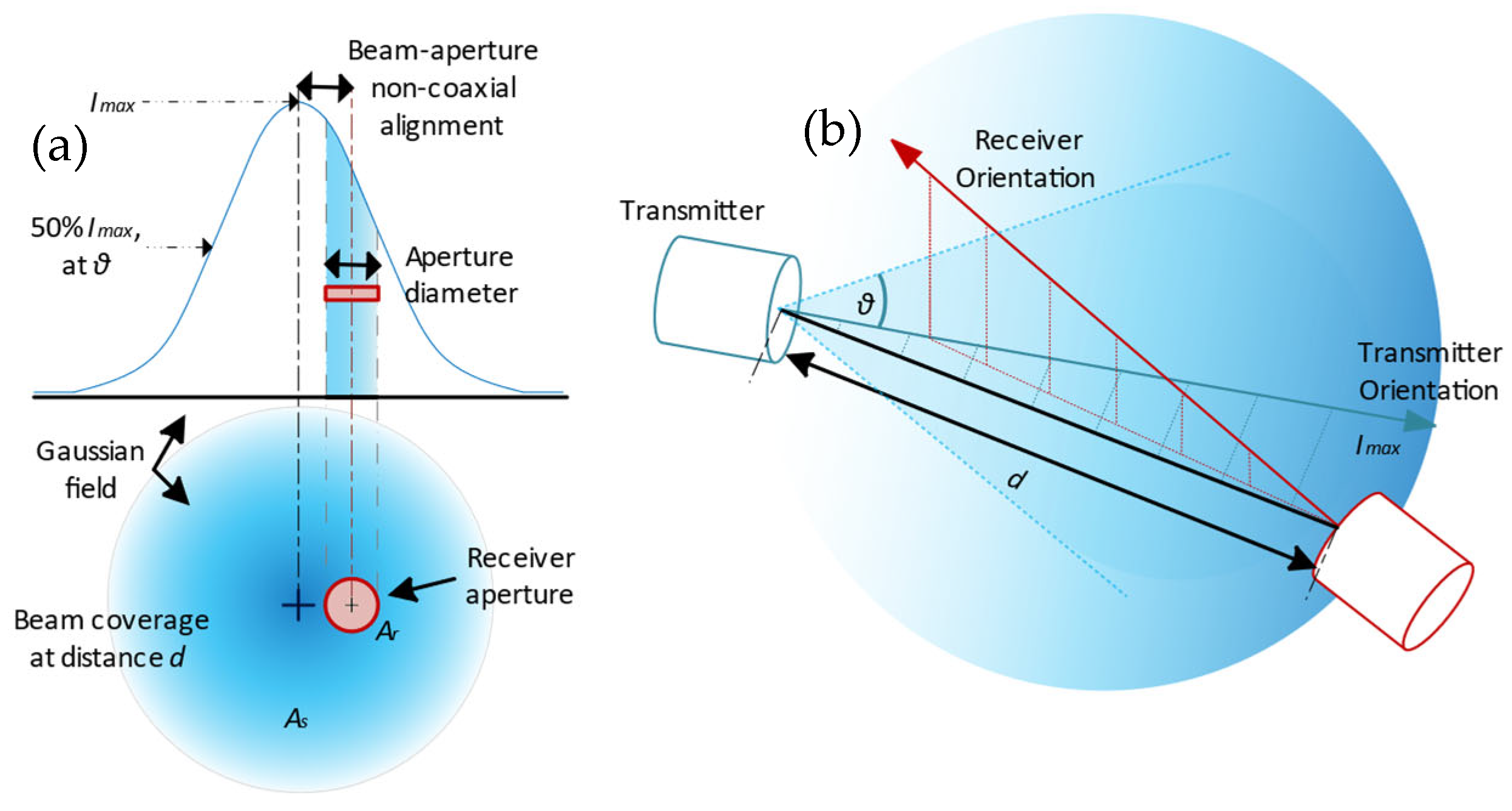
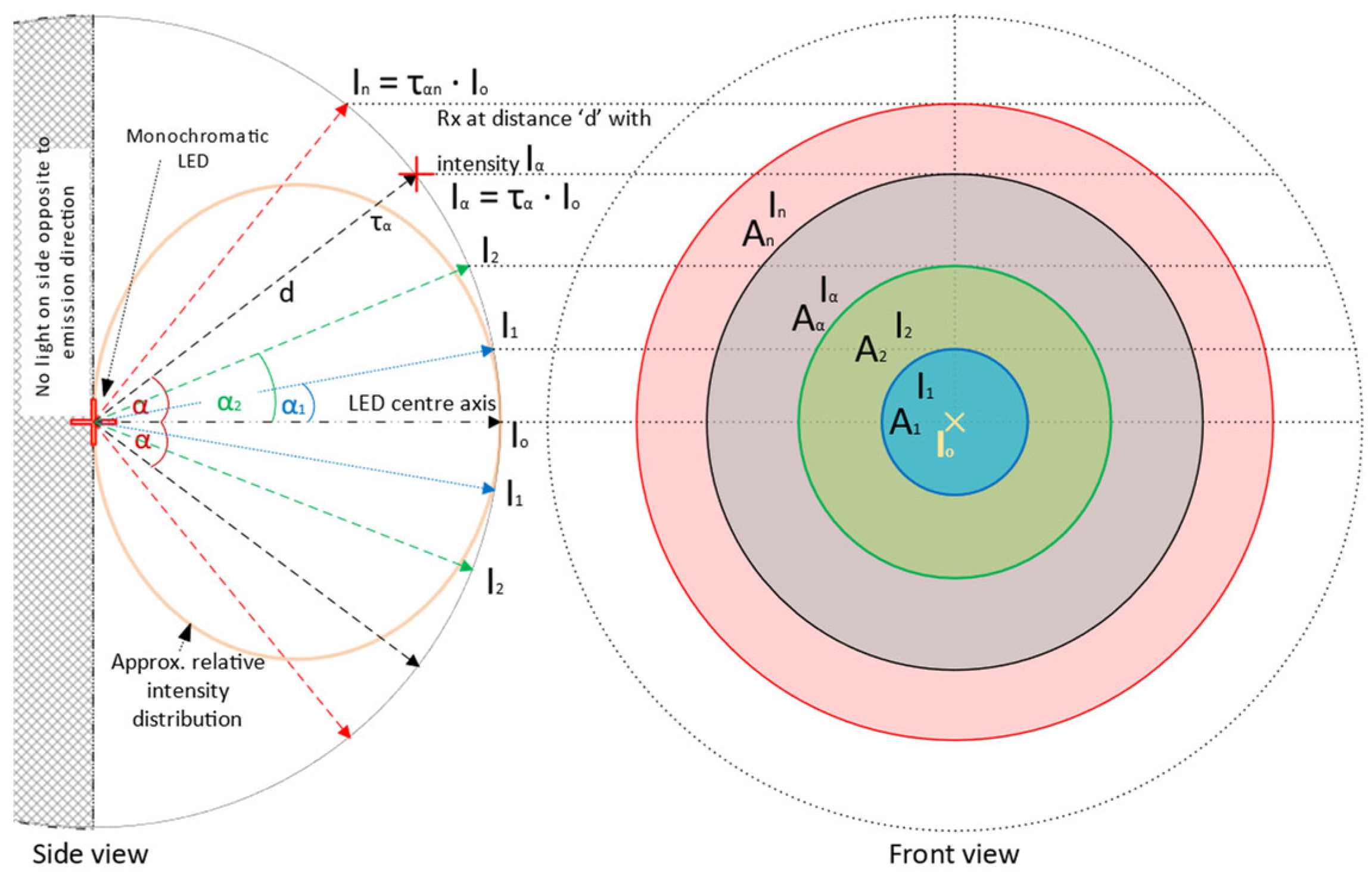
3. Preliminaries
4. Devised Model for Received Power
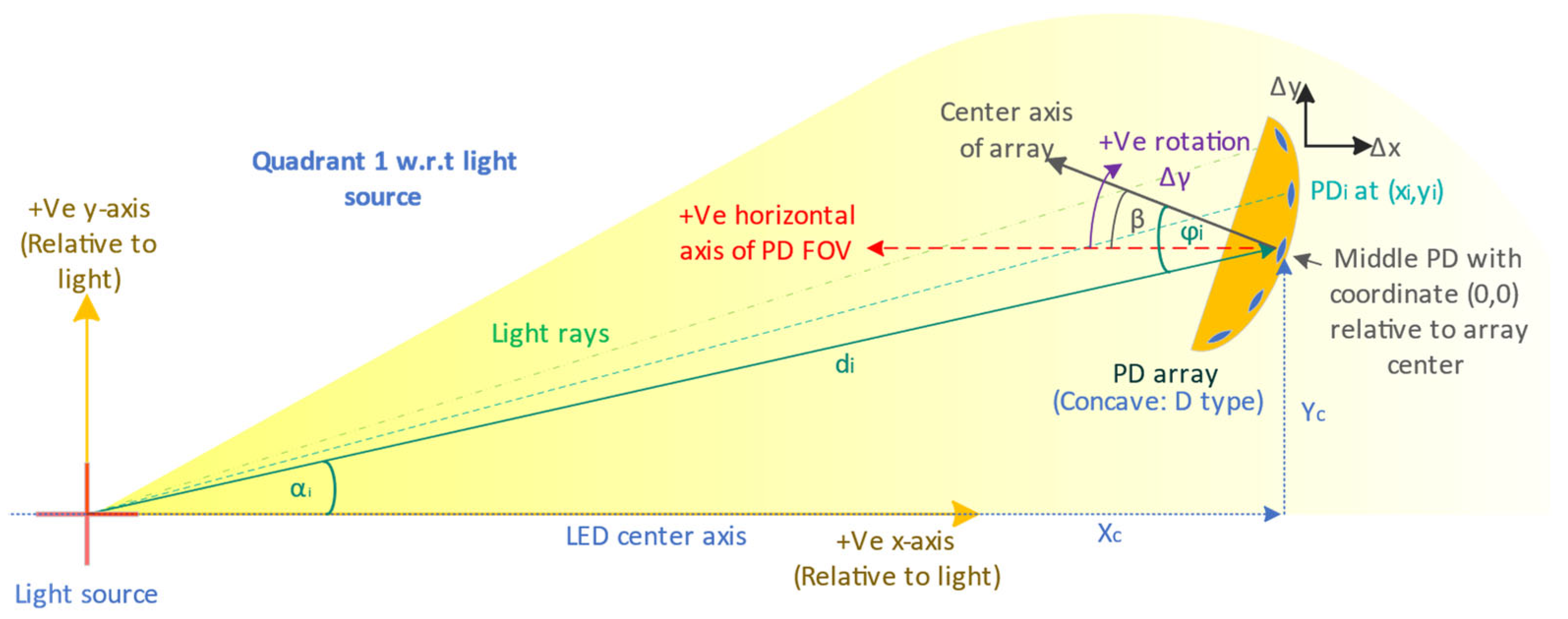
5. Geometric Implications for Optimizing PD Arrays for Received Power
5.1. Parameters and Simulation Design
5.2. Algorithm
| Algorithm 1 Array Received Power | |
| Input: | |
| Output: | |
| 1: | Calculate: |
| 2: | |
| 3: | |
| 4: | Evaluate new relative coordinates of PD to middle PD: |
| 5: | |
| 6: | while do |
| 7: | while do |
| 8: | for each PD do |
| 9: | |
| 10: | |
| 11: | |
| 12: | |
| 13: | |
| 14: | |
| 15: | Total power: |
| 16: | end for |
| 17: | |
| 18: | end while |
| 19: | |
| 20: | end while |
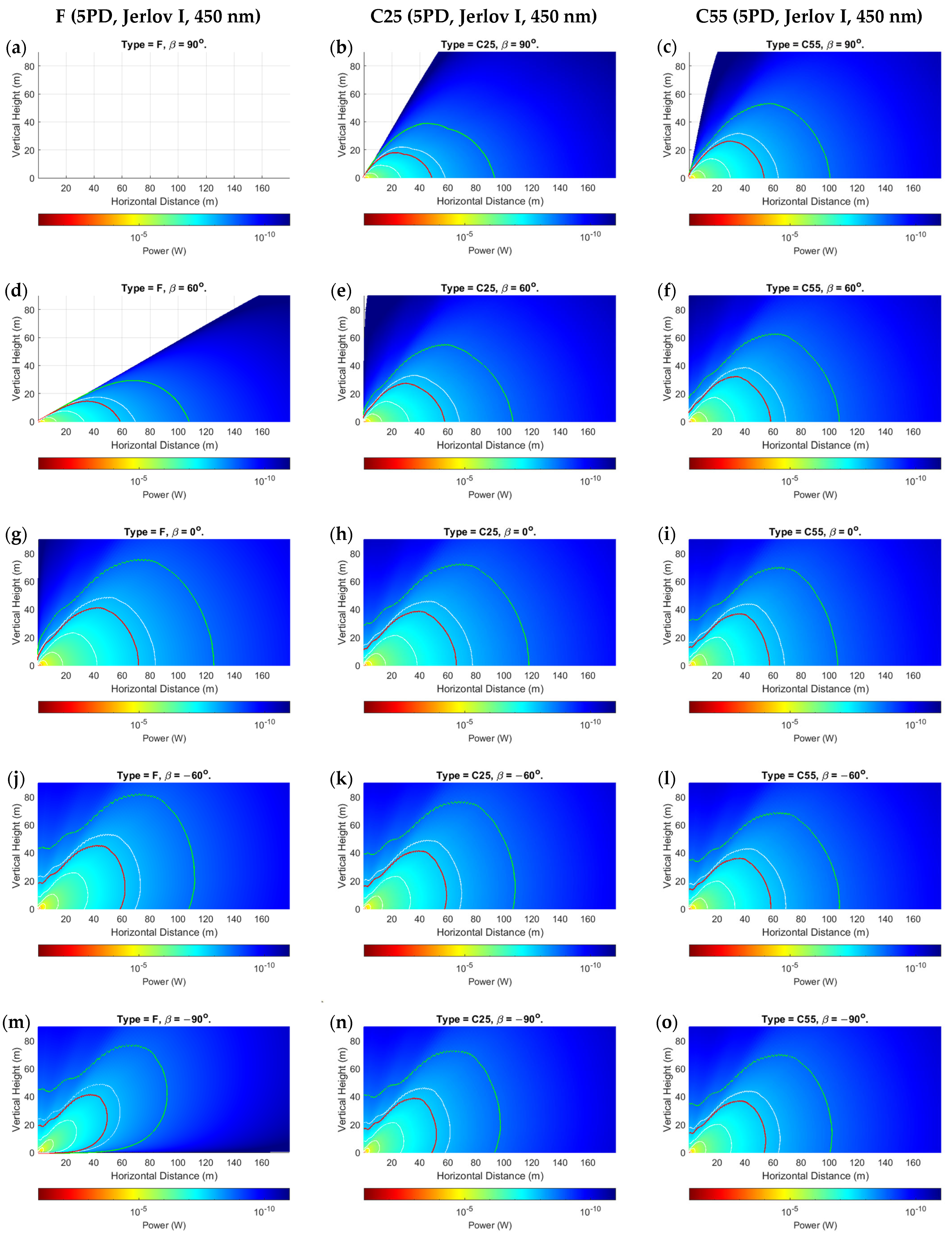
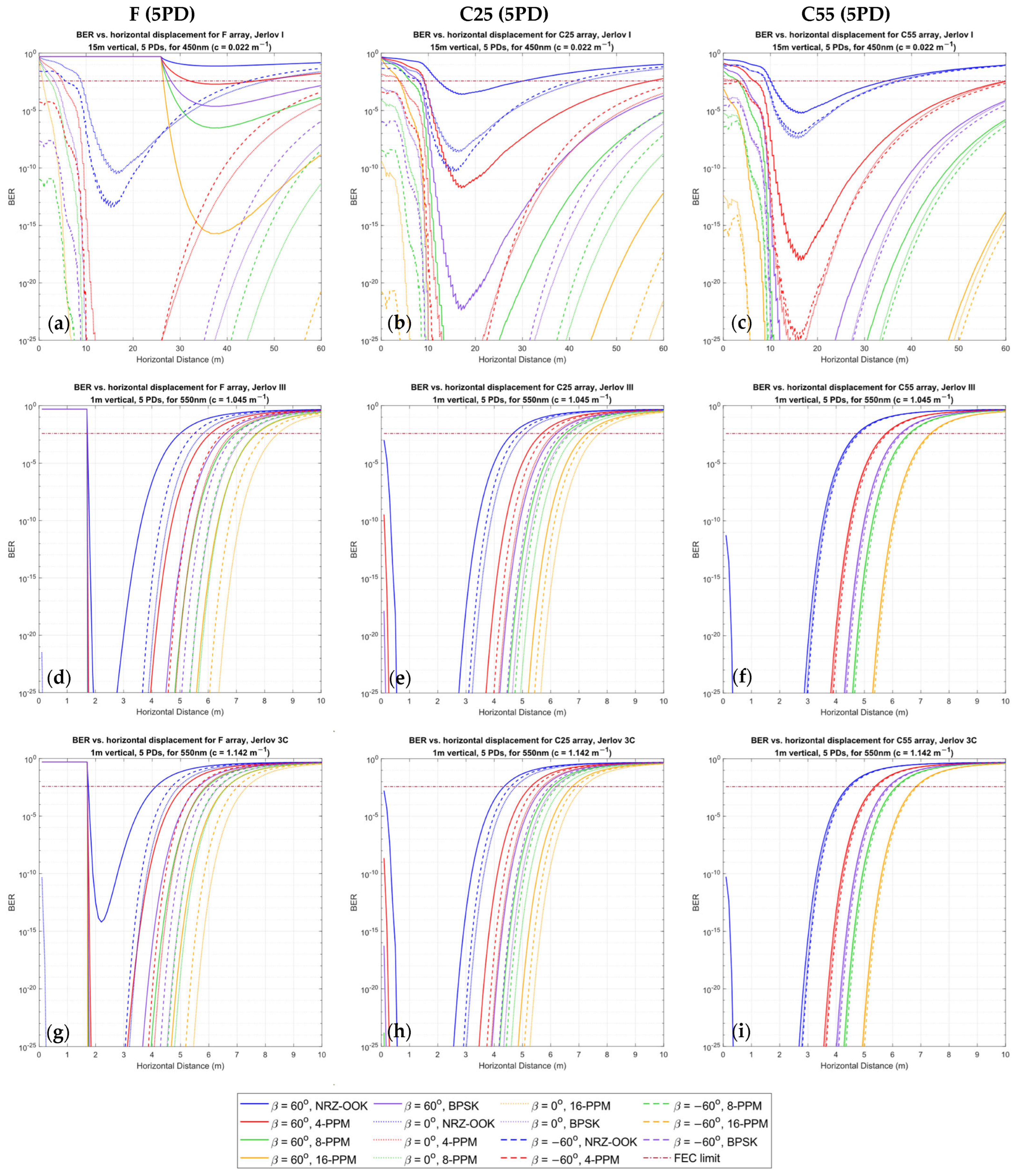
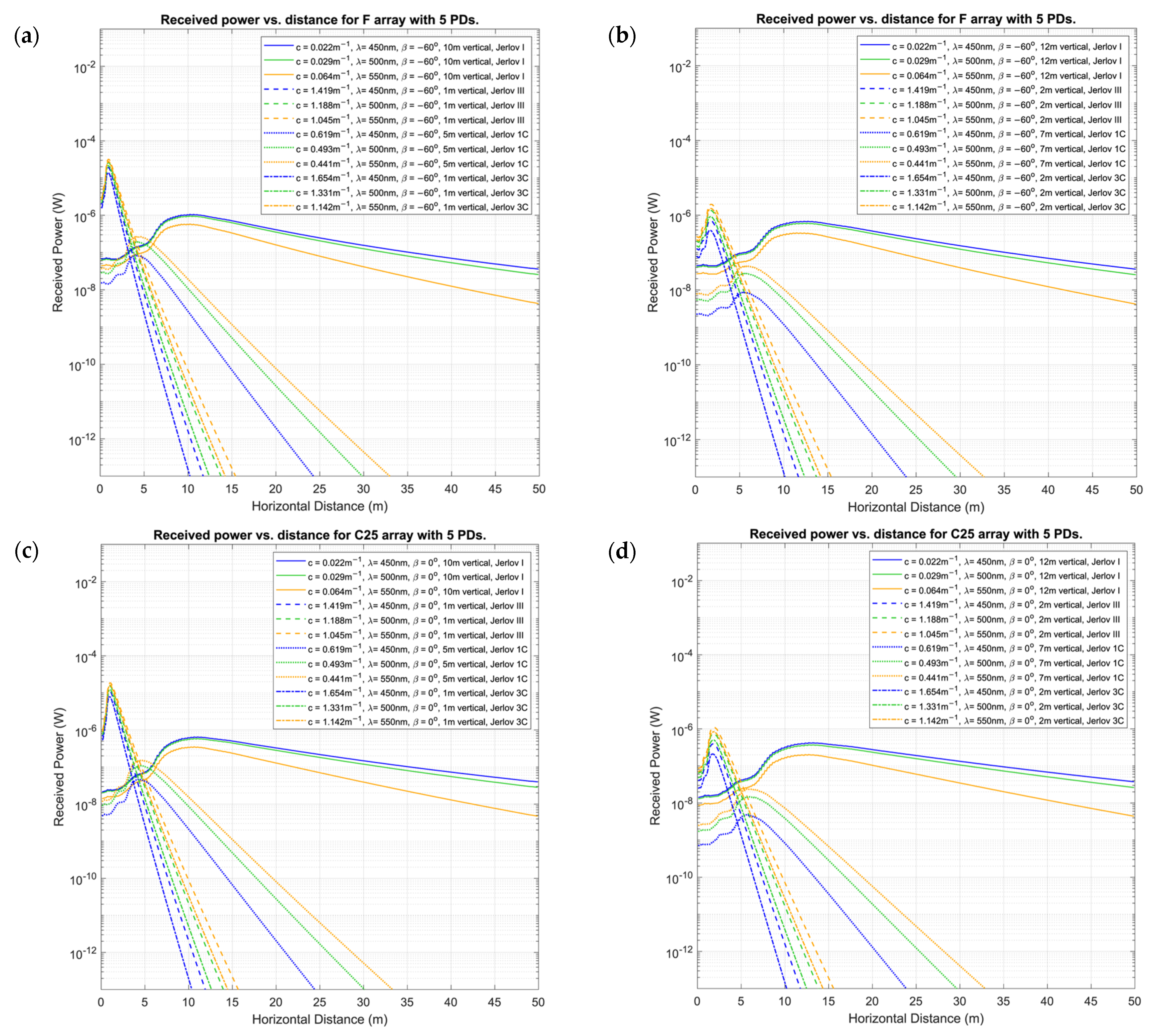
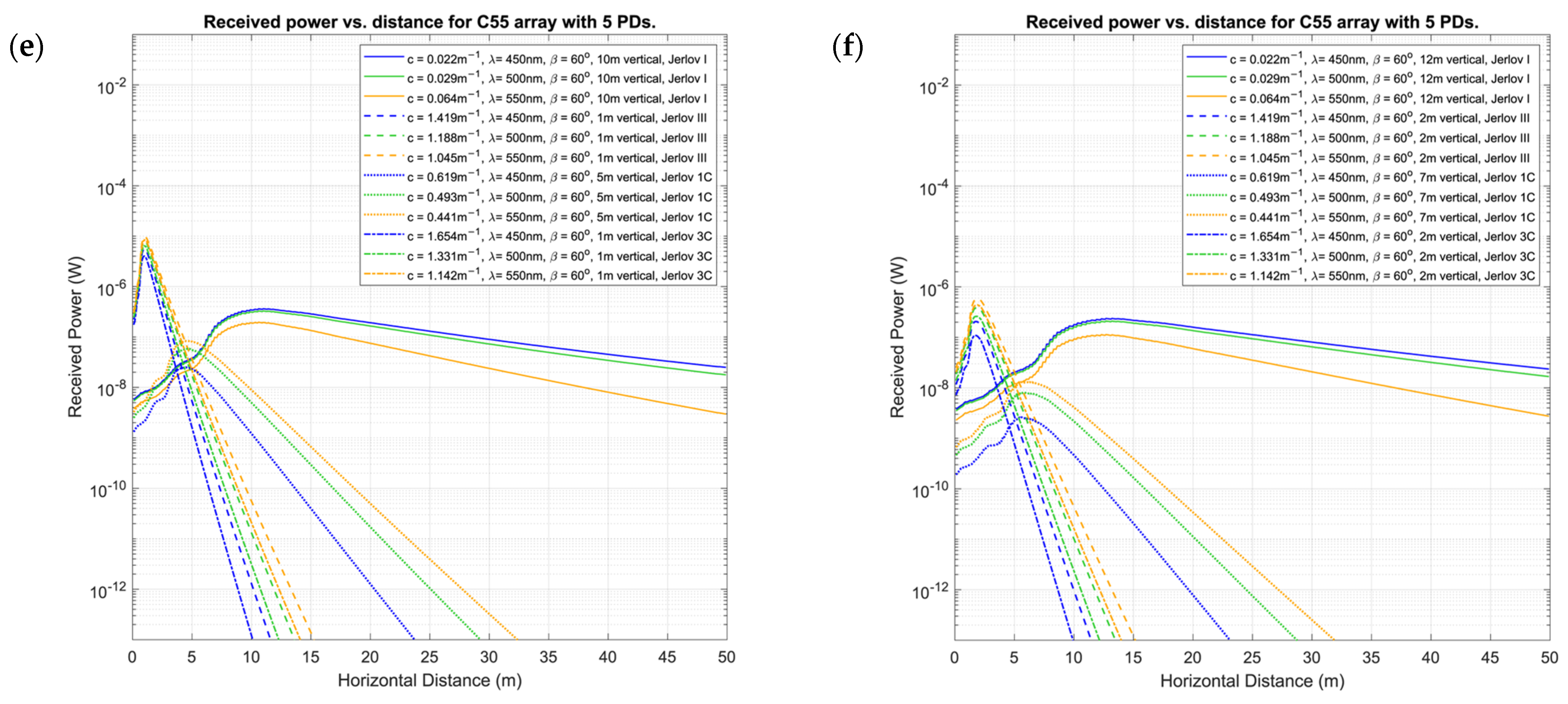
6. Results and Discussion
6.1. Organization of Results
6.2. Discussion
- Flat array designs are optimal for links where Tx–Rx alignment can be strictly maintained. This will need to be controlled dynamically as the UOWC moves to maintain orthogonality to the light ray. If not, the response may be very unpredictable and disadvantageous. There is also a significant risk of total blindness.
- Curved arrays are good overall for mobile UOWCs as they have large overall FOVs. This produces more predictable outcomes and, overall, less drastic BER variation. However, the spread-out PD configurations mean that there will always be some PDs at non-optimal AOIs to light. This may cause an irregular high-and-low received-power response until a peak power is observed at a certain horizontal distance for a given height from the Tx. The horizontal location of this peak power increases with increasing distance.
- The number of PDs used in the array plays a less significant role in optimal performance than the overall FOV of the array, especially as the distance from the transmitter increases. Overall, a convex shape may be better for curved arrays.
- As the clarity of the water improves, the range of link coverage could be improved much more significantly by utilizing more bandwidth-efficient modulation schemes.
- In the presence of non-uniform optical intensity distributions, the optimal BER location for all flat and curved arrays in mobile UOWCs will be sandwiched between two or more high-BER regions contingent on the intensity profile and angular distribution of the PDs.
- Where designers may want to address localization via the optical link, using received-signal-intensity (RSSI)-based methods may not be feasible as multiple loci produce equal received power. However, isolating the attenuation factor by using two or more distinct wavelengths may be a beneficial strategy.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Attenuation coefficient | |
| Relative intensity of light at an angle | |
| Number of annuli | |
| Planar surface area of a PD | |
| Output optical power of emitter | |
| Number of PDs in array | |
| Total number of PDs in array | |
| ith PD’s coordinate relative to middle PD | |
| ith PD’s inclination relative to middle PD axis | |
| Minimum and maximum horizontal test limit | |
| Minimum and maximum vertical test limit | |
| Horizontal distance increment interval | |
| Vertical height increment interval | |
| Rotation angle of array |
References
- Copping, A.E.; Green, R.E.; Cavagnaro, R.J.; Jenne, D.S.; Greene, D.; Martinez, J.J.; Yang, Y. Powering the Blue Economy-Ocean Observing Use Cases Report; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2020.
- Waduge, T.G.; Al-Anbuky, A.; Vopel, K.C. Optical Signals and Prospects Towards Multimedia in Underwater Wireless and Mobile Communication. In Proceedings of the 2022 27th Asia Pacific Conference on Communications (APCC), Jeju Island, Republic of Korea, 19–21 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 48–53. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Underwater Optical Wireless Communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Ali, M.F.; Jayakody, D.N.K.; Li, Y. Recent trends in underwater visible light communication (UVLC) systems. IEEE Access 2022, 10, 22169–22225. [Google Scholar] [CrossRef]
- Han, B.; Zhao, W.; Zheng, Y.; Meng, J.; Wang, T.; Han, Y.; Wang, W.; Su, Y.; Duan, T.; Xie, X. Experimental demonstration of quasi-omni-directional transmitter for underwater wireless optical communication based on blue LED array and freeform lens. Opt. Commun. 2019, 434, 184–190. [Google Scholar] [CrossRef]
- Tong, Z.; Yang, X.; Chen, X.; Zhang, H.; Zhang, Y.; Zou, H.; Zhao, L.; Xu, J. Quasi-omnidirectional transmitter for underwater wireless optical communication systems using a prismatic array of three high-power blue LED modules. Opt. Express 2021, 29, 20262–20274. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Yuan, Y.; Yin, H.; Zhao, H.; Fu, X. Optimization of LED Array Spatial Coverage Characteristics in Underwater Wireless Optical Communication. J. Mar. Sci. Eng. 2023, 11, 253. [Google Scholar] [CrossRef]
- Romdhane, I.; Kaddoum, G. A Reinforcement-Learning-Based Beam Adaptation for Underwater Optical Wireless Communications. IEEE Internet Things J. 2022, 9, 20270–20281. [Google Scholar] [CrossRef]
- Cui, Z.; Yue, P.; Yi, X.; Li, J. Improving the Performance of Underwater Wireless Optical Communications by Pointing Adjustable Beam Arrays. IEEE Trans. Veh. Technol. 2022, 72, 483–497. [Google Scholar] [CrossRef]
- Yildiz, S.; Baglica, I.; Kebapci, B.; Elamassie, M.; Uysal, M. Reflector-aided underwater optical channel modeling. Opt. Lett. 2022, 47, 5321–5324. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Cao, F.; Gu, Y.; Han, Z.; Liu, J.; Huang, B.; Xu, X.; Zeng, H. Broadband and sensitive two-dimensional halide perovskite photodetector for full-spectrum underwater optical communication. Nano Res. 2020, 14, 1210–1217. [Google Scholar] [CrossRef]
- Kang, C.H.; Alkhazragi, O.; Sinatra, L.; Alshaibani, S.; Wang, Y.; Li, K.H.; Kong, M.; Lutfullin, M.; Bakr, O.M.; Ng, T.K.; et al. All-inorganic halide-perovskite polymer-fiber-photodetector for high-speed optical wireless communication. Opt. Express 2022, 30, 9823–9840. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Luo, L.; Huang, Y.; Wei, S.; Zou, J.; He, A.; Huang, B.; Li, X.; Zhao, J.; Shen, K.; et al. Macroscopic and microscopic defect management in blue/green photodetectors for underwater wireless optical communication. J. Mater. Chem. C 2022, 10, 5970–5980. [Google Scholar] [CrossRef]
- Xu, X.; Fu, Y.; Shi, Z.; Li, C.; Kuai, Y.; Hu, Z.; Cao, Z.; Li, S. Stable and self-healing perovskite for high-speed underwater optical wireless communication. J. Mater. Chem. C 2024, 12, 3907–3914. [Google Scholar] [CrossRef]
- Lou, Y.; Ahmed, N. Underwater Communications and Networks; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Lin, R.; Liu, X.; Zhou, G.; Qian, Z.; Cui, X.; Tian, P. InGaN micro-LED array enabled advanced underwater wireless optical communication and underwater charging. Adv. Opt. Mater. 2021, 9, 2002211. [Google Scholar] [CrossRef]
- Liu, A.; Zhang, R.; Lin, B.; Yin, H. Multi-degree-of-freedom for underwater optical wireless communication with improved transmission performance. J. Mar. Sci. Eng. 2022, 11, 48. [Google Scholar] [CrossRef]
- Simpson, J.A.; Hughes, B.L.; Muth, J.F. Smart transmitters and receivers for underwater free-space optical communication. IEEE J. Sel. Areas Commun. 2012, 30, 964–974. [Google Scholar] [CrossRef]
- Rust, I.C.; Asada, H.H. A dual-use visible light approach to integrated communication and localization of underwater robots with application to non-destructive nuclear reactor inspection. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2445–2450. [Google Scholar]
- Hoeher, P.A.; Sticklus, J.; Harlakin, A. Underwater Optical Wireless Communications in Swarm Robotics: A Tutorial. IEEE Commun. Surv. Tutor. 2021, 23, 2630–2659. [Google Scholar] [CrossRef]
- AQUAmodem® Op2, Aquatec Group Ltd, Basingstoke, UK. Available online: https://www.aquatecgroup.com/aquamodem/aquamodem-op2 (accessed on 19 April 2024).
- BlueComm 200, Sonardyne, Hampshire, UK. Available online: https://www.sonardyne.com/products/bluecomm-200-wireless-underwater-link/ (accessed on 19 April 2024).
- LUMA, Hydromea, Renens, Switzerland. Available online: https://www.hydromea.com/underwater-wireless-communication (accessed on 19 April 2024).
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Solonenko, M.G.; Mobley, C.D. Inherent optical properties of Jerlov water types. Appl. Opt. 2015, 54, 5392–5401. [Google Scholar] [CrossRef] [PubMed]
- Arnon, S. Underwater optical wireless communication network. Opt. Eng. 2010, 49, 015001. [Google Scholar] [CrossRef]
- Haas, H.; Sarbazi, E.; Marshoud, H.; Fakidis, J. Visible-light communications and light fidelity. In Optical Fiber Telecommunications VII; Elsevier: Amsterdam, The Netherlands, 2020; pp. 443–493. [Google Scholar]
- OSRAM LED ENGIN LuxiGen®, LZ4-00G108 Color LEDs—Ams-osram—Ams, ams-osram. Available online: https://ams-osram.com/products/leds/color-leds/osram-led-engin-luxigen-lz4-00g108 (accessed on 21 June 2023).
- 200-12-22-041. DigiKey Electronics. Available online: https://www.digikey.co.nz/en/products/detail/advanced-photonix/200-12-22-041/1012514 (accessed on 19 April 2024).
- Elganimi, T.Y. Studying the BER performance, power-and bandwidth-efficiency for FSO communication systems under various modulation schemes. In Proceedings of the 2013 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, 3–5 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Petzold, T.J. Volume Scattering Functions for Selected Ocean Waters; Scripps Institution of Oceanography: La Jolla, CA, USA, 1972. [Google Scholar]
- Hanson, F.; Radic, S. High bandwidth underwater optical communication. Appl. Opt. 2008, 47, 277–283. [Google Scholar] [CrossRef] [PubMed]




| Water Type | a (m−1) | b (m−1) | c (m−1) |
|---|---|---|---|
| Clear ocean | 0.114 | 0.037 | 0.151 |
| Coastal ocean | 0.179 | 0.220 | 0.339 |
| Turbid harbor | 0.366 | 1.829 | 2.195 |
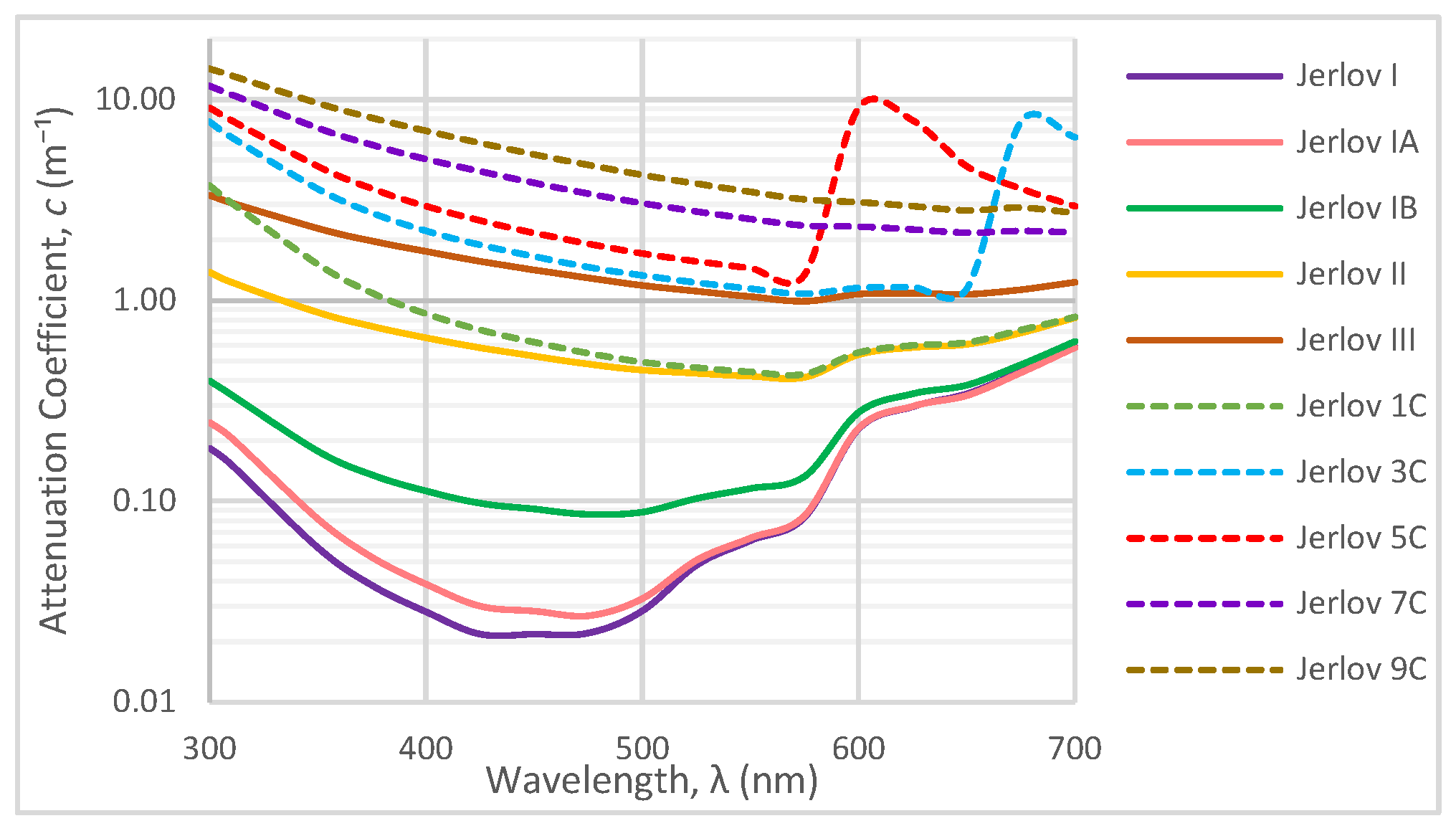
| Jerlov Type | (m−1) | (m−1) | (m−1) |
|---|---|---|---|
| Jerlov I | 0.022 | 0.029 | 0.064 |
| Jerlov IA | 0.028 | 0.033 | 0.066 |
| Jerlov IB | 0.092 | 0.088 | 0.116 |
| Jerlov II | 0.528 | 0.450 | 0.420 |
| Jerlov III | 1.419 | 1.188 | 1.045 |
| Jerlov 1C | 0.619 | 0.493 | 0.441 |
| Jerlov 3C | 1.654 | 1.331 | 1.142 |
| Jerlov 5C | 2.167 | 1.711 | 1.447 |
| Jerlov 7C | 3.842 | 3.050 | 2.545 |
| Jerlov 9C | 5.333 | 4.213 | 3.468 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Govinda Waduge, T.; Seet, B.-C.; Vopel, K. Geometric Implications of Photodiode Arrays on Received Power Distribution in Mobile Underwater Optical Wireless Communication. Sensors 2024, 24, 3490. https://doi.org/10.3390/s24113490
Govinda Waduge T, Seet B-C, Vopel K. Geometric Implications of Photodiode Arrays on Received Power Distribution in Mobile Underwater Optical Wireless Communication. Sensors. 2024; 24(11):3490. https://doi.org/10.3390/s24113490
Chicago/Turabian StyleGovinda Waduge, Tharuka, Boon-Chong Seet, and Kay Vopel. 2024. "Geometric Implications of Photodiode Arrays on Received Power Distribution in Mobile Underwater Optical Wireless Communication" Sensors 24, no. 11: 3490. https://doi.org/10.3390/s24113490
APA StyleGovinda Waduge, T., Seet, B.-C., & Vopel, K. (2024). Geometric Implications of Photodiode Arrays on Received Power Distribution in Mobile Underwater Optical Wireless Communication. Sensors, 24(11), 3490. https://doi.org/10.3390/s24113490







