A Ground-Based Electrostatically Suspended Accelerometer
Abstract
1. Introduction
2. Structural Design and Operation Principles
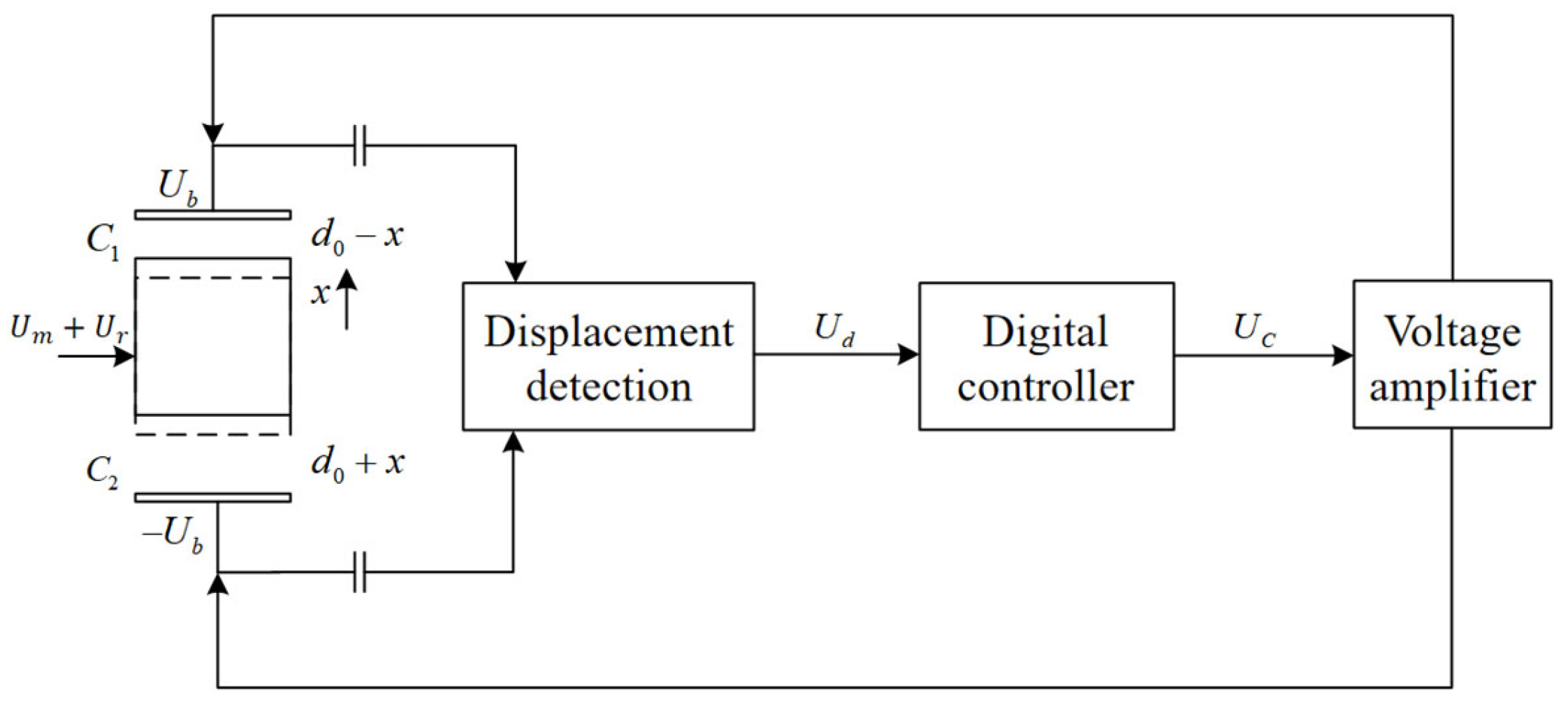
2.1. System Overview
2.2. Designed Structure
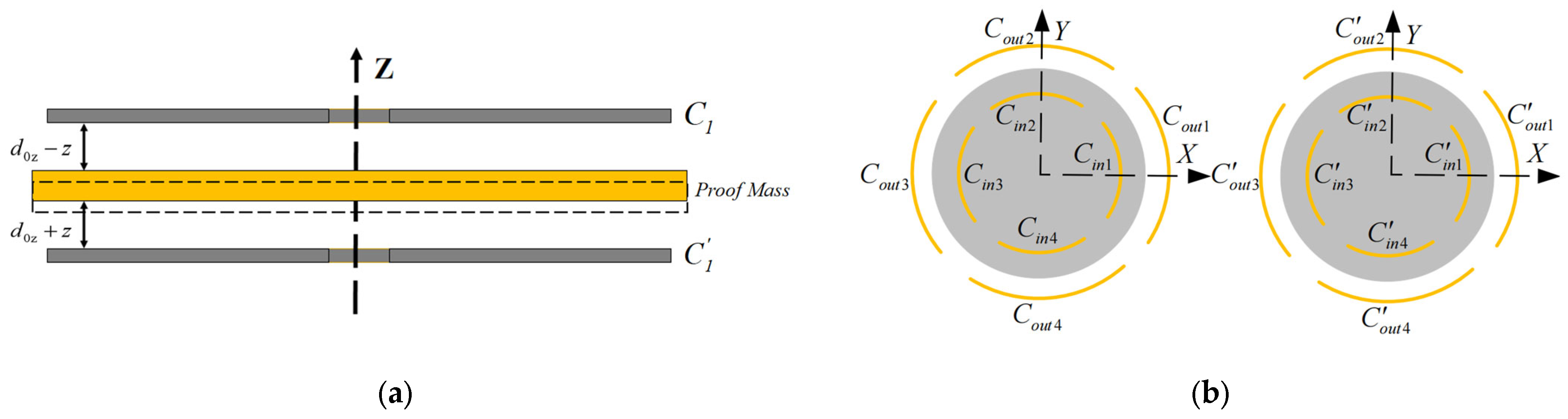
3. Displacement Detection of Proof Mass
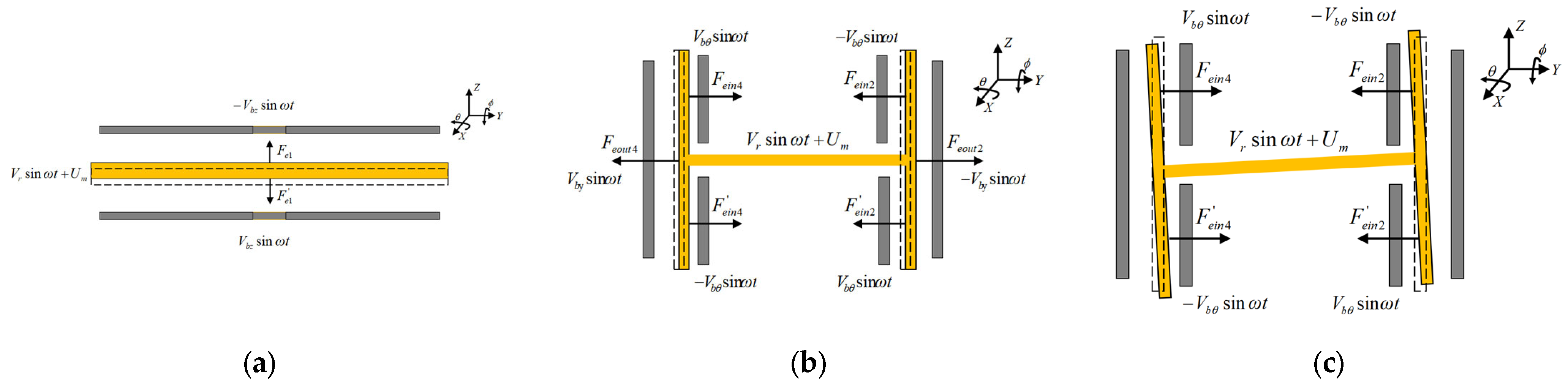
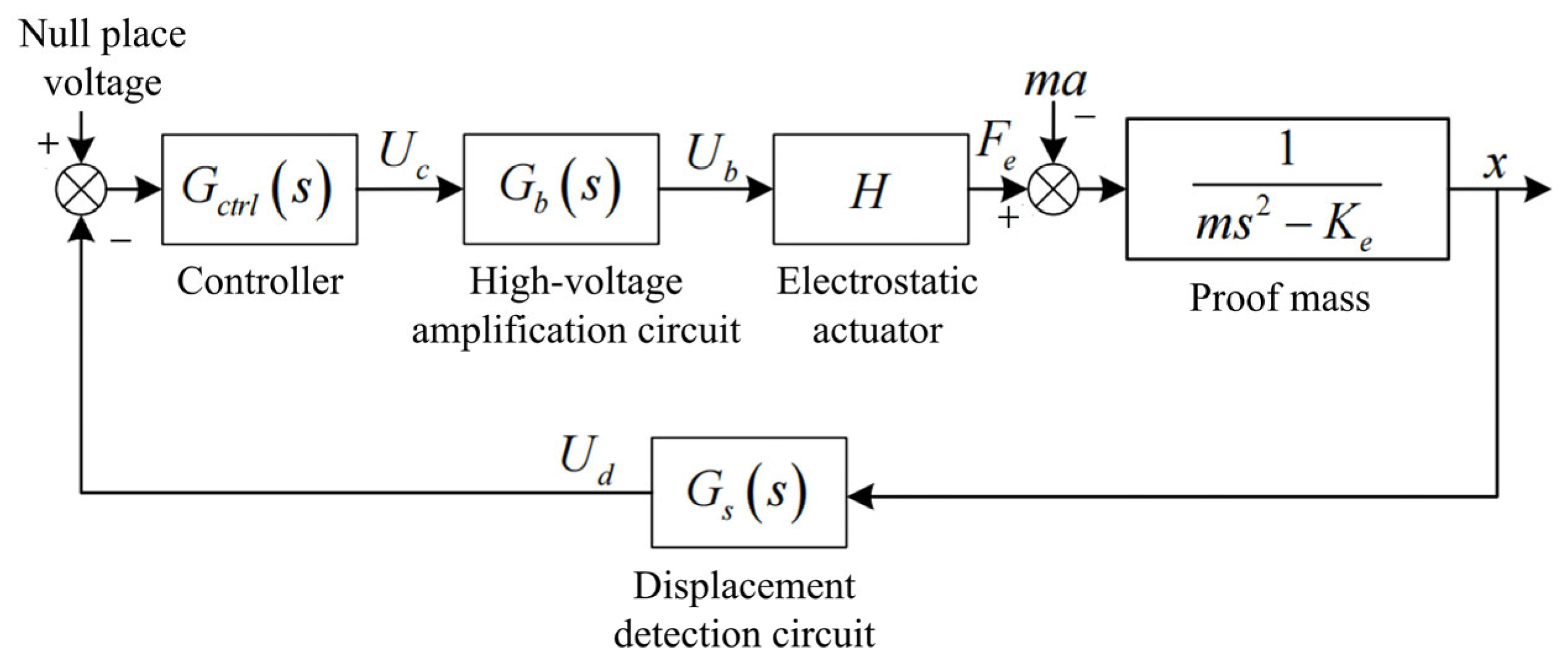
4. Electrostatic Suspension Control Principle
5. Controller Design
5.1. Control Method of Initial Levitation Process
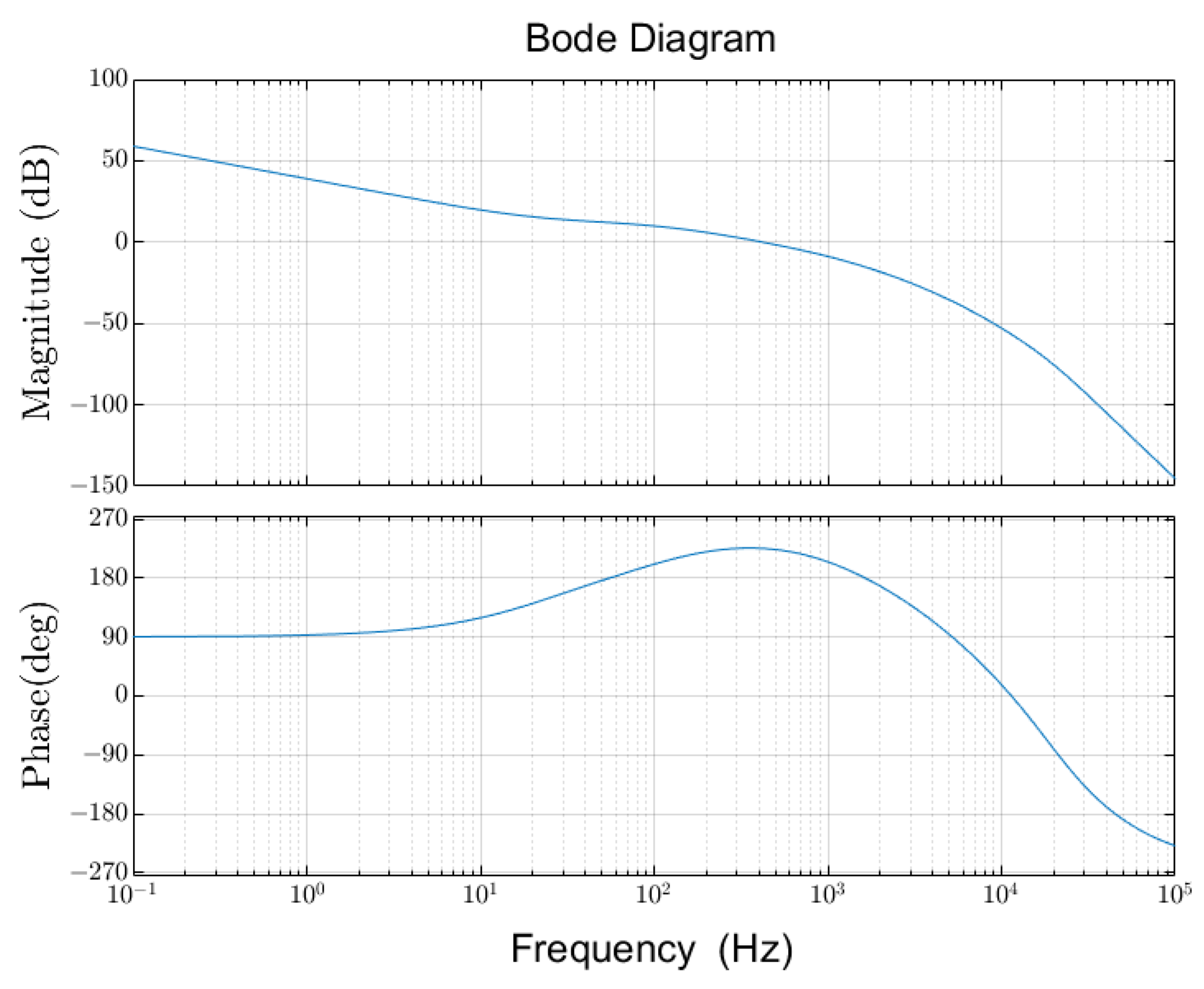
5.2. Control Method of Suspension Stage
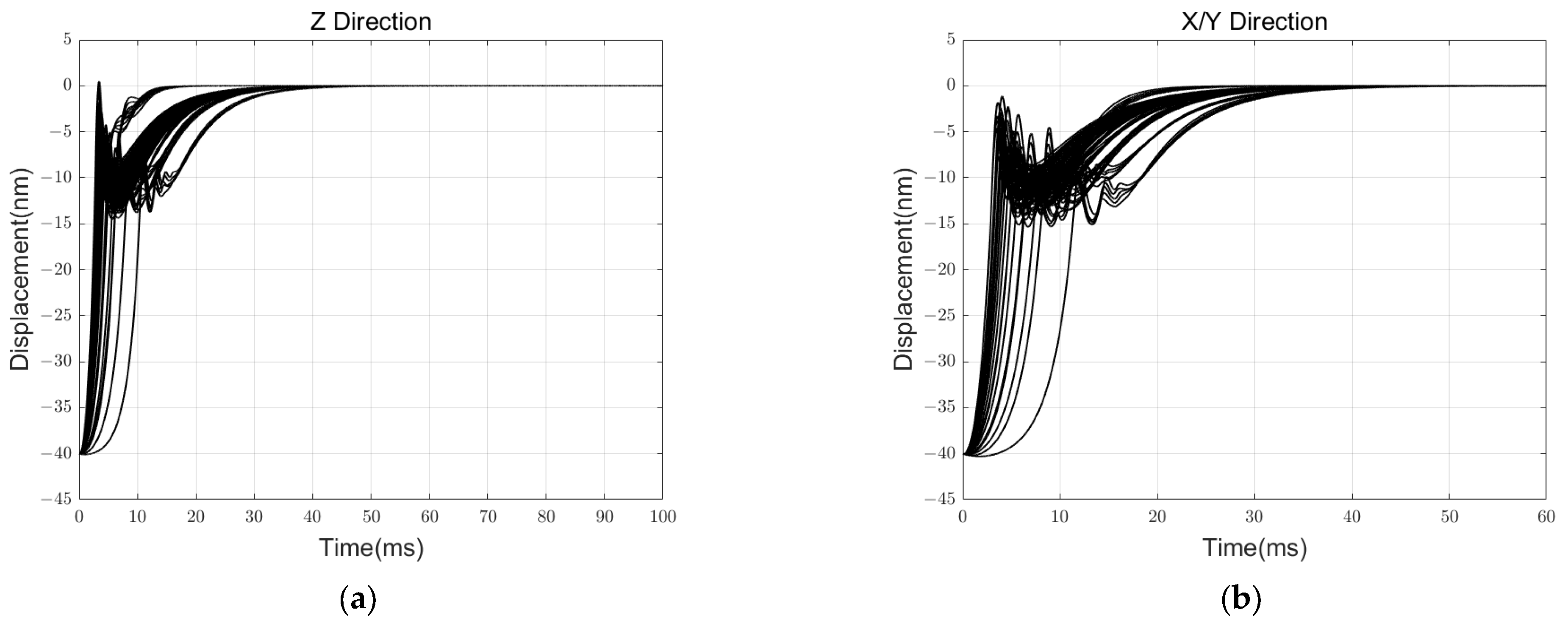
5.3. Results of Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, F.; Liu, W.; Chen, W.; Zhang, W.; Wu, X. Design, fabrication and levitation experiments of a micromachined electrostatically suspended six-axis accelerometer. Sensors 2011, 11, 11206–11234. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Bai, Y.; Li, H.; Qu, S.; Tan, D.; Wang, W.; Wu, S.; Yu, J.; Zhou, Z. Calibration and validation of a space electrostatic accelerometer onboard Tianzhou-1 cargo spacecraft using GNSS and attitude data. Aerosp. Sci. Technol. 2023, 138, 108320. [Google Scholar] [CrossRef]
- Touboul, P.; Metris, G.; Lebat, V.; Robert, A. The MICROSCOPE experiment, ready for the in-orbit test of the equivalence principle. Class. Quantum Gravity 2012, 29, 184010. [Google Scholar] [CrossRef]
- Mance, D. Development of Electronic System for Sensing and Actuation of Test Mass of the Inertial Sensor LISA. [Razvoj Elektroničkog Sustava za Očitavanje i Pokretanje Test Mase Inercijalnog Senzora LISA]. Ph.D. Thesis, University of Split, Split, Croatia, 2012. [Google Scholar]
- Luo, J.; Chen, L.-S.; Duan, H.-Z.; Gong, Y.-G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M. TianQin: A space-borne gravitational wave detector. Class. Quantum Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
- Feteih, S.E. Dynamically Testing of GP B Electrostatically Levitated Spherical Gyroscopes. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1991. [Google Scholar]
- Wu, C.-H. DC Electrostatic Gyro Suspension System for the Gravity Probe B Experiment. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1994. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Reigber, C.; Schwintzer, P. In CHAMP-A Challenging Microsatellite Payload for Geophysical Research and Application, Kleinsatelliten-Ein vielversprechender Weg in der Weltraumforschung und Raumfahrttechnik. 1995. Available online: https://gfzpublic.gfz-potsdam.de/pubman/faces/ViewItemFullPage.jsp;jsessionid=uehpYem5IWaITn9ErYdlMIIIUO4nqrZZNrIkwMxq.localhost?itemId=item_227107_1&view=EXPORT (accessed on 10 June 2024).
- Cai, L.; Zhou, Z.; Hsu, H.; Gao, F.; Zhu, Z.; Luo, J. Analytical error analysis for satellite gravity field determination based on two-dimensional Fourier method. J. Geod. 2013, 87, 417–426. [Google Scholar] [CrossRef][Green Version]
- Zhou, A.-N.; Bai, Y.-Z.; Cai, L.; Hu, M.; Li, H.-Y.; Liu, L.; Qu, S.-B.; Tan, D.-Y.; Wang, C.-R.; Wu, S.-C. An ultra-high sensitivity 70 g-TM electrostatic accelerometer for next generation satellite gravity measurement. Class. Quantum Gravity 2023, 40, 195004. [Google Scholar] [CrossRef]
- Weber, W.J.; Cavalleri, A.; Dolesi, R.; Fontana, G.; Hueller, M.; Vitale, S. Position sensors for LISA drag-free control. Class. Quantum Gravity 2002, 19, 1751. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.; Famiglietti, J.; Rodell, M. Spatial sensitivity of the Gravity Recovery and Climate Experiment (GRACE) time-variable gravity observations. J. Geophys. Res. Solid Earth 2005, 110, B08408. [Google Scholar] [CrossRef]
- Senobari, M. New results in airborne vector gravimetry using strapdown INS/DGPS. J. Geod. 2010, 84, 277–291. [Google Scholar] [CrossRef]
- Moryl, J.; Rice, H.; Shinners, S. The universal gravity module for enhanced submarine navigation. In Proceedings of the IEEE 1998 Position Location and Navigation Symposium (Cat. No. 98ch36153), Palm Springs, CA, USA, 20–23 April 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 324–331. [Google Scholar]
- Hu, S.; Pei, S.; Hu, M.; Bai, Y.; Li, H.; Liu, L.; Yang, B.; Wu, S.; Zhou, Z. Noise investigation of an electrostatic accelerometer by a high-voltage levitation method combined with a translation–tilt compensation pendulum bench. Rev. Sci. Instrum. 2021, 92, 064502. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Wu, S.C.; Zhou, Z.B.; Bai, Y.Z. Design and validation of a high-voltage levitation circuit for electrostatic accelerometers. Rev. Sci. Instrum. 2013, 84, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Liu, T.; Li, L.; Wu, Q. Design and fabrication of a differential electrostatic accelerometer for space-station testing of the equivalence principle. Sensors 2016, 16, 1262. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Bai, Y.; Hu, M.; Qu, S.; Zhou, Z. Amplitude stability analysis and experimental investigation of an AC excitation signal for capacitive sensors. Sens. Actuators A 2020, 309, 112020. [Google Scholar] [CrossRef]
- Bai, Y.Z.; Zhou, Z.B.; Tu, H.B.; Wu, S.C.; Cai, L.; Liu, L.; Luo, J. Capacitive position measurement for high-precision space inertial sensor. Front. Phys. China 2009, 4, 205. [Google Scholar] [CrossRef]
- Hu, M.; Bai, Y.Z.; Zhou, Z.B.; Li, Z.X.; Luo, J. Resonant frequency detection and adjustment method for a capacitive transducer with differential transformer bridge. Rev. Sci. Instrum. 2014, 85, 589–598. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Sun, B.; Han, F. Self-locking avoidance and stiffness compensation of a three-axis micromachined electrostatically suspended accelerometer. Sensors 2016, 16, 711. [Google Scholar] [CrossRef] [PubMed]
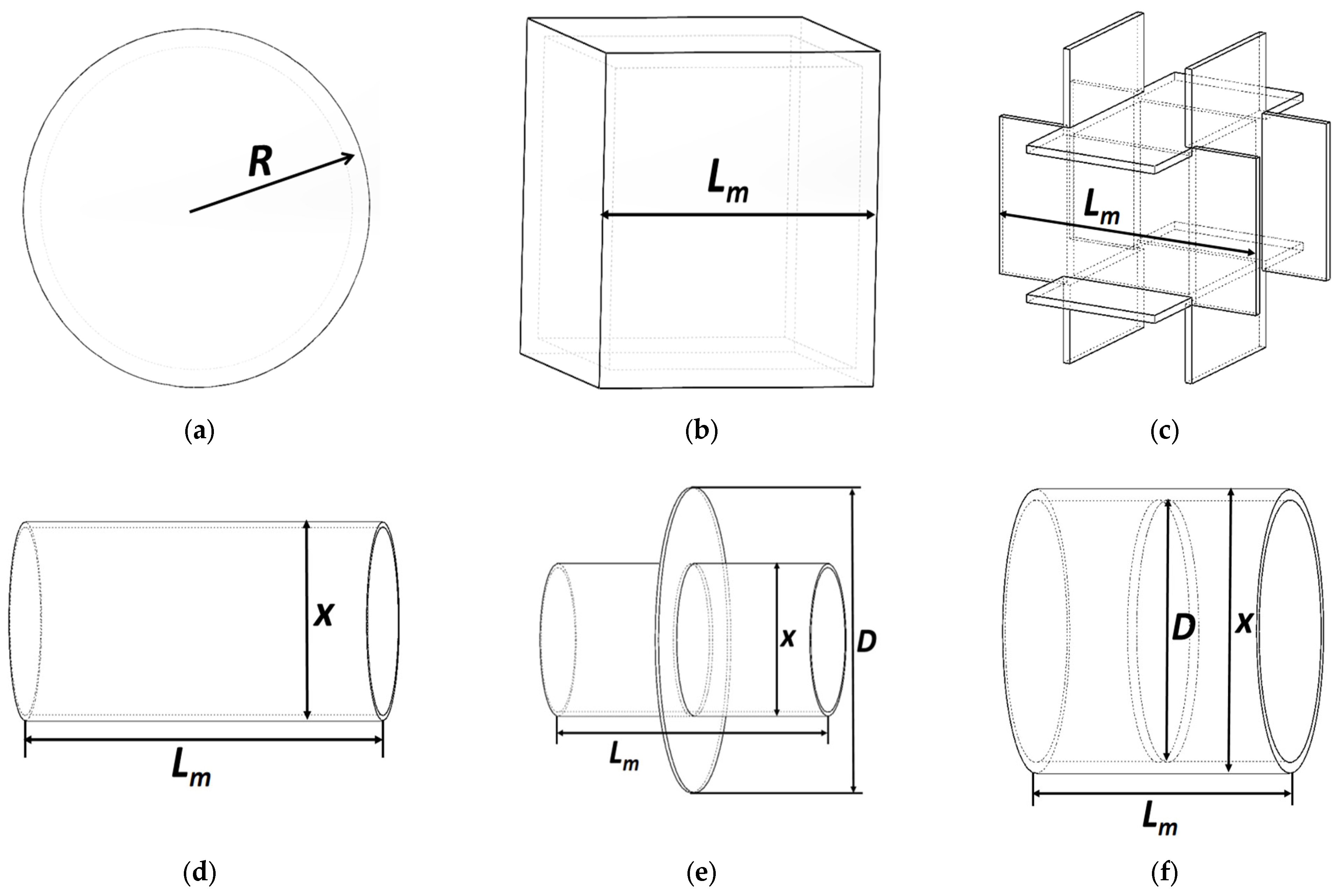








| Poof Mass Structure | Surface Area Formula | Surface Area Value | Mass Formula | ||
|---|---|---|---|---|---|
| Hollow sphere (Radius ) | 12.57 | 0.60 | 21.0 *2 | ||
| Hollow hexahedron (side length ) | 15.59 | 0.73 | 21.3 *2 | ||
| Six thin, hollow plates (side length ) | 7.80 | 0.39 | 20.0 *2 | ||
| Hollow cylinder | 23.23 | 0.58 | 40.1 | ||
| Hollow cylinder with an outer flange | 31.10 | 0.78 | 39.9 | ||
| Hollow cylinder with an inner flange | 22.97 | 0.57 | 40.3 |
| Design Parameters | Symbols |
|---|---|
| The inner diameter of the outer cylindrical electrode | |
| The length of the outer cylindrical electrode | |
| The included angle of the inner and outer cylindrical electrodes | |
| The diameter of the inner cylindrical electrode | |
| The length of the inner cylindrical electrode | |
| The surface area of the disk electrode in the Z-direction | |
| The gap between the electrode and the proof mass | |
| The electrostatic force arm length is for rotational freedom | |
| The capacitance of the outer cylindrical electrode | |
| The capacitance of the inner cylindrical electrode | |
| The capacitance of the disk electrode in the Z-direction | |
| The mass of the proof mass |
| Degree of Freedom | Electrodes for Displacement Detection and Suspension Voltage Application |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; He, X.; Wu, C.; Zhang, R. A Ground-Based Electrostatically Suspended Accelerometer. Sensors 2024, 24, 4029. https://doi.org/10.3390/s24124029
Liu H, He X, Wu C, Zhang R. A Ground-Based Electrostatically Suspended Accelerometer. Sensors. 2024; 24(12):4029. https://doi.org/10.3390/s24124029
Chicago/Turabian StyleLiu, Hanxiao, Xiaoxia He, Chenhui Wu, and Rong Zhang. 2024. "A Ground-Based Electrostatically Suspended Accelerometer" Sensors 24, no. 12: 4029. https://doi.org/10.3390/s24124029
APA StyleLiu, H., He, X., Wu, C., & Zhang, R. (2024). A Ground-Based Electrostatically Suspended Accelerometer. Sensors, 24(12), 4029. https://doi.org/10.3390/s24124029







