Determinants of Maximum Magnetic Anomaly Detection Distance
Abstract
:1. Introduction
1.1. Measurement Resolution
1.2. Background Noise
1.3. Magnetization
2. Basic Principles
2.1. Magnetic Field Anomaly Generated by Object
2.2. M-H Constitutive Relationships of Magnetic Object
2.3. Governing Equations for FEA
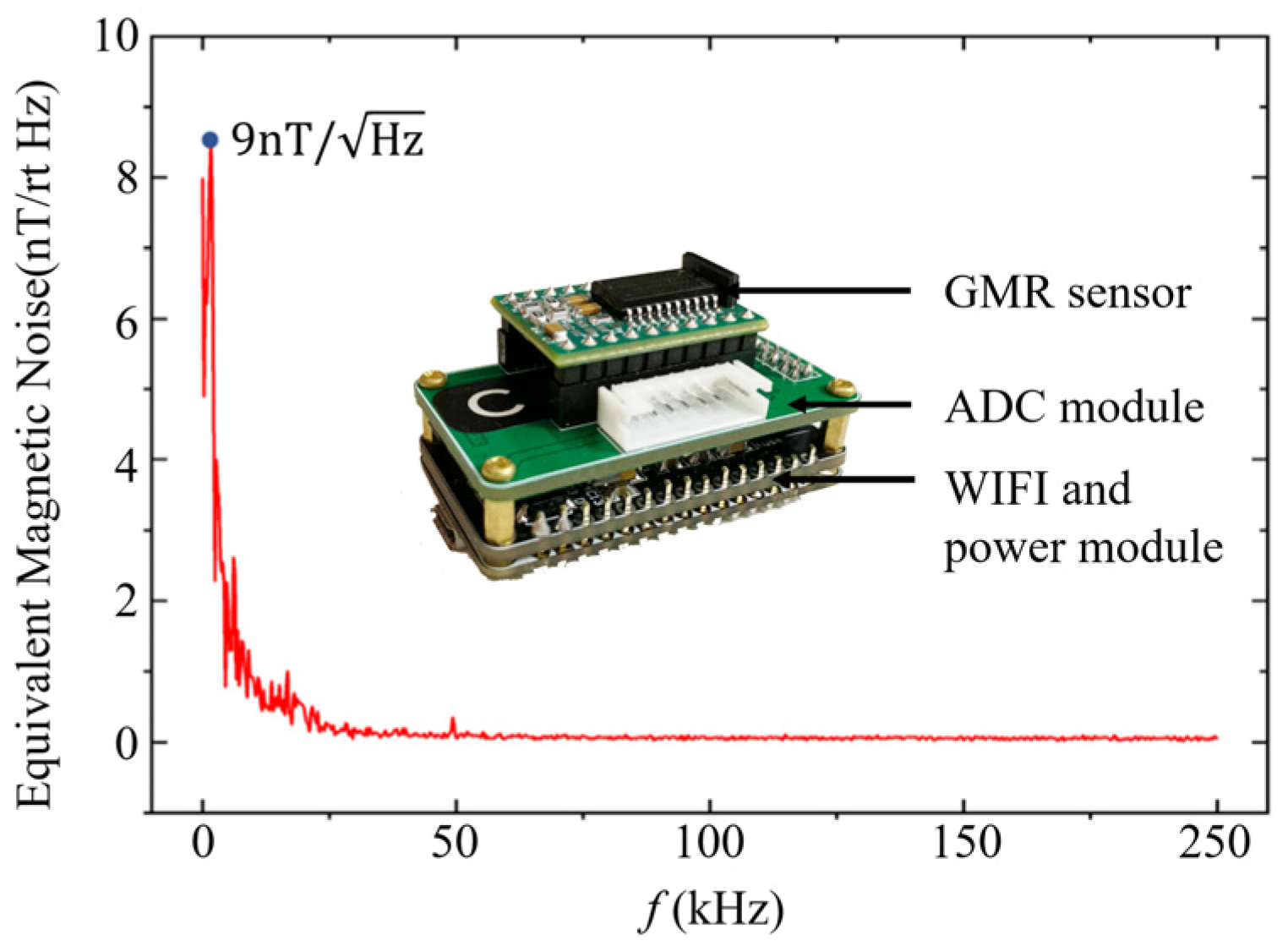
2.4. Measurement Resolution, Sensor Equivalent Magnetic Noise Spectrum Density and Background Magnetic Field Noise Spectrum Density
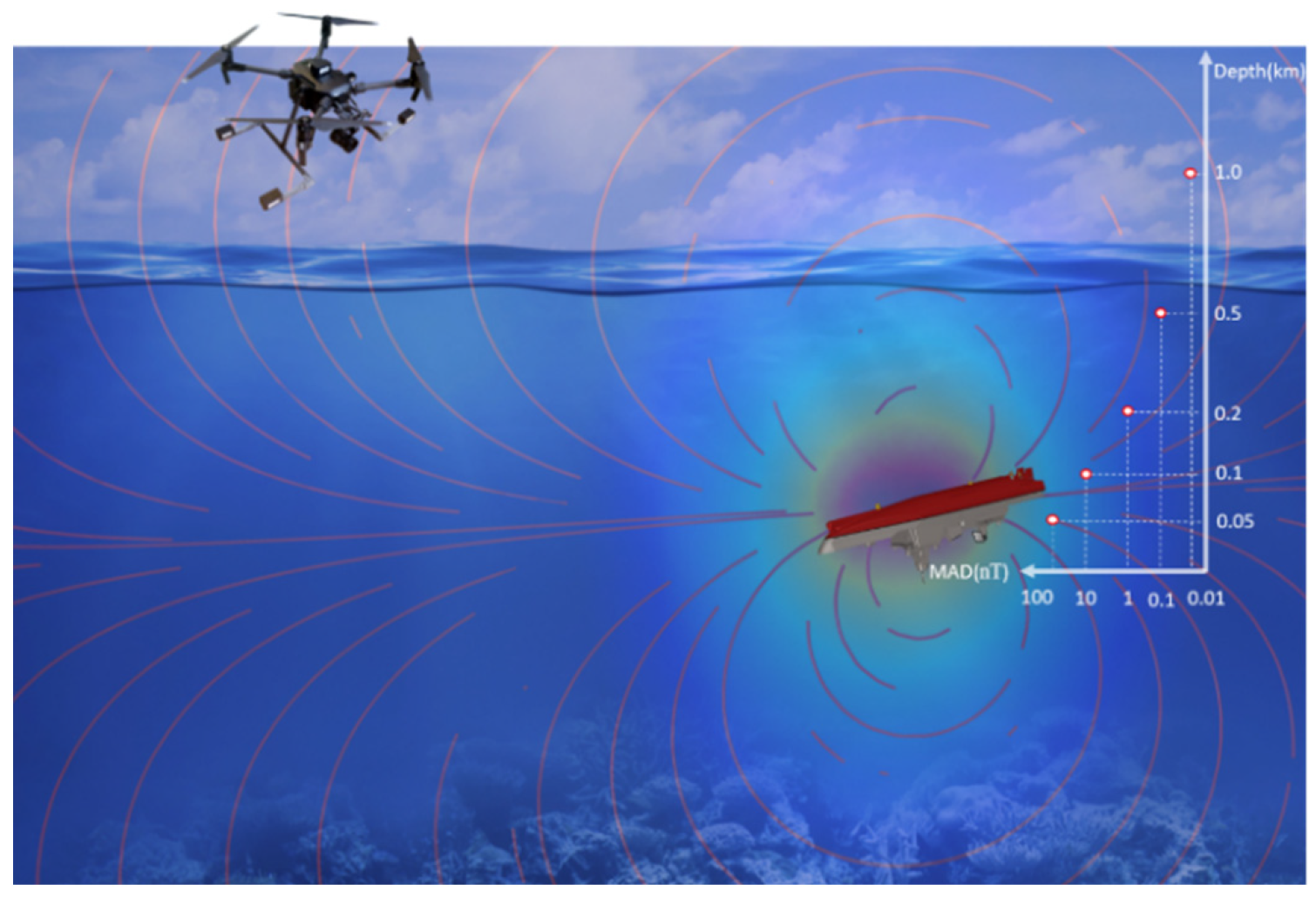
3. Experiments
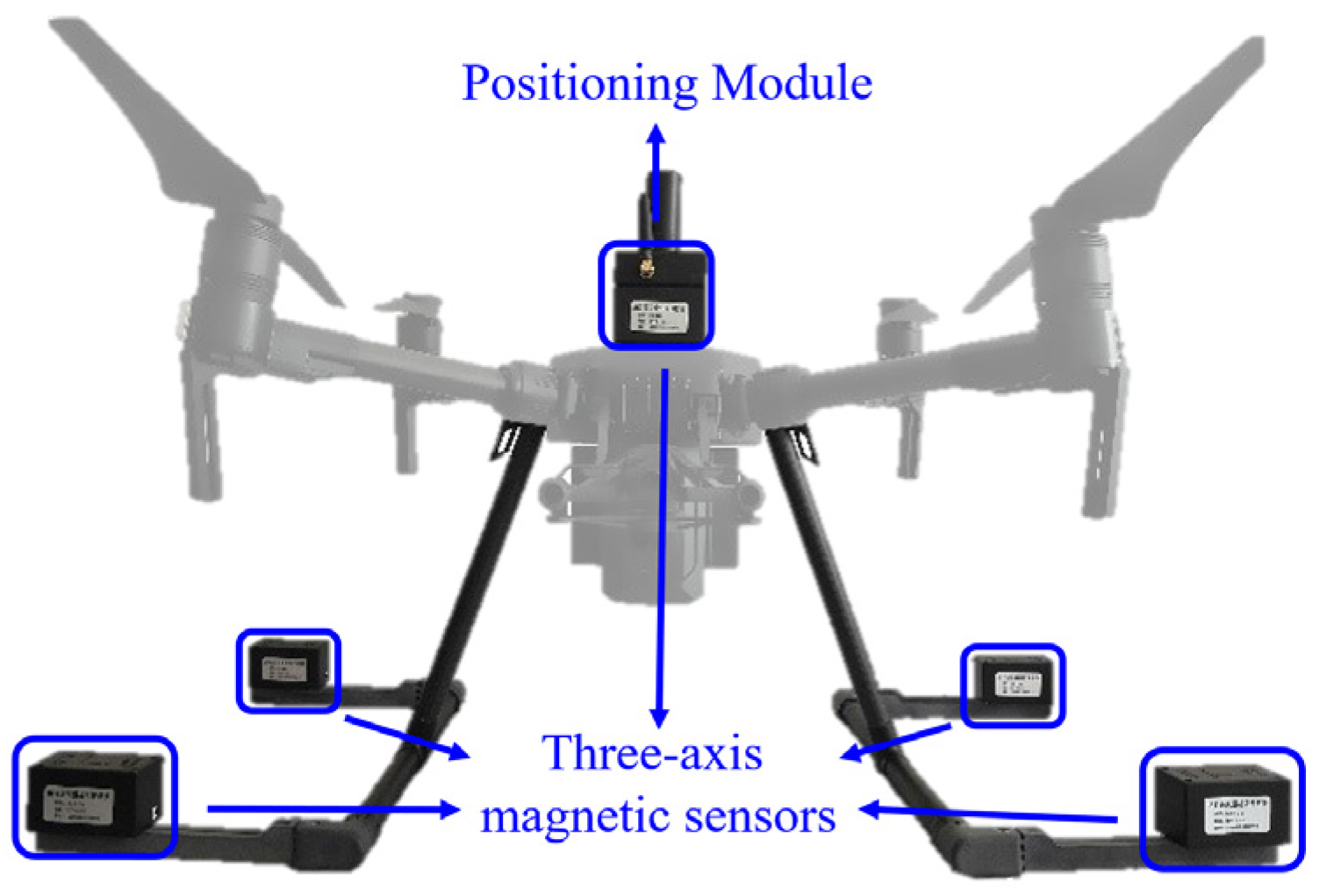
3.1. The MAD System
3.2. Cargo Ship as Soft-Magnetic Marine Object
3.3. NdFeB Magnet as Magnetic Marker Object
4. Numerical Model
4.1. Finite Element Analysis of Cargo Ship MAD
4.2. Finite Element Analysis of Magnet Marker MAD
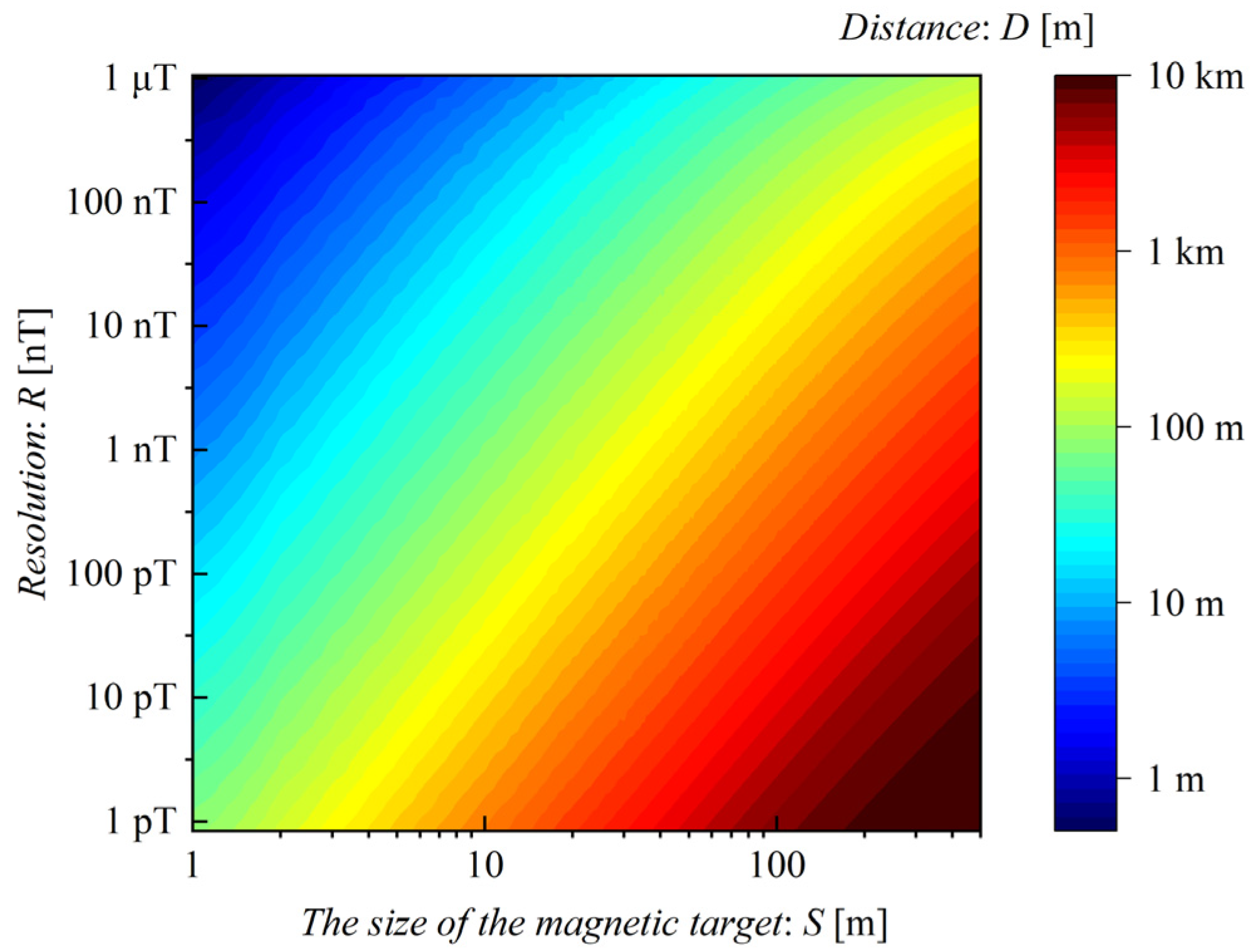
5. Determination of Detection Distance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.; Zhang, J.H.; Li, J.H.; Liu, S.Q.; Miao, P.X.; Shi, Y.C.; Zhao, E.M. A brief review of magnetic anomaly detection. Meas. Sci. Technol. 2021, 32, 13. [Google Scholar] [CrossRef]
- Butler, D.K.; Simms, J.E.; Furey, J.S.; Bennett, H.H. Review of Magnetic Modeling for UXO and Applications to Small Items and Close Distances. J. Environ. Eng. Geophys. 2012, 17, 53–73. [Google Scholar] [CrossRef]
- Mu, Y.X.; Xie, W.P.; Zhang, X.J. The Joint UAV-Borne Magnetic Detection System and Cart-Mounted Time Domain Electromagnetic System for UXO Detection. Remote Sens. 2021, 13, 2343. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. 75th Anniversary—The historical development of the magnetic method in exploration. Geophysics 2005, 70, 33ND–61ND. [Google Scholar] [CrossRef]
- Okada, K. Breakthrough technologies for mineral exploration. Miner. Econ. 2022, 35, 429–454. [Google Scholar] [CrossRef]
- Passaro, S. Marine electrical resistivity tomography for shipwreck detection in very shallow water: A case study from Agropoli (Salerno, southern Italy). J. Archaeol. Sci. 2010, 37, 1989–1998. [Google Scholar] [CrossRef]
- Ege, Y.; Kalender, O.; Nazlibilek, S. Direction finding of moving ferromagnetic objects inside water by magnetic anomaly. Sens. Actuator A-Phys. 2008, 147, 52–59. [Google Scholar] [CrossRef]
- Trammell, H.S.; Perry, A.R.; Kumar, S.; Czipott, P.V.; Whitecotton, B.R.; McManus, T.J.; Walsh, D.O. Using unmanned aerial vehicle-borne magnetic sensors to detect and locate improvised explosive devices and unexploded ordnance. In Proceedings of the Conference on Sensors, and Command, Control, Communications, and Intelligence (C31) Technologies for Homeland Security and Homeland Defense IV, Orlando, FL, USA, 28 March–1 April 2005; pp. 963–971. [Google Scholar]
- Kolster, M.E.; Wigh, M.D.; da Silva, E.L.S.; Vilhelmsen, T.B.; Dossing, A. High-Speed Magnetic Surveying for Unexploded Ordnance Using UAV Systems. Remote Sens. 2022, 14, 1134. [Google Scholar] [CrossRef]
- Jin, H.H.; Guo, J.; Wang, H.B.; Zhuang, Z.H.; Qin, J.; Wang, T.L. Magnetic Anomaly Detection and Localization Using Orthogonal Basis of Magnetic Tensor Contraction. IEEE Trans. Geosci. Remote Sensing 2020, 58, 5944–5954. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Di, W.N.; Chen, R.; Deng, T.Y.; Wang, Y.H.; You, H.R.; Lu, L.; Han, T.; Jiao, J.; Luo, H.S. Modeling and experimental investigation of magnetic anomaly detection using advanced triaxial magnetoelectric sensors. Sens. Actuator A-Phys. 2022, 346, 11. [Google Scholar] [CrossRef]
- Liang, S.J.; Sun, S.Y.; Lu, H.F. Application of Airborne Electromagnetics and Magnetics for Mineral Exploration in the Baishiquan-Hongliujing Area, Northwest China. Remote Sens. 2021, 13, 903. [Google Scholar] [CrossRef]
- Legault, J.M.; Niemi, J.; Brett, J.S.; Zhao, S.K.; Han, Z.H.; Plastow, G.C. Passive airborne EM and ground IP\resistivity results over the Romero intermediate sulphidation epithermal gold deposits, Dominican Republic. Explor. Geophys. 2016, 47, 191–200. [Google Scholar] [CrossRef]
- Wang, Y.J.; Gao, J.Q.; Li, M.H.; Shen, Y.; Hasanyan, D.; Li, J.F.; Viehland, D. A review on equivalent magnetic noise of magnetoelectric laminate sensors. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2014, 372, 13. [Google Scholar] [CrossRef] [PubMed]
- Butta, M.; Sasada, I. Orthogonal Fluxgate with Annealed Wire Core. IEEE Trans. Magn. 2013, 49, 62–65. [Google Scholar] [CrossRef]
- Clem, T.R. Sensor technologies for hunting buried sea mines. In Proceedings of the MTS/IEEE Oceans 2002 Conference, Biloxi, MS, USA, 29–31 October 2002; pp. 452–460. [Google Scholar]
- Overway, D.; Clem, T.; Bono, J.; Purpura, J.; Allen, G.; Van Wye, H.; King, D. Evaluation of the polatomic P-2000 laser pumped He-4 Magnetometer/Gradiometer. In Proceedings of the MTS/IEEE Oceans 2002 Conference, Biloxi, MI, USA, 29–31 October 2002; pp. 952–960. [Google Scholar]
- Stolz, R.; Schiffler, M.; Becken, M.; Thiede, A.; Schneider, M.; Chubak, G.; Marsden, P.; Bergshjorth, A.B.; Schaefer, M.; Terblanche, O. SQUIDs for magnetic and electromagnetic methods in mineral exploration. Miner. Econ. 2022, 35, 467–494. [Google Scholar] [CrossRef]
- Lenz, J.; Edelstein, A.S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Yang, S.L.; Zhang, J. Current Progress of Magnetoresistance Sensors. Chemosensors 2021, 9, 211. [Google Scholar] [CrossRef]
- Wei, S.R.; Liao, X.Q.; Zhang, H.; Pang, J.H.; Zhou, Y. Recent Progress of Fluxgate Magnetic Sensors: Basic Research and Application. Sensors 2021, 21, 1500. [Google Scholar] [CrossRef] [PubMed]
- Bichurin, M.; Petrov, R.; Sokolov, O.; Leontiev, V.; Kuts, V.; Kiselev, D.; Wang, Y.J. Magnetoelectric Magnetic Field Sensors: A Review. Sensors 2021, 21, 6232. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Yuan, J.S. Methods of Differential Submarine Detection Based on Magnetic Anomaly and Technology of Probes Arrangement. In Proceedings of the 2nd International Workshop on Materials Engineering and Computer Sciences (IWMECS), Jinan, China, 10–11 October 2015; pp. 446–449. [Google Scholar]
- Shangguan, Y.Q.; Yuan, J.S.; Zou, J. A localization method for submarines based on array probes magnetic measurement at two positions to overcome the influence of background field. Int. J. Appl. Electromagn. Mech. 2017, 55, 205–212. [Google Scholar] [CrossRef]
- Phelps, G.; Bracken, R.; Spritzer, J.; White, D. Achieving sub-nanoTesla precision in multirotor UAV aeromagnetic surveys. J. Appl. Geophys. 2022, 206, 16. [Google Scholar] [CrossRef]
- Ginzburg, B.; Frumkis, L.; Kaplan, B.Z. Processing of magnetic scalar gradiometer signals using orthonormalized functions. Sens. Actuator A-Phys. 2002, 102, 67–75. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, M.Y. Magnetic Anomaly Detection for Simultaneous Moving Target and Magnetometer. In Proceedings of the 3rd Asia-Pacific Conference on Antennas and Propagation (APCAP), Harbin, China, 26–29 July 2014; pp. 884–888. [Google Scholar]
- Frumkis, L.; Ginzburg, B.; Salomonski, N.; Kaplan, B.Z. Optimization of scalar magnetic gradiometer signal processing. Sens. Actuator A-Phys. 2005, 121, 88–94. [Google Scholar] [CrossRef]
- Humphrey, K.P.; Horton, T.J.; Keene, M.N. Detection of mobile targets from a moving platform using an actively shielded, adaptively balanced SQUID gradiometer. IEEE Trans. Appl. Supercond. 2005, 15, 753–756. [Google Scholar] [CrossRef]
- Lucivero, V.G.; Lee, W.; Kornack, T.W.; Limes, M.E.; Foley, E.L.; Romalis, M.V. Femtotesla Nearly-Quantum-Noise-Limited Pulsed Gradiometer at Earth-Scale Fields. Phys. Rev. Appl. 2022, 18, 6. [Google Scholar] [CrossRef]
- Yabukami, S.; Kikuchi, H.; Yamaguchi, M.; Arai, K.I.; Takahashi, K.; Itagaki, A.; Wako, N. Motion capture system of magnetic markers using three-axial magnetic field sensor. IEEE Trans. Magn. 2000, 36, 3646–3648. [Google Scholar] [CrossRef]
- Kurita, T.; Taruno, K.; Nakamura, S.; Takei, H.; Enokido, K.; Kuwayama, T.; Kanada, Y.; Akashi-Tanaka, S.; Matsuyanagi, M.; Hankyo, M.; et al. Magnetically Guided Localization Using a Guiding-Marker System(R) and a Handheld Magnetic Probe for Nonpalpable Breast Lesions: A Multicenter Feasibility Study in Japan. Cancers 2021, 13, 2923. [Google Scholar] [CrossRef] [PubMed]
- Enpuku, K.; Sakakibara, T.; Yoshida, T. Liquid-Phase Detection of Biological Targets Using Magnetoresistive Sensor and Magnetic Markers. IEEE Trans. Magn. 2014, 50, 4. [Google Scholar] [CrossRef]
- Murshudov, R.; Watson, J.M.; Liang, C.W.; Sexton, J.; Missous, M. Optimising sensor pitch for magnetic flux leakage imaging systems. Insight 2021, 63, 416–421. [Google Scholar] [CrossRef]
- Taylor, C.R.; Abramson, H.G.; Herr, H.M. Low-Latency Tracking of Multiple Permanent Magnets. IEEE Sens. J. 2019, 19, 11458–11468. [Google Scholar] [CrossRef]







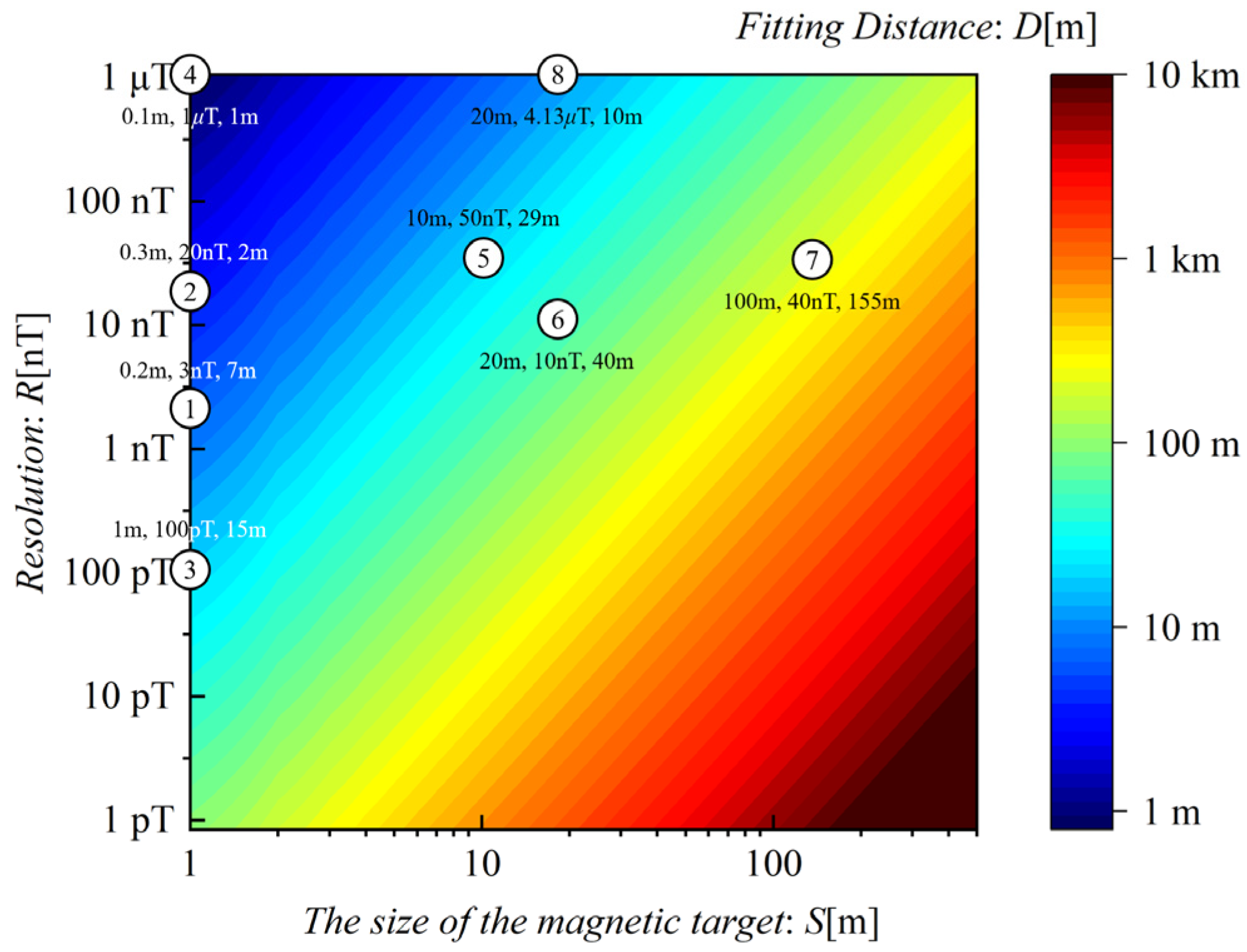
| No. Sensors (Noise Density) | Object (Size) | Measurement Resolution | Detectable Distance |
|---|---|---|---|
| 1. Fluxgate () | Land UXO (0.2 m) | 3 nT | 7 m@2005 [8] |
| 2. Magneto-electric () | UXO Simulation (0.3 m) | 20 nT | 2 m@2021 [3] |
| 3. Optically pumped () | Land UXO (1 m) | 100 pT | 15 m@2022 [9] |
| 4. Fluxgate () | UXO Simulation (0.1 m) | 1 μT | 1 m@2020 [10] |
| 5. Magneto-electric () | Ship (≈10 m) | 50 nT | 29 m@2022 [11] |
| 6. Electro-magnetic () | Gold Deposit (20 m) | 10 nT | 40 m@2021 [12] |
| 7. Electro-magnetic () | Gold Deposit (100 m) | 40 nT | 155 m@2018 [13] |
| 8. GMR () | Cargo Ship (20 m) | 4.13 μT | 10 m@This Work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Luo, J.; Zhang, J.; Li, J.; Zhang, Y.; Zhang, W.; Zhang, M. Determinants of Maximum Magnetic Anomaly Detection Distance. Sensors 2024, 24, 4028. https://doi.org/10.3390/s24124028
Li H, Luo J, Zhang J, Li J, Zhang Y, Zhang W, Zhang M. Determinants of Maximum Magnetic Anomaly Detection Distance. Sensors. 2024; 24(12):4028. https://doi.org/10.3390/s24124028
Chicago/Turabian StyleLi, Hangcheng, Jiaming Luo, Jiajun Zhang, Jing Li, Yi Zhang, Wenwei Zhang, and Mingji Zhang. 2024. "Determinants of Maximum Magnetic Anomaly Detection Distance" Sensors 24, no. 12: 4028. https://doi.org/10.3390/s24124028





