Modeling and Performance Study of Vehicle-to-Infrastructure Visible Light Communication System for Mountain Roads
Abstract
:1. Introduction
1.1. Related Works
1.2. Contributions
- A typical V2I–VLC communication scenario on a mountain road is considered. This consideration is more practical and specific, thus reflecting the V2I–VLC performance in real application scenarios.
- In the proposed scenario, the outdoor VLC channel is modeled taking into account AT and multiple propagation characteristics. In addition, vehicle mobility is considered in the modeling process, and dynamic V2I–VLC models are emphasized.
- Based on the channel model, closed-form expressions for the performance metrics of the LOS and NLOS links in the proposed scenario are derived. These performance metrics include average path loss, received optical power, channel capacity, and outage probability.
- Further, the derived theoretical expressions are compared with numerical simulation results in order to verify the accuracy of the derived theoretical expressions.
- Furthermore, the proposed propagation model is thoroughly investigated and analyzed in this paper, as well as compared with existing studies.
1.3. Paper Organization
2. System Model and Channel Modeling Methods
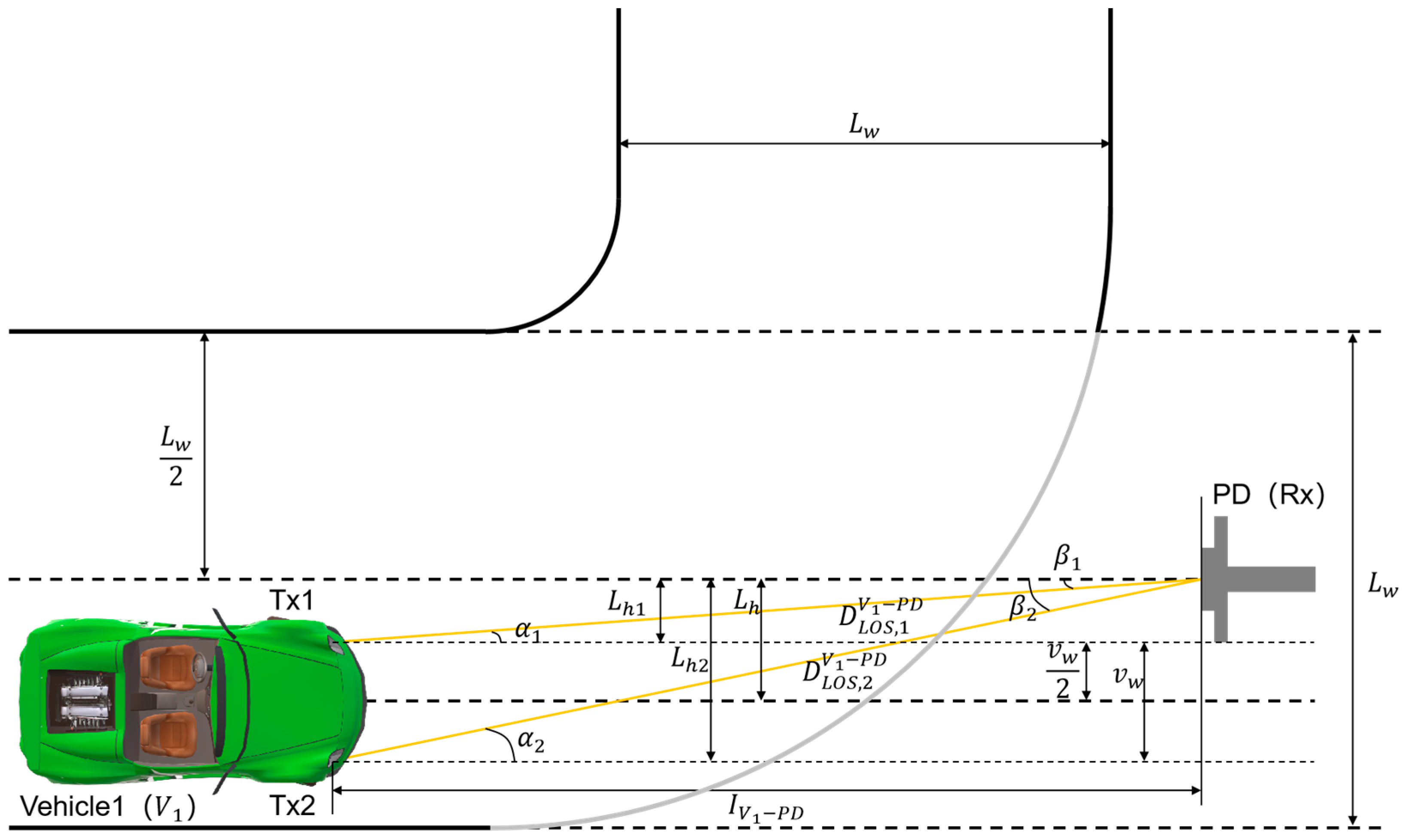
2.1. System Model
2.1.1. System Model for LOS Scenarios
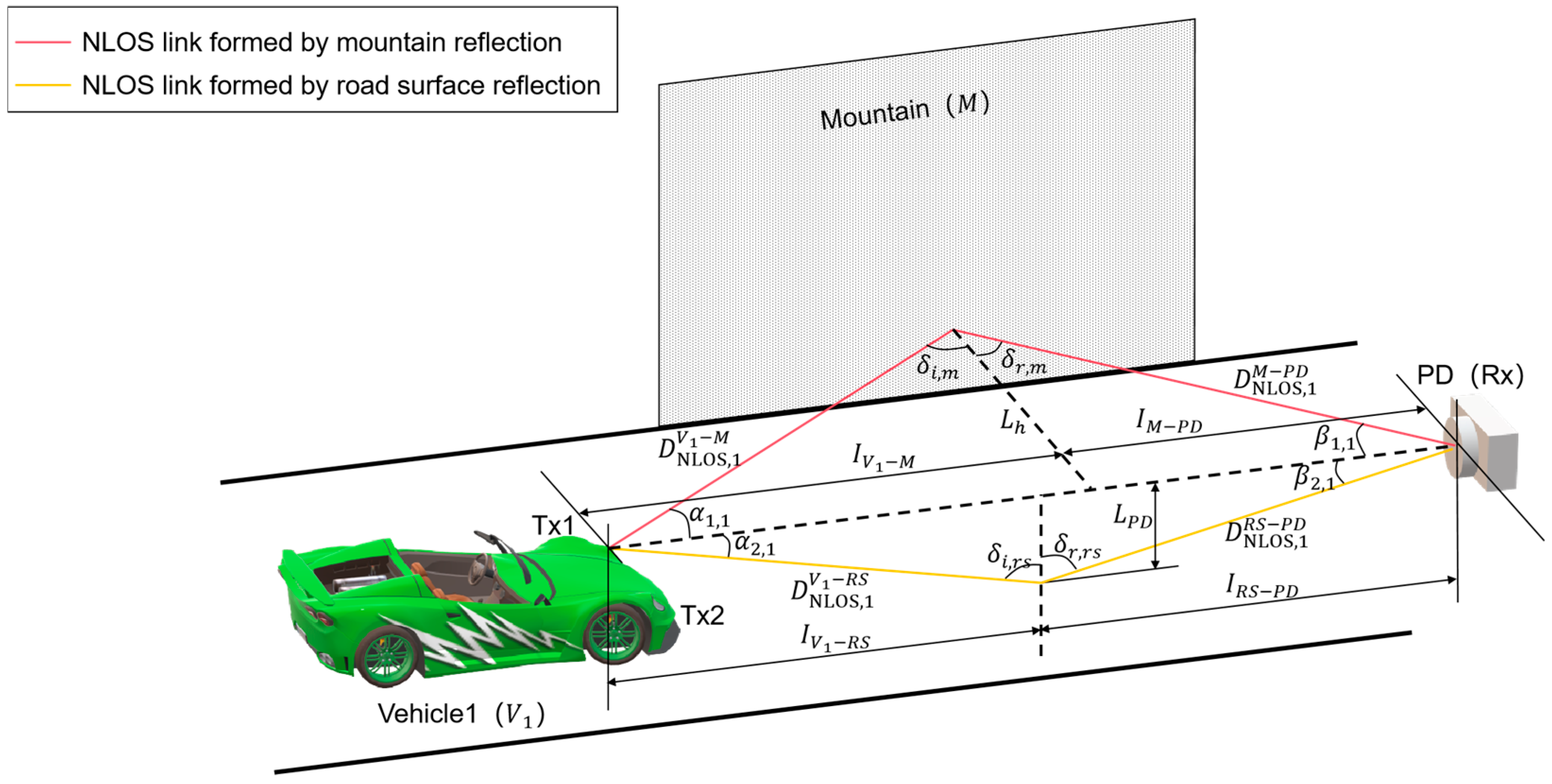
2.1.2. System Model for NLOS Scenarios
2.2. Channel Modeling Methods
3. Performance Analysis Methods
3.1. Expressions for Path Loss and Average Path Loss
3.1.1. The Average Path Loss for LOS Links
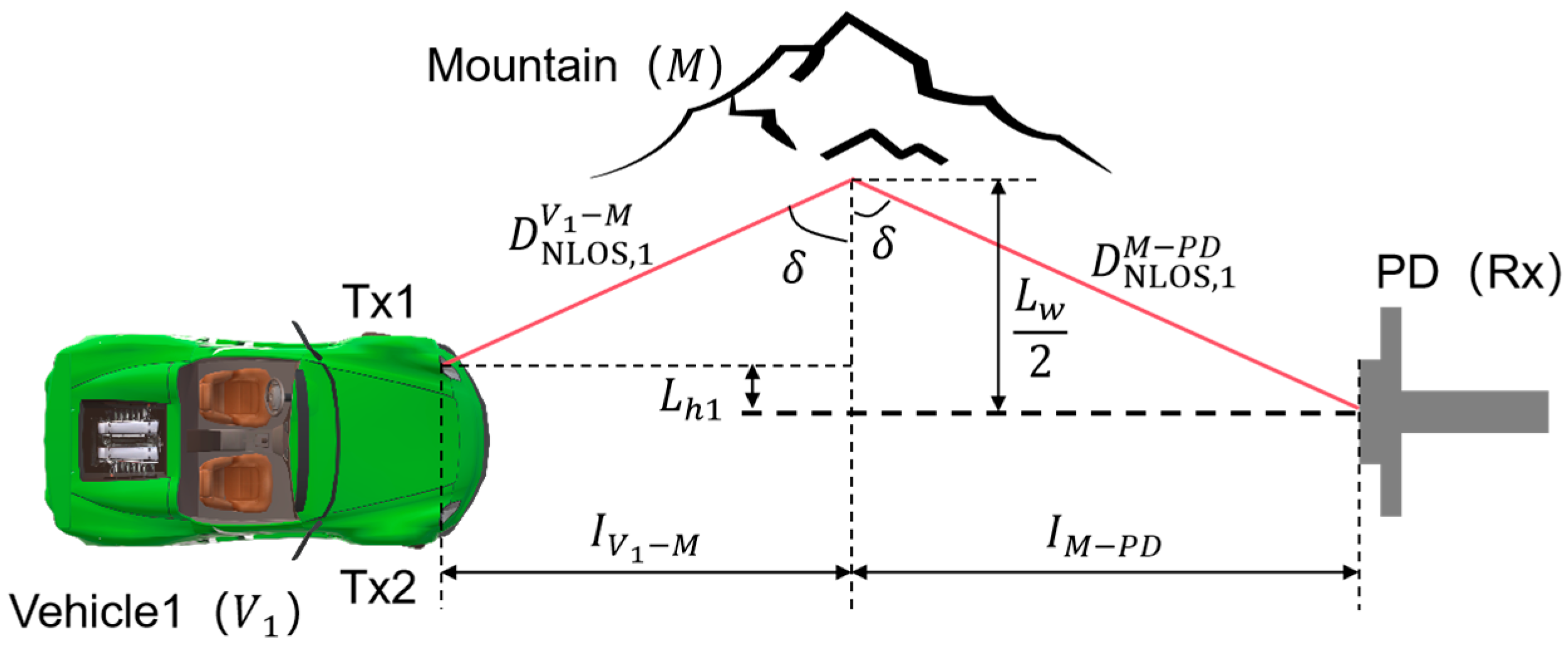
3.1.2. The Average Path Loss of the NLOS Link Formed by M
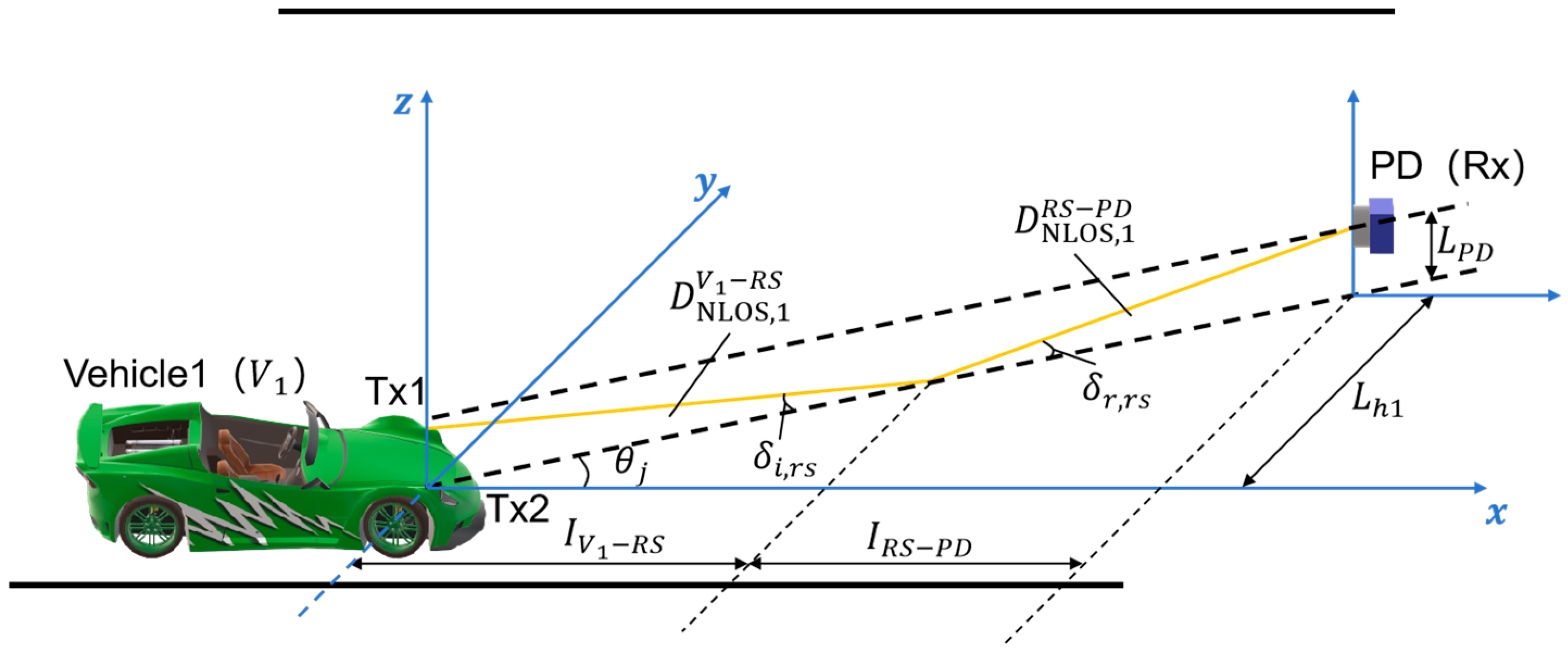
3.1.3. The Average Path Loss of the NLOS Link Formed by RS
3.2. Expressions for Received Optical Power
3.3. Expressions for Channel Capacity
3.4. Expressions for Outage Probability
4. Results
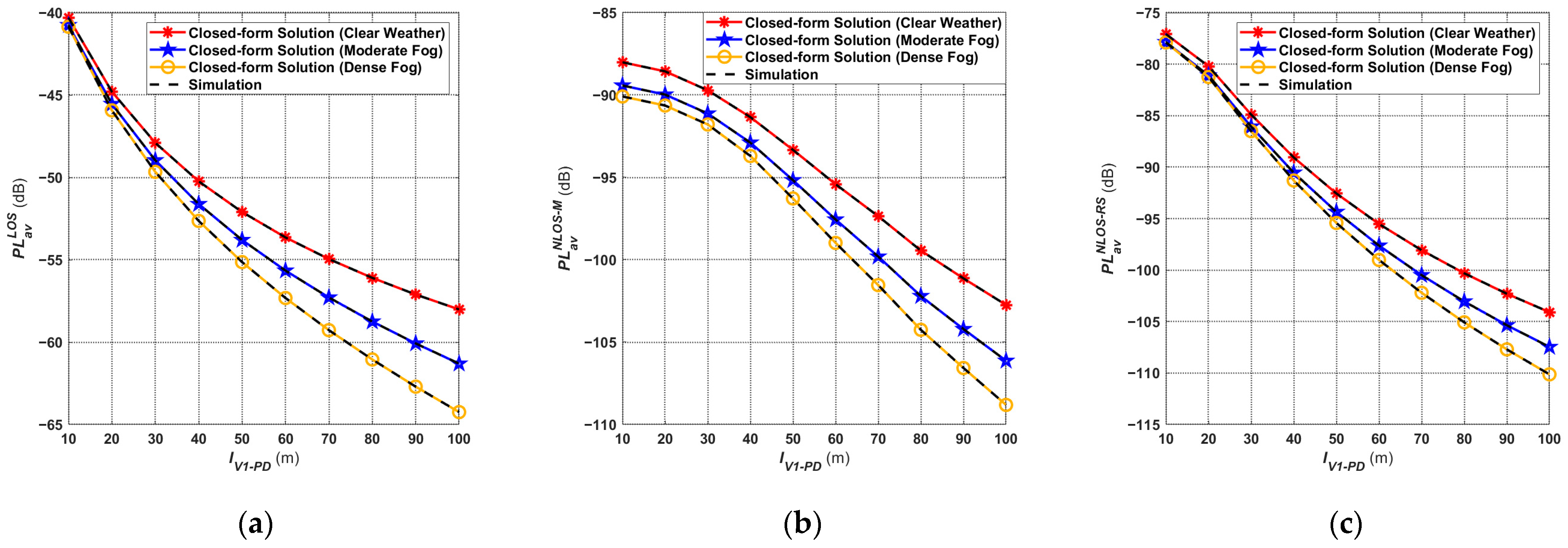
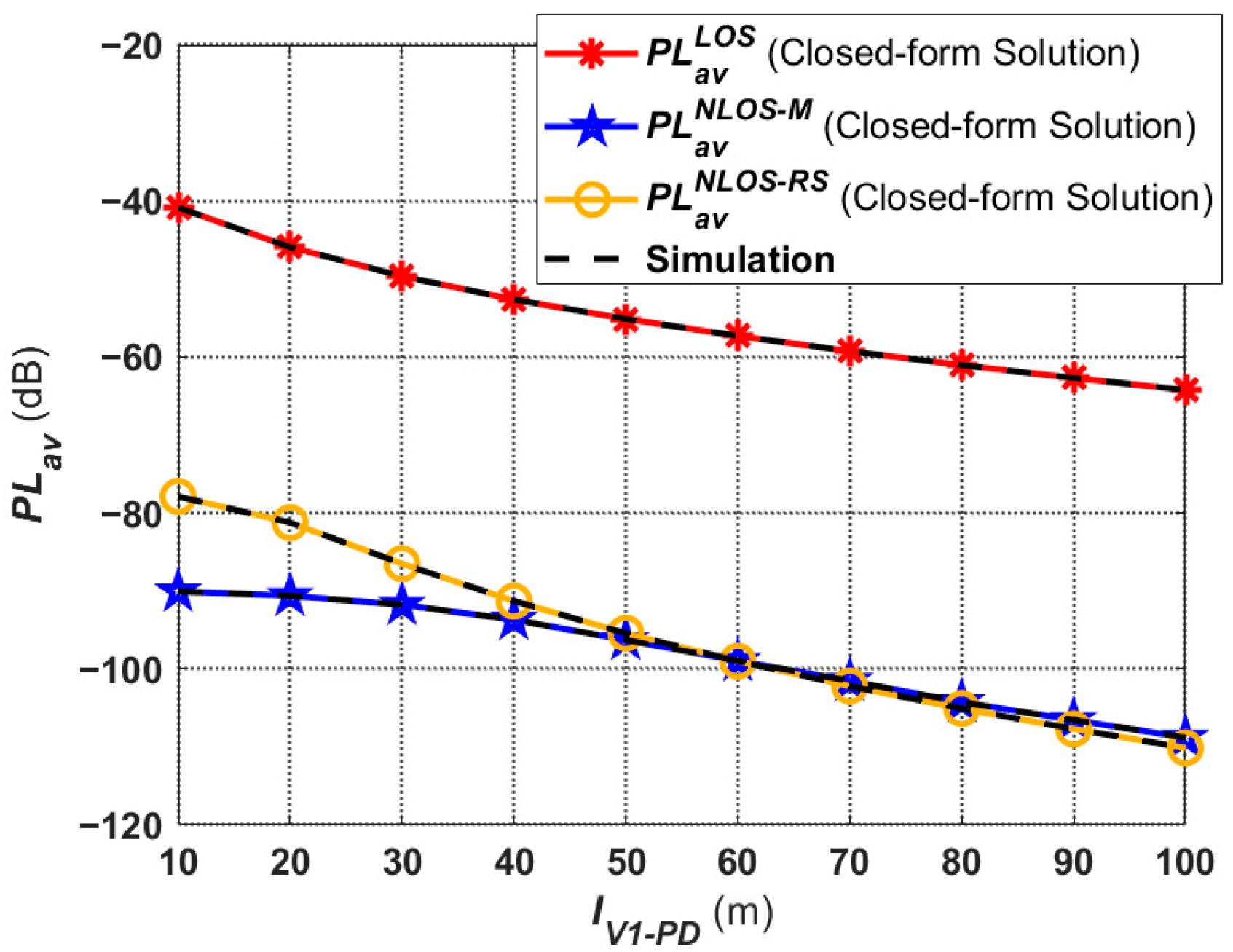
4.1. Average Path Loss
4.2. Received Optical Power
4.3. Channel Capacity
4.4. Outage Probability
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Case 1 of Tx1: Tx1 is located to the left of the center axis of the PD
- 2.
- Case 2 of Tx1: Tx1 is located to the right of the center axis of the PD
Appendix B
- Case 1 of Tx1: Tx1 is located to the left of the center axis of the PD
- 2.
- Case 2 of Tx1: Tx1 is located to the right of the center axis of the PD
Appendix C
- Case 1 of Tx1: Tx1 is located to the left of the center axis of the PD
- 2.
- Case 2 of Tx1: Tx1 is located to the right of the center axis of the PD
References
- Global Status Report on Road Safety 2023. Available online: https://www.who.int/publications/i/item/9789240086517 (accessed on 13 December 2023).
- Ahmed, S.K.; Mohammed, M.G.; Abdulqadir, S.O.; El-Kader, R.G.A.; El-Shall, N.A.; Chandran, D.; Rehman, M.E.U.; Dhama, K. Road Traffic Accidental Injuries and Deaths: A Neglected Global Health Issue. Health Sci. Rep. 2023, 6, e1240. [Google Scholar] [CrossRef] [PubMed]
- Shaaban, K.; Shamim, M.H.M.; Abdur-Rouf, K. Visible Light Communication for Intelligent Transportation Systems: A Review of the Latest Technologies. J. Traffic Transp. Eng. (Engl. Ed.) 2021, 8, 483–492. [Google Scholar] [CrossRef]
- Cailean, A.-M.; Dimian, M. Current Challenges for Visible Light Communications Usage in Vehicle Applications: A Survey. IEEE Commun. Surv. Tutorials 2017, 19, 2681–2703. [Google Scholar] [CrossRef]
- Eldeeb, H.B.; Hosney, M.; Elsayed, H.M.; Badr, R.I.; Uysal, M.; Selmy, H.A.I. Optimal Resource Allocation and Interference Management for Multi-User Uplink Light Communication Systems With Angular Diversity Technology. IEEE Access 2020, 8, 203224–203236. [Google Scholar] [CrossRef]
- Al Hasnawi, R.; Marghescu, I. A Survey of Vehicular VLC Methodologies. Sensors 2024, 24, 598. [Google Scholar] [CrossRef]
- Vieira, M.; Vieira, M.A.; Louro, P.; Vieira, P. Vehicular Visible Light Communication: A Road-to-Vehicle Proof of Concept. In Proceedings of the Optical Sensing and Detection V; Berghmans, F., Mignani, A.G., Eds.; SPIE: Strasbourg, France, 2018; p. 20. [Google Scholar]
- Bazzi, A.; Masini, B.M.; Zanella, A.; Calisti, A. Visible Light Communications as a Complementary Technology for the Internet of Vehicles. Comput. Commun. 2016, 93, 39–51. [Google Scholar] [CrossRef]
- Chaabna, A.; Babouri, A.; Chouabia, H.; Hafsi, T.; Meguetta, Z.E.; Zhang, X. Experimental Demonstration of V2V Communication System Based on VLC Technology for Smart Transportation. In Artificial Intelligence and Heuristics for Smart Energy Efficiency in Smart Cities; Hatti, M., Ed.; Lecture Notes in Networks and Systems; Springer International Publishing: Cham, Switzerland, 2022; Volume 361, pp. 653–661. [Google Scholar]
- Vieira, M.; Vieira, M.A.; Louro, P.; Vieira, P. Cooperative Communication between Vehicles and Road Infrastructures through Visible Light. In Proceedings of the SENSORDEVICES 2019; IARIA: Nice, France, 2019; pp. 26–31. [Google Scholar]
- Cailean, A.; Cagneau, B.; Chassagne, L.; Topsu, S.; Alayli, Y.; Blosseville, J.-M. Visible Light Communications: Application to Cooperation between Vehicles and Road Infrastructures. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; IEEE: Los Alamitos, CA, USA, 2012; pp. 1055–1059. [Google Scholar]
- Liu, J.; Chan, P.W.C.; Ng, D.W.K.; Lo, E.S.; Shimamoto, S. Hybrid Visible Light Communications in Intelligent Transportation Systems with Position Based Services. In Proceedings of the 2012 IEEE Globecom Workshops, Anaheim, CA, USA, 3–7 December 2012; IEEE: Los Alamitos, CA, USA, 2012; pp. 1254–1259. [Google Scholar]
- Irfan, M.; Habib, U.; Muhammad, F.; Ali, F.; Alwadie, A.S.; Ullah, S.; Glowacz, A.; Glowacz, W. Optical-Interference Mitigation in Visible Light Communication for Intelligent Transport Systems Applications. Energies 2020, 13, 5064. [Google Scholar] [CrossRef]
- Memedi, A.; Tsai, H.-M.; Dressler, F. Impact of Realistic Light Radiation Pattern on Vehicular Visible Light Communication. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; IEEE: Los Alamitos, CA, USA, 2017; pp. 1–6. [Google Scholar]
- Sharda, P. Next Generation Based Vehicular Visible Light Communications: A Novel Transmission Scheme. IEEE Trans. Veh. Technol. 2024, 1–9. [Google Scholar] [CrossRef]
- Eldeeb, H.B.; Naser, S.; Bariah, L.; Muhaidat, S. Energy and Spectral Efficiency Analysis for RIS-Aided V2V-Visible Light Communication. IEEE Commun. Lett. 2023, 27, 2373–2377. [Google Scholar] [CrossRef]
- Yahia, S.; Meraihi, Y.; Gabis, A.B.; Ramdane-Cherif, A. On the Performance of MIMO Vehicular Visible Light Communications. In Advances in Computational Intelligence and Communication; Hina, M.D., Ramdane-Cherif, A., Zitouni, R., Soukane, A., Eds.; EAI/Springer Innovations in Communication and Computing; Springer International Publishing: Cham, Switzerland, 2023; pp. 51–61. [Google Scholar]
- Liu, W.; He, X. Performance Analysis of MIMO Visible Light Based V2V Communications. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; IEEE: Los Alamitos, CA, USA, 2019; pp. 1–4. [Google Scholar]
- Aly, B.; Elamassie, M.; Eldeeb, H.B.; Uysal, M. Experimental Investigation of Lens Combinations on the Performance of Vehicular VLC. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020; IEEE: Los Alamitos, CA, USA, 2020; pp. 1–5. [Google Scholar]
- Ley-Bosch, C.; Alonso-Gonzalez, I.; Sanchez-Rodriguez, D.; Quintana-Suarez, M.A. Analysis of the Effects of the Hidden Node Problem in IEEE 802.15.7 Uplink Performance. In Proceedings of the 2015 International Conference on Computer, Information and Telecommunication Systems (CITS), Gijon, Spain, 15–17 July 2015; IEEE: Los Alamitos, CA, USA, 2015; pp. 1–5. [Google Scholar]
- Khan, L.U. Visible Light Communication: Applications, Architecture, Standardization and Research Challenges. Digit. Commun. Netw. 2017, 3, 78–88. [Google Scholar] [CrossRef]
- Memedi, A.; Dressler, F. Vehicular Visible Light Communications: A Survey. IEEE Commun. Surv. Tutorials 2021, 23, 161–181. [Google Scholar] [CrossRef]
- Nagura, T.; Yamazato, T.; Katayama, M.; Yendo, T.; Fujii, T.; Okada, H. Improved Decoding Methods of Visible Light Communication System for ITS Using LED Array and High-Speed Camera. In Proceedings of the 2010 IEEE 71st Vehicular Technology Conference, Taipei, Taiwan, 16–19 May 2010; IEEE: Los Alamitos, CA, USA, 2010; pp. 1–5. [Google Scholar]
- Nawaz, T.; Seminara, M.; Caputo, S.; Mucchi, L.; Cataliotti, F.S.; Catani, J. IEEE 802.15.7-Compliant Ultra-Low Latency Relaying VLC System for Safety-Critical ITS. IEEE Trans. Veh. Technol. 2019, 68, 12040–12051. [Google Scholar] [CrossRef]
- Cailean, A.-M.; Dimian, M.; Done, A. Enhanced Design of Visible Light Communication Sensor for Automotive Applications: Experimental Demonstration of a 130 Meters Link. In Proceedings of the 2018 Global LIFI Congress (GLC), Paris, France, 8–9 February 2018; IEEE: Los Alamitos, CA, USA, 2018; pp. 1–4. [Google Scholar]
- Naser, S.; Sofotasios, P.C.; Bariah, L.; Jaafar, W.; Muhaidat, S.; Al-Qutayri, M.; Dobre, O.A. Rate-Splitting Multiple Access: Unifying NOMA and SDMA in MISO VLC Channels. IEEE Open J. Veh. Technol. 2020, 1, 393–413. [Google Scholar] [CrossRef]
- Arafa, N.A.; Arafa, M.S.; Abd El-atty, S.M.; El-Samie, F.E.A.; Eldeeb, H.B. Capacity Analysis of Infrastructure-to-Vehicle Visible Light Communication with an Optimized Non-Orthogonal Multiple Access Scheme. Opt. Quant. Electron. 2023, 55, 840. [Google Scholar] [CrossRef]
- Eldeeb, H.B.; Yanmaz, E.; Uysal, M. MAC Layer Performance of Multi-Hop Vehicular VLC Networks with CSMA/CA. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020; IEEE: Los Alamitos, CA, USA, 2020; pp. 1–6. [Google Scholar]
- Yahia, S.; Meraihi, Y.; Gabis, A.B.; Ramdane-Cherif, A. Multi-Directional Vehicle-To-Vehicle Visible Light Communication With Angular Diversity Technology. In Proceedings of the 2020 2nd International Workshop on Human-Centric Smart Environments for Health and Well-being (IHSH), Boumerdes, Algeria, 9–10 February 2021; IEEE: Los Alamitos, CA, USA, 2021; pp. 160–164. [Google Scholar]
- Eldeeb, H.B.; Elamassie, M.; Sait, S.M.; Uysal, M. Infrastructure-to-Vehicle Visible Light Communications: Channel Modelling and Performance Analysis. IEEE Trans. Veh. Technol. 2022, 71, 2240–2250. [Google Scholar] [CrossRef]
- Kumar, N.; Terra, D.; Lourenco, N.; Nero Alves, L.; Aguiar, R.L. Visible Light Communication for Intelligent Transportation in Road Safety Applications. In Proceedings of the 2011 7th International Wireless Communications and Mobile Computing Conference, Istanbul, Turkey, 4–8 July 2011; IEEE: Los Alamitos, CA, USA, 2011; pp. 1513–1518. [Google Scholar]
- Yamazato, T.; Kinoshita, M.; Arai, S.; Souke, E.; Yendo, T.; Fujii, T.; Kamakura, K.; Okada, H. Vehicle Motion and Pixel Illumination Modeling for Image Sensor Based Visible Light Communication. IEEE J. Select. Areas Commun. 2015, 33, 1793–1805. [Google Scholar] [CrossRef]
- Viriyasitavat, W.; Yu, S.-H.; Tsai, H.-M. Short Paper: Channel Model for Visible Light Communications Using off-the-Shelf Scooter Taillight. In Proceedings of the 2013 IEEE Vehicular Networking Conference, Boston, MA, USA, 16–18 December 2013; IEEE: Los Alamitos, CA, USA, 2013; pp. 170–173. [Google Scholar]
- Uysal, M.; Ghassemlooy, Z.; Bekkali, A.; Kadri, A.; Menouar, H. Visible Light Communication for Vehicular Networking: Performance Study of a V2V System Using a Measured Headlamp Beam Pattern Model. IEEE Veh. Technol. Mag. 2015, 10, 45–53. [Google Scholar] [CrossRef]
- Kim, Y.H.; Cahyadi, W.A.; Chung, Y.H. Experimental Demonstration of VLC-Based Vehicle-to-Vehicle Communications Under Fog Conditions. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Elamassie, M.; Karbalayghareh, M.; Miramirkhani, F.; Kizilirmak, R.C.; Uysal, M. Effect of Fog and Rain on the Performance of Vehicular Visible Light Communications. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; IEEE: Porto, Portugal, 2018; pp. 1–6. [Google Scholar]
- Eldeeb, H.B.; Miramirkhani, F.; Uysal, M. A Path Loss Model for Vehicle-to-Vehicle Visible Light Communications. In Proceedings of the 2019 15th International Conference on Telecommunications (ConTEL), Graz, Austria, 3–5 July 2019; IEEE: Graz, Austria, 2019; pp. 1–5. [Google Scholar]
- Mishra, S.; Maheshwari, R.; Grover, J.; Vaishnavi, V. Investigating the Performance of a Vehicular Communication System Based on Visible Light Communication (VLC). Int. J. Inf. Technol. 2022, 14, 877–885. [Google Scholar] [CrossRef]
- Sharda, P.; Bhatnagar, M.R.; Ghassemlooy, Z. Modeling of a Vehicle-to-Vehicle Based Visible Light Communication System Under Shadowing and Investigation of the Diversity-Multiplexing Tradeoff. IEEE Trans. Veh. Technol. 2022, 71, 9460–9474. [Google Scholar] [CrossRef]
- Xie, Y.; Xu, D.; Zhang, T.; Yu, K.; Hussain, A.; Guizani, M. VLC-Assisted Safety Message Dissemination in Roadside Infrastructure-Less IoV Systems: Modeling and Analysis. IEEE Internet Things J. 2024, 11, 8185–8198. [Google Scholar] [CrossRef]
- Akanegawa, M.; Tanaka, Y.; Nakagawa, M. Basic Study on Traffic Information System Using LED Traffic Lights. IEEE Trans. Intell. Transport. Syst. 2001, 2, 197–203. [Google Scholar] [CrossRef]
- Kahn, J.M.; Barry, J.R. Wireless Infrared Communications. Proc. IEEE 1997, 85, 265–298. [Google Scholar] [CrossRef]
- Karbalayghareh, M.; Miramirkhani, F.; Eldeeb, H.B.; Kizilirmak, R.C.; Sait, S.M.; Uysal, M. Channel Modelling and Performance Limits of Vehicular Visible Light Communication Systems. IEEE Trans. Veh. Technol. 2020, 69, 6891–6901. [Google Scholar] [CrossRef]
- Eldeeb, H.B.; Elamassie, M.; Uysal, M. Vehicle-to-Infrastructure Visible Light Communications: Channel Modelling and Capacity Calculations. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020; IEEE: Los Alamitos, CA, USA, 2020; pp. 1–6. [Google Scholar]
- Cervinka, D.; Ahmad, Z.; Salih, O.; Rajbhandari, S. A Study of Yearly Sunlight Variance Effect on Vehicular Visible Light Communication for Emergency Service Vehicles. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020; IEEE: Los Alamitos, CA, USA, 2020; pp. 1–6. [Google Scholar]
- Eldeeb, H.B.; Uysal, M. Visible Light Communication-Based Outdoor Broadcasting. In Proceedings of the 2021 17th International Symposium on Wireless Communication Systems (ISWCS), Berlin, Germany, 6–9 September 2021; IEEE: Los Alamitos, CA, USA, 2021; pp. 1–6. [Google Scholar]
- Sharda, P.; Reddy, G.S.; Bhatnagar, M.R.; Ghassemlooy, Z. A Comprehensive Modeling of Vehicle-to-Vehicle Based VLC System Under Practical Considerations, an Investigation of Performance, and Diversity Property. IEEE Trans. Commun. 2022, 70, 3320–3332. [Google Scholar] [CrossRef]
- Sharda, P.; Bhatnagar, M.R. Vehicular Visible Light Communication System: Modeling and Visualizing Critical Outdoor Propagation Characteristics. IEEE Trans. Veh. Technol. 2023, 72, 14317–14329. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Performance Evaluation of Visible-Light Wireless Communication System Using White LED Lightings. In Proceedings of the Proceedings. ISCC 2004. Ninth International Symposium on Computers and Communications (IEEE Cat. No.04TH8769), Alexandria, Egypt, 28 June–1 July 2004; IEEE: Alexandria, Egypt, 2004; Volume 1, pp. 258–263. [Google Scholar]
- Lapidoth, A.; Moser, S.M.; Wigger, M.A. On the Capacity of Free-Space Optical Intensity Channels. IEEE Trans. Inform. Theory. 2009, 55, 4449–4461. [Google Scholar] [CrossRef]
- Chaaban, A.; Morvan, J.-M.; Alouini, M.-S. Free-Space Optical Communications: Capacity Bounds, Approximations, and a New Sphere-Packing Perspective. IEEE Trans. Commun. 2016, 64, 1176–1191. [Google Scholar] [CrossRef]
- Yin, L.; Haas, H. Physical-Layer Security in Multiuser Visible Light Communication Networks. IEEE J. Select. Areas Commun. 2018, 36, 162–174. [Google Scholar] [CrossRef]





| Classification | [30] | [31] | [32] | [36,37] | [39] | Our Proposed Work |
|---|---|---|---|---|---|---|
| VLC Scenario | I2V | V2I | I2V, V2I and V2V | V2V | V2V | V2I |
| System Model | Both LOS and NLOS | Only LOS | Only LOS | Only LOS | Both LOS and NLOS | Both LOS and NLOS |
| Modeling Approach | Using the non- sequential ray tracing function of OpticStudio® | Based on Lambertian radiation model and hardware simulation | Based on Image sensors | Using the non- sequential ray tracing function of Zemax® | Considering AT and shadow effects | Channel modeling method considering AT |
| Tx | LED streetlights | LED arrays conforming to Lambertian radiation patterns | LED arrays and LED headlights | LED headlights | LED taillights | LED headlights |
| Rx | PD-based receivers | PD-based receivers | High-speed camera-based receiver | PD-based receivers | PD-based receivers | PD-based receivers |
| Comparative Study of LOS and NLOS | × | × | × | × | √ | √ |
| Considering AT and Various Propagation Characteristics | × | × | × | √ | √ | √ |
| Deriving Closed-form Expressions for Channel Models and Performance Indicators | × | √ | × | √ | × | √ |
| Symbol | Variable Name | Value |
|---|---|---|
| Aperture Diameter of PD | 0.02 m | |
| Road Width | 4.5 m | |
| Vehicle Width | 1.8 m | |
| (Clear Weather) | Extinction Coefficient (Clear Weather) | 0 |
| (Moderate Fog) | Extinction Coefficient (Moderate Fog) | 0.00782 |
| (Dense Fog) | Extinction Coefficient (Dense Fog) | 0.01565 |
| (Clear Weather) | Weather Correction Factor 1 (Clear Weather) | 0.0175 |
| (Moderate Fog) | Weather Correction Factor 1 (Moderate Fog) | 0.0172 |
| (Dense Fog) | Weather Correction Factor 1 (Dense Fog) | 0.0170 |
| (Clear Weather) | Weather Correction Factor 2 (Clear Weather) | 0.1585 |
| (Moderate Fog) | Weather Correction Factor 2 (Moderate Fog) | 0.1600 |
| (Dense Fog) | Weather Correction Factor 2 (Dense Fog) | 0.1550 |
| Height of Headlights and PD | 0.7 m | |
| Variance of the Zero Mean AWGN Noise | 1 | |
| Variance of the Lognormal Distribution | 0.2 | |
| Photoelectric Conversion Efficiency of PD | 1 | |
| Output Power of a Single Tx | 30 W | |
| System Bandwidth | 20 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Liu, H.; Cheng, G. Modeling and Performance Study of Vehicle-to-Infrastructure Visible Light Communication System for Mountain Roads. Sensors 2024, 24, 5541. https://doi.org/10.3390/s24175541
Yang W, Liu H, Cheng G. Modeling and Performance Study of Vehicle-to-Infrastructure Visible Light Communication System for Mountain Roads. Sensors. 2024; 24(17):5541. https://doi.org/10.3390/s24175541
Chicago/Turabian StyleYang, Wei, Haoran Liu, and Guangpeng Cheng. 2024. "Modeling and Performance Study of Vehicle-to-Infrastructure Visible Light Communication System for Mountain Roads" Sensors 24, no. 17: 5541. https://doi.org/10.3390/s24175541
APA StyleYang, W., Liu, H., & Cheng, G. (2024). Modeling and Performance Study of Vehicle-to-Infrastructure Visible Light Communication System for Mountain Roads. Sensors, 24(17), 5541. https://doi.org/10.3390/s24175541





