Estimating Lab-Quake Source Parameters: Spectral Inversion from a Calibrated Acoustic System
Abstract
:1. Introduction
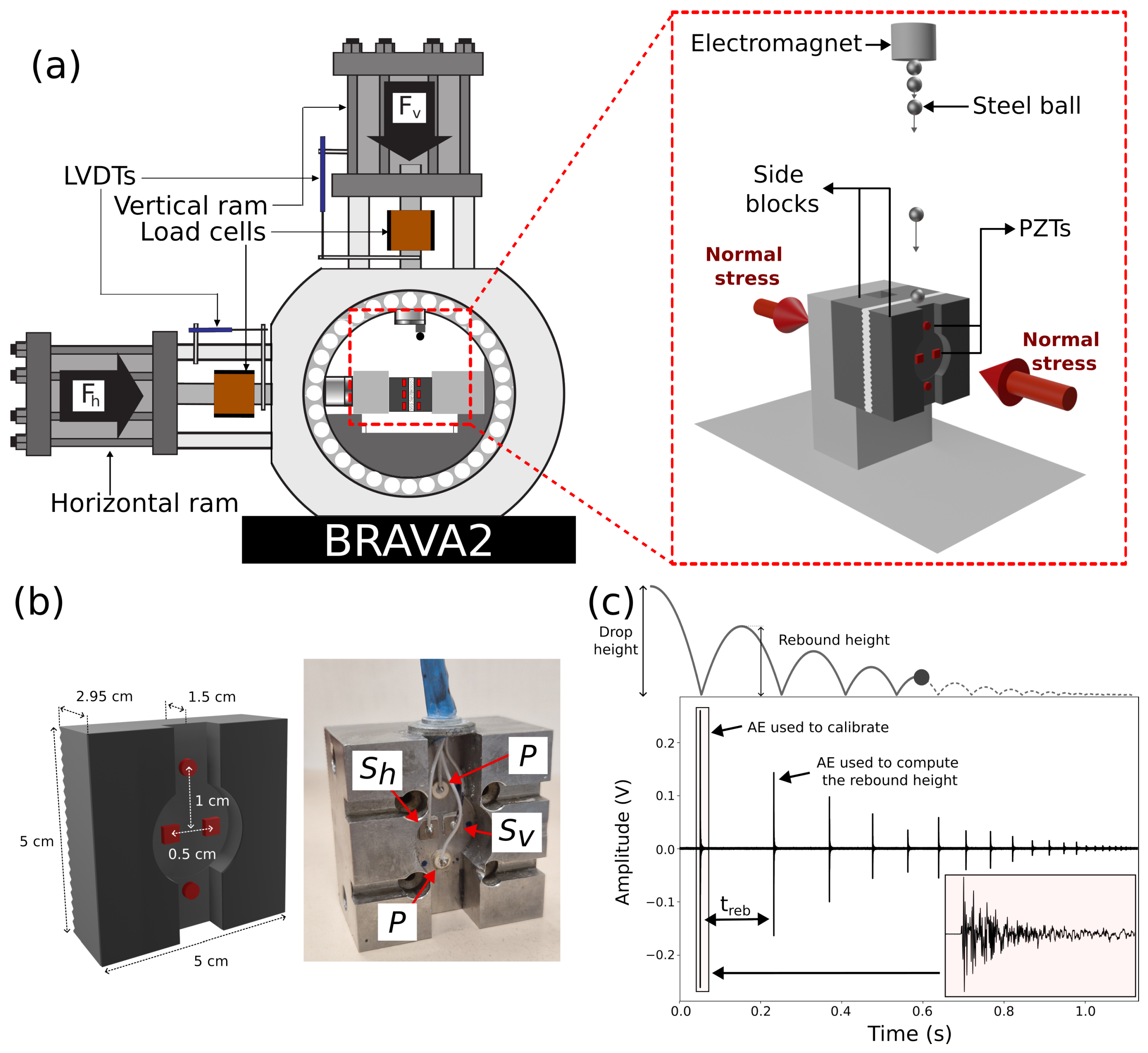
2. Calibration Test Setup
2.1. Deformation Apparatus
2.2. Acoustic System
2.3. Ball-Drop Setup and Procedure
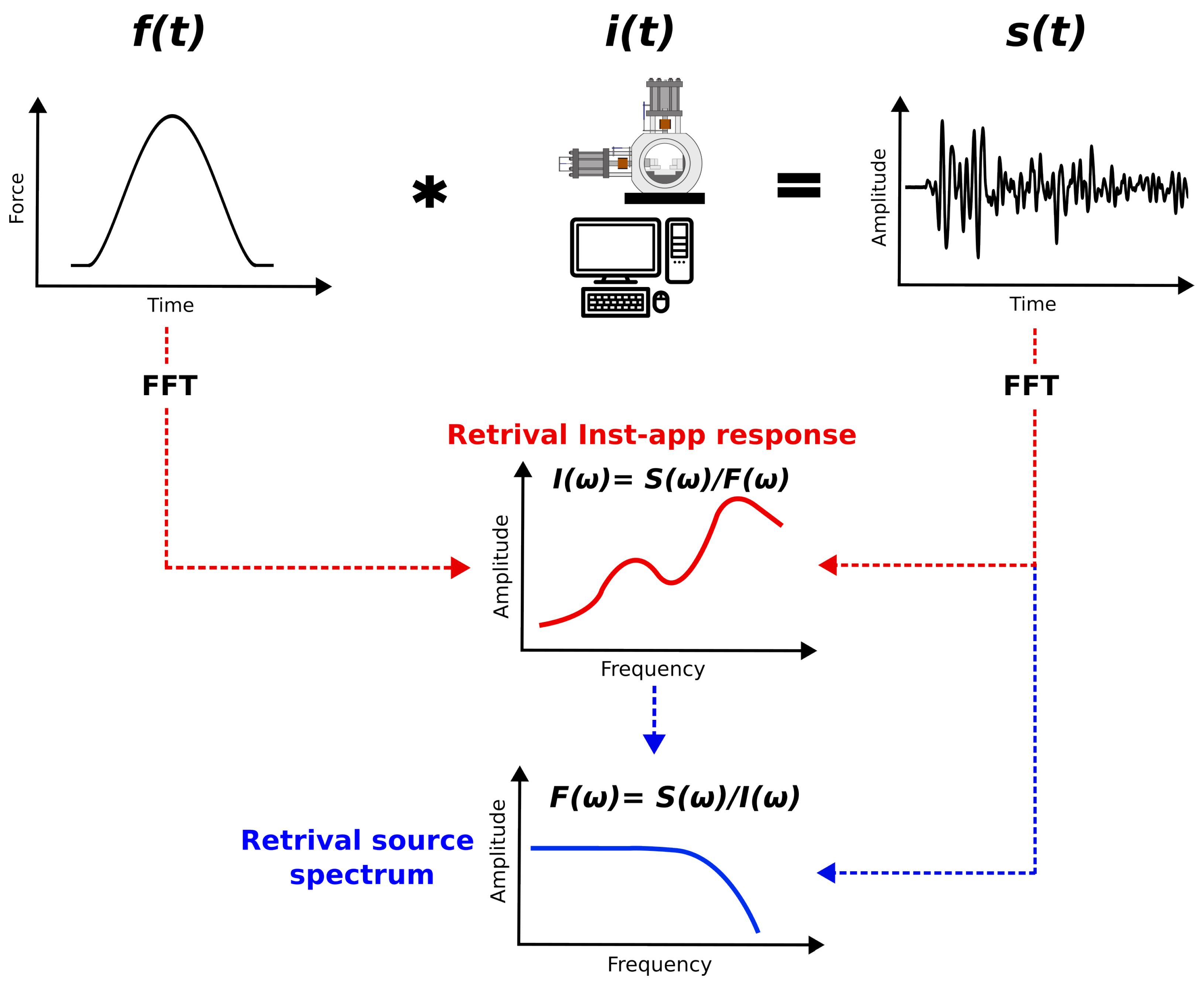
3. Theoretical Framework
4. Absolute AE System Calibration
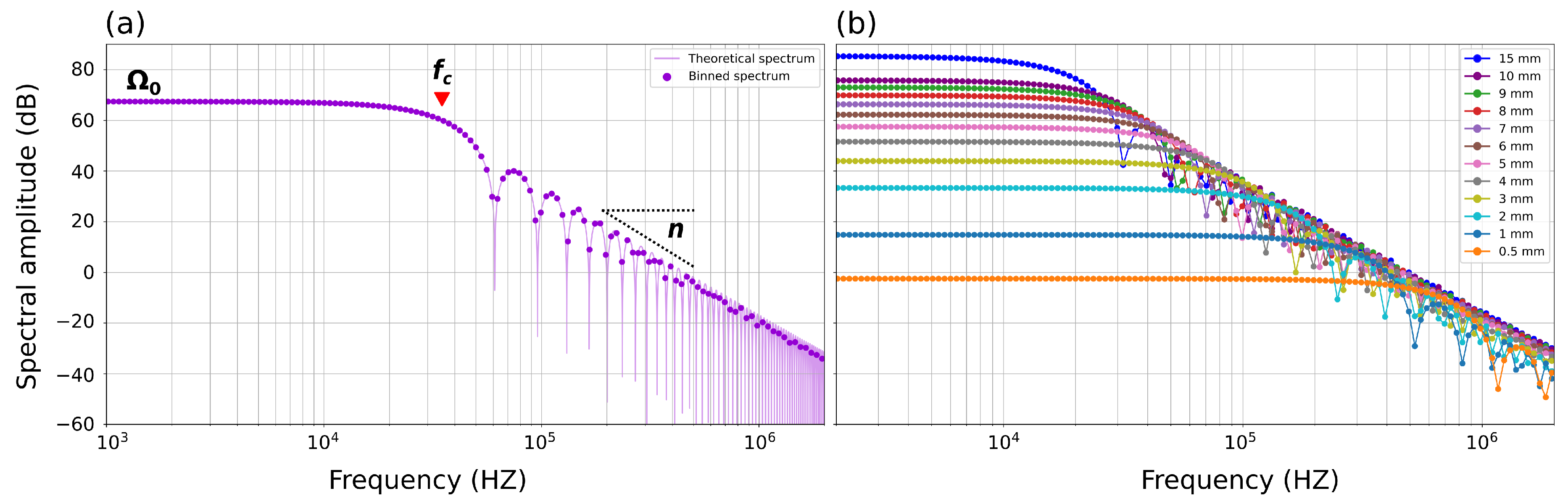
4.1. Theoretical Force–Time Function
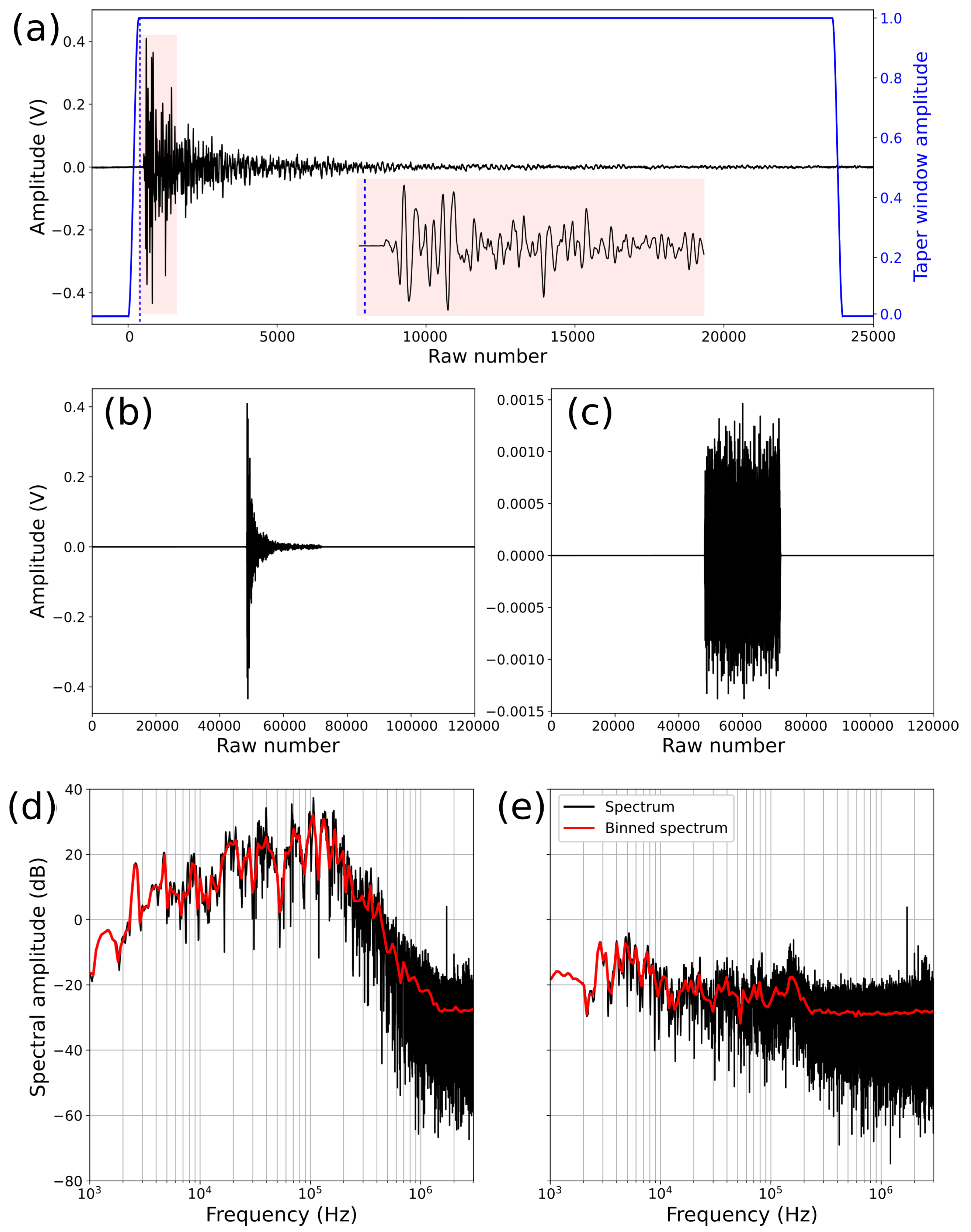
4.2. Waveform Analysis
4.3. Spectral Analysis
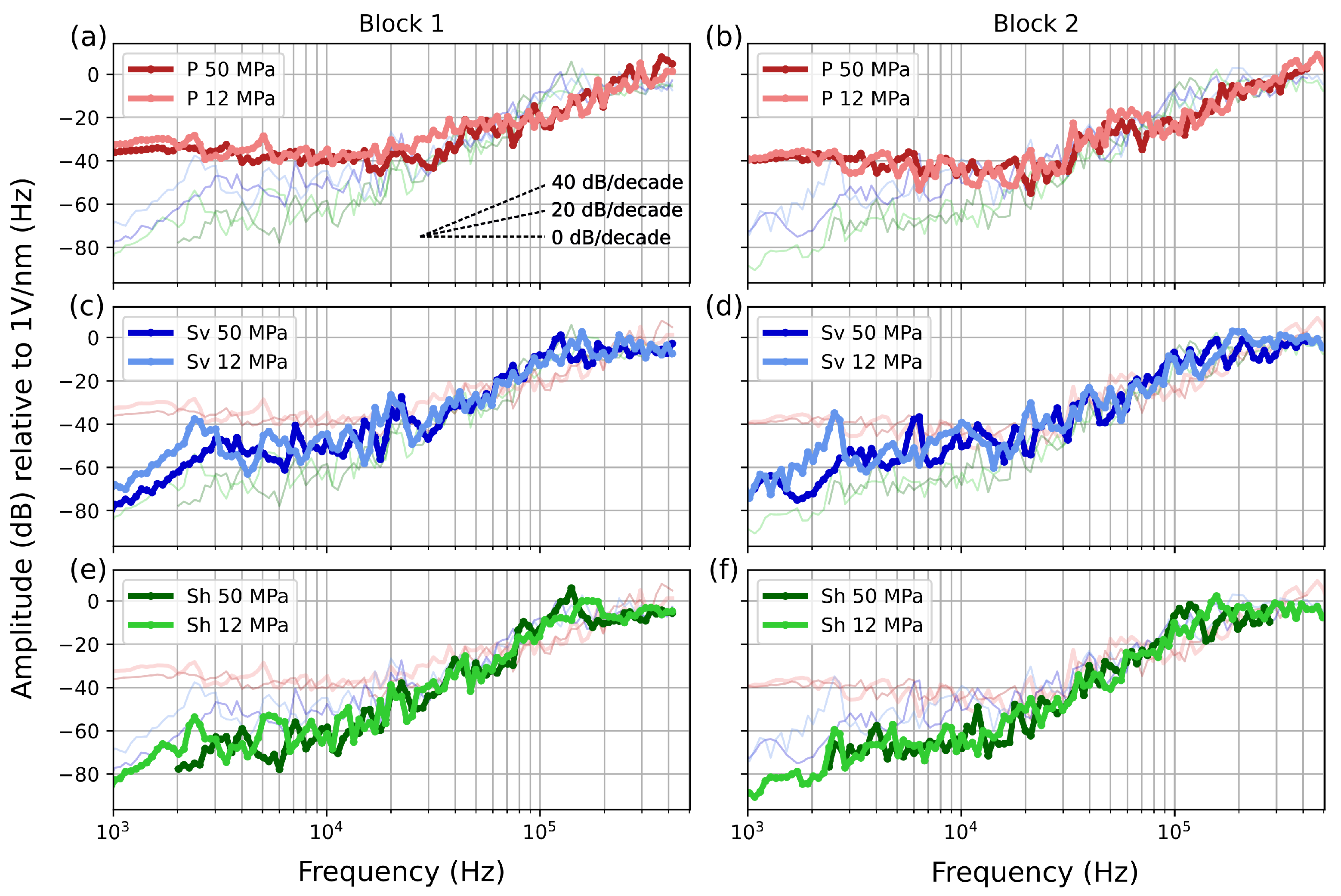
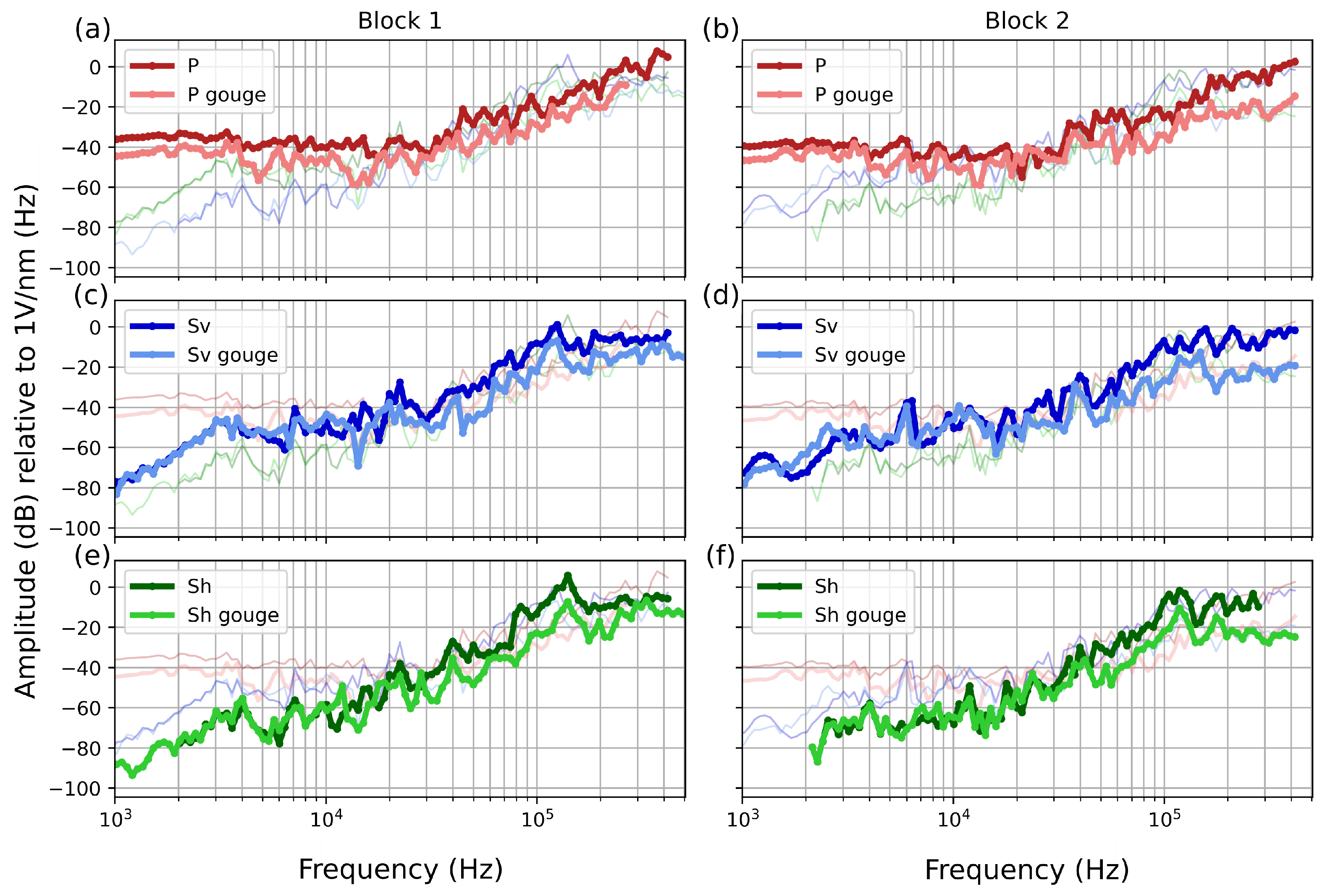
4.4. Instrument Apparatus Responses and Effect of Normal Stress and Gouge on Sensor Sensitivity
4.5. Source Spectrum Derivation
5. Test Experiment
5.1. Experimental Setup
5.2. Acoustic Emission Waveform during Lab Quake
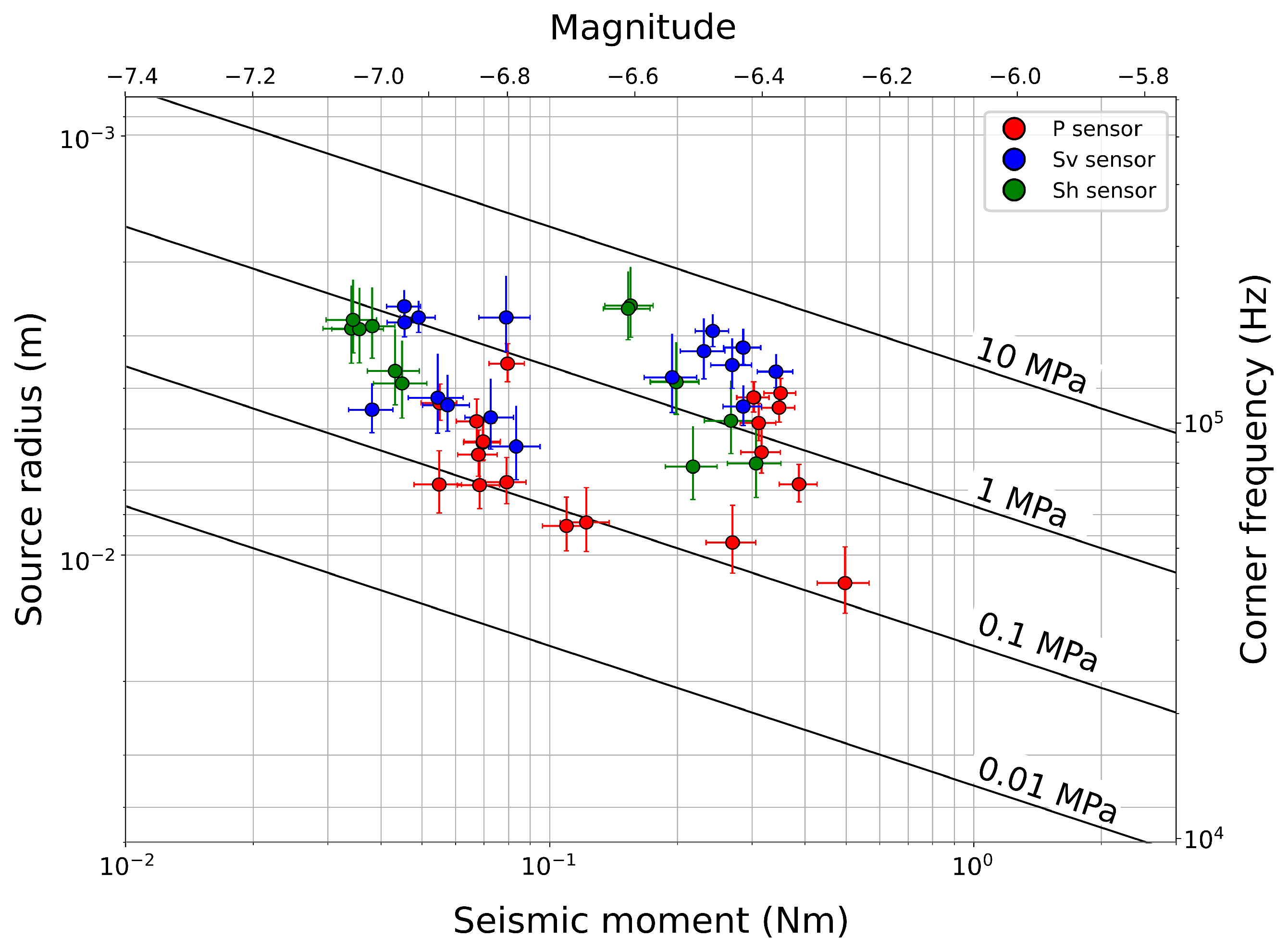
5.3. Source Parameter Derivation
6. Applicability and Limits
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mogi, K. Study of elastic shocks caused by the fracture of heterogeneous materials and its relations to earthquake phenomena. Bull. Earthq. Res. Inst. Univ. Tokyo 1962, 40, 125–173. [Google Scholar]
- Scholz, C.H. Experimental study of the fracturing process in brittle rock. J. Geophys. Res. 1968, 73, 1447–1454. [Google Scholar] [CrossRef]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Scholz, C.H. Microfractures, aftershocks, and seismicity. Bull. Seismol. Soc. Am. 1968, 58, 1117–1130. [Google Scholar]
- Scholz, C.H. Microfracturing and the inelastic deformation of rock in compression. J. Geophys. Res. 1968, 73, 1417–1432. [Google Scholar] [CrossRef]
- Lockner, D. The role of acoustic emission in the study of rock fracture. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 883–899. [Google Scholar] [CrossRef]
- Johnson, P.A.; Ferdowsi, B.; Kaproth, B.M.; Scuderi, M.; Griffa, M.; Carmeliet, J.; Guyer, R.A.; Le Bas, P.-Y.; Trugman, D.T.; Marone, C. Acoustic emission and microslip precursors to stick-slip failure in sheared granular material. Geophys. Res. Lett. 2013, 40, 5627–5631. [Google Scholar] [CrossRef]
- Kwiatek, G.; Goebel, T.H.W.; Dresen, G. Seismic moment tensor and b value variations over successive seismic cycles in laboratory stick-slip experiments. Geophys. Res. Lett. 2014, 41, 5838–5846. [Google Scholar] [CrossRef]
- Lei, X.; Li, S.; Liu, L. Seismic b-value for foreshock AE events preceding repeated stick-slips of pre-cut faults in granite. Appl. Sci. 2018, 8, 2361. [Google Scholar] [CrossRef]
- Rivière, J.; Lv, Z.; Johnson, P.A.; Marone, C. Evolution of b-value during the seismic cycle: Insights from laboratory experiments on simulated faults. Earth Planet. Sci. Lett. 2018, 482, 407–413. [Google Scholar] [CrossRef]
- Marty, S.; Schubnel, A.; Bhat, H.S.; Aubry, J.; Fukuyama, E.; Latour, S.; Nielsen, S.; Madariaga, R. Nucleation of laboratory earthquakes: Quantitative analysis and scalings. J. Geophys. Res. Solid Earth 2023, 128, e2022JB026294. [Google Scholar] [CrossRef]
- Goebel, T.H.W.; Kwiatek, G.; Becker, T.W.; Brodsky, E.E.; Dresen, G. What allows seismic events to grow big?: Insights from b-value and fault roughness analysis in laboratory stick-slip experiments. Geology 2017, 45, 815–818. [Google Scholar] [CrossRef]
- Bolton, D.C.; Marone, C.; Saffer, D.; Trugman, D.T. Foreshock properties illuminate nucleation processes of slow and fast laboratory earthquakes. Nat. Commun. 2023, 14, 3859. [Google Scholar] [CrossRef] [PubMed]
- Dresen, G.; Kwiatek, G.; Goebel, T.; Ben-Zion, Y. Seismic and aseismic preparatory processes before large stick–slip failure. Pure Appl. Geophys. 2020, 177, 5741–5760. [Google Scholar] [CrossRef]
- Marty, S.; Passelègue, F.X.; Aubry, J.; Bhat, H.S.; Schubnel, A.; Madariaga, R. Origin of high-frequency radiation during laboratory earthquakes. Geophys. Res. Lett. 2019, 46, 3755–3763. [Google Scholar] [CrossRef]
- Selvadurai, P.A.; Glaser, S.D. Laboratory-developed contact models controlling instability on frictional faults. J. Geophys. Res. Solid Earth 2015, 120, 4208–4236. [Google Scholar] [CrossRef]
- McLaskey, G.C.; Glaser, S.D. Micromechanics of asperity rupture during laboratory stick slip experiments. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Kwiatek, G.; Charalampidou, E.-M.; Dresen, G.; Stanchits, S. An improved method for seismic moment tensor inversion of acoustic emissions through assessment of sensor coupling and sensitivity to incidence angle. Int. J. Rock Mech. Min. Sci. 2014, 65, 153–161. [Google Scholar] [CrossRef]
- Manthei, G. Characterization of acoustic emission sources in a rock salt specimen under triaxial compression. Bull. Seismol. Soc. Am. 2005, 95, 1674–1700. [Google Scholar] [CrossRef]
- Goodfellow, S.D.; Young, R.P. A laboratory acoustic emission experiment under in situ conditions. Geophys. Res. Lett. 2014, 41, 3422–3430. [Google Scholar] [CrossRef]
- McLaskey, G.C.; Lockner, D.A. Calibrated acoustic emission system records M-3.5 to M-8 events generated on a saw-cut granite sample. Rock Mech. Rock Eng. 2016, 49, 4527–4536. [Google Scholar] [CrossRef]
- Aki, K. Scaling law of seismic spectrum. J. Geophys. Res. 1967, 72, 1217–1231. [Google Scholar] [CrossRef]
- Abercrombie, R.E. Resolution and uncertainties in estimates of earthquake stress drop and energy release. Philos. Trans. R. Soc. A 2021, 379, 20200131. [Google Scholar] [CrossRef] [PubMed]
- Cocco, M.; Tinti, E.; Cirella, A. On the scale dependence of earthquake stress drop. J. Seismol. 2016, 20, 1151–1170. [Google Scholar] [CrossRef]
- Ide, S.; Beroza, G.C. Does apparent stress vary with earthquake size? Geophys. Res. Lett. 2001, 28, 3349–3352. [Google Scholar] [CrossRef]
- Yoshimitsu, N.; Kawakata, H.; Takahashi, N. Magnitude-7 level earthquakes: A new lower limit of self-similarity in seismic scaling relationships. Geophys. Res. Lett. 2014, 41, 4495–4502. [Google Scholar] [CrossRef]
- Bindi, D.; Spallarossa, D.; Picozzi, M.; Oth, A.; Morasca, P.; Mayeda, K. The community stress-drop validation study—Part I: Source, propagation, and site decomposition of Fourier spectra. Seismol. Soc. Am. 2023, 94, 1980–1991. [Google Scholar] [CrossRef]
- Bindi, D.; Spallarossa, D.; Picozzi, M.; Oth, A.; Morasca, P.; Mayeda, K. The community stress-drop validation study—Part II: Uncertainties of the source parameters and stress drop analysis. Seismol. Soc. Am. 2023, 94, 1992–2002. [Google Scholar] [CrossRef]
- Baltay, A.; Abercrombie, R.; Chu, S.; Taira, T. The SCEC/USGS Community Stress Drop Validation Study Using the 2019 Ridgecrest Earthquake Sequence. Seismica 2024, 3. [Google Scholar] [CrossRef]
- Blanke, A.; Kwiatek, G.; Goebel, T.H.; Bohnhoff, M.; Dresen, G. Stress drop–Magnitude dependence of acoustic emissions during laboratory stick-slip. Geophys. J. Int. 2021, 224, 1371–1380. [Google Scholar] [CrossRef]
- Selvadurai, P.A. Laboratory insight into seismic estimates of energy partitioning during dynamic rupture: An observable scaling breakdown. J. Geophys. Res. Solid Earth 2019, 124, 11350–11379. [Google Scholar] [CrossRef]
- Lei, X.; Ma, S. Laboratory acoustic emission study for earthquake generation process. Earthq. Sci. 2014, 27, 627–646. [Google Scholar] [CrossRef]
- Ono, K. Calibration methods of acoustic emission sensors. Materials 2016, 9, 508. [Google Scholar] [CrossRef]
- Grosse, C.U.; Ohtsu, M.; Aggelis, D.G.; Shiotani, T. (Eds.) Acoustic Emission Testing: Basics for Research—Applications in Engineering; Springer Nature: Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- McLaskey, G.C.; Lockner, D.A.; Kilgore, B.D.; Beeler, N.M. A robust calibration technique for acoustic emission systems based on momentum transfer from a ball drop. Bull. Seismol. Soc. Am. 2015, 105, 257–271. [Google Scholar] [CrossRef]
- Wu, B.S.; McLaskey, G.C. Contained laboratory earthquakes ranging from slow to fast. J. Geophys. Res. Solid Earth 2019, 124, 10270–10291. [Google Scholar] [CrossRef]
- Scuderi, M.M.; Tinti, E.; Cocco, M.; Collettini, C. The role of shear fabric in controlling breakdown processes during laboratory slow-slip events. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020405. [Google Scholar] [CrossRef]
- Giorgetti, C.; Carpenter, B.M.; Collettini, C. Frictional behavior of talc-calcite mixtures. J. Geophys. Res. Solid Earth 2015, 120, 6614–6633. [Google Scholar] [CrossRef]
- Noël, C.; Giorgetti, C.; Collettini, C.; Marone, C. The effect of shear strain and shear localization on fault healing. Geophys. J. Int. 2024, 236, 1206–1215. [Google Scholar] [CrossRef]
- Hough, S.E. Empirical Green’s function analysis: Taking the next step. J. Geophys. Res. Solid Earth 1997, 102, 5369–5384. [Google Scholar] [CrossRef]
- Baltay, A.S.; Beroza, G.C.; Ide, S. Radiated energy of great earthquakes from teleseismic empirical Green’s function deconvolution. Pure Appl. Geophys. 2014, 171, 2841–2862. [Google Scholar] [CrossRef]
- Abercrombie, R.E. Investigating uncertainties in empirical Green’s function analysis of earthquake source parameters. J. Geophys. Res. Solid Earth 2015, 120, 4263–4277. [Google Scholar] [CrossRef]
- Thomas, A.M.; Beroza, G.C.; Shelly, D.R. Constraints on the source parameters of low-frequency earthquakes on the San Andreas Fault. Geophys. Res. Lett. 2016, 43, 1464–1471. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Frank, W.B.; Abercrombie, R.E.; Obara, K.; Kato, A. What makes low-frequency earthquakes low frequency. Sci. Adv. 2023, 9, eadh3688. [Google Scholar] [CrossRef] [PubMed]
- McLaskey, G.C.; Glaser, S.D. Acoustic emission sensor calibration for absolute source measurements. J. Nondestruct. Eval. 2012, 31, 157–168. [Google Scholar] [CrossRef]
- Goldsmith, W.; Frasier, J.T. Impact— The Theory and Physical Behavior of Colliding Solids. J. Appl. Mech. 1961, 28, 639. [Google Scholar] [CrossRef]
- Wu, B.S.; McLaskey, G.C. Broadband calibration of acoustic emission and ultrasonic sensors from generalized ray theory and finite element models. J. Nondestruct. Eval. 2018, 37, 8. [Google Scholar] [CrossRef]
- Leeman, J.R.; Saffer, D.M.; Scuderi, M.M.; Marone, C. Laboratory observations of slow earthquakes and the spectrum of tectonic fault slip modes. Nat. Commun. 2016, 7, 11104. [Google Scholar] [CrossRef]
- Leeman, J.R.; Marone, C.; Saffer, D.M. Frictional mechanics of slow earthquakes. J. Geophys. Res. Solid Earth 2018, 123, 7931–7949. [Google Scholar] [CrossRef]
- Scuderi, M.M.; Marone, C.; Tinti, E.; Stefano, G.D.; Collettini, C. Precursory changes in seismic velocity for the spectrum of earthquake failure modes. Nat. Geosci. 2016, 9, 695–700. [Google Scholar] [CrossRef]
- Scuderi, M.M.; Collettini, C.; Viti, C.; Tinti, E.; Marone, C. Evolution of shear fabric in granular fault gouge from stable sliding to stick slip and implications for fault slip mode. Geology 2017, 45, 731–734. [Google Scholar] [CrossRef]
- Tinti, E.; Scuderi, M.M.; Scognamiglio, L.; Stefano, G.D.; Marone, C.; Collettini, C. On the evolution of elastic properties during laboratory stick-slip experiments spanning the transition from slow slip to dynamic rupture. J. Geophys. Res. Solid Earth 2016, 121, 8569–8594. [Google Scholar] [CrossRef]
- Brune, J.N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
- Venkataraman, A.; Beroza, G.C.; Ide, S.; Imanishi, K.; Ito, H.; Iio, Y. Measurements of spectral similarity for microearthquakes in western Nagano, Japan. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Madariaga, R. Dynamics of an expanding circular fault. Bull. Seismol. Soc. Am. 1976, 66, 639–666. [Google Scholar] [CrossRef]
- Madariaga, R.; Sergio, R. Earthquake dynamics on circular faults: A review 1970–2015. J. Seismol. 2016, 20, 1235–1252. [Google Scholar] [CrossRef]
- Kaneko, Y.; Shearer, P.M. Variability of seismic source spectra, estimated stress drop, and radiated energy, derived from cohesive-zone models of symmetrical and asymmetrical circular and elliptical ruptures. J. Geophys. Res. Solid Earth 2015, 120, 1053–1079. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology; University Science Books: Herndon, VA, USA, 2002. [Google Scholar]






| Density | 7800 kg/m3 | |
| Elastic stiffness coefficient (shear direction) | N/m2 | |
| Elastic stiffness coefficient (axial direction) | N/m2 | |
| Elastic compliance coefficient | m2/N | |
| Poisson’s ratio | 0.35 |
| Ball Diameter (mm) | (N) | (Ns) | (kHz) | |
|---|---|---|---|---|
| 15 | 102.11 | 0.00310 | 18,579.44 | 18.237 |
| 10 | 51.47 | 0.00104 | 6185.67 | 27.608 |
| 9 | 41.5 | 0.00075 | 4480.6 | 30.702 |
| 8 | 32.66 | 0.00052 | 3125.33 | 34.569 |
| 7 | 24.90 | 0.00035 | 2077.93 | 39.542 |
| 6 | 18.22 | 0.00022 | 1297.28 | 46.171 |
| 5 | 12.60 | 0.00013 | 749.96 | 55.452 |
| 4 | 8.03 | 379.72 | 69.373 | |
| 3 | 4.499 | 157.67 | 92.574 | |
| 2 | 1.99 | 46.53 | 138.975 | |
| 1 | 0.49 | 5.52 | 278.176 | |
| 0.5 | 0.15 | 0.75 | 561.749 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pignalberi, F.; Mastella, G.; Giorgetti, C.; Scuderi, M.M. Estimating Lab-Quake Source Parameters: Spectral Inversion from a Calibrated Acoustic System. Sensors 2024, 24, 5824. https://doi.org/10.3390/s24175824
Pignalberi F, Mastella G, Giorgetti C, Scuderi MM. Estimating Lab-Quake Source Parameters: Spectral Inversion from a Calibrated Acoustic System. Sensors. 2024; 24(17):5824. https://doi.org/10.3390/s24175824
Chicago/Turabian StylePignalberi, Federico, Giacomo Mastella, Carolina Giorgetti, and Marco Maria Scuderi. 2024. "Estimating Lab-Quake Source Parameters: Spectral Inversion from a Calibrated Acoustic System" Sensors 24, no. 17: 5824. https://doi.org/10.3390/s24175824






