A Novel Robust Position Integration Optimization-Based Alignment Method for In-Flight Coarse Alignment
Abstract
1. Introduction
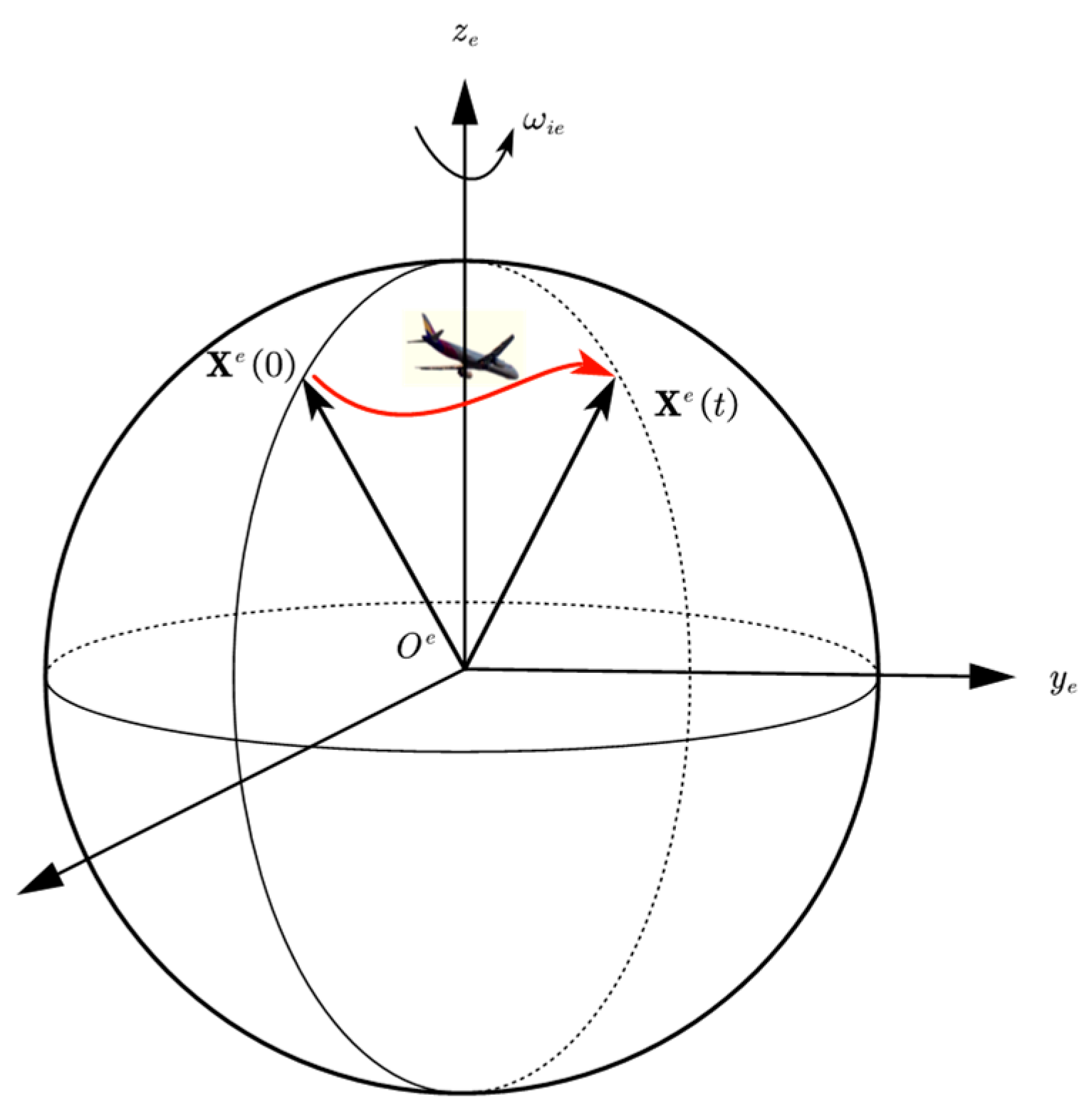
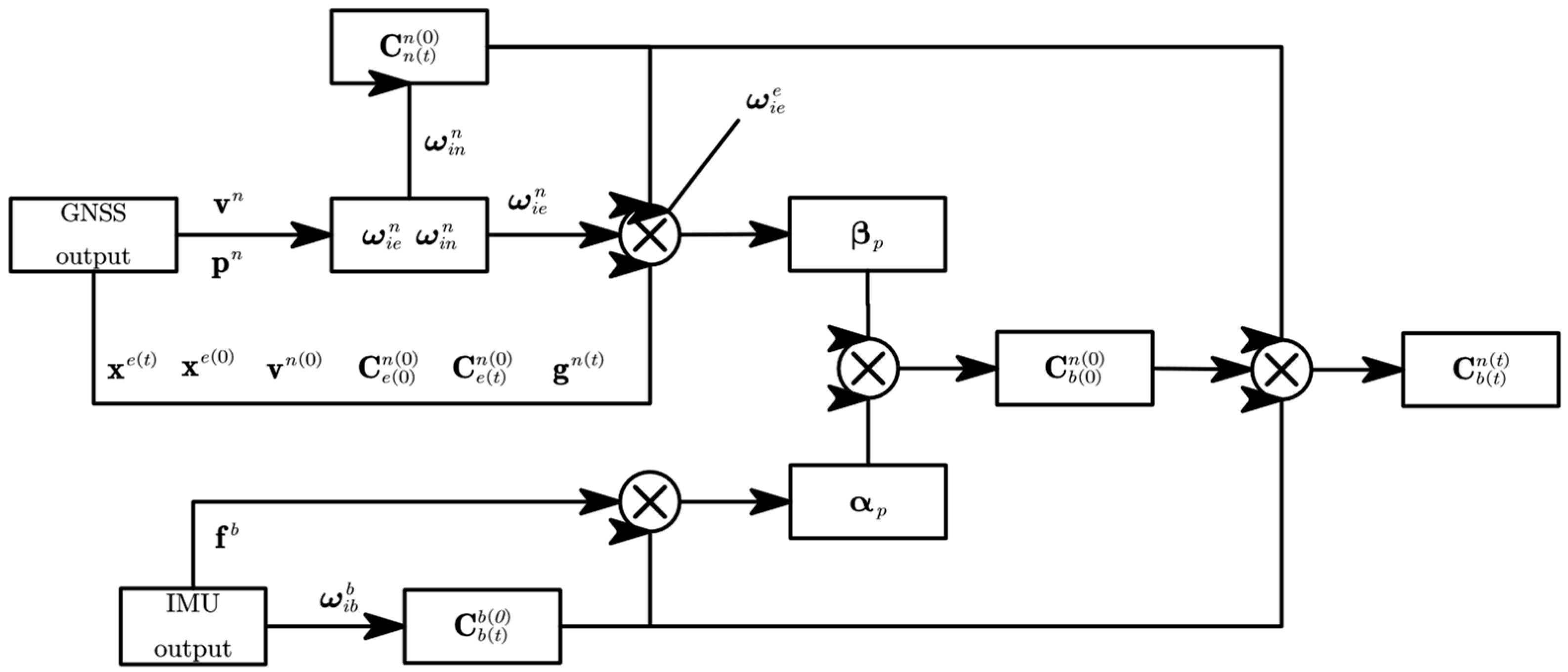
2. Robust Position Integration Alignment Method Aided by GNSS
2.1. Traditional OBA Method
2.2. Novel Robust Position Integration Formula
3. Simulations and Experiments
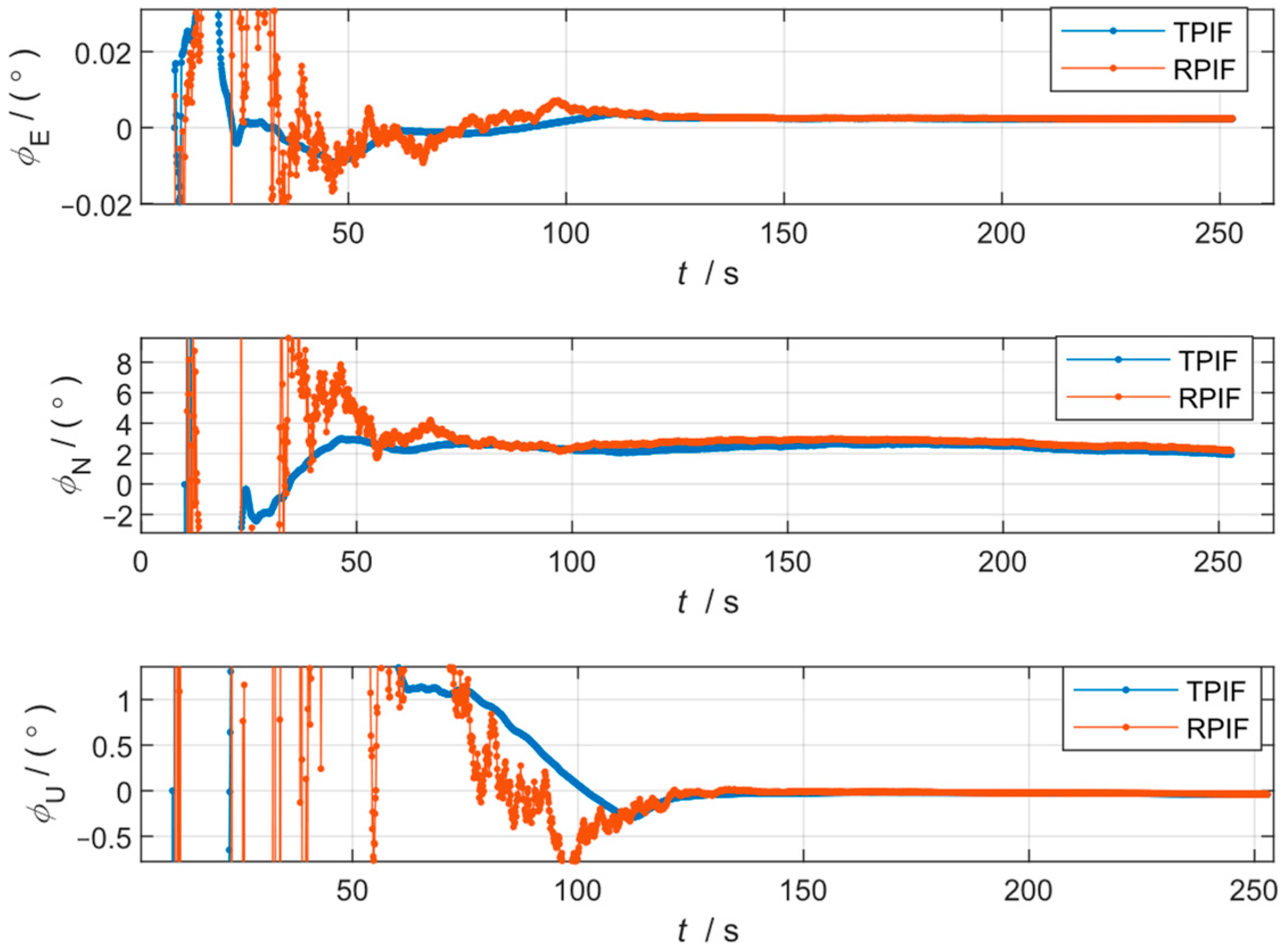
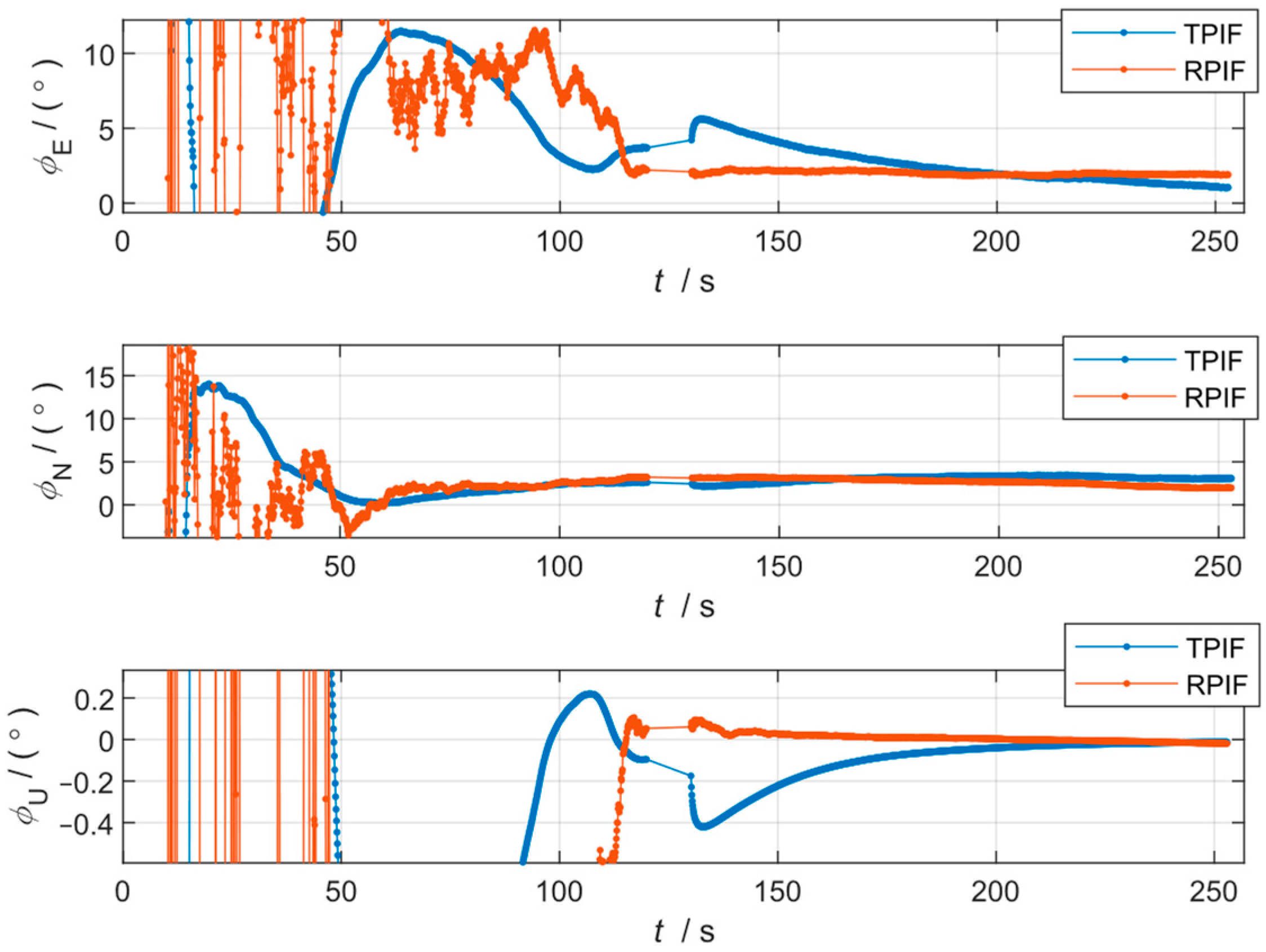
3.1. Simulation Results and Analysis
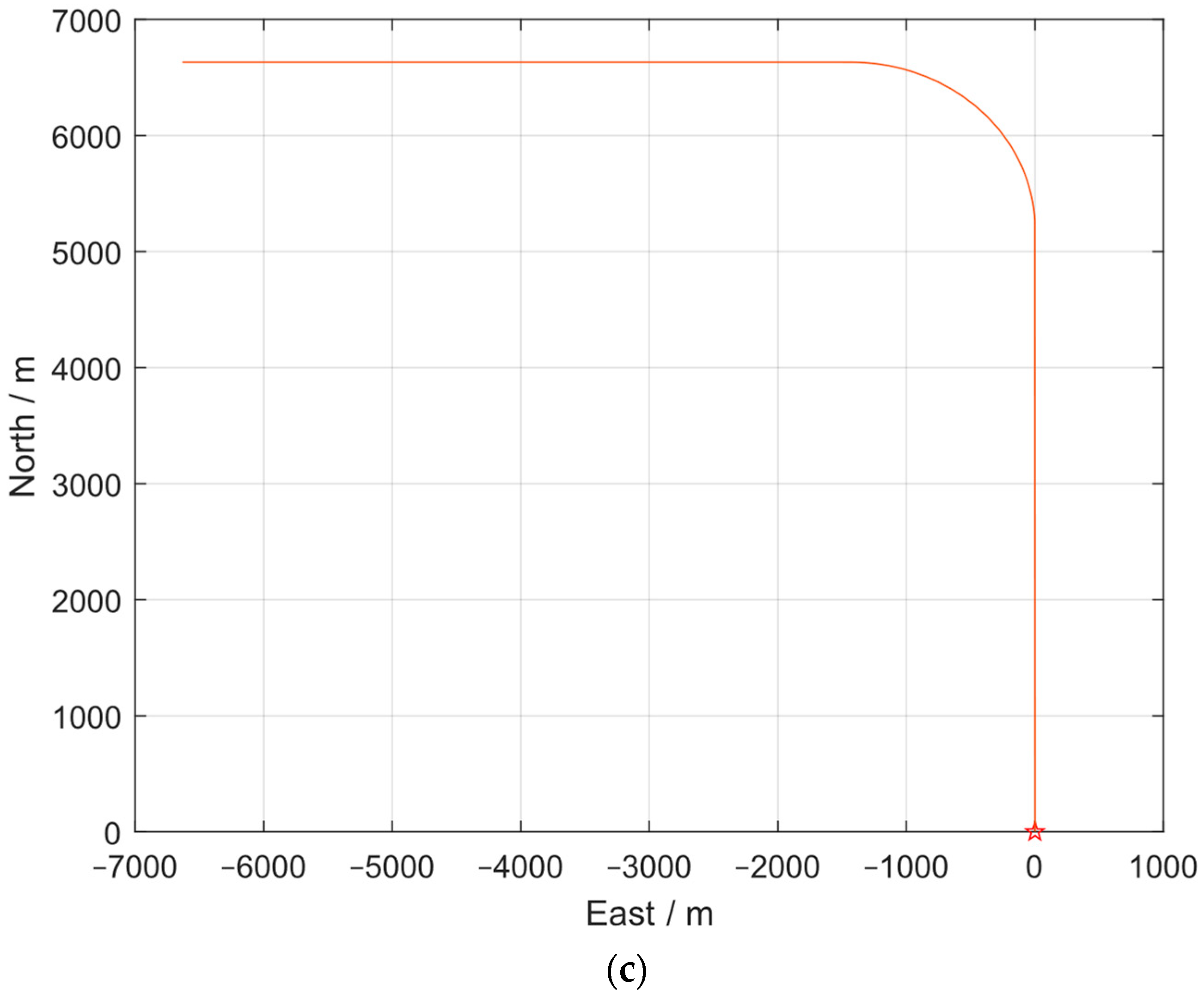
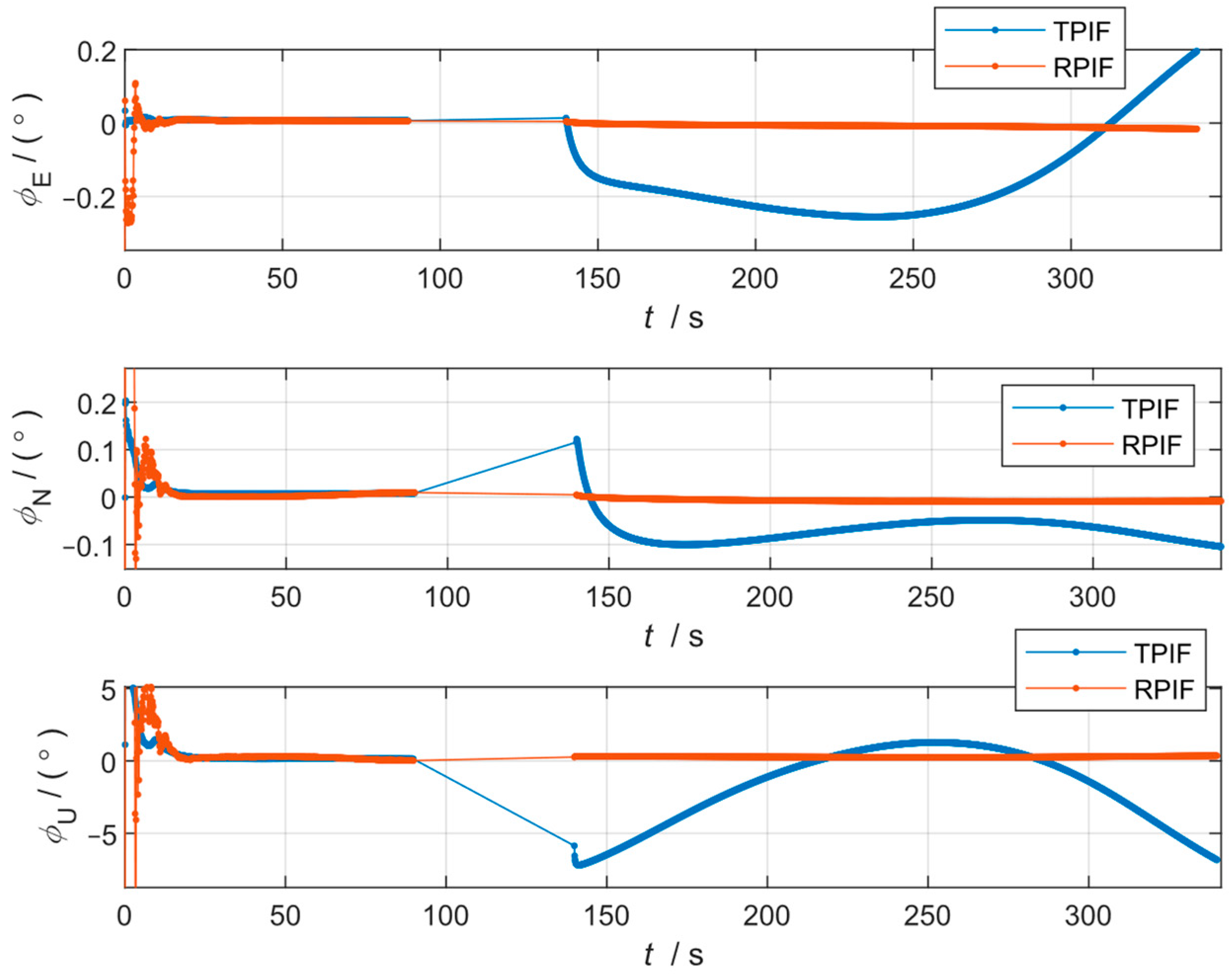
3.2. Field Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Savage, P.G. Strapdown Analytics; Strapdown Associates: Maple Plain, MN, USA, 2000. [Google Scholar]
- Jekeli, C. Inertial Navigation Systems with Geodetic Applications; Walter de Gruyter GmbH & Co KG: New York, NY, USA, 2012. [Google Scholar]
- Qin, Y.; Yan, G.; Gu, D.; Zheng, J. A Clever Way of SINS Coarse Alignment despite Rocking Ship. J. Northwestern Polytech. Univ. 2005, 23, 684. [Google Scholar]
- Yan, G.M.; Qin, Y.Y.; Wei, Y.X.; Zhang, L.C.; Yan, W.S. New initial alignment algorithm for SINS on moving base. Syst. Eng. Electron. 2009, 31, 634–637. [Google Scholar]
- Wu, M.; Wu, Y.; Hu, X.; Hu, D. Optimization-based alignment for inertial navigation systems: Theory and algorithm. Aerosp. Sci. Technol. 2011, 15, 1–17. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, X. Velocity/Position Integration Formula Part I: Application to In-Flight Coarse Alignment. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1006–1023. [Google Scholar] [CrossRef]
- Chang, L.; Qin, F.; Li, A. A Novel Backtracking Scheme for Attitude Determination-Based Initial Alignment. IEEE Trans. Autom. Sci. Eng. 2015, 12, 384–390. [Google Scholar] [CrossRef]
- Lubin, C.; Baiqing, H.; Yang, L. Backtracking Integration for Fast Attitude Determination-Based Initial Alignment. IEEE Trans. Instrum. Meas. 2015, 64, 795–803. [Google Scholar] [CrossRef]
- Chang, L.B.; Li, Y.; Xue, B.Y. Initial Alignment for a Doppler Velocity Log-Aided Strapdown Inertial Navigation System With Limited Information. IEEE-Asme Trans. Mechatron. 2017, 22, 329–338. [Google Scholar] [CrossRef]
- Xu, X.; Sun, Y.F.; Gui, J.; Yao, Y.Q.; Zhang, T. A Fast Robust In-Motion Alignment Method for SINS With DVL Aided. IEEE Trans. Veh. Technol. 2020, 69, 3816–3827. [Google Scholar] [CrossRef]
- Guo, S.; Wu, M.; Xu, J.; Zha, F. b-frame velocity aided coarse alignment method for dynamic SINS. IET Radar Sonar Navig. 2018, 12, 833–838. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Luo, L.; Fang, T.; Li, N.; Wang, G.Q. An Improved Coarse Alignment Algorithm for Odometer-Aided SINS Based on the Optimization Design Method. Sensors 2018, 18, 195. [Google Scholar] [CrossRef]
- Xu, X.; Ning, X.; Yao, Y.; Li, K. In-Motion Coarse Alignment Method for SINS/GPS Integration in Polar Region. IEEE Trans. Veh. Technol. 2022, 71, 6110–6118. [Google Scholar] [CrossRef]
- Chang, L.B.; Li, J.S.; Li, K.L. Optimization-Based Alignment for Strapdown Inertial Navigation System: Comparison and Extension. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1697–1713. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Z.; Du, S.Y.; Li, Y.F.; Zhang, Y.G. A High-Accuracy GPS-Aided Coarse Alignment Method for MEMS-Based SINS. IEEE Trans. Instrum. Meas. 2020, 69, 7914–7932. [Google Scholar] [CrossRef]
- Xu, X.; Xu, D.C.; Zhang, T.; Zhao, H.M. In-Motion Coarse Alignment Method for SINS/GPS Using Position Loci. IEEE Sens. J. 2019, 19, 3930–3938. [Google Scholar] [CrossRef]
- He, Q.E.; He, G.B.; Yang, H.Z.; Chen, S.; Wang, J.Q.; Liu, S. In-Motion Rapid and Robust Heading Alignment of Low-Cost Inertial Measurement Units Using Position Loci for Indoor Navigation. IEEE Sens. J. 2024, 24, 19454–19465. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control. Dynam 1981, 4, 70–77. [Google Scholar] [CrossRef]
- Wahba, G. Problem 65-1: A Least Squares Estimate of Satellite Attitude. Siam Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Black, H.D. A passive system for determining the attitude of a satellite. AIAA J. 1963, 2, 14. [Google Scholar] [CrossRef]
- Markley, F.L. Attitude Determination from Vector Observations: A Fast Optimal Matrix Algorithm. J. Astronaut. Sci. 1993, 41, 19930015542. [Google Scholar]
- Mortari, D. ESOQ: A closed-form solution to the Wahba problem. J. Astronaut. Sci. 1997, 45, 195–204. [Google Scholar] [CrossRef]
- Mortari, D. Second Estimator of the Optimal Quaternion. J. Guid. Control Dyn. 2000, 23, 885–887. [Google Scholar] [CrossRef]
- Yan, G.; Chen, R.; Guo, K. Equivalence analysis between SVD and QUEST for multi-vector attitude determination. J. Chin. Inert. Technol. 2019, 27, 568–572. [Google Scholar]

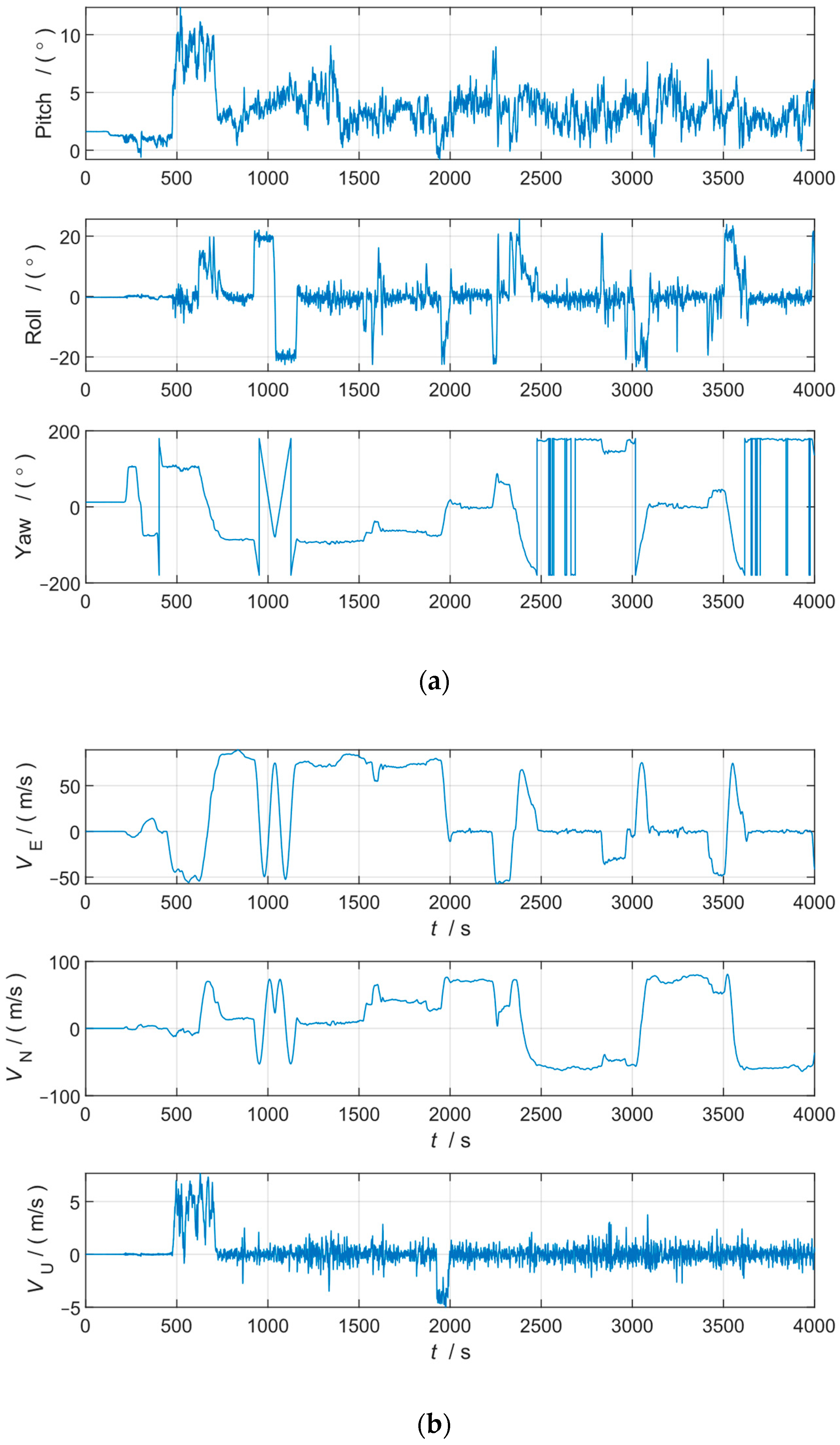
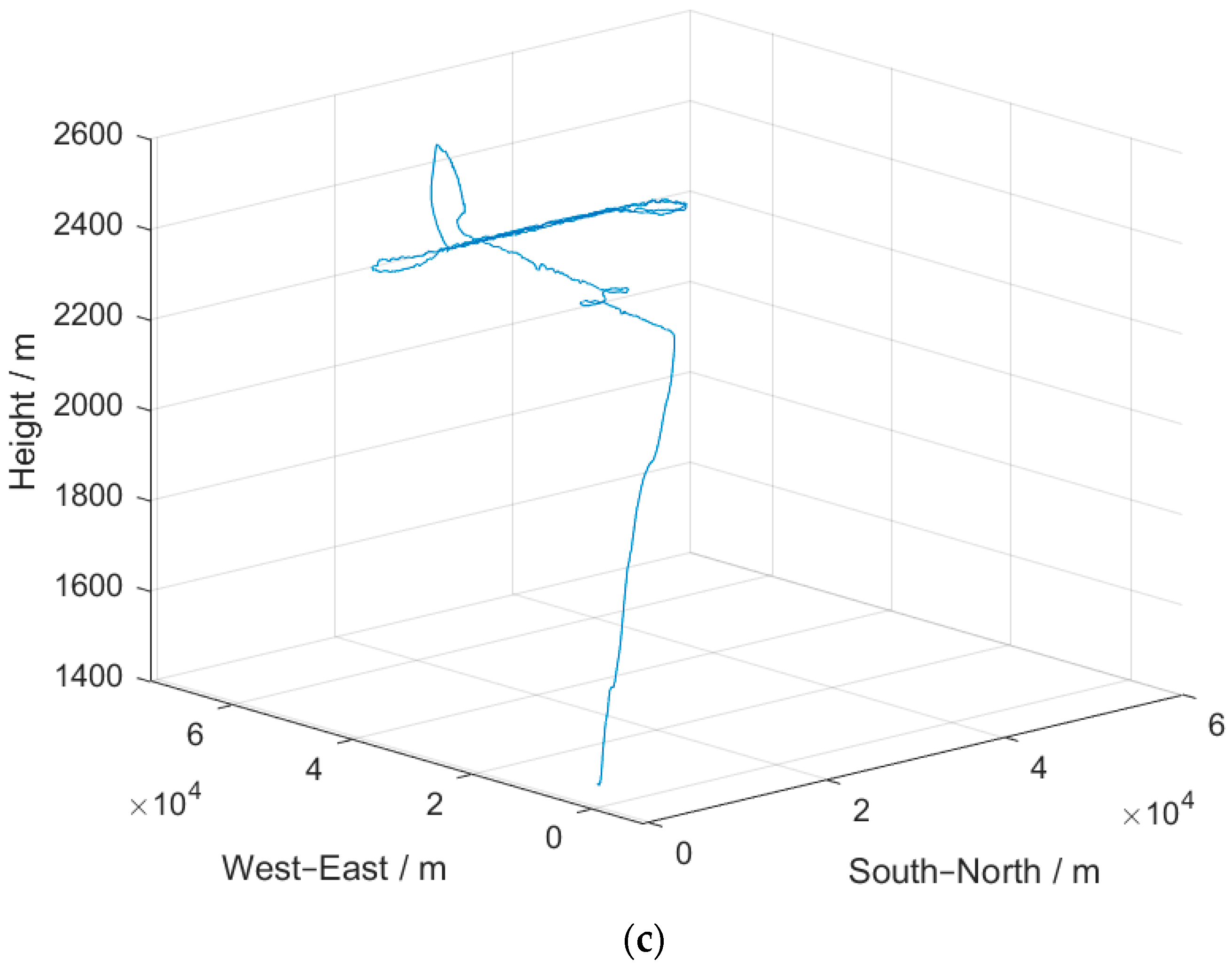
| No. | State | Duration |
| 1 | Moving north with 50 m/s speed | 100 s |
| 2 | Left turning | 53 s |
| 3 | Moving west with 50 m/s speed | 100 s |
| Alignment results under the first simulation condition | |||
| Alignment methods | East misalignment (deg) | North misalignment (deg) | Upward misalignment (deg) |
| TPIF | 0.002 | 0.002 | −0.041 |
| RPIF | 0.002 | 0.002 | −0.038 |
| Alignment results under the second simulation condition | |||
| Alignment methods | East misalignment (deg) | North misalignment (deg) | Upward misalignment (deg) |
| TPIF | 0.001 | 0.003 | −0.013 |
| RPIF | 0.002 | 0.002 | −0.019 |
| Alignment Methods | East Misalignment (deg) | North Misalignment (deg) | Upward Misalignment (deg) |
|---|---|---|---|
| TPIF | 0.192 | −0.106 | −6.826 |
| RPIF | 0.027 | −0.041 | 0.191 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, X.; Huang, J.; Li, J. A Novel Robust Position Integration Optimization-Based Alignment Method for In-Flight Coarse Alignment. Sensors 2024, 24, 7000. https://doi.org/10.3390/s24217000
Ning X, Huang J, Li J. A Novel Robust Position Integration Optimization-Based Alignment Method for In-Flight Coarse Alignment. Sensors. 2024; 24(21):7000. https://doi.org/10.3390/s24217000
Chicago/Turabian StyleNing, Xiaoge, Jixun Huang, and Jianxun Li. 2024. "A Novel Robust Position Integration Optimization-Based Alignment Method for In-Flight Coarse Alignment" Sensors 24, no. 21: 7000. https://doi.org/10.3390/s24217000
APA StyleNing, X., Huang, J., & Li, J. (2024). A Novel Robust Position Integration Optimization-Based Alignment Method for In-Flight Coarse Alignment. Sensors, 24(21), 7000. https://doi.org/10.3390/s24217000





