Recognition of Impact Load on Connecting-Shaft Rotor System Based on Motor Current Signal Analysis
Abstract
:1. Introduction
2. Methods and Principles
2.1. Preprocessing Methods for Current Information
2.1.1. Fast Fourier Transform
2.1.2. Singular Value Decomposition
2.1.3. Wavelet Packet Energy Feature Extraction
2.2. LVQNN Screening Method
2.2.1. Network Structure
2.2.2. Learning Algorithm
- LVQ1 algorithm.
- LVQ2 algorithm.
2.2.3. Model Establishment
3. Results and Analysis
3.1. Measurement and Acquisition of Motor Current Signal
3.2. Preprocessing the Motor Current Signal
3.2.1. FFT Processing
3.2.2. SVD Processing
3.2.3. Energy Feature Extraction
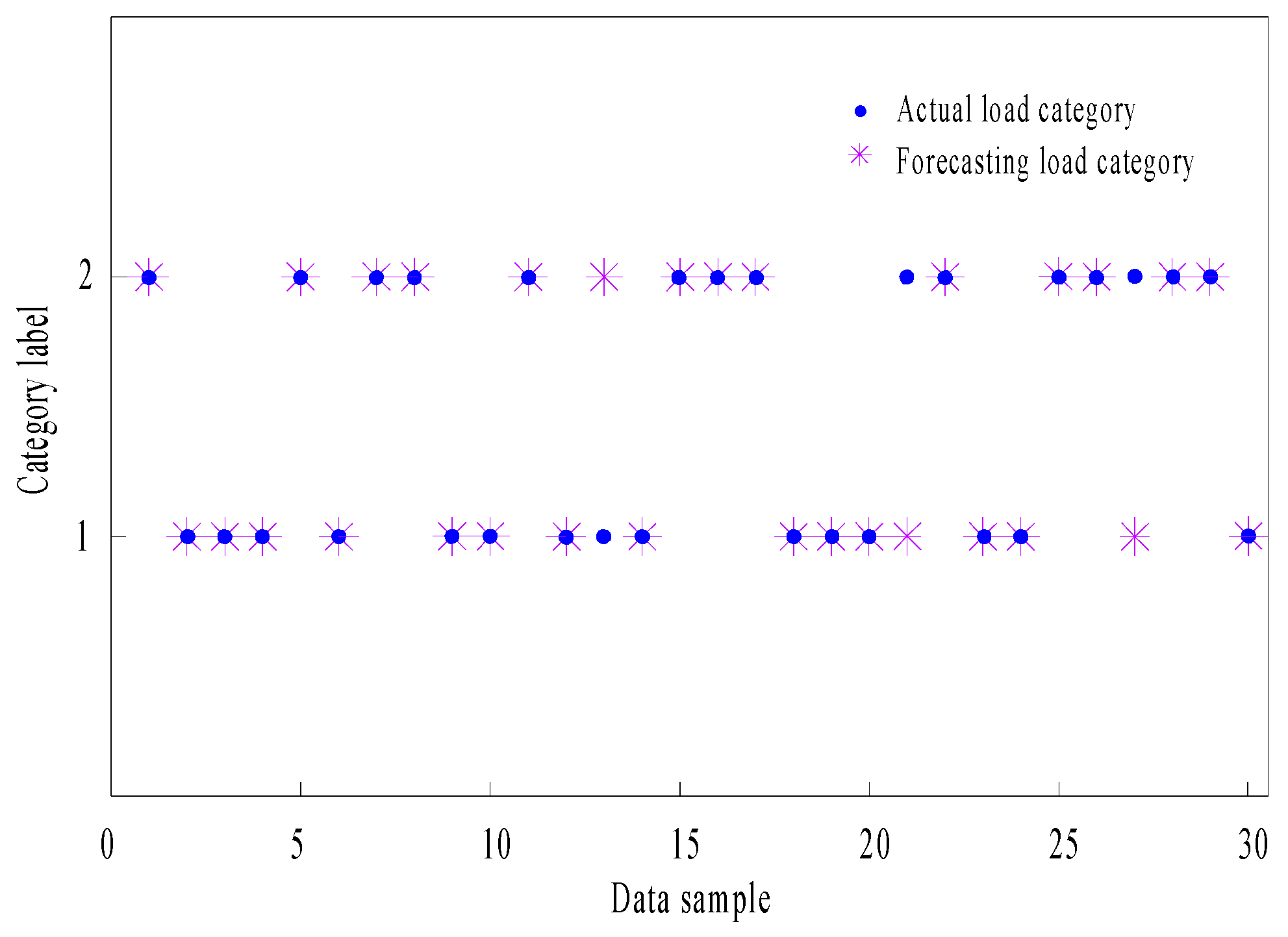
3.3. Load Recognition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, R.C.; Zhou, C.L. Parametrically Excited Vibration of Electromechanical Coupling System of a Rolling Mill Main Drive Based on Rotor Induction Current Influence. J. Vib. Shock 2016, 35, 1–6. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Liu, Y.; Valera-Medina, A.; Robinson, F. Strip Snap Analytics in Cold Rolling Process Using Machine Learning. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 368–373. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Zhang, H.; Chen, Y.; Li, Z.; Li, G.H.; Fu, Z. Load Identification Method of Driving System Based on Genetic Neural Network. J. Vib. Shock 2022, 41, 54–61+89. [Google Scholar] [CrossRef]
- Liu, Y.R.; Wang, L. Multiobjective-clustering-based Optimal Heterogeneous Sensor Placement Method for Thermo-mechanical Load Identification. Int. J. Mech. Sci. 2023, 253, 108369. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kwon, D.K.; Kareem, A. Frequency Domain Identification of Modal Characteristics and Loads from Output-only Measurements. Comput.-Aided. Civ. Inf. 2023, 38, 2092–2108. [Google Scholar] [CrossRef]
- Petersen, O.W.; Oiseth, O.; Lourens, E. Investigation of Dynamic Wind Loads on A Long-span Suspension Bridge Identified from Measured Acceleration Data. J. Wind Eng. Ind. Aerodyn. 2020, 196, 104045. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.J. Identification of Load Categories in Rotor System Based on Vibration Analysis. Sensors 2017, 17, 1676. [Google Scholar] [CrossRef]
- Xu, F.; Chen, H.H.; Bao, M. Force Identification for Mechanical Vibration: State-of-the Art and Prospect. China Mech. Eng. 2002, 13, 526–531. [Google Scholar] [CrossRef]
- Movahedian, B.; Boroomand, B. Inverse Identification of Time-harmonic Loads Acting on Thin Plates Using Approximated Green’s Functions. Inverse Probl. Sci. Eng. 2016, 24, 1475–1493. [Google Scholar] [CrossRef]
- Li, M.Q.; Wang, L.J.; Luo, C.S.; Wu, H.C. A New Improved Fractional Tikhonov Regularization Method for Moving Force Identification. Structures 2024, 60, 105840. [Google Scholar] [CrossRef]
- Fu, C.Y.; Shan, D.S.; Li, Q. Damage Location Identification of Railway Bridge Based on Vibration Response Caused by Vehicles. J. Southwest Jiaotong Univ. 2011, 46, 719–725. [Google Scholar] [CrossRef]
- Troclet, B.; Alestra, S.; Srithammavanh, V. A Time Domain Inverse Method for Identification of Random Acoustic Sources at Launch Vehicle Lift-Off. J. Vib. Acoust. 2011, 133, 021010. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, Q.; Shuai, Z.J.; Li, W.Y. Review of Research and Development Status of Dynamic Load Identification in Time Domain. Noise Vib. Control 2014, 34, 6–11. [Google Scholar] [CrossRef]
- Lin, J.H.; Guo, X.L.; Zhi, H.; Howsonb, W.P.; Williams, F.W. Computer Simulation of Structural Random Loading Identification. Comput. Struct. 2001, 79, 375–387. [Google Scholar] [CrossRef]
- Ryerkerk, M.L.; Averill, R.C.; Deb, K.; Goodman, E.D. Solving Metameric Variable-length Optimization Problems Using Genetic Algorithms. Genet. Program. Evolvable Mach. 2017, 18, 247–277. [Google Scholar] [CrossRef]
- Wang, X.M. Neural Network Introduction; Science Press: Beijing, China, 2017. [Google Scholar]
- Zang, T.L.; Zou, D.Y.; Huang, F.; Shen, N. Combined Three Feature Selection Mechanisms with LVQ Neural Network for Colon Cancer Diagnosis. In Proceedings of the 8th International Symposium on Neural Networks, Guilin, China, 29–31 May 2011; pp. 467–474. [Google Scholar]
- Zhang, Z.; Lu, H.; Li, B.B.; Ding, L.J. Research on Data-Driven Self-Diagnosis for Measurement Errors in Capacitor Voltage Transformers. IEEE Trans. Instrum. Meas. 2024, 73, 1–12. [Google Scholar] [CrossRef]
- Mark, W.D.; Lee, H.; Patrick, R.J.D. A Simple Frequency-domain Algorithm for Early Detection of Damaged Gear Teeth. Mech. Syst. Signal Process. 2010, 24, 2807–2823. [Google Scholar] [CrossRef]
- Lin, Q.; Yu, S.L. A Portable Digital Torsional Vibration Analysis System and Its Signal Processing. Adv. Mater. Res. 2012, 490–495, 1903–1907. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Advanced Sensor Technologies for Non-destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Waheed, M.F.; Bernadin, S. In-Situ Analysis of Vibration and Acoustic Data in Additive Manufacturing. In Proceedings of the IEEE SoutheastCon 2024 Conference on Engineering the Future, Atlanta, USA, 15–24 March 2024; pp. 812–817. [Google Scholar]
- Shang, M.J.; Qin, W.Y.; Li, H.T. Improving the Performance of Vibration Energy Harvesting from Weak Excitations by a Lever-type Mechanism. Mech. Syst. Signal Process. 2025, 222, 111766. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Frequency Domain Averaging Based Experimental Evaluation of Gear Fault without Tachometer for Fluctuating Speed Conditions. Mech. Syst. Signal Process. 2017, 85, 278–295. [Google Scholar] [CrossRef]
- Léonard, F. Time Domain Cyclostationarity Signal-processing Tools. Mech. Syst. Signal Process. 2015, 62–63, 100–112. [Google Scholar] [CrossRef]
- Cao, J.H.; Yang, Z.B.; Sun, R.B.; Teng, G.R. OPR-free Single Probe Blade Tip Timing for Monitoring Rotating Blade. Int. J. Mech. Sci. 2023, 247, 108174. [Google Scholar] [CrossRef]
- Nazarko, P.; Ziemiański, L. Application of Elastic Waves and Neural Networks for the Prediction of Forces in Bolts of Flange Connections Subjected to Static Tension Tests. Materials 2020, 13, 3607. [Google Scholar] [CrossRef] [PubMed]
- Rafaq, M.S.; Shaikh, M.F.; Park, Y.; Lee, S.B. Reliable Airgap Search Coil Based Detection of Induction Motor Rotor Faults under False Negative Motor Current Signature Analysis Indications. IEEE Trans. Ind. Inform. 2022, 18, 3276–3285. [Google Scholar] [CrossRef]
- Farhat, M.H.; Gelman, L.; Abdullahi, A.O.; Ball, A.; Conaghan, G.; Kluis, W. Novel Fault Diagnosis of a Conveyor Belt Mis-tracking via Motor Current Signature Analysis. Sensors 2023, 23, 3652. [Google Scholar] [CrossRef] [PubMed]
- Niu, G.; Dong, X.; Chen, Y.J. Motor Fault Diagnostics Based on Current Signatures: A Review. IEEE Trans. Instrum. Meas. 2023, 72, 3520919. [Google Scholar] [CrossRef]
- Benamira, N.; Dekhane, A.; Bouraiou, A.; Atoui, I. Exploring the Effects of Overvoltage Unbalances on Three Phase Induction Motors: Insights from Motor Current Spectral Analysis and Discrete Wavelet Transform Energy Assessment. Comput. Electr. Eng. 2024, 117, 109242. [Google Scholar] [CrossRef]
- Poncelas, O.; Rosero, J.A.; Cusido, J.; Ortega, J.A.; Romeral, L. Design and Application of Rogowski Coil Current Sensor without Integrator for Fault Detection in Induction Motors. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 Jun–2 July 2008; pp. 1958–1963. [Google Scholar]
- Gu, F.; Shao, Y.; Hu, N.; Naid, A.; Ball, A.D. Electrical Motor Current Signal Analysis Using a Modified Bispectrum for Fault Diagnosis of Downstream Mechanical Equipment. Mech. Syst. Signal Process. 2011, 25, 360–372. [Google Scholar] [CrossRef]
- Ahonen, T.; Kortelainen, J.T.; Tamminen, J.K.; Ahola, J. Centrifugal Pump Operation Monitoring with Motor Phase Current Measurement. Int. J. Electr. Power Energy Syst. 2012, 42, 188–195. [Google Scholar] [CrossRef]
- Han, Y.J.; Yuan, J.P.; Luo, Y.; Zou, J.M. Operation Diagnosis for Centrifugal Pumps Using Stator Current-based Indicators. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 237, 1075–1087. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.Y.; Tipsuwan, Y.; Hung, J.C. Neural-network-based Motor Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2000, 47, 1060–1069. [Google Scholar] [CrossRef]
- Nasar, R.A.; Alzarooni, T.; AL-Shudeifat, M.A. On Modeling and Damage Detection Methodologies in Rotor Systems. Nonlinear Dyn. 2024, 112, 16657–16710. [Google Scholar] [CrossRef]
- Ogbulafor, U.E.; Feng, G.J.; Mones, Z.; Gu, F.S.; Ball, A.D. Application of Wavelet Packet Transform and Envelope Analysis to Non-Stationary Vibration Signals for Fault Diagnosis of a Reciprocating Compressor. In Proceedings of the 1st World Congress on Condition Monitoring (WCCM), London, UK, 13–16 June 2017; pp. 1748–1759. [Google Scholar]
- Konguvel, E.; Kannan, M. A Survey on FFT/IFFT Processors for Next Generation Telecommunication Systems. J. Circuits Syst. Comput. 2018, 27, 1830001. [Google Scholar] [CrossRef]
- Schneider, M. A Review of Nonlinear FFT-based Computational Homogenization Methods. Acta. Mech. 2021, 232, 2051–2100. [Google Scholar] [CrossRef]
- Zhang, R.X.; Hang, S.J.; Sun, Z.S.; Nie, F.P.; Wang, R.; Li, X.L. Anchor-based Fast Spectral Ensemble Clustering. Inf. Fusion 2025, 113, 102587. [Google Scholar] [CrossRef]
- Li, Y.Q.; Zhang, M.M.; Tang, M.A. Data-effective Black-box EDFA Gain Model with Singular Value Decomposition. In Proceedings of the Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022; pp. 985–987. [Google Scholar] [CrossRef]
- Chiyonobu, M.; Miyamae, T.; Takata, M.; Harayama, J.; Kimura, K.; Nakamura, Y. Singular Value Decomposition for Complex Matrices Using Two-Sided Jacobi Method. J. Supercomput. 2024, 80, 11719–11740. [Google Scholar] [CrossRef]
- Golafshan, R.; Sanliturk, K.Y. SVD and lHankel Matrix Based De-noising Approach for Ball Bearing Fault Detection and Its Assessment Using Artificial Faults. Mech. Syst. Signal Process. 2016, 70–71, 36–50. [Google Scholar] [CrossRef]
- Oliveira, R.M.; Maldonado, D.J.G.; Batou, A.; Ritto, T.G. Application of Random Matrix Theory Combined with the Singular Value Decomposition to Journal Bearings Uncertainty Analysis. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 213. [Google Scholar] [CrossRef]
- Lakdawala, Z.; Kassem, H.; Schulte, J. Enhancing Standard CFD Based Practices for Site Assessment Through Polynomial Surrogates for Estimating Uncertainty in Wind Speed. In Proceedings of the Wind Europe Annual Event Conference, Bilbao, Spain, 20–22 March 2024; p. 012016. [Google Scholar] [CrossRef]
- Weiland, S.; van Belzen, F. Singular Value Decompositions and Low Rank Approximations of Tensors. IEEE Trans. Signal Process. 2010, 58, 1171–1182. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.G.; Zhao, X.Z. Feature Frequency Extraction Based on Singular Value Decomposition and Its Application on Rotor Faults Diagnosis. J. Vib. Control 2019, 25, 1246–1262. [Google Scholar] [CrossRef]
- Chen, J.H.; Qiu, W.G.; Zhao, X.W.; Wang, H.L. Vibration Characteristics Analysis of the Metro Tunnel Subarea Blasting Based on Wavelet Packet Technique. J. Vib. Shock 2022, 41, 222–228+255. [Google Scholar] [CrossRef]
- Fan, B.Y.; Zhao, W.G.; Ju, J.H.; Tian, X.S.; Zheng, W.K.; Yang, Y. Research on Wavelet Packet Energy Entropy Extraction Method for Acoustic Signal of Tunnel Lining Cavity. Meas. Sci. Technol. 2024, 35, 106133. [Google Scholar] [CrossRef]
- Li, Z.Z.; Gao, P.X.; Zhao, D.Z.; Liu, J.R. Application of Wavelet Packet and Fractal Combination Technology in Analyzing Aero-engine Hydraulic Pipeline Vibration Signals with Variable Pressure. Comput. Eng. Sci. 2016, 38, 807–813. [Google Scholar] [CrossRef]
- Lee, Y.; Park, C.; Kim, N.; Ahn, J.; Jeong, J. LSTM-Autoencoder Based Anomaly Detection Using Vibration Data of Wind Turbines. Sensors 2024, 24, 2833. [Google Scholar] [CrossRef]
- Vong, C.M.; Wong, P.K.; Tam, L.M. Ignition Pattern Analysis for Automotive Engine Trouble Diagnosis Using Wavelet Packet Transform and Support Vector Machines. Chin. J. Mech. Eng. 2011, 24, 870–878. [Google Scholar] [CrossRef]
- Hussain, A.; Janjua, T.A.; Malik, A.N.; Najib, A.; Khan, S.A. Health Monitoring of CNC Machining Processes Using Machine Learning and Wavelet Packet Transform. Mech. Syst. Signal Process. 2024, 212, 111326. [Google Scholar] [CrossRef]
- de Boer, J.; Dedja, K.; Vens, C.S. LVQ: Interpretable Supervised Clustering and Prediction in Survival Analysis via Learning Vector Quantization. Pattern. Recogn. 2024, 153, 110497. [Google Scholar] [CrossRef]
- Nogueira, M.A.; Abreu, P.H.; Martins, P.; Machado, P.; Duarte, H.; Santos, J. An Artificial Neural Networks Approach for Assessment Treatment Response in Oncological Patients Using PET/CT Images. BMC Med. Imaging 2017, 17, 13. [Google Scholar] [CrossRef]
- Han, H.; Luo, S.H.; Chen, S.M.; Yuan, L.; Shi, G.Z.; Yang, Y.F.; Fei, L.X. A Transient Stability Enhancement Framework Based on Rapid Fault-Type Identification for Virtual Synchronous Generators. Int. J. Electr. Power Energy Syst. 2023, 155, 109545. [Google Scholar] [CrossRef]
- Li, J.M.; Lin, H.J.; Liang, C.B.; Teng, Z.S.; Cheng, D. Detection Method of Power Quality Disturbances Based on Double Resolutions Transform and Learning Vector Quantization Neural Network. Trans. China Electrotech. Soc. 2019, 34, 3453–3463. [Google Scholar] [CrossRef]
- Shobha; Nalini, N. Performance Study of Data Fusion Using Kalman Filter and Learning Vector Quantization. In Proceedings of the 2nd International Conference on Sustainable Expert Systems (ICSES 2021), Lalitpur, Nepal, 17–18 September 2021; Volume 351, pp. 79–88. [Google Scholar] [CrossRef]
- Akarslan, E. Learning Vector Quantization Based Predictor Model Selection for Hourly Load Demand Forecasting. Appl. Soft Comput. 2022, 117, 108421. [Google Scholar] [CrossRef]

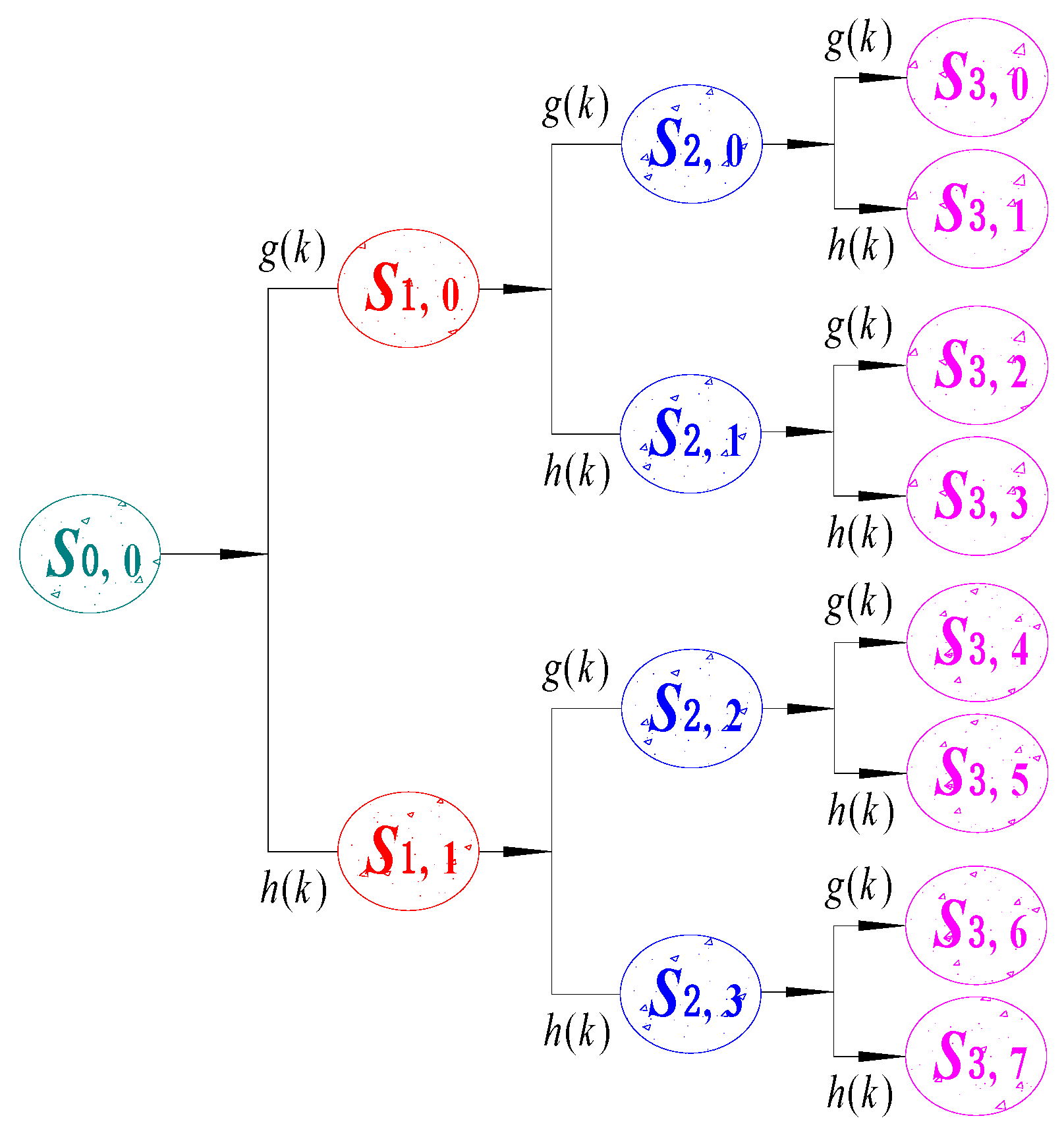




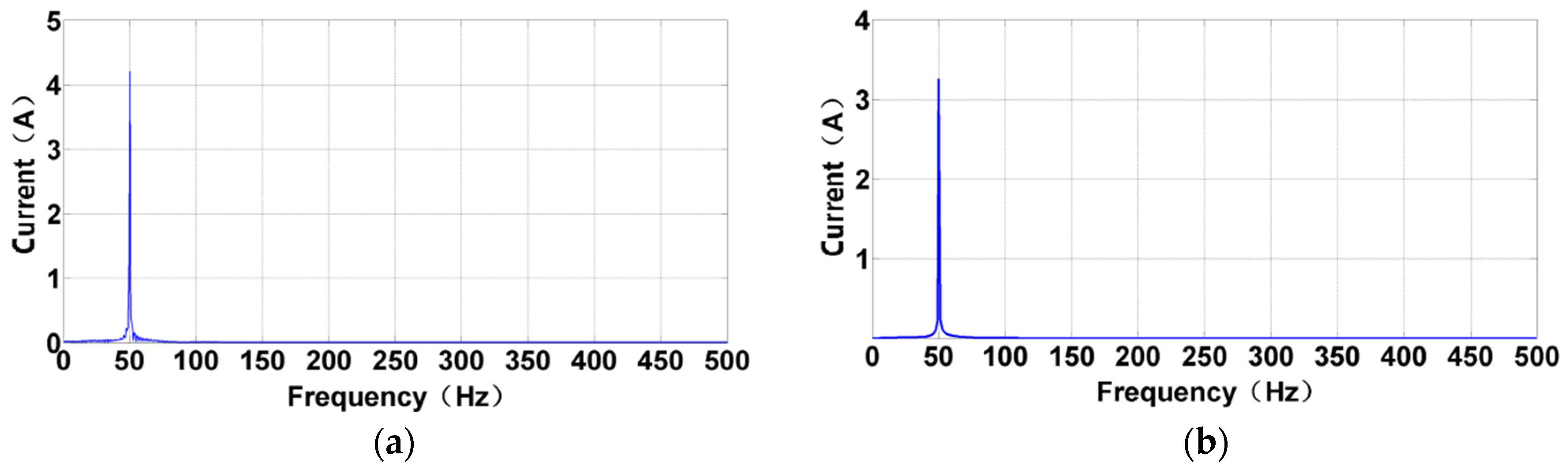
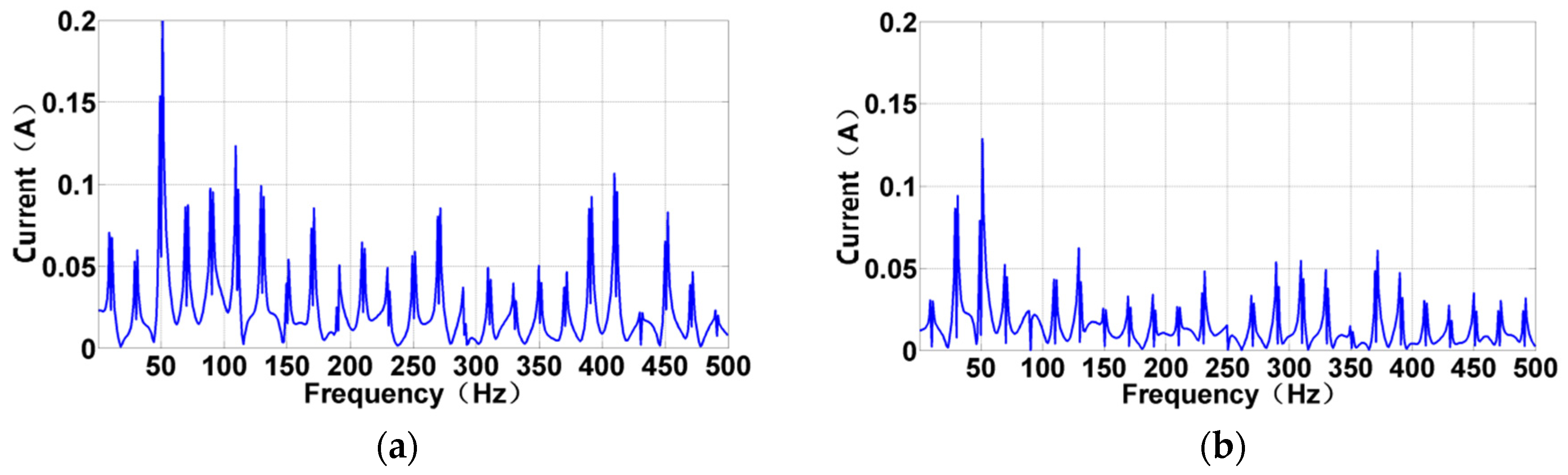
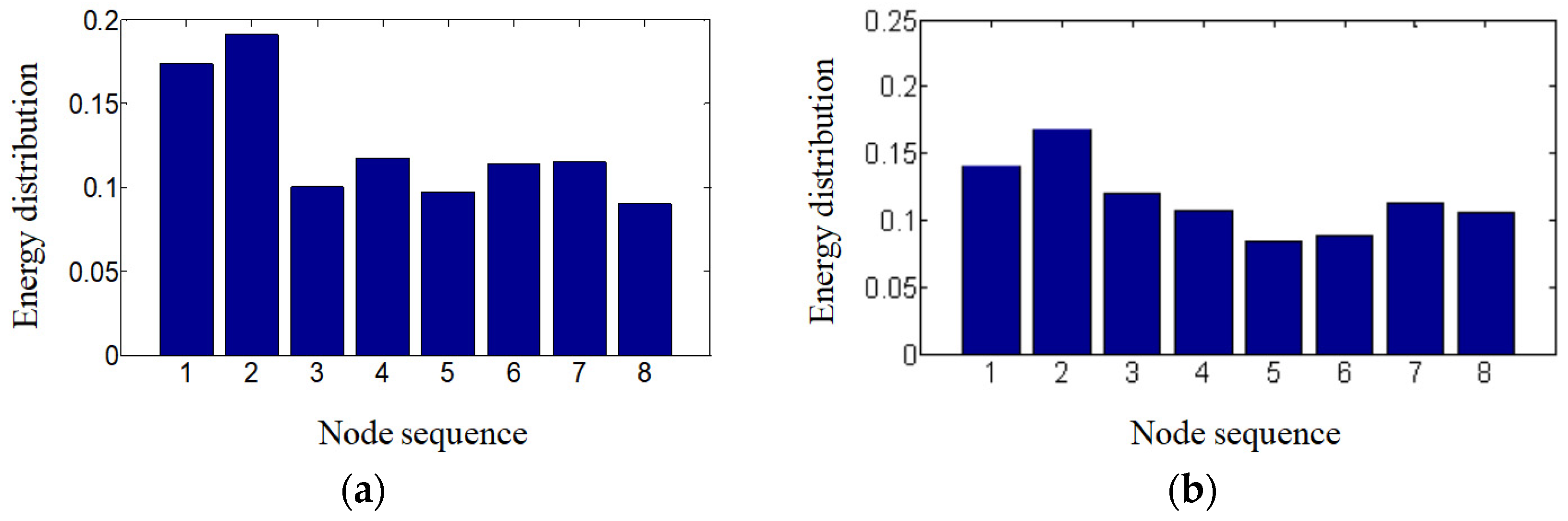

| Energy Node | Frequency Band (Hz) | Energy Node | Frequency Band (Hz) |
|---|---|---|---|
| (3, 0) | 0~15.625 | (3, 4) | 62.50~78.125 |
| (3, 1) | 15.625~31.25 | (3, 5) | 78.125~93.75 |
| (3, 2) | 31.25~46.875 | (3, 6) | 93.75~109.375 |
| (3, 3) | 46.875~62.50 | (3, 7) | 109.375~125.0 |
| Load | P0 | P1 | P2 | P3 | P4 | P5 | P6 | P7 |
|---|---|---|---|---|---|---|---|---|
| Impact | 0.1568 | 0.1558 | 0.1381 | 0.0400 | 0.1505 | 0.1078 | 0.0734 | 0.1777 |
| 0.0625 | 0.0363 | 0.3669 | 0.1959 | 0.0186 | 0.0124 | 0.2003 | 0.1072 | |
| 0.1597 | 0.1433 | 0.1204 | 0.1348 | 0.1119 | 0.1036 | 0.1191 | 0.1072 | |
| Steady | 0.1040 | 0.1510 | 0.1065 | 0.1388 | 0.1624 | 0.0858 | 0.1457 | 0.1058 |
| 0.1140 | 0.1565 | 0.1600 | 0.1024 | 0.1744 | 0.0439 | 0.1445 | 0.1044 | |
| 0.1255 | 0.0979 | 0.1012 | 0.1712 | 0.0778 | 0.1671 | 0.0771 | 0.1823 |
| Load | P0 | P1 | P2 | P3 | P4 | P5 | P6 | P7 |
|---|---|---|---|---|---|---|---|---|
| Impact | 0.0636 | 0.0369 | 0.3662 | 0.1954 | 0.0187 | 0.0126 | 0.1997 | 0.1069 |
| 0.1215 | 0.1149 | 0.1456 | 0.1530 | 0.1448 | 0.1791 | 0.0793 | 0.0620 | |
| Steady | 0.0546 | 0.0266 | 0.3724 | 0.2009 | 0.0204 | 0.0119 | 0.2048 | 0.1084 |
| 0.1074 | 0.1309 | 0.1309 | 0.2051 | 0.1697 | 0.0950 | 0.0703 | 0.0908 |
| Error Analysis | Impact Loads | Steady Loads | All loads |
|---|---|---|---|
| Number of correct recognitions | 14 | 13 | 27 |
| Number of incorrect recognitions | 1 | 2 | 3 |
| Accuracy | 93.33% | 86.67% | 90% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Yang, Z.; Bao, Q.; Zhang, J. Recognition of Impact Load on Connecting-Shaft Rotor System Based on Motor Current Signal Analysis. Sensors 2024, 24, 7008. https://doi.org/10.3390/s24217008
Zhang K, Yang Z, Bao Q, Zhang J. Recognition of Impact Load on Connecting-Shaft Rotor System Based on Motor Current Signal Analysis. Sensors. 2024; 24(21):7008. https://doi.org/10.3390/s24217008
Chicago/Turabian StyleZhang, Kun, Zhaojian Yang, Qingbao Bao, and Jianwen Zhang. 2024. "Recognition of Impact Load on Connecting-Shaft Rotor System Based on Motor Current Signal Analysis" Sensors 24, no. 21: 7008. https://doi.org/10.3390/s24217008
APA StyleZhang, K., Yang, Z., Bao, Q., & Zhang, J. (2024). Recognition of Impact Load on Connecting-Shaft Rotor System Based on Motor Current Signal Analysis. Sensors, 24(21), 7008. https://doi.org/10.3390/s24217008





