Leveraging Environmental Contact and Sensor Feedback for Precision in Robotic Manipulation
Abstract
:1. Introduction
2. Review of Methods
- Methods for solving inverse kinematics;
- Methods based on optimization approach.
2.1. Methods for Solving Inverse Kinematics
2.2. Optimization Approach
- If the matrix is invertible, a unique solution for is obtained.
- If the matrix is singular but the system is solvable, any solution is considered optimal.
- If the system is not solvable, the optimization problem is either unbounded or infeasible.
- The matrix is non-singular.
- .
- .
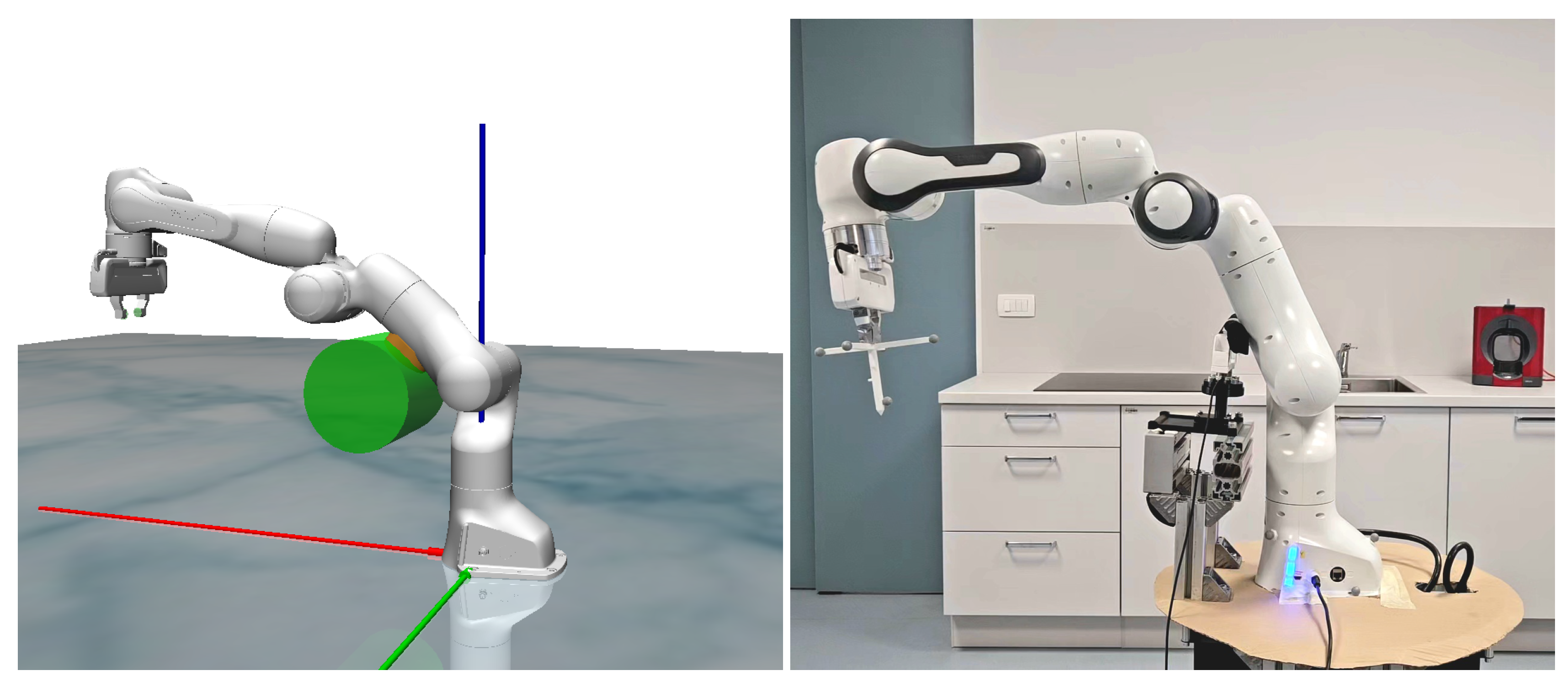
3. Exploiting Leaning on Surface for Accurate End-Effector Motion
3.1. Gradient Projection and Jacobian Pseudo Inverse
3.2. Gradient Projection and Jacobian Weighting
3.3. Augmented Jacobian
3.4. Quadratic Programming
- Positive definiteness: for all the , and if , then .
- Absolute homogeneity: , for all and .
- Subadditivity/Triangle inequality: for all .
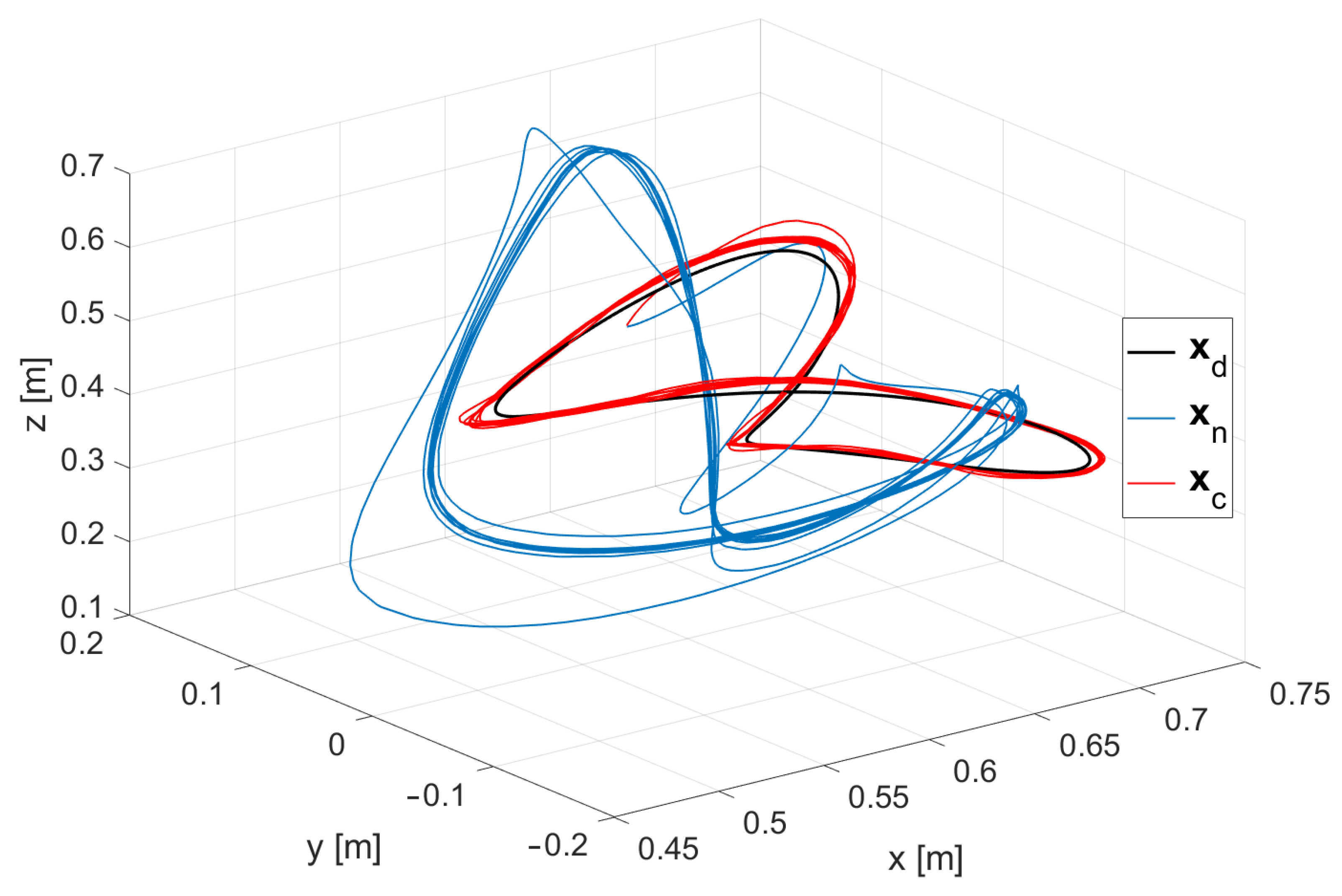
4. Evaluation, Results, and Comparison of Multiple Methods
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOF | Degrees of freedom |
| SVD | Singular Value Decomposition |
| JP | Jacobian Pseudo-inverse |
| JT | Jacobian Transpose |
| SD | Selective Damping |
| JD | Jacobian Damping |
| JF | Filtered Jacobian |
| ED | Error Damping |
| IED | Improved Error Damping |
| SVF | Singular Value Filtering |
| JW | Jacobian Weighting |
| JC | Joint Clamping |
| JA | Augmented Jacobian |
| WJA | Weighted Augmented Jacobian |
| GP | Gradient Projection |
| TP | Task Priority |
| CTP | Continuous Task Priority |
| AI | Artificial Intelligence |
References
- Campilho, R.D.S.G.; Silva, F.J.G. Industrial Process Improvement by Automation and Robotics. Machines 2023, 11, 1011. [Google Scholar] [CrossRef]
- Castillo, J.F.; Ortiz, J.H.; Velásquez, M.F.D.; Saavedra, D.F. COBOTS in industry 4.0: Safe and efficient interaction. In Collaborative and Humanoid Robots; IntechOpen: Rijeka, Croatia, 2021; Volume 13. [Google Scholar] [CrossRef]
- Peshkin, M.; Colgate, J.E. Cobots. Ind. Robot. Int. J. 1999, 26, 335–341. [Google Scholar] [CrossRef]
- Pearce, M.; Mutlu, B.; Shah, J.; Radwin, R. Optimizing makespan and ergonomics in integrating collaborative robots into manufacturing processes. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1772–1784. [Google Scholar] [CrossRef]
- Bisen, A.S.; Payal, H. Collaborative robots for industrial tasks: A review. Mater. Today Proc. 2022, 52, 500–504. [Google Scholar] [CrossRef]
- Šifrer, J.; Petrič, T. A Novel Approach Exploiting Contact Points on Robot Structures for Enhanced End-Effector Accuracy. In Advances in Service and Industrial Robotics; Springer: Cham, Switzerland, 2024; pp. 329–336. [Google Scholar]
- Liu, L.; Guo, F.; Zou, Z.; Duffy, V.G. Application, Development and Future Opportunities of Collaborative Robots (Cobots) in Manufacturing: A Literature Review. Int. J. Hum.-Comput. Interact. 2024, 40, 915–932. [Google Scholar] [CrossRef]
- Lackner, J.R. The Importance of Being in Touch. Front. Neurol. 2021, 12, 646640. [Google Scholar] [CrossRef]
- Popp, W.L.; Richner, L.; Lambercy, O.; Shirota, C.; Barry, A.; Gassert, R.; Kamper, D.G. Effects of wrist posture and stabilization on precision grip force production and muscle activation patterns. J. Neurophysiol. 2023, 130, 596–607. [Google Scholar] [CrossRef]
- Couto, C.R.; Leite, C.M.F.; Campos, C.E.; Portes, L.L.; dos Santos, S.P.; Cruz, M.P.; Sousa, M.C.A.; Ugrinowitsch, H. Enhanced Performance Stabilization Increases Performance Variability in a Virtual Interception Task. Percept. Mot. Ski. 2021, 128, 546–559. [Google Scholar] [CrossRef] [PubMed]
- Therapy Skill Builders. Forearm, Hand, and Finger Control. A Division of Communication Skill Builders/602-323-7500. 1991. Available online: https://resources.finalsite.net/images/v1677526428/sdcoenet/ecziqkimggbtlbsznasu/Forearm_and_finger_control.pdf (accessed on 21 October 2024).
- Zhang, Y.; Parker, L.E. Multi-robot task scheduling. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: New York, NY, USA, 2013; pp. 2992–2998. [Google Scholar]
- Chiaverini, S.; Oriolo, G.; Walker, I.D. Kinematically Redundant Manipulators. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 245–268. [Google Scholar] [CrossRef]
- Benhabib, B.; Goldenberg, A.A.; Fenton, R.G. A solution to the inverse kinematics of redundant manipulators. J. Robot. Syst. 1985, 2, 373–385. [Google Scholar] [CrossRef]
- Šifrer, J. Preučevanje Pristopov Vodenja Redundantnih Robotskih Mehanizmov. Master’s Thesis, Univerza v Ljubljani, Ljubljana, Slovenia, 2023. [Google Scholar]
- Colome, A.; Torras, C. Redundant inverse kinematics: Experimental comparative review and two enhancements. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5333–5340. [Google Scholar] [CrossRef]
- Buss, S.R. Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares methods. IEEE J. Robot. Autom. 2004, 17, 16. [Google Scholar]
- Buss, S.R.; Kim, J.S. Selectively Damped Least Squares for Inverse Kinematics. J. Graph. Tools 2005, 10, 37–49. [Google Scholar] [CrossRef]
- Siciliano, B.; Member, S.; Egeland, O. Review of the Damped Least-Squares Inverse Kinematics with Experiments on an Industrial Robot Manipulator. IEEE Trans. Control Syst. Technol. 1994, 2, 123–134. [Google Scholar]
- Chiaverini, S.; Egeland, O.; Kanestrom, R. Achieving user-defined accuracy with damped least-squares inverse kinematics. In Proceedings of the Fifth International Conference on Advanced Robotics ’Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991; IEEE: New York, NY, USA, 1991; Volume 1, pp. 672–677. [Google Scholar] [CrossRef]
- Chan, S.K.; Lawrence, P.D. general inverse kinematics with the error damped pseudoinverse. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988. [Google Scholar]
- Sugihara, T. Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method. IEEE Trans. Robot. 2011, 27, 984–991. [Google Scholar] [CrossRef]
- Colome, A.; Torras, C. Closed-Loop Inverse Kinematics for Redundant Robots: Comparative Assessment and Two Enhancements. IEEE/ASME Trans. Mechatron. 2015, 20, 944–955. [Google Scholar] [CrossRef]
- Park, J.; Choi, Y.; Chung, W.K.; Youm, Y. Multiple tasks kinematics using weighted pseudo-inverse for kinematically redundant manipulators. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; IEEE: New York, NY, USA, 2001; Volume 4, pp. 4041–4047. [Google Scholar] [CrossRef]
- Raunhardt, D.; Boulic, R. Progressive Clamping. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; IEEE: New York, NY, USA, 2007; pp. 4414–4419. [Google Scholar] [CrossRef]
- Sciavicco, L.; Siciliano, B. A dynamic solution to the inverse kinematic problem for redundant manipulators. In Proceedings of the 1987 IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1987; Volume 4, pp. 1081–1087. [Google Scholar] [CrossRef]
- Sciavicco, L.; Siciliano, B. Solving the Inverse Kinematic Problem for Robotic Manipulators; Springer: Boston, MA, USA, 1987; pp. 107–114. [Google Scholar] [CrossRef]
- Sciavicco, L.; Siciliano, B. A solution algorithm to the inverse kinematic problem for redundant manipulators. IEEE J. Robot. Autom. 1988, 4, 403–410. [Google Scholar] [CrossRef]
- Egeland, O. Task-space tracking with redundant manipulators. IEEE J. Robot. Autom. 1987, 3, 471–475. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, X.; Hu, T.; Tan, Q.; Hou, Y. Weighted augmented Jacobian matrix with a variable coefficient method for kinematics mapping of space teleoperation based on human–robot motion similarity. Adv. Space Res. 2016, 58, 1401–1416. [Google Scholar] [CrossRef]
- Zghal, H.; Dubey, R.; Euler, J. Efficient gradient projection optimization for manipulators with multiple degrees of redundancy. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; IEEE Computer Society Press: Washington, DC, USA, 1990; pp. 1006–1011. [Google Scholar] [CrossRef]
- Maciejewski, A.A.; Klein, C.A. Obstacle Avoidance for Kinematically Redundant Manipulators in Dynamically Varying Environments. Int. J. Robot. Res. 1985, 4, 109–117. [Google Scholar] [CrossRef]
- Sadati, S.M.H.; Naghibi, S.E.; Shiva, A.; Walker, I.D.; Althoefer, K.; Nanayakkara, T. Mechanics of Continuum Manipulators, a Comparative Study of Five Methods with Experiments. In Proceedings of the Towards Autonomous Robotic Systems, Guildford, UK, 19–21 July 2017; Gao, Y., Fallah, S., Jin, Y., Lekakou, C., Eds.; Springer: Cham, Switzerland, 2017; pp. 686–702. [Google Scholar]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Whitney, D.E. The Mathematics of Coordinated Control of Prosthetic Arms and Manipulators. J. Dyn. Syst. Meas. Control 1972, 94, 303–309. Available online: https://asmedigitalcollection.asme.org/dynamicsystems/article-abstract/94/4/303/400875/The-Mathematics-of-Coordinated-Control-of?redirectedFrom=fulltext (accessed on 28 October 2024). [CrossRef]
- Liegeois, A. Automatic Supervisory Control of the Configuration and Behavior of Multibody Mechanisms. IEEE Trans. Syst. Man Cybern. 1977, 7, 868–871. [Google Scholar] [CrossRef]
- Klein, C.A.; Chirco, A.I. Dynamic simulation of a kinematically redundant manipulator system. J. Robot. Syst. 1987, 4, 5–23. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of robotic mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B.; Dastres, R. Optimization of energy consumption in industrial robots, a review. Cogn. Robot. 2023, 3, 142–157. [Google Scholar] [CrossRef]
- Tassi, F.; De Momi, E.; Ajoudani, A. An adaptive compliance Hierarchical Quadratic Programming controller for ergonomic human–robot collaboration. Robot. Comput.-Integr. Manuf. 2022, 78, 102381. [Google Scholar] [CrossRef]
- Zhang, M.; Li, C.; Shang, Y.; Liu, Z. Cycle Time and Human Fatigue Minimization for Human-Robot Collaborative Assembly Cell. IEEE Robot. Autom. Lett. 2022, 7, 6147–6154. [Google Scholar] [CrossRef]
- Hollerbach, J.; Suh, K. Redundancy resolution of manipulators through torque optimization. IEEE J. Robot. Autom. 1987, 3, 308–316. [Google Scholar] [CrossRef]
- Cheng, F.T.; Wang, W.M.; Kung, F.C. Priority considerations for multiple goals of redundant manipulators. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 2–5 October 1994; IEEE: New York, NY, USA, 1994; Volume 1, pp. 264–269. [Google Scholar] [CrossRef]
- Chamitoff, G.E.; Saenz-Otero, A.; Katz, J.G.; Ulrich, S.; Morrell, B.J.; Gibbens, P.W. Real-time maneuver optimization of space-based robots in a dynamic environment: Theory and on-orbit experiments. Acta Astronaut. 2018, 142, 170–183. [Google Scholar] [CrossRef]
- Cheng, F.T.; Chen, T.H.; Wang, Y.S.; Sun, Y.Y. Obstacle avoidance for redundant manipulators using the compact QP method. In Proceedings of the [1993] Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; IEEE Computer Society: Los Alamitos, CA, USA, 1993; pp. 262–269. [Google Scholar] [CrossRef]
- Zhou, L.; Tokekar, P. Multi-robot coordination and planning in uncertain and adversarial environments. Curr. Robot. Rep. 2021, 2, 147–157. [Google Scholar] [CrossRef]
- Bertsekas, D.; Nedic, A.; Ozdaglar, A. Convex Analysis and Optimization; Athena Scientific: Nashua, NH, USA, 2003; Volume 1. [Google Scholar]
- Hager, W.W.; Park, S. The gradient projection method with exact line search. J. Glob. Optim. 2004, 30, 103–118. [Google Scholar] [CrossRef]
- Polyak, B.T. Newton’s method and its use in optimization. Eur. J. Oper. Res. 2007, 181, 1086–1096. [Google Scholar] [CrossRef]
- Nearchou, A.C.; Aspragathos, N.A. A genetic path planning algorithm for redundant articulated robots. Robotica 1997, 15, 213–224. [Google Scholar] [CrossRef]
- da Graça Marcos, M.; Machado, J.A.T.; Azevedo-Perdicoúlis, T.P. Trajectory planning of redundant manipulators using genetic algorithms. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2858–2869. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, K.; Han, L.; Guan, S. Modeling and Control of Robotic Manipulators Based on Artificial Neural Networks: A Review. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1307–1347. [Google Scholar] [CrossRef]




| Name | Abb. | Equation (=) | Ref. |
|---|---|---|---|
| Jacobian Pseudo-inverse | JP | [16] | |
| Jacobian Transpose | JT | [17] | |
| Selective Damping | SD | [18] | |
| Damped Jacobian | JD | [19] | |
| Filtered Jacobian | JF | [20] | |
| Error Damping | ED | [21] | |
| Improved Error Damping | IED | [22] | |
| Singular Value Filtering | SVF | [16] |
| Method | Advantages | Disadvantages |
|---|---|---|
| Jacobian Pseudo-inverse (JP) | Solves the minimization problem effectively for redundant manipulators. | Produces large joint velocities near singularities, leading to numerical instability. |
| Jacobian Transpose (JT) | Avoids the large velocity gains of JP near singularities. | Suffers from conditioning issues similar to JP, especially near singular configurations. |
| Selective Damping (SD) | Reduces joint velocities specifically in problematic directions without affecting all directions. | Does not fully address the rank loss near singularities; precision is reduced in damped directions. |
| Damped Jacobian (JD) | Increases stability near singularities by adding a small damping term. | Reduces overall accuracy due to the uniform increase in all singular values. |
| Filtered Jacobian (JF) | Adaptive damping near singularities, improving control in those situations. | Can still result in significant precision loss near small singular values. |
| Error Damping (ED) | Reduces large joint velocities when the target is far away, ensuring smoother control. | Ineffective near singularities, as the error norm is not sufficient to handle instability in those cases. |
| Improved Error Damping (IED) | Better damping adjustment near singularities, improving control stability. | More complex to implement, and still struggles in extreme singular configurations. |
| Singular Value Filtering (SVF) | Maintains full rank and ensures bounded condition numbers, improving stability near singularities. | Precision may be reduced when operating close to very small singular values. |
| Name | Abbreviation | Equation | References |
|---|---|---|---|
| Jacobian Weighting | JW | [24] | |
| Gradient Projection | GP | [31] | |
| Joint Clamping | JC | [25] | |
| Augmented Jacobian | JA | [26] | |
| Weighted Augmented Jacobian | WJA | [30] | |
| Task Priority | TP | [32] | |
| Continuous Task Priority | CTP | [16] |
| Name | Average Time of the Control Loop | Standard Deviation of the Control Loop Time | Error of the End Effector | Standard Deviation of the End-Effector Error |
|---|---|---|---|---|
| Gradient Projection and Jacobian Pseudo-inverse | 0.0022 | 0.0025 | 0.4162 | 0.0076 |
| Gradient Projection and Jacobian Weighting | 0.0020 | 0.0024 | 0.2754 | 0.0053 |
| Weighted Augmented Jacobian | 0.0023 | 0.0026 | 0.3336 | 0.0063 |
| Quadratic programming | 0.0078 | 0.0050 | 2.096 | 0.0741 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šifrer, J.; Petrič, T. Leveraging Environmental Contact and Sensor Feedback for Precision in Robotic Manipulation. Sensors 2024, 24, 7006. https://doi.org/10.3390/s24217006
Šifrer J, Petrič T. Leveraging Environmental Contact and Sensor Feedback for Precision in Robotic Manipulation. Sensors. 2024; 24(21):7006. https://doi.org/10.3390/s24217006
Chicago/Turabian StyleŠifrer, Jan, and Tadej Petrič. 2024. "Leveraging Environmental Contact and Sensor Feedback for Precision in Robotic Manipulation" Sensors 24, no. 21: 7006. https://doi.org/10.3390/s24217006
APA StyleŠifrer, J., & Petrič, T. (2024). Leveraging Environmental Contact and Sensor Feedback for Precision in Robotic Manipulation. Sensors, 24(21), 7006. https://doi.org/10.3390/s24217006






