Comparison of Classical and Inverse Calibration Equations in Chemical Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Relative Humidity Sensors
2.2. Saturated Salt Solutions
2.3. Calibration of Humidity Sensors
2.4. Establish the Calibration Equation
2.4.1. The Classical Equation
2.4.2. The Inverse Equation
2.5. The Evaluation Criteria for Calibration
2.6. Compare the Predictive Performance for Two Calibration Equations
2.6.1. The Criteria for the Predictive Performance of Two Calibration Equations
- The minimum value, ei,min.
- The maximum value, ei,max.
- Mean absolute error (MAE):where is the absolute value.
- 4.
- Root mean square error (RMSE):
2.6.2. The Criteria for the Comparison of the Predictive Performance of Two Calibration Equations
2.7. Data Splitting
2.8. The Calculation of the New Measurement
- The inverse equation.
- 2.
- The classical equation.
2.9. Data Source for Comparing Two Calibration Equations
- Higher-order polynomial equation:
- 2.
- Exponential decay equation:
- 3.
- Power equation:
- 4.
- Exponential rise to maximum equations (ERTM equations):
3. Results
3.1. The Capacitive Humidity Sensor
3.1.1. The Calibration Equation of Capacitive Humidity Sensors
- The classical equation
- 2.
- The inverse equation of capacitive humidity sensors
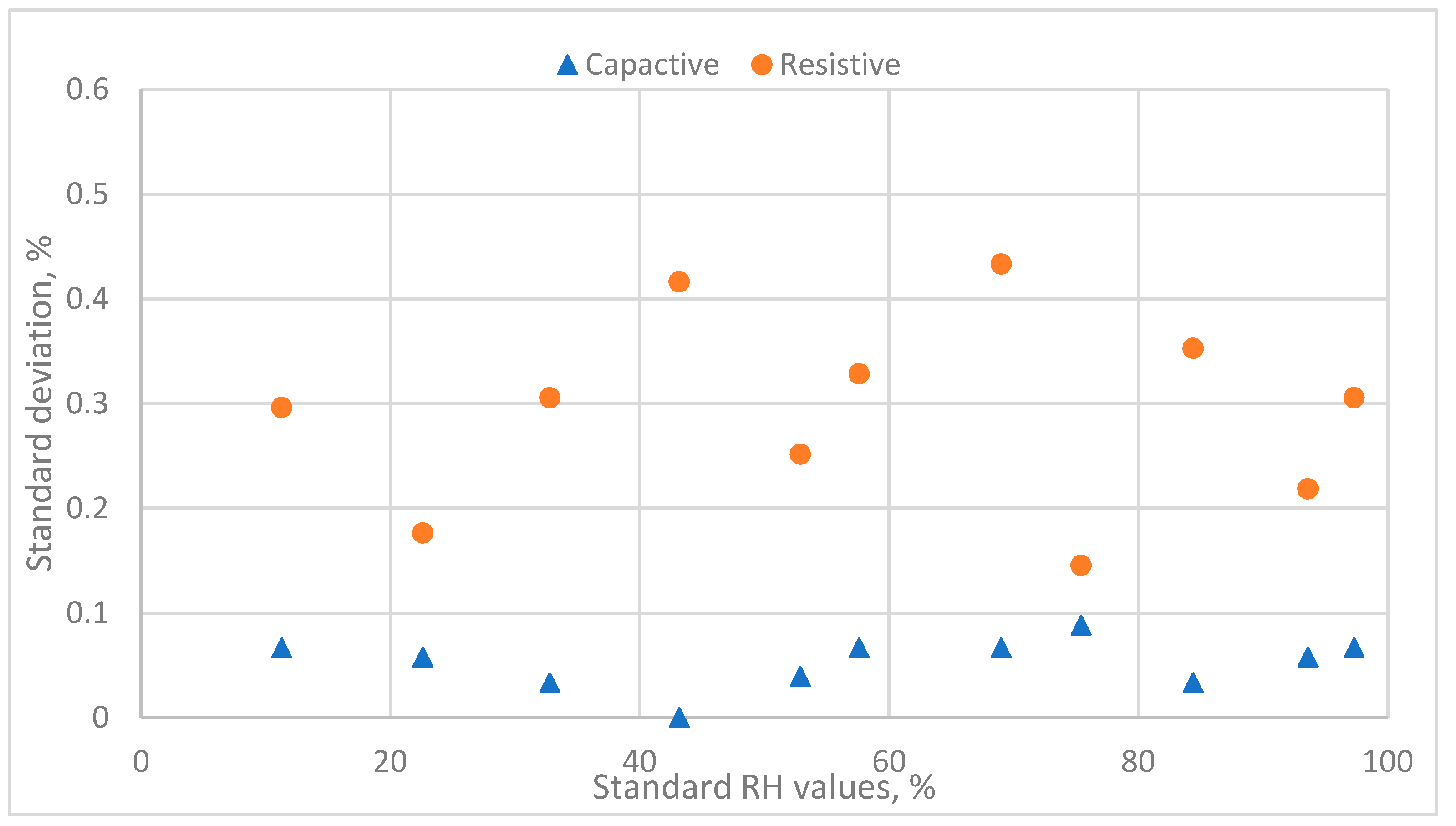
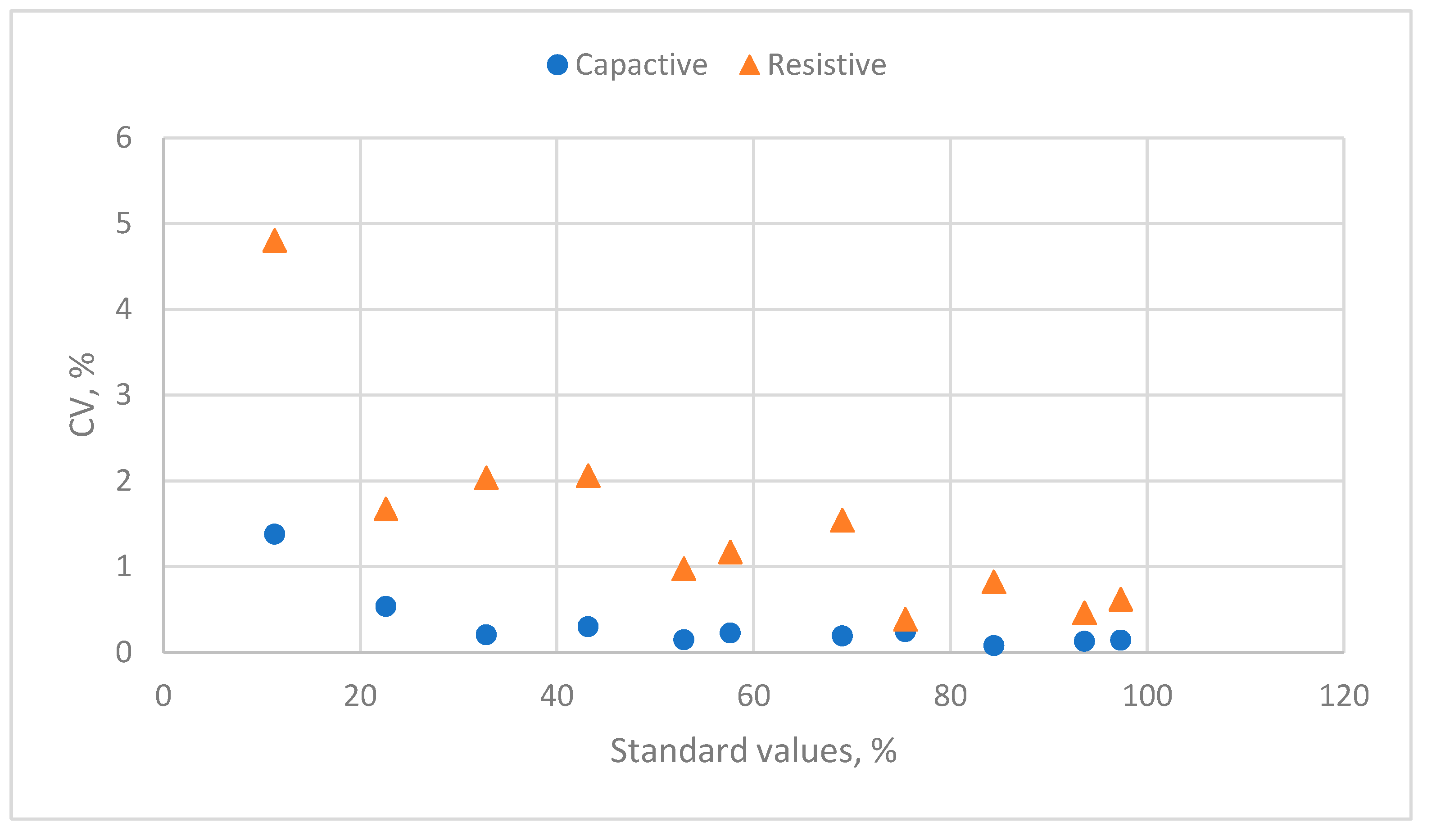
3.1.2. The Evaluation of the Calibration Equation of Capacitive Humidity Sensors
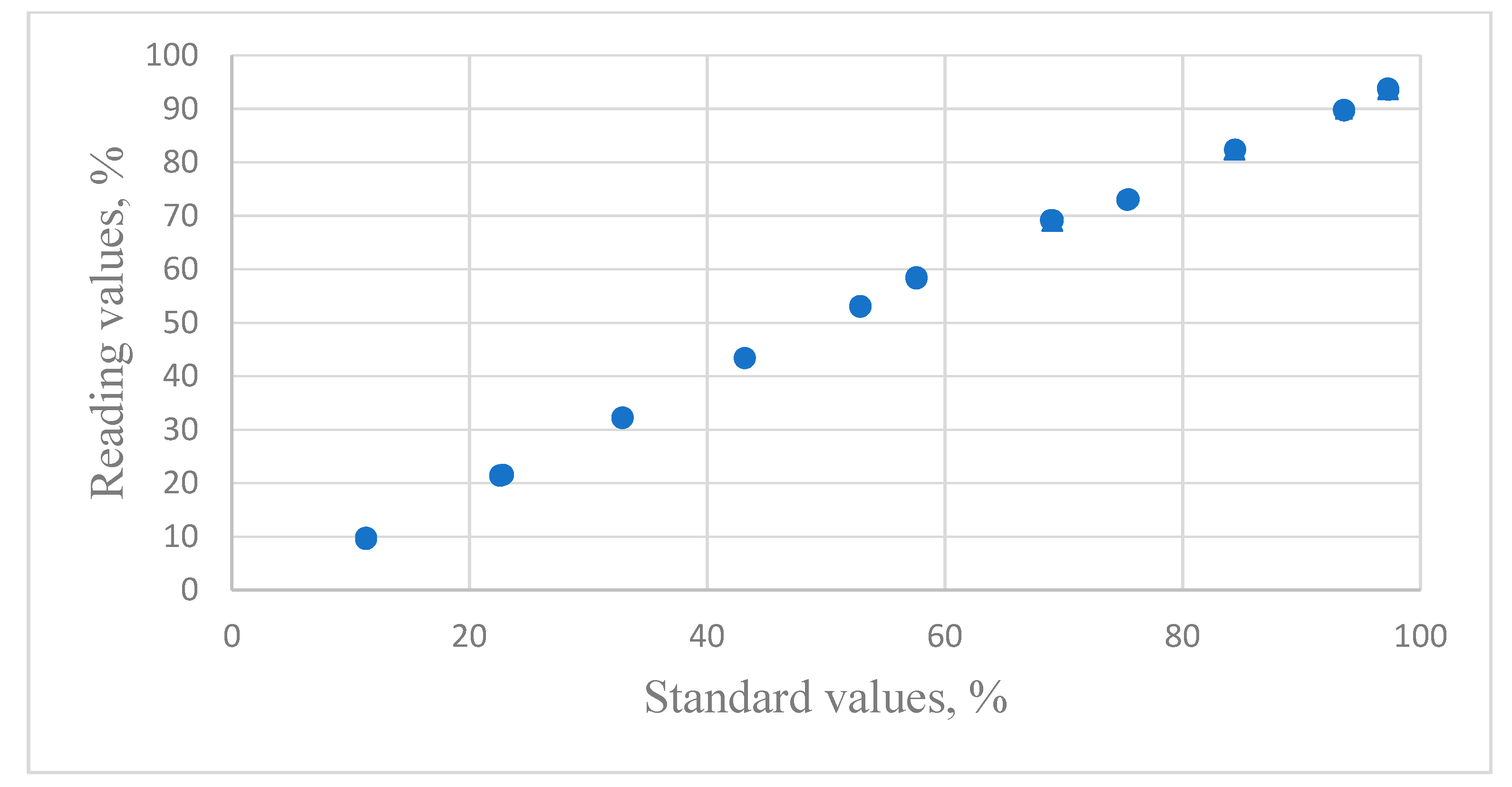
3.2. The Resistive Humidity Sensor
3.2.1. The Calibration Equation of Resistive Humidity Sensors
- The classical equation.
- 2.
- The inverse equation.
3.2.2. The Evaluation of the Calibration Equation of Resistive Humidity Sensors
3.3. The Evaluation of Two Calibration Equations from Previous Data in the Literature
3.3.1. The Measurement of Chloromethane Concentration with GC-MS
3.3.2. Using Spectrophotometry to Measure Albumin
- The classical equation is
- 2.
- The inverse equation is
3.3.3. The Measurement of Anti-IgG by Biophotonic Sensing Cells
3.3.4. The Measurement of Drug Concentration in Blood with an HPLC Assay
- The classical equation iswhere R2 = 0.9921, and sy = 0.0348.
- The inverse equation iswhere R2 = 0.9912, and sx = 0.0896.
3.3.5. Detection of EtP Compound by QqQ-MS
3.3.6. The Measurement of Sulfides by Flow Injection Analysis
3.3.7. Measurement of Daidzein by HPLC Analysis
3.3.8. Measurement of Cocaine Concentration by LC-MS-MS
3.3.9. Measurement of Benzaldehyde Using Pulse Polarography
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EURACHEM Working Group. The Fitness for Purpose of Analytical Methods. In A Laboratory Guide to Method Validation and Related Topics, 1st ed.; EURACHEM: London, UK, 1998. [Google Scholar]
- IUPAC. Recommendation, guidelines for calibration in analytical chemistry. Part I. Fundamentals and single component calibration. Pure Appl. Chem. 1998, 70, 993–1014. [Google Scholar] [CrossRef]
- Barwick, V. Preparation of Calibration Curves: A Guide to Best Practice; VAM, LGC/VAM/2003/032. 2003. Available online: https://www.researchgate.net/publication/334063221_Preparation_of_Calibration_Curves_A_Guide_to_Best_Practice (accessed on 10 June 2024).
- Rozet, E.; Ceccato, A.; Hubert, C.; Ziemons, E.; Oprean, R.; Rudaz, S.; Boulanger, B.; Hubert, P. Analysis of recent pharmaceutical regulatory documents on analytical method validation. J. Chromatogr. A 2007, 1158, 111–125. [Google Scholar] [CrossRef] [PubMed]
- Sanagi, M.M.; Nasir, Z.; Ling, S.L.; Hermawan, D.; Ibrahim, W.A.W.; Naim, A.A. A practical approach for linearity assessment of calibration curves under the International Union of Pure and Applied Chemistry (IUPAC) Guidelines for an in-house validation of method of analysis. J. AOAC Intern. 2010, 93, 1322–1330. [Google Scholar] [CrossRef]
- Myers, R.H. Classical and Modern Regression with Applications, 2nd ed.; Duxbury Press: Monterey, CA, USA, 1990. [Google Scholar]
- Krutchkoff, R.G. Classical and inverse regression methods of calibration. Technometrics 1967, 9, 25–439. [Google Scholar] [CrossRef]
- Krutchkoff, R.G. Classical and inverse regression methods of calibration in extrapolation. Technometrics 1969, 11, 605–608. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.L.; De Jong, S. Inverse calibration predicts better than classical calibration. Fresenius’ J. Anal. Chem. 1998, 361, 2–9. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Inverse vs. classical calibration for small data sets. Fresenius’ J. Anal. Chem. 2000, 368, 585–588. [Google Scholar] [CrossRef]
- Shalabh. Least squares estimators in measurement error models under the balanced loss function. Test 2001, 10, 301–308. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Simple algorithms for nonlinear calibration by the classical and standard additions methods. Analyst 2005, 130, 370–378. [Google Scholar] [CrossRef]
- Parker, P.A.; Vining, G.G.; Wilson, S.R.; Szarka, J.L., III; Johnson, N.G. The prediction properties of classical and inverse regression for the simple linear calibration problem. J. Qual. Technol. 2010, 42, 332–347. [Google Scholar] [CrossRef]
- Besalú, E. The connection between inverse and classical calibration. Talanta 2013, 116, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Granovskii, V.; Siraia, T. Direct and inverse calibration curves of measuring instruments: Selection and fitting. In 16th International Congress of Metrology; EDP Sciences: Les Ulis, France, 2013; p. 04006. [Google Scholar]
- Witkovsky, V.; Wimmer, G. Inverse and direct prediction and its effect on measurement uncertainty in polynomial comparative calibration. In Proceedings of the 2019 12th International Conference on Measurement, Smolenice, Slovakia, 27–29 May 2019. [Google Scholar]
- Delgado, R. Misuse of Beer-Lambert Law and other calibration curves. R. Soc. Open Sci. 2022, 9, 211103. [Google Scholar] [CrossRef] [PubMed]
- François, N.; Govaerts, B.; Boulanger, B. Optimal designs for inverse prediction in univariate nonlinear calibration models. Chemom. Intell. Lab. Syst. 2004, 74, 283–292. [Google Scholar] [CrossRef]
- Kannan, N.; Keating, J.P.; Mason, R.L. A comparison of classical and inverse estimators in the calibration problem. Comm. Statist. Theory Methods 2007, 36, 83–95. [Google Scholar] [CrossRef]
- Chen, H.Y.; Chen, C. Evaluation of calibration equations by using regression analysis: An example of chemical analysis. Sensors 2022, 22, 447. [Google Scholar] [CrossRef]
- Mulholland, M.; Hibbert, D.B. Linearity and the limitations of least squares calibration. J. Chromatogr. A 1997, 762, 73–82. [Google Scholar] [CrossRef]
- Desimoni, E. A program for the weighted linear least-squares regression of unbalanced response arrays. Analyst 1999, 124, 1191–1196. [Google Scholar] [CrossRef]
- Lavagnini, I.; Magno, F. A statistical overview on univariate calibration, inverse regression, and detection limits: Application to gas chromatography/mass spectrometry technique. Mass Spectrom. Rev. 2007, 26, 1–18. [Google Scholar] [CrossRef]
- Ortiz, M.C.; Sánchez, M.S.; Sarabia, L.A. Quality of analytical measurements: Univariate regression. In Comprehensive Chemometrics. Chemical and Biochemical Data Analysis; Brown, S.D., Tauler, R., Walczak, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 127–169. [Google Scholar]
- Rawski, R.I.; Sanecki, P.T.; Kijowska, K.M.; Skital, P.M.; Saletnik, D.E. Regression analysis in analytical chemistry. Determination and validation of linear and quadratic regression dependencies. S. Afr. J. Chem. 2016, 69, 166–173. [Google Scholar] [CrossRef]
- Desharnais, B.; Camirand-lemyre, F.; Mireault, P.; Skinner, C.D. Procedure for the selection and validation of a calibration model I—Description and application. J. Anal. Toxicol. 2017, 41, 261–268. [Google Scholar] [CrossRef]
- Martin, J.; de Adana, D.D.R.; Asuero, A.G. Fitting models to data: Residual analysis, a primer. In Uncertainty Quantification and Model Calibration; Hessling, J.P., Ed.; IntechOpen Ltd.: London, UK, 2017; Chapter 7; p. 133. [Google Scholar]
- Martin, J.; Gracia, A.R.; Asuero, A.G. Fitting nonlinear calibration curves: No models perfect. J. Anal. Sci. Methods Instrum. 2017, 7, 1–17. [Google Scholar] [CrossRef]
- Lavín, Á.; Vicente, J.D.; Holgado, M.; Laguna, M.F.; Casquel, R.; Santamaría, B.; Maigler, M.V.; Hernández, A.L.; Ramírez, Y. On the determination of uncertainty and limit of detection in label-free biosensors. Sensors 2018, 18, 2038. [Google Scholar] [CrossRef]
- Greenspan, L. Humidity fixed points of binary saturated aqueous solutions. J. Res. Natl. Bur. Stand. 1977, 81A, 89–96. [Google Scholar] [CrossRef]
- OMIL. The Scale of Relative Humidity of Air Certified Against Saturated Salt Solutions. In OMIL R 121; Organization Internationale De Metrologie Legale: Paris, France, 1996. [Google Scholar]
- Chen, H.Y.; Chen, C. Determination of optimal measurement points for calibration equations—Examples by RH sensors. Sensors 2019, 19, 1213. [Google Scholar] [CrossRef] [PubMed]
- Weisberg, S. Applied Linear Regression, 4th ed.; Wiley: New York, NY, USA, 2013; p. 384. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D. Applied regression analysis. In Springer Texts in Statistics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Chen, C. Evaluation of resistance–temperature calibration equations for NTC thermistors. Measurement 2009, 42, 1103–1111. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Rab, S.; Suman, R. Significance of sensors for industry 4.0: Roles, capabilities, and applications. Sens. Int. 2021, 2, 100110. [Google Scholar] [CrossRef]
- Voorter, P.J.; McKay, A.; Dai, J.; Paravagna, O.; Cameron, N.R.; Junkers, T. Solvent-independent molecular weight determination of polymers based on a truly universal calibration. Angew. Chem. Int. Ed. 2022, 61, e202114536. [Google Scholar] [CrossRef]
- Visconti, G.; Boccard, J.; Feinberg, M.; Rudaz, S. From fundamentals in calibration to modern methodologies: A tutorial for small molecules quantification in liquid chromatography–mass spectrometry bioanalysis. Anal. Chim. Acta 2023, 1240, 340711. [Google Scholar] [CrossRef]
- Olsson, C.O.A.; Igual-Muñoz, A.N.; Mischler, S. Methods for calibrating the electrochemical quartz crystal microbalance: Frequency to mass and compensation for viscous load. Chemosensors 2023, 11, 456. [Google Scholar] [CrossRef]
- Gómez-Astorga, M.J.; Villagra-Mendoza, K.; Masís-Meléndez, F.; Ruíz-Barquero, A.; Rimolo-Donadio, R. Calibration of low-cost moisture sensors in a biochar-amended sandy loam soil with different salinity levels. Sensors 2024, 24, 5958. [Google Scholar] [CrossRef]
- Veiga-del-Baño, J.M.; Oliva, J.; Cámara, M.Á.; Andreo-Martínez, P.; Motas, M. Matrix-matched calibration for the quantitative analysis of pesticides in pepper and wheat flour: Selection of the best calibration model. Agriculture 2024, 14, 1014. [Google Scholar] [CrossRef]


| Study | Equipment | Target | Standard Range | Response Range | Calibration Equation | Statistic Criteria |
|---|---|---|---|---|---|---|
| Mulholland and Hibbert [21] | HPLC 1 | Daidzein | 0.162–10.96 mg/50 mL | 0.243–30.75 peak area | Linear y = X1.1 | R2, residual plot |
| Desimoni [22] | Flow injection analysis | Sulfides | 0.88–81.2 μm | 0.170–15.94 μA | Linear | R2, residual plot |
| Lavagnini and Magno [23] | GC-MS 2 | Chloromethane | 0~4 μg/L | 0.111975~0.465813 peak area ratio | Linear polynomial | s, residual plot |
| Ortiz et al. [24] | Pulse polarography | Benzaldehyde | 0.0198~0.1740 mnol/L | 0.033~0.366 μA | Linear | Residual plots, S |
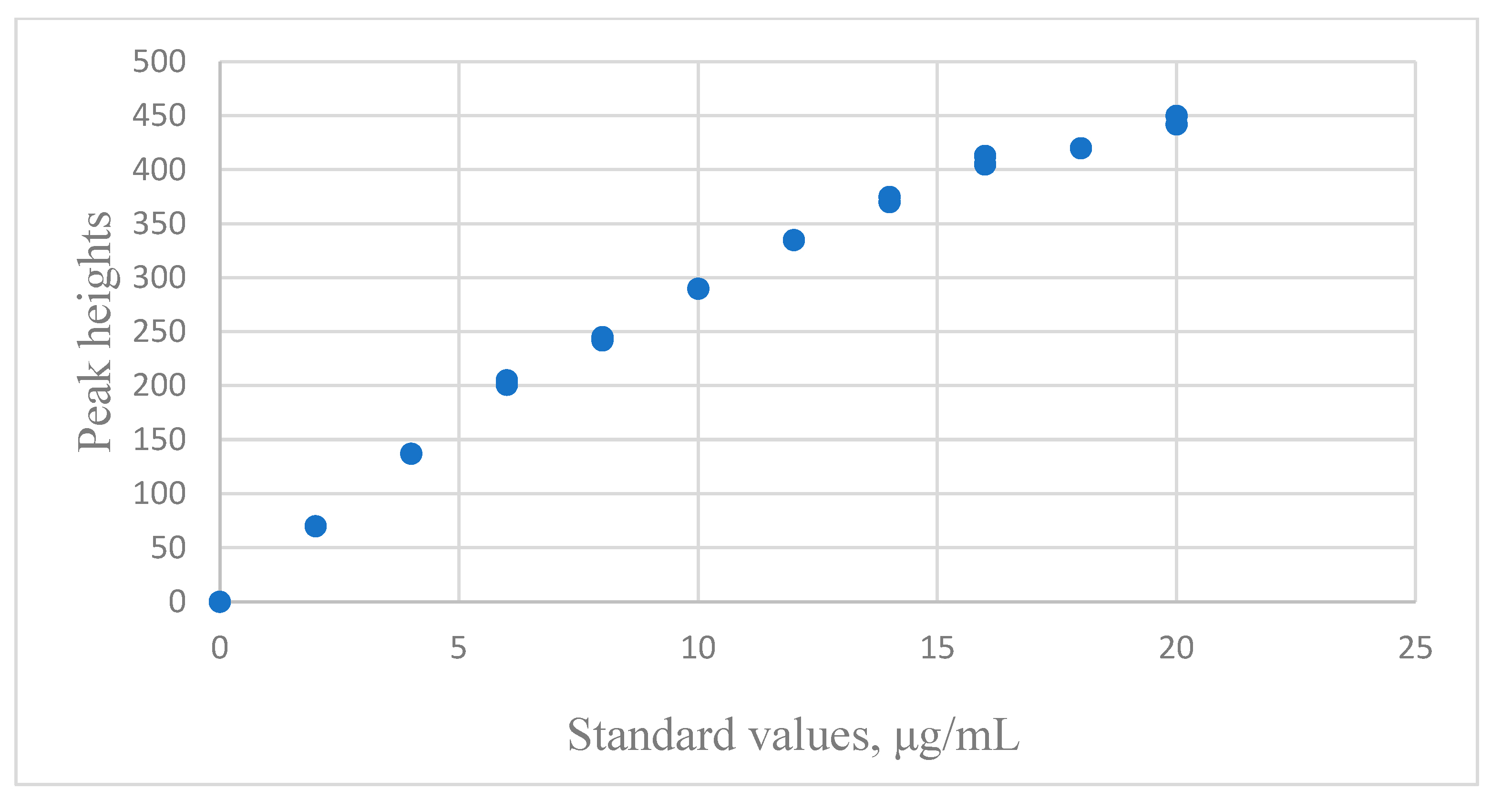
| Rawski et al. [25] | Spectrophotometry | Albumin | 0~20 μg/mL | 0~450 peak height × 10−3 | Linear | Lack of fit, R2 |
| Desharnais et al. [26] | LC-MS 3 | Cocaine | 5~1000 ng/mL | 0.049~9.209 area ratio | Linear | Partial F-test |
| Martin et al. [27] | HPLC | Blood | 0~90 ng/mL | 0.002~0.272 area ratio | High-order polynomial | R2 Residual plots |
| Martin et al. [28] | LC-QqQ-MS 4 | PrP | 2150–3,054,469 | Linear | R2 | |
| array | ||||||
| Lavin et al. [29] | BICELLS 5 | Anti-IgG | 1~100 μg/mL | 0.00~6.14 | Polynomial | AICs 5, R2 |
| Resistive Sensor | Capacitive Sensor | |
|---|---|---|
| Name | THT-B121 | HMP 140A |
| Sensing element | Macro-molecule HPR-MQ | HUMICAP |
| Operating range | 0–60 °C | 0–50 °C |
| Measuring range | 10–99% RH | 0–100% |
| Nonlinearity and repeatability | ±0.25% RH | ±0.2% RH |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −1.9395 | −1.0464 |
| ei,max | 0.2198 | 0.2414 |
| 0.9855 | 0.4944 | |
| 1.229 | 0.6064 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −1.9150 | −0.9950 |
| ei,max | 0.7311 | 0.8908 |
| 0.5431 | 0.5536 | |
| 0.4894 | 0.4807 |
| Classical Equation | Residual Plots | |
|---|---|---|
| 1. | 0.9842 | F.P. |
| 2. | 0.9893 | U.D. |
| 3. | 0.9863 | U.D. |
| 4. | 0.9873 | U.D. |
| 5. | 0.9867 | F.P. |
| Inverse Equation | Residual Plots | |
| 0.9773 | F.D. | |
| 2. x = | 0.9791 | U.D. |
| 3. x | 0.9691 | U.D. |
| 4. | 0.9841 | U.D. |
| 5. x | 0.9793 | F.P. |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −0.3859 | −0.3835 |
| ei,max | 1.4983 | 0.9350 |
| 0.4758 | 0.3328 | |
| 0.2695 | 0.2043 |
| Classical Equation | sy | Residual Plots | |
|---|---|---|---|
| 1. | 0.9651 | 29.081 | F.P. |
| 2. | 0.9980 | 5.5069 | F.P. |
| 3. | 0.9985 | 6.0221 | U.D. |
| 4. | 0.9985 | 6.1770 | U.D. |
| 5. | 0.9939 | 12.184 | F.P. |
| Inverse Equation | sx | Residual Plots | |
| 0.9651 | 1.2876 | F.P. | |
| 2. | 0.994 | 0.5430 | U.D. |
| 3. | 0.9522 | 1.5030 | F.P. |
| 4. | 0.9646 | 1.3361 | F.P. |
| 5. | 0.992 | 0.6153 | U.D. |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −0.4849 | −0.7791 |
| ei,max | 1.1608 | 1.3347 |
| 0.4770 | 0.5416 | |
| 0.4147 | 0.4214 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −8.0672 | −10.2422 |
| ei max | 4.3461 | 5.8671 |
| 2.2862 | 2.2715 | |
| 2.9587 | 3.3921 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −0.5011 | −0.475 |
| ei,max | 0.4713 | 0.482 |
| 0.1924 | 0.1847 | |
| 0.1171 | 0.1110 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −33.0861 | −34.4825 |
| ei,max | 22.0372 | 23.6656 |
| 15.6931 | 15.5105 | |
| 12.6058 | 13.3721 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −0.3948 | −0.1498 |
| ei,max | 0.4439 | 0.2781 |
| 0.2134 | 0.1355 | |
| 0.2449 | 0.1137 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −0.0698 | −0.1562 |
| ei,max | 0.1701 | 0.0684 |
| 0.0837 | 0.0823 | |
| 0.0668 | 0.073 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −71.2154 | −82.0002 |
| ei,max | 46.0926 | 36.4611 |
| 47.4945 | 27.3709 | |
| 35.4701 | 12.6038 |
| Criterion | Classical Equation | Inverse Equation |
|---|---|---|
| ei,min | −0.02174 | −0.01608 |
| ei,max | 0.00858 | 0.007406 |
| 0.008197 | 0.006503 | |
| 0.009711 | 0.007014 |
| REMAE 1 (Accuracy) | RERMSE 2 (Precision) | |
|---|---|---|
| I. Hygrometer | ||
| 1. Capacitive | 49.83% | 50.66% |
| 2. Resistance | −1.93% | 1.78% |
| II. Literature data 1. GC-MS [23] 2. Flow injection Analysis [22] 3. LC-MS-MS [26] 4. Pulse polarography [24] 5. Spectrophotometry [25] 6. BICELLS (biophotonic sensing cells) [29] 7. HPLC [27] (drug in blood) 8. LC-QqQ-MS [28] 9. HPLC [21] (daidzein) | 48.56% 36.5% 42.37% 20.67% −13.54% −0.64% 4.0% 1.16% 1.67% | 46.53% 53.57% 64.47% 27.78% −1.62% 14.65% 5.2% −6.08% −9.28% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-Y.; Chen, C. Comparison of Classical and Inverse Calibration Equations in Chemical Analysis. Sensors 2024, 24, 7038. https://doi.org/10.3390/s24217038
Chen H-Y, Chen C. Comparison of Classical and Inverse Calibration Equations in Chemical Analysis. Sensors. 2024; 24(21):7038. https://doi.org/10.3390/s24217038
Chicago/Turabian StyleChen, Hsuan-Yu, and Chiachung Chen. 2024. "Comparison of Classical and Inverse Calibration Equations in Chemical Analysis" Sensors 24, no. 21: 7038. https://doi.org/10.3390/s24217038
APA StyleChen, H.-Y., & Chen, C. (2024). Comparison of Classical and Inverse Calibration Equations in Chemical Analysis. Sensors, 24(21), 7038. https://doi.org/10.3390/s24217038







