Running Gait Complexity During an Overground, Mass-Participation Five-Kilometre Run
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants & Protocol
2.2. Data Processing
2.3. Statistical Analysis
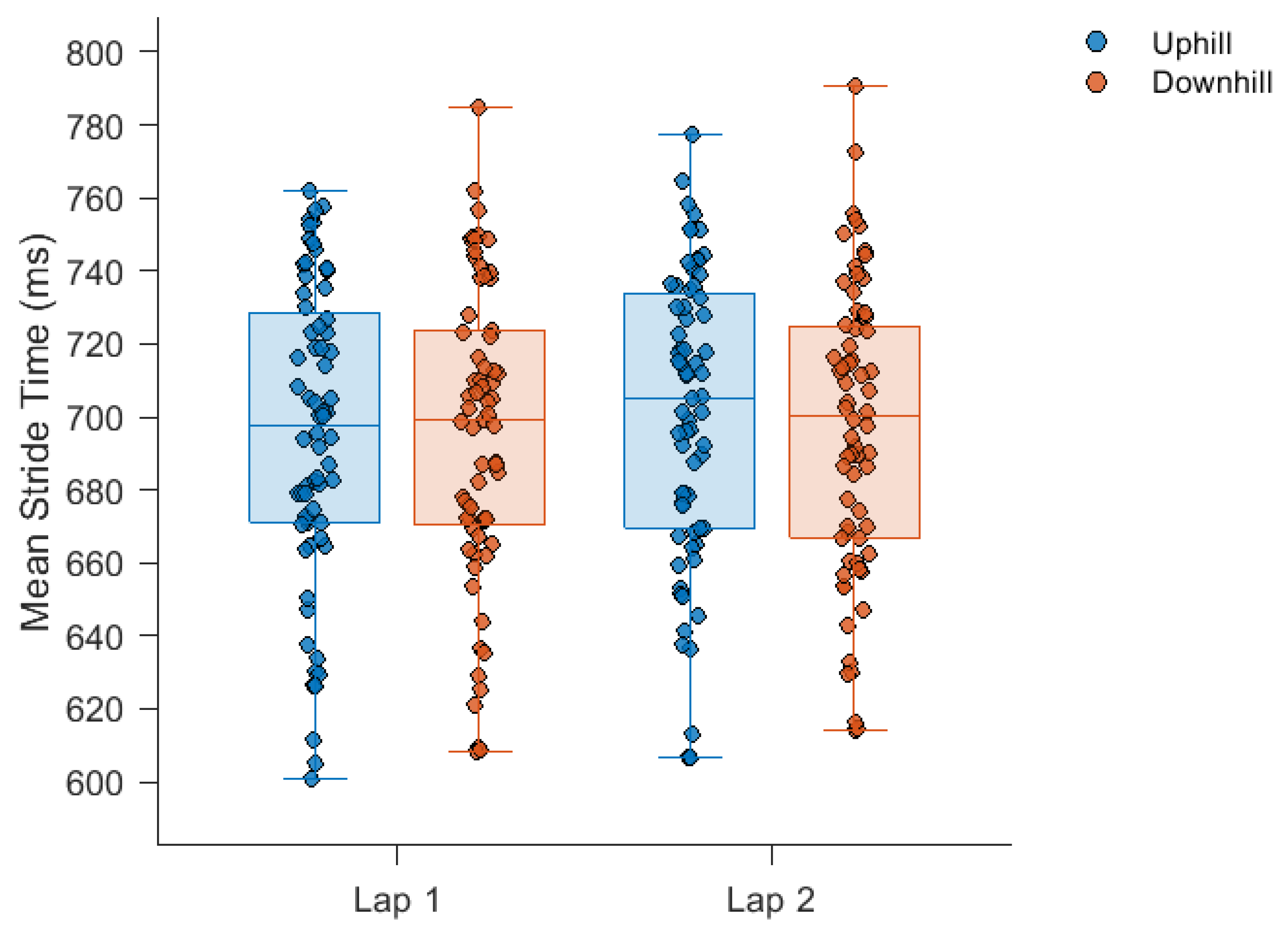
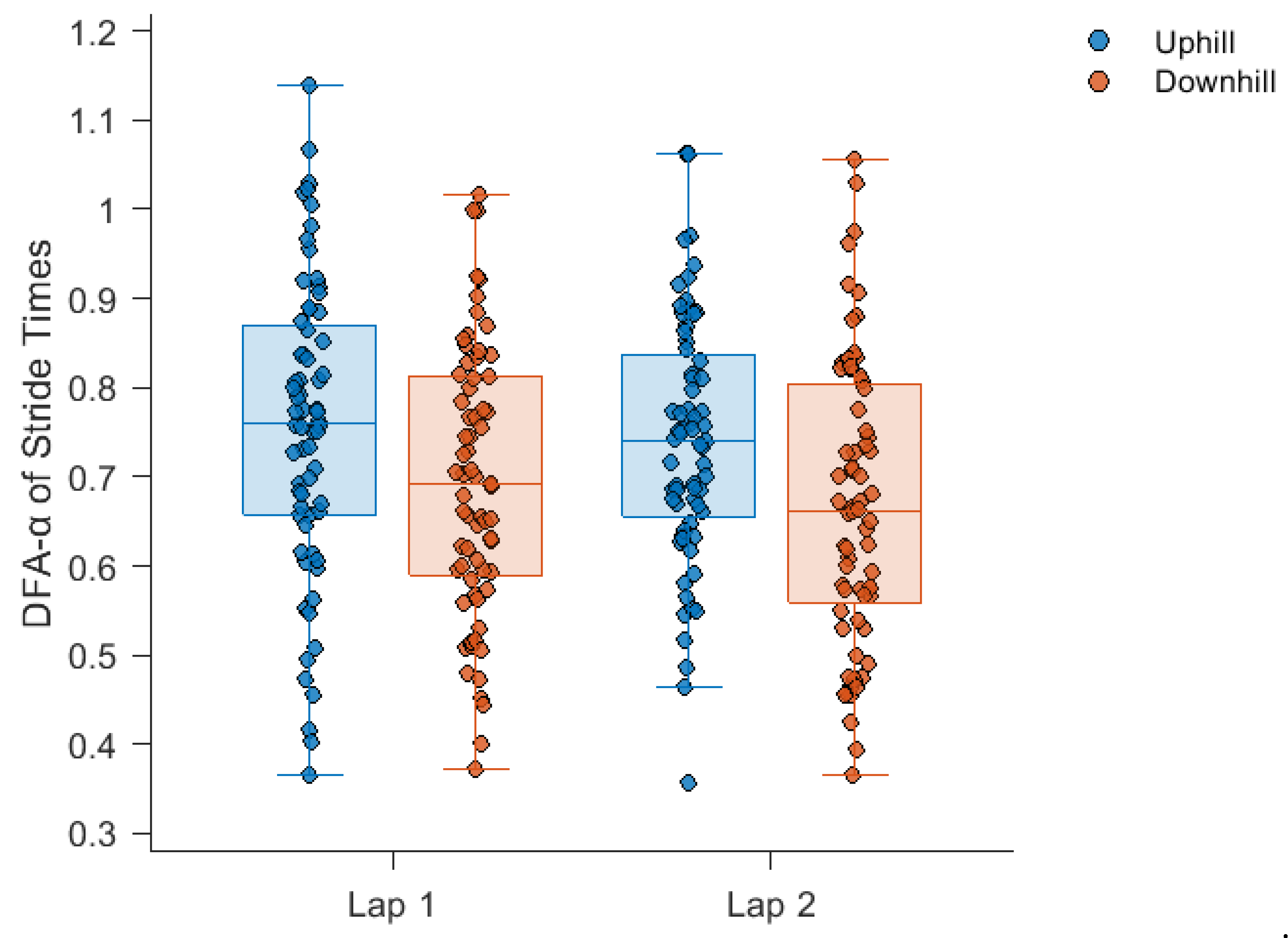
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bartlett, R.; Wheat, J.; Robins, M. Is movement variability important for sports biomechanists? Sports Biomech. 2007, 6, 224–243. [Google Scholar] [CrossRef] [PubMed]
- Davids, K.; Glazier, P.; Araújo, D.; Bartlett, R. Movement Systems as Dynamical Systems. Sports Med. 2003, 33, 245–260. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, S.T.; Souza, T.R.; Verhagen, E.; Van Emmerik, R.; Bittencourt, N.F.N.; Mendonça, L.D.M.; Andrade, A.G.P.; Resende, R.A.; Ocarino, J.M. Sports Injury Forecasting and Complexity: A Synergetic Approach. Sports Med. 2020, 50, 1757–1770. [Google Scholar] [CrossRef] [PubMed]
- James, C. Considerations of movement variability in biomechanics research. In Innovative Analyses of Human Movement; Human Kinetics: Champaign, IL, USA, 2004; pp. 29–62. [Google Scholar]
- Kakouris, N.; Yener, N.; Fong, D.T.P. A systematic review of running-related musculoskeletal injuries in runners. J. Sport Health Sci. 2021, 10, 513–522. [Google Scholar] [CrossRef]
- Hunter, B.; Karsten, B.; Greenhalgh, A.; Burnley, M.; Muniz-Pumares, D. The Application of non-linear methods to quantify changes to movement dynamics during running: A scoping review. J. Sports Sci. 2023, 41, 481–494. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Van Emmerik, R.E.A.; Ducharme, S.W.; Amado, A.C.; Hamill, J. Comparing dynamical systems concepts and techniques for biomechanical analysis. J. Sport Health Sci. 2016, 5, 3–13. [Google Scholar] [CrossRef]
- Duarte, M.; Sternad, D. Complexity of human postural control in young and older adults during prolonged standing. Exp. Brain Res. 2008, 191, 265–276. [Google Scholar] [CrossRef]
- Lipsitz, L.A. Dynamics of Stability: The Physiologic Basis of Functional Health and Frailty. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2002, 57, B115–B125. [Google Scholar] [CrossRef]
- Wilson, T.J.; Likens, A.D. Running gait produces long range correlations: A systematic review. Gait Posture 2023, 102, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Meardon, S.A.; Hamill, J.; Derrick, T.R. Running injury and stride time variability over a prolonged run. Gait Posture 2011, 33, 36–40. [Google Scholar] [CrossRef] [PubMed]
- Brahms, C.M.; Zhao, Y.; Gerhard, D.; Barden, J.M. Long-range correlations and stride pattern variability in recreational and elite distance runners during a prolonged run. Gait Posture 2022, 92, 487–492. [Google Scholar] [CrossRef] [PubMed]
- Zignoli, A.; Godin, A.; Mourot, L. Indoor running temporal variability for different running speeds, treadmill inclinations, and three different estimation strategies. PLoS ONE 2023, 18, e0287978. [Google Scholar] [CrossRef]
- Hunter, B.; Karsten, B.; Greenhalgh, A.; Burnley, M.; Leuchanka, A.; Clark, T.; Muniz, D. Fractal Analyses of Gait Variability During a Marathon; International Society of Biomechanics in Sports Proceedings. In Proceedings of the 39th Conference of the International Society of Biomechanics in Sport Conference, Canberra, Australia, 3–6 August 2021; Available online: https://researchprofiles.herts.ac.uk/en/publications/fractal-analyses-of-gait-variability-during-a-marathon (accessed on 25 July 2023).
- Mo, S.; Chow, D.H.K. Stride-to-stride variability and complexity between novice and experienced runners during a prolonged run at anaerobic threshold speed. Gait Posture 2018, 64, 7–11. [Google Scholar] [CrossRef]
- Norris, M.; Kenny, I.C.; Healy, R.; Anderson, R. Possibilities for Real-time DFA Based Injury Detection and Skill Level Differentiation. Procedia Eng. 2016, 147, 700–705. [Google Scholar] [CrossRef]
- Ducharme, S.W.; Liddy, J.J.; Haddad, J.M.; Busa, M.A.; Claxton, L.J.; van Emmerik, R.E.A. Association between stride time fractality and gait adaptability during unperturbed and asymmetric walking. Hum. Mov. Sci. 2018, 58, 248–259. [Google Scholar] [CrossRef]
- Taunton, J.E.; Ryan, M.B.; Clement, D.B.; McKenzie, D.C.; Lloyd-Smith, D.R.; Zumbo, B.D.; Run, V.S. “In Training” clinics. Br. J. Sports Med. 2003, 37, 239–244. [Google Scholar] [CrossRef]
- Benson, L.C.; Räisänen, A.M.; Clermont, C.A.; Ferber, R. Is This the Real Life, or Is This Just Laboratory? A Scoping Review of IMU-Based Running Gait Analysis. Sensors 2022, 22, 1722. [Google Scholar] [CrossRef]
- van Gelder, L.M.A.; Barnes, A.; Wheat, J.S.; Heller, B.W. Runners’ responses to a biofeedback intervention aimed to reduce tibial acceleration differ within and between individuals. J. Biomech. 2023, 157, 111686. [Google Scholar] [CrossRef]
- 100 Millionth Instance of Participation and Nine Million Registered Parkrunners, Parkrun UK Blog. 2023. Available online: https://blog.parkrun.com/uk/2023/11/28/100-millionth-instance-of-participation-and-nine-million-registered-parkrunners/ (accessed on 19 March 2024).
- Barnes, A.; Wheat, J.; Milner, C.E. Fore- and Rearfoot Kinematics in High- and Low-Arched Individuals during Running. Foot Ankle Int. 2011, 32, 710–716. [Google Scholar] [CrossRef]
- Brayne, L.; Barnes, A.; Heller, B.; Wheat, J. Using a wireless consumer accelerometer to measure tibial acceleration during running: Agreement with a skin-mounted sensor. Sports Eng. 2018, 21, 487–491. [Google Scholar] [CrossRef]
- Sinclair, J.; Hobbs, S.J.; Protheroe, L.; Edmundson, C.J.; Greenhalgh, A. Determination of Gait Events Using an Externally Mounted Shank Accelerometer. J. Appl. Biomech. 2013, 29, 118–122. [Google Scholar] [CrossRef]
- Ducharme, S.W.; Turner, D.S.; Pleuss, J.D.; Moore, C.C.; Schuna, J.M.; Tudor-Locke, C.; Aguiar, E.J. Using Cadence to Predict the Walk-to-Run Transition in Children and Adolescents: A Logistic Regression Approach. J. Sports Sci. 2021, 39, 1039–1045. [Google Scholar] [CrossRef]
- Ueno, H.; Nakazawa, S.; Takeuchi, Y.; Sugita, M. Relationship between Step Characteristics and Race Performance during 5000-m Race. Sports 2021, 9, 131. [Google Scholar] [CrossRef]
- Phinyomark, A.; Larracy, R.; Scheme, E. Fractal Analysis of Human Gait Variability via Stride Interval Time Series. Front. Physiol. 2020, 11, 333. [Google Scholar] [CrossRef]
- Warlop, T.B.; Bollens, B.; Detrembleur, C.; Stoquart, G.; Lejeune, T.; Crevecoeur, F. Impact of series length on statistical precision and sensitivity of autocorrelation assessment in human locomotion. Hum. Mov. Sci. 2017, 55, 31–42. [Google Scholar] [CrossRef]
- Almurad, Z.M.H.; Delignières, D. Evenly spacing in Detrended Fluctuation Analysis. Phys. A Stat. Mech. Appl. 2016, 451, 63–69. [Google Scholar] [CrossRef]
- Liddy, J.J.; Haddad, J.M. Evenly spaced Detrended Fluctuation Analysis: Selecting the number of points for the diffusion plot. Phys. A Stat. Mech. Appl. 2018, 491, 233–248. [Google Scholar] [CrossRef]
- Kroese, D.P.; Botev, Z.I. Spatial Process Generation. arXiv 2013, arXiv:1308.0399. [Google Scholar] [CrossRef]
- Delignières, D. Correlation Properties of (Discrete) Fractional Gaussian Noise and Fractional Brownian Motion. Math. Probl. Eng. 2015, 2015, e485623. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Jordan, K.; Challis, J.H.; Newell, K.M. Speed influences on the scaling behavior of gait cycle fluctuations during treadmill running. Hum. Mov. Sci. 2007, 26, 87–102. [Google Scholar] [CrossRef] [PubMed]
- Jordan, K.; Challis, J.H.; Newell, K.M. Long range correlations in the stride interval of running. Gait Posture 2006, 24, 120–125. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, T.R.; Noakes, T.D.; McGregor, S.J. Effect of Treadmill versus Overground Running on the Structure of Variability of Stride Timing. Percept. Mot. Skills 2014, 118, 331–346. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, J.M. Gait dynamics, fractals and falls: Finding meaning in the stride-to-stride fluctuations of human walking. Hum. Mov. Sci. 2007, 26, 555–589. [Google Scholar] [CrossRef]
- Snyder, K.L.; Farley, C.T. Energetically optimal stride frequency in running: The effects of incline and decline. J. Exp. Biol. 2011, 214, 2089–2095. [Google Scholar] [CrossRef]
- Weart, A.N.; Szymanek, E.B.; Miller, E.M.; Goss, D.L. The stability of step rate throughout a 3200 meter run. Gait Posture 2019, 71, 284–288. [Google Scholar] [CrossRef]
- Townshend, A.D.; Worringham, C.J.; Stewart, I.B. Spontaneous Pacing during Overground Hill Running. Med. Sci. Sports Exerc. 2010, 42, 160. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, B.; Heller, B.; van Gelder, L.; Barnes, A.; Reeves, J.; Wheat, J. Running Gait Complexity During an Overground, Mass-Participation Five-Kilometre Run. Sensors 2024, 24, 7252. https://doi.org/10.3390/s24227252
Jones B, Heller B, van Gelder L, Barnes A, Reeves J, Wheat J. Running Gait Complexity During an Overground, Mass-Participation Five-Kilometre Run. Sensors. 2024; 24(22):7252. https://doi.org/10.3390/s24227252
Chicago/Turabian StyleJones, Ben, Ben Heller, Linda van Gelder, Andrew Barnes, Joanna Reeves, and Jon Wheat. 2024. "Running Gait Complexity During an Overground, Mass-Participation Five-Kilometre Run" Sensors 24, no. 22: 7252. https://doi.org/10.3390/s24227252
APA StyleJones, B., Heller, B., van Gelder, L., Barnes, A., Reeves, J., & Wheat, J. (2024). Running Gait Complexity During an Overground, Mass-Participation Five-Kilometre Run. Sensors, 24(22), 7252. https://doi.org/10.3390/s24227252




