Ultrasonic Through-Metal Communication Based on Deep-Learning-Assisted Echo Cancellation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Echoing Problem
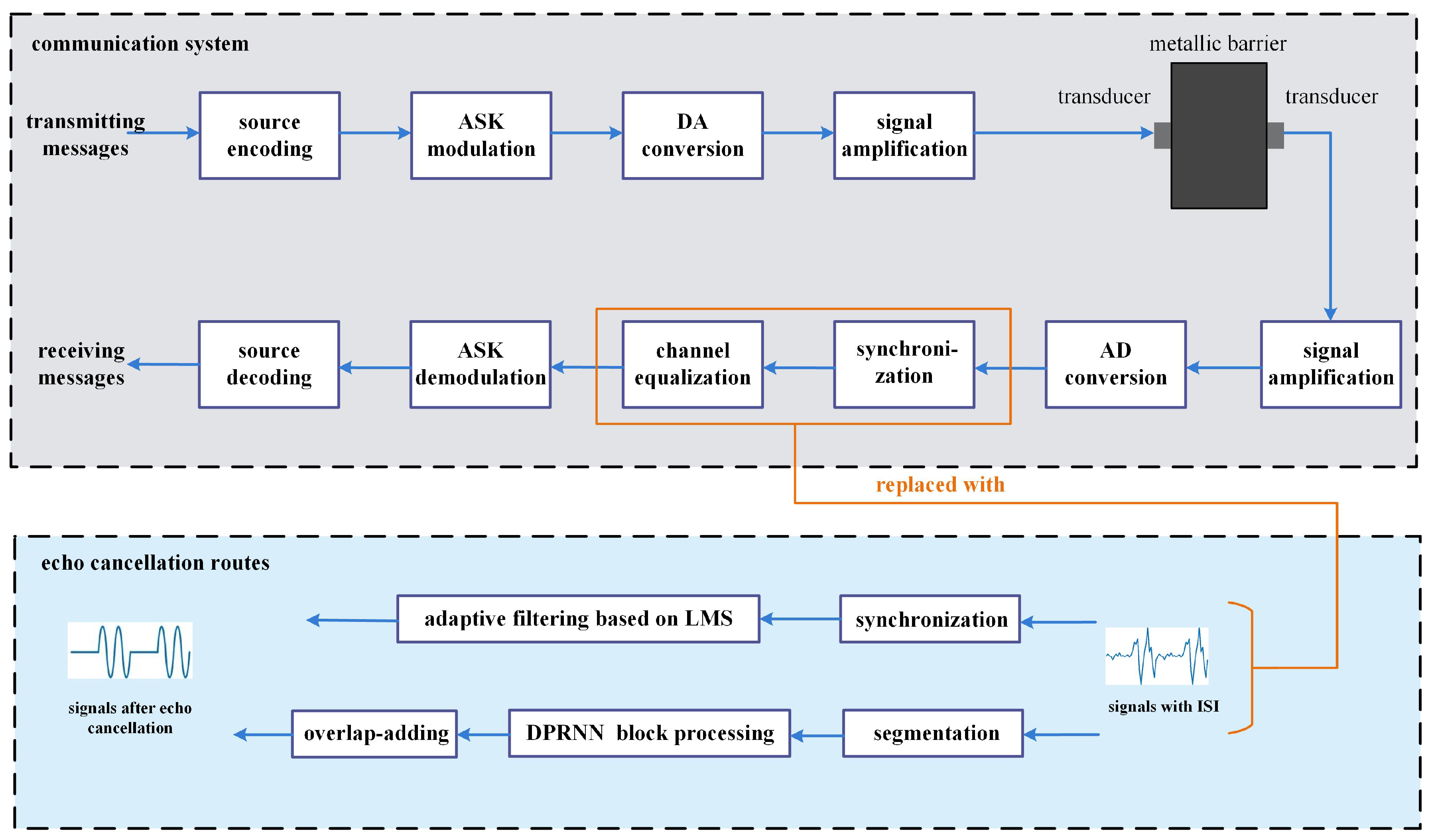
2.2. System Architecture
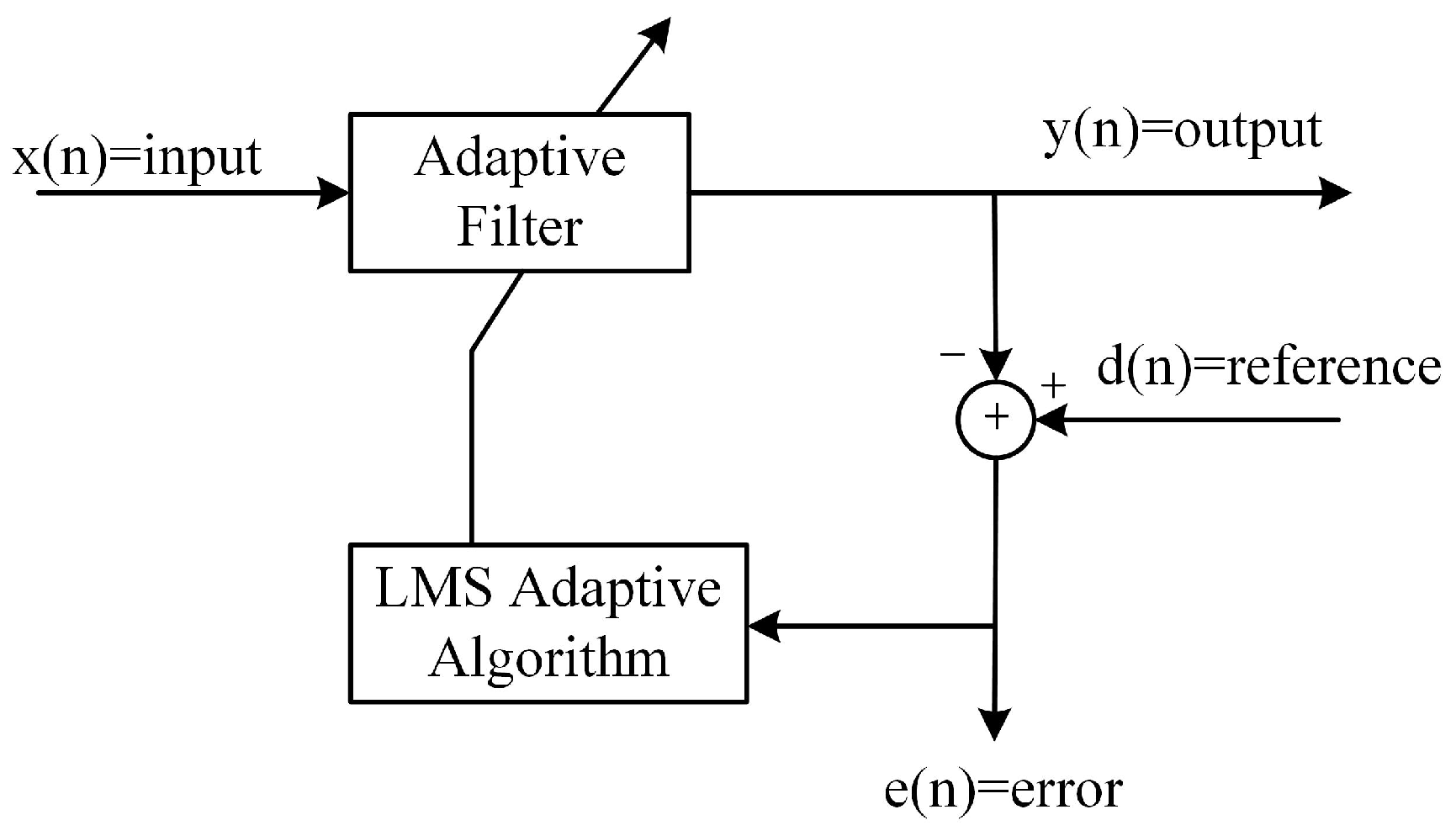
2.3. Echo Cancellation Approach I: Adaptive Filtering
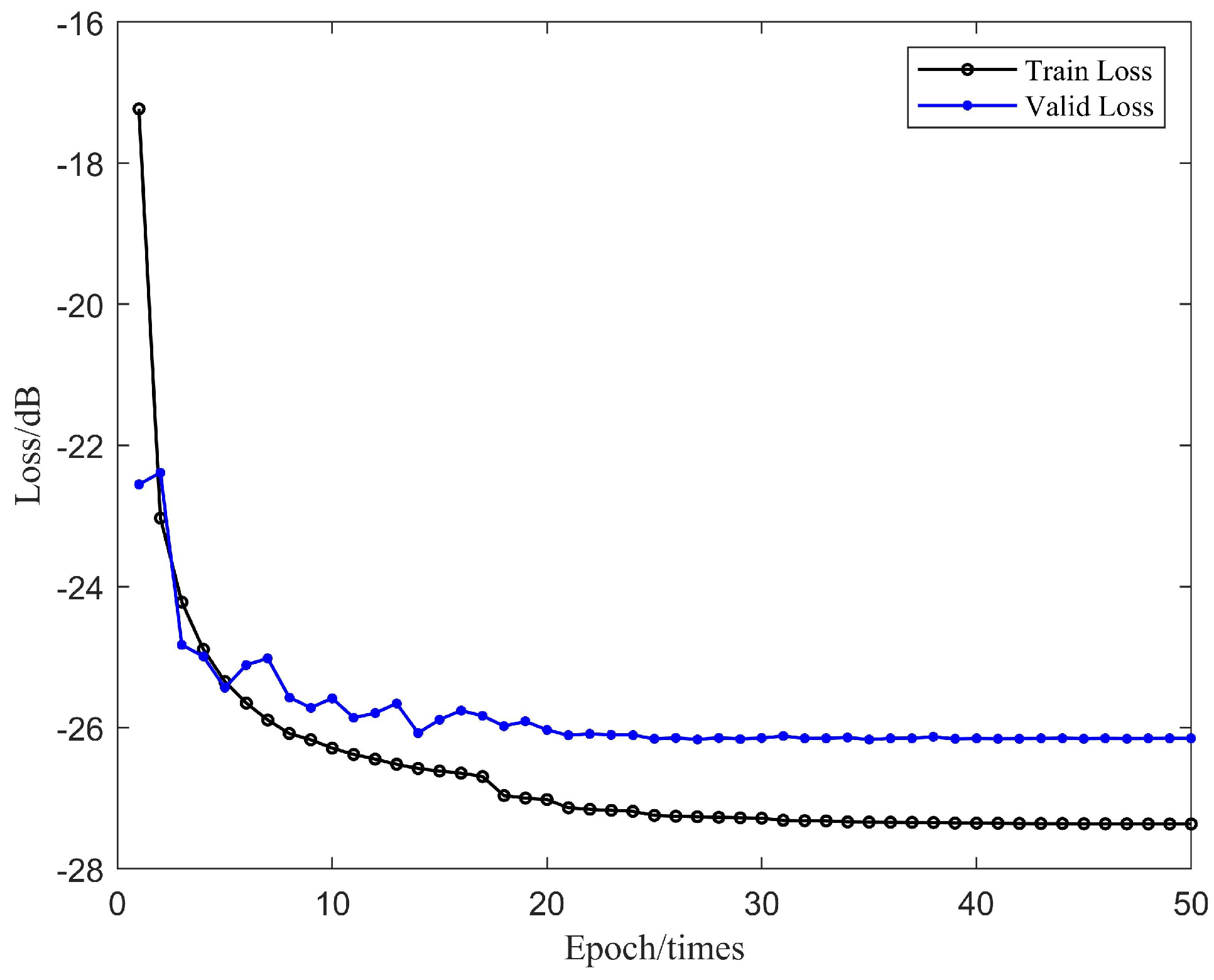
2.4. Echo Cancellation Approach II: DPRNN
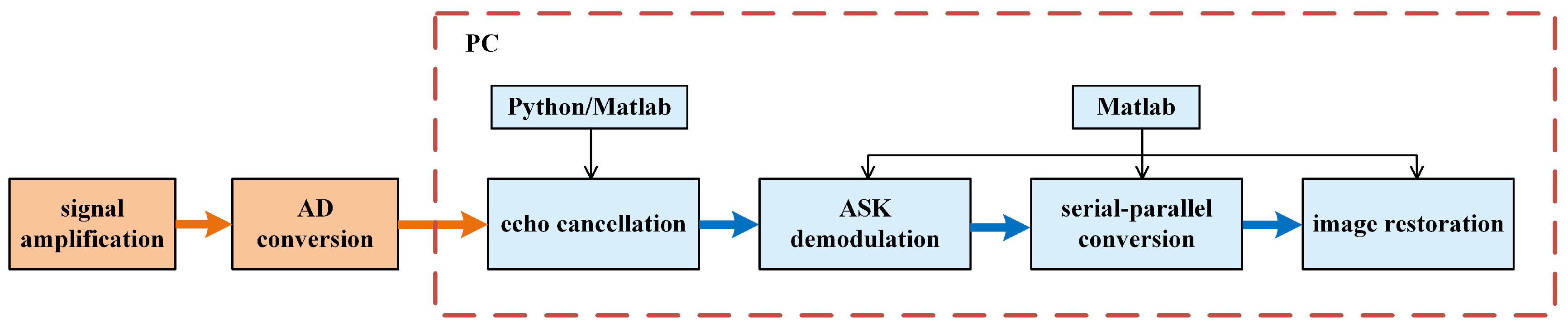
2.5. Implementation of Signal Transmission
3. Results
3.1. Data Transmission
3.1.1. Generating Initial Received Signals with Different SNRs
3.1.2. Quality Evaluation Indexes of Signal Recovery
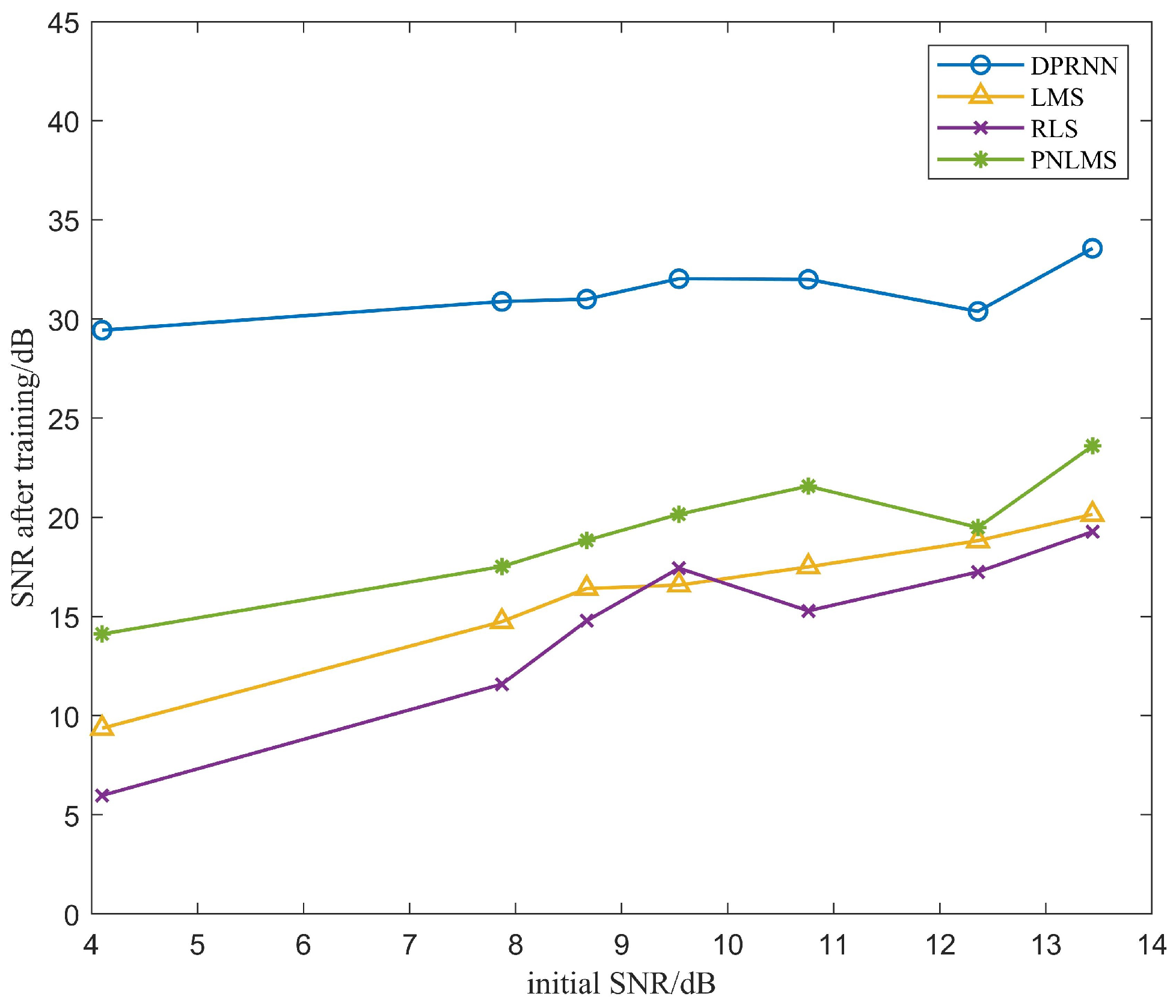
3.1.3. Comparison of Echo Cancellation Performance
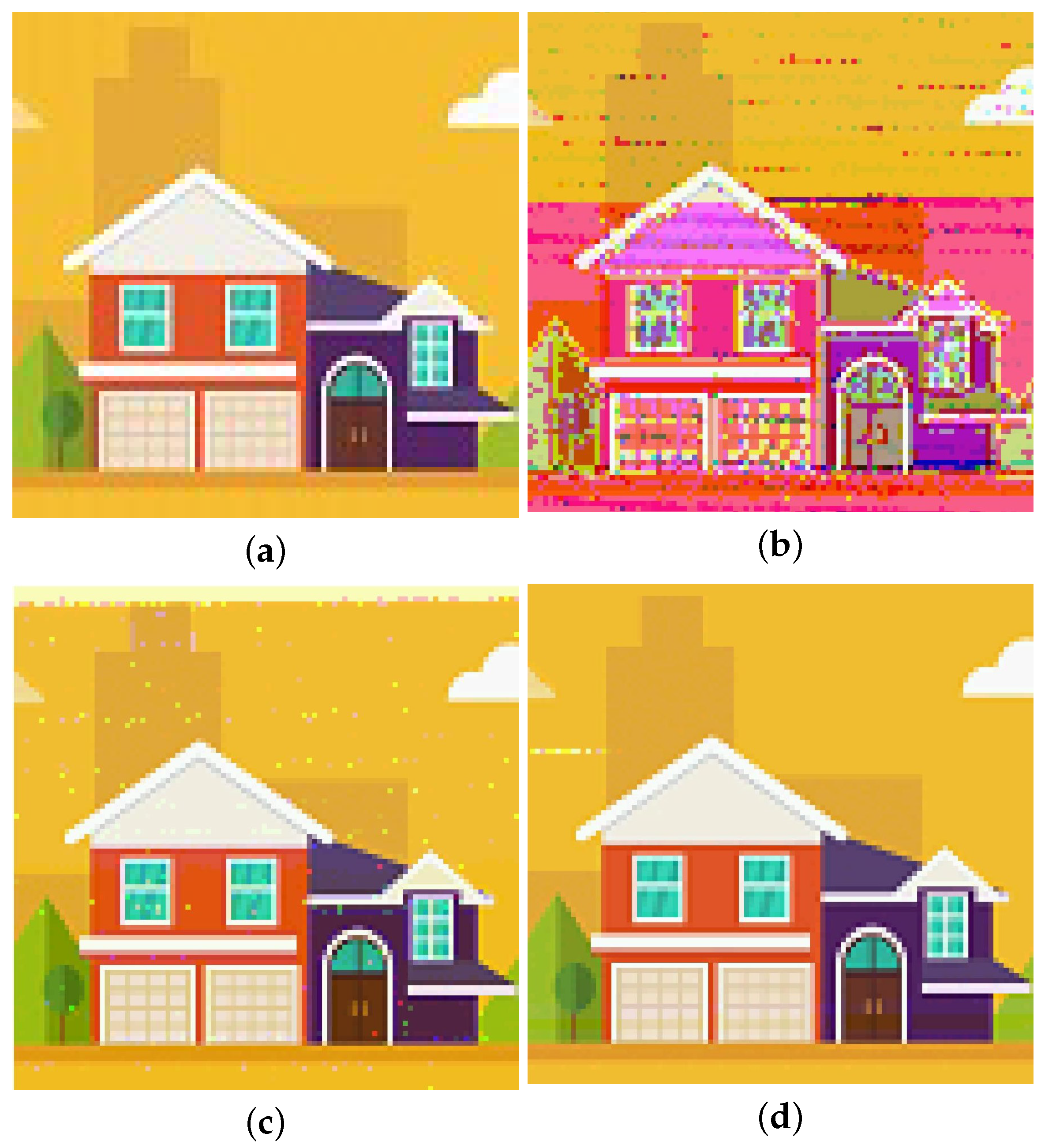
3.2. Image Transmission
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DPRNN | Dual-path Recurrent Neural Network |
| SNR | Signal-to-noise Ratio |
| PSNR | Peak-signal-to-noise Ratio |
| SSIM | Structural Similarity Index Measure |
| ISI | Intersymbol Interference |
| RF | Radio Frequency |
| LMS | Least Mean Square |
| NLMS | Normalize Least Mean Square |
| OFDM | Orthogonal Frequency Division Multiplexing |
| PAPR | Peak-to-average Power Ratio |
| DL | Deep Learning |
| SISNR | Scale-invariant Signal-to-noise Ratio |
| NCC | Normalized Correlation Coefficient |
| BER | Bit Error Rate |
References
- Bahouth, R.; Benmeddour, F.; Moulin, E.; Assaad, J. Lamb wave wireless communication through healthy and damaged channels with symmetrical and asymmetrical steps and notches. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2390–2399. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Wu, Y.; Qian, F.; Jung, H.; Kaluvan, S.; Huijin, H.; Zhang, C.; Reed, F.K.; Ericson, M.N.; Zhang, H. Self-powered Through-wall communication for dry cask storage monitoring. Ann. Nucl. Energy 2022, 177, 109306. [Google Scholar] [CrossRef]
- Guo, H.; Prince, M.; Ramsey, J.; Turner, J.; Allen, M.; Samuels, C.; Nuako, J.A. A Low-cost Through-metal Communication System for Sensors in Metallic Pipes. IEEE Sens. J. 2023, 23, 8952–8960. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saulnier, G.J.; Wilt, K.W.; Curt, E.; Scarton, H.A.; Litman, R.B. Low-power, low-rate ultrasonic communications system transmitting axially along a cylindrical pipe using transverse waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1788–1796. [Google Scholar] [CrossRef] [PubMed]
- Bielinski, M.; Wanuga, K.; Sosa, G.; Primerano, R.; Kam, M.; Dandekar, K.R. Transceiver design for high-data rate through-metal communication in naval applications. Nav. Eng. J. 2013, 125, 121–126. [Google Scholar]
- Pereira, R.B.; Braga, A.M.; Kubrusly, A.C. Ultrasonic Energy and Data Transfer through a Metal—Liquid Multi-Layer Channel Enhanced by Automatic Gain and Carrier Control. Sensors 2023, 23, 4697. [Google Scholar] [CrossRef] [PubMed]
- Sugino, C.; Gerbe, R.; Baca, E.; Reinke, C.; Ruzzene, M.; Erturk, A.; El-Kady, I. Machined phononic crystals to block high-order Lamb waves and crosstalk in through-metal ultrasonic communication systems. Appl. Phys. Lett. 2022, 120, 191705. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Z.; Yang, H.; Wu, M.; Yang, J. Ultrasonic Wireless Communication through Metal Barriers. Sound Vib. 2019, 53, 2–15. [Google Scholar] [CrossRef]
- Yang, D.-X.; Hu, Z.; Zhao, H.; Hu, H.-F.; Sun, Y.-Z.; Hou, B.-J. Through-metal-wall power delivery and data transmission for enclosed sensors: A review. Sensors 2015, 15, 31581–31605. [Google Scholar] [CrossRef]
- Pujari, S.S.; Panda, A.; Dash, P. Design & Implementation of FPGA based Adaptive Filter for Echo Cancellation. In Proceedings of the International Conference for Convergence for Technology—2014, Pune, India, 6–8 April 2014. [Google Scholar]
- Pauline, S.H.; Samiappan, D.; Kumar, R.; Anand, A.; Kar, A. Variable tap-length non-parametric variable step-size NLMS adaptive filtering algorithm for acoustic echo cancellation. Appl. Acoust. 2020, 159, 107074. [Google Scholar] [CrossRef]
- Dogariu, L.M.; Paleologu, C.; Benesty, J.; Ciochină, S. On the Performance of a Data-Reuse Fast RLS Algorithm for Acoustic Echo Cancellation. In Proceedings of the 2022 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Sofia, Bulgaria, 6–9 June 2022; pp. 135–140. [Google Scholar]
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Lee, K.A.; Gan, W.S.; Kuo, S.M. Subband Adaptive Filtering: Theory and Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Guo, G.; Yu, Y.; de Lamare, R.C.; Zheng, Z.; Lu, L.; Cai, Q. Proximal normalized subband adaptive filtering for acoustic echo cancellation. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 2174–2188. [Google Scholar] [CrossRef]
- Bahraini, T.; Sadigh, A.N. Proposing a robust RLS based subband adaptive filtering for audio noise cancellation. Appl. Acoust. 2024, 216, 109755. [Google Scholar] [CrossRef]
- Primerano, R.; Wanuga, K.; Dorn, J.; Kam, M.; Dandekar, K. Echo-cancellation for ultrasonic data transmission through a metal channel. In Proceedings of the 2007 41st Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 14–16 March 2007; pp. 841–845. [Google Scholar]
- Primerano, R.; Kam, M.; Dandekar, K. High bit rate ultrasonic communication through metal channels. In Proceedings of the 2009 43rd Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 18–20 March 2009; pp. 902–906. [Google Scholar]
- Tian, D.; Yang, D.; Hou, B. Identification and Communication Simulation of an Ultrasonic Through-metal-wall Channel. In Proceedings of the 2nd International Conference on Computer Engineering, Information Science & Application Technology, Wuhan, China, 8–9 July 2016; Volume 74, pp. 621–625. [Google Scholar]
- Xu, L.S.; Yang, W.; Tian, H.X. A Channel Estimation Method for Ultrasonic Through-Metal Communication. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 823–832. [Google Scholar] [CrossRef] [PubMed]
- Oya, J.R.G.; Miguel, J.M.A.; Doblado, J.G.; Chavero, F.M.; Fort, E.H.; Lecuyer, V.B.; Martín, A.J.L. Subsampling ofdm-based ultrasonic data communication through metallic channels for monitoring of cargo containers. IEEE Trans. Intell. Transp. Syst. 2018, 20, 4245–4250. [Google Scholar]
- Xu, L.; Yang, W.; Tian, H.; Wu, T. Bit-filling algorithm for fast subcarrier-selecting in ultrasonic through-metalcommunication. J. Commun. 2020, 41, 11. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Soltani, M.; Pourahmadi, V.; Mirzaei, A.; Sheikhzadeh, H. Deep learning-based channel estimation. IEEE Commun. Lett. 2019, 23, 652–655. [Google Scholar] [CrossRef]
- Shen, B.; Huang, C.; Xu, W.; Yang, T.; Cui, S. Blind channel codes recognition via deep learning. IEEE J. Sel. Areas Commun. 2021, 39, 2421–2433. [Google Scholar] [CrossRef]
- Mattu, S.R.; Theagarajan, L.N.; Chockalingam, A. Deep channel prediction: A DNN framework for receiver design in time-varying fading channels. IEEE Trans. Veh. Technol. 2022, 71, 6439–6453. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, X. A Robust and Cascaded Acoustic Echo Cancellation Based on Deep Learning. In Proceedings of the INTERSPEECH, Shanghai, China, 25–29 October 2020; pp. 3940–3944. [Google Scholar]
- Ivry, A.; Cohen, I.; Berdugo, B. Nonlinear acoustic echo cancellation with deep learning. arXiv 2021, arXiv:2106.13754. [Google Scholar]
- Butterweck, H.-J. A wave theory of long LMS adaptive filters. In Proceedings of the 2000 10th European Signal Processing Conference, Tampere, Finland, 4–8 September 2000; pp. 1–4. [Google Scholar]
- Luo, Y.; Chen, Z.; Yoshioka, T. Dual-path RNN: Efficient long sequence modeling for time-domain single-channel speech separation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 46–50. [Google Scholar]
- Li, C.; Luo, Y.; Han, C.; Li, J.; Yoshioka, T.; Zhou, T.; Delcroix, M.; Kinoshita, K.; Boeddeker, C.; Qian, Y. Dual-path RNN for long recording speech separation. In Proceedings of the 2021 IEEE Spoken Language Technology Workshop (SLT), Shenzhen, China, 19–22 January 2021; pp. 865–872. [Google Scholar]
- Wijayakusuma, A.; Gozali, D.R.; Widjaja, A.; Ham, H. Implementation of Real-Time Speech Separation Model Using Time-Domain Audio Separation Network (TasNet) and Dual-Path Recurrent Neural Network (DPRNN). Proc. Comput. Sci. 2021, 179, 762–772. [Google Scholar] [CrossRef]
- Zhu, J.; Yeh, R.A.; Hasegawa-Johnson, M. Multi-decoder DPRNN: Source separation for variable number of speakers. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 3420–3424. [Google Scholar]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]

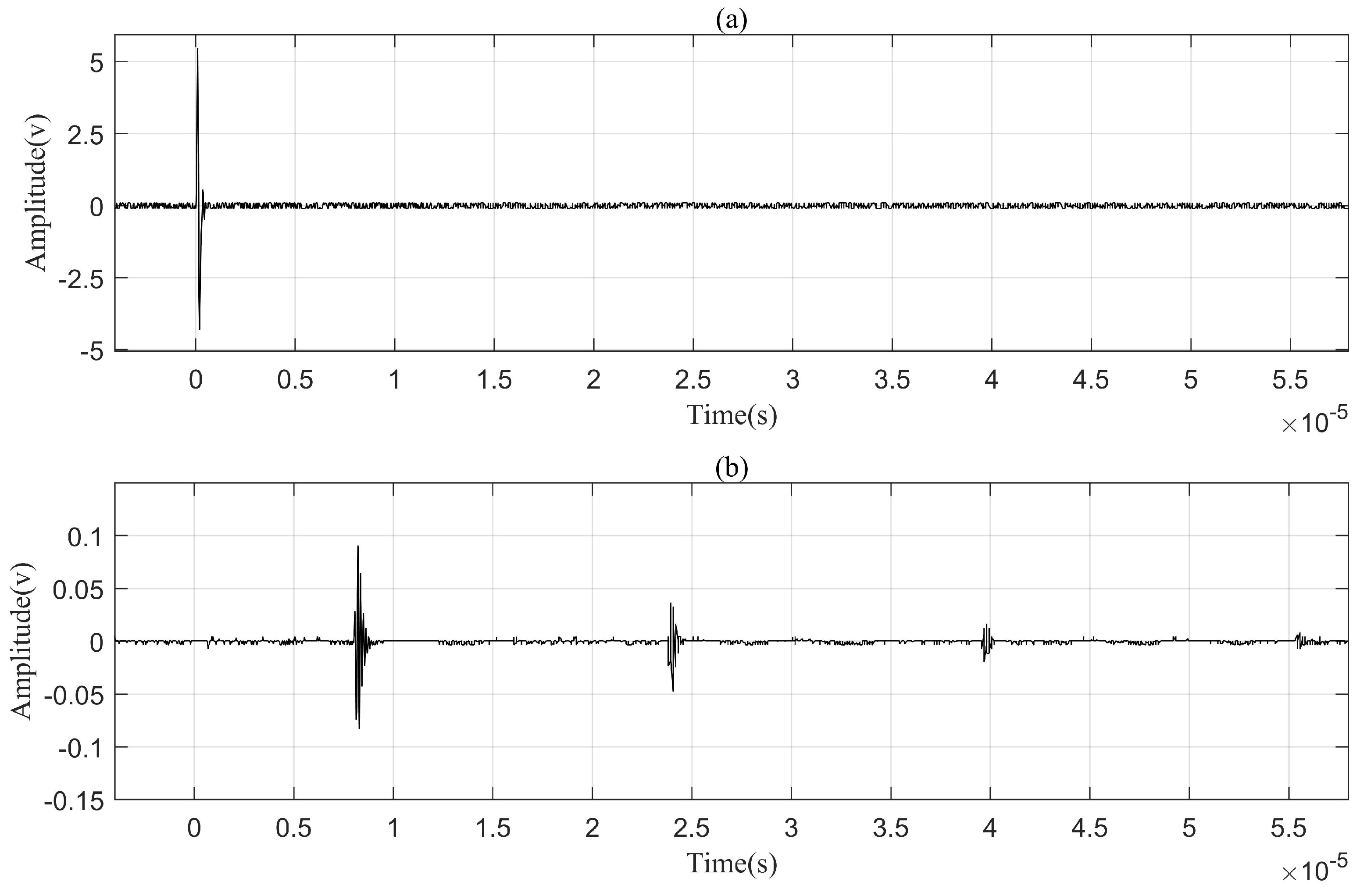




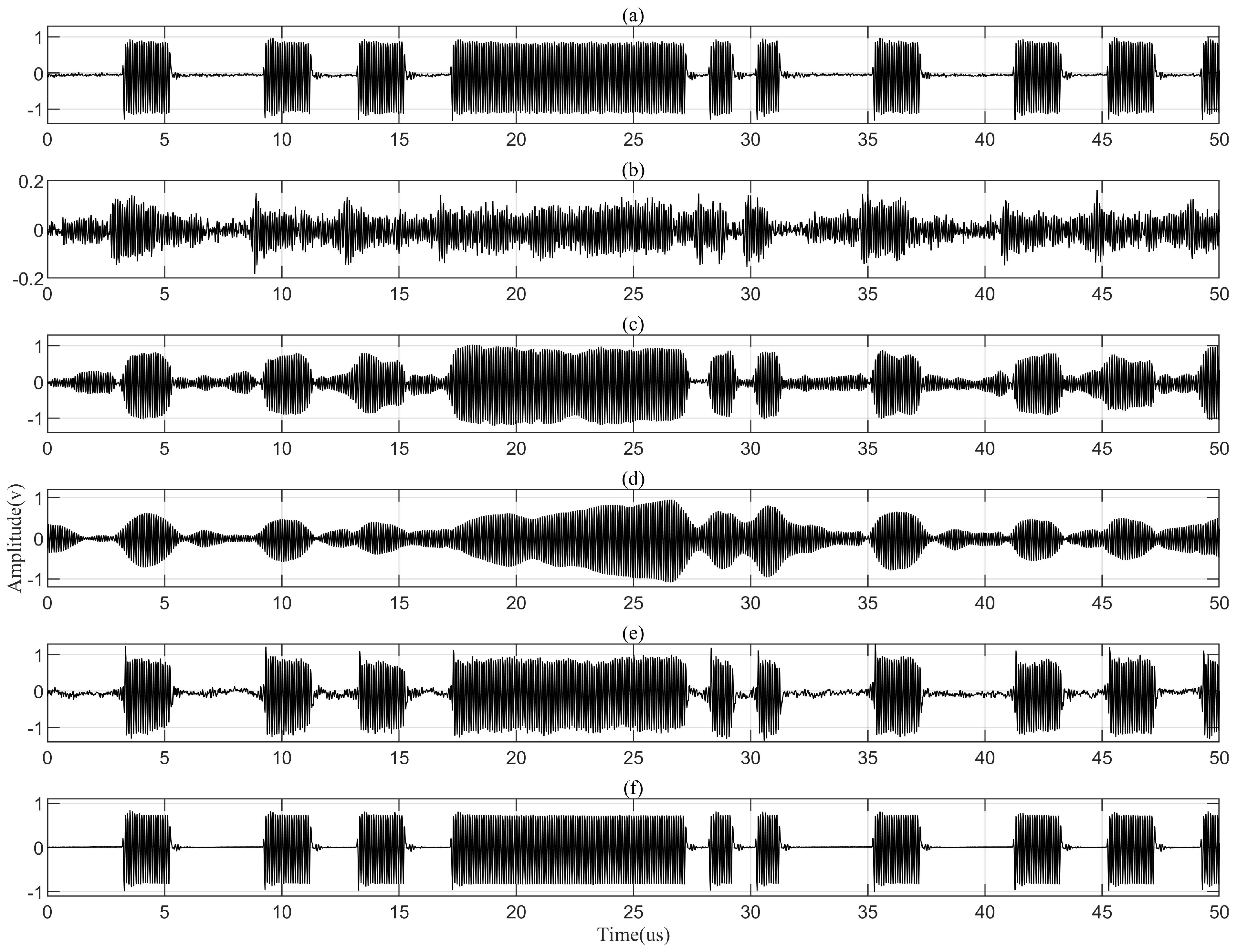

| Channel Length/mm | 30 | 40 | 50 | 50 | 50 | 50 | 60 |
| Offset Distance/mm | 0 | 0 | 0 | 6 | 12 | 18 | 0 |
| SNR/dB | 12.36 | 10.76 | 13.44 | 9.54 | 7.87 | 4.10 | 8.67 |
| Evaluation Index | ||||
|---|---|---|---|---|
| SNR (dB) | 9.331 | 14.112 | 5.974 | 29.437 |
| SISNR (dB) | 22.911 | 43.688 | 16.243 | 113.826 |
| NCC | 0.7533 | 0.8952 | 0.6391 | 0.9829 |
| BER | 5.593 × | 2.182 × | 3.742 × | 3.502 × |
| ERLE | 6.47 | 17.82 | 4.22 | 32.53 |
| Evaluation Index | Image without Echo Cancellation | Image with LMS Filter | Image with DPRNN Model |
|---|---|---|---|
| PSNR/dB | 11.8911 | 19.1776 | 24.8396 |
| SSIM | 0.4144 | 0.8911 | 0.9471 |
| 17.1429 | 5.6638 | 3.6256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Jiang, M.; Zhang, J.; Gu, M.; Cao, Z. Ultrasonic Through-Metal Communication Based on Deep-Learning-Assisted Echo Cancellation. Sensors 2024, 24, 2141. https://doi.org/10.3390/s24072141
Zhang J, Jiang M, Zhang J, Gu M, Cao Z. Ultrasonic Through-Metal Communication Based on Deep-Learning-Assisted Echo Cancellation. Sensors. 2024; 24(7):2141. https://doi.org/10.3390/s24072141
Chicago/Turabian StyleZhang, Jinya, Min Jiang, Jingyi Zhang, Mengchen Gu, and Ziping Cao. 2024. "Ultrasonic Through-Metal Communication Based on Deep-Learning-Assisted Echo Cancellation" Sensors 24, no. 7: 2141. https://doi.org/10.3390/s24072141
APA StyleZhang, J., Jiang, M., Zhang, J., Gu, M., & Cao, Z. (2024). Ultrasonic Through-Metal Communication Based on Deep-Learning-Assisted Echo Cancellation. Sensors, 24(7), 2141. https://doi.org/10.3390/s24072141






