An Effective Single-Station Cooperative Node Localization Technique Using Multipath Spatiotemporal Information
Abstract
:1. Introduction
- We propose a novel and sophisticated single-station passive positioning algorithm for estimating the locations of cooperative nodes. This algorithm first constructs virtual mirror observation points based on MPCs for target detection. Then, by matching spatiotemporal information according to energy characteristics, it acquires the optimal solution for the positioning function, thereby achieving precise target location estimation.
- This paper introduces a dual-antenna unambiguous direction-finding technique to acquire the spatial information of MPCs, using channel ratios in a manner similar to circular synthetic aperture radar (SAR). This approach eliminates the need for clock synchronization, avoids the requirement for antenna array configurations, and imposes no specific waveform constraints, while still accurately estimating the directions of multiple incoming waves.
- Simulations and experimental results demonstrate that the positioning system presented in this paper achieves a positioning error within 0.1 m, while providing a more streamlined, cost-effective, and compact hardware implementation that requires only two receiving antennas in the sensor configuration to achieve high-precision location estimation of collaborative nodes. As a result, it sheds light on a more practical and versatile approach for real-world positioning applications.
2. System Method
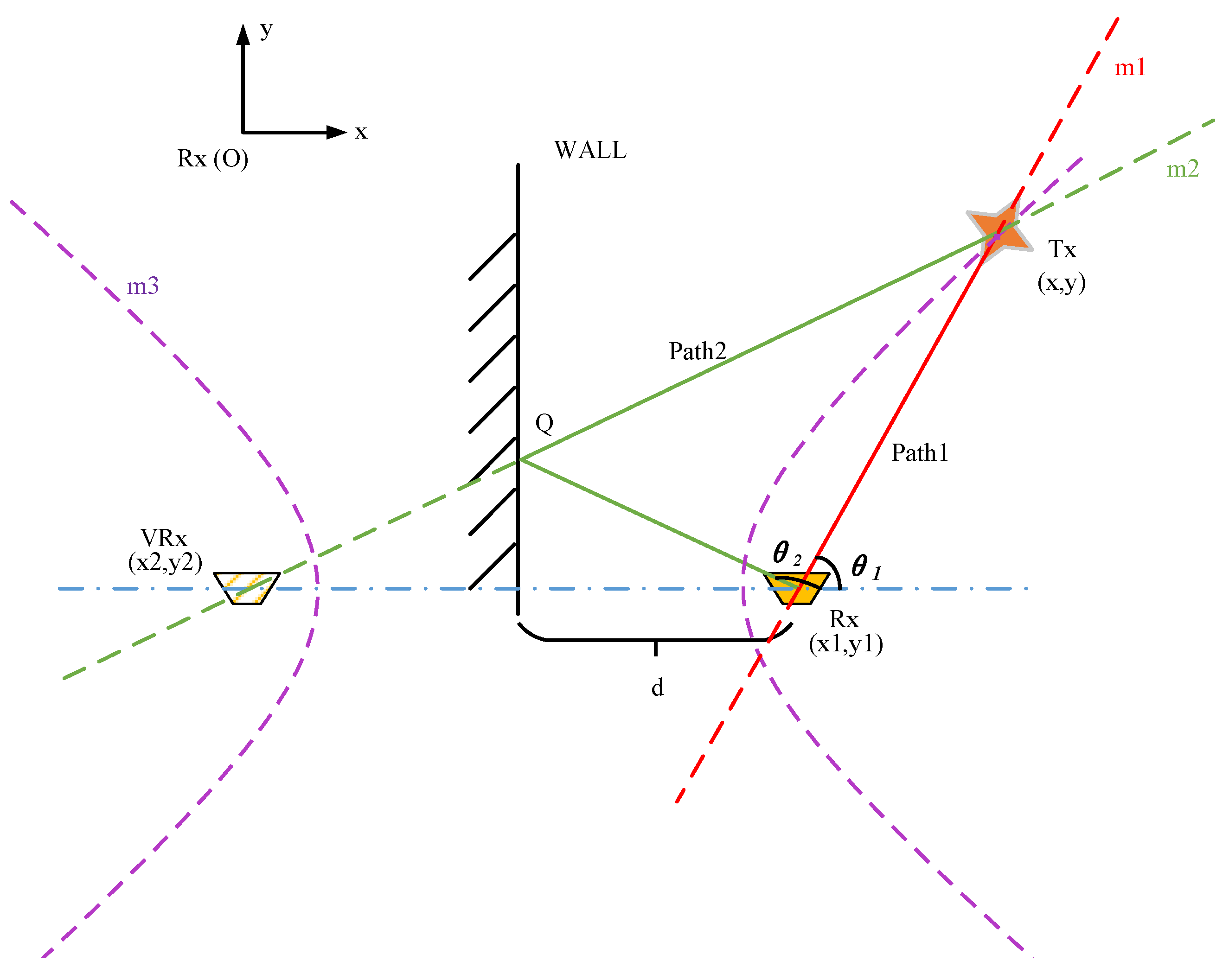
2.1. Mathematical Model
2.2. Model Solution
2.3. Extraction of Spatial Information Based on MPCs
| Algorithm 1: Extraction of Spatial Information Based on MPCs | ||
| Input: data files, each containing sample points of I/Q data from both moving and stationary antennas at - different angular position. | ||
| Output: A file with spatial angles and corresponding power values . | ||
| 1. | for each data file do | |
| 2. | Read the file to extract the angular position and corresponding I/Q samples from both the moving antenna reception and the stationary antenna reception . | |
| 3. | Store as the and , as the in the mapping table . | |
| 4. | end | |
| 5. | for each in do | |
| 6. | Extract the data and for sample points, respectively. | |
| 7. | Compute the ratio of to and store the result in the updated mapping table , with the calculation of performed as follows: | |
| . | ||
| 8. | end | |
| 9. | for , with a step size of do | |
| 10. | for each in do | |
| 11. | Calculate the received power at spatial angle based on Equation (16). | |
| 12. | end | |
| 13. | Store the current angle in the array , and the corresponding power in the array . | |
| 14. | end | |
| 15. | Save the arrays and as a file for further analysis. | |
2.4. Complete Procedure Analysis
| Algorithm 2: An Effective Single-Station Cooperative Node Localization Technique Using Multipath Spatiotemporal Information | |
| Input: data files, each containing sample points of I/Q data from both moving and stationary antennas at - different angular position; The transmitted waveform of the cooperative target . | |
| Output: Estimated coordinates of . | |
| 1. | Execute Algorithm 1 to extract a file containing spatial angles and corresponding power values based on the input data files. |
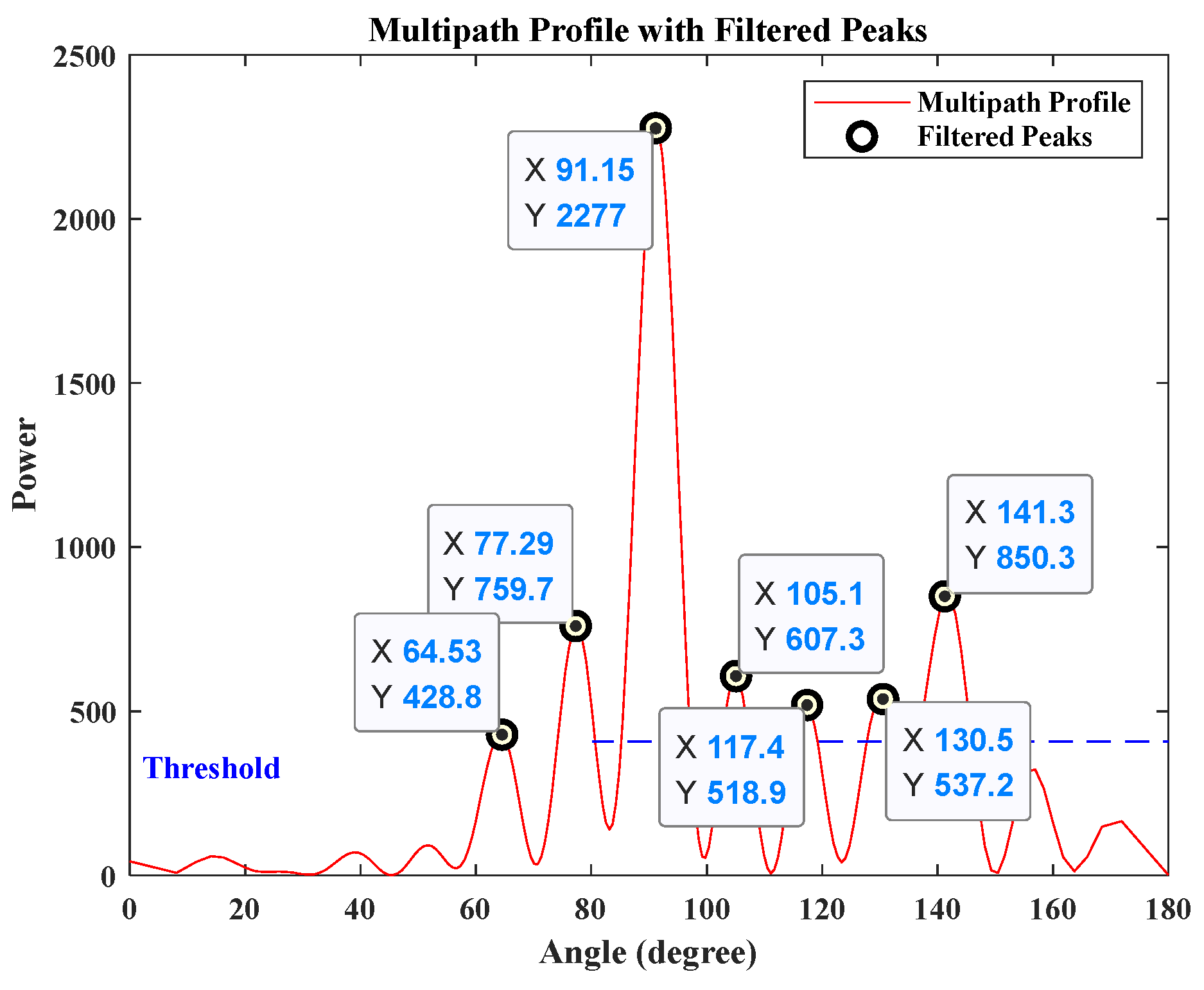
| 2. | Load the file to obtain the spatial spectrum and identify the direct path arrival angle and potential values for the reflected path arrival angle based on a predefined threshold. |
| 3. | Calculate the possible coordinates of according to Equation (4). |
| 4. | Perform matched filtering on the stationary antenna’s received data with the transmitted waveform to obtain the time-domain energy distribution. |
| 5. | Determine the direct path delay and possible values for the delay differences between the reflected and main path based on a predefined threshold. |
| 6. | Match the candidate coordinates derived from spatial analysis with the corresponding time delay differences obtained through temporal analysis based on energy. |
| 7. | Compute the coordinates of as specified in Equation (14). |
3. Experiments and Discussions
3.1. Simulation Experiment
3.1.1. Feasibility Analysis
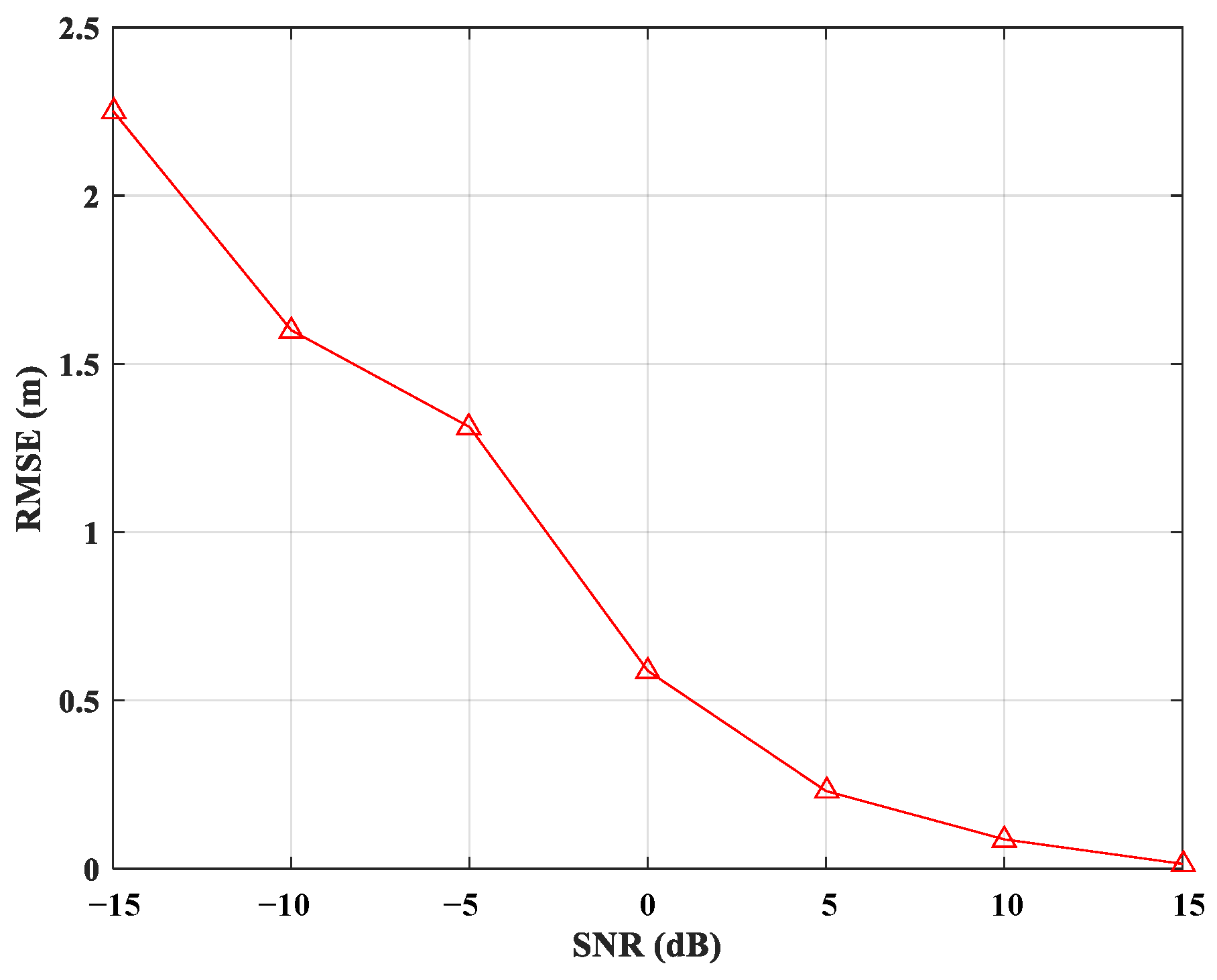
3.1.2. Influencing Factors Analysis
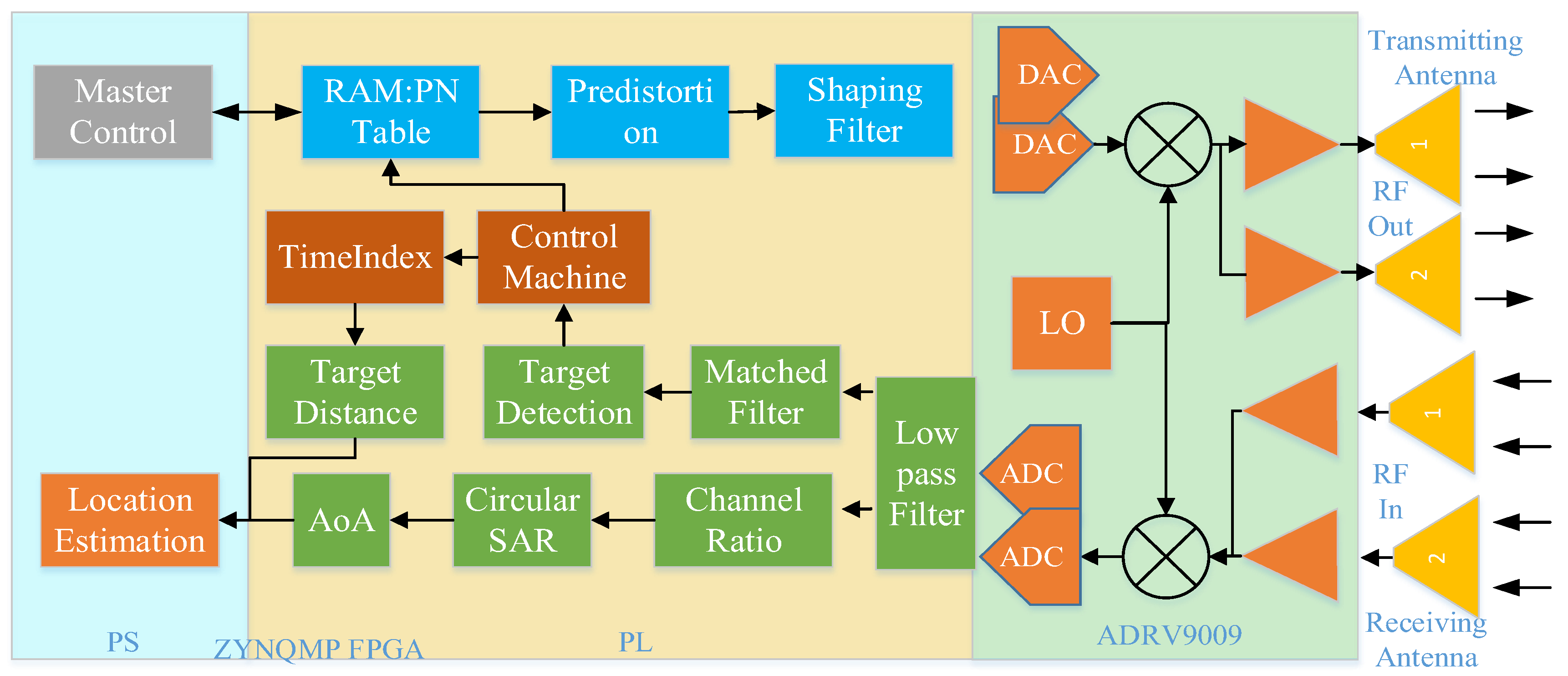
3.2. System Design
3.3. Anechoic Chamber Scenario Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nawaz, H.; Tahir, A.; Ahmed, N.; Fayyaz, U.U.; Mahmood, T.; Jaleel, A.; Gogate, M.; Dashtipour, K.; Masud, U.; Abbasi, Q. Ultra-Low-Power, High-Accuracy 434 MHz Indoor Positioning System for Smart Homes Leveraging Machine Learning Models. Entropy 2021, 23, 1401. [Google Scholar] [CrossRef] [PubMed]
- Tomic, S.; Beko, M.; Camarinha-Matos, L.M.; Oliveira, L.B. Distributed Localization with Complemented RSS and AOA Measurements: Theory and Methods. Appl. Sci. 2020, 10, 272. [Google Scholar] [CrossRef]
- Săcăleanu, D.-I.; Matache, M.-G.; Roșu, Ș.-G.; Florea, B.-C.; Manciu, I.-P.; Perișoară, L.-A. IoT-Enhanced Decision Support System for Real-Time Greenhouse Microclimate Monitoring and Control. Technologies 2024, 12, 230. [Google Scholar] [CrossRef]
- Mutalemwa, L.C.; Shin, S. Achieving Source Location Privacy Protection in Monitoring Wireless Sensor Networks through Proxy Node Routing. Sensors 2019, 19, 1037. [Google Scholar] [CrossRef] [PubMed]
- Nantogma, S.; Ran, W.; Liu, P.; Yu, Z.; Xu, Y. Immunized Token-Based Approach for Autonomous Deployment of Multiple Mobile Robots in Burnt Area. Remote Sens. 2021, 13, 4135. [Google Scholar] [CrossRef]
- Shahzad, F.; Sheltami, T.R.; Shakshuki, E.M. DV-maxHop: A fast and accurate range-free localization algorithm for anisotropic wireless networks. IEEE Trans. Mob. Comput. 2017, 16, 2494–2505. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Ma, K.; Xu, L. A Cooperative Relative Localization System for Distributed Multi-Agent Networks. IEEE Trans. Veh. Technol. 2023, 72, 14828–14843. [Google Scholar] [CrossRef]
- Ruan, L.; Li, G.; Dai, W.; Tian, S. Cooperative Relative Localization for UAV Swarm in GNSS-Denied Environment: A Coalition Formation Game Approach. IEEE Internet Things J. 2022, 9, 11560–11577. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Shen, Y. Cooperative tracking by multi-agent systems using signals of opportunity. IEEE Trans. Commun. 2020, 68, 93–105. [Google Scholar] [CrossRef]
- Liu, J.; Hu, G. Relative Localization Estimation for Multiple Robots via the Rotating Ultra-Wideband Tag. IEEE Robot. Autom. Lett. 2023, 8, 4187–4194. [Google Scholar] [CrossRef]
- Cai, Y.; Shen, Y. An integrated localization and control framework for multi-agent formation. IEEE Trans. Signal Process. 2019, 67, 1941–1956. [Google Scholar] [CrossRef]
- Li, X.; Ma, K.; Wang, J.; Shen, Y. An integrated design of cooperative localization and motion control. In Proceedings of the 2019 IEEE International Conference on Communications, Shanghai, China, 20–24 May 2019. [Google Scholar] [CrossRef]
- Lei, Z.; Yang, K.; Ma, Y. Passive localization in the deep ocean based on cross-correlation function matching. J. Acoust. Soc. Am. 2016, 139, 196–201. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.-H.; Oh, C.-H. RSS-based cooperative localization algorithm using virtual reference node in wireless sensor networks. In Proceedings of the 2009 11th International Conference on Advanced Communication Technology, Gangwon, Republic of Korea, 15–18 February 2009. [Google Scholar]
- Wang, S.; Jiang, X.; Wymeersch, H. Cooperative Localization in Wireless Sensor Networks with AOA Measurements. IEEE Trans. Wirel. Commun. 2022, 21, 6760–6773. [Google Scholar] [CrossRef]
- Chen, H.; Wang, G.; Wu, X. Cooperative Multiple Target Nodes Localization Using TOA in Mixed LOS/NLOS Environments. IEEE Sens. J. 2020, 20, 1473–1484. [Google Scholar] [CrossRef]
- Al-Qahtani, K.M.; Al-Ahmari, A.S.; Muqaibel, A.H. Improved residual weighting for NLOS mitigation in TDOA-based UWB positioning systems. In Proceedings of the 2014 21st International Conference on Telecommunications, Lisbon, Portugal, 4–7 May 2014. [Google Scholar] [CrossRef]
- Bar-Shalom, O.; Weiss, A.J. Transponder-Aided Single Platform Geolocation. IEEE Trans. Signal Process. 2013, 61, 1239–1248. [Google Scholar] [CrossRef]
- Sun, X.; Gao, X.; Li, G.Y.; Han, W. Single-Site Localization Based on a New Type of Fingerprint for Massive MIMO-OFDM Systems. IEEE Trans. Veh. Technol. 2018, 67, 6134–6145. [Google Scholar] [CrossRef]
- Zhou, Z.; Xiao, Z.; Zeng, Y. Single-BS Simultaneous Environment Sensing and UE Localization Without LoS Path by Exploiting Near-Field Scatterers. IEEE Commun. Lett. 2024, 28, 2071–2075. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Wu, L.; Dang, J.; Liu, P. 5G Communication Signal Based Localization with a Single Base Station. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference, Victoria, BC, Canada, 18 November–16 December 2020. [Google Scholar] [CrossRef]
- Liang, J.; He, J.; Yu, W.; Truong, T.-K. Single-Site 3-D Positioning in Multipath Environments Using DOA-Delay Measurements. IEEE Commun. Lett. 2021, 25, 2559–2563. [Google Scholar] [CrossRef]
- Jespersen, M.H.; Serup, D.E.; Nielsen, M.H.; Hannesbo, M.H. An indoor multipath-assisted single-anchor UWB localization method. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium, Chengdu, China, 6–10 May 2018. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Liu, Y.; Wu, L.; Zhang, Z.; Dang, J. Multi-RIS-assisted Millimeter Wave Single Base Station Localization. In Proceedings of the 2023 4th Information Communication Technologies Conference, Nanjing, China, 17–19 May 2023. [Google Scholar] [CrossRef]
- IEEE 802.15.4a; IEEE Standard for Local and Metropolitan Area Networks—Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs)—Physical Layer (PHY) Specifications for Ultra Wideband (UWB). IEEE: New York, USA, 2007. [CrossRef]
- Philips, D.R.; Salami, E.; Ramiah, H.; Kanesan, J. Location Accuracy Optimization in Bluetooth Low Energy (BLE) 5.1-Based Indoor Positioning System (IPS)—A Machine Learning Approach. IEEE Access 2023, 11, 140186–140201. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, Y. Research on Interferometer Direction Finding Technology Based on Digital Beam forming. In Proceedings of the 2022 7th International Conference on Signal and Image Processing, Suzhou, China, 20–22 July 2022. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, J.-K.; Ryu, H.-K.; Park, Y.-J. Multiple Array Spacings for an Interferometer Direction Finder with High Direction-Finding Accuracy in a Wide Range of Frequencies. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 563–566. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Q.; Lu, W.; Lv, Z.; Lin, B.; Dong, N. An Efficient Phase Interferometer Direction-Finding Algorithm Based on Circular Array. In Proceedings of the 2023 IEEE 6th International Conference on Computer and Communication Engineering Technology, Beijing, China, 4–6 August 2023. [Google Scholar] [CrossRef]
- Aswathi, P.; Mathew, M.R.; Krishna, D.D.; Krishna, P.M. Direction Finding by Time Modulated Linear Antenna Arrays Using Root-MUSIC Algorithm. In Proceedings of the 2024 IEEE Wireless Antenna and Microwave Symposium, Visakhapatnam, India, 29 February–3 March 2024. [Google Scholar] [CrossRef]
- Peshkov, I.W.; Zaitseva, I.N.; Nechaev, Y.B. The Estimation of Radio Direction-Finding Performance in volume Antenna Arrays with Directive Radiators by Music Method. In Proceedings of the 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications, Minsk, Belarus, 4–5 July 2018. [Google Scholar] [CrossRef]
- Shu, Q.; Wang, Y.; Li, H.; Li, Z. Design of Software Radio Direction Finding System Based on an Improved MUSIC Algorithm. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication, Dalian, China, 19–21 December 2017. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Zhang, Z. Joint 2D-DOD, 2D-DOA, and Polarization Angles Estimation for Bistatic EMVS-MIMO Radar via PARAFAC Analysis. IEEE Trans. Veh. Technol. 2020, 69, 1626–1638. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F.; He, J.; Truong, T.-K. EMVS-MIMO Radar With Sparse Rx Geometry: Tensor Modeling and 2-D Direction Finding. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8062–8075. [Google Scholar] [CrossRef]
- Wang, J.; Katabi, D. Dude, Where’s My Card?: RFID Positioning That Works with Multipath and Non-line of Sight. In Proceedings of the ACM SIGCOMM 2013 conference on SIGCOMM, Hong Kong, China, 12–16 August 2013. [Google Scholar] [CrossRef]








| Reference | Technique | Research Findings | Challenges |
|---|---|---|---|
| [18] | Maximum likelihood algorithm with multiple transponders assistance | Single-step processing without explicit estimation of TOA/TDOA or AOA | Requirement for multi-antenna array configuration and higher computational complexity |
| [19] | Fingerprint matching based on hybrid AOA/PDP | Reduced matching complexity, search latency, and storage overhead, with enhanced accuracy | Requires complex matrix operations and multi-antenna access points |
| [20] | Exploiting near-field effects of XL arrays | Achieve superior accuracy and robustness with similar complexity compared with benchmark methods | Similarly demand advanced matrix decomposition and large-scale antenna arrays |
| [21] | Hybrid AOA/TOA method leveraging 5G signals | Improved positioning accuracy | Require time and frequency synchronization, along with spatial spectrum computation and multi-antenna configuration. |
| Proposed work in this paper | AOA/TDOA hybrid method based on multipath | Require only two antennas, with no complex calculations or time/frequency synchronization, while maintaining high accuracy | Future work will optimize this proposed approach for high-accuracy localization in complex, NLOS environments |
| Reference | Computational Complexity | Notes |
|---|---|---|
| [18] | : number of passive transponders | |
| [19] | : number of OFDM symbols : number of subcarriers : number of antennas : number of grids searched | |
| [20] | : maximum delay compensation : number of antennas : length of the cyclic prefix (in sampling points) : total number of reference points | |
| Proposed method in this paper | : number of angular positions : number of samples at each position |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, D.; Li, X.; Zhou, L.; Yang, C.; Cui, Y.; Bai, L.; Chen, Y. An Effective Single-Station Cooperative Node Localization Technique Using Multipath Spatiotemporal Information. Sensors 2025, 25, 631. https://doi.org/10.3390/s25030631
Bai D, Li X, Zhou L, Yang C, Cui Y, Bai L, Chen Y. An Effective Single-Station Cooperative Node Localization Technique Using Multipath Spatiotemporal Information. Sensors. 2025; 25(3):631. https://doi.org/10.3390/s25030631
Chicago/Turabian StyleBai, Di, Xinran Li, Lingyun Zhou, Chunyong Yang, Yongqiang Cui, Liyun Bai, and Yunhao Chen. 2025. "An Effective Single-Station Cooperative Node Localization Technique Using Multipath Spatiotemporal Information" Sensors 25, no. 3: 631. https://doi.org/10.3390/s25030631
APA StyleBai, D., Li, X., Zhou, L., Yang, C., Cui, Y., Bai, L., & Chen, Y. (2025). An Effective Single-Station Cooperative Node Localization Technique Using Multipath Spatiotemporal Information. Sensors, 25(3), 631. https://doi.org/10.3390/s25030631






