Laterally Excited Bulk Acoustic Wave Resonators with Rotated Electrodes Using X-Cut LiNbO3 Thin-Film Substrates
Abstract
1. Introduction
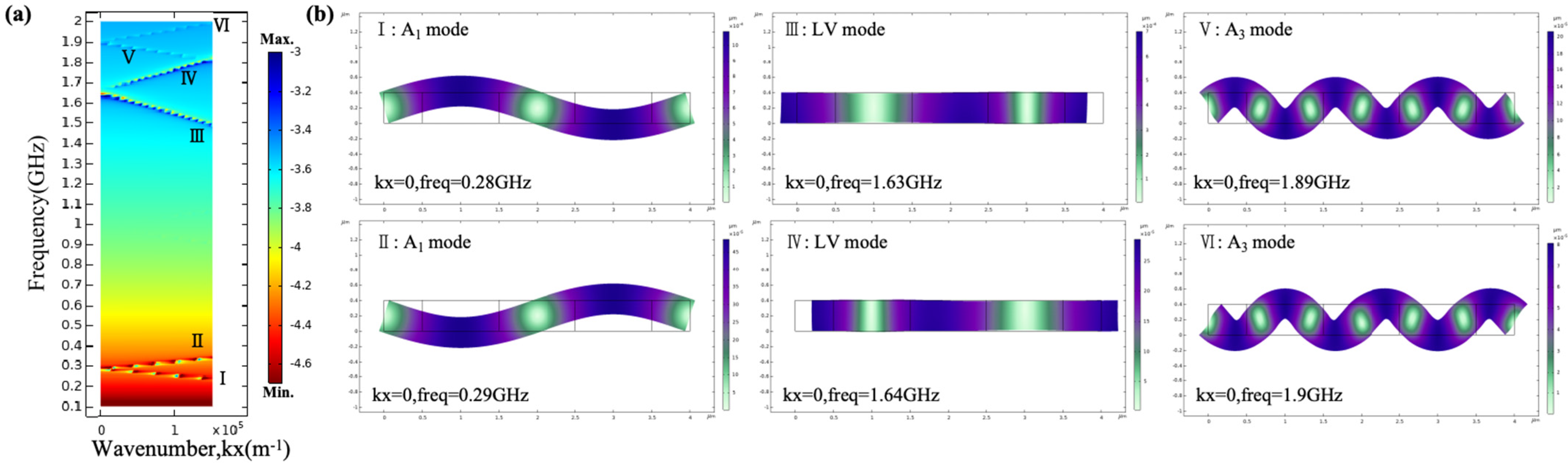
2. Modeling and Simulation
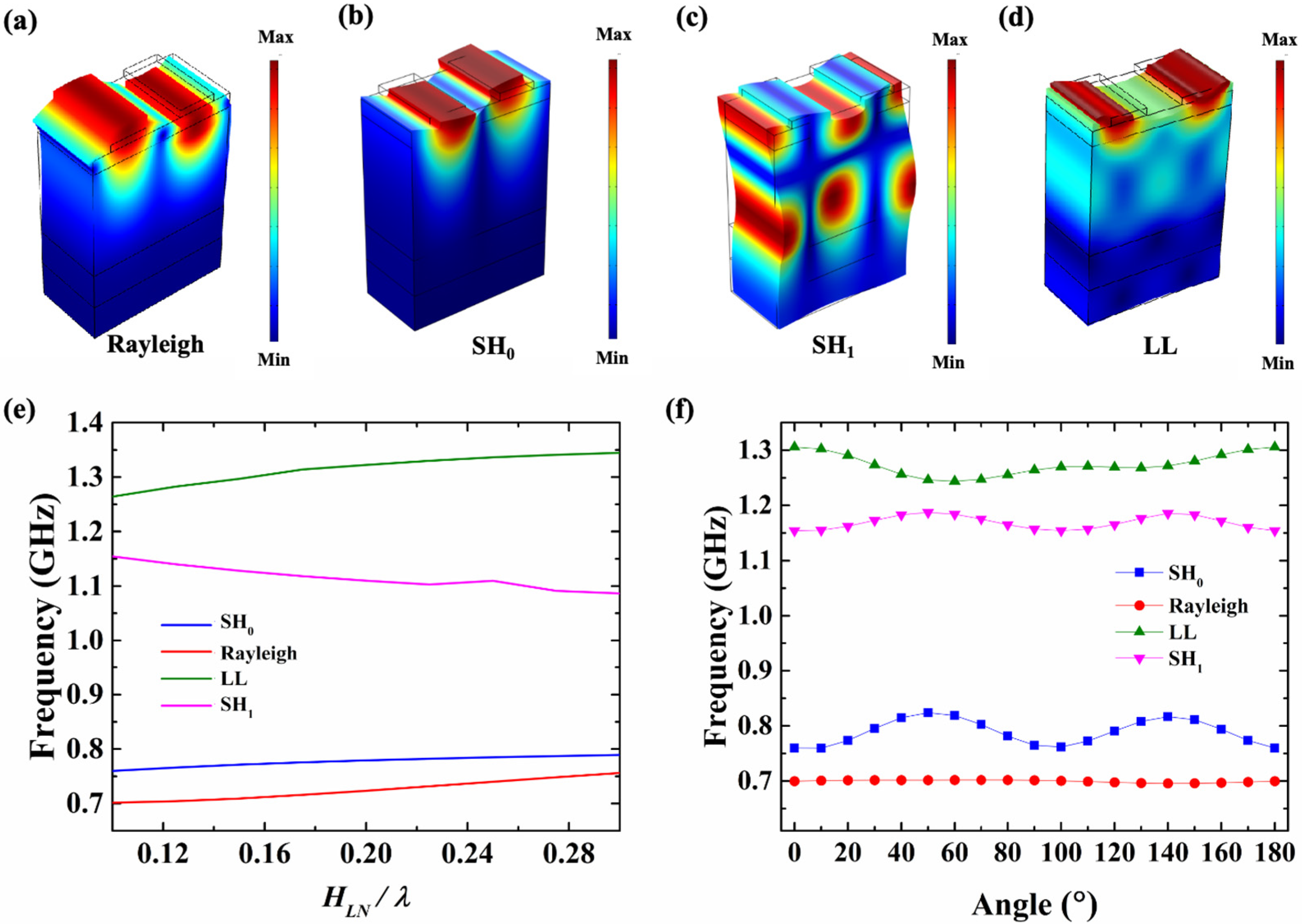
2.1. Device Modeling
2.2. Analysis of Rotation Angle
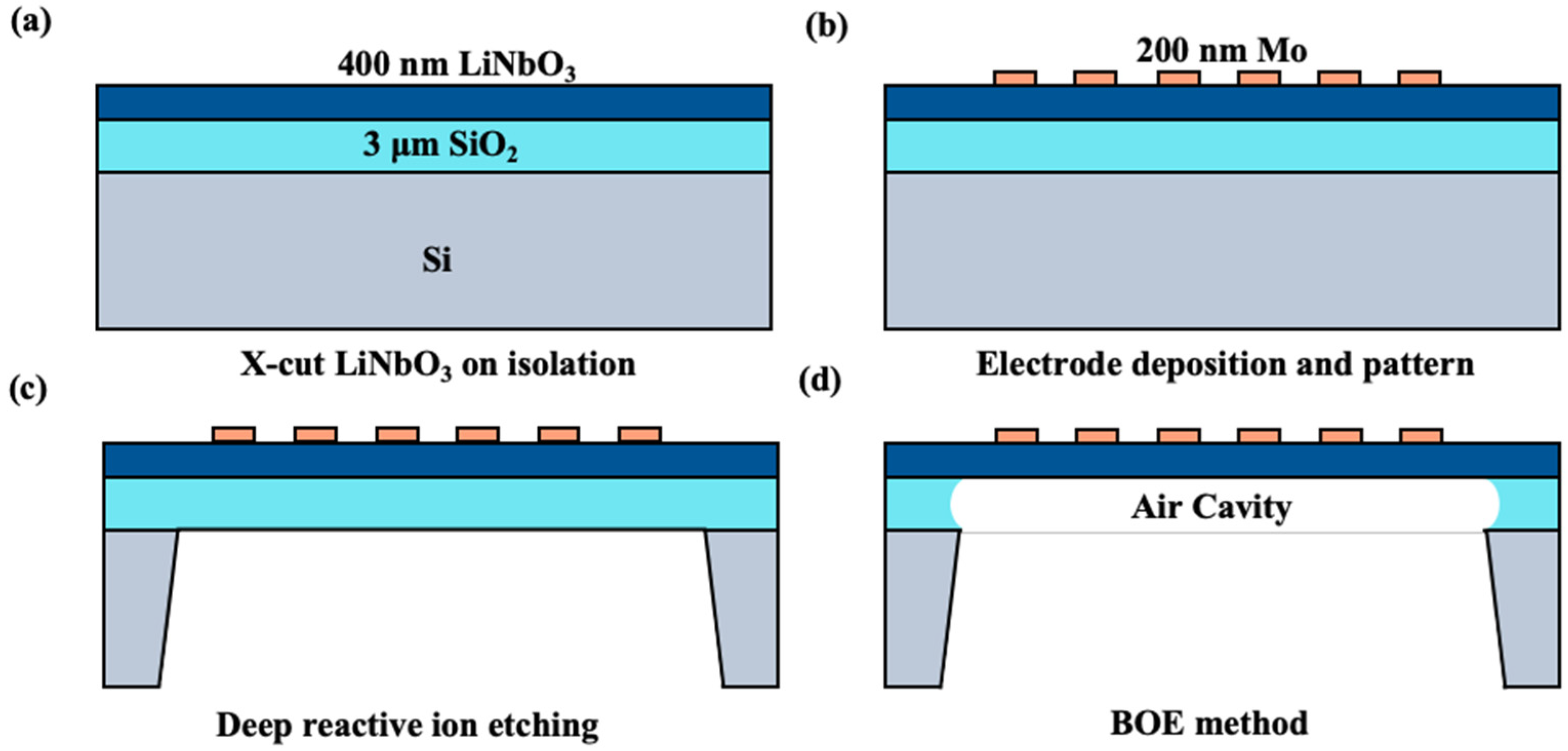
3. Fabrication and Characterization
3.1. Impedance Curve and MBVD Model Fitting
3.2. Impact of Rotation Angle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Branch, D.W.; Jensen, D.S.; Nordquist, C.D.; Siddiqui, A.; Douglas, J.K.; Eichenfield, M.; Friedmann, T.A. Investigation of a Solid-State Tuning Behavior in Lithium Niobate. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 67, 365–373. [Google Scholar] [CrossRef] [PubMed]
- Kadota, M.; Ogami, T.; Yamamoto, K.; Tochishita, H.; Negoro, Y. High-frequency lamb wave device composed of MEMS structure using LiNbO3 thin film and air gap. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2564–2571. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Omura, M.; Kishimoto, Y.; Hashimoto, K. Comparative Study of Acoustic Wave Devices Using Thin Piezoelectric Plates in the 3-5-GHz Range. IEEE Trans. Microw. Theory Tech. 2019, 67, 915–921. [Google Scholar] [CrossRef]
- Xu, H.; Fu, S.; Shen, J.; Su, R.; Li, H.; Zeng, F.; Song, C.; Wang, W.; Pan, F. Enlarging Rayleigh Elimination Window through Modulating Substrate and LiNbO3 Cut Angle for Fabricating LNOI-Based Spurious-Free Wideband SAW Filters. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022. [Google Scholar]
- Pirro, M.; Colombo, L.; Michetti, G.; Piazza, G.; Rinaldi, M. X-cut LiNbO3 Coupled Resonators for Narrow-band Filtering Applications. In Proceedings of the 2020 Joint Conference of the IEEE International Frequency Control Symposium and International Symposium on Applications of Ferroelectrics (IFCS-ISAF), Keystone, CO, USA, 19–23 July 2020. [Google Scholar]
- Bousquet, M.; Borel, E.; Joulie, A.; Perreau, P.; Soulat, E.; Maeder-Pachurka, C.; Delaguillaumie, F.; Castellan, G.; Enyedi, G.; Delprato, J.; et al. LiNbO3 Film Bulk Acoustic Resonator for n79 band. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022. [Google Scholar]
- Xu, H.; Fu, S.; Su, R.; Liu, P.; Zhang, S.; Lu, Z.; Xiao, B.; Wang, R.; Song, C.; Zeng, F.; et al. SAW Filters on LiNbO3/SiC Heterostructure for 5G n77 and n78 Band Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 1157–1169. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhang, S.; Wu, J.; Zheng, P.; Zhang, L.; Xu, H.; An, Z.; You, T.; Ou, X. Ultrawide-Band SAW Devices Using SH0 Mode Wave with Increased Velocity for 5G Front-Ends. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021. [Google Scholar]
- Su, R.; Fu, S.; Shen, J.; Lu, Z.; Xu, H.; Wang, R.; Song, C.; Zeng, F.; Wang, W.; Pan, F. Wideband Surface Acoustic Wave Filter at 3.7 GHz with Spurious Mode Mitigation. IEEE Trans. Microw. Theory Tech. 2023, 71, 480–487. [Google Scholar] [CrossRef]
- Song, Y.H.; Gong, S. Wideband Spurious-Free Lithium Niobate RF-MEMS Filters. J. Microelectromech. Syst. 2017, 26, 820–828. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Xu, H.; Fu, S.; Shen, J.; Lu, Z.; Su, R.; Wang, R.; Song, C.; Zeng, F.; Wang, W.; Pan, F. Large-Range Spurious Mode Elimination for Wideband SAW Filters on LiNbO3/SiO2/Si Platform by LiNbO3 Cut Angle Modulation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3117–3125. [Google Scholar] [CrossRef] [PubMed]
- Hsu, T.H.; Tseng, K.J.; Li, M.H. Thin-film lithium niobate-on-insulator (LNOI) shear horizontal surface acoustic wave resonators. J. Micromech. Microeng. 2021, 31, 054003. [Google Scholar] [CrossRef]
- Asakawa, S.; Mizuno, J.; Hayashi, J.; Suzuki, M.; Kakio, S.; Tezuka, A.; Kuwae, H.; Yokota, H.; Yonai, T.; Kishida, K. Analysis of Longitudinal Leaky SAW on LiNbO3 Thin Plate/Amorphous Layer/Quartz Structure. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019. [Google Scholar]
- Yang, Y.; Gao, A.; Lu, R.; Gong, S. 5 GHz lithium niobate MEMS resonators with high FoM of 153. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017. [Google Scholar]
- Yang, K.; Lin, F.; Fang, J.; Chen, J.; Tao, H.; Sun, H.; Zuo, C. Nanosheet Lithium Niobate Acoustic Resonator for mmWave Frequencies. IEEE Electron Device Lett. 2024, 45, 272–275. [Google Scholar] [CrossRef]
- Bousquet, M.; Enyedi, G.; Dechamp, J.; Zussy, M.; Kuisseu, P.S.P.; Mazen, F.; Billard, C.; Reinhardt, A.; Bertucchi, M.; Perreau, P.; et al. Single-mode high frequency LiNbO3 Film Bulk Acoustic Resonator. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019. [Google Scholar]
- Song, Y.H.; Gong, S. Arraying SH0 Lithium Niobate laterally vibrating resonators for mitigation of higher order spurious modes. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016. [Google Scholar]
- Plessky, V.P.; Koskela, J.; Yandrapalli, S. Crystalline Y-cut Lithium Niobate Layers for the Bulk Acoustic Wave Resonator (YBAR). In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020. [Google Scholar]
- Gong, S.; Piazza, G. Design and Analysis of Lithium–Niobate-Based High Electromechanical Coupling RF-MEMS Resonators for Wideband Filtering. IEEE Trans. Microw. Theory Tech. 2013, 61, 403–414. [Google Scholar] [CrossRef]
- Lu, R.; Yang, Y.; Link, S.; Gong, S. A1 Resonators in 128° Y-cut Lithium Niobate with Electromechanical Coupling of 46.4%. J. Microelectromech. Syst. 2020, 29, 313–319. [Google Scholar] [CrossRef]
- Plessky, V.; Yandrapalli, S.; Turner, P.J.; Villanueva, L.G.; Koskela, J.; Faizan, M.; Pastina, A.D.; Garcia, B.; Costa, J.; Hammond, R.B. Laterally excited bulk wave resonators (XBARs) based on thin Lithium Niobate platelet for 5GHz and 13 GHz filters. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019. [Google Scholar]
- Yandrapalli, S.; Eroglu SE, K.; Plessky, V.; Atakan, H.B.; Villanueva, L.G. Study of Thin Film LiNbO3 Laterally Excited Bulk Acoustic Resonators. J. Microelectromech. Syst. 2022, 31, 217–225. [Google Scholar] [CrossRef]
- Wen, Z.; Liu, W.; Luo, T.; Tong, X.; Xie, Y.; Gu, X.; Liu, Y.; Cai, Y.; Guo, S.; Wang, J.; et al. A laterally excited bulk acoustic resonator with scattering vias in electrodes. Appl. Phys. Lett. 2023, 123, 093501. [Google Scholar] [CrossRef]
- Li, T.; Du, B.; Zhong, H.; Wang, H. Large Coupling Surface Acoustic Wave Resonator Based on SiO2/5°Y-X LiNbO3 Structure. In Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Guangzhou, China, 27–29 November 2022. [Google Scholar]
- Zhang, S.; Lu, R.; Zhou, H.; Link, S.; Yang, Y.; Li, Z.; Huang, K.; Ou, X.; Gong, S. Surface Acoustic Wave Devices Using Lithium Niobate on Silicon Carbide. IEEE Trans. Microw. Theory Tech. 2020, 68, 3653–3666. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Wu, J.; Zheng, P.; Yao, H.; Chen, Y.; Huang, K.; Zhao, X.; Zhou, M.; Ou, X. 3D Hybrid Acoustic Resonator with Coupled Frequency Responses of Surface Acoustic Wave and Bulk Acoustic Wave. In Proceedings of the 2023 IEEE 36th International Conference on Micro Electro Mechanical Systems (MEMS), Munich, Germany, 15–19 January 2023. [Google Scholar]
- Feld, D.A.; Parker, R.; Ruby, R.; Bradley, P.; Dong, S. After 60 years: A new formula for computing quality factor is warranted. In Proceedings of the 2008 IEEE Ultrasonics Symposium, Beijing, China, 2–5 November 2008. [Google Scholar]
- Su, R.; Fu, S.; Xu, H.; Lu, Z.; Liu, P.; Xiao, B.; Wang, R.; Zeng, F.; Song, C.; Wang, W.; et al. 5.9 GHz Longitudinal Leaky SAW Filter with FBW of 9.2% and IL of 1.8 dB Using LN/Quartz Structure. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 1434–1437. [Google Scholar] [CrossRef]
- Lee, Z.Q.; Hsu, T.H.; Tsai, C.H.; Lin, C.C.; Yu, Y.C.; Tung, S.S.; Li, M.H. L-Band LiNbO3/SiO2/Sapphire Longitudinal Leaky Saw (LLSAW) Resonators with High Figure of Merit. In Proceedings of the 2024 IEEE 37th International Conference on Micro Electro Mechanical Systems (MEMS), Austin, TX, USA, 21–25 January 2024. [Google Scholar]
- Su, R.; Shen, J.; Lu, Z.; Xu, H.; Niu, Q.; Xu, Z.; Zeng, F.; Song, C.; Wang, W.; Fu, S.; et al. Wideband and Low-Loss Surface Acoustic Wave Filter Based on 15° YX-LiNbO3/SiO2/Si Structure. IEEE Electron Device Lett. 2021, 42, 438–441. [Google Scholar] [CrossRef]
- Colombo, L.; Kochhar, A.; Vidal-Álvarez, G.; Simeoni, P.; Soysal, U.; Piazza, G. Sub-GHz X-Cut Lithium Niobate S0 Mode MEMS Resonators. J. Microelectromech. Syst. 2022, 31, 888–900. [Google Scholar] [CrossRef]
- Rosenbaum, J.F. Bulk Acoustic Wave Theory and Devices. 1988. Available online: https://cir.nii.ac.jp/crid/1130000795964581760 (accessed on 5 March 2025).




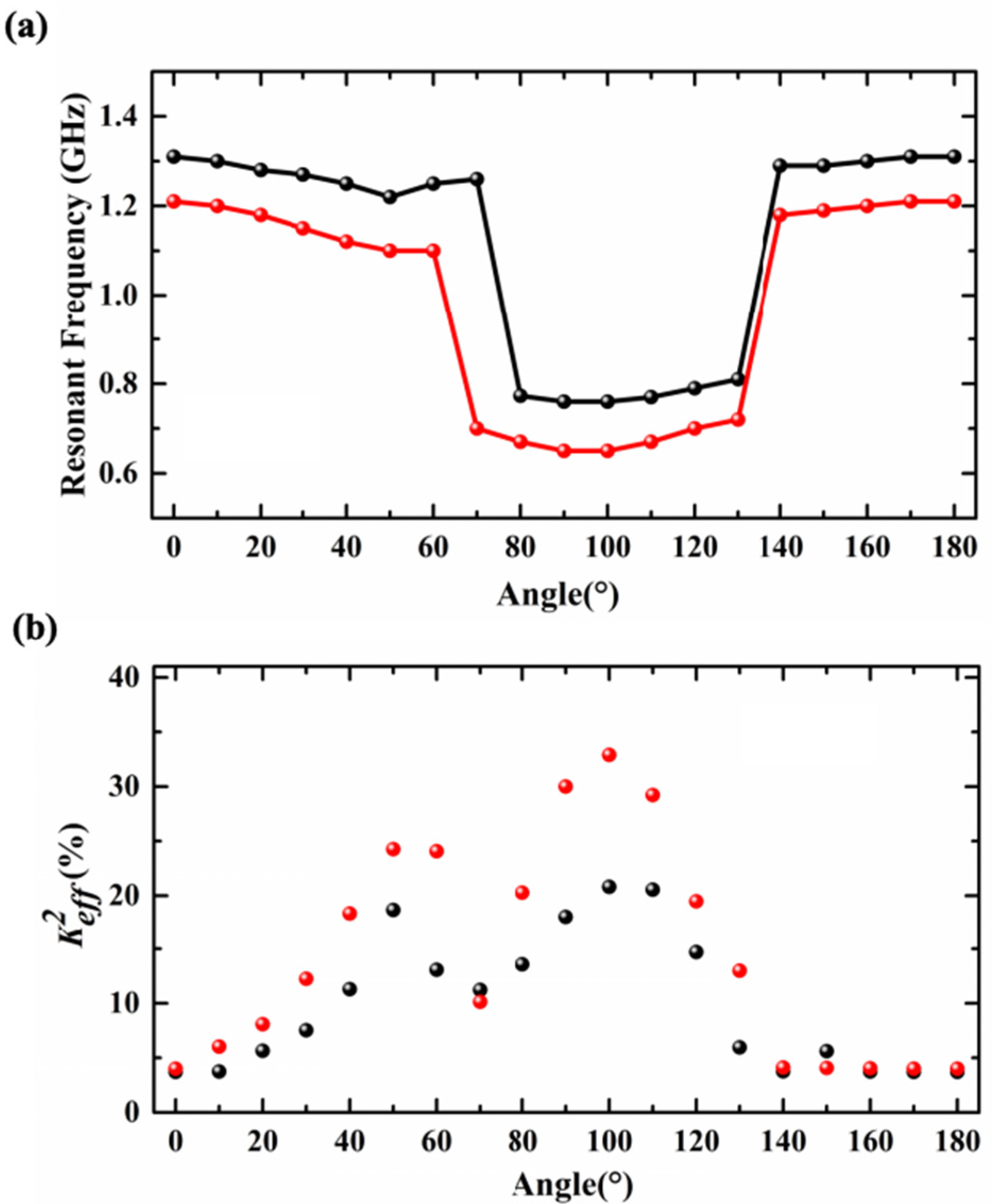
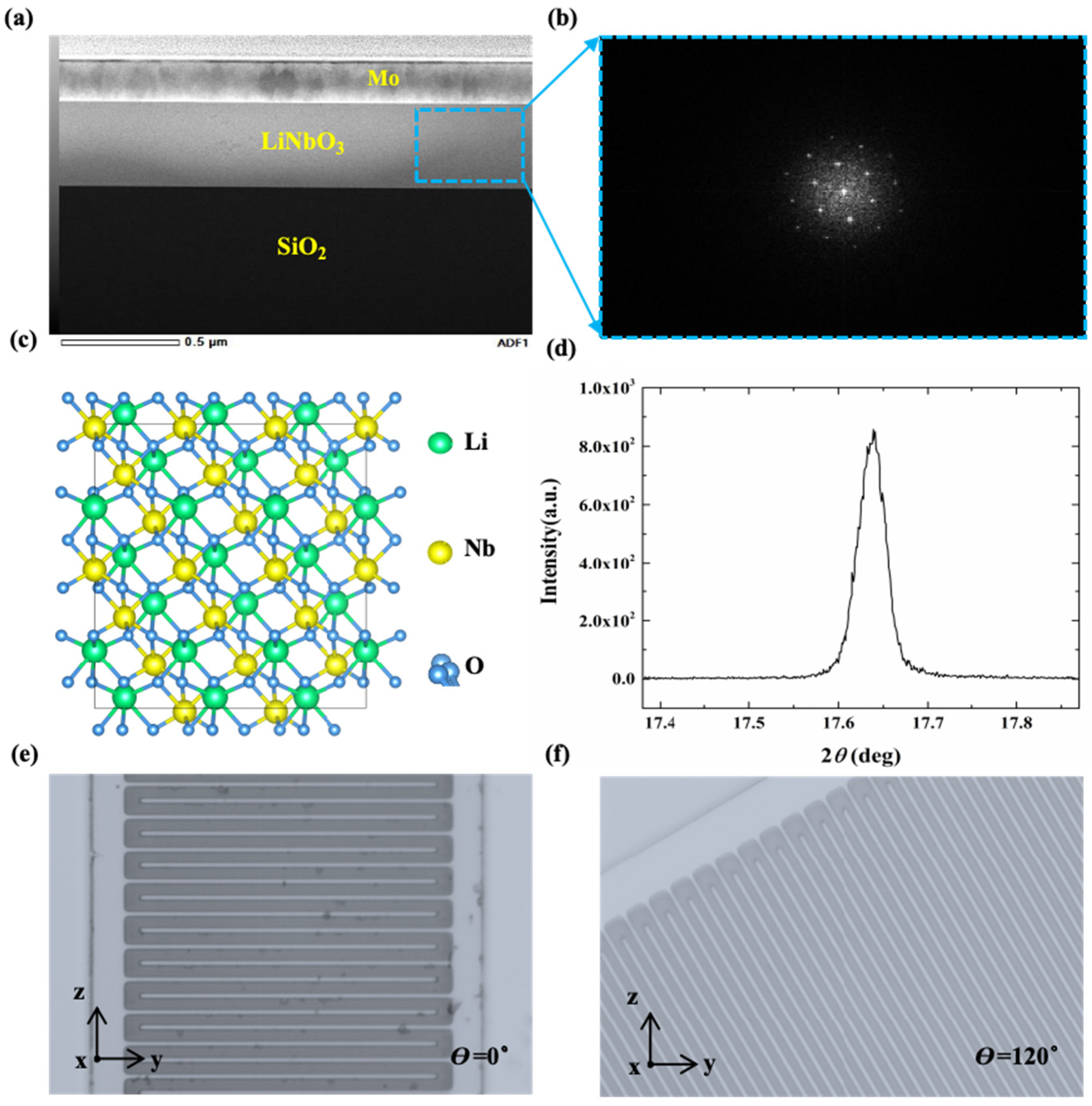

| (°) 1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| fs (GHz) 2 | 1.31 | 1.3 | 1.28 | 1.27 | 1.25 | 1.22 | 1.25 | 1.26 | 0.773 |
| (%) 3 | 3.71 | 3.74 | 5.65 | 7.53 | 11.3 | 18.69 | 13.08 | 11.22 | 13.57 |
| (°) 1 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
| fs (GHz) 2 | 18.05 | 20.81 | 20.56 | 14.69 | 5.95 | 3.77 | 5.61 | 3.74 | 3.71 |
| (%) 3 | 30 | 32.9 | 29.22 | 19.48 | 12.99 | 4.11 | 4.08 | 4.04 | 4.01 |
| (°) 1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| fs (GHz) 2 | 1.21 | 1.2 | 1.18 | 1.15 | 1.12 | 1.1 | 1.1 | 0.7 | 0.67 |
| (%) 3 | 4.01 | 6.02 | 8.09 | 12.24 | 18.35 | 24.27 | 24.07 | 10.14 | 20.28 |
| (°) 1 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
| fs (GHz) 2 | 0.65 | 0.65 | 0.67 | 0.7 | 0.72 | 1.18 | 1.19 | 1.2 | 1.21 |
| (%) 3 | 30 | 32.9 | 29.22 | 19.48 | 12.99 | 4.11 | 4.08 | 4.04 | 4.01 |
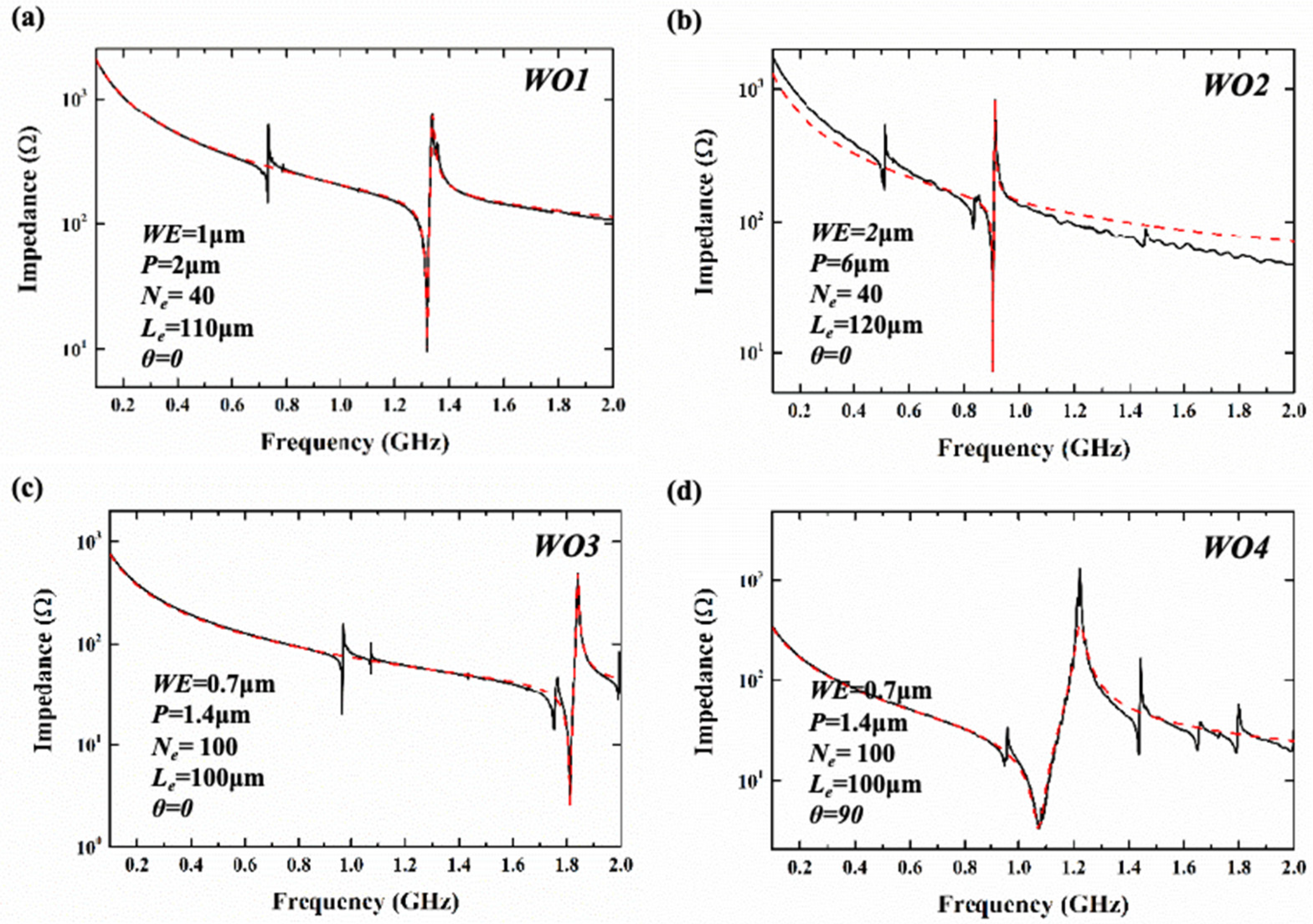
| Resonator | WO1 | WO2 | WO3 | WO4 |
|---|---|---|---|---|
| Mode | LLSAW | LLSAW | LLSAW | SH0-SAW |
| fs (GHz) | 1.319 | 0.904 | 1.812 | 1.074 |
| (%) | 3.45 | 1.62 | 3.70 | 26.60 |
| Bode-Qmax | 708 | 1309 | 705 | 228 |
| C0 (pF) | 0.736 | 1.197 | 2.06 | 3.641 |
| R0 ) | 27 | 19.55 | 1.3 | 1.5 |
| RS ) | 0.408 | 0.65 | 0.4 | 1.2 |
| RM ) | 9.31 | 6.6 | 2.2 | 2 |
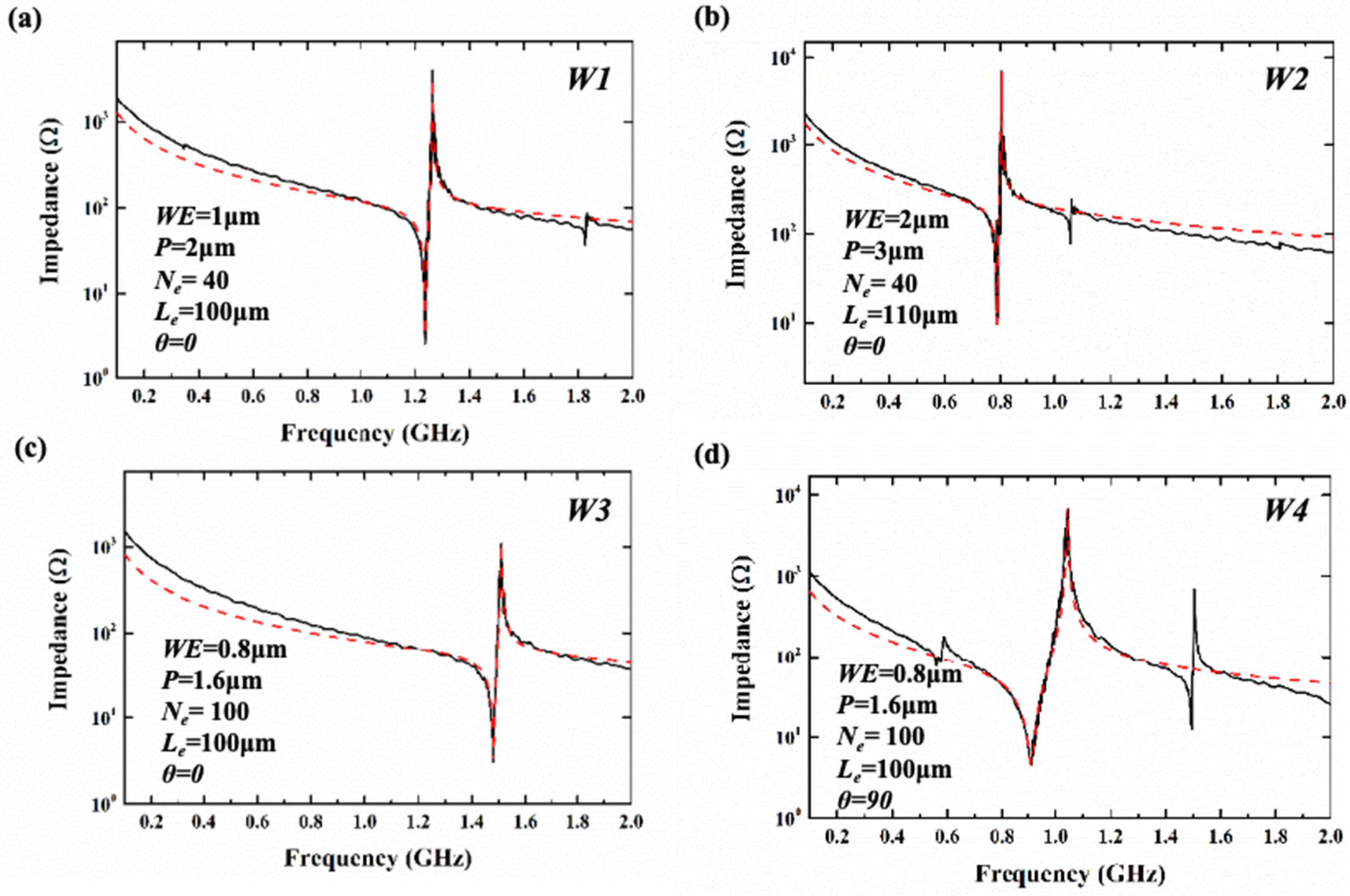
| Resonator | W1 | W2 | W3 | W4 |
|---|---|---|---|---|
| Mode | S0 | S0 | S0 | SH0 |
| fs (GHz) | 1.237 | 0.787 | 1.48 | 0.91 |
| (%) | 5.16 | 4.82 | 4.65 | 27.66 |
| Bode-Qmax | 1237 | 803 | 740 | 288 |
| C0 (pF) | 1.202 | 0.876 | 1.881 | 1.87 |
| R0 ) | 1.9 | 1.4 | 0.76 | 0.5 |
| RS ) | 1.1 | 3.65 | 1 | 0.48 |
| RM ) | 1.4 | 5.99 | 2.12 | 4.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liu, W.; Wen, Z.; Zeng, M.; Cai, Y.; Sun, C. Laterally Excited Bulk Acoustic Wave Resonators with Rotated Electrodes Using X-Cut LiNbO3 Thin-Film Substrates. Sensors 2025, 25, 1740. https://doi.org/10.3390/s25061740
Liu J, Liu W, Wen Z, Zeng M, Cai Y, Sun C. Laterally Excited Bulk Acoustic Wave Resonators with Rotated Electrodes Using X-Cut LiNbO3 Thin-Film Substrates. Sensors. 2025; 25(6):1740. https://doi.org/10.3390/s25061740
Chicago/Turabian StyleLiu, Jieyu, Wenjuan Liu, Zhiwei Wen, Min Zeng, Yao Cai, and Chengliang Sun. 2025. "Laterally Excited Bulk Acoustic Wave Resonators with Rotated Electrodes Using X-Cut LiNbO3 Thin-Film Substrates" Sensors 25, no. 6: 1740. https://doi.org/10.3390/s25061740
APA StyleLiu, J., Liu, W., Wen, Z., Zeng, M., Cai, Y., & Sun, C. (2025). Laterally Excited Bulk Acoustic Wave Resonators with Rotated Electrodes Using X-Cut LiNbO3 Thin-Film Substrates. Sensors, 25(6), 1740. https://doi.org/10.3390/s25061740






