Two Degrees of Freedom Synchronous Motion Modulation Technique Using MEMS Voltage-Controlled Oscillator-Based Phase-Locked Loop for Magnetoresistive Sensing
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview
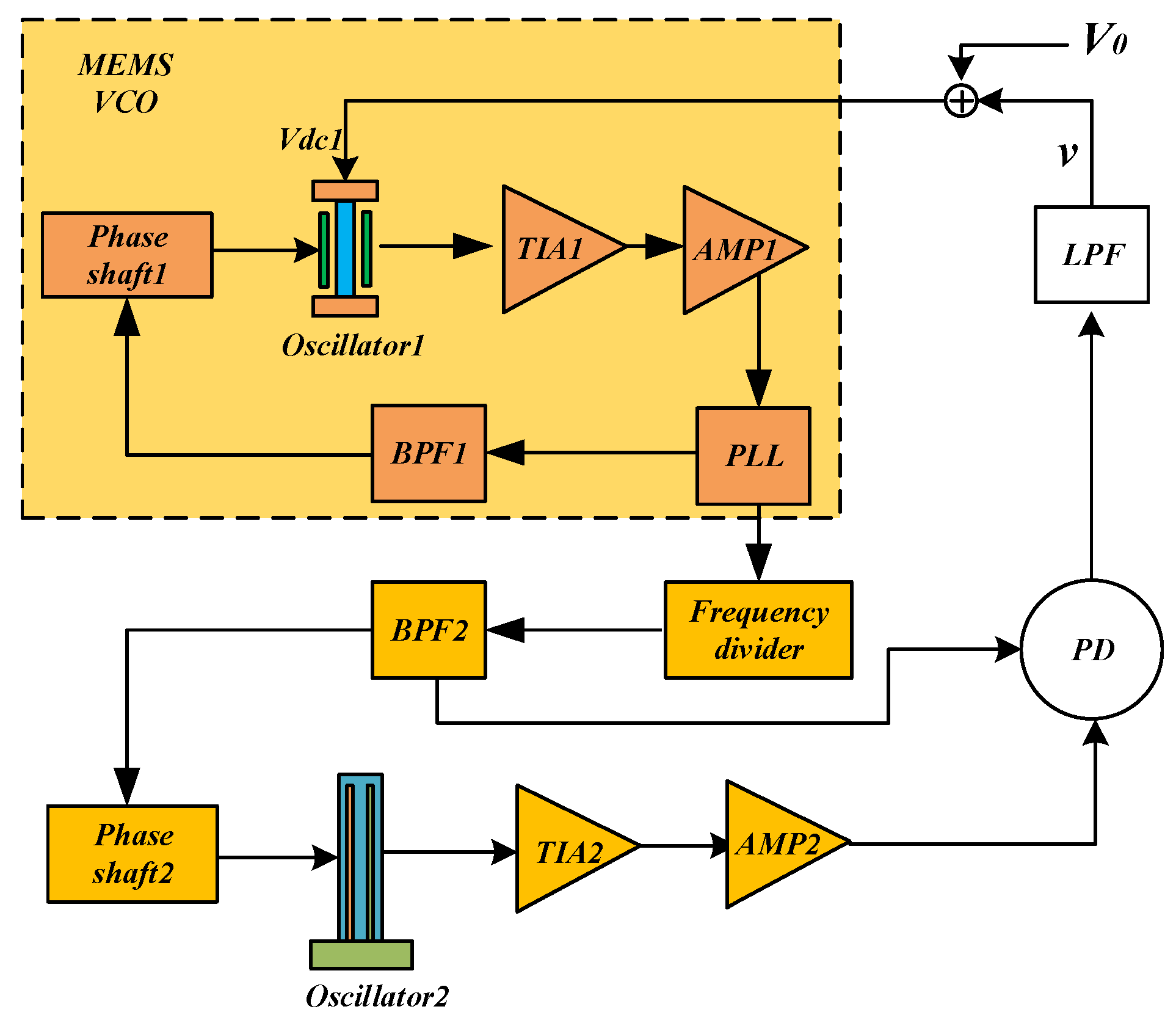
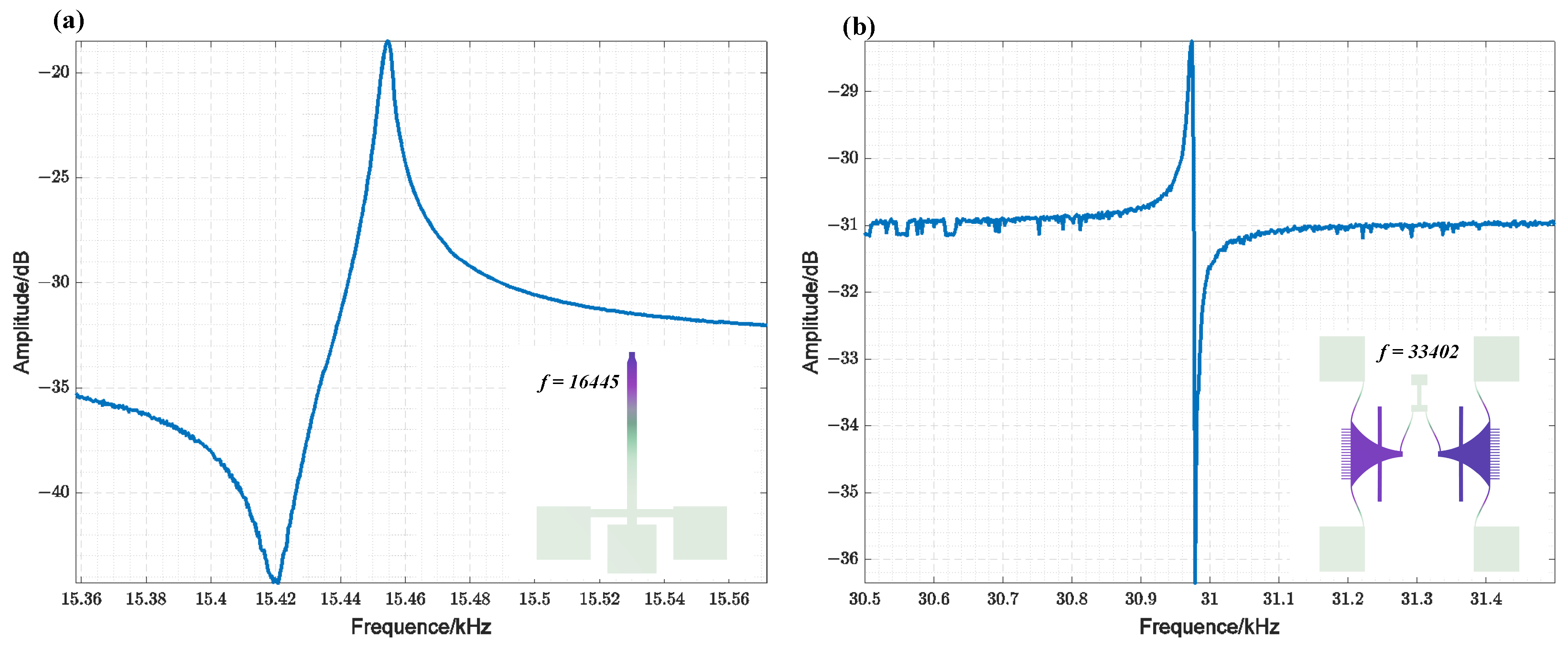
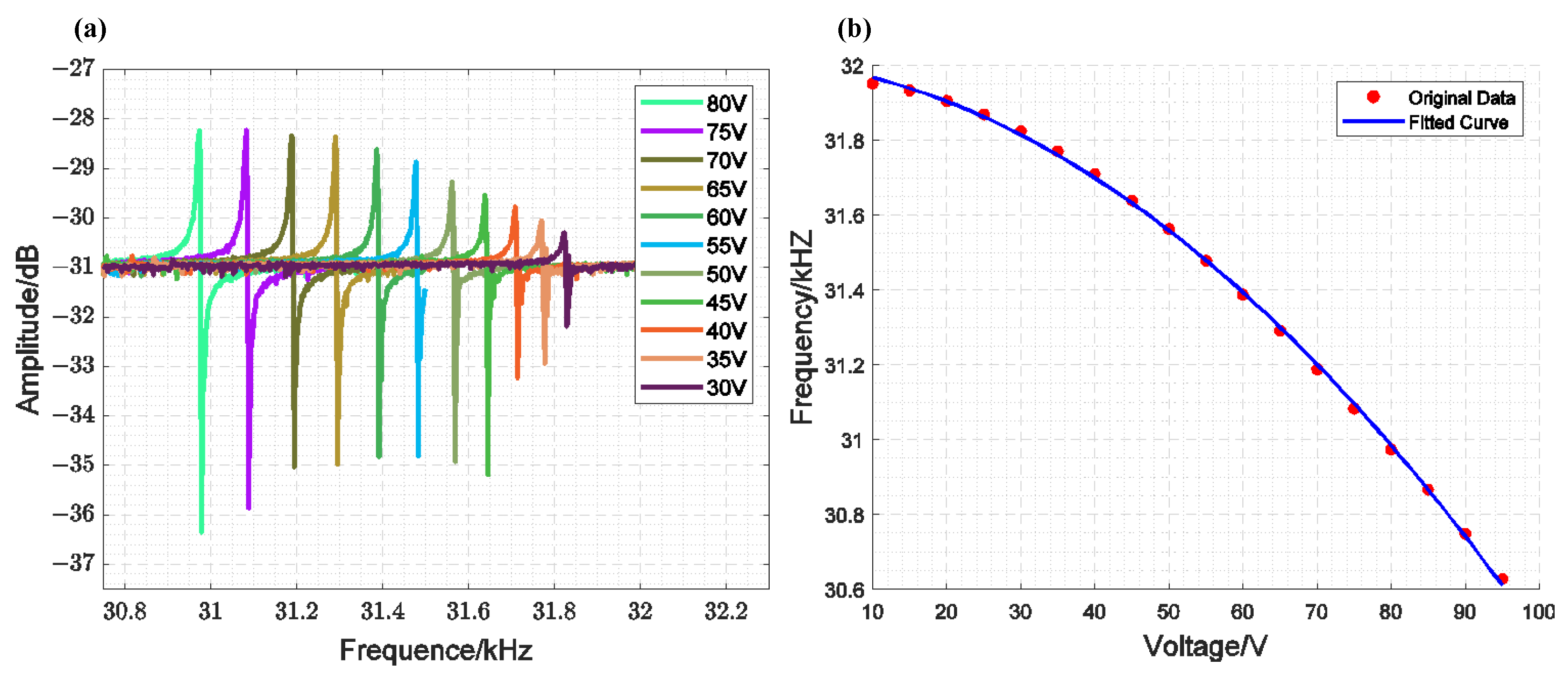
2.2. MEMS-VCO
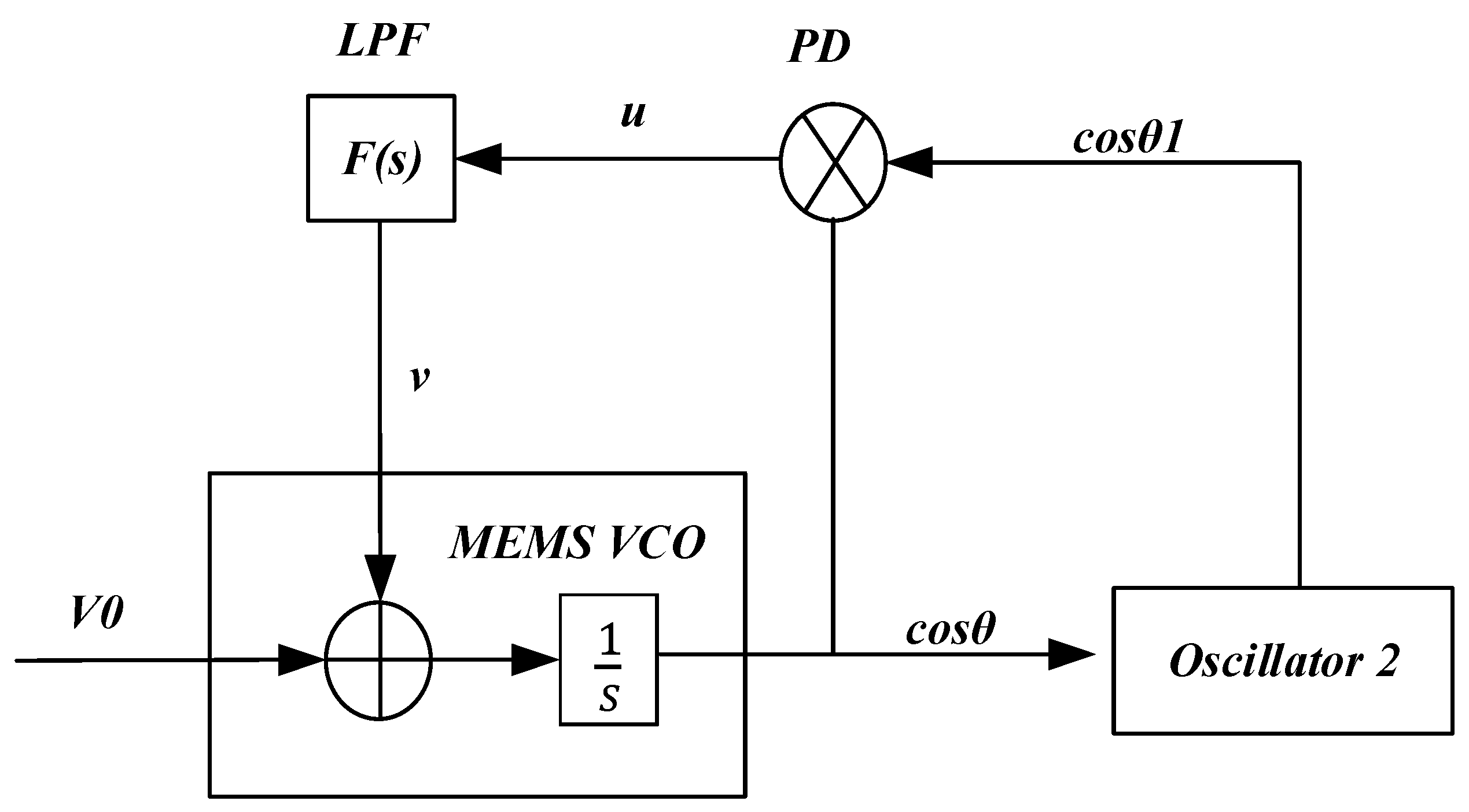
2.3. System Model
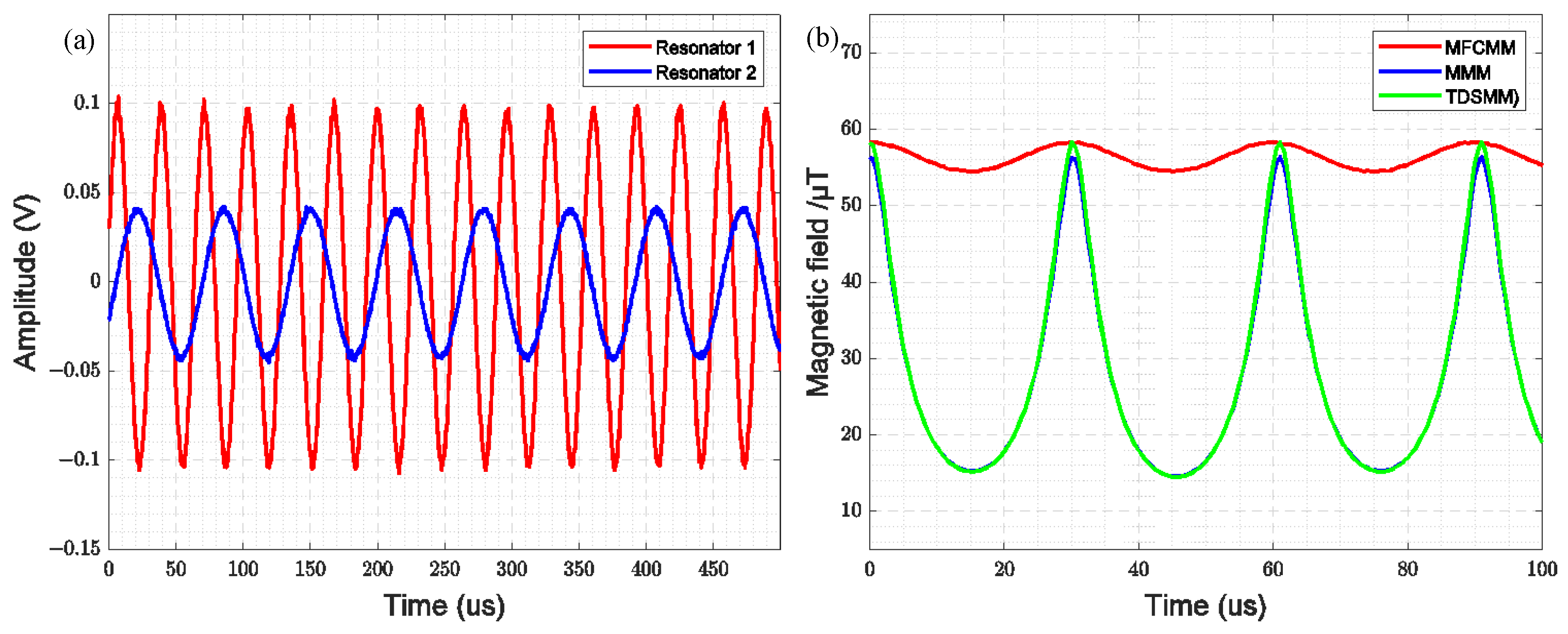
2.4. Theoretical Analysis and Simulation of TDSMM
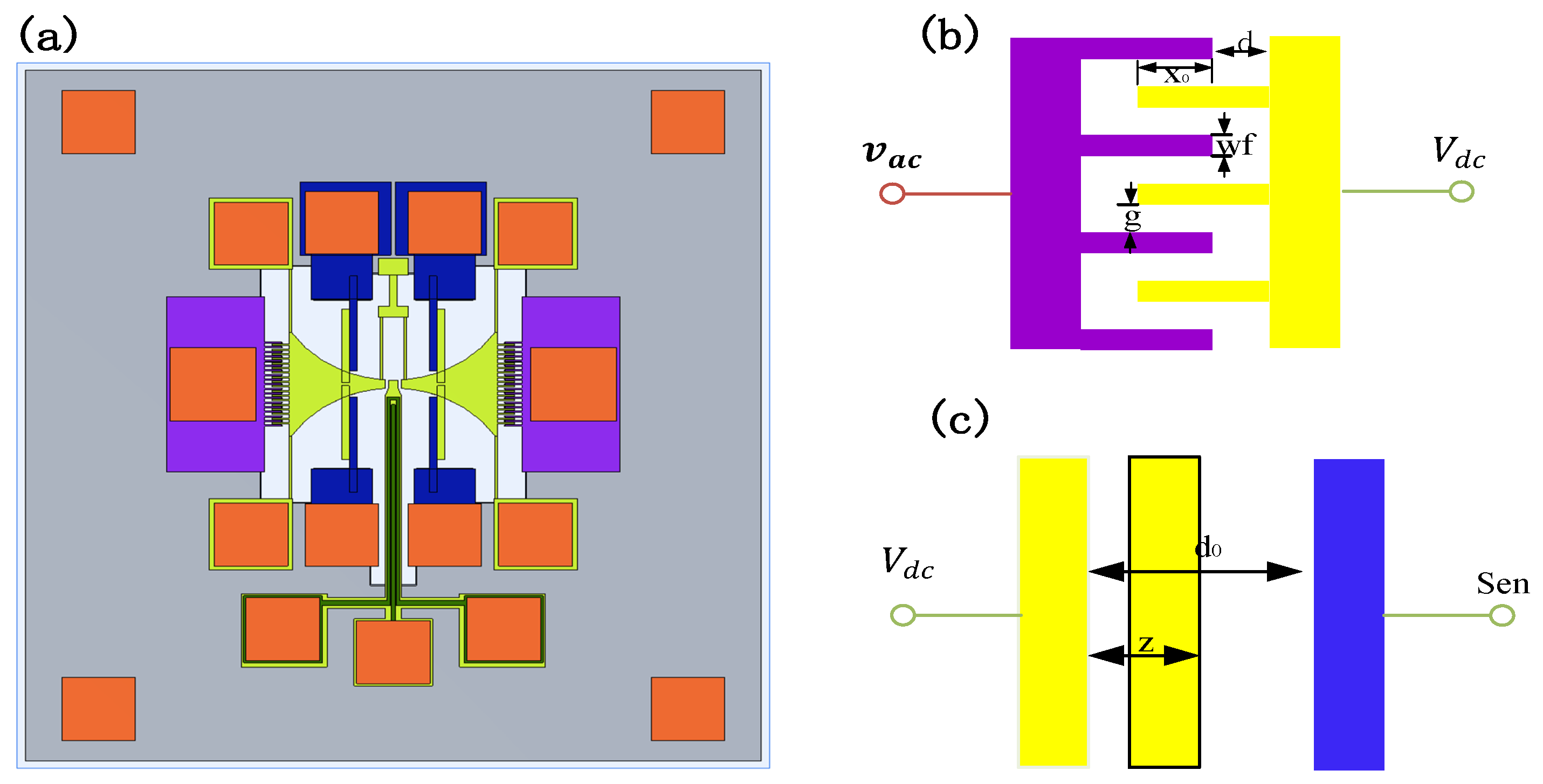
2.5. Mechanical Structure
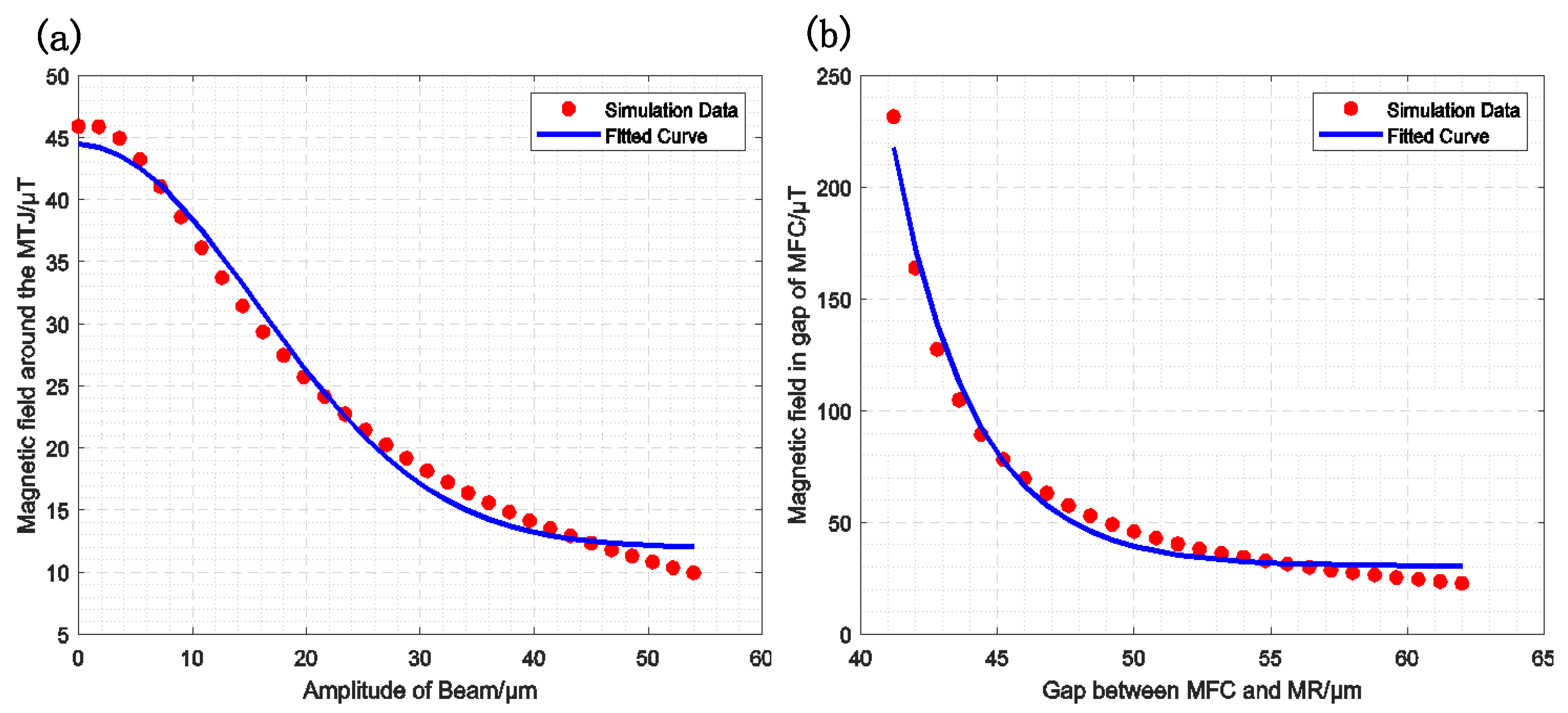
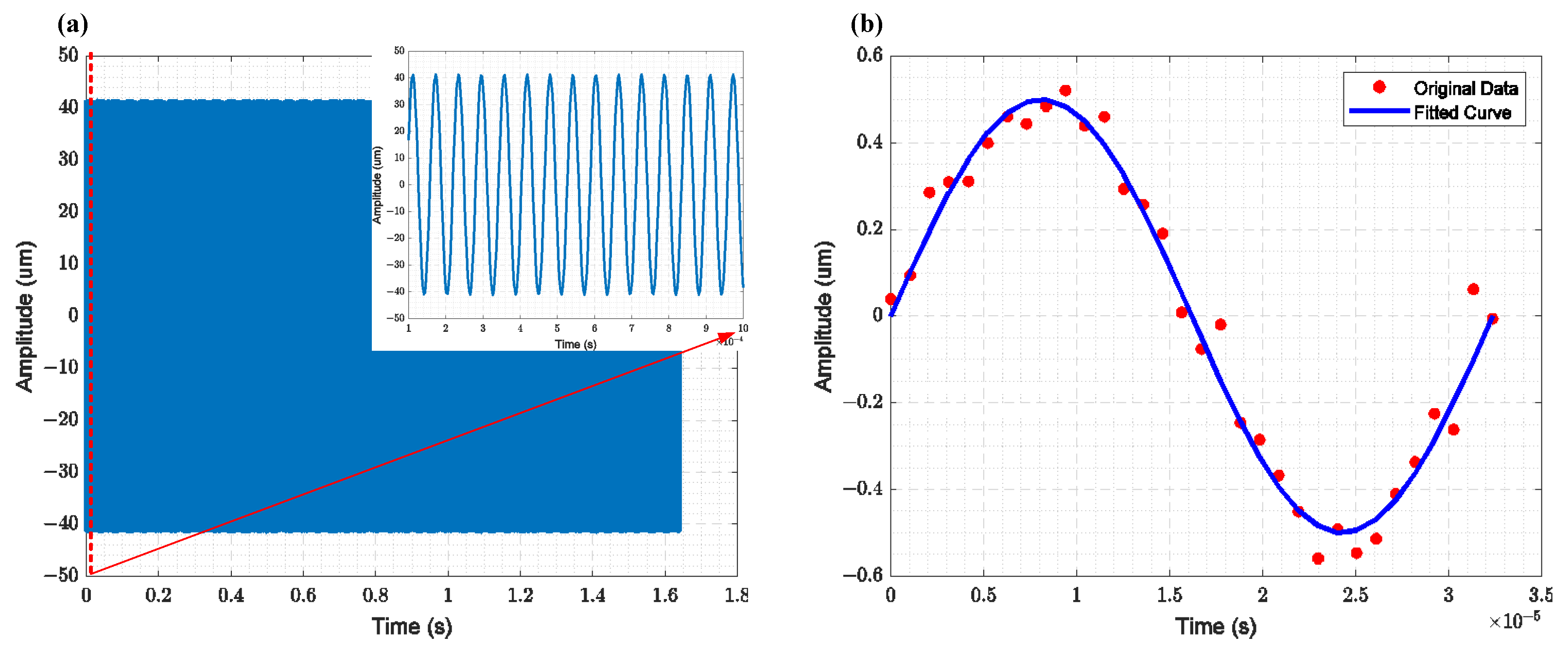
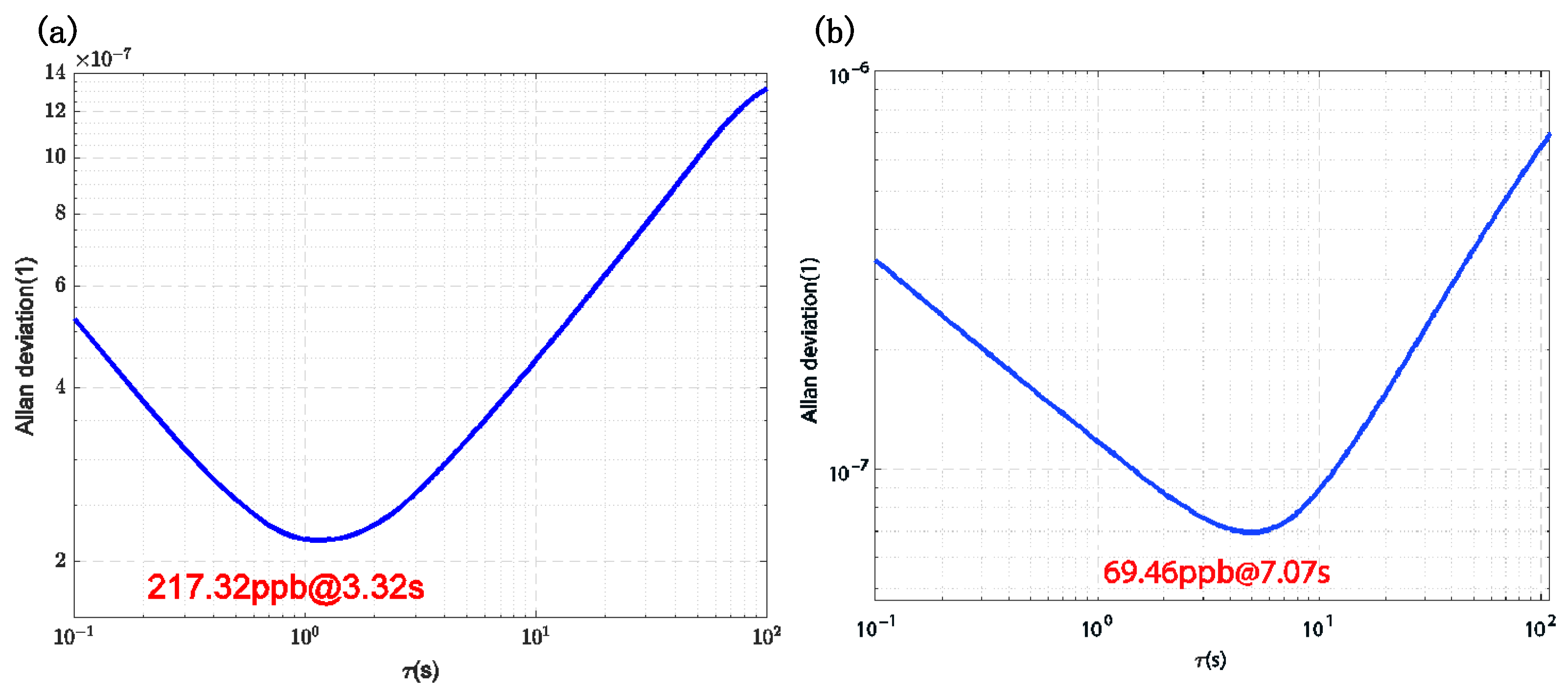
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, C.; Zhu, K.; Freitas, S.C.d.; Chang, J.Y.; Davies, J.E.; Eames, P.; Freitas, P.P.; Kazakova, O.; Kim, C.; Leung, C.W.; et al. Magnetoresistive Sensor Development Roadmap (Non-Recording Applications). IEEE Trans. Magn. 2019, 55, 1–30. [Google Scholar] [CrossRef]
- Ren, C.; Bayin, Q.; Feng, S.; Fu, Y.; Ma, X.; Guo, J. Biomarkers detection with magnetoresistance-based sensors. Biosens. Bioelectron. 2020, 165, 112340. [Google Scholar] [CrossRef] [PubMed]
- Su, D.; Wu, K.; Saha, R.; Peng, C.; Wang, J.-P. Advances in Magnetoresistive Biosensors. Micromachines 2020, 11, 34. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J. Current Progress of Magnetoresistance Sensors. Chemosensors 2021, 9, 211. [Google Scholar] [CrossRef]
- Khan, M.A.; Sun, J.; Li, B.; Przybysz, A.; Kosel, J. Magnetic sensors-A review and recent technologies. Eng. Res. Express 2021, 3, 022005. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Kaiser, C.; Panchula, A.; Rice, P.M.; Hughes, B.; Samant, M.; Yang, S.-H. Giant tunnelling magnetoresistance at room temperature with MgO (100) tunnel barriers. Nat. Mater. 2004, 3, 862–867. [Google Scholar] [CrossRef]
- Han, X.; Ali, S.S.; Liang, S. MgO(001) barrier based magnetic tunnel junctions and their device applications. Sci. China Phys. Mech. Astron. 2013, 56, 29–60. [Google Scholar] [CrossRef]
- Lei, Z.Q.; Li, G.J.; Egelhoff, W.F.; Lai, P.T.; Pong, P.W.T. Review of Noise Sources in Magnetic Tunnel Junction Sensors. IEEE Trans. Magn. 2011, 47, 602–612. [Google Scholar] [CrossRef]
- Hu, J.; Pan, M.; Tian, W.; Chen, D.; Zhao, J.; Luo, F. 1/f noise suppression of giant magnetoresistive sensors with vertical motion flux modulation. Appl. Phys. Lett. 2012, 100, 244102. [Google Scholar] [CrossRef]
- Ozbay, A.; Gokce, A.; Flanagan, T.; Stearrett, R.A.; Nowak, E.R.; Nordman, C. Low frequency magnetoresistive noise in spin-valve structures. Appl. Phys. Lett. 2009, 94, 202506. [Google Scholar] [CrossRef]
- Pan, M.; Hu, J.; Tian, W.; Chen, D.; Zhao, J. Magnetic flux vertical motion modulation for 1/f noise reduction of magnetic tunnel junctions. Sens. Actuators A Phys. 2012, 179, 92–97. [Google Scholar] [CrossRef]
- Guerrero, R.; Pannetier-Lecoeur, M.; Fermon, C.; Cardoso, S.; Ferreira, R.; Freitas, P.P. Low frequency noise in arrays of magnetic tunnel junctions connected in series and parallel. J. Appl. Phys. 2009, 105, 113922. [Google Scholar] [CrossRef]
- Paz, E.; Serrano-Guisan, S.; Ferreira, R.; Freitas, P.P. Room temperature direct detection of low frequency magnetic fields in the 100 pT/Hz0.5 range using large arrays of magnetic tunnel junctions. J. Appl. Phys. 2014, 115, 17E501. [Google Scholar] [CrossRef]
- Jander, A.; Nordman, C.A.; Pohm, A.V.; Anderson, J.M. Chopping techniques for low-frequency nanotesla spin-dependent tunneling field sensors. J. Appl. Phys. 2003, 93, 8382–8384. [Google Scholar] [CrossRef]
- Edelstein, A.S.; Fischer, G.A. Minimizing 1/f noise in magnetic sensors using a microelectromechanical system flux concentrator. J. Appl. Phys. 2002, 91, 7795–7797. [Google Scholar] [CrossRef]
- Edelstein, A.S.; Fischer, G.A.; Pedersen, M.; Nowak, E.R.; Cheng, S.F.; Nordman, C.A. Progress toward a thousandfold reduction in 1/f noise in magnetic sensors using an ac microelectromechanical system flux concentrator (invited). J. Appl. Phys. 2006, 99, 08B317. [Google Scholar] [CrossRef]
- Hu, J.; Pan, M.; Tian, W.; Chen, D.; Zhao, J. Magnetostatic detection using magnetoresistive sensors with vertical motion flux modulation. Rev. Sci. Instrum. 2012, 83, 055009. [Google Scholar] [CrossRef] [PubMed]
- Guedes, A.; Macedo, R.; Jaramillo, G.; Cardoso, S.; Freitas, P.P.; Horsley, D.A. Hybrid GMR Sensor Detecting 950 pT/sqrt(Hz) at 1 Hz and Room Temperature. Sensors 2018, 18, 790. [Google Scholar] [CrossRef]
- Tian, W.; Hu, J.; Pan, M.; Chen, D.; Zhao, J. Magnetic Flux Vertical Motion Modulation for 1/f Noise Suppression in Magnetoresistance Field Sensors Using MEMS Device. IEEE Trans. Magn. 2016, 52, 1–6. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.; Zou, X. Magnetic Flux Synchronous Motion Modulation for Improving the Low-Frequency Magnetic Field Detection Limit of Magnetoresistive Sensor Using MEMS Resonators. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Jiao, Q.; Luo, J.; Jin, Z.; Zou, X.; Chen, J. Two-dimensional synchronous motion modulation MEMS structure for suppressing 1/f noise in magnetoresistive sensors. AIP Adv. 2023, 13, 125223. [Google Scholar] [CrossRef]
- Lyu, H.; Liu, Z.; Wang, Z.; Yang, W.; Xiong, X.; Chen, J.; Zou, X. A high-resolution MEMS magnetoresistive sensor utilizing magnetic tunnel junction motion modulation driven by the piezoelectric resonator. Appl. Phys. Lett. 2022, 121, 123504. [Google Scholar] [CrossRef]
- Ma, L.; Wang, J.; Wang, Z.; Wang, K.; Zhai, Z.; Cai, P.; Xiong, X.; Zou, X. An Intrinsically Temperature-Drift Suppression Phase-Locked Loop with MEMS Voltage Controlled Oscillator for Micromechanical Resonant Accelerometer. J. Microelectromech. Syst. 2022, 31, 901–911. [Google Scholar] [CrossRef]
- Wei, X.; Xu, M.; Yang, Q.; Xu, L.; Qi, Y.; Ren, Z.; Ren, J.; Huan, R.; Jiang, Z. MEMS Huygens Clock Based on Synchronized Micromechanical Resonators. Engineering 2024, 36, 124–131. [Google Scholar] [CrossRef]
- Elshurafa, A.M.; Khirallah, K.; Tawfik, H.H.; Emira, A.; Aziz, A.K.S.A.; Sedky, S.M. Nonlinear Dynamics of Spring Softening and Hardening in Folded-MEMS Comb Drive Resonators. J. Microelectromech. Syst. 2011, 20, 943–958. [Google Scholar] [CrossRef]
- Shaw, K.; Nai, Y.H.; Haswell, S. Application of Microfluidic Methodology for the Analysis of DNA. Micromachines 2018, 9, 18. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Yuldashev, M.V.; Yuldashev, R.V. Hold-In, Pull-In, and Lock-In Ranges of PLL Circuits: Rigorous Mathematical Definitions and Limitations of Classical Theory. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2454–2464. [Google Scholar] [CrossRef]
- Sohanian-Haghighi, H.; Davaie-Markazi, A.H. Resonance Tracking of Nonlinear MEMS Resonators. IEEE/ASME Trans. Mechatron. 2012, 17, 617–621. [Google Scholar] [CrossRef]
- Sun, X.; Horowitz, R.; Komvopoulos, K. Stability and Resolution Analysis of a Phase-Locked Loop Natural Frequency Tracking System for MEMS Fatigue Testing. J. Dyn. Syst. Meas. Control 2002, 124, 599–605. [Google Scholar] [CrossRef]
- Azgin, K.; Valdevit, L. The effects of tine coupling and geometrical imperfections on the response of DETF resonators. J. Micromech. Microeng. 2013, 23, 125011. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.; Yang, W.; Zheng, T.; Jiao, Q.; Zou, X. Dynamic behaviours of double-ended tuning fork based comb-driven microelectromechanical resonators for modulating magnetic flux synchronously. J. Micromech. Microeng. 2022, 32, 014003. [Google Scholar] [CrossRef]
- Qi, Z.; Wang, B.; Zhai, Z.; Wang, Z.; Xiong, X.; Yang, W.; Bie, X.; Wang, Y.; Zou, X. Bridging piezoelectric and electrostatic effects: A novel piezo-MEMS pitch/roll gyroscope with sub 10°/h bias instability. Microsyst. Nanoeng. 2024, 10, 160. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Zhai, Z.; Wang, B.; Yang, W.; Xiong, X.; Wang, Z.; Lv, H.; Bie, X.; Zou, X. Bridging Piezoelectric And Electrostatic Effects: A Novel Pitch/Roll Gyroscope. In Proceedings of the 2024 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 25–28 March 2024; pp. 1–4. [Google Scholar]
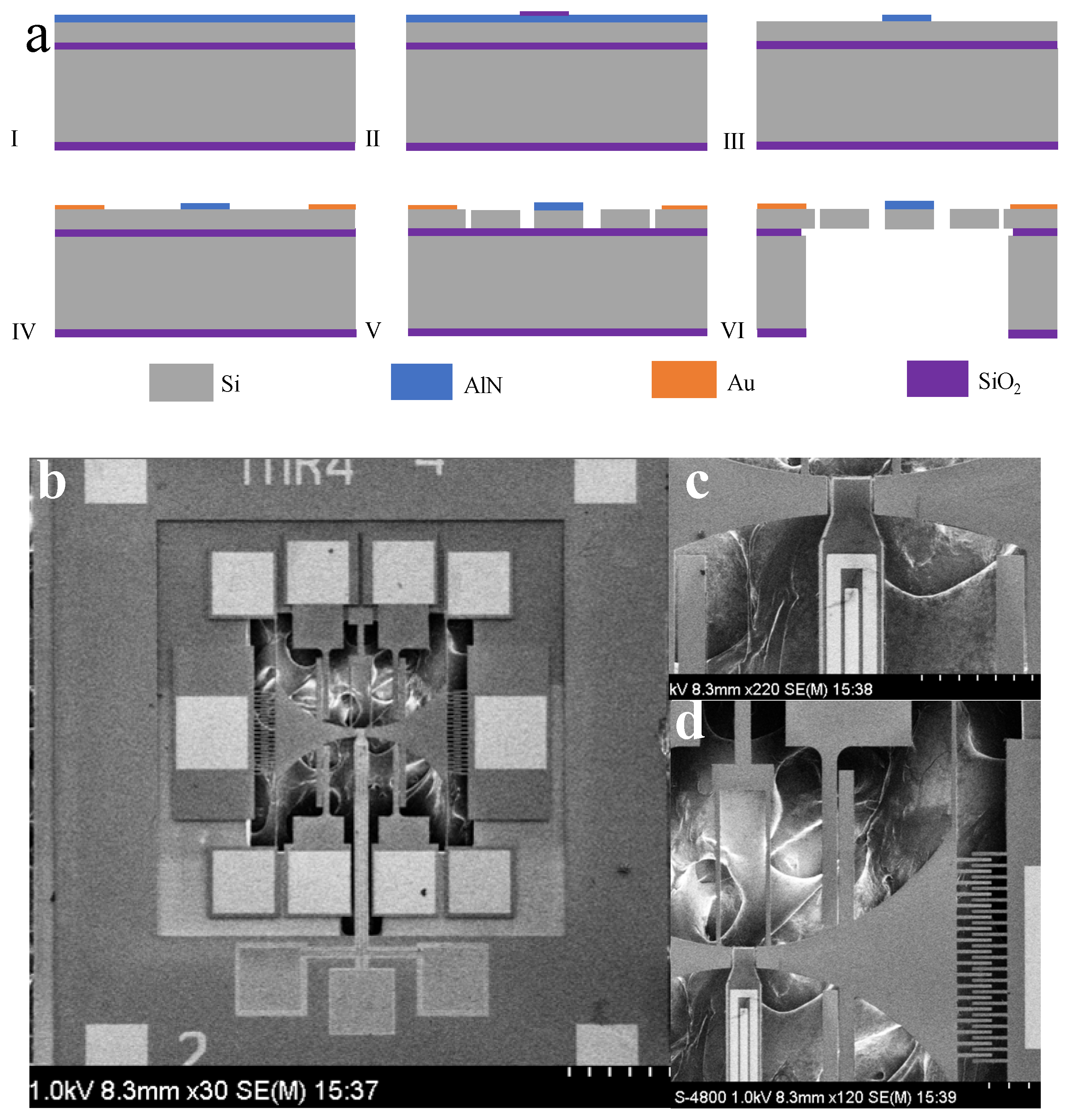

| Parameter | Value [μm] |
|---|---|
| AIN thickness | 1 |
| Length of beam | 820 |
| Width of beam (upper) | 45 |
| Width of beam (nether) | 70 |
| Length of DETF beam | 300 |
| Length of short side of transverse mass | 40 |
| Length of long side of transverse mass | 490 |
| Length of long side of transverse mass | 390 |
| Gap of transverse mass | 50 |
| Gap of parallel plate | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Qi, Z.; Lyu, H.; Jiao, Q.; Chen, C.; Zou, X. Two Degrees of Freedom Synchronous Motion Modulation Technique Using MEMS Voltage-Controlled Oscillator-Based Phase-Locked Loop for Magnetoresistive Sensing. Sensors 2025, 25, 1835. https://doi.org/10.3390/s25061835
Shi Z, Qi Z, Lyu H, Jiao Q, Chen C, Zou X. Two Degrees of Freedom Synchronous Motion Modulation Technique Using MEMS Voltage-Controlled Oscillator-Based Phase-Locked Loop for Magnetoresistive Sensing. Sensors. 2025; 25(6):1835. https://doi.org/10.3390/s25061835
Chicago/Turabian StyleShi, Zhenyu, Zhenxiang Qi, Haoqi Lyu, Qifeng Jiao, Chen Chen, and Xudong Zou. 2025. "Two Degrees of Freedom Synchronous Motion Modulation Technique Using MEMS Voltage-Controlled Oscillator-Based Phase-Locked Loop for Magnetoresistive Sensing" Sensors 25, no. 6: 1835. https://doi.org/10.3390/s25061835
APA StyleShi, Z., Qi, Z., Lyu, H., Jiao, Q., Chen, C., & Zou, X. (2025). Two Degrees of Freedom Synchronous Motion Modulation Technique Using MEMS Voltage-Controlled Oscillator-Based Phase-Locked Loop for Magnetoresistive Sensing. Sensors, 25(6), 1835. https://doi.org/10.3390/s25061835






