Collecting Performance Prediction for the Rubber Collector in Horizontal Wellbore Based on AutoML
Abstract
1. Introduction
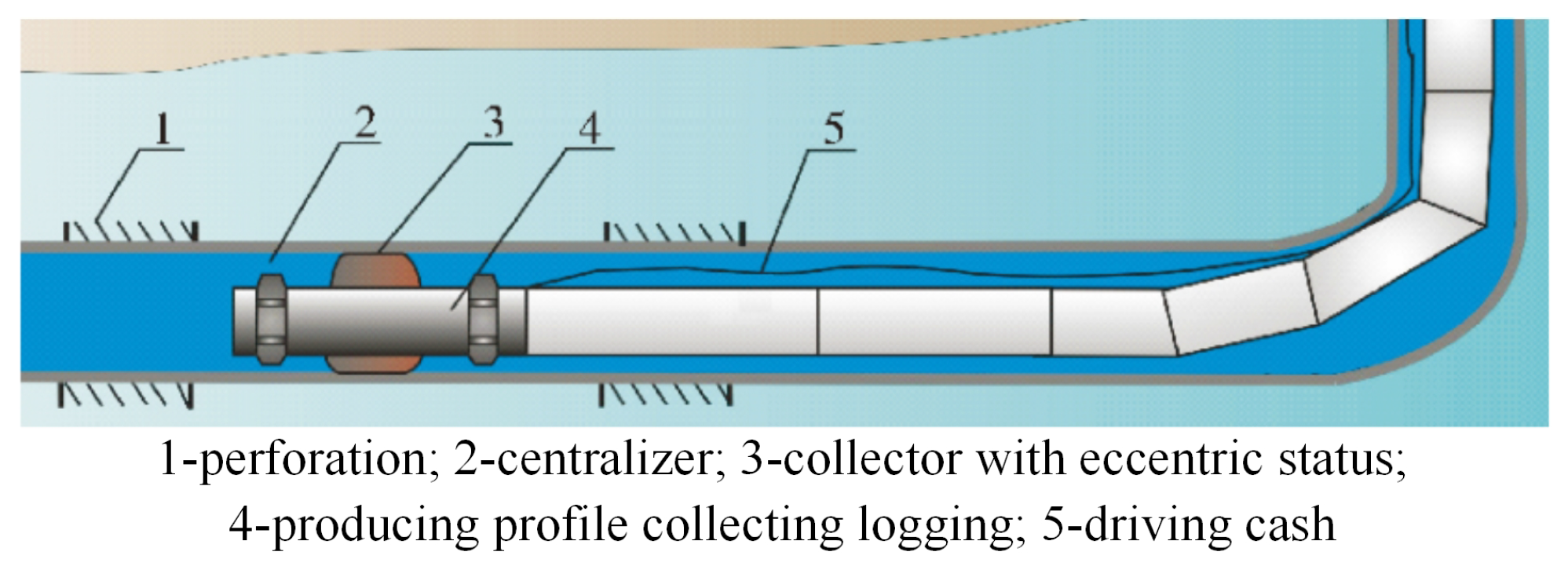
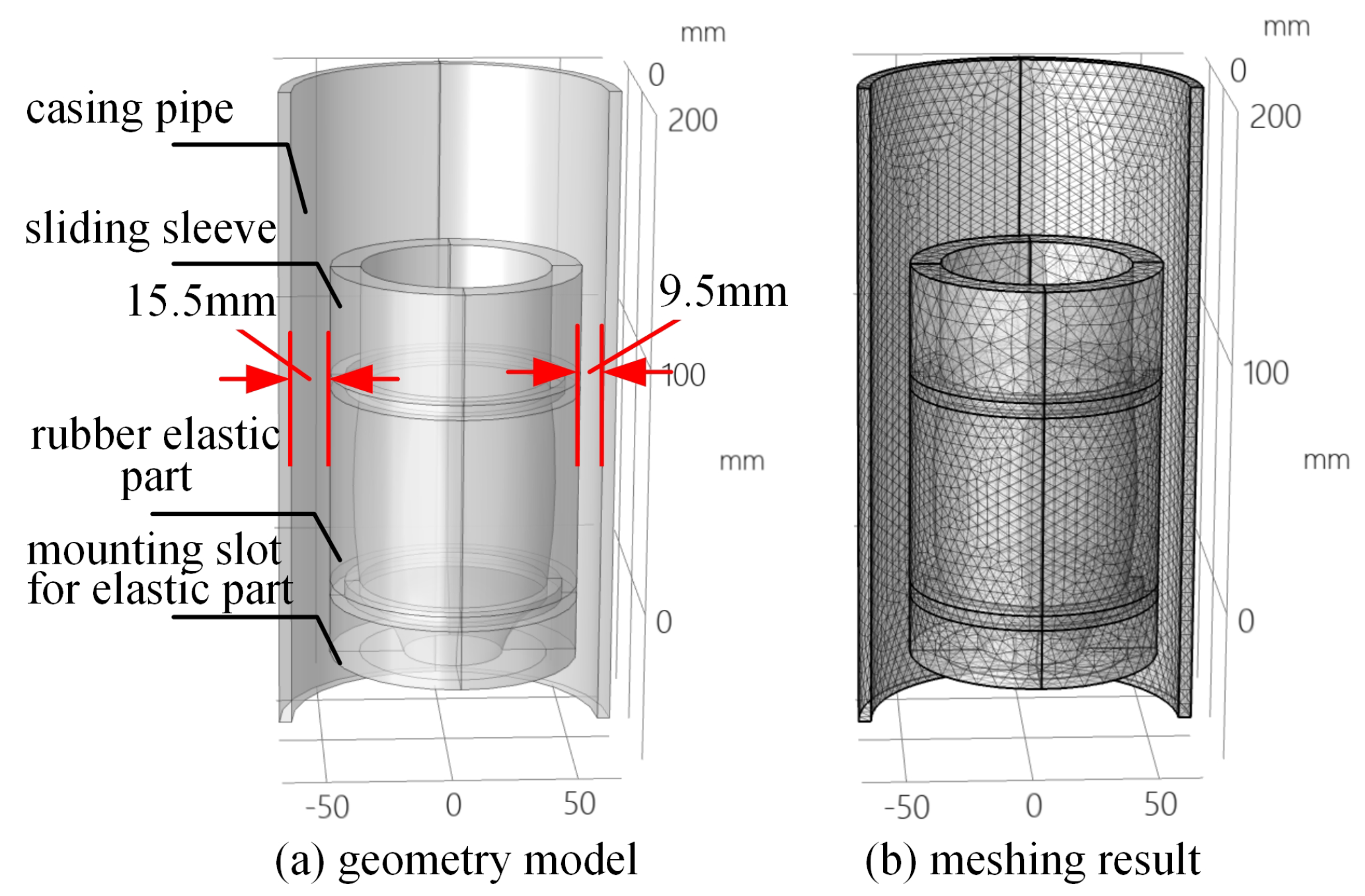
2. Simulated Modeling of a Rubber Collector in Horizontal Wellbore
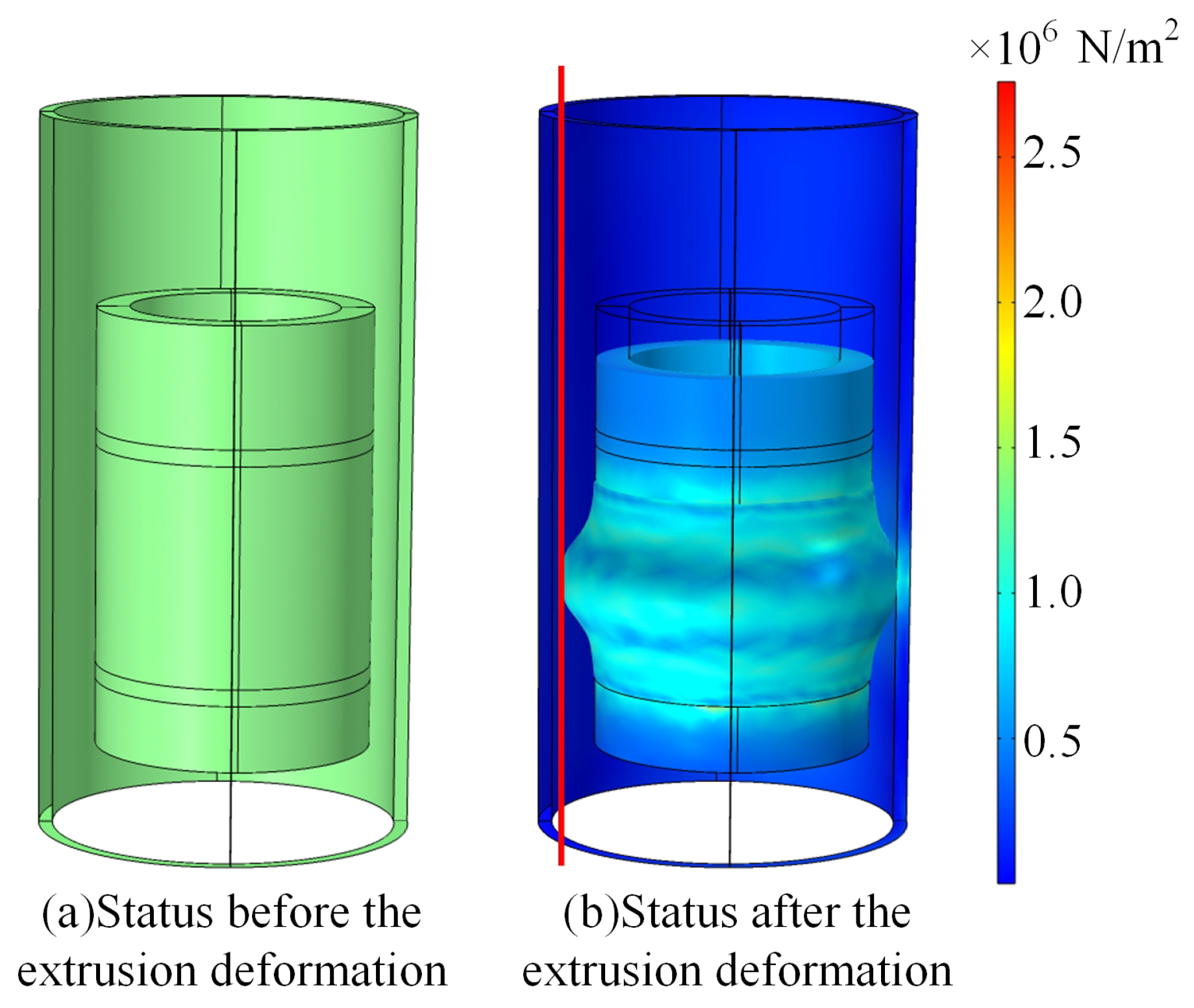
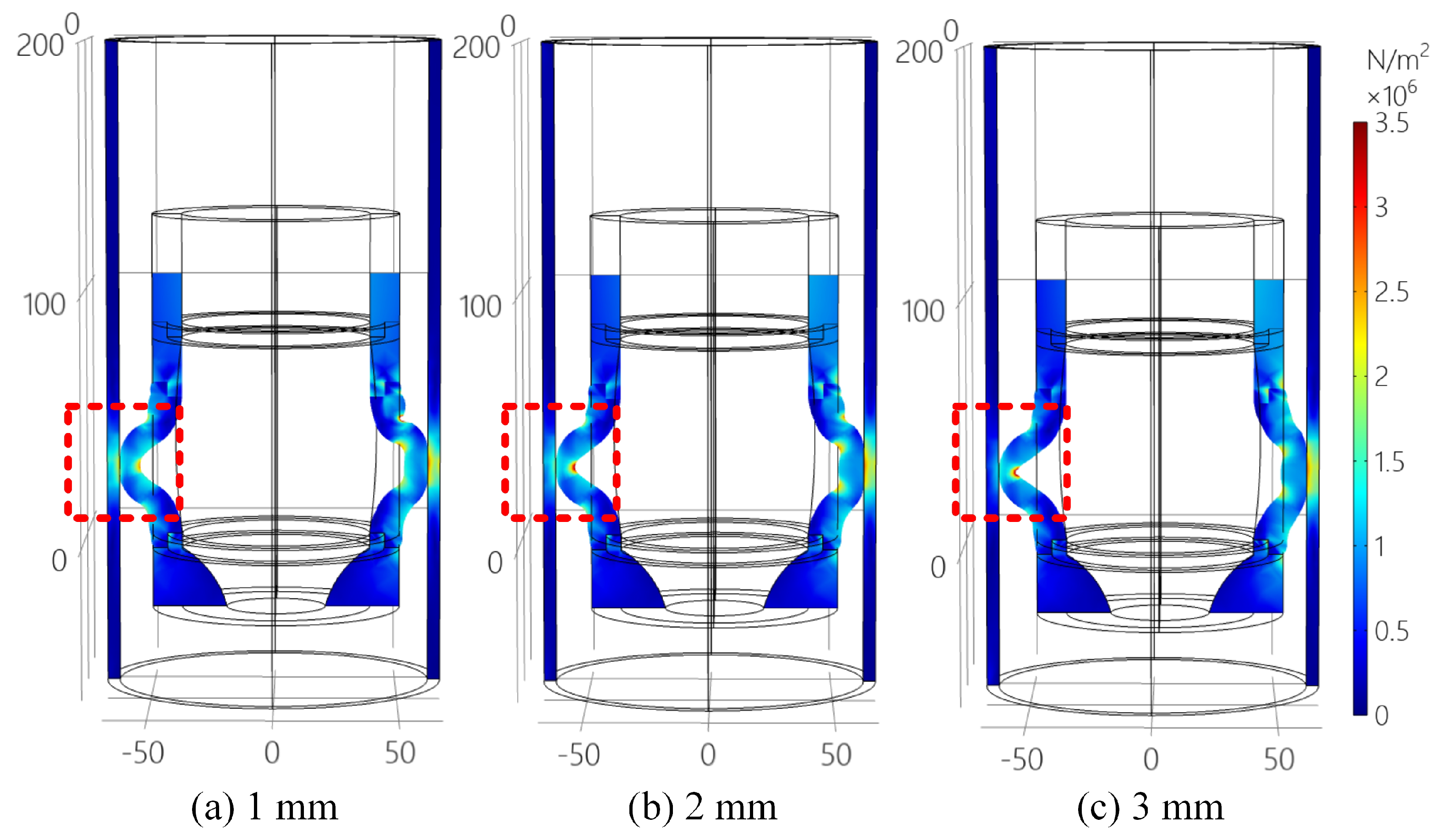
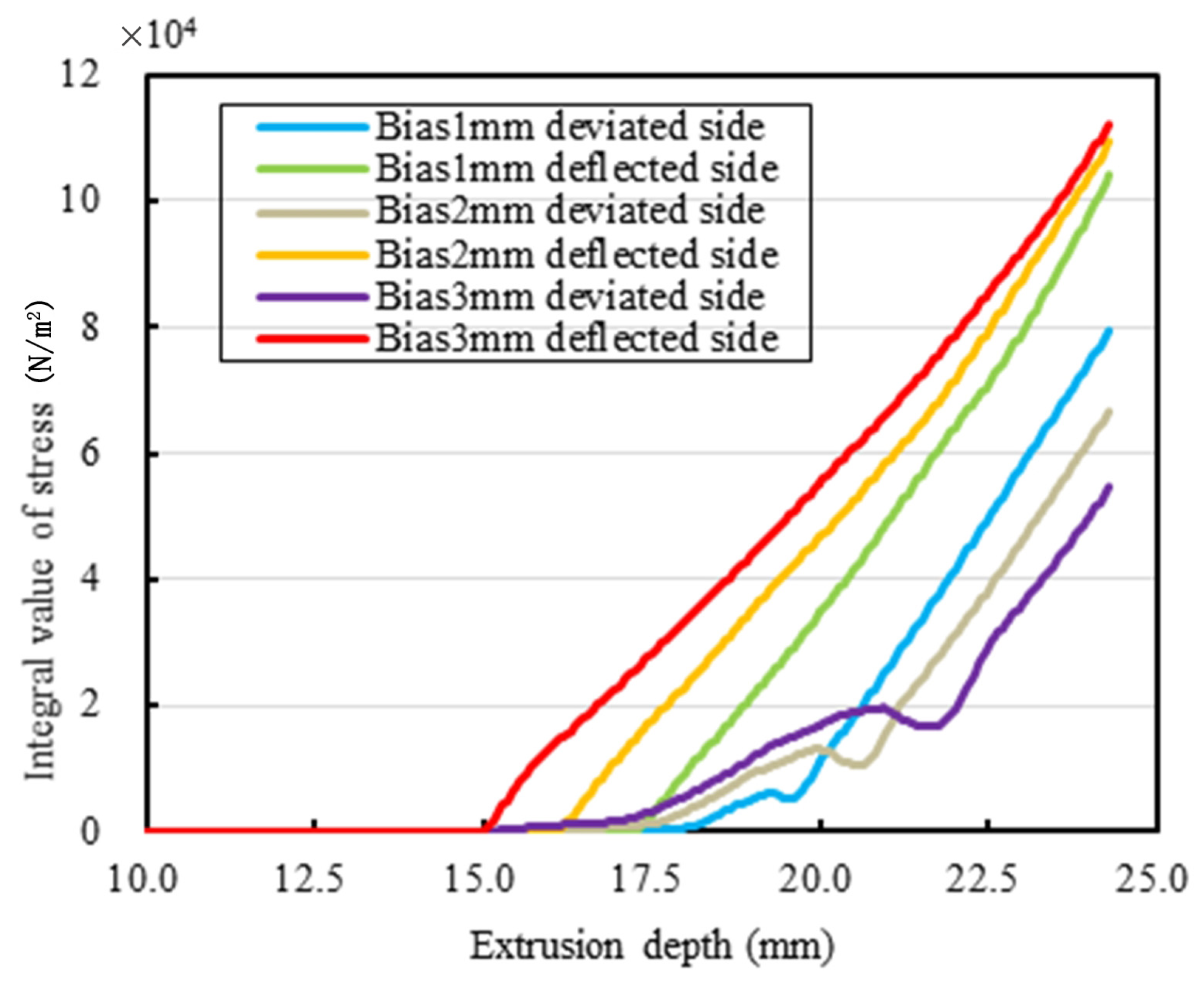
3. Simulated Analyses of the Collecting Performance of the Rubber Collector with Different Eccentric Degrees
4. Prediction of the Collecting Performance of the Rubber Collector in Horizontal Wellbore Based on AutoML
4.1. Dataset Collection
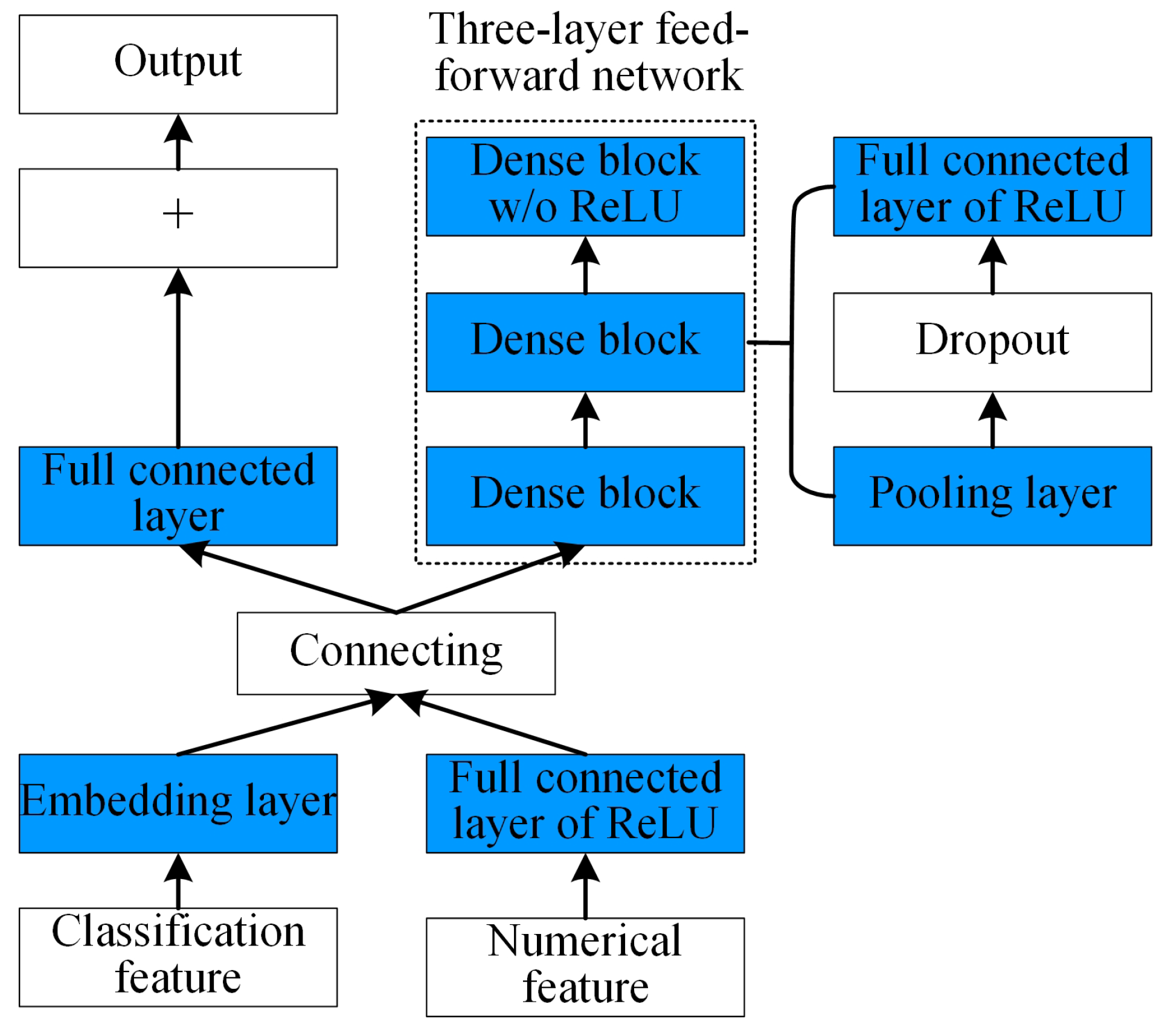
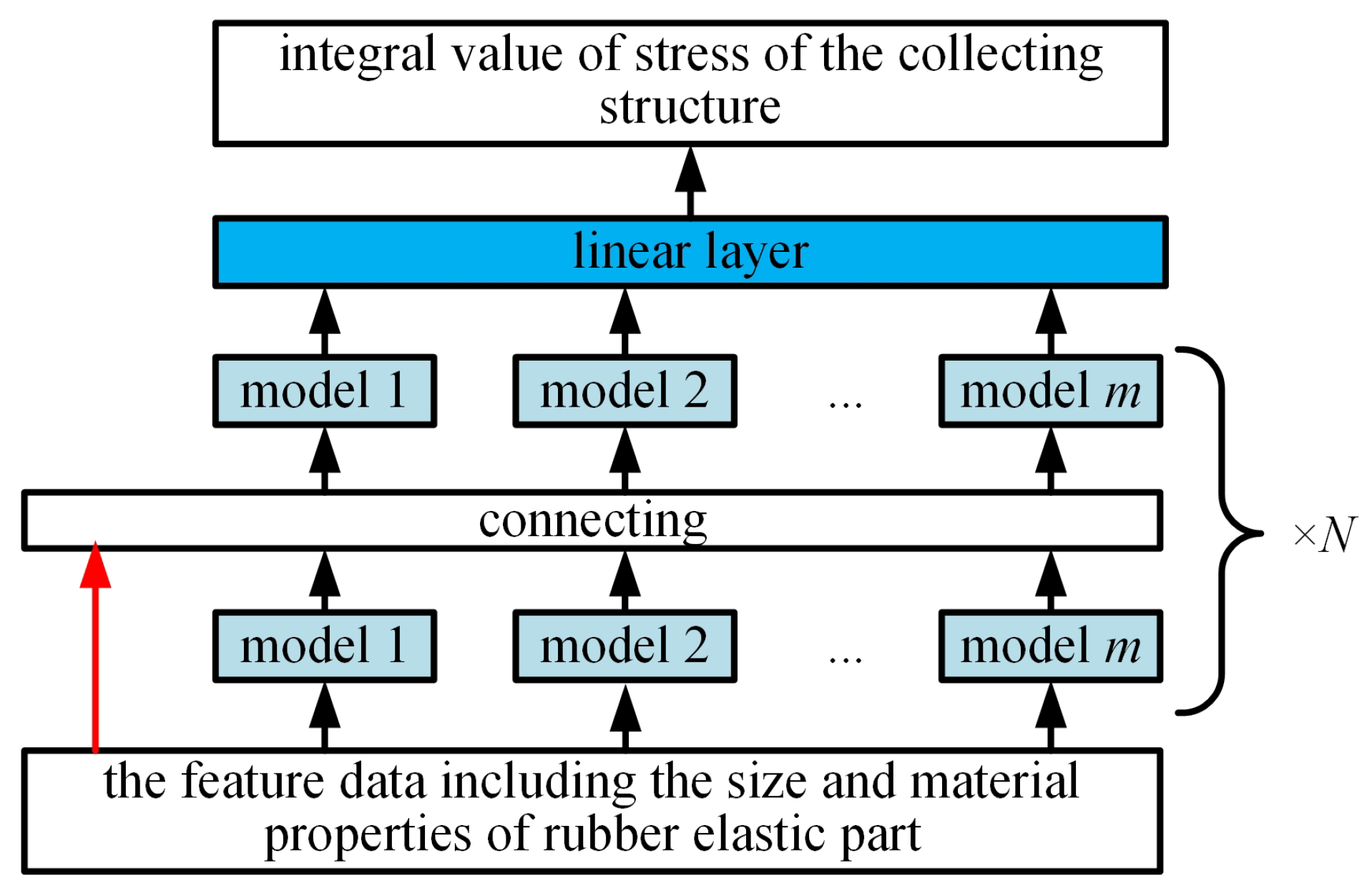
4.2. Basic Architecture of the Prediction Model of the Collecting Performance Based on AutoML
4.3. Model Fusing with the Machine Learning Algorithm
4.4. Training Process
| Algorithm 1: Detailed training process of the collecting performance prediction. Training strategy of the prediction model of the collecting performance of the eccentric rubber collector based on AutoGluon | |
| Input: Data (X: feature of rubber elastic part, Y: collecting performance); M: set of sub-models; L: stacking layer number. | |
| Output: Prediction result of collecting performance of each model. | |
| 1: | automatic feature engineering |
| 2: | for l = 1 to L do integrating each layer, L = 4 |
| 3: | for i = 1 to n do n-times repetition, n = 2 |
| 4: | Divide the data into k parts randomly , k = 5 |
| 5: | for j = 1 to k do k-fold cross-validation and bagging integration |
| 6: | for each model type m in M do |
| 7: | train the model m on , |
| 8: | validate on , and the prediction value of each fold |
| 9: | end for |
| 10: | end for |
| 11: | end for |
| 12: | Average over the of all folds, |
| 13: | Update X, X = concatenate (X, ) |
| 14: | end for |
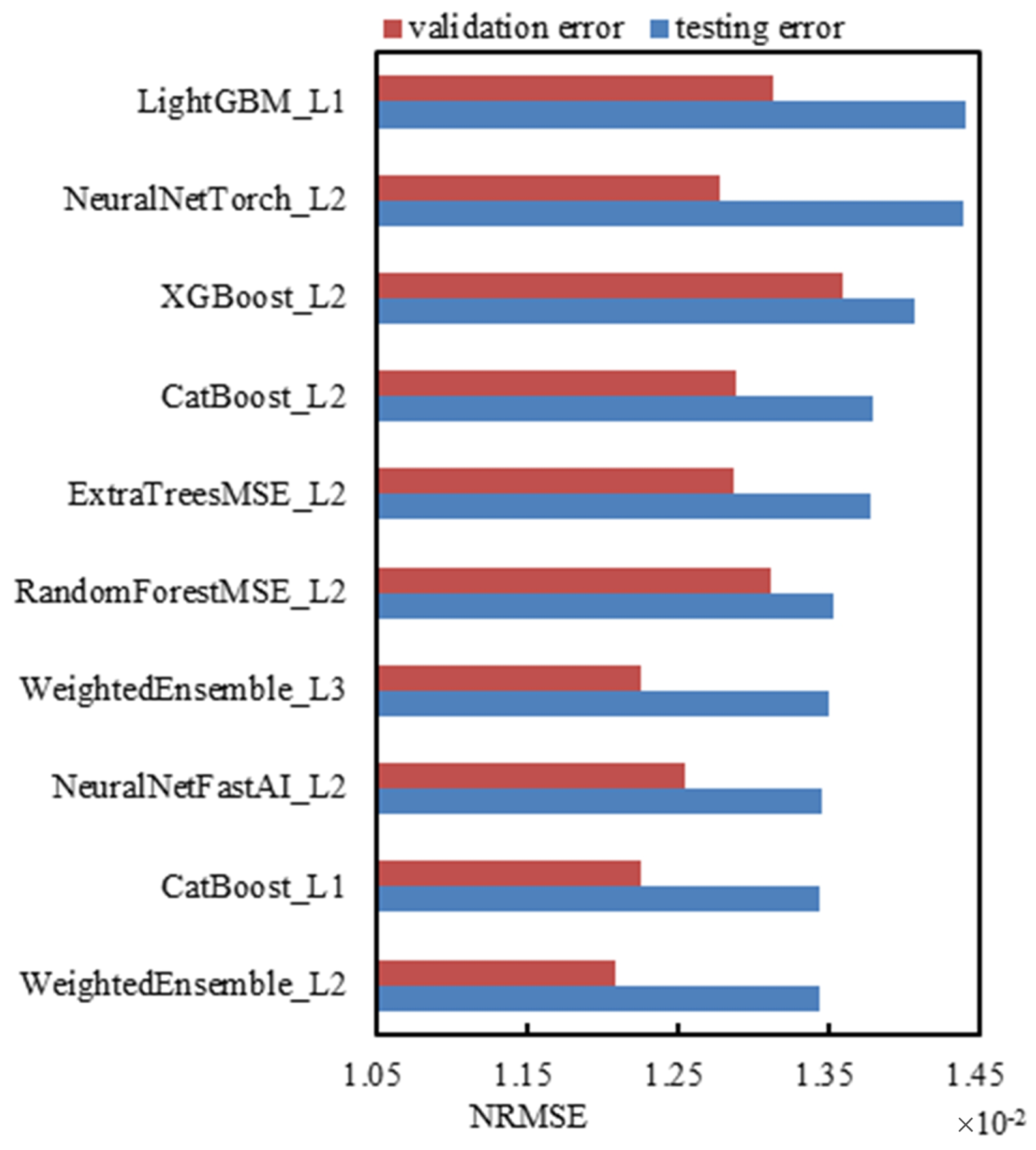
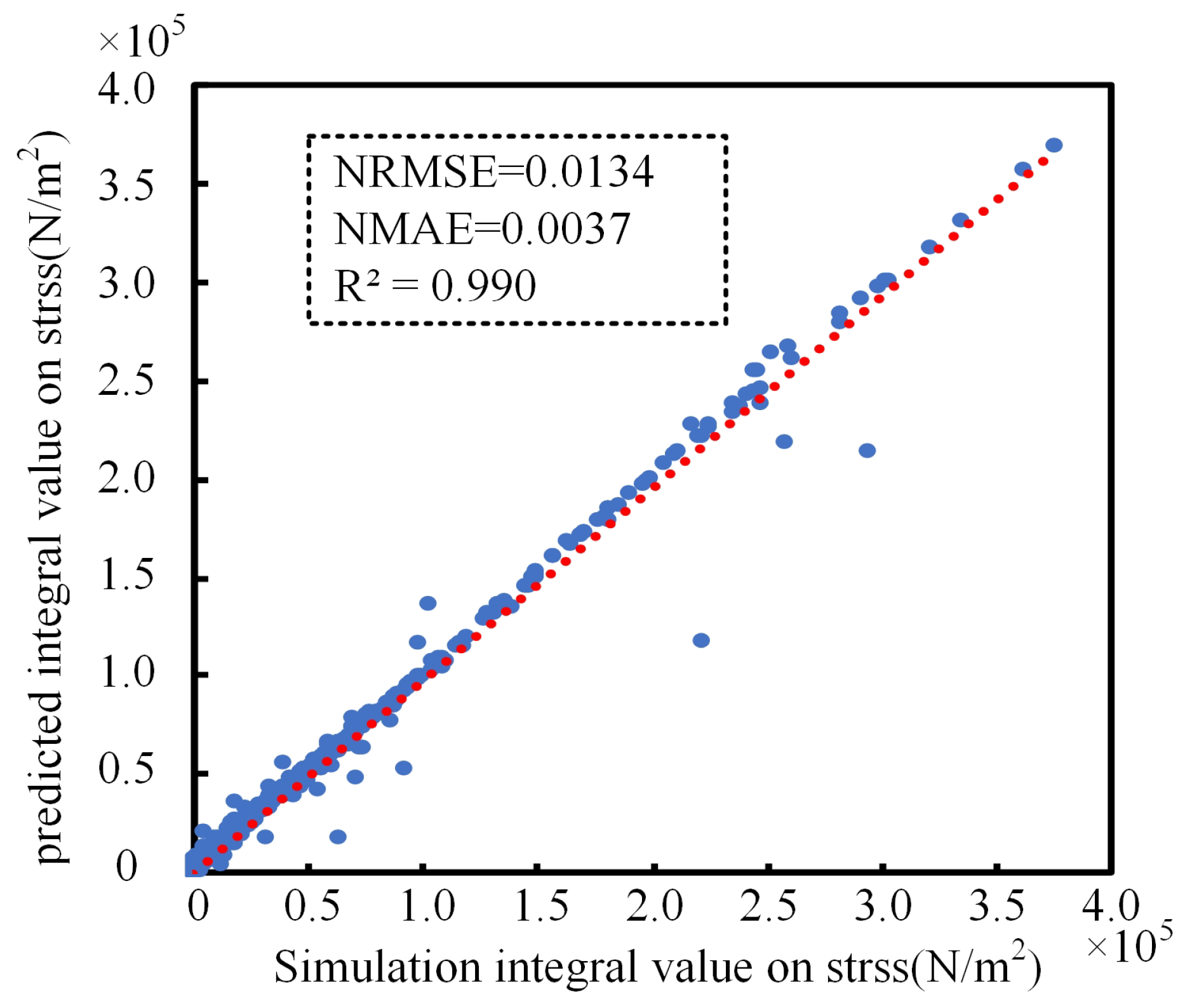
4.5. Prediction Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pu, C.; Zheng, H.; Yang, Z.; Gao, Z. Research status and development trend of the formation mechanism of complex fractures by staged volume fracturing in horizontal wells. Acta Pet. Sin. 2020, 41, 1734–1743. [Google Scholar] [CrossRef]
- Zhu, H.; Guo, J.; Huang, W.; Ji, Y.; Jing, X.; Lv, Y. Development and application of memory type fluid production profile logging technology in low liquid output horizontal wells. Drill. Prod. Technol. 2018, 41, 50–52. [Google Scholar] [CrossRef]
- Kong, L.; Li, L.; Kong, W.; Liu, X.; Li, Y.; Zhang, S. Overview of logging technique in oil production horizontal and high deviated wells. J. Yanshan Univ. 2015, 39, 1–8. [Google Scholar] [CrossRef]
- Li, X.; Qin, Y.; Chen, S.; Ge, H.; Tian, F. The horizontal well logging instrument conveying technology and its applications. China Pet. Mach. 2014, 42, 98–102. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Liu, S.; Liu, J.; Gao, Y.; Li, C. Gas-water flow law in horizontal wellbore and its influencing factors. Acta Pet. Sin. 2019, 40, 1244–1254. [Google Scholar] [CrossRef]
- Kong, W.H.; Li, H.; Li, L.; Xing, G.L. Water cut measurement of horizontal oil-water flow using trielectrode capacitance sensor. IEEE Trans. Ind. Electron. 2022, 69, 13686–13695. [Google Scholar] [CrossRef]
- Chen, D.B.; Zhu, R.D.; Wu, T.; Zhang, C.; Dai, Q.X. Finite element analysis of intelligent packer rubber based on Mooney-Rivlin model. J. Yangtze Univ. 2013, 10, 99–101. [Google Scholar] [CrossRef]
- Wu, W.; Fu, Y.; Niu, W. Numerical simulation of responses for cased-hole density logging. J. Geophys. Eng. 2013, 10, 054006. [Google Scholar] [CrossRef]
- Karmaker, S.K.; Hassan, M.M.; Smith, M.J.; Xu, L.; Zhai, C.; Veeramachaneni, K. AutoML to Date and Beyond: Challenges and Opportunities. ACM Comput. Surv. 2022, 54, 1–36. [Google Scholar] [CrossRef]
- Xin, D.; Wu, E.Y.; Lee, D.J.L.; Salehi, N.; Parameswaran, A. Whither AutoML? Understanding the Role of Automation in Machine Learning Workflows. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Online, 8–13 May 2021; Volume 83, pp. 1–16. [Google Scholar] [CrossRef]
- de Souza, D.C.M.; Cabrita, L.; Galinha, C.F.; Rato, T.J.; Reis, M.S. A Spectral AutoML approach for industrial soft sensor development: Validation in an oil refinery plant. Comput. Chem. Eng. 2021, 150, 107324. [Google Scholar] [CrossRef]
- Nikitin, N.; Revin, I.; Hvatov, A.; Vychuzhanin, P.; Kalyuzhnaya, A.V. Hybrid and automated machine learning approaches for oil fields development: The case study of volve field, north sea. Comput. Geosci. 2022, 161, 105061. [Google Scholar] [CrossRef]
- Yang, D. Application of coiled tubing bridge plug technology to deep gas well in Daqing oilfield. Well Test. 2016, 25, 54–58. [Google Scholar] [CrossRef]
- Qu, X.; Li, C.; Su, M.; Yuan, B.; Yun, X.; Qu, X. Segmented testing technology for horizontal wells with coiled tubing. Well Test. 2021, 30, 68–72. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, L.; Wu, G. Inflation and bifurcation of a compressible spherical membrane. Chin. J. Solid Mech. 2009, 30, 42–47. [Google Scholar] [CrossRef]
- Lalo, D.F.; Greco, M.; Meroniuc, M.; Thipprakmas, S. Numerical modeling and experimental characterization of elastomeric pads bonded in a conical spring under multiaxial loads and pre-compression. Math. Probl. Eng. 2019, 2019, 5182629. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Z.; Ma, X. Study on parameter characteristics of rubber Mooney-Rivlin model. Noise Vib. Control 2018, 38, 427–430. [Google Scholar]
- Yang, C.; Li, B.; Zheng, X.; Zhang, D. The evaluation of sealing and reliability of packer rubber based on working temperature. Chin. J. Appl. Mech. 2017, 34, 1079–1085. [Google Scholar]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl.-Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Ferreira, L.; Pilastri, A.; Martins, C.; Pires, P.M.; Cortez, P. A comparison of AutoML tools for machine learning, deep learning and xgboost. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]




| Name | Value | Note |
|---|---|---|
| Pipe_thick | 5 [mm] | Thickness of casing pipe |
| Pipe_height | 200 [mm] | Length of casing pipe |
| Pipe_r | 62.5 [mm] | Inner diameter of casing pipe |
| Rubber_r | 32–38 [mm] | Outer diameter of rubber |
| Rubber_thick | 9–15 [mm] | Thickness of rubber |
| Rubber_height | 80–120 [mm] | Length of the rubber |
| Press | 0–35 [mm] | Axial extrusion range |
| Concave | 8–14 [mm] | Thickness of concave center |
| K | 3.56–21.34 [MPa] | Bulk modulus of elastic part |
| Bias | 1–5 [mm] | Eccentric degree |
| Name | Value | Note |
|---|---|---|
| Rubber_r | 38 [mm] | Outer diameter of the rubber |
| Rubber_thick | 12 [mm] | Thickness of the rubber |
| Rubber_height | 80 [mm] | Length of the rubber |
| 0.436 [MPa] | Mooney-Rivlin parameter | |
| 0.109 [MPa] | Mooney-Rivlin parameter | |
| Concave | 9 [mm] | Thickness of the concave center |
| Name | Value | Note |
|---|---|---|
| Rubber_r | 36 [mm] | Outer diameter of the rubber |
| Rubber_thick | 16 [mm] | Thickness of the rubber |
| Rubber_height | 105 [mm] | Length of the rubber |
| 0.436 [MPa] | Mooney-Rivlin parameter | |
| 0.109 [MPa] | Mooney-Rivlin parameter | |
| Concave | 13 [mm] | Thickness of the concave center |
| Parameter | Number | Average Value | Variance | Minimum Value | Maximum Value |
|---|---|---|---|---|---|
| 4789 | 26,594 | 49,202 | 0 | 385,176 | |
| 4789 | 0.5723 | 0.3887 | 0 | 1.926 | |
| 4789 | 0.2354 | 0.2186 | 0 | 0.963 | |
| Rubber_r | 4789 | 36.3 | 2.4 | 30 | 36 |
| Rubber_thick | 4789 | 14.1 | 1.99 | 12 | 16 |
| Rubber_height | 4789 | 93.2 | 12.48 | 80 | 105 |
| Press | 4789 | 18.78 | 1.55 | 0 | 30 |
| Concave | 4789 | 10.77 | 2.15 | 9 | 14 |
| K | 4789 | 7.74 | 7,475,537 | − | 2.13 |
| Bias | 4789 | 3.43 | 1.55 | 0 | 8 |
| Hyper-Parameter | Value | Note |
|---|---|---|
| num_epochs | 10 | Iterating number of NN model |
| learning_rate | ~ | Learning rate of NN model |
| activation | ‘relu’, ‘tanh’, ‘softrelu’ | Activation function of NN model |
| dropout_prob | 0–0.5 | Dropout of NN model |
| num_boost_round | 100 | Iterating number of GBM model |
| num_leaves | 26–66 | Leaf number of tree model |
| num_bag_folds | 5 | 5-fold cross-validation |
| num_bag_sets | 2 | Iterating number of Bagging |
| num_stack_levels | 4 | Layer number of stacking integration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Li, Y.; Chen, L.; Wang, X.; Kong, W. Collecting Performance Prediction for the Rubber Collector in Horizontal Wellbore Based on AutoML. Sensors 2025, 25, 1836. https://doi.org/10.3390/s25061836
Li S, Li Y, Chen L, Wang X, Kong W. Collecting Performance Prediction for the Rubber Collector in Horizontal Wellbore Based on AutoML. Sensors. 2025; 25(6):1836. https://doi.org/10.3390/s25061836
Chicago/Turabian StyleLi, Shaohua, Yang Li, Longlin Chen, Xianbin Wang, and Weihang Kong. 2025. "Collecting Performance Prediction for the Rubber Collector in Horizontal Wellbore Based on AutoML" Sensors 25, no. 6: 1836. https://doi.org/10.3390/s25061836
APA StyleLi, S., Li, Y., Chen, L., Wang, X., & Kong, W. (2025). Collecting Performance Prediction for the Rubber Collector in Horizontal Wellbore Based on AutoML. Sensors, 25(6), 1836. https://doi.org/10.3390/s25061836






