An Efficient 3D Measurement Method for Shiny Surfaces Based on Fringe Projection Profilometry
Abstract
1. Introduction
- (1)
- Dual-frequency heterodyne (DFH) complementary decoding to improve measurement efficiency. Conventional dual-frequency interpolation methods require at least six fringe patterns for phase unwrapping, but our proposed method only needs five, improving measurement efficiency. Additionally, we introduced a phase order complement strategy that does not require extra projected patterns, utilizing the captured fringe patterns themselves to correct potential phase ambiguities.
- (2)
- Polarizers to eliminate specular reflection. The existence of specular reflection is a challenge in the 3D measurement of shiny surfaces. To address this, previous methods have included multi-exposure, adaptive projection, and algorithmic compensation. However, due to specular reflection, even when projection light is dim, saturation can still occur, making it impossible to compute valid phase information, leading to the exclusion of these regions. By introducing polarizers, we can physically reduce the impact of specular reflection and effectively capture fringes in shiny regions.
- (3)
- Multi-scale convolutional neural network to enhance fringe quality. This approach works synergistically with the polarizer-based solution. While polarizers reduce specular reflections, they also darken the entire scene. Previous neural network-based methods either directly predict fringes in saturated regions or map the saturated phase to the ideal phase. These approaches require the network to infer the fringe or phase information in large saturated regions, which becomes difficult when the scene’s dynamic range is wide, resulting in more missing fringe information. In contrast, our method addresses the saturation problem by using polarizers to directly reduce the saturation of fringes and applies a neural network to enhance the accuracy of fringes, especially in dark regions. These dark regions contain object information but are susceptible to noise and step-like effects due to the camera’s intensity resolution limitations. Our method improves the accuracy of object fringes and reduces the impact of dark fringe areas. Previous methods often require estimation and reconstruction for missing information, while our approach focuses on denoising and refining existing information, so it is relatively easy to train the network. By combining physical solutions (polarization) with deep learning, we solve the overexposure problem in fringes, reducing the difficulty of network tasks and allowing the network to focus on noise reduction in dark fringes while maintaining 3D measurement accuracy.
2. Principle
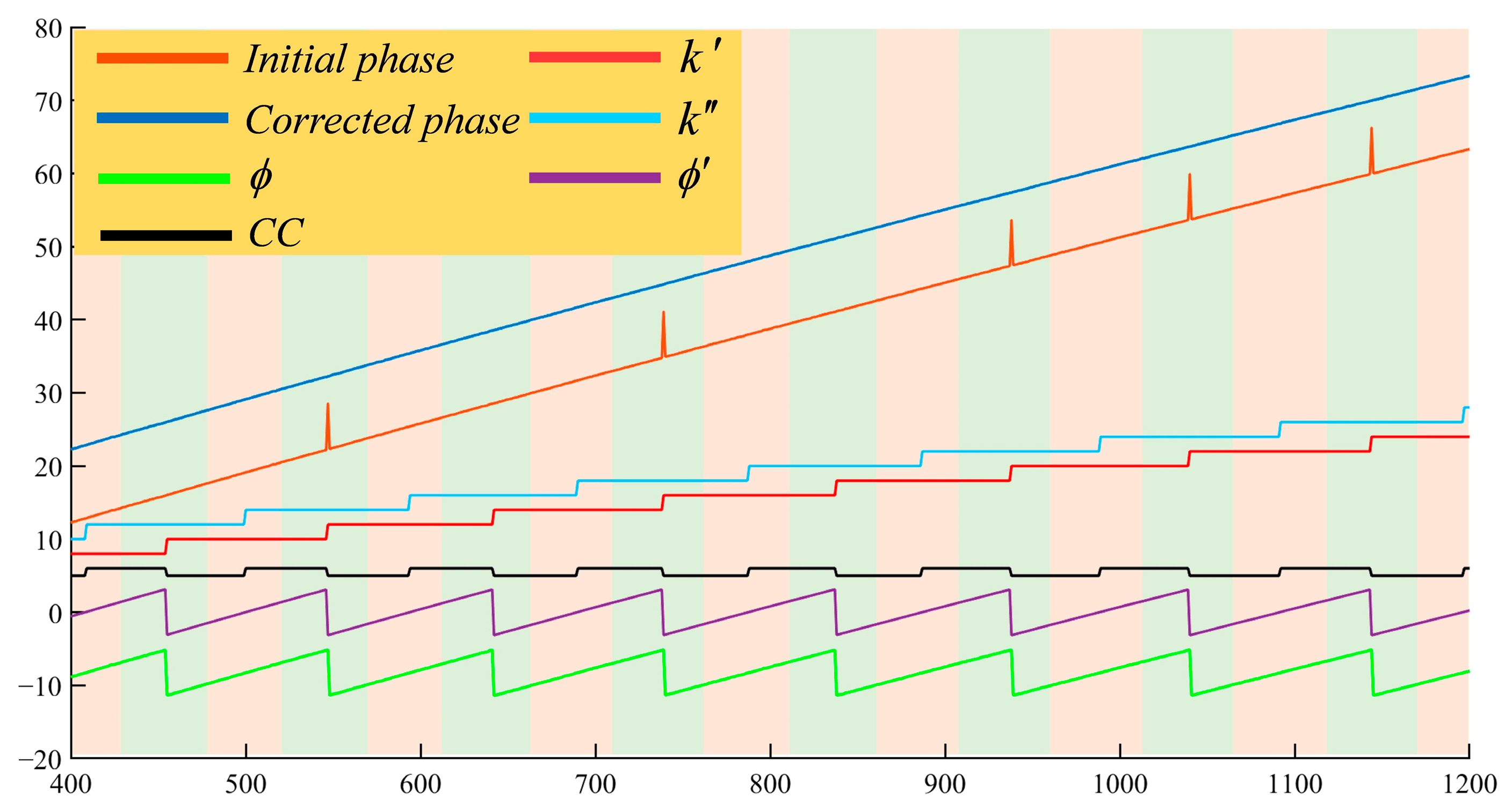
2.1. Dual-Frequency Heterodyne Complementary Decoding Method
2.2. Polarizers Eliminate Specular Reflection
2.3. Multi-Scale Convolutional Neural Network for Enhancing Fringe Quality
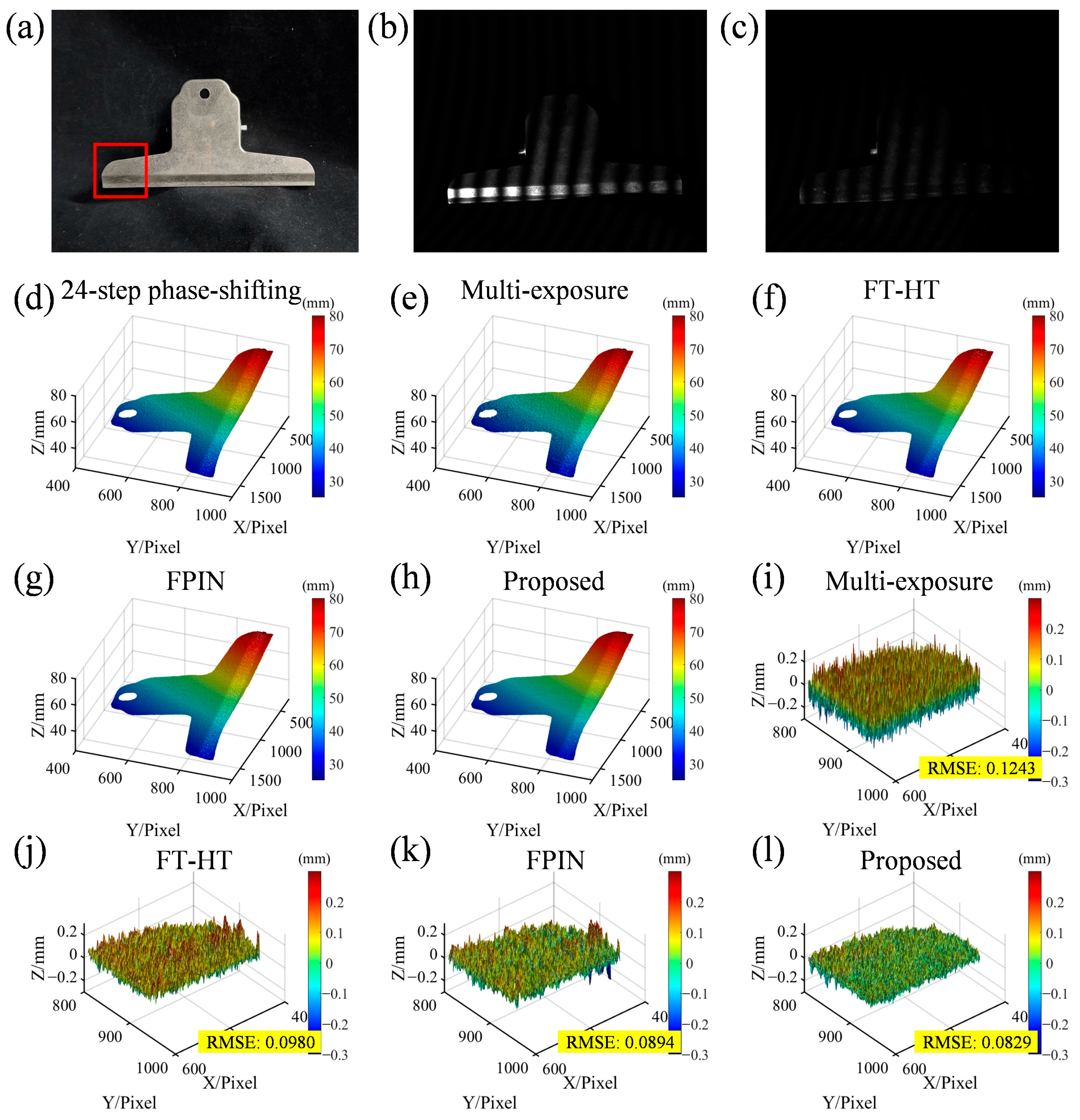
3. Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Lasers Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, L.; Zuo, C.; Tao, T.; Chen, Q.; Gu, G. High dynamic range 3D measurements with fringe projection profilometry: A review. Meas. Sci. Technol. 2018, 29, 122001. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High dynamic range scanning technique. Opt. Eng. 2009, 48, 033604. [Google Scholar]
- Waddington, C.; Kofman, J. Saturation avoidance by adaptive fringe projection in phase-shifting 3D surface-shape measurement. In Proceedings of the 2010 International Symposium on Optomechatronic Technologies, Toronto, ON, Canada, 25–27 October 2010; pp. 1–4. [Google Scholar]
- Du, J.; Yang, F.; Guo, H.; Zhu, J.; Zhou, P. Parameter selection on a multi-exposure fusion method for measuring surfaces with varying reflectivity in microscope fringe projection profilometry. Appl. Opt. 2024, 63, 3506–3517. [Google Scholar] [CrossRef]
- Feng, L.; Kang, J.; Li, H.; Zhang, Z.; Sun, Z.; Wu, B. Automatic exposure control method for 3D shape measurement of specular surface based on digital fringe projection. Meas. Sci. Technol. 2023, 34, 105201. [Google Scholar] [CrossRef]
- Xiang, S.; Huang, Z.; Deng, H.; Wu, J.; Yang, Y.; Yu, L. Adaptive pattern fusion for multi-reflectivity objects in fringe projection profilometry. Opt. Lasers Eng. 2024, 174, 107978. [Google Scholar] [CrossRef]
- Cheng, T.; Qin, L.; Li, Y.; Hou, J.; Xiao, C. An adaptive multi-exposure scheme for the structured light profilometry of highly reflective surfaces using complementary binary gray code. IEEE Trans. Instrum. Meas. 2024, 73, 5007912. [Google Scholar] [CrossRef]
- Jiang, C.; Bell, T.; Zhang, S. High dynamic range real-time 3D shape measurement. Opt. Express 2016, 24, 7337. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y. A new method for high dynamic range 3D measurement combining adaptive fringe projection and original-inverse fringe projection. Opt. Lasers Eng. 2023, 163, 107490. [Google Scholar] [CrossRef]
- Qi, Z.; Wang, Z.; Huang, J.; Xing, C.; Gao, J. Highlight removal based on the regional-projection fringe projection method. Opt. Eng. 2018, 57, 041404. [Google Scholar] [CrossRef]
- Chen, T.; Lensch, H.P.A.; Fuchs, C.; Seidel, H.-P. Polarization and phase-shifting for 3D scanning of translucent objects. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Salahieh, B.; Chen, Z.; Rodriguez, J.; Liang, R. Multi-polarization fringe projection imaging for high dynamic range objects. Opt. Express 2014, 22, 10064–10071. [Google Scholar] [PubMed]
- Tan, J.; Su, W.; He, Z.; Bai, Y.; Dong, B.; Xie, S. Generic saturation-induced phase error correction for structured light 3D shape measurement. Opt. Lett. 2022, 47, 3387–3390. [Google Scholar] [PubMed]
- Li, H.; Wei, H.; Liu, J.; Deng, G.; Zhou, S.; Wang, W.; He, L.; Tian, P. Fringe projection profilometry based on saturated fringe restoration in high dynamic range scenes. Sensors 2023, 23, 3133. [Google Scholar] [PubMed]
- Wei, H.; Li, H.; Liu, J.; Deng, G.; Zhou, S. A method for suppressing saturation-induced errors in fringe projection profilometry by fringe restoration assisted via Euler formula-based method and intersection points. IEEE Trans. Instrum. Meas. 2024, 73, 5031816. [Google Scholar]
- Zhang, L.; Chen, Q.; Zuo, C.; Feng, S. High-speed high dynamic range 3D shape measurement based on deep learning. Opt. Lasers Eng. 2020, 143, 106245. [Google Scholar]
- Yang, G.; Yang, M.; Zhou, N.; Wang, Y. High dynamic range fringe pattern acquisition based on deep neural network. Opt. Commun. 2022, 512, 128047. [Google Scholar]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar]
- Zhang, S. Digital multiple wavelength phase shifting algorithm. In Proceedings of the Optical Inspection and Metrology for Non-Optics Industries, San Diego, CA, USA, 3–4 August 2009; Volume 7432, p. 74320N. [Google Scholar]
- Zhang, Q.; Su, X.; Xiang, L.; Sun, X. 3-D shape measurement based on complementary Gray-code light. Opt. Lasers Eng. 2012, 50, 574–579. [Google Scholar]
- Qian, J.M.; Feng, S.; Li, Y.; Tao, T.; Han, J.; Chen, Q.; Zuo, C. Single-shot absolute 3D shape measurement with deep-learning-based color fringe projection profilometry. Opt. Lett. 2020, 45, 1842–1845. [Google Scholar]
- Yao, P.; Gai, S.; Da, F. Super-resolution technique for dense 3D reconstruction in fringe projection profilometry. Opt. Lett. 2021, 46, 4442–4445. [Google Scholar]
- Li, Y.; Wu, Z.; Shen, J.; Zhang, Q. Real-time 3D shape measurement of dynamic scenes using fringe projection profilometry: Lightweight NAS-optimized dual frequency deep learning approach. Opt. Express 2023, 31, 40803–40823. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Liu, J.; Wang, X.; He, Z.; Su, W.; Huang, T.; Xie, S. Large depth range binary-focusing projection 3D shape reconstruction via unpaired data learning. Opt. Lasers Eng. 2024, 181, 108442. [Google Scholar] [CrossRef]
- Tan, J.; Niu, H.; Su, W.; He, Z. Structured light 3D shape measurement for translucent media base on deep Bayesian inference. Opt. Laser Technol. 2025, 181, 111758. [Google Scholar] [CrossRef]
- Chen, W.; Feng, S.; Yin, W.; Li, Y.; Qian, J.; Chen, Q.; Zuo, C. Deep-learning-enabled temporally super-resolved multiplexed fringe projection profilometry: High-speed kHz 3D imaging with low-speed camera. PhotoniX 2024, 5, 25. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Qian, J.; Feng, S.; Chen, Q.; Zuo, C. Single-shot super-resolved fringe projection profilometry (SSSR-FPP): 100,000 frames-per-second 3D imaging with deep learning. Light Sci. Appl. 2025, 14, 70. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Li, H.; Li, X.; Wang, S.; Deng, G.; Zhou, S. An Efficient 3D Measurement Method for Shiny Surfaces Based on Fringe Projection Profilometry. Sensors 2025, 25, 1942. https://doi.org/10.3390/s25061942
Wei H, Li H, Li X, Wang S, Deng G, Zhou S. An Efficient 3D Measurement Method for Shiny Surfaces Based on Fringe Projection Profilometry. Sensors. 2025; 25(6):1942. https://doi.org/10.3390/s25061942
Chicago/Turabian StyleWei, Hao, Hongru Li, Xuan Li, Sha Wang, Guoliang Deng, and Shouhuan Zhou. 2025. "An Efficient 3D Measurement Method for Shiny Surfaces Based on Fringe Projection Profilometry" Sensors 25, no. 6: 1942. https://doi.org/10.3390/s25061942
APA StyleWei, H., Li, H., Li, X., Wang, S., Deng, G., & Zhou, S. (2025). An Efficient 3D Measurement Method for Shiny Surfaces Based on Fringe Projection Profilometry. Sensors, 25(6), 1942. https://doi.org/10.3390/s25061942




