Research on the Transformer Failure Diagnosis Method Based on Fluorescence Spectroscopy Analysis and SBOA Optimized BPNN
Abstract
1. Introduction
- The characteristic gas content does not change significantly, does not exceed the gas standard warning value, and cannot issue an early warning for latent hidden dangers in time;
- The intelligence is low and the auxiliary discrimination method is not flexible;
2. Materials and Methods
2.1. Materials
2.1.1. Experimental Samples
2.1.2. Spectral Acquisition
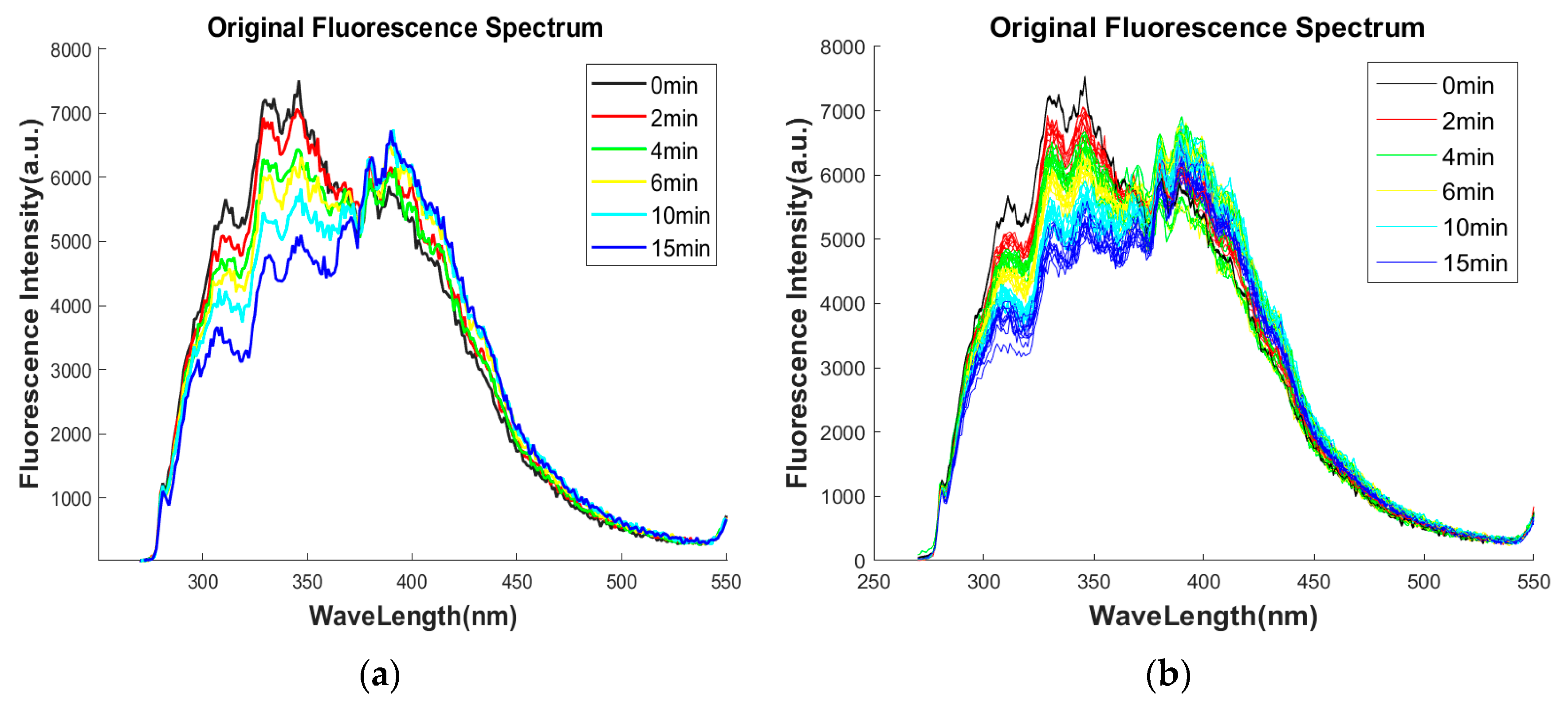
2.1.3. Original Spectral Analysis
2.2. Methods
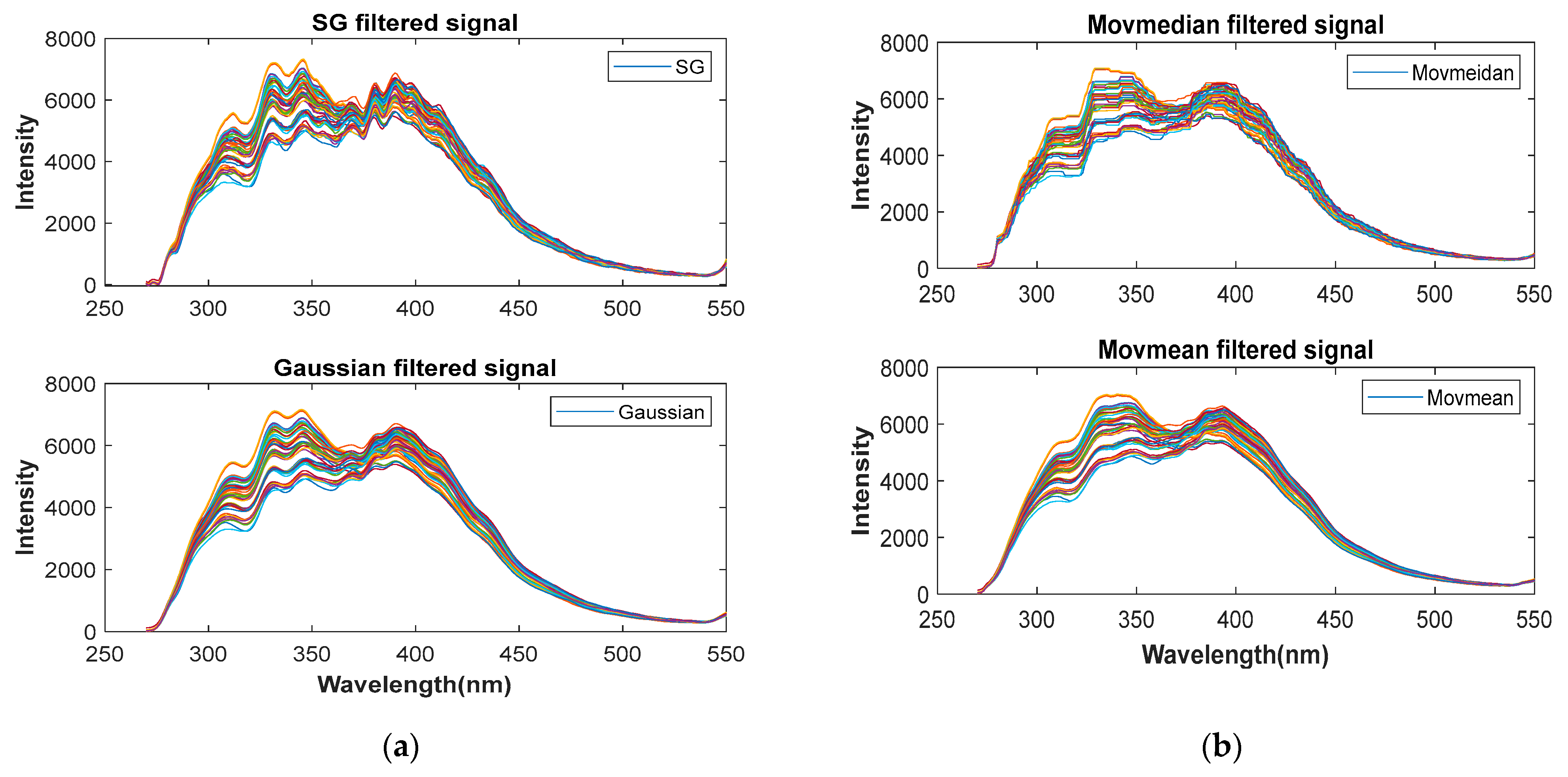
2.2.1. Spectral Preprocessing
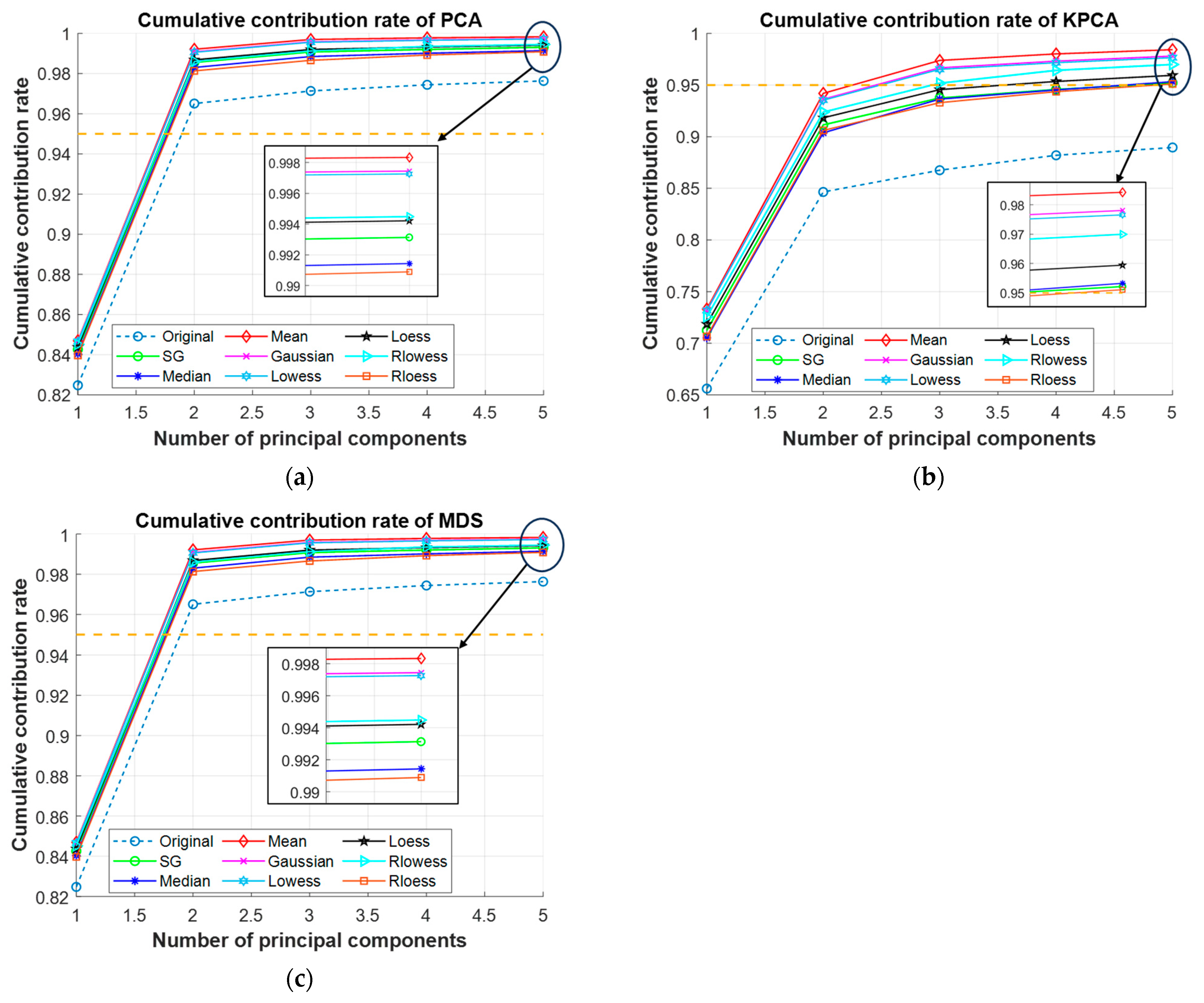
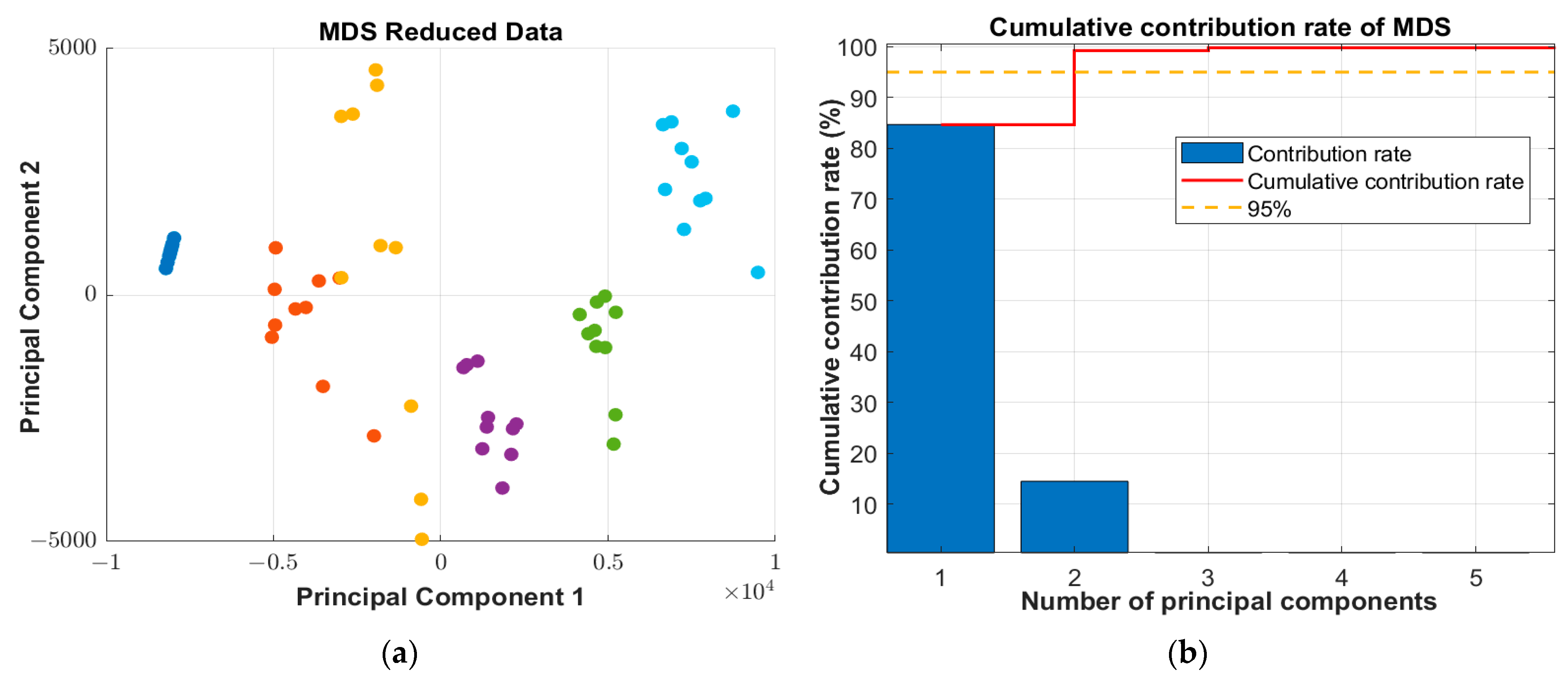
2.2.2. Dimensionality Reduction
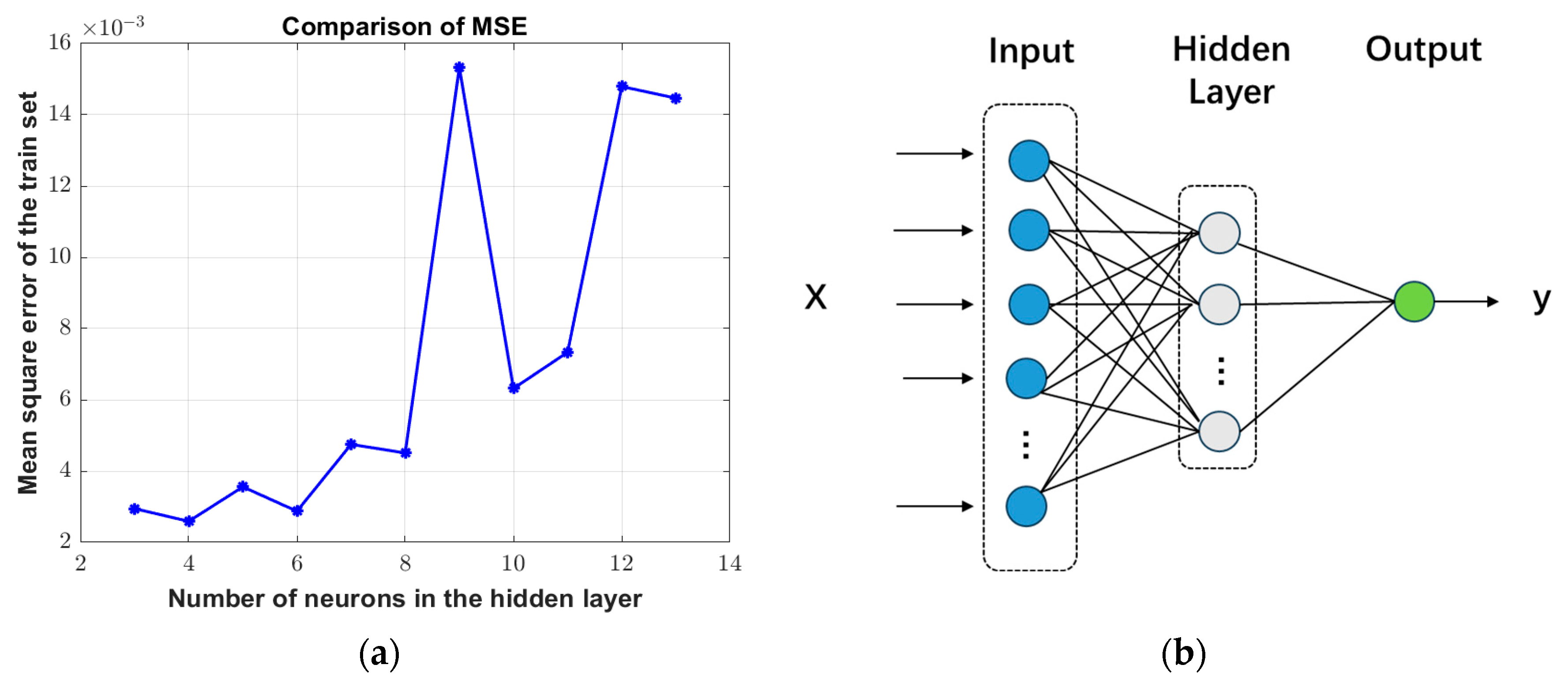
2.2.3. BP Neural Network
2.2.4. PSO Optimization
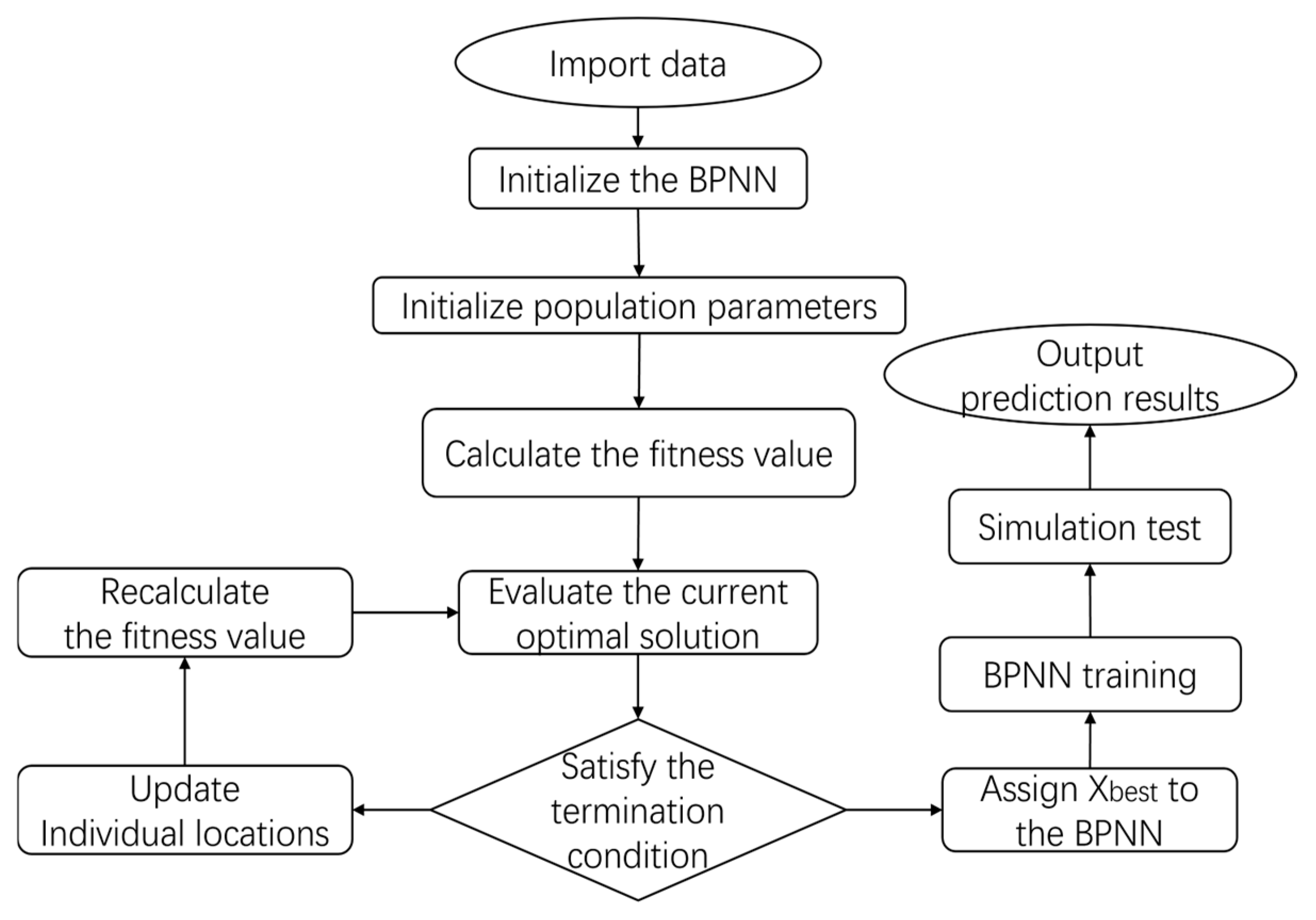
2.2.5. SBOA Optimization
- Step 1: Initialization stage:
- Step 2: Exploration stage P1:
- Hunting for prey:
- 2.
- Exhaust Prey:
- 3.
- Attack prey:
- Step 3: Development stage P2: there are two strategies for escaping from pursuit.
- Step 4: until the iterative termination condition is satisfied, the best solution is output.
3. Results and Discussion
3.1. Spectral Preprocessing
3.2. Dimensionality Reduction
3.3. BP Neural Network
3.4. PSO Optimization
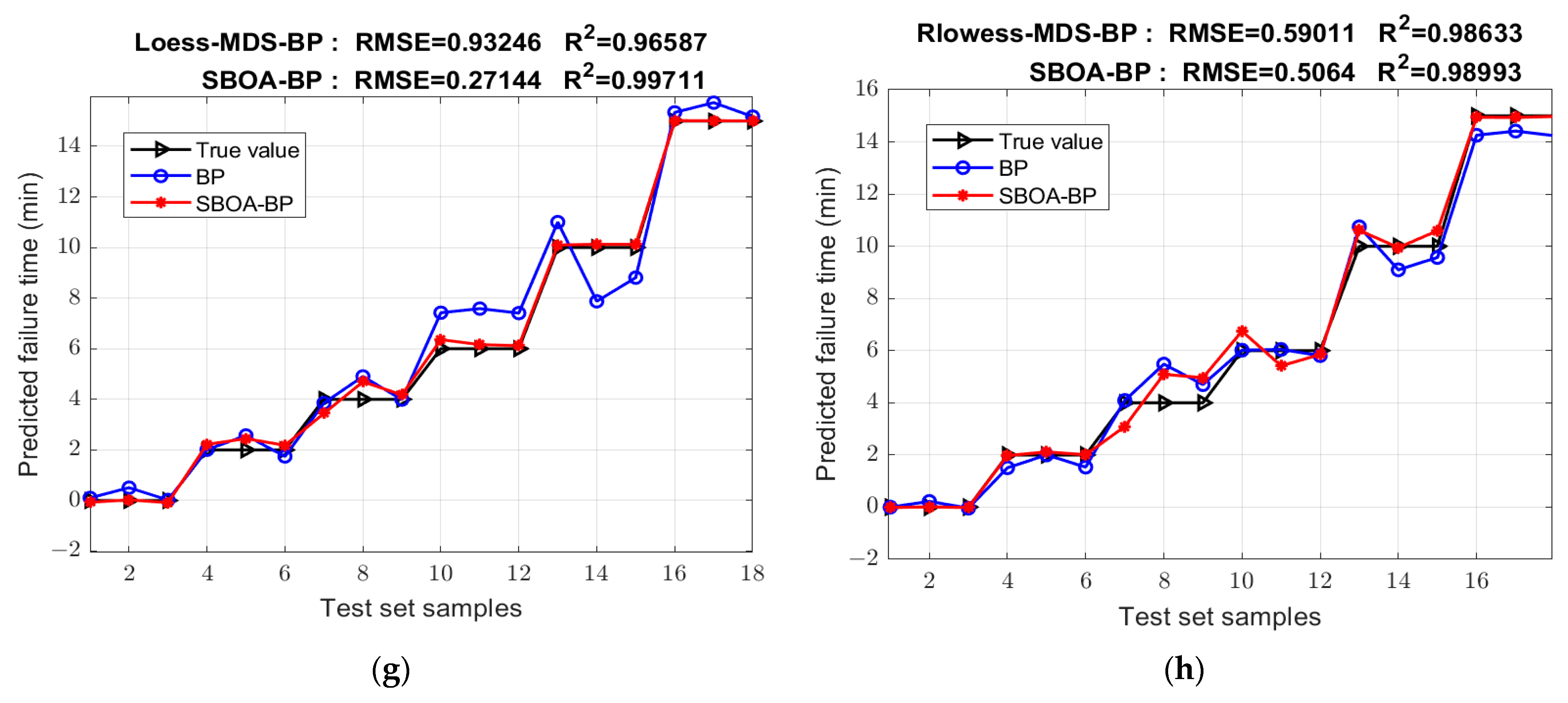
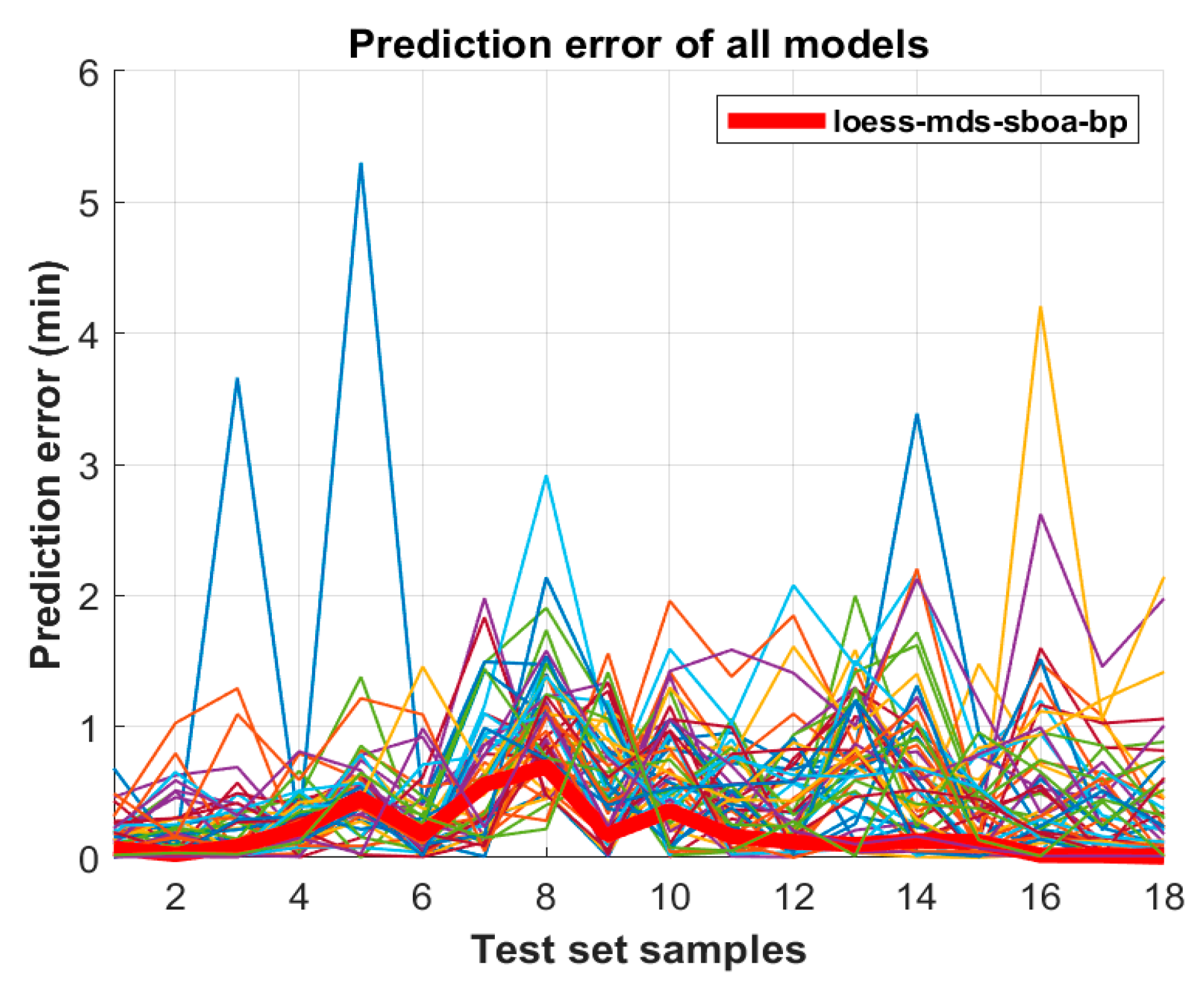
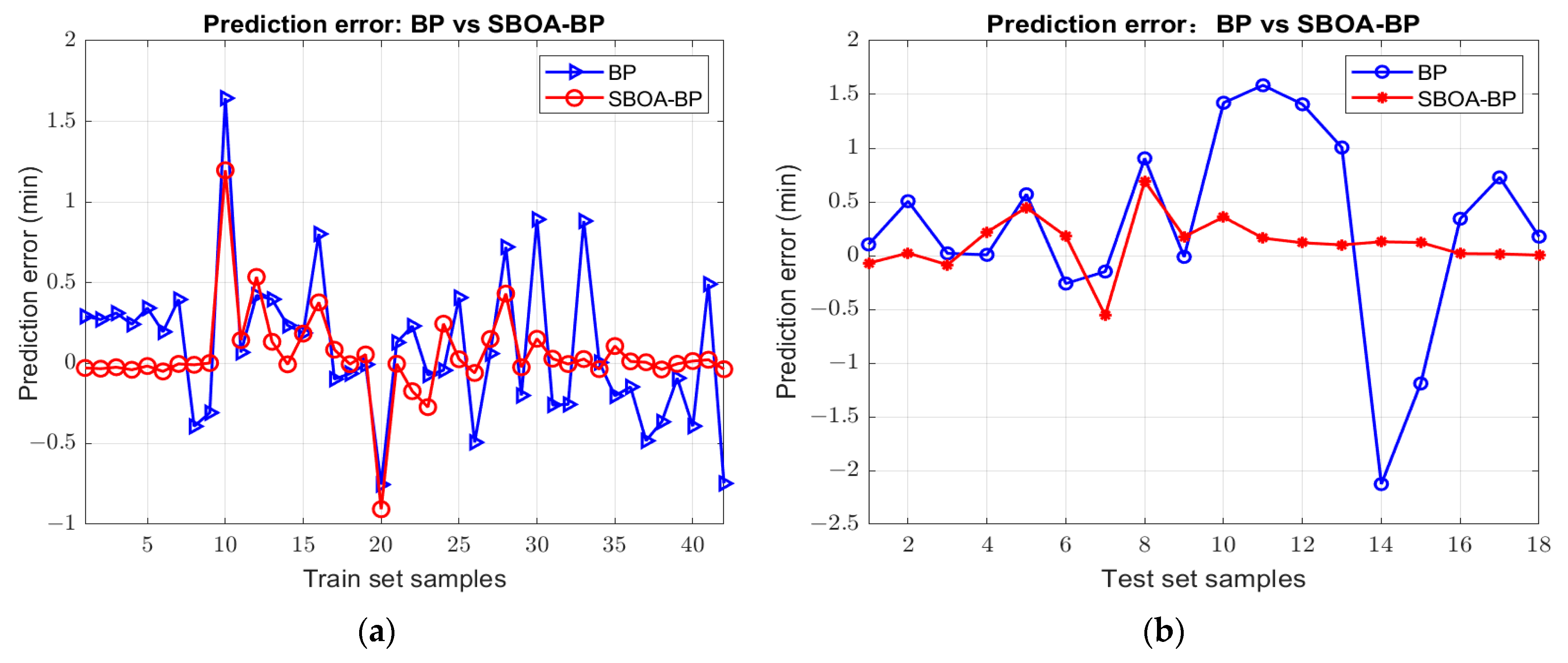
3.5. SBOA Optimization
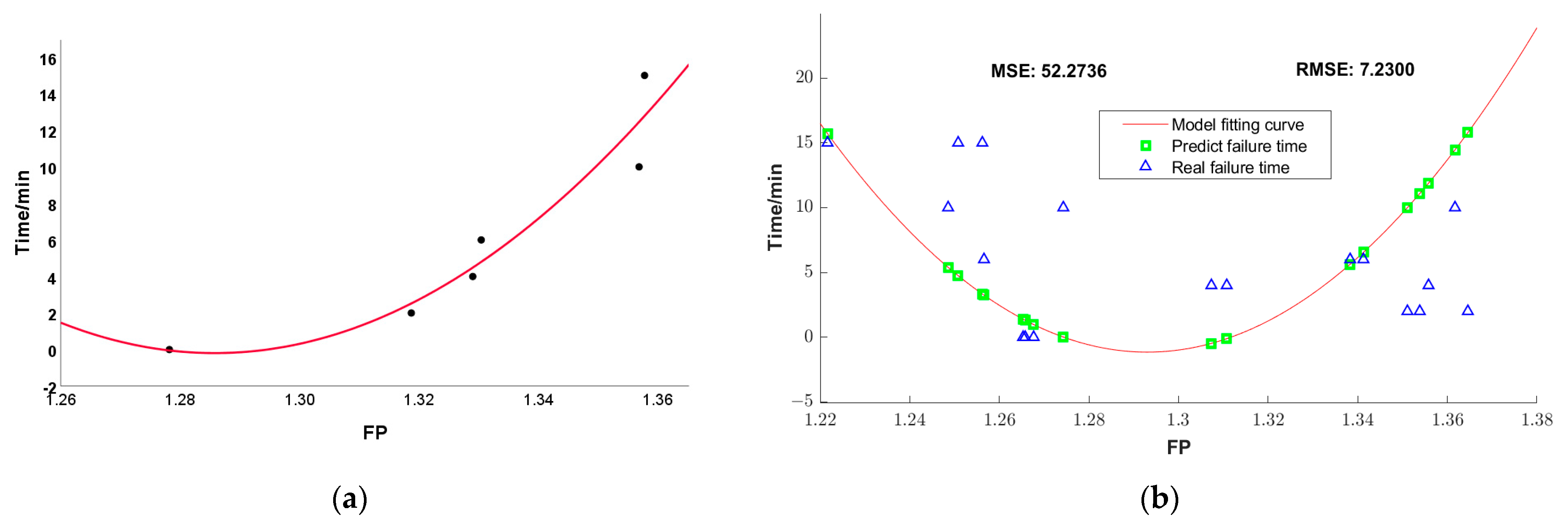
3.6. Fluorescence Double-Color Ratio
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Liu, Z.; Shi, Z.; Ma, L.; Du, H.; Han, D. Fault Diagnosis of the Power Transformer Based on PSO-SVM. In Proceedings of the 11th International Conference on Communications, Signal Processing, and Systems, Changbaishan, China, 23–24 July 2022. [Google Scholar] [CrossRef]
- Dhiman, A.; Kumar, R. Fault Diagnosis of a Transformer using Fuzzy Model and PSO optimized SVM. In Proceedings of the 2023 IEEE 8th International Conference for Convergence in Technology (I2CT 2023), Pune, India, 7–9 April 2023. [Google Scholar] [CrossRef]
- Zeng, B.; Guo, J.; Zhu, W.; Xiao, Z.; Yuan, F.; Huang, S. A Transformer Fault Diagnosis Model Based on Hybrid Grey Wolf Optimizer and LS-SVM. Energies 2019, 12, 4170. [Google Scholar] [CrossRef]
- Yang, X.L.; Yue, M.; Jia, T.B.; Sun, A.Q. Transformer Fault Diagnosis Based on DGA Information Fusion. In Proceedings of the 2023 4th International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE 2023), Hangzhou, China, 25–27 August 2023; pp. 241–244. [Google Scholar] [CrossRef]
- Ghoneim, S.S.M.; Taha, I.B.M. A new approach of DGA interpretation technique for transformer fault diagnosis. Int. J. Electr. Power. Energy Syst. 2016, 81, 265–274. [Google Scholar] [CrossRef]
- Sahoo, S.; Chowdary, K.V.V.S.R.; Das, S. DGA and AI Technique for Fault Diagnosis in Distribution Transformer. In Proceedings of the Lecture Notes in Electrical Engineering, Bhubaneswar, India, 5–6 March 2020; pp. 35–46. [Google Scholar] [CrossRef]
- Shi, Y.H.; Yang, Y.; Liao, Y.; Hong, L.Z.; Liao, M.Y.; Pang, S. Transformer fault diagnosis based on improved particle swarm optimization SVM. Eng. J. Wuhan Univ. 2023, 56, 1238–1244. [Google Scholar] [CrossRef]
- Kong, W.; Wan, F.; Lei, Y.; Wang, C.; Sun, H.; Wang, R.; Chen, W. Dynamic Detection of Decomposition Gases in Eco-Friendly C5F10O Gas-Insulated Power Equipment by Fiber-Enhanced Raman Spectroscopy. Anal Chem. 2024, 96, 15313–15321. [Google Scholar] [CrossRef]
- Si, S.H.; Zhao, J.Z.; Zou, G.L.; Liu, F.; Liu, C.; Yan, G.Y. Application of Fluorescence Spectroscopy in Identification of Aromatic Components in Single Oil Inclusions. Spectrosc. Spectral Anal. 2020, 40, 1736–1740. [Google Scholar] [CrossRef]
- Deepa, S.; Sarathi, R.; Mishra, A.K. Synchronous fluorescence and excitation emission characteristics of transformer oil ageing. Talanta 2006, 70, 811–817. [Google Scholar] [CrossRef] [PubMed]
- Suwarno; Pasaribu, R. Effects of thermal aging on paper characteristics in paper-mineral oil composite insulation. In Proceedings of the 2017 International Symposium on Electrical Insulating Materials, Toyohashi, Japan, 11–15 September 2017; pp. 705–708. [Google Scholar] [CrossRef]
- Boyekong, G.O.; Mengounou, G.M.; Nkouetcha, E.T.; Imano, A.M. Analysis of the Dielectric and Physicochemical Performances of Thermally Aged Natural Monoester Insulating Liquids. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2498–2506. [Google Scholar] [CrossRef]
- Markova, L.V.; Myshkin, N.K.; Makarenko, V.M. Fluorescence Method for Quick Transformer Oil Monitoring. Chem. Technol. Fuels Oils 2016, 52, 194–202. [Google Scholar] [CrossRef]
- Zhao, Y.; Leng, W.; Lin, Q.; Song, Y.M.; Zhang, Y.K.; Li, K.P.; Liu, J.Y.; Xu, F. Study on Insulation States Monitoring Technology of Transformer Insulating Oils Based on Three-dimensional Fluorescence Spectroscopy. Insul. Mater. 2022, 55, 87–91. [Google Scholar] [CrossRef]
- Yan, P.C.; Zhang, C.Y.; Sun, Q.S.; Shang, S.H.; Yin, N.N.; Zhang, X.F. LIF Technology and ELM Algorithm Power Transformer Fault Diagnosis Research. Spectrosc. Spectral Anal. 2022, 42, 1459–1464. [Google Scholar] [CrossRef]
- Dai, R.Y. Research on Rapid Fault Diagnosis of Transformers Based on Fluorescence Spectroscopy. Master’s Thesis, Anhui University of Science & Technology, Huainan, China, 2022. [Google Scholar] [CrossRef]
- Yan, P.C.; Zhang, C.Y.; Mei, K.F.; Chen, F.X.; Wang, Y.H. Research on fault diagnosis of transformer based on laser induced fluorescence technology. J. Mol. Struct. 2022, 1258, 132645. [Google Scholar] [CrossRef]
- Hu, F.; Hu, J.; Dai, R.; Guan, Y.; Shen, X.; Gao, B.; Wang, K.; Liu, Y.; Yao, X. Selection of characteristic wavelengths using SMA for laser induced fluorescence spectroscopy of power transformer oil. Spectrochim. Acta Part A 2023, 288, 122140. [Google Scholar] [CrossRef]
- Zou, D.; Li, Z.; Quan, H.; Peng, Q.; Wang, S.; Hong, Z.; Dai, W.; Zhou, T.; Yin, J. Transformer fault classification for diagnosis based on DGA and deep belief network. Energy Rep. 2023, 9, 250–256. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Fan, X.; Zhang, W.; Zhuo, R.; Hao, J.; Shi, Z. An Integrated Model for Transformer Fault Diagnosis to Improve Sample Classification near Decision Boundary of Support Vector Machine. Energies 2020, 13, 6678. [Google Scholar] [CrossRef]
- Hu, L.; Yin, L.; Mo, F.; Liang, Z.; Ruan, Z.; Wang, Y. A classification and prediction model with the sparrow search-probabilistic neural network algorithm for transformer fault diagnosis. Int. J. Sens. Netw. 2024, 44, 249–257. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, F.X.; Wang, A.J.; Li, D.C.; Song, Y.M.; Wu, J.; Cui, F.X.; Li, Y.Y.; Cao, Z.C. Research on Electric Breakdown Fault Diagnosis Model of Transformer Insulated Oil Based on Fluorescent Double-Color Ratio. Spectrosc. Spectral Anal. 2022, 42, 1134–1138. [Google Scholar] [CrossRef]
- Mu, L.; Li, D.C.; Wang, A.J.; Xie, J.; Zhao, Y.; Sun, X.B. Fluorescence Spectroscopy-based very Sensitive Detection Technique for Insulating Oil Conditions. In Proceedings of the 2023 International Conference on Optoelectronic Information and Functional Materials (OIFM 2023), Guangzhou, China, 14–16 April 2023. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Liu, X.; Liu, X. Research on a Fault Diagnosis Method of an A-Class Thermal Insulation Panel Production Line Based on Multi-Sensor Data Fusion. Appl. Sci. 2022, 12, 9642. [Google Scholar] [CrossRef]
- Xie, Y.C.; Wang, R.F.; Cao, Y.; Liu, K.; Gao, X.M. Research on Detecting CO2 with off-Beam Quartz-Enhanced Photoacoustic Spectroscopy at 2.004 μm. Spectrosc. Spectral Anal. 2000, 40, 2664–2669. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, K.; Zheng, L. Transformer Fault Diagnosis Method Based on TimesNet and Informer. Actuators 2024, 13, 74. [Google Scholar] [CrossRef]
- Song, Z.; Xiao, D.; Wei, Y.; Zhao, R.; Wang, X.; Tang, J. The Research on Complex Lithology Identification Based on Well Logs: A Case Study of Lower 1st Member of the Shahejie Formation in Raoyang Sag. Energies 2023, 16, 1748. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 1–102. [Google Scholar] [CrossRef]







| Degree | Acquisition Time | Numbers |
|---|---|---|
| 0 min | 1 March 2024 | 10 |
| 2 min | 1 March 2024 | 10 |
| 4 min | 1 March 2024 | 10 |
| 6 min | 1 March 2024 | 10 |
| 10 min | 1 March 2024 | 10 |
| 15 min | 1 March 2024 | 10 |
| Acquisition Parameters | Value |
|---|---|
| Excitation wavelength | 280 nm |
| Emission wavelength | 270 nm–600 nm |
| Excitation slit width | 1.5 nm |
| Emission slit width | 1.5 nm |
| Integration time | 100 ms |
| Excitation scan step size | 5.0 nm |
| Emission scan step size | 1.0 nm |
| Evaluation Indicators | Original | SG | Median | Mean | Gaussian | Lowess | Loess | Rlowess | Rloess |
|---|---|---|---|---|---|---|---|---|---|
| MAE | 1.8317 | 1.1962 | 1.3435 | 0.72386 | 0.80052 | 0.86717 | 0.97859 | 0.73532 | 1.1972 |
| MSE | 7.5201 | 2.1821 | 3.0601 | 1.2868 | 1.3843 | 1.5284 | 1.5227 | 0.94403 | 2.2853 |
| RMSE | 2.7423 | 1.4772 | 1.7493 | 1.1344 | 1.1766 | 1.2363 | 1.234 | 0.97161 | 1.5117 |
| R2 | 0.70477 | 0.91433 | 0.87987 | 0.94948 | 0.94566 | 0.94 | 0.94022 | 0.96294 | 0.91028 |
| Evaluation Indicators | Original | SG | Mean | Gaussian | Lowess | Loess | Rlowess | |
|---|---|---|---|---|---|---|---|---|
| PCA | MAE | 0.35217 | 0.31527 | 0.52965 | 0.70788 | 0.41558 | 0.53789 | 0.61502 |
| MSE | 0.23524 | 0.14999 | 0.35175 | 0.83849 | 0.27578 | 0.49177 | 0.95938 | |
| RMSE | 0.48502 | 0.38728 | 0.59309 | 0.91569 | 0.52514 | 0.70126 | 0.97948 | |
| R2 | 0.99076 | 0.99411 | 0.98619 | 0.96708 | 0.98917 | 0.98069 | 0.96234 | |
| KPCA | MAE | 0.61273 | 0.86364 | 0.54661 | 0.62488 | 1.1149 | 0.68433 | 0.67522 |
| MSE | 1.2029 | 1.2103 | 0.74745 | 0.56053 | 2.9142 | 0.64992 | 0.72844 | |
| RMSE | 1.0967 | 1.1001 | 0.86455 | 0.74868 | 1.7071 | 0.80618 | 0.85349 | |
| R2 | 0.95278 | 0.95249 | 0.97066 | 0.97799 | 0.88559 | 0.97449 | 0.9714 | |
| MDS | MAE | 0.60583 | 0.8366 | 0.43934 | 0.65861 | 0.5407 | 0.69559 | 0.43913 |
| MSE | 0.57823 | 1.1271 | 0.35401 | 0.8975 | 0.54504 | 0.86949 | 0.34823 | |
| RMSE | 0.76042 | 1.0616 | 0.59499 | 0.94736 | 0.73827 | 0.93246 | 0.59011 | |
| R2 | 0.9773 | 0.95575 | 0.9861 | 0.96477 | 0.9786 | 0.96587 | 0.98633 | |
| Gaussian- PCA | Loess-PCA | Rlowess- PCA | Original-KPCA | Lowess- KPCA | SG- MDS | Mean- MDS | |
|---|---|---|---|---|---|---|---|
| MAE | 0.56972 | 0.46691 | 0.5522 | 0.73889 | 0.76997 | 0.32626 | 0.31647 |
| MSE | 0.57442 | 0.35049 | 0.54673 | 0.94695 | 0.84421 | 0.23481 | 0.20332 |
| RMSE | 0.7579 | 0.59202 | 0.73941 | 0.97311 | 0.91881 | 0.48457 | 0.45091 |
| R2 | 0.97745 | 0.98624 | 0.97854 | 0.96282 | 0.96686 | 0.99078 | 0.99202 |
| Rlowess- PCA | Original-KPCA | SG- KPCA | Gaussian-KPCA | Lowess- KPCA | Lowess- MDS | Loess- MDS | Rlowess- MDS | |
|---|---|---|---|---|---|---|---|---|
| MAE | 0.57971 | 0.42633 | 0.58447 | 0.30992 | 0.92728 | 0.51085 | 0.19345 | 0.33531 |
| MSE | 0.69486 | 0.53103 | 0.52652 | 0.22168 | 1.6783 | 0.46405 | 0.073678 | 0.25644 |
| RMSE | 0.83359 | 0.72872 | 0.72562 | 0.47083 | 1.2955 | 0.68121 | 0.27144 | 0.5064 |
| R2 | 0.97272 | 0.97915 | 0.97933 | 0.9913 | 0.93411 | 0.98178 | 0.99711 | 0.98993 |
| 0 min | 2 min | 4 min | 6 min | 10 min | 15 min | |
|---|---|---|---|---|---|---|
| FP | 1.2782 | 1.3187 | 1.3290 | 1.3305 | 1.3569 | 1.3578 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, D.; Wang, A. Research on the Transformer Failure Diagnosis Method Based on Fluorescence Spectroscopy Analysis and SBOA Optimized BPNN. Sensors 2025, 25, 2296. https://doi.org/10.3390/s25072296
Chen X, Li D, Wang A. Research on the Transformer Failure Diagnosis Method Based on Fluorescence Spectroscopy Analysis and SBOA Optimized BPNN. Sensors. 2025; 25(7):2296. https://doi.org/10.3390/s25072296
Chicago/Turabian StyleChen, Xueqing, Dacheng Li, and Anjing Wang. 2025. "Research on the Transformer Failure Diagnosis Method Based on Fluorescence Spectroscopy Analysis and SBOA Optimized BPNN" Sensors 25, no. 7: 2296. https://doi.org/10.3390/s25072296
APA StyleChen, X., Li, D., & Wang, A. (2025). Research on the Transformer Failure Diagnosis Method Based on Fluorescence Spectroscopy Analysis and SBOA Optimized BPNN. Sensors, 25(7), 2296. https://doi.org/10.3390/s25072296






