Validation of Smartphones in Arbitrary Positions Against Force Plate Standard for Balance Assessment
Abstract
1. Introduction
2. Materials and Methods
2.1. Trial Overview
2.2. Data Acquisition
2.3. Analysis
2.3.1. Rigid Body Kinematics
2.3.2. Inverted Pendulum Model: Force Plate COP Displacement to COM Acceleration
2.3.3. Inverted Pendulum Model: Smartphone COM Acceleration to COP Displacement
2.4. Finite Difference
2.5. Filtering
2.6. Error Propagation
2.7. Results Correlation
2.8. Analysis Summary
3. Results
3.1. Center of Mass Acceleration Comparison
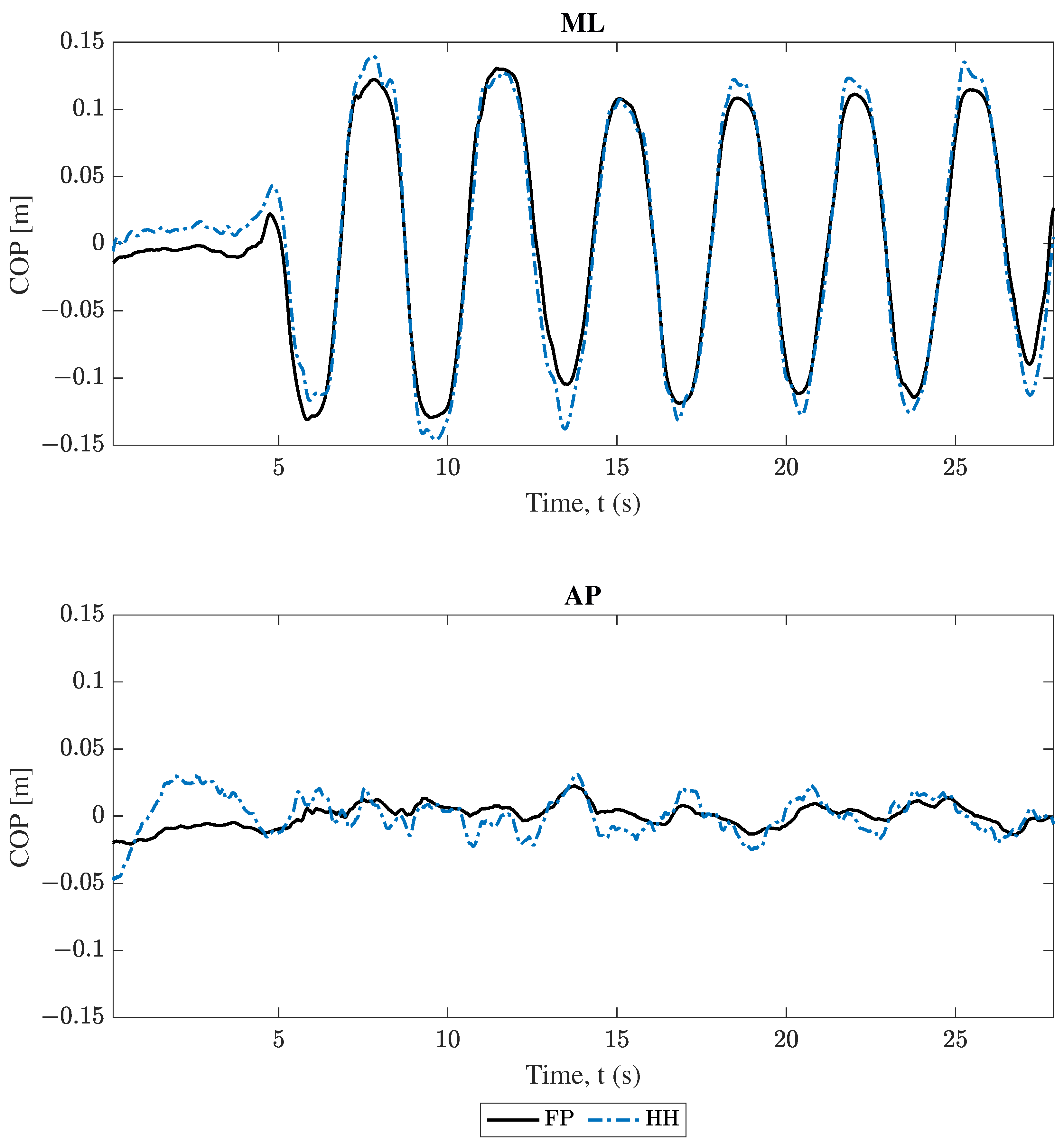
3.2. Center of Pressure Comparison
3.3. Data Correlation
3.4. Root Mean Square Error
4. Discussion
4.1. Key Findings
4.2. Device Location Comparison: Handheld Versus Back Harness Phone
4.3. Model Results Comparison: COM Acceleration Versus COP Position
4.4. Limitations
4.4.1. Model Limitations
4.4.2. Filtering
4.5. Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Inverted Pendulum Derivation
Appendix A.1. Assumptions and Definitions

| Name | Symbolic Form |
|---|---|
| Angular Acceleration | |
| COP Position | |
| COM Position | |
| Ground reaction force | |
| Angle of Body Rotation | |
| Ankle Height | h |
Appendix A.2. Static Analysis

Appendix A.3. Dynamic Analysis

Appendix A.4. Linking Static and Dynamic Results
References
- CDC. National Estimates of the 10 Leading Causes of Nonfatal Injuries Treated in Hospital Emergency Departments, United States—2017; CDC: Atlanta, GA, USA, 2019. [Google Scholar]
- Chen, B.; Liu, P.; Xiao, F.; Liu, Z.; Wang, Y. Review of the upright balance assessment based on the force plate. Int. J. Environ. Res. Public Health 2021, 18, 2696. [Google Scholar] [CrossRef]
- Hsieh, K.L.; Roach, K.L.; Wajda, D.A.; Sosnoff, J.J. Smartphone technology can measure postural stability and discriminate fall risk in older adults. Gait Posture 2019, 67, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Lattanzi, E.; Freschi, V.; Delpriori, S.; Klopfenstein, L.C.; Bogliolo, A. Standing balance assessment by measurement of body center of gravity using smartphones. IEEE Access 2020, 8, 96438–96448. [Google Scholar] [CrossRef]
- Horak, F.B.; Mancini, M. Objective biomarkers of balance and gait for Parkinson’s disease using body-worn sensors. Mov. Disord. 2013, 28, 1544–1551. [Google Scholar] [CrossRef]
- Ozinga, S.J.; Linder, S.M.; Alberts, J.L. Use of mobile device accelerometry to enhance evaluation of postural instability in Parkinson disease. Arch. Phys. Med. Rehabil. 2017, 98, 649–658. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Youm, S.; Jeon, Y.; Park, S.H. Development of a balance analysis system for early diagnosis of Parkinson’s disease. Int. J. Ind. Ergon. 2015, 48, 139–148. [Google Scholar] [CrossRef]
- Toots, A.; Littbrand, H.; Lindelöf, N.; Wiklund, R.; Holmberg, H.; Nordström, P.; Lundin-Olsson, L.; Gustafson, Y.; Rosendahl, E. Effects of a high-intensity functional exercise program on dependence in activities of daily living and balance in older adults with dementia. J. Am. Geriatr. Soc. 2016, 64, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.R.; Chiu, Y.L.; Chiang, S.L.; Chen, H.Y.; Sung, W.H. Development of a smartphone-based balance assessment system for subjects with stroke. Sensors 2019, 20, 88. [Google Scholar] [CrossRef]
- Logan, S.W.; Kipling Webster, E.; Getchell, N.; Pfeiffer, K.A.; Robinson, L.E. Relationship between fundamental motor skill competence and physical activity during childhood and adolescence: A systematic review. Kinesiol. Rev. 2015, 4, 416–426. [Google Scholar] [CrossRef]
- Maïano, C.; Hue, O.; April, J. Effects of motor skill interventions on fundamental movement skills in children and adolescents with intellectual disabilities: A systematic review. J. Intellect. Disabil. Res. 2019, 63, 1163–1179. [Google Scholar] [CrossRef]
- Miranda-Cantellops, N.; Tiu, T.K. Berg Balance Testing; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- Lima, C.A.; Ricci, N.A.; Nogueira, E.C.; Perracini, M.R. The Berg Balance Scale as a clinical screening tool to predict fall risk in older adults: A systematic review. Physiotherapy 2018, 104, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Blum, L.; Korner-Bitensky, N. Usefulness of the Berg Balance Scale in stroke rehabilitation: A systematic review. Phys. Ther. 2008, 88, 559–566. [Google Scholar] [CrossRef]
- Duarte, M.; Freitas, S.M.S.F.; Zatsiorsky, V. Control of equilibrium in humans. In Motor Control; Oxford University Press: Oxford, UK, 2010; pp. 219–242. [Google Scholar]
- Błaszczyk, J.W. The use of force-plate posturography in the assessment of postural instability. Gait Posture 2016, 44, 1–6. [Google Scholar] [CrossRef]
- Berger, L.; Chuzel, M.; Buisson, G.; Rougier, P. Undisturbed upright stance control in the elderly: Part 1. Age-related changes in undisturbed upright stance control. J. Mot. Behav. 2005, 37, 348–358. [Google Scholar] [CrossRef]
- Corriveau, H.; Hébert, R.; Raîche, M.; Dubois, M.F.; Prince, F. Postural stability in the elderly: Empirical confirmation of a theoretical model. Arch. Gerontol. Geriatr. 2004, 39, 163–177. [Google Scholar] [CrossRef] [PubMed]
- Masani, K.; Vette, A.H.; Kouzaki, M.; Kanehisa, H.; Fukunaga, T.; Popovic, M.R. Larger center of pressure minus center of gravity in the elderly induces larger body acceleration during quiet standing. Neurosci. Lett. 2007, 422, 202–206. [Google Scholar] [CrossRef]
- LeMoyne, R.; Mastroianni, T.; Cozza, M.; Coroian, C.; Grundfest, W. Implementation of an iPhone for characterizing Parkinson’s disease tremor through a wireless accelerometer application. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; IEEE: New York, NY, USA, 2010. [Google Scholar]
- Mayagoitia, R.E.; Lötters, J.C.; Veltink, P.H.; Hermens, H. Standing balance evaluation using a triaxial accelerometer. Gait Posture 2002, 16, 55–59. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Wang, Y.; Banda, J. Gait characteristic analysis and identification based on the iPhone’s accelerometer and gyrometer. Sensors 2014, 14, 17037–17054. [Google Scholar] [CrossRef]
- Winter, D. Biomechanics and Motor Control of Human Movement; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Anthony, E.C.; Kam, O.K.; Klisch, S.M.; Hazelwood, S.J.; Berg-Johansen, B. Balance assessment using a handheld smartphone with Principal Component Analysis for anatomical calibration. Sensors 2024, 24, 5467. [Google Scholar] [CrossRef]
- Estimate Phone Orientation Using Sensor Fusion. Available online: https://www.mathworks.com/help/nav/ug/estimate-phone-orientation-using-sensor-fusion.html (accessed on 30 January 2025).
- NASA. Anthropometry and Biomechanics. In Man-Systems Integration Standards; NASA: Washington, DC, USA, 1995; Volume 1. [Google Scholar]
- McGinnis, P. Biomechanics of Sport and Exercise; Human Kinetics: Champaign, IL, USA, 2013. [Google Scholar]
- Winter, D.A.; Patla, A.E.; Prince, F.; Ishac, M.; Gielo-Perczak, K. Stiffness Control of Balance in Quiet Standing. J. Neurophysiol. 1998, 80, 1211–1221. [Google Scholar] [CrossRef] [PubMed]
- Ledebt, A.; Brenière, Y. Dynamical implication of anatomical and mechanical parameters in gait initiation process in children. Hum. Mov. Sci. 1994, 13, 801–815. [Google Scholar] [CrossRef]
- Breniere, Y. Why we walk the way we do. J. Mot. Behav. 1996, 28, 291. [Google Scholar] [CrossRef]
- Fornberg, B. Generation of Finite Difference Formulas on Arbitrarily Spaced Grids. Math. Comput. 1988, 51, 699–706. [Google Scholar] [CrossRef]
- Taylor, C.R. Finite Difference Coefficients Calculator. 2016. Available online: https://web.media.mit.edu/~crtaylor/calculator.html (accessed on 4 April 2024).
- Crenna, F.; Rossi, G.B.; Berardengo, M. Filtering Biomechanical Signals in Movement Analysis. Sensors 2021, 21, 4580. [Google Scholar] [CrossRef] [PubMed]
- Doherty, C.; Zhao, L.; Ryan, J.; Komaba, Y.; Inomata, A.; Caulfield, B. Quantification of postural control deficits in patients with recent concussion: An inertial-sensor based approach. Clin. Biomech. 2017, 42, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Mancini, M.; Horak, F.B.; Zampieri, C.; Carlson-Kuhta, P.; Nutt, J.G.; Chiari, L. Trunk accelerometry reveals postural instability in untreated Parkinson’s disease. Park. Relat. Disord. 2011, 17, 557–562. [Google Scholar] [CrossRef]
- Yu, B.; Gabriel, D.; Noble, L.; An, K.N. Estimate of the Optimum Cutoff Frequency for the Butterworth Low-Pass Digital Filter. J. Appl. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. In Studies in Individual Differences: The Search for Intelligence; Appleton-Century-Crofts: Norwalk, CT, USA, 1961. [Google Scholar]
- Presley, B.; Sklar, J.; Hazelwood, S.; Berg-Johansen, B.; Klisch, S. Balance Assessment Using a Smartwatch Inertial Measurement Unit with Principal Component Analysis for Anatomical Calibration. Sensors 2023, 23, 4585. [Google Scholar] [CrossRef]
- Roeing, K.L.; Hsieh, K.L.; Sosnoff, J.J. A systematic review of balance and fall risk assessments with mobile phone technology. Arch. Gerontol. Geriatr. 2017, 73, 222–226. [Google Scholar] [CrossRef]
- Karlsson, A.; Frykberg, G. Correlations between force plate measures for assessment of balance. Clin. Biomech. 2000, 15, 365–369. [Google Scholar] [CrossRef]
- Shim, D.; Park, D.; Yoo, B.; Choi, J.O.; Hong, J.; Choi, T.Y.; Park, E.S.; Rha, D.W. Evaluation of sitting and standing postural balance in cerebral palsy by center-of-pressure measurement using force plates: Comparison with clinical measurements. Gait Posture 2022, 92, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Eom, G.M.; Kwon, Y.R.; Kim, D.Y.; Ko, J.; Kim, J.W. The influence of height on test-retest reliability of postural balance measures in healthy young adults. J. Mech. Med. Biol. 2022, 22. [Google Scholar] [CrossRef]
- Kot, A.; Nawrocka, A. Double inverted pendulum for human hip strategy of balance modelling. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 29 May–1 June 2016; IEEE: New York, NJ, USA, 2016; pp. 368–371. [Google Scholar]
- Khan, M.H.; Zöller, M.; Farid, M.S.; Grzegorzek, M. Marker-Based Movement Analysis of Human Body Parts in Therapeutic Procedure. Sensors 2020, 20, 3312. [Google Scholar] [CrossRef]
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 2018, 21, 1281–1289. [Google Scholar] [CrossRef]
- Nath, T.; Mathis, A.; Chen, A.C.; Patel, A.; Bethge, M.; Mathis, M.W. Using DeepLabCut for 3D markerless pose estimation across species and behaviors. Nat. Protoc. 2019, 14, 2152–2176. [Google Scholar] [CrossRef] [PubMed]


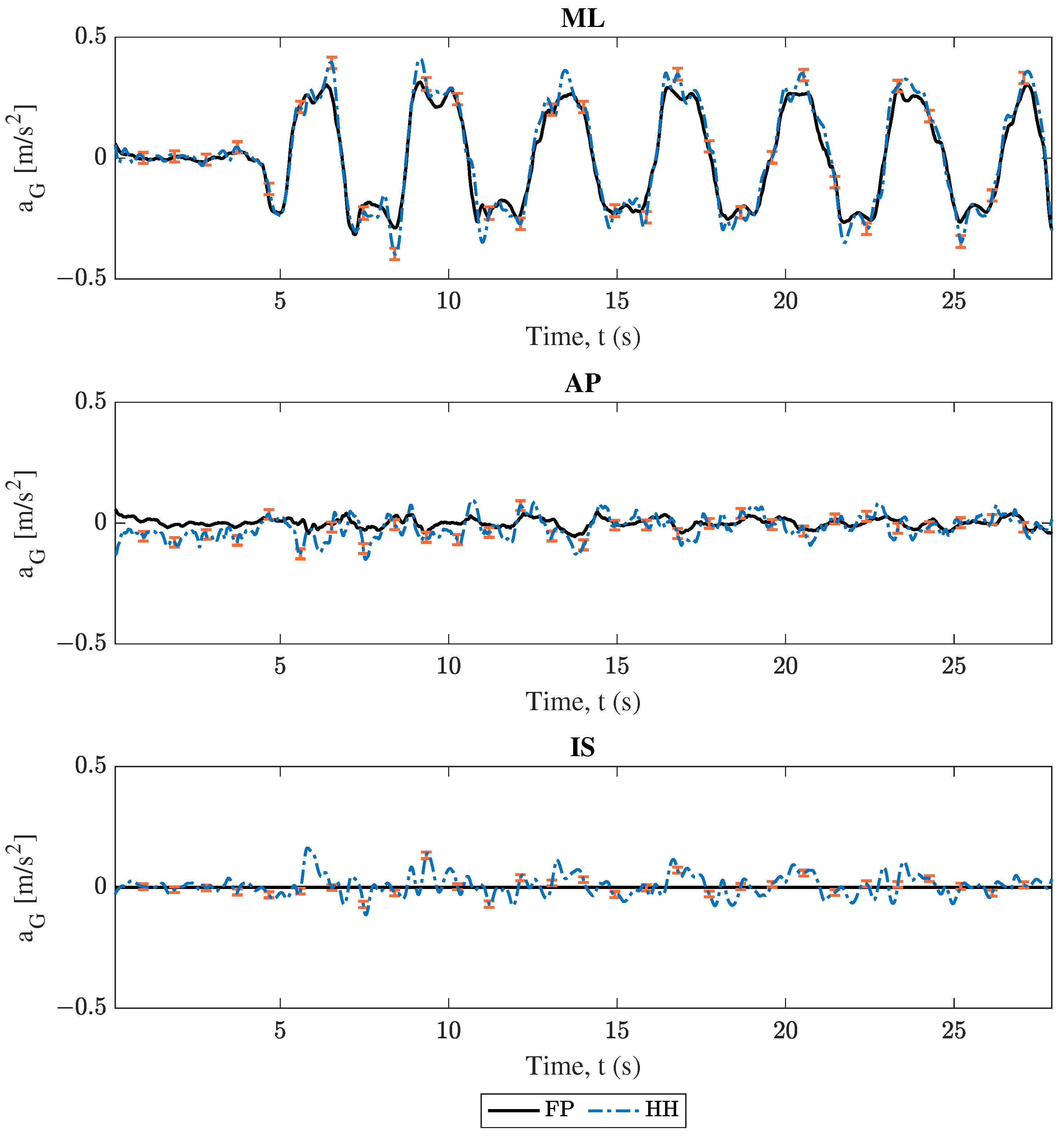
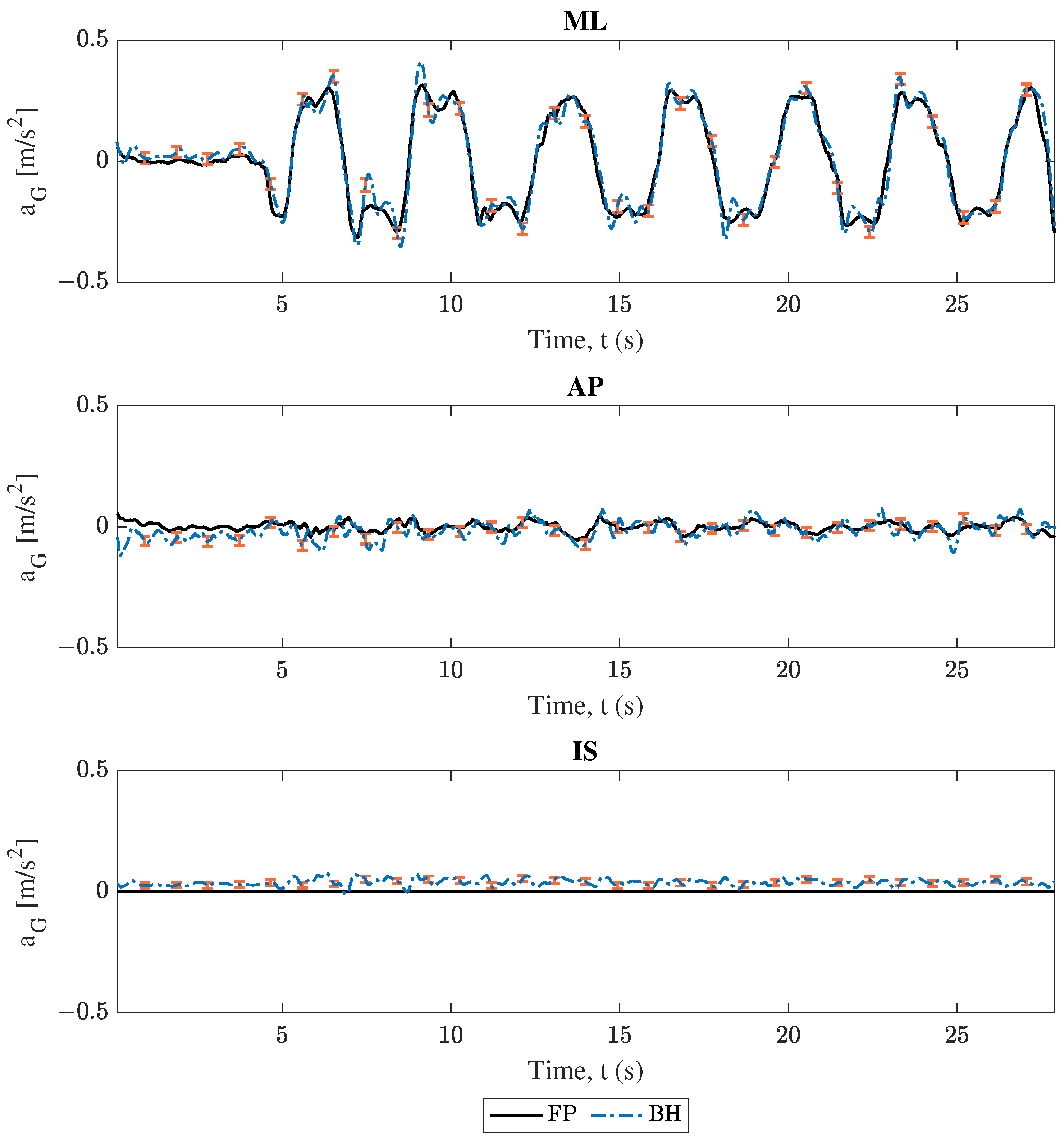
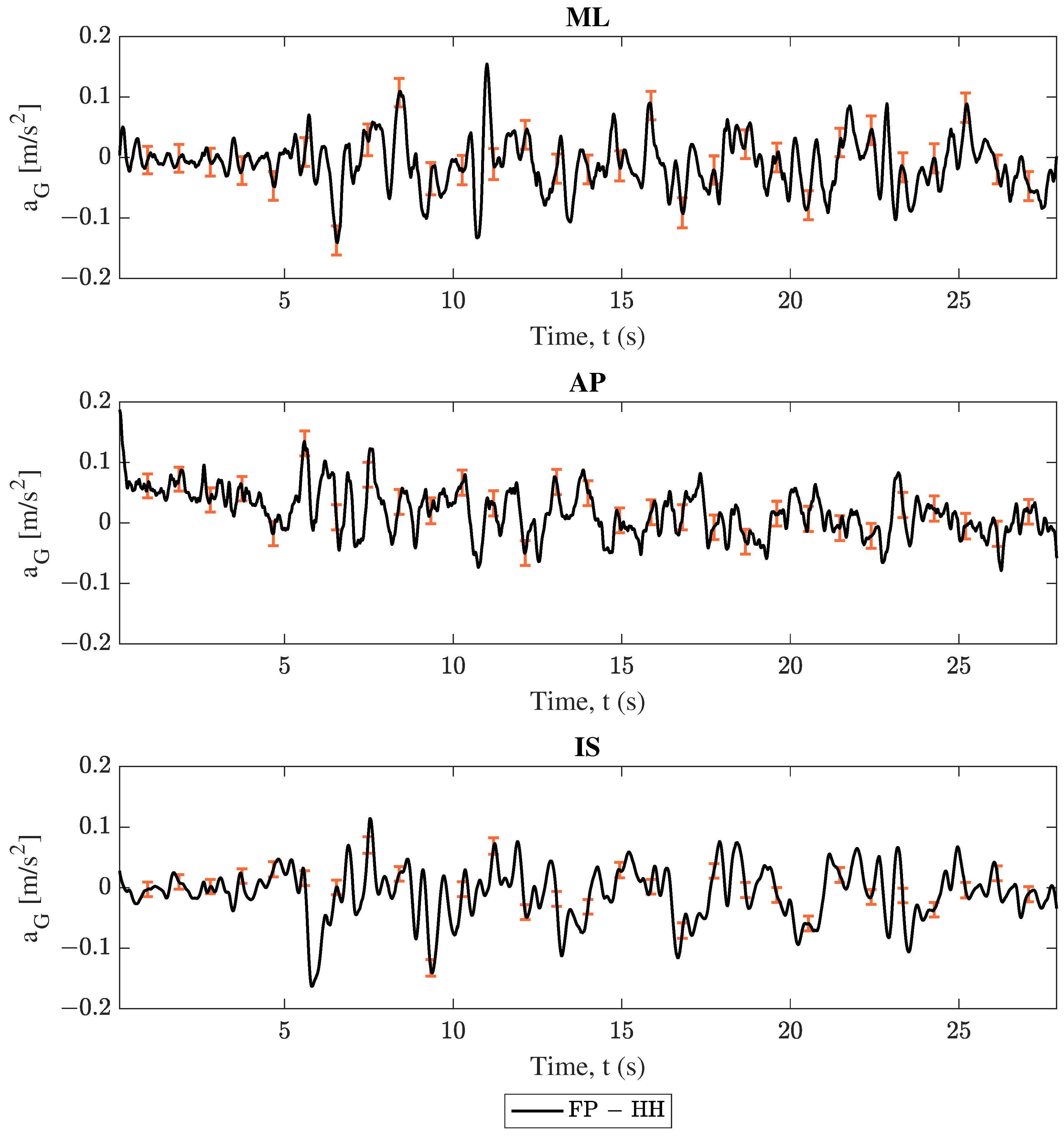


| Trial | Engaged Direction | Motion Description |
|---|---|---|
| 1 | None | Stable balance |
| 2 | ML | Swaying in medio–lateral direction |
| 3 | AP | Swaying in antero–posterior direction |
| 4 | Both | Random swaying in both directions |
| Trial | COM Acceleration | COP Position | |||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Comp. | Handheld | Back Harness | Handheld | Back Harness | ||||
| 1 | Norm | 0.271 | 0.000 | 0.334 | 0.000 | −0.133 | 0.000 | −0.018 | 0.446 |
| ML | 0.404 | 0.000 | 0.566 | 0.000 | 0.385 | 0.000 | 0.6949 | 0.0000 | |
| AP | 0.333 | 0.000 | 0.470 | 0.000 | −0.102 | 0.000 | −0.1594 | 0.0000 | |
| IS | −0.000 | 1.000 | 0.000 | 1.000 | |||||
| 2 | Norm | 0.934 | 0.000 | 0.915 | 0.000 | 0.963 | 0.000 | 0.9622 | 0.0000 |
| ML | 0.985 | 0.000 | 0.980 | 0.000 | 0.988 | 0.000 | 0.9883 | 0.0000 | |
| AP | 0.442 | 0.000 | 0.498 | 0.000 | 0.459 | 0.000 | 0.4594 | 0.0000 | |
| IS | 0.000 | 1.000 | 0.000 | 1.000 | |||||
| 3 | Norm | 0.949 | 0.000 | 0.874 | 0.000 | 0.855 | 0.000 | 0.7561 | 0.0000 |
| ML | 0.597 | 0.000 | 0.649 | 0.000 | 0.521 | 0.000 | 0.1587 | 0.0000 | |
| AP | 0.991 | 0.000 | 0.983 | 0.000 | 0.970 | 0.000 | 0.9462 | 0.0000 | |
| IS | −0.000 | 1.000 | −0.000 | 1.000 | |||||
| 4 | Norm | 0.742 | 0.000 | 0.811 | 0.0000 | 0.728 | 0.000 | 0.7153 | 0.0000 |
| ML | 0.921 | 0.000 | 0.962 | 0.000 | 0.910 | 0.000 | 0.9503 | 0.0000 | |
| AP | 0.956 | 0.000 | 0.962 | 0.000 | 0.948 | 0.000 | 0.9073 | 0.0000 | |
| IS | −0.000 | 1.000 | −0.000 | 1.000 | |||||
| Trial | COM Acceleration RMSE | COP Position RMSE | |||
|---|---|---|---|---|---|
| No. | Comp. | Handheld | Back Harness | Handheld | Back Harness |
| 1 | Norm | 0.0419 | 0.0373 | 0.0049 | 0.0035 |
| ML | 0.0157 | 0.0194 | 0.0025 | 0.0022 | |
| AP | 0.0300 | 0.0152 | 0.0069 | 0.0053 | |
| IS | 0.0345 | 0.0359 | |||
| 2 | Norm | 0.0497 | 0.0412 | 0.0137 | 0.0120 |
| ML | 0.0434 | 0.0393 | 0.0143 | 0.0126 | |
| AP | 0.0451 | 0.0339 | 0.0129 | 0.0102 | |
| IS | 0.0434 | 0.0397 | |||
| 3 | Norm | 0.0827 | 0.0777 | 0.0235 | 0.0227 |
| ML | 0.0289 | 0.0316 | 0.0057 | 0.0078 | |
| AP | 0.0775 | 0.0743 | 0.0238 | 0.0235 | |
| IS | 0.0403 | 0.0409 | |||
| 4 | Norm | 0.0967 | 0.0784 | 0.0178 | 0.0174 |
| ML | 0.0965 | 0.0665 | 0.0154 | 0.0116 | |
| AP | 0.1056 | 0.0858 | 0.0197 | 0.0204 | |
| IS | 0.0761 | 0.0429 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellsworth, G.J.; Klisch, S.M.; Berg-Johansen, B.; Ocegueda, E. Validation of Smartphones in Arbitrary Positions Against Force Plate Standard for Balance Assessment. Sensors 2025, 25, 2639. https://doi.org/10.3390/s25092639
Ellsworth GJ, Klisch SM, Berg-Johansen B, Ocegueda E. Validation of Smartphones in Arbitrary Positions Against Force Plate Standard for Balance Assessment. Sensors. 2025; 25(9):2639. https://doi.org/10.3390/s25092639
Chicago/Turabian StyleEllsworth, German Jack, Stephen M. Klisch, Britta Berg-Johansen, and Eric Ocegueda. 2025. "Validation of Smartphones in Arbitrary Positions Against Force Plate Standard for Balance Assessment" Sensors 25, no. 9: 2639. https://doi.org/10.3390/s25092639
APA StyleEllsworth, G. J., Klisch, S. M., Berg-Johansen, B., & Ocegueda, E. (2025). Validation of Smartphones in Arbitrary Positions Against Force Plate Standard for Balance Assessment. Sensors, 25(9), 2639. https://doi.org/10.3390/s25092639









