Automated Recognition and Measurement of Corrugated Pipes for Precast Box Girder Based on RGB-D Camera and Deep Learning
Abstract
Highlights
- Corrugated pipes were identified using semantic segmentation techniques applied to reinforcement cage point clouds acquired by cost-effective RGB-D sensors.
- After the segmentation, registration, and fitting processes, an optimal configuration was proposed with maximum measurement errors < 6 mm.
- It addresses the limitations of the automatic recognition of corrugated pipes caused by occlusion interference from rebars and precast molds.
- It replaces labor-intensive manual work in precast quality control, enhancing the efficiency and precision of the corrugated pipe recognition and measurement.
Abstract
1. Introduction
- (1)
- This paper develops an innovative integrated method for precise corrugated pipe recognition and measurement, combining registration algorithms, semantic segmentation, and fitting techniques, successfully meeting engineering standard requirements.
- (2)
- This paper comprehensively evaluates the applicability of different registration algorithms and compares the performance between traditional and neural network approaches in corrugated pipe curve fitting, providing valuable references for future pipe measurement research.
- (3)
- The proposed methodology addresses manual detection limitations by improving efficiency, reducing subjectivity, and enhancing operational safety in prestressed corrugated pipe measurement.
- (4)
- This paper proposes a cost-effective automated measurement solution using RGB-D sensors, offering an economically viable paradigm for advancing the practical implementation of automated pipe measurement technologies.
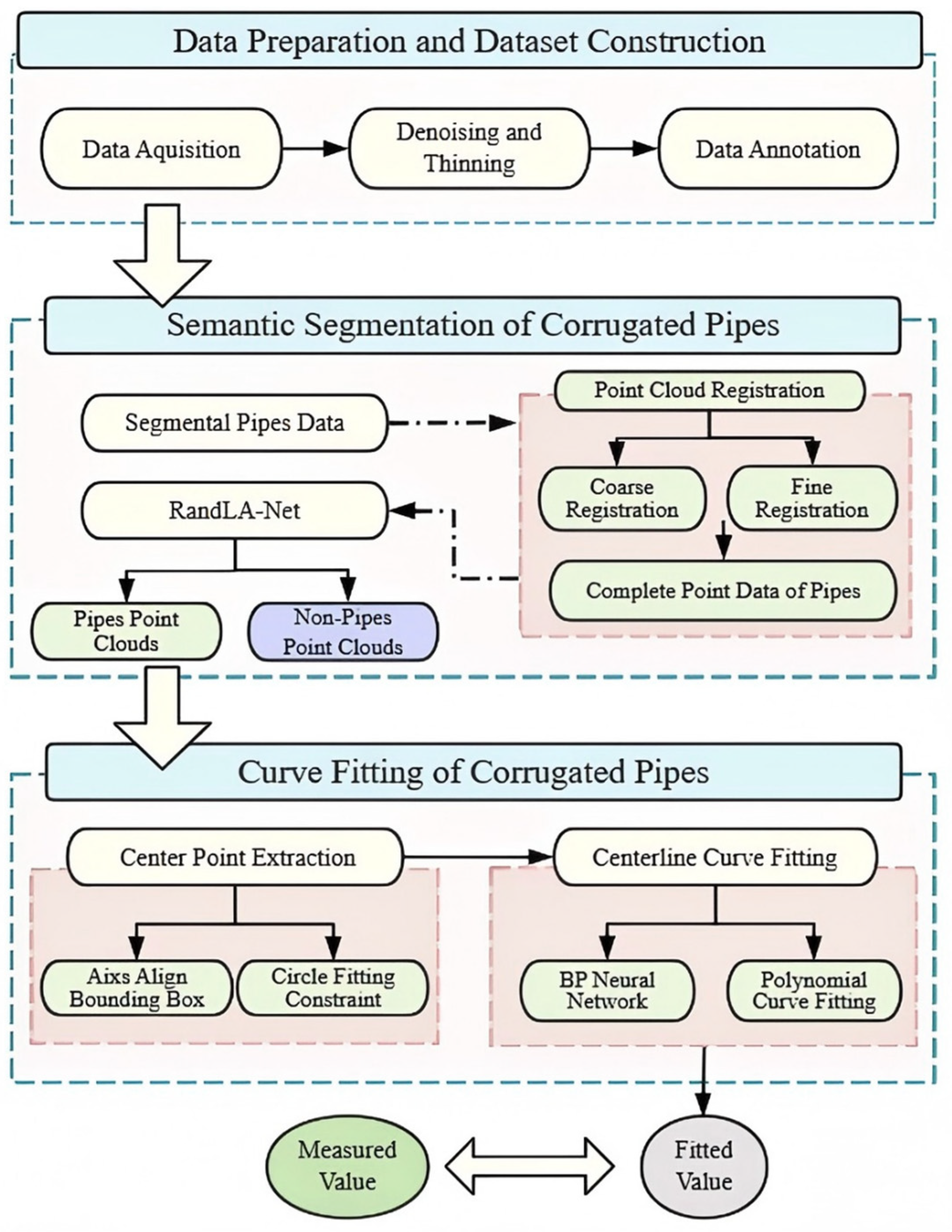
2. Methodology
3. Data Preparation and Registration
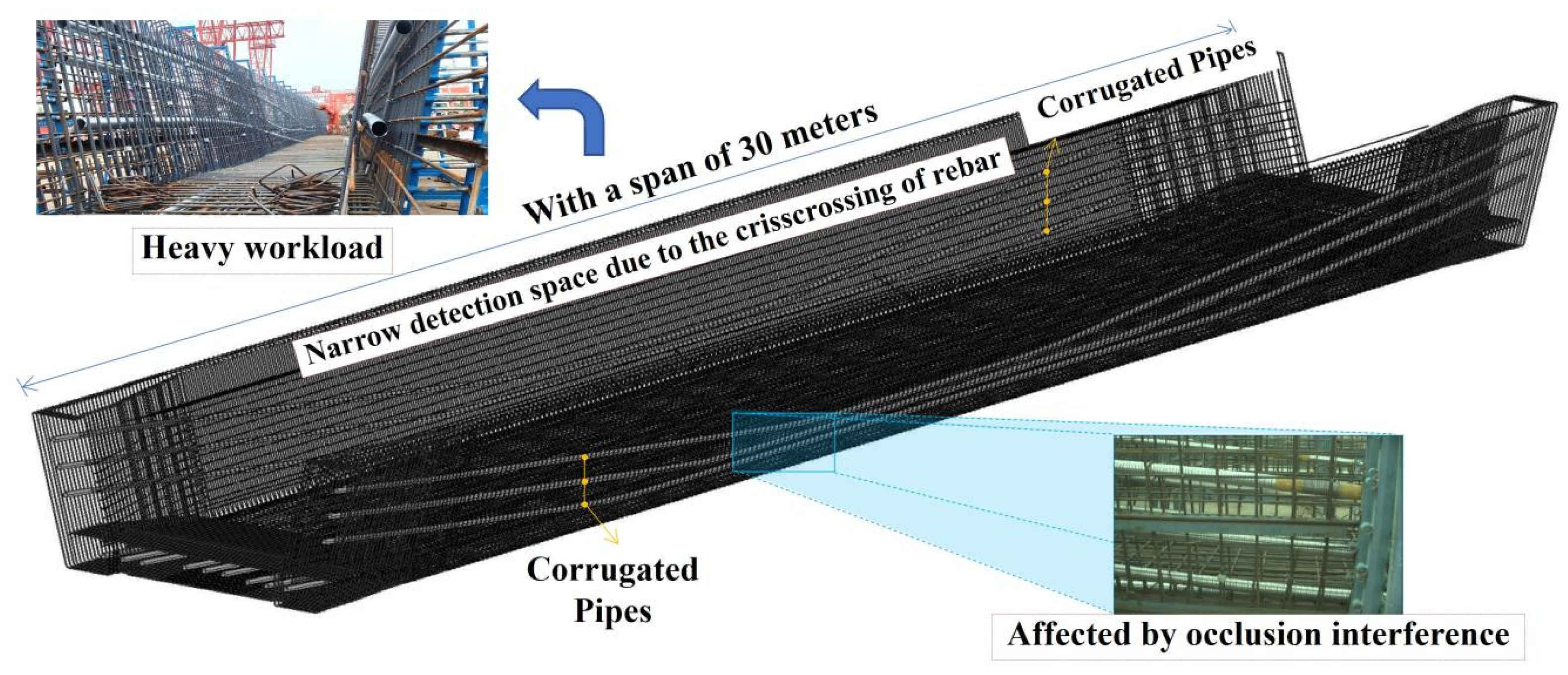
3.1. Data Acquisition and Dataset Construction
3.2. Point Cloud Registration
3.2.1. Algorithm Introduction
3.2.2. Evaluation Metrics
- (1)
- Fitness
- (2)
- Root Mean Square Error (RMSEInlier)
3.3. Point Cloud Preprocessing
4. Recognition and Measurement of Corrugated Pipes
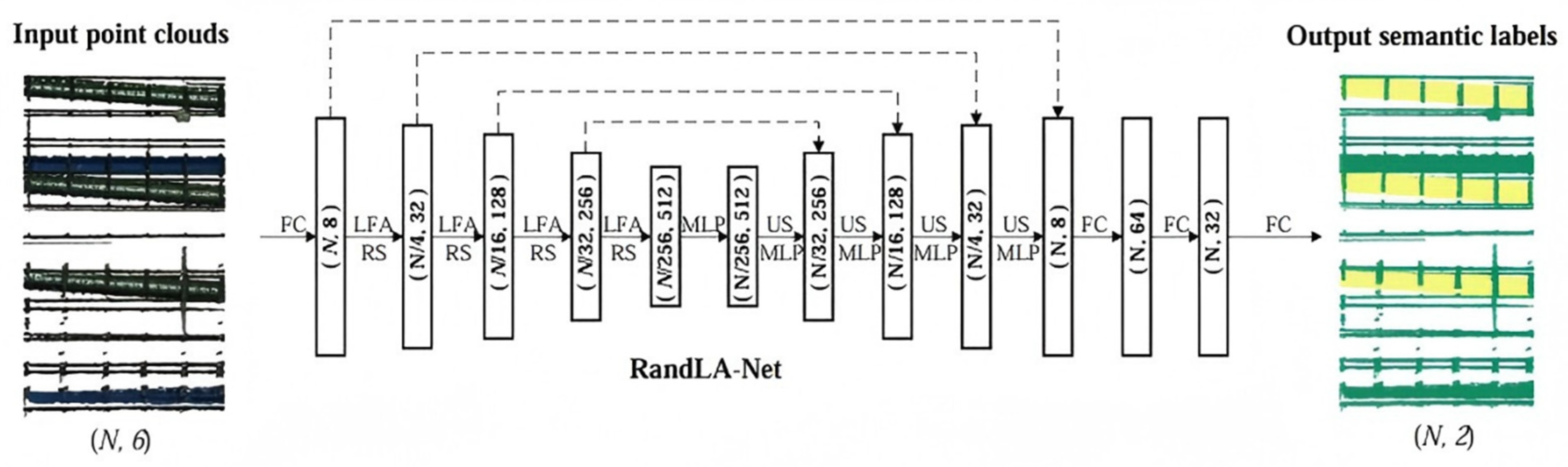
4.1. Semantic Segmentation of Pipes
4.2. Semantic Segmentation Results and Analysis
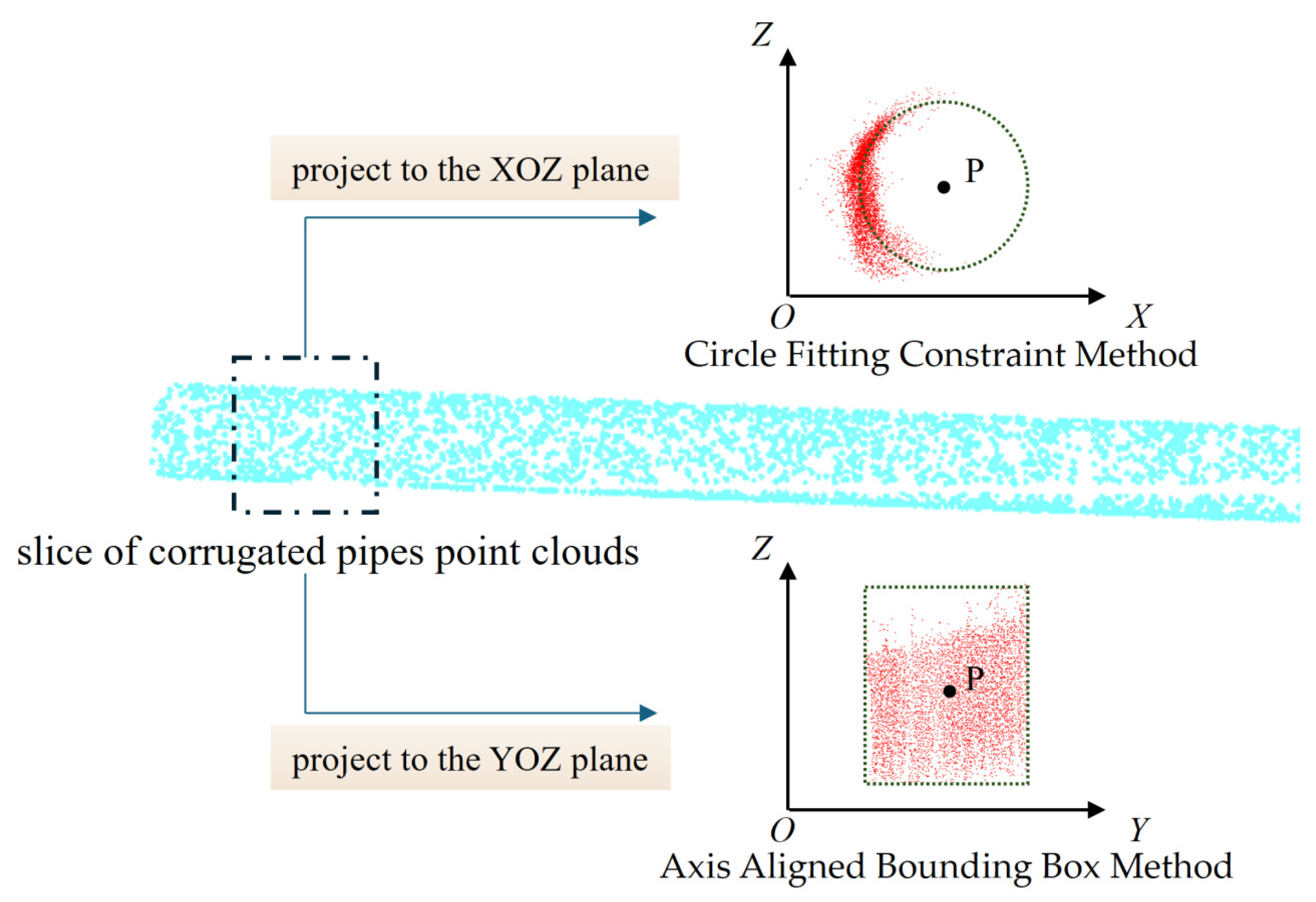
4.3. Center Point Extraction and Curve Fitting Methods
- Center Point Extraction Methods
- 2.
- Curve Fitting Methods
5. Experimental Results and Analysis
6. Discussion and Conclusions
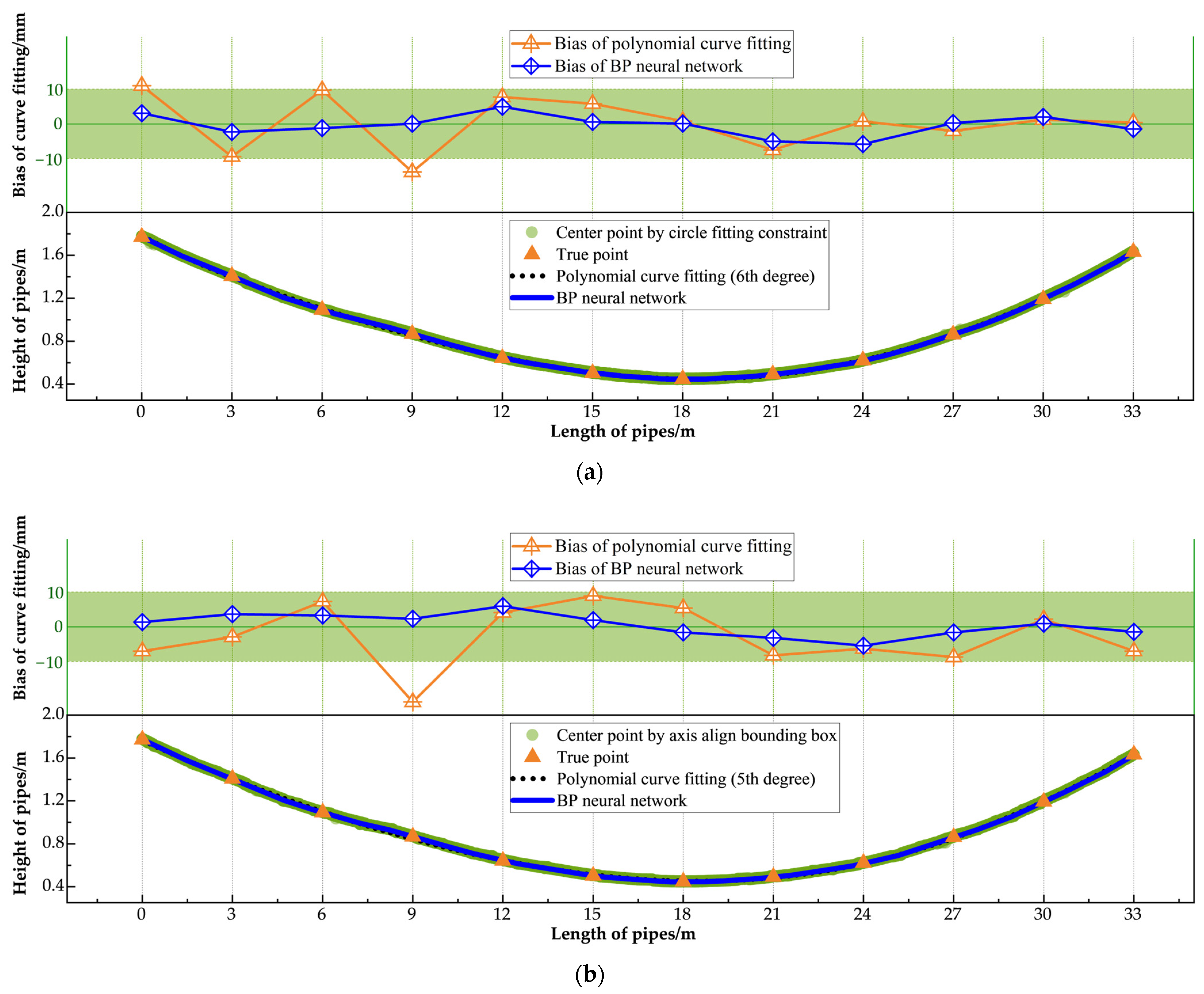
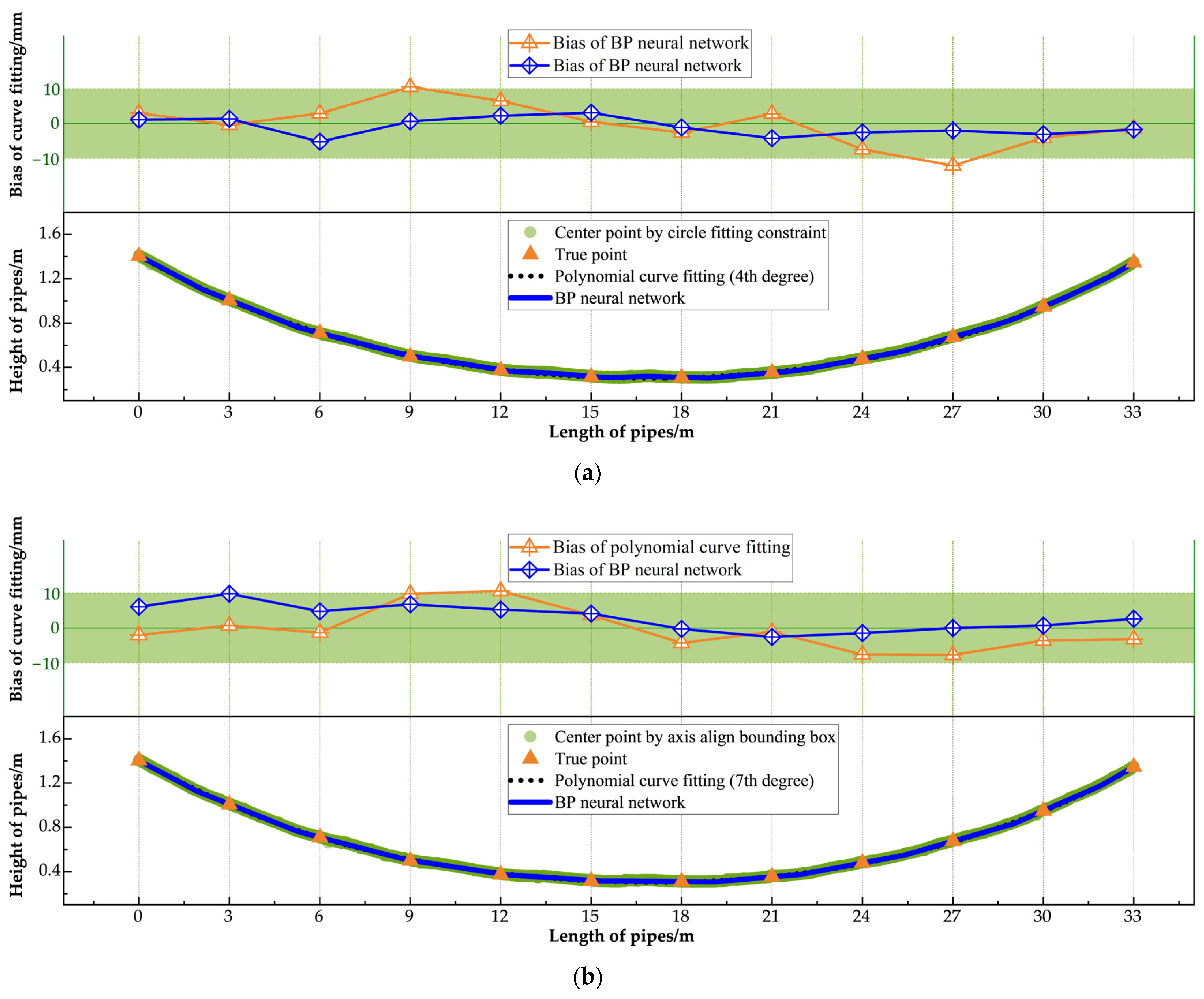
- Under the proposed optimal fitting method (BP neural network combined with the circle fitting constraint method), the average detection errors for the three pipes were 2.2 mm, 1.4 mm, and 1.6 mm, respectively, with maximum detection errors of −5.8 mm, −4.2 mm, and −5.7 mm, all of which meet the requirements of construction standards.
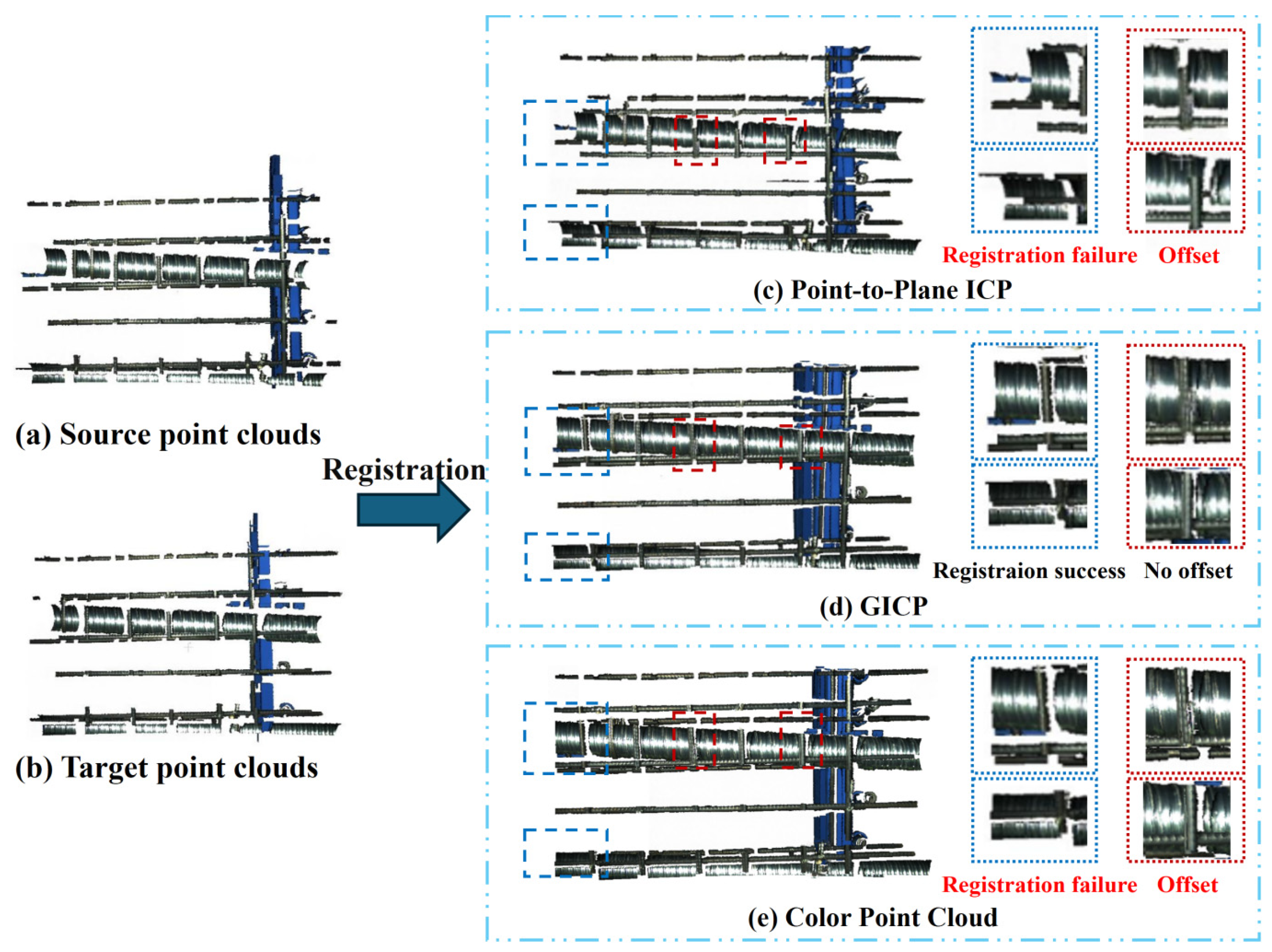
- The proposed point cloud registration method integrates both coarse and fine registration stages to achieve accurate alignment. During the coarse registration stage, the RANSAC algorithm combined with Fast Point Feature Histograms (FPFHs) was employed for initial alignment by iteratively estimating optimal feature correspondences. In the fine registration stage, three methods, Point-to-Plane ICP, Generalized ICP (GICP), and color-assisted point cloud registration, were evaluated and compared. Based on key metrics, including alignment accuracy, the RMSE of inlier pairs, and computation time, GICP was identified as the most suitable method for the fine registration of point clouds in precast segmental box girders.
- BP neural networks and polynomial curve fitting were employed to model the centerlines of the pipes. The BP neural network demonstrated significantly greater robustness, effectively managing the irregular and dispersed center points in the data over traditional polynomial curve fitting. It consistently maintained fitting biases within the permissible error range, achieving reliable and accurate performance even under challenging conditions.
7. Limitation and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Tang, S.; Zheng, H.; Zhou, C.; Zhu, M. Flexural Behavior of a 30-Meter Full-Scale Simply Supported Prestressed Concrete Box Girder. Appl. Sci. 2020, 10, 3076. [Google Scholar] [CrossRef]
- Liang, Z.; Gong, C.; Liang, W.; Zhang, S.; Li, X. Behavior of Confined Headed Bar Connection for Precast Reinforced Concrete Member Assembly. Appl. Sci. 2023, 13, 827. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, K.; Wu, S.; Xiong, T.; Bai, Y.; Li, W. Vertical Cracking at Girder Ends during Post-Tensioning of Prefabricated Prestress Concrete Bridge T-Girders. Struct. Concr. 2021, 22, 3094–3108. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, L.; Ou, J.; Chen, X. Nondestructive Testing and Health Monitoring Techniques for Structural Effective Prestress. Struct. Control Health Monit. 2023, 2023, 8940008. [Google Scholar] [CrossRef]
- Li, K.; Zheng, Y.; Liu, C. Mechanism Analysis of Small Box Girder Diseases and Summary of Reinforcement Treatment Strategies. J. Phys. Conf. Ser. 2020, 1578, 012184. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, K.; Zheng, Y. Comparison and Applicability Research of Prestressed Duct Pumpness Contemporary Major Nondestructive Detection Technology. IOP Conf. Ser. Mater. Sci. Eng. 2018, 439, 042064. [Google Scholar] [CrossRef]
- Wang, H.; Ye, Z.; Wang, D.; Jiang, H.; Liu, P. Synthetic Datasets for Rebar Instance Segmentation Using Mask R-CNN. Buildings 2023, 13, 585. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, J.C.P.; Sohn, H. Automated Estimation of Reinforced Precast Concrete Rebar Positions Using Colored Laser Scan Data. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 787–802. [Google Scholar] [CrossRef]
- Chen, W.; Qu, G.; Li, W. Application of impact-echo method in the localization of prestressed bellows. J. Highw. Transp. 2018, 14, 55–56+105. (In Chinese) [Google Scholar]
- Wu, B.; Chen, S.; Pu, Y.; Yang, M.; Zhang, S.; Yuan, H.; Zhao, C.; Zhang, H. Application of High Frequency Ground Penetrating Radar in the Linear Detection of Metal Corrugated Pipe of Bridge. Hunan Commun. Sci. Technol. 2018, 44, 138–142. (In Chinese) [Google Scholar]
- Chen, H.; Lin, C. Research on Location and Data Processing of Ground Penetrating Radar for Prestressed Pipe in Bridges. Chin. J. Eng. Geophys. 2020, 17, 101–106. (In Chinese) [Google Scholar]
- Xu, M.; Yin, N.; Yang, M.; Zhou, L. A New Non destructive Testing Technique for Concrete Railway Bridge Using Ground Penetrating Radar. Chin. Railw. Sci. 1999, 3, 63–70. (In Chinese) [Google Scholar]
- Guo, Y. The Construction Technology of PC-beam Pre-stressed Duct’ sThree-dimensional Integrate Precision Location. Railw. Constr. Technol. 2013, 1, 55–58. (In Chinese) [Google Scholar]
- Guo, Q.; Shi, K.; Xu, J.; Teng, Q.; Zhang, X. Design of Corrugated Pipe Position Monitoring System in Bridge Prestressed Construction. Instruct. Tech. Sens. 2019, 11, 49–52. (In Chinese) [Google Scholar]
- Park, S.; Kim, S. Semantic Segmentation of Heavy Construction Equipment Based on Point Cloud Data. Buildings 2024, 14, 2393. [Google Scholar] [CrossRef]
- Ahn, H.; Lee, C.; Kim, M.; Kim, T.; Lee, D.; Kwon, W.; Cho, H. Applicability of Smart Construction Technology: Prioritization and Future Research Directions. Autom. Constr. 2023, 153, 104953. [Google Scholar] [CrossRef]
- Li, S.; Zhang, B.; Zheng, J.; Wang, D.; Liu, Z. Development of Automated 3D LiDAR System for Dimensional Quality Inspection of Prefabricated Concrete Elements. Sensors 2024, 24, 7486. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Li, J. Review on Automated Quality Inspection of Precast Concrete Components. Autom. Constr. 2023, 150, 104828. [Google Scholar] [CrossRef]
- Shu, J.; Li, W.; Zhang, C.; Gao, Y.; Xiang, Y.; Ma, L. Point Cloud-Based Dimensional Quality Assessment of Precast Concrete Components Using Deep Learning. J. Build. Eng. 2023, 70, 106391. [Google Scholar] [CrossRef]
- Chen, W.; Fu, X.; Chen, W.; Peng, Z. Intelligent Detection of Rebar Size and Position Using Improved DeeplabV3+. Appl. Sci. 2023, 13, 11094. [Google Scholar] [CrossRef]
- Peng, Z.; Li, J.; Hao, H. Computer Vision-Based Displacement Identification and Its Application to Bridge Condition Assessment under Operational Conditions. Smart Constr. 2024, 1, 3. [Google Scholar] [CrossRef]
- Sun, A.; An, X.; Li, P.; Lv, M.; Liu, W. Near Real-Time 3D Reconstruction of Construction Sites Based on Surveillance Cameras. Buildings 2025, 15, 567. [Google Scholar] [CrossRef]
- Piekarczuk, A.; Mazurek, A.; Szer, J.; Szer, I. A Case Study of 3D Scanning Techniques in Civil Engineering Using the Terrestrial Laser Scanning Technique. Buildings 2024, 14, 3703. [Google Scholar] [CrossRef]
- Teng, J.; Sun, H.; Liu, P.; Jiang, S. An Improved TransMVSNet Algorithm for Three-Dimensional Reconstruction in the Unmanned Aerial Vehicle Remote Sensing Domain. Sensors 2024, 24, 2064. [Google Scholar] [CrossRef]
- Trzeciak, M.; Brilakis, I. Dense 3D Reconstruction of Building Scenes by AI-Based Camera–Lidar Fusion and Odometry. J. Comput. Civ. Eng. 2023, 37, 04023010. [Google Scholar] [CrossRef]
- Truong-Hong, L.; Lindenbergh, R. Extracting Structural Components of Concrete Buildings from Laser Scanning Point Clouds from Construction Sites. Adv. Eng. Inform. 2022, 51, 101490. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Z.; Liu, Z.; Zhang, Y.; Cai, R.; Hu, X.; Yang, R.; Wang, G. Multi-Task Intelligent Monitoring of Construction Safety Based on Computer Vision. Buildings 2024, 14, 2429. [Google Scholar] [CrossRef]
- Mhmoud Alzubi, K.; Salah Alaloul, W.; Malkawi, A.B.; Al Salaheen, M.; Hannan Qureshi, A.; Ali Musarat, M. Automated Monitoring Technologies and Construction Productivity Enhancement: Building Projects Case. Ain Shams Eng. J. 2023, 14, 102042. [Google Scholar] [CrossRef]
- Chian, E.; Fang, W.; Goh, Y.M.; Tian, J. Computer Vision Approaches for Detecting Missing Barricades. Autom. Constr. 2021, 131, 103862. [Google Scholar] [CrossRef]
- Wu, H.; Zhong, B.; Li, H.; Love, P.; Pan, X.; Zhao, N. Combining Computer Vision with Semantic Reasoning for On-Site Safety Management in Construction. J. Build. Eng. 2021, 42, 103036. [Google Scholar] [CrossRef]
- Kong, T.; Fang, W.; Love, P.E.D.; Luo, H.; Xu, S.; Li, H. Computer Vision and Long Short-Term Memory: Learning to Predict Unsafe Behaviour in Construction. Adv. Eng. Inform. 2021, 50, 101400. [Google Scholar] [CrossRef]
- Peng, Z.; Li, J.; Hao, H.; Zhong, Y. Smart Structural Health Monitoring Using Computer Vision and Edge Computing. Eng. Struct. 2024, 319, 118809. [Google Scholar] [CrossRef]
- Onososen, A.O.; Musonda, I.; Onatayo, D.; Saka, A.B.; Adekunle, S.A.; Onatayo, E. Drowsiness Detection of Construction Workers: Accident Prevention Leveraging Yolov8 Deep Learning and Computer Vision Techniques. Buildings 2025, 15, 500. [Google Scholar] [CrossRef]
- Al Shafian, S.; Hu, D. Integrating Machine Learning and Remote Sensing in Disaster Management: A Decadal Review of Post-Disaster Building Damage Assessment. Buildings 2024, 14, 2344. [Google Scholar] [CrossRef]
- Ai, D.; Jiang, G.; Lam, S.-K.; He, P.; Li, C. Computer Vision Framework for Crack Detection of Civil Infrastructure—A Review. Eng. Appl. Artif. Intell. 2023, 117, 105478. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, Y.; Liu, Y.; Shu, J. Automated Recognition and Measurement Based on Three-Dimensional Point Clouds to Connect Precast Concrete Components. Autom. Constr. 2022, 133, 104000. [Google Scholar] [CrossRef]
- Zhong, B.; Wu, H.; Ding, L.; Love, P.E.D.; Li, H.; Luo, H.; Jiao, L. Mapping Computer Vision Research in Construction: Developments, Knowledge Gaps and Implications for Research. Autom. Constr. 2019, 107, 102919. [Google Scholar] [CrossRef]
- Shu, J.; Zhang, X.; Li, W.; Zeng, Z.; Zhang, H.; Duan, Y. Point Cloud and Machine Learning-Based Automated Recognition and Measurement of Corrugated Pipes and Rebars for Large Precast Concrete Beams. Autom. Constr. 2024, 165, 105493. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef]
- Kim, M.-K.; Wang, Q.; Li, H. Non-Contact Sensing Based Geometric Quality Assessment of Buildings and Civil Structures: A Review. Autom. Constr. 2019, 100, 163–179. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, J.; Qiu, H.; Sun, J. Intelligent Inspection Method for Rebar Installation Quality of Reinforced Concrete Slab Based on Point Cloud Processing and Semantic Segmentation. Buildings 2024, 14, 3693. [Google Scholar] [CrossRef]
- Wang, Q.; Tan, Y.; Mei, Z. Computational Methods of Acquisition and Processing of 3D Point Cloud Data for Construction Applications. Arch. Computat. Methods Eng. 2020, 27, 479–499. [Google Scholar] [CrossRef]
- Mostafa, K.; Hegazy, T. Review of Image-Based Analysis and Applications in Construction. Autom. Constr. 2021, 122, 103516. [Google Scholar] [CrossRef]
- Yoon, S.; Wang, Q.; Sohn, H. Optimal Placement of Precast Bridge Deck Slabs with Respect to Precast Girders Using 3D Laser Scanning. Autom. Constr. 2018, 86, 81–98. [Google Scholar] [CrossRef]
- Kim, M.-K.; Sohn, H.; Chang, C.-C. Automated Dimensional Quality Assessment of Precast Concrete Panels Using Terrestrial Laser Scanning. Autom. Constr. 2014, 45, 163–177. [Google Scholar] [CrossRef]
- Li, F.; Kim, M.-K. Mirror-Aided Registration-Free Geometric Quality Inspection of Planar-Type Prefabricated Elements Using Terrestrial Laser Scanning. Autom. Constr. 2021, 121, 103442. [Google Scholar] [CrossRef]
- Xiao, Y.; Feng, C.; Taguchi, Y.; Kamat, V.R. User-Guided Dimensional Analysis of Indoor Building Environments from Single Frames of RGB-D Sensors. J. Comput. Civ. Eng. 2017, 31, 04017006. [Google Scholar] [CrossRef]
- Bellés, C.; Pla, F. A Kinect-Based System for 3D Reconstruction of Sewer Manholes. Comput.-Aided Civ. Eng. 2015, 30, 906–917. [Google Scholar] [CrossRef]
- Rebolj, D.; Pučko, Z.; Babič, N.Č.; Bizjak, M.; Mongus, D. Point Cloud Quality Requirements for Scan-vs-BIM Based Automated Construction Progress Monitoring. Autom. Constr. 2017, 84, 323–334. [Google Scholar] [CrossRef]
- Kim, M.-K.; Thedja, J.P.P.; Wang, Q. Automated Dimensional Quality Assessment for Formwork and Rebar of Reinforced Concrete Components Using 3D Point Cloud Data. Autom. Constr. 2020, 112, 103077. [Google Scholar] [CrossRef]
- Wu, C.; Yuan, Y.; Tang, Y.; Tian, B. Application of terrestrial laser scanning (TLS) in the architecture, engineering and construction (AEC) industry. Sensors 2021, 22, 265. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wang, G.; Liu, Z.; Liu, L.; Zou, Y.; Li, S.; Yang, R.; Hu, X.; Li, S.; Wang, D. The Automated Inspection of Precast Utility Tunnel Segments for Geometric Quality Based on the BIM and LiDAR. Buildings 2024, 14, 2717. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Deng, Y. Semantic Segmentation and Extraction of 3D Laser Point Cloud Orbit Objects Based on Deep Learning. Master’s Thesis, Wuhan University, Wuhan, China, 2020. (In Chinese). [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Learning Semantic Segmentation of Large-Scale Point Clouds With Random Sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 8338–8354. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Zhao, Q.; Hu, B.; Pu, D.; Liu, K. Tunnel Longitudinal Deformation Detection Based on Deep Learning and Laser Point Cloud. Yunnan Water Power 2023, 39, 45–51. (In Chinese) [Google Scholar]
- Jia, X.; Zhu, Q.; Ge, X.; Ma, R.; Zhang, D.; Liu, T. Robust Guardrail Instantiation and Trajectory Optimization of Complex Highways Based on Mobile Laser Scanning Point Clouds. Photogramm. Eng. Remote Sens. 2023, 89, 151–161. [Google Scholar] [CrossRef]
- Mattheuwsen, L.; Bassier, M.; Vergauwen, M. Storm Drain Detection and Localisation on Mobile LIDAR Data Using a Pre-Trained Randla-Net Semantic Segmentation Network. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2022, 43, 237–244. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Inspection and Evaluation Quality Standards for Highway Engineering Section 1 Civil Engineering: JTG F80/1-2017; China Communications Press Co., Ltd.: Beijing, China, 2018. (In Chinese) [Google Scholar]



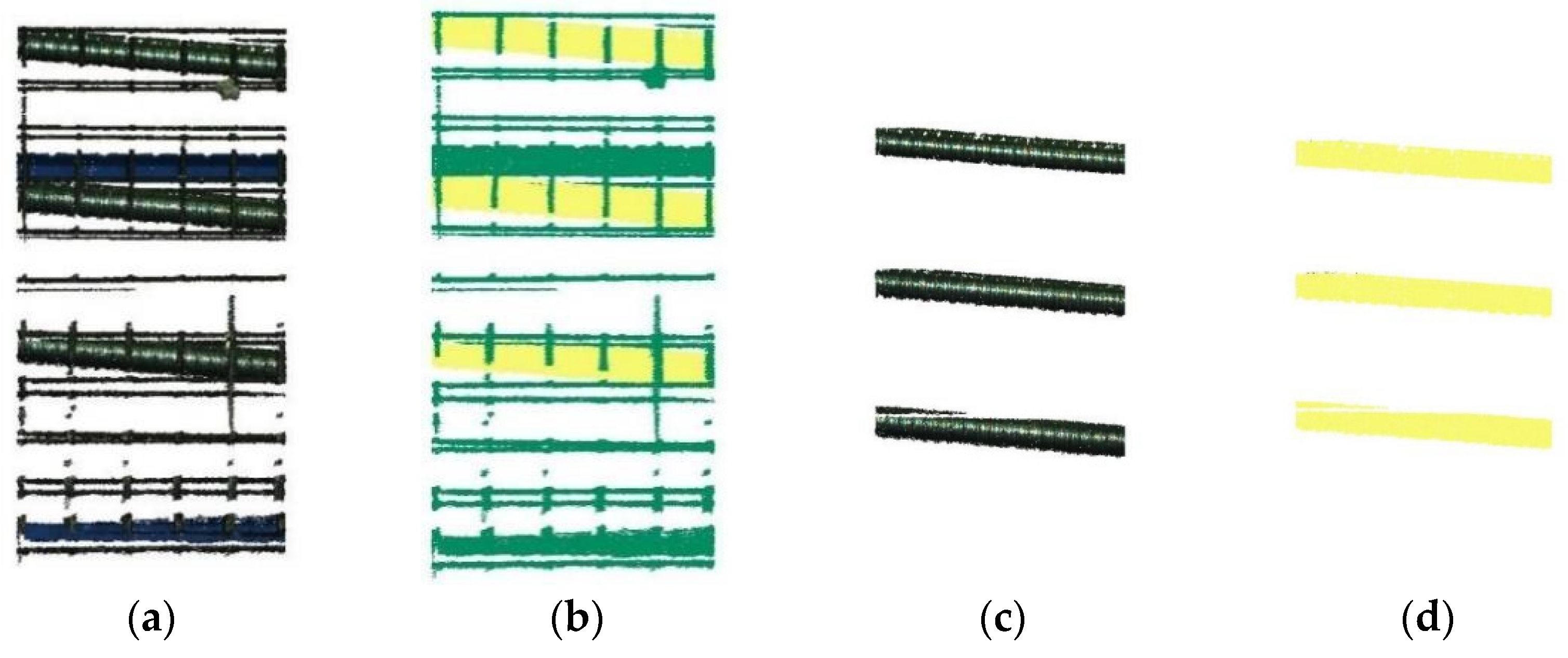


| Model | Detection Range (m) | Field of View (mm) | Color Resolution | Spatial Resolution (mm) |
|---|---|---|---|---|
Zivid One+ L | 1.2–3 | 2069 × 1310@3000 | 1920 × 1200 | 1.11@300 |
| Algorithms | Fitness | RMSEInliner (mm) | Registration Time (s) |
|---|---|---|---|
| Point-to-Plane ICP | 0.378 | 1.47 | 0.056 |
| GICP | 0.374 | 1.46 | 0.188 |
| Color assisted | 3.19 × 10−6 | 7.52 | 72.733 |
| Model Name | OA (%) | mAcc(%) | mIoU (%) | IoUbellows (%) | IoUnonbellows (%) |
|---|---|---|---|---|---|
| Model | 99.97 | 99.96 | 99.94 | 99.92 | 99.96 |
| Fitting Scheme | No. A Bellow | No. B Bellow | No. C Bellow | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | Maxerror (mm) | P * | MAE | RMSE | Maxerror (mm) | P * | MAE | RMSE | Maxerror (mm) | P * | |
| Circle fitting constraint with BP neural network | 2.2 | 3.0 | −5.8 | 9 | 2.4 | 2.7 | −4.2 | 8 | 1.6 | 2.1 | −5.7 | 9 |
| Axis align bounding box with BP neural network | 2.7 | 3.1 | 5.9 | 5 | 3.7 | 4.7 | 9.8 | 2 | 2.2 | 2.6 | 4.2 | 7 |
| Circle fitting constraint with polynomial curve fitting | 5.9 | 7.4 | −13.8 | 4 | 4.5 | 5.8 | −12.0 | 10 | 15.8 | 23.9 | −59.6 | 12 |
| Axis align bounding box with polynomial curve fitting | 7.5 | 8.8 | −21.6 | 4 | 4.7 | 5.7 | 10.6 | 5 | 16.1 | 24.1 | −64.5 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Huang, Z.; Wang, D.; Liu, P.; Jiang, H.; Du, X. Automated Recognition and Measurement of Corrugated Pipes for Precast Box Girder Based on RGB-D Camera and Deep Learning. Sensors 2025, 25, 2641. https://doi.org/10.3390/s25092641
Zhu J, Huang Z, Wang D, Liu P, Jiang H, Du X. Automated Recognition and Measurement of Corrugated Pipes for Precast Box Girder Based on RGB-D Camera and Deep Learning. Sensors. 2025; 25(9):2641. https://doi.org/10.3390/s25092641
Chicago/Turabian StyleZhu, Jiongyi, Zixin Huang, Dejiang Wang, Panpan Liu, Haili Jiang, and Xiaoqing Du. 2025. "Automated Recognition and Measurement of Corrugated Pipes for Precast Box Girder Based on RGB-D Camera and Deep Learning" Sensors 25, no. 9: 2641. https://doi.org/10.3390/s25092641
APA StyleZhu, J., Huang, Z., Wang, D., Liu, P., Jiang, H., & Du, X. (2025). Automated Recognition and Measurement of Corrugated Pipes for Precast Box Girder Based on RGB-D Camera and Deep Learning. Sensors, 25(9), 2641. https://doi.org/10.3390/s25092641






