Optimization of OPM-MEG Layouts with a Limited Number of Sensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Measurements of Auditory Evoked Fields (AEFs)
2.2. Transforming SQUID-MEG Measurements to the OPM-MEG System
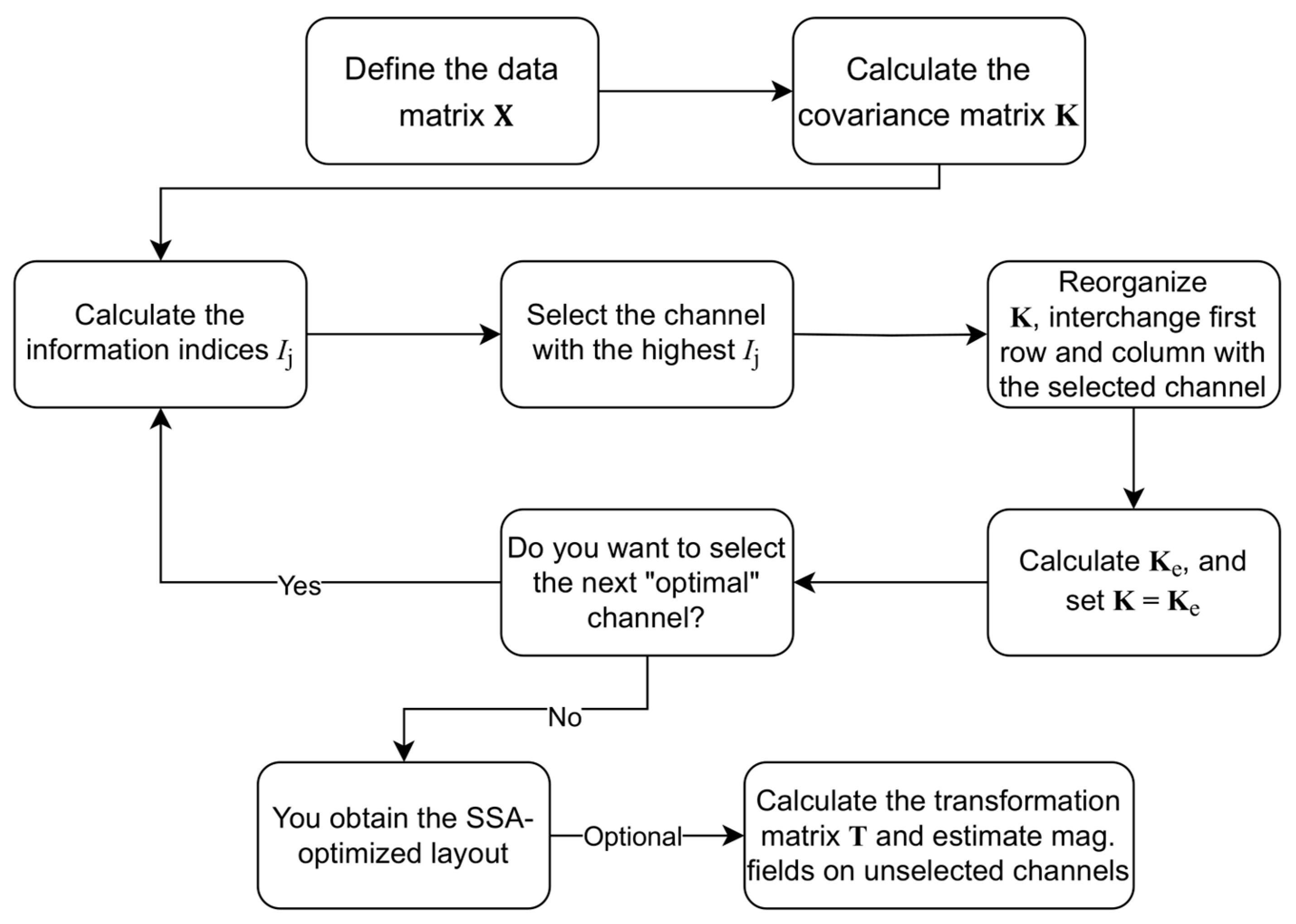
2.3. Sequential Selection Algorithm (SSA)
2.4. Protocols for Applying the SSA on OPM-MEG MFMs
- We treat the radial and tangential channels as independent, giving 160 channels, 80 radial and 80 tangential. This approach selects channels using the SSA algorithm.
- During the SSA selection, we chose channels (same as with approach I). Finally, we add the channel pair (exact location, different measuring component) that has not yet been selected. This gives of selected measurement sites and channels.
- This approach is a combination of approaches I and II. When we select one channel (radial or tangential) during the SSA, we also choose the channel pair. Similarly, as II, this gives us of selected measurement sites and channels.
- With this approach, we combine the radial and tangential MFMs into a common basis with twice the number of all MFMs. We consider the measurement system to be 80-channel. The transfer matrix () in Equation (6) is the same for radial and tangential channels.
2.5. Evaluation Parameters
2.5.1. Root-Mean-Square Error, Relative Difference, and Correlation Coefficient
2.5.2. Localization Error
3. Results
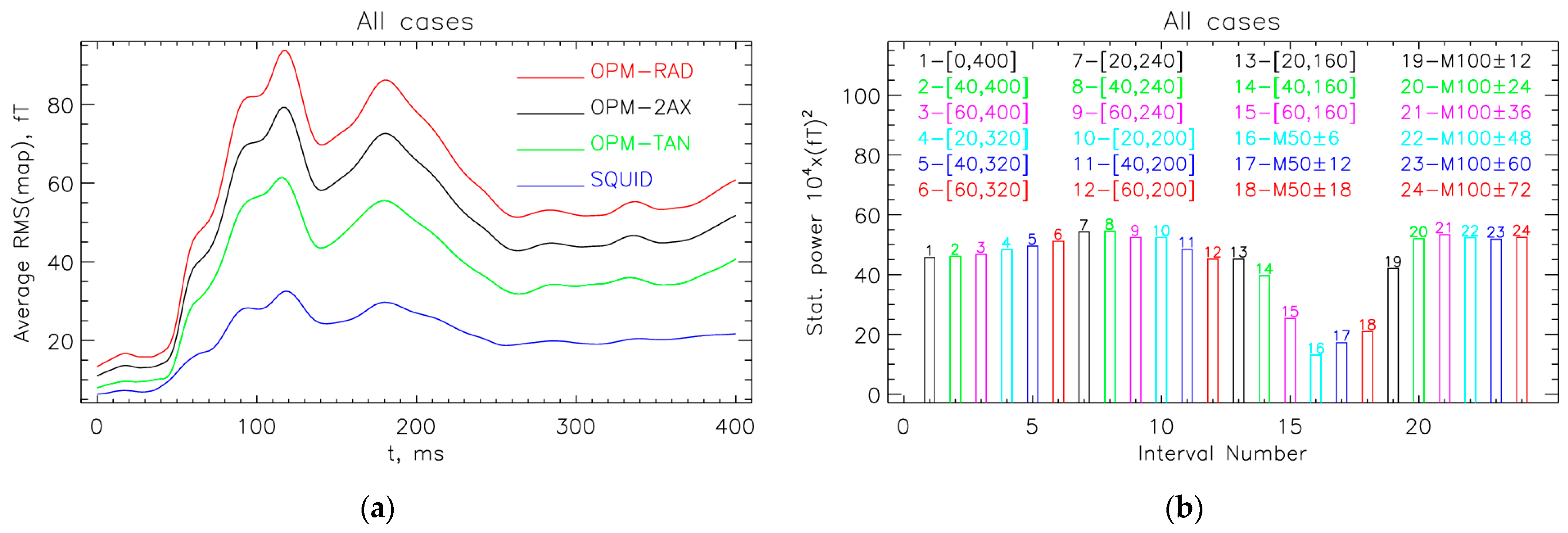
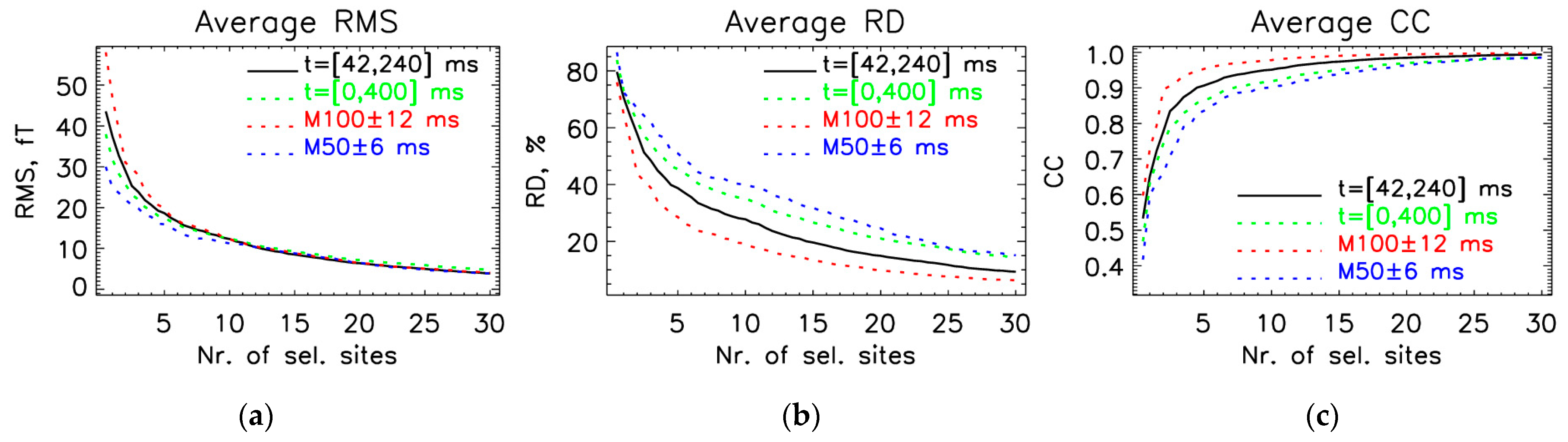
3.1. Interval with the Largest Statistical Power
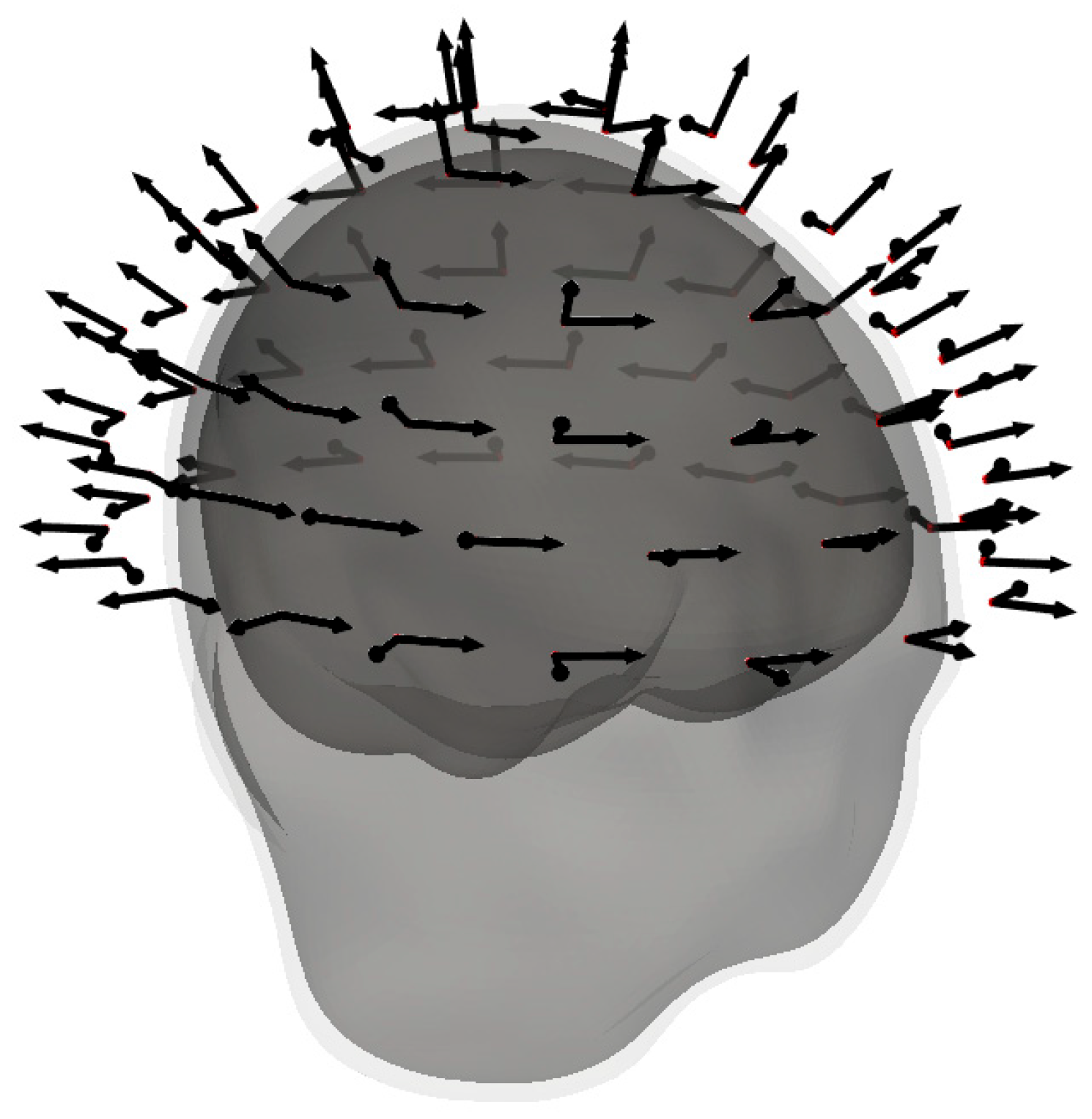
3.2. Optimal Locations for the OPM-2AX System
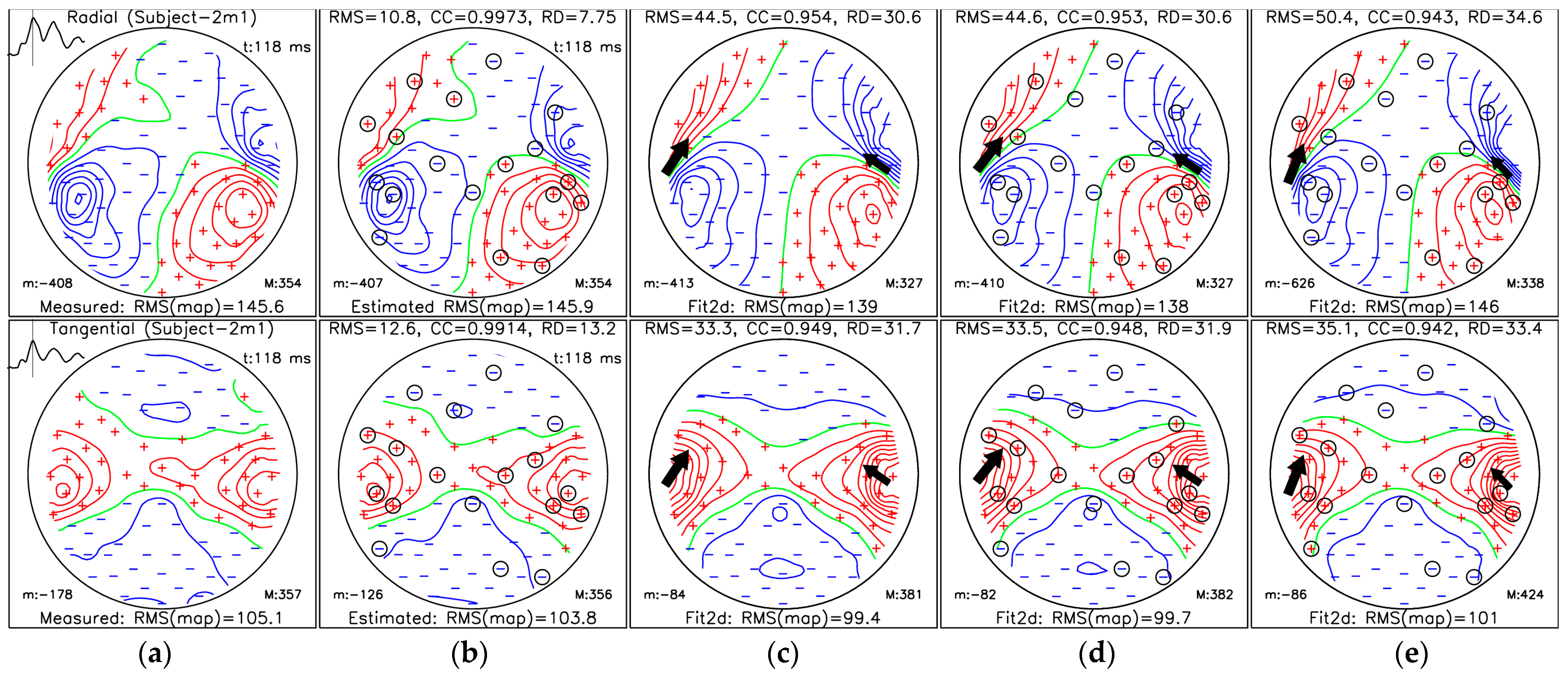
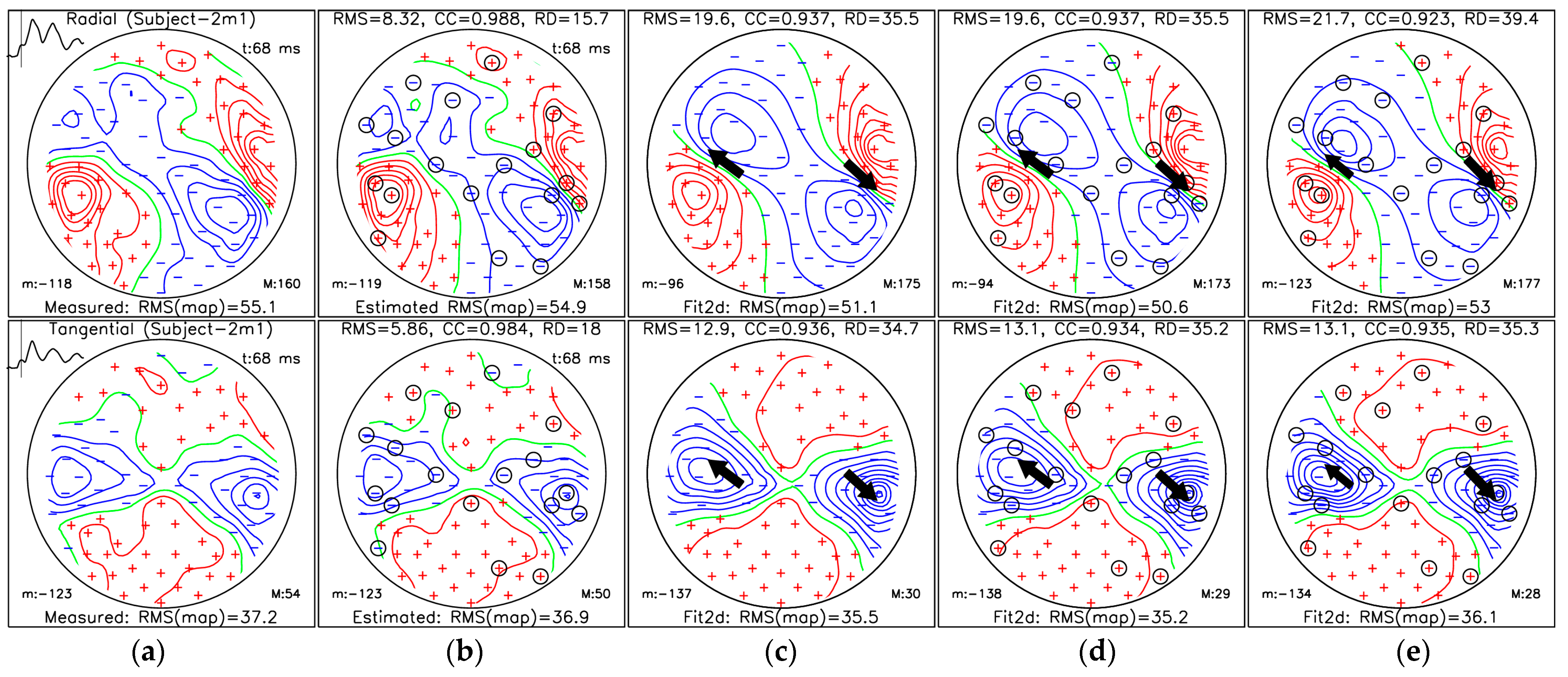
3.3. Localization of Sources for the M50 and M100 Peaks
- (a)
- MFM for measured data;
- (b)
- MFM of estimated data from selected measuring sites (36 channels) using protocol III for the OPM-2AX system;
- (c)
- MFM estimated for the ECD fit using measured data from all measuring sites;
- (d)
- MFM estimated for the ECD fit using SSA-estimated data from selected measuring sites;
- (e)
- MFMs estimated for the ECD fit using data only from selected measuring sites.
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| MEG | Magnetoencephalography |
| SQUID | Superconducting quantum interference device |
| OPM | Optically pumped magnetometer |
| MFM | Magnetic field map |
| ROI | Region of interest |
| SSA | Sequential selection algorithm |
| AEF | Auditory evoked field |
| MNE | Minimum norm estimation |
| ECD | Equivalent current dipole |
| CC | Correlation coefficient |
| RMS | Root mean square |
| MSR | Magnetically shielded room |
| MRI | Magnetic resonance imaging |
| ECG | Electrocardiography |
| SNR | Signal-to-noise ratio |
| BEM | Boundary element method |
Appendix A
Appendix A.1. Theoretical Background of Meg Forward Modeling of Sources Inside a Multi-Layer Shell Model
Appendix A.2. Theoretical Background of the Minimum Norm Estimate (MNE) Method
Appendix A.3. Implementation Details of the System Transformation Using MNE and BEM from the Software Package Mne-Python
Appendix B
RMS of MFM Values for SQUID Measurements

References
- Hämäläinen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 1993, 65, 413–497. [Google Scholar] [CrossRef]
- Jaklevic, R.C.; Lambe, J.; Silver, A.H.; Mercereau, J.E. Quantum Interference Effects in Josephson Tunneling. Phys. Rev. Lett. 1964, 12, 159–160. [Google Scholar] [CrossRef]
- Faley, M.I.; Dammers, J.; Maslennikov, Y.V.; Schneiderman, J.F.; Winkler, D.; Koshelets, V.P.; Shah, N.J.; Dunin-Borkowski, R.E. High-Tc SQUID biomagnetometers. Supercond. Sci. Technol. 2017, 30, 083001. [Google Scholar] [CrossRef]
- Kim, K.; Begus, S.; Xia, H.; Lee, S.-K.; Jazbinsek, V.; Trontelj, Z.; Romalis, M.V. Multi-channel atomic magnetometer for magnetoencephalography: A configuration study. NeuroImage 2014, 89, 143–151. [Google Scholar] [CrossRef]
- Budker, D.; Romalis, M. Optical magnetometry. Nat. Phys. 2007, 3, 227–234. [Google Scholar] [CrossRef]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef]
- Iivanainen, J.; Stenroos, M.; Parkkonen, L. Measuring MEG closer to the brain: Performance of on-scalp sensor arrays. NeuroImage 2017, 147, 542–553. [Google Scholar] [CrossRef]
- Marhl, U.; Sander, T.; Jazbinšek, V. Simulation Study of Different OPM-MEG Measurement Components. Sensors 2022, 22, 3184. [Google Scholar] [CrossRef]
- Shah, V.; Osborne, J.; Orton, J.; Alem, O. Fully integrated, standalone zero field optically pumped magnetometer for biomagnetism. In Steep Dispersion Engineering and Opto-Atomic Precision Metrology XI; Shahriar, S.M., Scheuer, J., Eds.; SPIE: San Francisco, CA, USA, 2018; p. 51. [Google Scholar]
- Alem, O.; Mhaskar, R.; Jimenez-Martinez, R.; Sheng, D.; LeBlanc, J.; Trahms, L.; Sander, T.; Kitching, J.; Knappe, S. Magnetic field imaging with microfabricated optically-pumped magnetometers. Opt. Express 2017, 25, 7849–7858. [Google Scholar] [CrossRef]
- Knappe, S.; Sander, T.; Trahms, L. Optically Pumped Magnetometers for MEG. In Magnetoencephalography; Supek, S., Aine, C.J., Eds.; Springer: Cham, Switzerland, 2019; pp. 1301–1312. ISBN 978-3-030-00086-8. [Google Scholar]
- Marhl, U.; Jodko-Władzińska, A.; Brühl, R.; Sander, T.; Jazbinšek, V. Transforming and comparing data between standard SQUID and OPM-MEG systems. PLoS ONE 2022, 17, e0262669. [Google Scholar] [CrossRef]
- Brickwedde, M.; Anders, P.; Kühn, A.A.; Lofredi, R.; Holtkamp, M.; Kaindl, A.M.; Grent-‘t-Jong, T.; Krüger, P.; Sander, T.; Uhlhaas, P.J. Applications of OPM-MEG for translational neuroscience: A perspective. Transl. Psychiatry 2024, 14, 341. [Google Scholar] [CrossRef] [PubMed]
- Seymour, R.A.; Alexander, N.; Mellor, S.; O’Neill, G.C.; Tierney, T.M.; Barnes, G.R.; Maguire, E.A. Using OPMs to measure neural activity in standing, mobile participants. NeuroImage 2021, 244, 118604. [Google Scholar] [CrossRef] [PubMed]
- Vivekananda, U.; Mellor, S.; Tierney, T.M.; Holmes, N.; Boto, E.; Leggett, J.; Roberts, G.; Hill, R.M.; Litvak, V.; Brookes, M.J.; et al. Optically pumped magnetoencephalography in epilepsy. Ann. Clin. Transl. Neurol. 2020, 7, 397–401. [Google Scholar] [CrossRef]
- Pedersen, M.; Abbott, D.F.; Jackson, G.D. Wearable OPM-MEG: A changing landscape for epilepsy. Epilepsia 2022, 63, 2745–2753. [Google Scholar] [CrossRef]
- Gage, N.M.; Siegel, B.; Callen, M.; Roberts, T.P.L. Cortical sound processing in children with autism disorder: An MEG investigation. NeuroReport 2003, 14, 2047–2051. [Google Scholar] [CrossRef]
- Roberts, T.P.L.; Matsuzaki, J.; Blaskey, L.; Bloy, L.; Edgar, J.C.; Kim, M.; Ku, M.; Kuschner, E.S.; Embick, D. Delayed M50/M100 evoked response component latency in minimally verbal/nonverbal children who have autism spectrum disorder. Mol. Autism 2019, 10, 34. [Google Scholar] [CrossRef]
- Demopoulos, C.; Yu, N.; Tripp, J.; Mota, N.; Brandes-Aitken, A.N.; Desai, S.S.; Hill, S.S.; Antovich, A.D.; Harris, J.; Honma, S.; et al. Magnetoencephalographic Imaging of Auditory and Somatosensory Cortical Responses in Children with Autism and Sensory Processing Dysfunction. Front. Hum. Neurosci. 2017, 11, 259. [Google Scholar] [CrossRef]
- Demopoulos, C.; Kopald, B.E.; Bangera, N.; Paulson, K.; David Lewine, J. Rapid auditory processing of puretones is associated with basic components of language in individuals with autism spectrum disorders. Brain Lang. 2023, 238, 105229. [Google Scholar] [CrossRef]
- Kikuchi, M.; Yoshimura, Y.; Mutou, K.; Minabe, Y. Magnetoencephalography in the study of children with autism spectrum disorder. Psychiatry Clin. Neurosci. 2016, 70, 74–88. [Google Scholar] [CrossRef]
- Port, R.G.; Edgar, J.C.; Ku, M.; Bloy, L.; Murray, R.; Blaskey, L.; Levy, S.E.; Roberts, T.P.L. Maturation of auditory neural processes in autism spectrum disorder—A longitudinal MEG study. NeuroImage Clin. 2016, 11, 566–577. [Google Scholar] [CrossRef]
- Beltrachini, L.; von Ellenrieder, N.; Eichardt, R.; Haueisen, J. Optimal design of on-scalp electromagnetic sensor arrays for brain source localisation. Hum. Brain Mapp. 2021, 42, 4869–4879. [Google Scholar] [CrossRef] [PubMed]
- Lux, R.L.; Smith, C.R.; Wyatt, R.F.; Abildskov, J.A. Limited Lead Selection for Estimation of Body Surface Potential Maps in Electrocardiography. IEEE Trans. Biomed. Eng. 1978, 25, 270–276. [Google Scholar] [CrossRef]
- Marhl, U.; Sander, T.; Jazbinšek, V. Using a Limited Number of Sensors in MEG or the Feasibility of Partial Head Coverage OPM MEG. In Proceedings of the 2024 47th MIPRO ICT and Electronics Convention (MIPRO), Opatija, Croatia, 20–24 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1134–1138. [Google Scholar]
- Jazbinsek, V.; Hren, R.; Trontelj, Z. High resolution ECG and MCG mapping: Simulation study of single and dual accessory pathways and influence of lead displacement and limited lead selection on localisation results. Bull. Pol. Acad. Sci. Tech. Sci. 2005, 53, 195–205. [Google Scholar]
- Jazbinšek, V.; Hren, R.; Trontelj, Z. Influence of limited lead selection on source localization in magnetocardiography and electrocardiography. Int. Congr. Ser. 2007, 1300, 492–495. [Google Scholar] [CrossRef]
- Jazbinšek, V.; Burghoff, M.; Kosch, O.; Steinhoff, U.; Hren, R.; Trahms, L.; Trontelj, Z. Selection of optimal recording sites in electrocardiography and magnetocardiography. Biomed. Eng. Biomed. Tech. 2004, 48, 174–177. [Google Scholar]
- Shimogawara, M.; Tanaka, H.; Kazumi, K.; Haruta, Y. MEGvision magnetoencephalograph system and its applications. Yokogawa Tech. Rep. Engl. Ed. 2004, 38, 23–27. [Google Scholar]
- Fischl, B. FreeSurfer. NeuroImage 2012, 62, 774–781. [Google Scholar] [CrossRef]
- Gramfort, A. MEG and EEG data analysis with MNE-Python. Front. Neurosci. 2013, 7, 267. [Google Scholar] [CrossRef]
- Gramfort, A.; Luessi, M.; Larson, E.; Engemann, D.A.; Strohmeier, D.; Brodbeck, C.; Parkkonen, L.; Hämäläinen, M.S. MNE software for processing MEG and EEG data. NeuroImage 2014, 86, 446–460. [Google Scholar] [CrossRef]
- Lux, R.L. Karhunen-loeve representation of ECG data. J. Electrocardiol. 1992, 25, 195–198. [Google Scholar] [CrossRef]
- Lux, R.L.; Burgess, M.J.; Wyatt, R.F.; Evans, A.K.; Vincent, G.M.; Abildskov, J.A. Clinically practical lead systems for improved electrocardiography: Comparison with precordial grids and conventional lead systems. Circulation 1979, 59, 356–363. [Google Scholar] [CrossRef] [PubMed]
- Lux, R.L.; Evans, A.K.; Burgess, M.J.; Wyatt, R.F.; Abildskov, J.A. Redundancy reduction for improved display and analysis of body surface potential maps. I. Spatial compression. Circ. Res. 1981, 49, 186–196. [Google Scholar] [CrossRef] [PubMed]
- Sarvas, J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys. Med. Biol. 1987, 32, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; ISBN 978-0-521-88068-8. [Google Scholar]
- Jazbinsek, V.; Hren, R. Assesment of Single-Dipole and Dual-Dipole Inverse Solutions in Electrocardiography. In Proceedings of the 5th European Conference of the International Federation for Medical and Biological Engineering, IFMBE Proceedings, Budapest, Hungary, 14–18 September 2011; Jobbágy, Á., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 37, pp. 323–326, ISBN 978-3-642-23507-8. [Google Scholar]
- Hren, R.; Stroink, G. Application of the surface harmonic expansions for modeling the human torso. IEEE Trans. Biomed. Eng. 1995, 42, 521–524. [Google Scholar] [CrossRef]
- Bergquist, J.; Rupp, L.; Zenger, B.; Brundage, J.; Busatto, A.; MacLeod, R.S. Body Surface Potential Mapping: Contemporary Applications and Future Perspectives. Hearts 2021, 2, 514–542. [Google Scholar] [CrossRef]
- Hubley-Kozey, C.L.; Mitchell, L.B.; Gardner, M.J.; Warren, J.W.; Penney, C.J.; Smith, E.R.; Horácek, B.M. Spatial Features in Body-Surface Potential Maps Can Identify Patients with a History of Sustained Ventricular Tachycardia. Circulation 1995, 92, 1825–1838. [Google Scholar] [CrossRef]
- Hren, R.; Horácek, B.M. Value of simulated body surface potential maps as templates in localizing sites of ectopic activation for radiofrequency ablation. Physiol. Meas. 1997, 18, 373–400. [Google Scholar] [CrossRef]
- SippensGroenewegen, A.; Spekhorst, H.; Van Hemel, N.M.; Kingma, J.H.; Hauer, R.N.; De Bakker, J.M.; Grimbergen, C.A.; Janse, M.J.; Dunning, A.J. Localization of the site of origin of postinfarction ventricular tachycardia by endocardial pace mapping. Body surface mapping compared with the 12-lead electrocardiogram. Circulation 1993, 88, 2290–2306. [Google Scholar] [CrossRef]
- SippensGroenewegen, A.; Spekhorst, H.; Van Hemel, N.M.; Kingma, J.H.; Hauer, R.N.; Janse, M.J.; Dunning, A.J. Body surface mapping of ectopic left ventricular activation. QRS spectrum in patients with prior myocardial infarction. Circ. Res. 1992, 71, 1361–1378. [Google Scholar] [CrossRef]
- Spekhorst, H.; SippensGroenewegen, A.; David, G.K.; Janse, M.J.; Dunning, A.J. Body surface mapping during percutaneous transluminal coronary angioplasty. QRS changes indicating regional myocardial conduction delay. Circulation 1990, 81, 840–849. [Google Scholar] [CrossRef] [PubMed]
- SippensGroenewegen, A.; Spekhorst, H.; Van Hemel, N.M.; Kingma, J.H.; Hauer, R.N.; Janse, M.J.; Dunning, A.J. Body surface mapping of ectopic left and right ventricular activation. QRS spectrum in patients without structural heart disease. Circulation 1990, 82, 879–896. [Google Scholar] [CrossRef] [PubMed]
- Dambrink, J.-H.E.; SippensGroenewegen, A.; Van Gilst, W.H.; Peels, K.H.; Grimbergen, C.A.; Kingma, J.H. Association of Left Ventricular Remodeling and Nonuniform Electrical Recovery Expressed by Nondipolar QRST Integral Map Patterns in Survivors of a First Anterior Myocardial Infarction. Circulation 1995, 92, 300–310. [Google Scholar] [CrossRef]
- SippensGroenewegen, A.; Spekhorst, H.; Van Hemel, N.M.; Kingma, J.H.; Hauer, R.N.W.; De Barker, J.M.T.; Grimbergen, C.A.; Janse, M.J.; Dunning, A.J. Value of body surface mapping in localizing the site of origin of ventricular tachycardia in patients with previous myocardial infarction. J. Am. Coll. Cardiol. 1994, 24, 1708–1724. [Google Scholar] [CrossRef]
- Mitchell, L.B.; Hubley-Kozey, C.L.; Smith, E.R.; Wyse, D.G.; Duff, H.J.; Gillis, A.M.; Horacek, B.M. Electrocardiographic body surface mapping in patients with ventricular tachycardia. Assessment of utility in the identification of effective pharmacological therapy. Circulation 1992, 86, 383–393. [Google Scholar] [CrossRef]
- Tsunakawa, H.; Nishiyama, G.; Kusahana, Y.; Harumi, K. Identification of susceptibility to ventricular tachycardia after myocardial infarction by nondipolarity of QRST area maps. J. Am. Coll. Cardiol. 1989, 14, 1530–1536. [Google Scholar] [CrossRef]
- Stellbrink, C.; Stegemann, E.; Killmann, R.; Mischke, K.; Schütt, H.; Hanrath, P. Analyse von QRST-Integral und QT-Dispersion mittels Body surface potential mapping bei Patienten mit malignen ventrikulären Arrhythmien. Herzschrittmachertherapie Elektrophysiologie 1997, 8, 107–112. [Google Scholar] [CrossRef]
- Green, L.S.; Lux, R.L.; Stilli, D.; Haws, C.W.; Taccardi, B. Fine detail in body surface potential maps: Accuracy of maps using a limited lead array and spatial and temporal data representation. J. Electrocardiol. 1987, 20, 21–26. [Google Scholar] [CrossRef]
- Peeters, H.A.P.; SippensGroenewegen, A.; Schoonderwoerd, B.A.; Wever, E.F.D.; Grimbergen, C.A.; Hauer, R.N.W.; Robles De Medina, E.O. Body-Surface QRST Integral Mapping: Arrhythmogenic Right Ventricular Dysplasia Versus Idiopathic Right Ventricular Tachycardia. Circulation 1997, 95, 2668–2676. [Google Scholar] [CrossRef]
- Hren, R.; Steinhoff, U.; Gessner, C.; Endt, P.; Goedde, P.; Agrawal, R.; Oeff, M.; Lux, R.L.; Trahms, L. Value of Magnetocardiographic QRST Integral Maps in the Identification of Patients at Risk of Ventricular Arrhythmias. Pacing Clin. Electrophysiol. 1999, 22, 1292–1304. [Google Scholar] [CrossRef]
- Göudde, P.; Agrawal, R.; Müuller, H.-P.; Czerski, K.; Endt, P.; Steinhoff, U.; Oeff, M.; Schultheiss, H.-P.; Behrens, S. Magnetocardiographic mapping of QRS fragmentation in patients with a history of malignant tachyarrhythmias. Clin. Cardiol. 2001, 24, 682–688. [Google Scholar] [CrossRef] [PubMed]
- Roth, B.J. The magnetocardiogram. Biophys. Rev. 2024, 5, 021305. [Google Scholar] [CrossRef]
- Endt, P.; Montonen, J.; Mäkijärvi, M.; Nenonen, J.; Steinhoff, U.; Trahms, L.; Katila, T. Identification of post-myocardial infarction patients with ventricular tachycardia by time-domain intra-QRS analysis of signal-averaged electrocardiogram and magnetocardiogram. Med. Biol. Eng. Comput. 2000, 38, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Korhonen, P.; Mointonen, J.; Mäkinärvi, M.; Katila, T.; Nieminen, M.S.; Toivonen, L. Late Fields of the Magnetocardiographic QRS Complex as Indicators of Propensity to Sustained Ventricular Tachycardia after Myocardial Infarction. J. Cardiovasc. Electrophysiol. 2000, 11, 413–420. [Google Scholar] [CrossRef]
- Stenroos, M.; Sarvas, J. Bioelectromagnetic forward problem: Isolated source approach revis(it)ed. Phys. Med. Biol. 2012, 57, 3517–3535. [Google Scholar] [CrossRef]
- Dale, A.M.; Fischl, B.; Sereno, M.I. Cortical Surface-Based Analysis. NeuroImage 1999, 9, 179–194. [Google Scholar] [CrossRef]



| N | Recording 1 | Date | Age |
|---|---|---|---|
| 1 | Subject-1f1 | 8 October 2018 | 30 |
| 2 | Subject-1f2 | 7 May 2019 | 31 |
| 3 | Subject-2m1 | 16 October 2019 | 26 |
| 4 | Subject-3f1 | 27 June 2019 | 31 |
| 5 | Subject-3f2 | 10 April 2019 | 31 |
| 6 | Subject-4m1 | 9 October 2018 | 36 |
| 7 | Subject-4m2 | 10 May 2019 | 37 |
| 8 | Subject-5m1 | 8 January 2020 | 31 |
| 9 | Subject-6f1 | 5 July 2018 | 33 |
| 10 | Subject-6f2 | 5 April 2019 | 34 |
| 11 | Subject-7m1 | 7 May 2019 | 54 |
| 12 | Subject-7m2 | 17 October 2019 | 54 |
| 13 | Subject-8m1 | 11 October 2019 | 26 |
| 14 | Subject-8m2 | 18 October 2019 | 26 |
| 15 | Subject-9m1 | 18 June 2018 | 57 |
| 16 | Subject-9m2 | 12 June 2019 | 58 |
| [0, 400] ms | [42, 240] ms | M100 ± 12 ms | M50 ± 6 ms | |
| RMS [fT] | 15.4 ± 4.2 | 16 ± 4.2 | 16.2 ± 3.9 | 13.6 ± 6.9 |
| RD [%] | 39.4 ± 18.6 | 32.7 ± 15.3 | 23.2 ± 10.3 | 44 ± 18.4 |
| CC | 0.897 ± 0.115 | 0.932 ± 0.076 | 0.968 ± 0.031 | 0.875 ± 0.108 |
| RMS [fT] | 12.4 ± 3.2 | 12.4 ± 3.1 | 13 ± 3 | 11.2 ± 3.9 |
| RD [%] | 32.5 ± 16.8 | 25.8 ± 13.1 | 18.4 ± 7.9 | 37.3 ± 16.2 |
| CC | 0.929 ± 0.087 | 0.957 ± 0.055 | 0.98 ± 0.02 | 0.914 ± 0.077 |
| RMS [fT] | 10 ± 2.7 | 9.5 ± 2.2 | 9.7 ± 2.4 | 9.5 ± 3.7 |
| RD [%] | 26.5 ± 14.9 | 20.1 ± 11.1 | 13.7 ± 5.3 | 31.7±13.6 |
| CC | 0.952 ± 0.065 | 0.973 ± 0.039 | 0.989 ± 0.009 | 0.939 ± 0.053 |
| RMS [fT] | 8.3 ± 2.1 | 7.7 ± 1.5 | 7.9 ± 1.8 | 7.9 ± 2.4 |
| RD [%] | 22.6 ± 13.6 | 16.4 ± 9.8 | 11.1 ± 3.8 | 27.2 ± 12.8 |
| CC | 0.964 ± 0.051 | 0.981 ± 0.03 | 0.993 ± 0.005 | 0.954 ± 0.046 |
| Measures | Measured Map Fit (c) | Estimated Map Fit (d) | Selected Chan. Fit (e) |
|---|---|---|---|
| [mm] | (44.5, 0.9, 15.2) | (44.8, 0.9, 15.4) | (51.8, −1.1, 14.6) |
| [mm] | (−37.8, 3.0, 6.2) | (−38.2, 4.1, 7.6) | (−41.6, 0.4, 5.3) |
| [µAm] | (10.5, −12.1, −30.1) | (10.4, −11.4, −29.6) | (5.9, −11.3, −22.0) |
| [µAm] | (−8.1, −26.3, −36.7) | (−9.4, −23.2, −34.8) | (−3.8, −25.9, −28.1) |
| [mm] | / | 0.3 | 7.5 |
| [mm] | / | 1.9 | 4.7 |
| [mm] | / | 1.9 | 8.9 |
| [°] | / | 0.8 | 6.8 |
| [°] | / | 3.2 | 8.3 |
| Measures | Measured Map Fit (c) | Estimated Map Fit (d) | Selected Chan. Fit (e) |
|---|---|---|---|
| [mm] | (49.7, −6.4, 27.3) | (50.9, −6.6, 26.1) | (51.2, −5.1, 28.7) |
| [mm] | (−34.1, 2.1, 41.7) | (−35.3, 2.0, 42.8) | (−43.6, 0.3, 44.8) |
| [µAm] | (−3.2, 2.9, 6.5) | (−2.8, 2.6, 6.2) | (−2.7, 3.0, 5.4) |
| [µAm] | (5.4, −3.3, 4.6) | (5.1, −3.1, 4.3) | (3.6, −2.4, 3.5) |
| [mm] | / | 1.7 | 2.4 |
| [mm] | / | 1.7 | 10.2 |
| [mm] | / | 2.4 | 10.5 |
| [°] | / | 1.6 | 5.0 |
| [°] | / | 0.2 | 3.8 |
| Evaluation of Estimated M100 | Localization— Estimated |
Localization— Sel. Sites Only | |||||
|---|---|---|---|---|---|---|---|
| [fT] | [%] | [mm] | [mm] | [mm] | [mm] | ||
| 6 | 17.3 ± 4.4 | 22.6 ± 10.1 | 0.971 ± 0.026 | 7.2 ± 8.6 | 6.9 ± 4.4 | 24.9 ± 23.7 | 22.9 ± 16.6 |
| 8 | 14.8 ± 3.4 | 19 ± 7.5 | 0.980 ± 0.015 | 7.2 ± 10.6 | 7.7 ± 13.1 | 10.9 ± 8.5 | 12.8 ± 18.1 |
| 9 | 13.7 ± 3.4 | 17.6 ± 7.2 | 0.983 ± 0.015 | 6.4 ± 10.7 | 2.3 ± 2.0 | 16.9 ± 11.8 | 12.5 ± 16.2 |
| 10 | 12.3 ± 3.1 | 16.4 ± 6.2 | 0.985 ± 0.013 | 6.5 ± 11.8 | 1.8 ± 1.1 | 9.9 ± 8.4 | 7.7 ± 7.0 |
| 12 | 10.2 ± 2.9 | 13.5 ± 4.6 | 0.990 ± 0.006 | 5.8 ± 12.3 | 2.0 ± 1.2 | 6.7 ± 4.7 | 11.7 ± 15.7 |
| 15 | 8.7 ± 2.2 | 11.3 ± 3.4 | 0.993 ± 0.004 | 5.0 ± 12.2 | 1.5 ± 1.2 | 6.3 ± 5.0 | 3.8 ± 3.4 |
| 18 | 7.3 ± 1.8 | 9.3 ± 3.0 | 0.995 ± 0.003 | 1.1 ± 1.2 | 1.0 ± 0.8 | 5.8 ± 4.9 | 3.5 ± 2.0 |
| 21 | 6.1 ± 1.3 | 7.9 ± 2.5 | 0.997 ± 0.002 | 0.8 ± 0.7 | 1.0 ± 1.0 | 8.1 ± 7.8 | 6.6 ± 7.6 |
| 24 | 5.1 ± 1.0 | 6.6 ± 2.1 | 0.998 ± 0.001 | 0.7 ± 0.5 | 0.8 ± 0.9 | 7.4 ± 8.0 | 4.2 ± 3.4 |
| 27 | 4.6 ± 1.0 | 5.8 ± 1.8 | 0.998 ± 0.001 | 0.7 ± 0.5 | 0.8 ± 0.7 | 7.2 ± 7.9 | 3.3 ± 2.6 |
| 30 | 4.1 ± 0.8 | 5.4 ± 1.9 | 0.998 ± 0.001 | 0.5 ± 0.3 | 0.6 ± 0.6 | 4.6 ± 3.3 | 7.5 ± 14.1 |
| Evaluation of Estimated M100 | Estimated | Selected | |||
|---|---|---|---|---|---|
| [fT] | [%] | [mm] | [mm] | ||
| 3 | 25.5 ± 6.7 | 32.3 ± 14.3 | 0.946 ± 0.047 | 0.9 ± 0.5 | 2.7 ± 3.1 |
| 4 | 19.2 ± 3.7 | 25.4 ± 13.5 | 0.963 ± 0.044 | 0.4 ± 0.4 | 1.8 ± 2.4 |
| 5 | 18.4 ± 3.4 | 24 ± 12.4 | 0.968 ± 0.035 | 0.5 ± 0.4 | 1.8 ± 2.4 |
| 6 | 17.2 ± 4.6 | 22.3 ± 11.6 | 0.971 ± 0.03 | 0.4 ± 0.4 | 1.2 ± 1.3 |
| 7 | 14.7 ± 4.7 | 18.9 ± 9.8 | 0.980 ± 0.019 | 0.3 ± 0.3 | 0.8 ± 0.6 |
| 8 | 12.9 ± 3.7 | 17.6 ± 8.6 | 0.984 ± 0.015 | 0.2 ± 0.2 | 0.6 ± 0.7 |
| 9 | 11.8 ± 3.6 | 16.2 ± 8.3 | 0.985 ± 0.016 | 0.2 ± 0.2 | 0.6 ± 0.7 |
| 12 | 8.3 ± 2.5 | 11.2 ± 6.3 | 0.993 ± 0.009 | 0.1 ± 0.2 | 0.6 ± 0.6 |
| 15 | 6.0 ± 1.9 | 7.6 ± 3.7 | 0.997 ± 0.004 | 0.1 ± 0.1 | 0.6 ± 0.6 |
| 18 | 4.6 ± 1.1 | 6.0 ± 2.8 | 0.998 ± 0.002 | 0.0 ± 0.0 | 0.5 ± 0.5 |
| 21 | 3.5 ± 0.8 | 4.5 ± 2.3 | 0.999 ± 0.001 | 0.0 ± 0.0 | 0.4 ± 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marhl, U.; Hren, R.; Sander, T.; Jazbinšek, V. Optimization of OPM-MEG Layouts with a Limited Number of Sensors. Sensors 2025, 25, 2706. https://doi.org/10.3390/s25092706
Marhl U, Hren R, Sander T, Jazbinšek V. Optimization of OPM-MEG Layouts with a Limited Number of Sensors. Sensors. 2025; 25(9):2706. https://doi.org/10.3390/s25092706
Chicago/Turabian StyleMarhl, Urban, Rok Hren, Tilmann Sander, and Vojko Jazbinšek. 2025. "Optimization of OPM-MEG Layouts with a Limited Number of Sensors" Sensors 25, no. 9: 2706. https://doi.org/10.3390/s25092706
APA StyleMarhl, U., Hren, R., Sander, T., & Jazbinšek, V. (2025). Optimization of OPM-MEG Layouts with a Limited Number of Sensors. Sensors, 25(9), 2706. https://doi.org/10.3390/s25092706






