MFBCE: A Multi-Focal Bionic Compound Eye for Distance Measurement
Abstract
1. Introduction
- We Design an MFBCE. This system integrates an onboard core processing unit to handle image data, thereby reducing reliance on GPUs. This design significantly decreases the weight and size of the bionic compound eye (Section 2).
- We propose a multi-eye distance measurement algorithm. By utilizing multiple lenses with different focal lengths to capture multi-scale target images and deriving the intrinsic relationships between these images, the algorithm overcomes the limitations of binocular methods, which require identical cameras and prior calibration. This approach improves the ranging accuracy of the system (Section 3).
- We conducted an analysis of distance measurement errors. The MFBCE, combined with the multi-eye distance measurement algorithm, was used to conduct experiments for error analysis (Section 4).
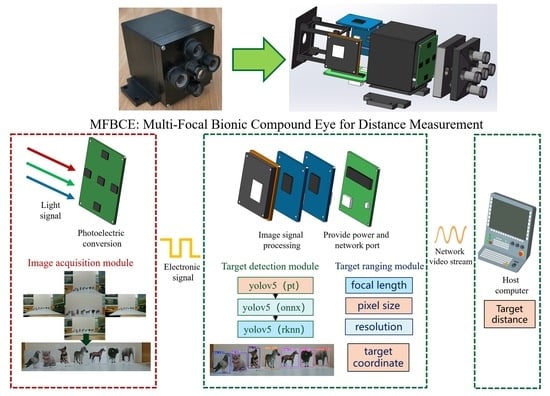
2. Design of MFBCE
2.1. Structure of MFBCE
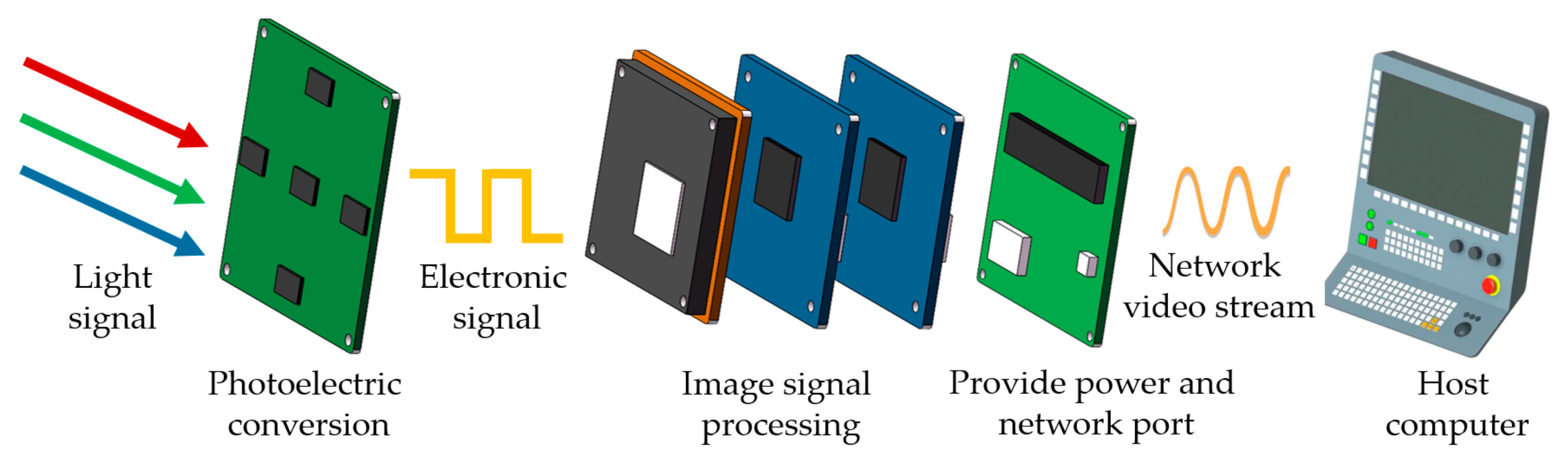
2.2. Principle of MFBCE
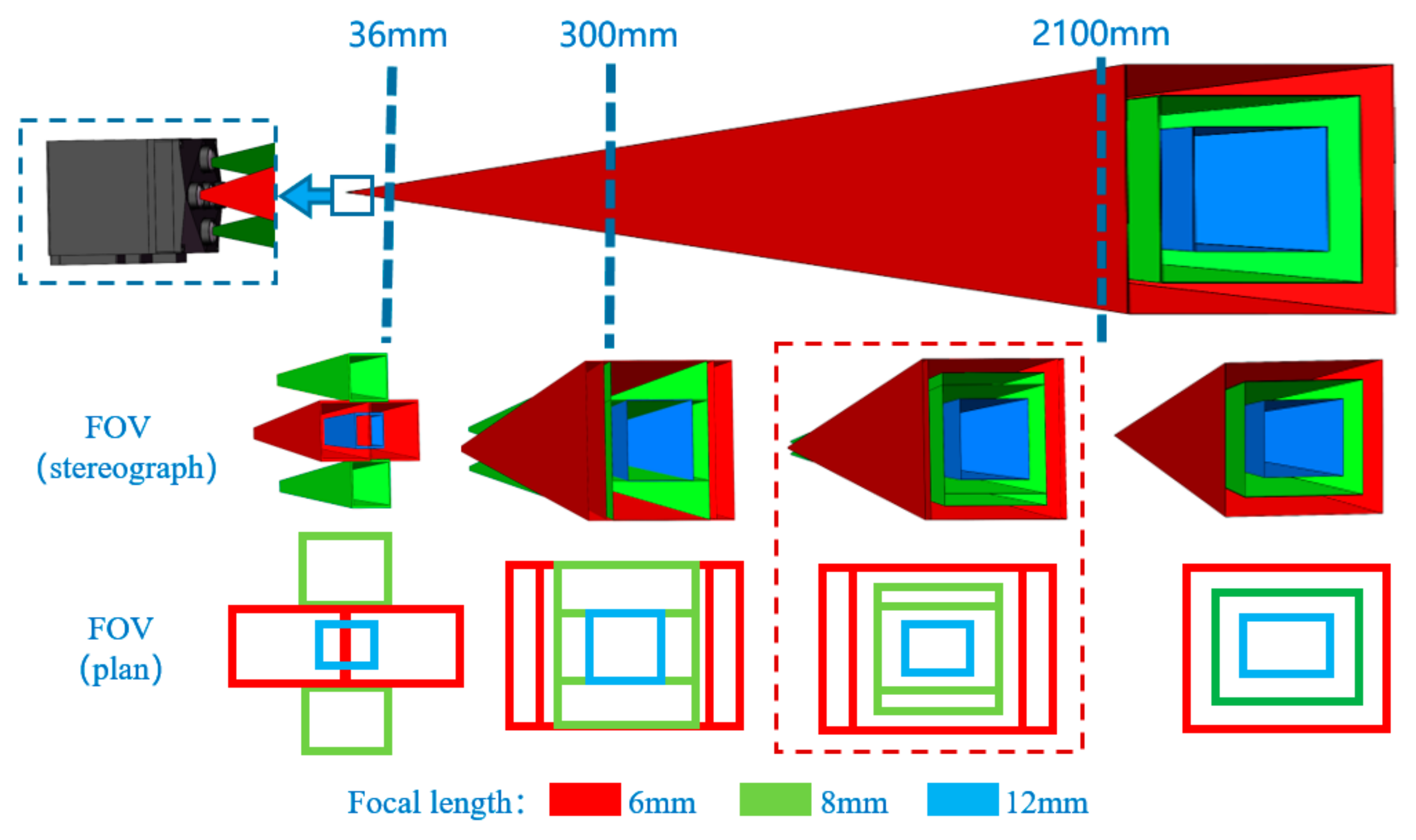
2.3. Field of View of MFBCE
- 36 mm: The FOV of four lenses at the top, bottom, left, and right intersect at this distance. Distances less than 36 mm create a blind area.
- 300 mm: The FOV of four lenses covers the center lens’s FOV at this distance.
- 300–2100 mm: The FOVs of the five lenses exhibit significant overlap, with noticeable differences caused by the parallax.
- Greater than 2100 mm: The overlap between the FOVs of the 6 mm focal length lenses reaches 98%, while the overlap between the 8 mm focal length lenses is 95%. The effect of parallax becomes smaller, and the system can be approximated as a coaxial system.
3. MFBCE Distance Measurement Algorithm
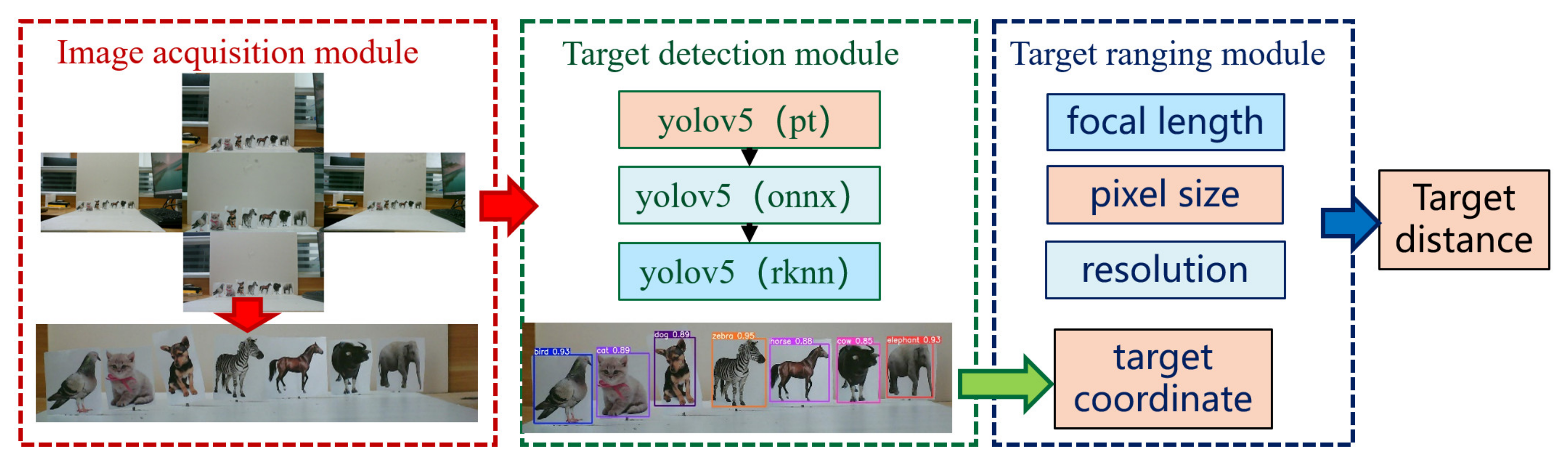
- Image acquisition module: MFBCE captures the target simultaneously using five lenses with different focal lengths. The use of lenses with varying focal lengths allows for the acquisition of multi-scale information, which provides a solid foundation for target detection and ranging.
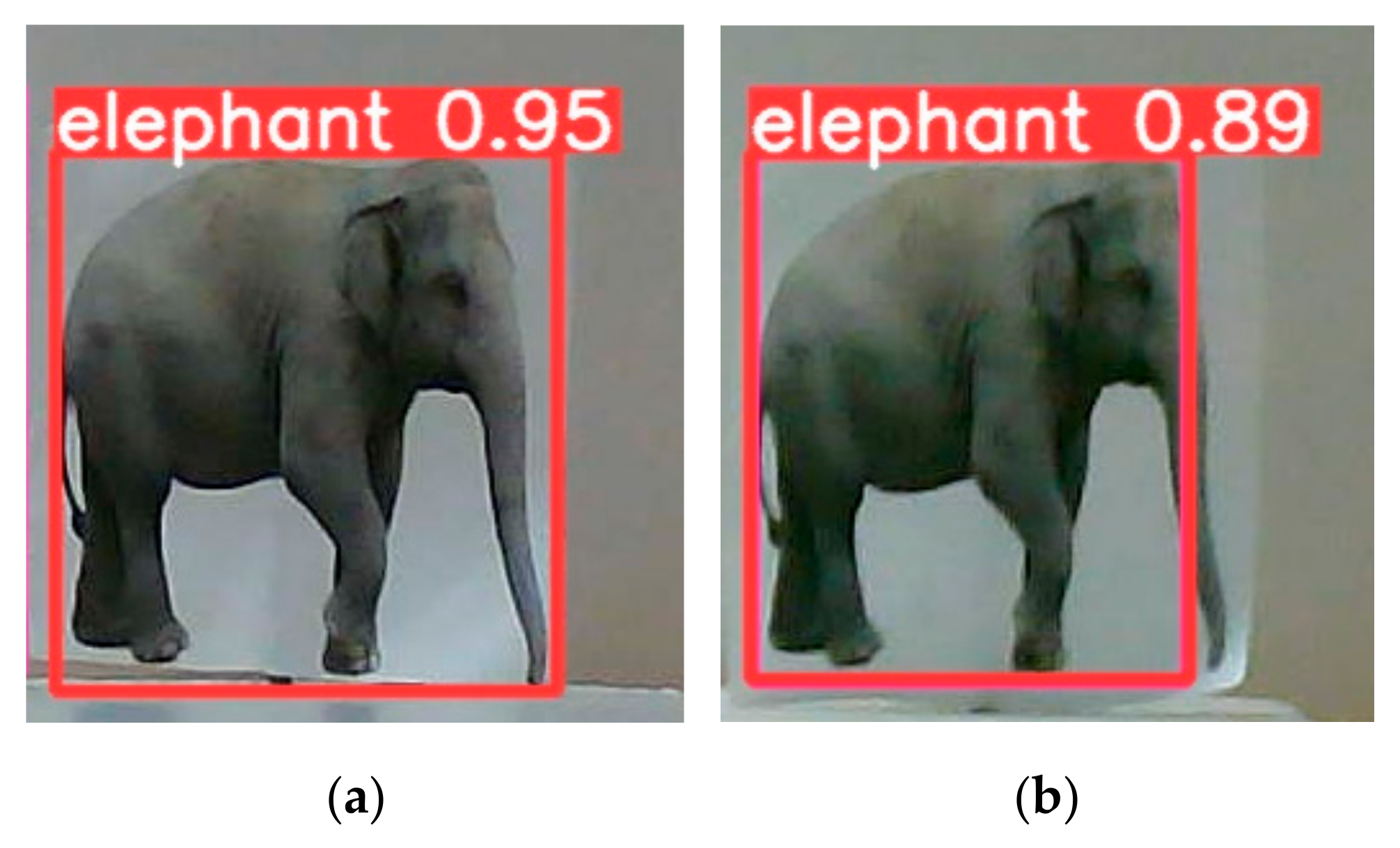
- Target detection module: The five acquired images are input into the intelligent vision chip of the MFBCE for target detection. In this study, we employ the YOLOv5 target detection algorithm [30,31]. Since traditional PyTorch models are not compatible with the RV1126 chip, the YOLOv5 model must be converted. First, the PyTorch model is converted into the ONNX (open neural network exchange), and then, the ONNX is further converted into the RKNN (rockchip neural network). RKNN is the deep learning neural network used by the RV1126 chip.
- Target ranging module: Through the image acquisition and target detection modules, the target bounding box and coordinates are obtained. Then, by integrating information such as the CMOS pixel size, camera resolution, lens’s focal length, and distance between lenses, the target’s distance can be calculated through theoretical derivation. This process is elaborated in detail in the following sections.
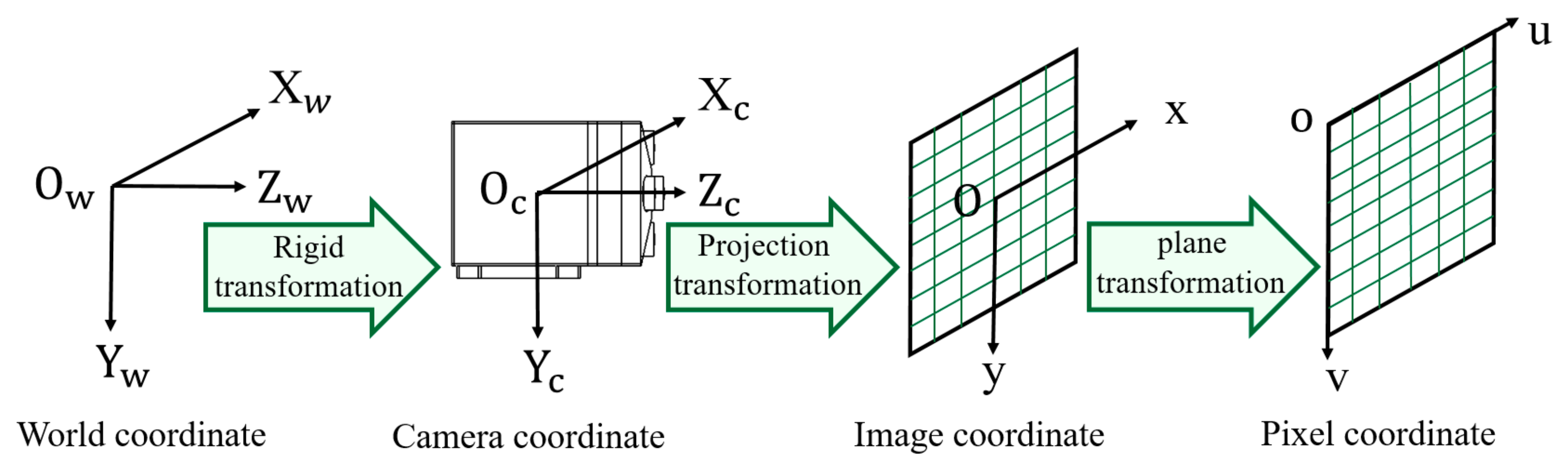
3.1. Monocular Vision Distance Measurement Model
3.2. Binocular Vision Distance Measurement Model
3.3. Multi-Eye Vision Distance Measurement Model
4. Experimental Results
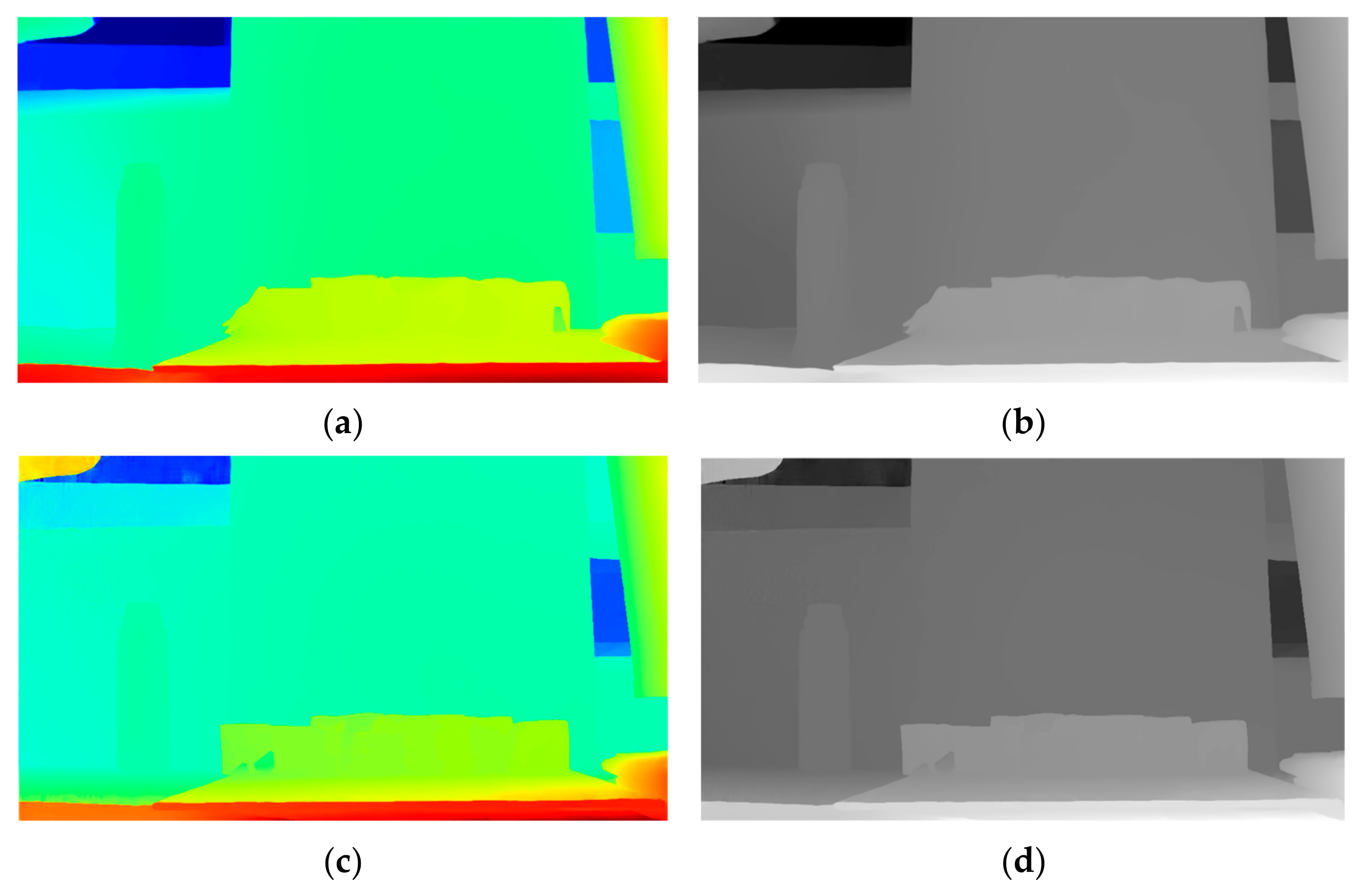
4.1. Binocular Ranging Experiments Between Lenses with Different Focal Lengths
4.2. Binocular Ranging Experiments with Different Algorithms
4.3. Binocular Ranging Experiments with Different Object Detection Accuracies
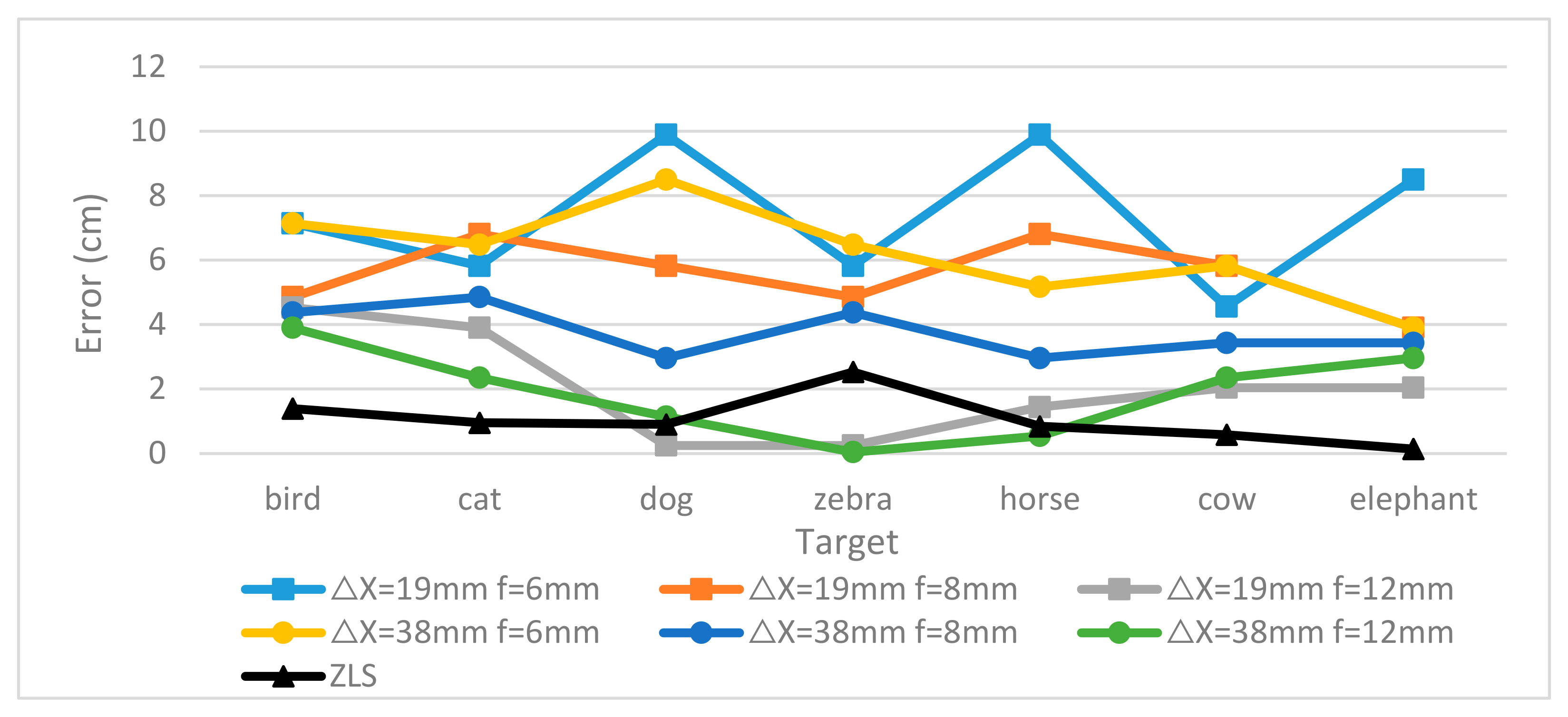
4.4. Comparison Experiment Between Binocular and Multi-Eye Ranging Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petrie, G.; Toth, C.K. Introduction to laser ranging, profiling, and scanning. In Topographic Laser Ranging and Scanning; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–28. [Google Scholar]
- Foley, J.M. Binocular distance perception. Psychol. Rev. 1980, 87, 411. [Google Scholar] [CrossRef] [PubMed]
- Blake, R.; Wilson, H. Binocular vision. Vis. Res. 2011, 51, 754–770. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Jiang, T.; Zhang, G.; Schoenemann, B.; Neri, F.; Zhu, M.; Bu, C.; Han, J.; Kuhnert, K.-D. Artificial compound eye: A survey of the state-of-the-art. Artif. Intell. Rev. 2017, 48, 573–603. [Google Scholar] [CrossRef]
- Wang, D.; Pan, Q.; Zhao, C.; Hu, J.; Xu, Z.; Yang, F.; Zhou, Y. A study on camera array and its applications. IFAC-PapersOnLine 2017, 50, 10323–10328. [Google Scholar] [CrossRef]
- Shogenji, R.; Kitamura, Y.; Yamada, K.; Miyatake, S.; Tanida, J. Bimodal fingerprint capturing system based on compound-eye imaging module. Appl. Opt. 2004, 43, 1355–1359. [Google Scholar] [CrossRef]
- Ma, M.; Guo, F.; Cao, Z.; Wang, K. Development of an artificial compound eye system for three-dimensional object detection. Appl. Opt. 2014, 53, 1166–1172. [Google Scholar] [CrossRef]
- Zhao, Z.-F.; Liu, J.; Zhang, Z.-Q.; Xu, L.-F. Bionic-compound-eye structure for realizing a compact integral imaging 3D display in a cell phone with enhanced performance. Opt. Lett. 2020, 45, 1491–1494. [Google Scholar] [CrossRef]
- Kagawa, K.; Yamada, K.; Tanaka, E.; Tanida, J. A three-dimensional multifunctional compound-eye endoscopic system with extended depth of field. Electron. Commun. Jpn. 2012, 95, 14–27. [Google Scholar] [CrossRef]
- Tanida, J.; Mima, H.; Kagawa, K.; Ogata, C.; Umeda, M. Application of a compound imaging system to odontotherapy. Opt. Rev. 2015, 22, 322–328. [Google Scholar] [CrossRef]
- Davis, J.; Barrett, S.; Wright, C.; Wilcox, M. A bio-inspired apposition compound eye machine vision sensor system. Bioinspir. Biomim. 2009, 4, 046002. [Google Scholar] [CrossRef]
- Venkataraman, K.; Lelescu, D.; Duparré, J.; McMahon, A.; Molina, G.; Chatterjee, P.; Mullis, R.; Nayar, S. Picam: An ultra-thin high performance monolithic camera array. ACM Trans. Graph. (TOG) 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Afshari, H.; Popovic, V.; Tasci, T.; Schmid, A.; Leblebici, Y. A spherical multi-camera system with real-time omnidirectional video acquisition capability. IEEE Trans. Consum. Electron. 2012, 58, 1110–1118. [Google Scholar] [CrossRef]
- Afshari, H.; Jacques, L.; Bagnato, L.; Schmid, A.; Vandergheynst, P.; Leblebici, Y. The PANOPTIC camera: A plenoptic sensor with real-time omnidirectional capability. J. Signal Process. Syst. 2013, 70, 305–328. [Google Scholar] [CrossRef]
- Cao, A.; Shi, L.; Deng, Q.; Hui, P.; Zhang, M.; Du, C. Structural design and image processing of a spherical artificial compound eye. Optik 2015, 126, 3099–3103. [Google Scholar] [CrossRef]
- Carles, G.; Chen, S.; Bustin, N.; Downing, J.; McCall, D.; Wood, A.; Harvey, A.R. Multi-aperture foveated imaging. Opt. Lett. 2016, 41, 1869–1872. [Google Scholar] [CrossRef]
- Popovic, V.; Seyid, K.; Pignat, E.; Çogal, Ö.; Leblebici, Y. Multi-camera platform for panoramic real-time HDR video construction and rendering. J. Real-Time Image Process. 2016, 12, 697–708. [Google Scholar] [CrossRef]
- Xue, J.; Qiu, S.; Wang, X.; Jin, W. A compact visible bionic compound eyes system based on micro-surface fiber faceplate. In Proceedings of the 2019 International Conference on Optical Instruments and Technology: Optoelectronic Imaging/Spectroscopy and Signal Processing Technology, Beijing, China, 2–4 November 2019; pp. 68–75. [Google Scholar]
- Horisaki, R.; Irie, S.; Ogura, Y.; Tanida, J. Three-dimensional information acquisition using a compound imaging system. Opt. Rev. 2007, 14, 347–350. [Google Scholar] [CrossRef]
- Lee, W.-B.; Lee, H.-N. Depth-estimation-enabled compound eyes. Opt. Commun. 2018, 412, 178–185. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, S.; Jin, W.Q.; Dai, J.L. Image Mosaic and Positioning Algorithms of Bionic Compound Eye Based on Fiber Faceplate. Binggong Xuebao/Acta Armamentarii 2018, 39, 1144–1150. [Google Scholar]
- Liu, J.; Zhang, Y.; Xu, H.; Wu, D.; Yu, W. Long-working-distance 3D measurement with a bionic curved compound-eye camera. Opt. Express 2022, 30, 36985–36995. [Google Scholar] [CrossRef]
- Oh, W.; Yoo, H.; Ha, T.; Oh, S. Local selective vision transformer for depth estimation using a compound eye camera. Pattern Recognit. Lett. 2023, 167, 82–89. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Liu, J.; Huang, Z.; Li, Y.; Wang, H.; Zhang, Y.; Yu, Y.; Yuan, X.; Qiu, L. Infrared Bionic Compound-Eye Camera: Long-Distance Measurement Simulation and Verification. Electronics 2025, 14, 1473. [Google Scholar] [CrossRef]
- Song, Y.M.; Xie, Y.; Malyarchuk, V.; Xiao, J.; Jung, I.; Choi, K.-J.; Liu, Z.; Park, H.; Lu, C.; Kim, R.-H. Digital cameras with designs inspired by the arthropod eye. Nature 2013, 497, 95–99. [Google Scholar] [CrossRef]
- Viollet, S.; Godiot, S.; Leitel, R.; Buss, W.; Breugnon, P.; Menouni, M.; Juston, R.; Expert, F.; Colonnier, F.; L’Eplattenier, G. Hardware architecture and cutting-edge assembly process of a tiny curved compound eye. Sensors 2014, 14, 21702–21721. [Google Scholar] [CrossRef]
- Leininger, B.; Edwards, J.; Antoniades, J.; Chester, D.; Haas, D.; Liu, E.; Stevens, M.; Gershfield, C.; Braun, M.; Targove, J.D. Autonomous real-time ground ubiquitous surveillance-imaging system (ARGUS-IS). In Proceedings of the Defense Transformation and Net-Centric Systems 2008, Orlando, FL, USA, 16–20 March 2008; pp. 141–151. [Google Scholar]
- Cheng, Y.; Cao, J.; Zhang, Y.; Hao, Q. Review of state-of-the-art artificial compound eye imaging systems. Bioinspir. Biomim. 2019, 14, 031002. [Google Scholar] [CrossRef]
- Phan, H.L.; Yi, J.; Bae, J.; Ko, H.; Lee, S.; Cho, D.; Seo, J.-M.; Koo, K.-i. Artificial compound eye systems and their application: A review. Micromachines 2021, 12, 847. [Google Scholar] [CrossRef]
- Jiang, P.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. A Review of Yolo algorithm developments. Procedia Comput. Sci. 2022, 199, 1066–1073. [Google Scholar] [CrossRef]
- Zhu, X.; Lyu, S.; Wang, X.; Zhao, Q. TPH-YOLOv5: Improved YOLOv5 based on transformer prediction head for object detection on drone-captured scenarios. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2778–2788. [Google Scholar]
- Griffin, B.A.; Corso, J.J. Depth from camera motion and object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1397–1406. [Google Scholar]
- Wang, X.; Li, D.; Zhang, G. Panoramic stereo imaging of a bionic compound-Eye based on binocular vision. Sensors 2021, 21, 1944. [Google Scholar] [CrossRef]
- Lipson, L.; Teed, Z.; Deng, J. Raft-stereo: Multilevel recurrent field transforms for stereo matching. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 218–227. [Google Scholar]
- Jiang, H.; Xu, R.; Jiang, W. An improved raftstereo trained with a mixed dataset for the robust vision challenge 2022. arXiv 2022, arXiv:2210.12785. [Google Scholar]
- Xu, G.; Wang, X.; Zhang, Z.; Cheng, J.; Liao, C.; Yang, X. IGEV++: Iterative multi-range geometry encoding volumes for stereo matching. arXiv 2024, arXiv:2409.00638. [Google Scholar]





| Parameter | Typical Value |
|---|---|
| Size | 60 mm × 60 mm × 80 mm |
| Weight | 275 g |
| Focal length | 6 mm, 8 mm, 12 mm |
| Inter-camera distance (baseline) | 19 mm |
| Optical format | 1/2.9 inch |
| Pixel size | 2.8 μm × 2.8 μm |
| Active pixel array | 1920 × 1080 |
| Focal Length | DFOV | HFOV | VFOV |
|---|---|---|---|
| 6 mm | 54.84° | 48.26° | 28.18° |
| 8 mm | 42.52° | 37.14° | 21.40° |
| 12 mm | 29.09° | 25.25° | 14.36° |
| Target | Stereo ΔX = 38 mm | ||
|---|---|---|---|
| 6 mm and 8 mm | 6 mm and 12 mm | 8 mm and 12 mm | |
| bird | 100.31 | 101.27 | 101.00 |
| cat | 104.92 | 101.07 | 100.56 |
| dog | 103.90 | 95.24 | 101.66 |
| zebra | 107.74 | 102.97 | 106.10 |
| horse | 97.86 | 98.95 | 102.49 |
| cow | 98.16 | 96.74 | 101.81 |
| elephant | 101.27 | 93.78 | 105.69 |
| MAE | 3.16 | 2.94 | 2.76 |
| RMSE | 3.95 | 3.48 | 3.44 |
| Target | Stereo ΔX = 38 mm, f = 8 mm | ||
|---|---|---|---|
| RAFT | IGEV++ | Ours (Detection) | |
| bird | 111.69 | 107.20 | 105.09 |
| cat | 110.54 | 106.67 | 105.09 |
| dog | 110.54 | 106.14 | 103.56 |
| zebra | 109.97 | 105.61 | 104.07 |
| horse | 109.40 | 105.61 | 102.56 |
| cow | 109.40 | 105.61 | 103.56 |
| elephant | 108.84 | 104.58 | 102.07 |
| MAE | 10.05 | 5.92 | 3.71 |
| RMSE | 10.09 | 5.97 | 3.86 |
| Distance (cm) | Stereo ΔX = 19 mm | Stereo ΔX = 38 mm | ||||||
|---|---|---|---|---|---|---|---|---|
| 6 mm | 8 mm | 12 mm | 6 mm | 8 mm | 12 mm | 12 mm 2 Pixel | 12 mm 1 Pixel | |
| 90 | 101.18 | 98.13 | 95.26 | 95.26 | 93.89 | 92.56 | 91.01 | 90.50 |
| 95 | 107.55 | 104.11 | 100.88 | 100.88 | 99.35 | 97.85 | 96.21 | 95.56 |
| 100 | 114.00 | 110.14 | 106.54 | 106.54 | 104.83 | 103.17 | 101.24 | 100.62 |
| 105 | 120.54 | 116.24 | 112.24 | 112.24 | 110.34 | 108.50 | 106.37 | 105.68 |
| 110 | 127.18 | 122.40 | 117.97 | 117.97 | 115.87 | 113.84 | 111.51 | 110.75 |
| 115 | 133.91 | 128.62 | 123.74 | 123.74 | 121.43 | 119.21 | 116.65 | 115.82 |
| 120 | 140.74 | 134.91 | 129.55 | 129.55 | 127.02 | 124.59 | 121.79 | 120.89 |
| Model | Size | mAPval 50–95 | mAPval 50 | Speed CPU b1 (ms) | Speed RV1126 (ms) | Params (M) |
|---|---|---|---|---|---|---|
| YOLOv5n | 640 | 28.0 | 45.7 | 45 | 33 | 1.9 |
| YOLOv5s | 640 | 37.4 | 56.8 | 98 | 65 | 7.2 |
| YOLOv5m | 640 | 45.4 | 64.1 | 224 | 144 | 21.2 |
| YOLOv5l | 640 | 49.0 | 67.3 | 430 | 280 | 46.5 |
| YOLOv5x | 640 | 50.7 | 68.9 | 766 | 502 | 86.7 |
| Target | Stereo ΔX = 19 mm | Stereo ΔX = 38 mm | Ours (MFBCE) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 6 mm | 8 mm | 12 mm | 6 mm | 8 mm | 12 mm | ZAM | ZRMS | ZLS | |
| bird | 107.14 | 104.85 | 104.53 | 107.14 | 104.37 | 103.90 | 102.52 | 102.53 | 101.39 |
| cat | 105.82 | 106.81 | 103.90 | 106.48 | 104.85 | 102.35 | 101.06 | 101.07 | 100.95 |
| dog | 109.89 | 105.82 | 100.25 | 108.50 | 102.96 | 101.14 | 101.11 | 101.15 | 100.90 |
| zebra | 105.82 | 104.85 | 100.25 | 106.48 | 104.37 | 99.96 | 103.85 | 103.86 | 102.53 |
| horse | 109.89 | 106.81 | 101.44 | 105.17 | 102.96 | 100.54 | 100.99 | 101.01 | 100.84 |
| cow | 104.56 | 105.82 | 102.04 | 105.82 | 103.43 | 102.35 | 99.49 | 99.50 | 99.42 |
| elephant | 108.50 | 103.90 | 102.04 | 103.90 | 103.43 | 102.96 | 99.94 | 99.98 | 99.86 |
| MAE | 7.37 | 5.55 | 2.06 | 6.21 | 3.77 | 1.90 | 1.44 | 1.45 | 1.05 |
| RMSE | 7.63 | 5.64 | 2.57 | 6.36 | 3.83 | 2.28 | 1.88 | 1.89 | 1.26 |
| Target | Ours (MFBCE) ZLS | |||||
|---|---|---|---|---|---|---|
| 100 cm | 120 cm | 140 cm | 160 cm | 180 cm | 200 cm | |
| bird | 101.39 | 121.77 | 144.22 | 172.89 | 193.07 | 218.60 |
| cat | 100.95 | 123.21 | 144.71 | 170.44 | 193.72 | 215.56 |
| dog | 100.90 | 123.60 | 147.20 | 169.00 | 195.22 | 216.10 |
| zebra | 102.53 | 122.94 | 147.27 | 171.00 | 192.91 | 214.67 |
| horse | 100.84 | 122.13 | 144.83 | 169.94 | 190.07 | 213.12 |
| cow | 99.42 | 122.06 | 144.97 | 168.24 | 193.03 | 210.84 |
| elephant | 99.86 | 121.34 | 144.54 | 169.44 | 185.09 | 209.53 |
| MAE | 1.05 | 2.43 | 5.39 | 10.15 | 11.87 | 14.03 |
| RMSE | 1.26 | 2.55 | 5.52 | 10.25 | 12.27 | 14.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Wang, X.; Xue, J.; Lv, S.; Wei, R. MFBCE: A Multi-Focal Bionic Compound Eye for Distance Measurement. Sensors 2025, 25, 2708. https://doi.org/10.3390/s25092708
Liu Q, Wang X, Xue J, Lv S, Wei R. MFBCE: A Multi-Focal Bionic Compound Eye for Distance Measurement. Sensors. 2025; 25(9):2708. https://doi.org/10.3390/s25092708
Chicago/Turabian StyleLiu, Qiwei, Xia Wang, Jiaan Xue, Shuaijun Lv, and Ranfeng Wei. 2025. "MFBCE: A Multi-Focal Bionic Compound Eye for Distance Measurement" Sensors 25, no. 9: 2708. https://doi.org/10.3390/s25092708
APA StyleLiu, Q., Wang, X., Xue, J., Lv, S., & Wei, R. (2025). MFBCE: A Multi-Focal Bionic Compound Eye for Distance Measurement. Sensors, 25(9), 2708. https://doi.org/10.3390/s25092708