Low Signal-to-Noise Ratio Optoelectronic Signal Reconstruction Based on Zero-Phase Multi-Stage Collaborative Filtering
Abstract
1. Introduction
- Zero-phase FIR Bandpass Filtering Mechanism: A novel filtering approach employing forward–backward processing combined with dynamic phase compensation to rigorously suppress phase distortion, ensuring high-fidelity signal representation throughout the processing chain.
- Four-stage Cascaded Collaborative Filtering Strategy: An adaptive, multi-stage filtering architecture that synergistically integrates adaptive sampling and sophisticated anti-aliasing techniques. This strategy optimally balances signal reconstruction fidelity, smoothness, and parameter sparsity for enhanced signal quality.
- Multi-scale Adaptive Transform Algorithm: A robust adaptive transformation algorithm, based on the fourth-order Daubechies wavelet, designed to achieve high-precision signal reconstruction while maintaining stability and effectiveness across diverse and challenging noise environments.
- Significant Performance Enhancement and Empirical Validation: Rigorous experimental evaluations show that the proposed MCFC framework achieves a remarkable SNR improvement of up to 45 dB for input signals with an SNR as low as −15 dB. Furthermore, correlation coefficients consistently exceeding 0.98 are maintained across various noise conditions, demonstrating superior performance and stability compared to traditional methods.
2. Methods
2.1. Theoretical Foundation of MCFC
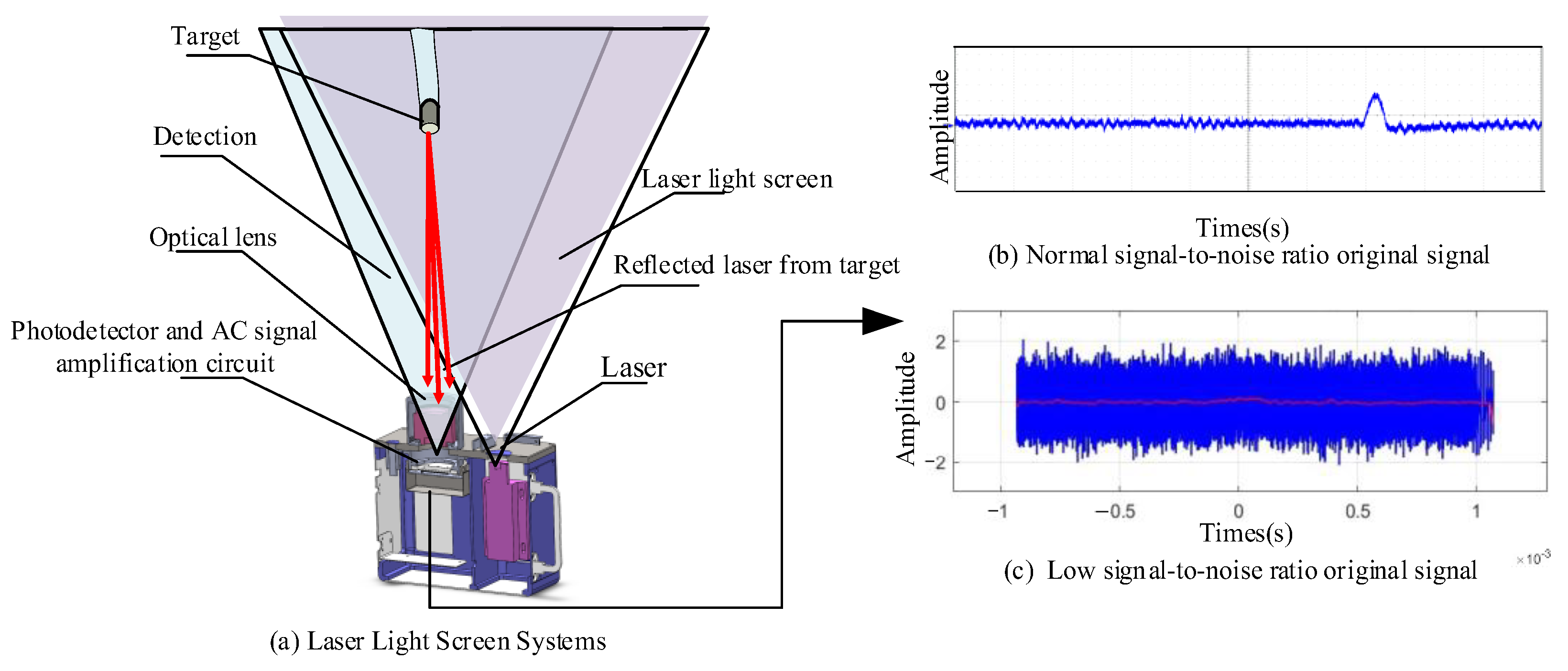
2.1.1. Problem Formalization
2.1.2. System Structure Design
2.1.3. Theoretical Optimality Proof
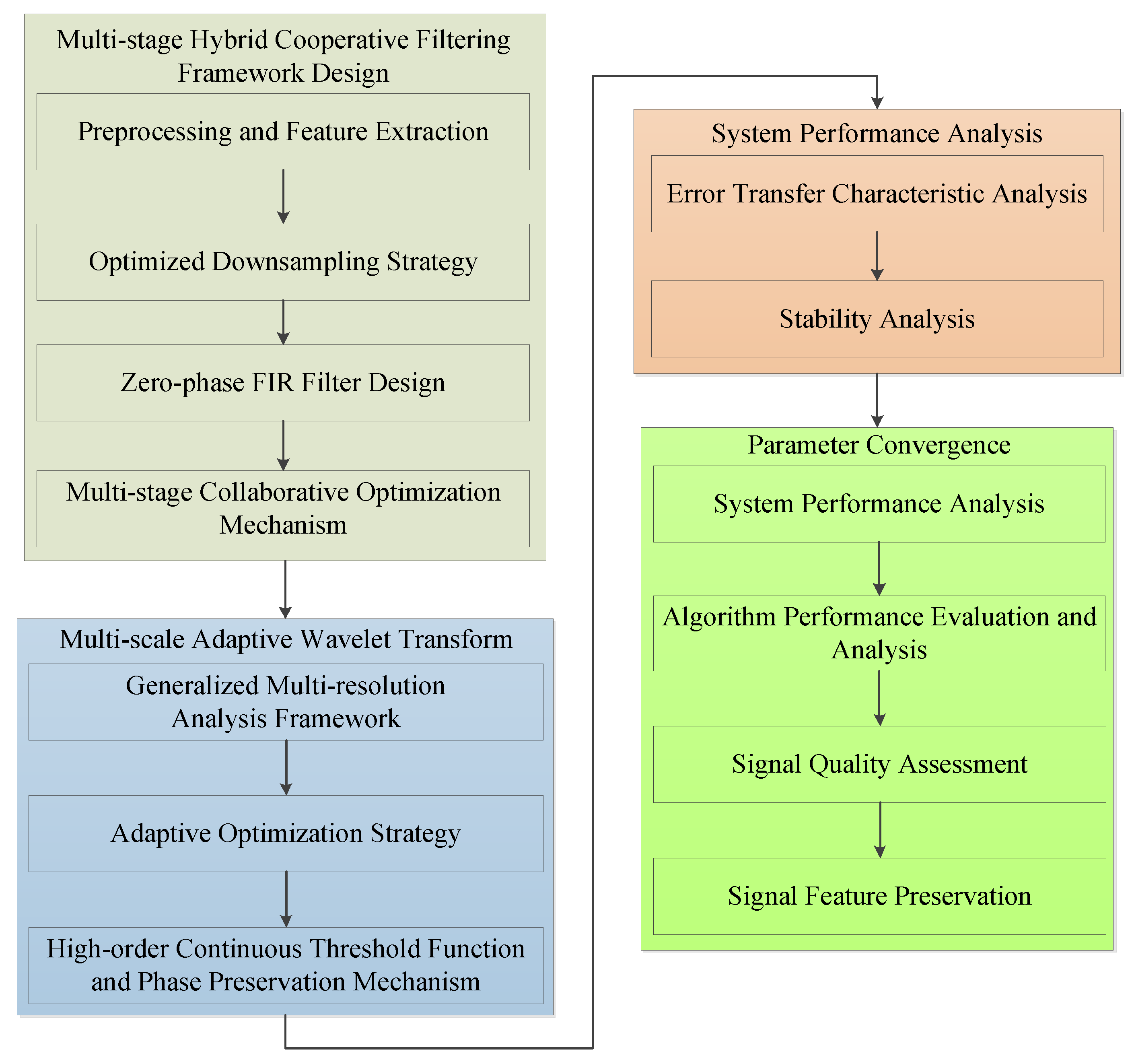
2.2. Multi-Stage Cooperative Filtering Framework Design
2.2.1. Preprocessing and Feature Extraction
- Dynamic Mean Compensation and Normalization
- 2.
- Signal Spectral Analysis
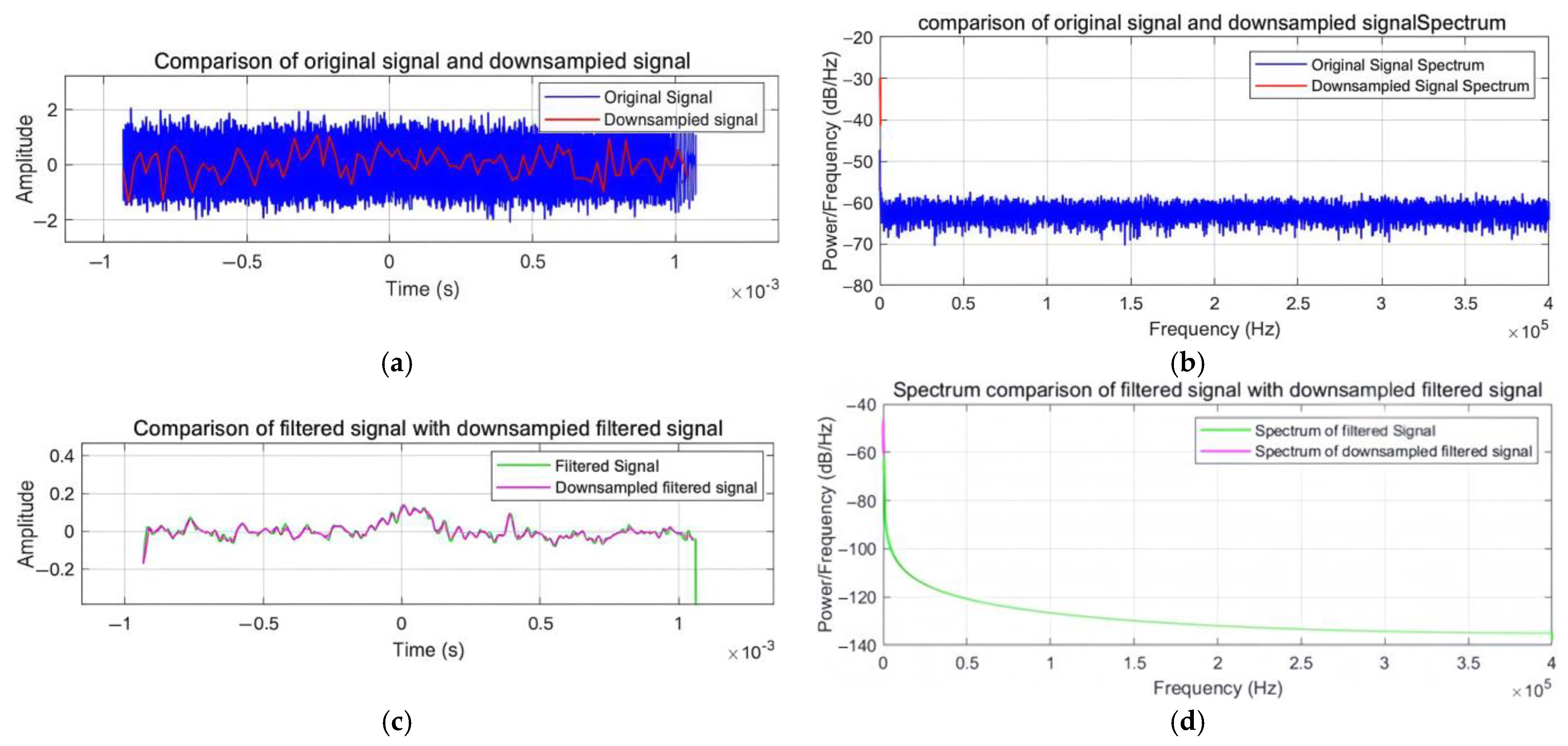
2.2.2. Optimized Downsampling Strategy
- Adaptive Sampling Rate Optimization
- 2.
- Anti-aliasing Processing Method
- 3.
- Signal Integrity Protection
2.2.3. Zero-Phase FIR Filter Design
- High-order FIR Filtering
- 2.
- Bidirectional Zero-phase Processing Mechanism
- (1)
- Forward Filtering Process:
- (2)
- Backward Filtering Process:
- 3.
- Global Phase Compensation
2.2.4. Multi-Stage Collaborative Optimization Mechanism
- Multi-objective Optimization Framework
- 2.
- Four-stage Cascade Filtering Structure
2.3. Multi-Scale Adaptive Wavelet Transform
2.3.1. Generalized Multi-Resolution Analysis Framework
2.3.2. Adaptive Optimization Strategy
2.3.3. High-Order Continuous Threshold Function and Phase Preservation Mechanism
2.4. System Performance Analysis
2.4.1. Error Transfer Characteristic Analysis
2.4.2. Stability Analysis
- Closed-loop Stability Analysis
- 2.
- Parameter Convergence
2.5. Algorithm Performance Evaluation and Analysis
2.5.1. Signal Quality Assessment
- Signal-to-Noise Ratio Gain (SNR):
- 2.
- Reconstruction Accuracy:
2.5.2. Signal Feature Preservation
- Waveform Distortion Degree
- 2.
- Spectral Preservation Degree
3. Results
3.1. Experimental Platform Setup
3.2. Algorithm Performance Verification
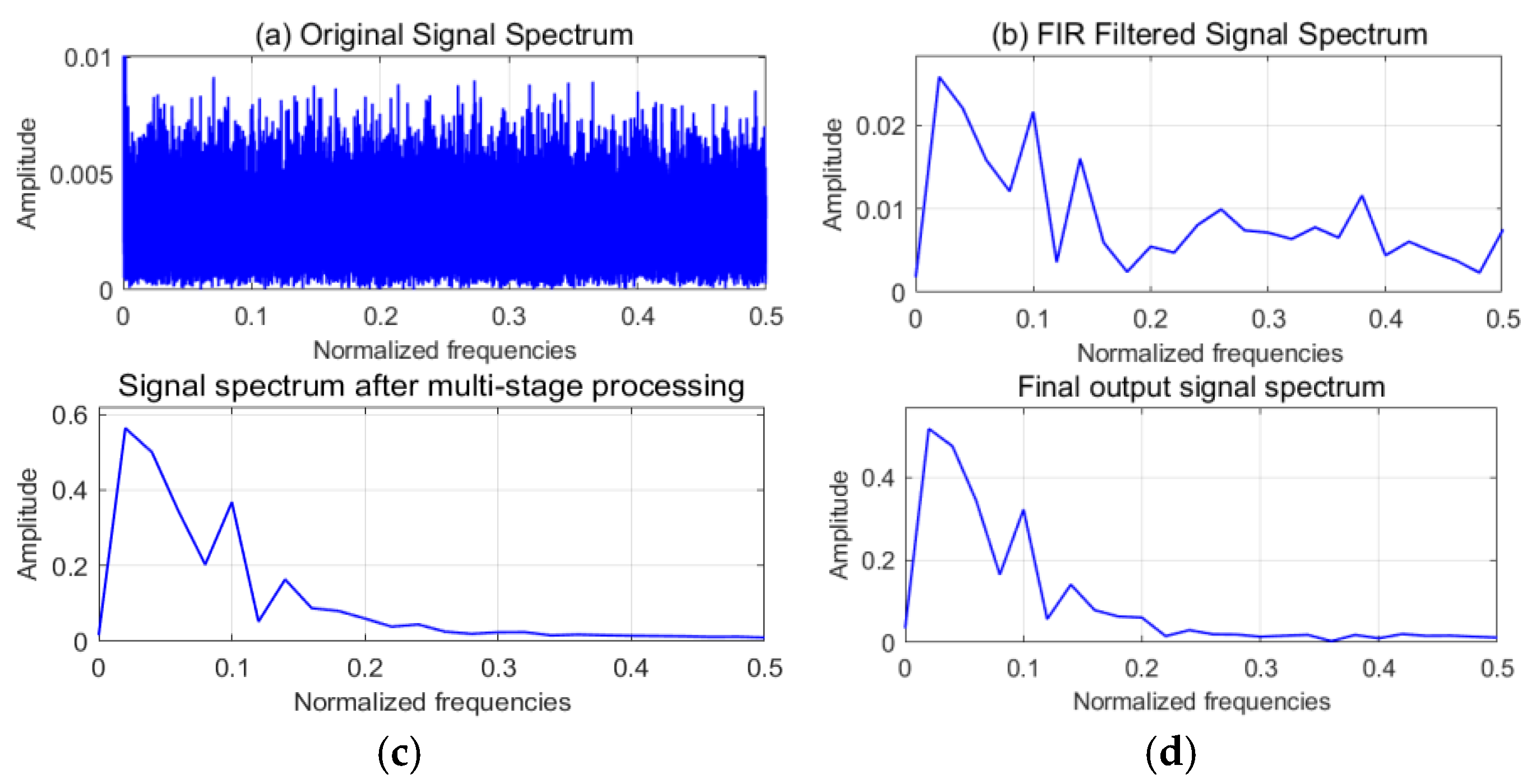
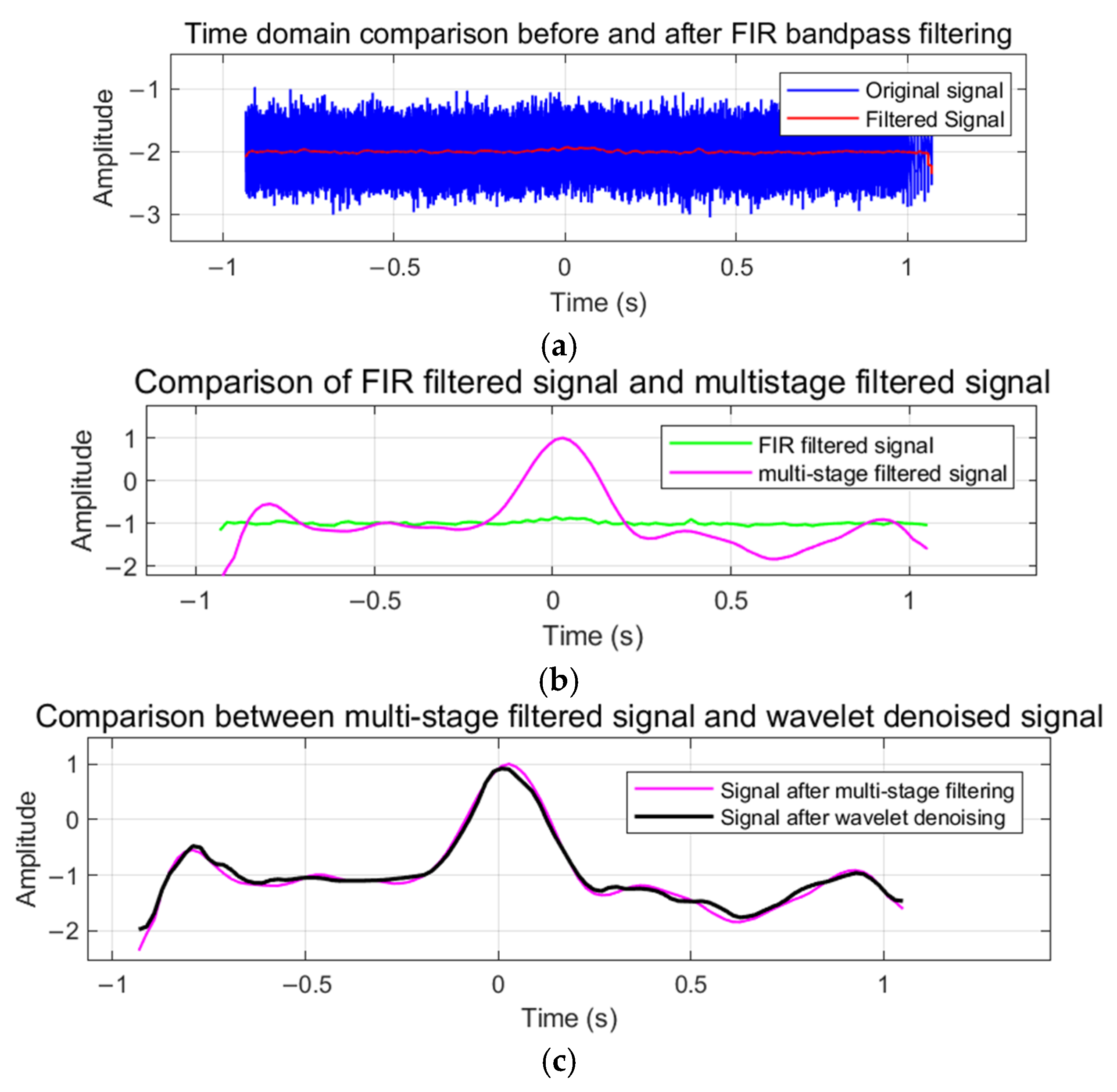
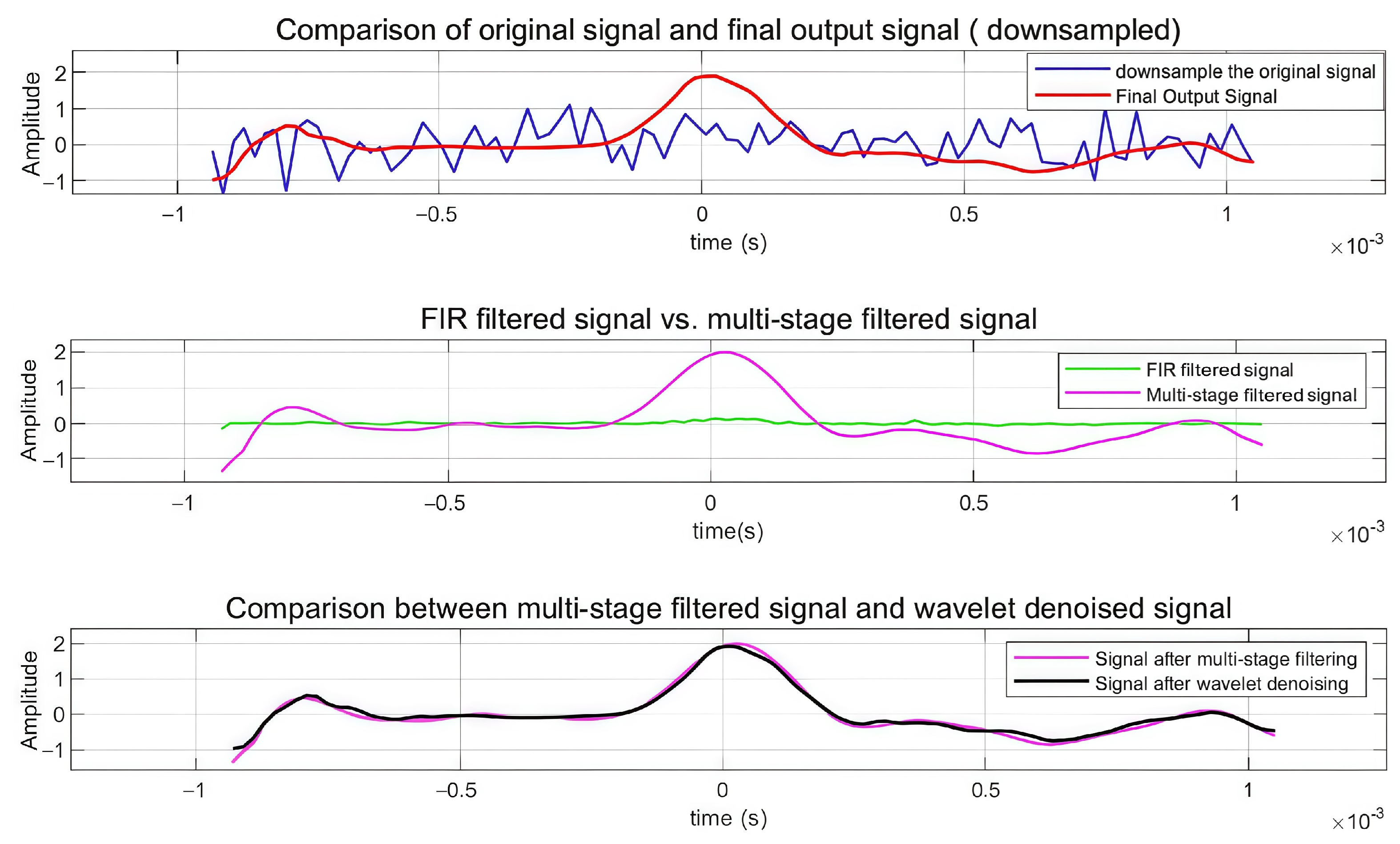
3.2.1. Multi-Stage Denoising Effect Verification
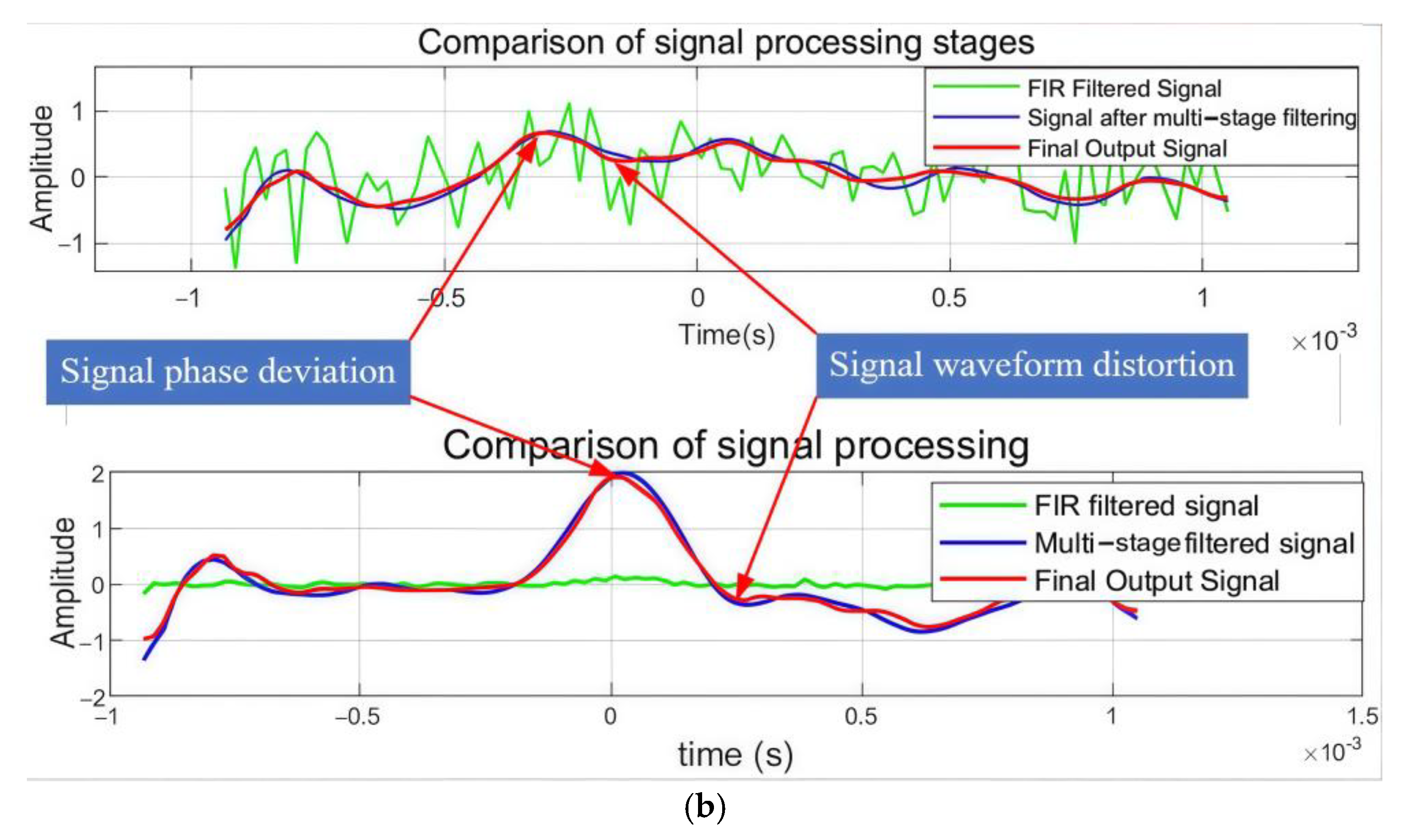
3.2.2. Phase Control Effect Analysis
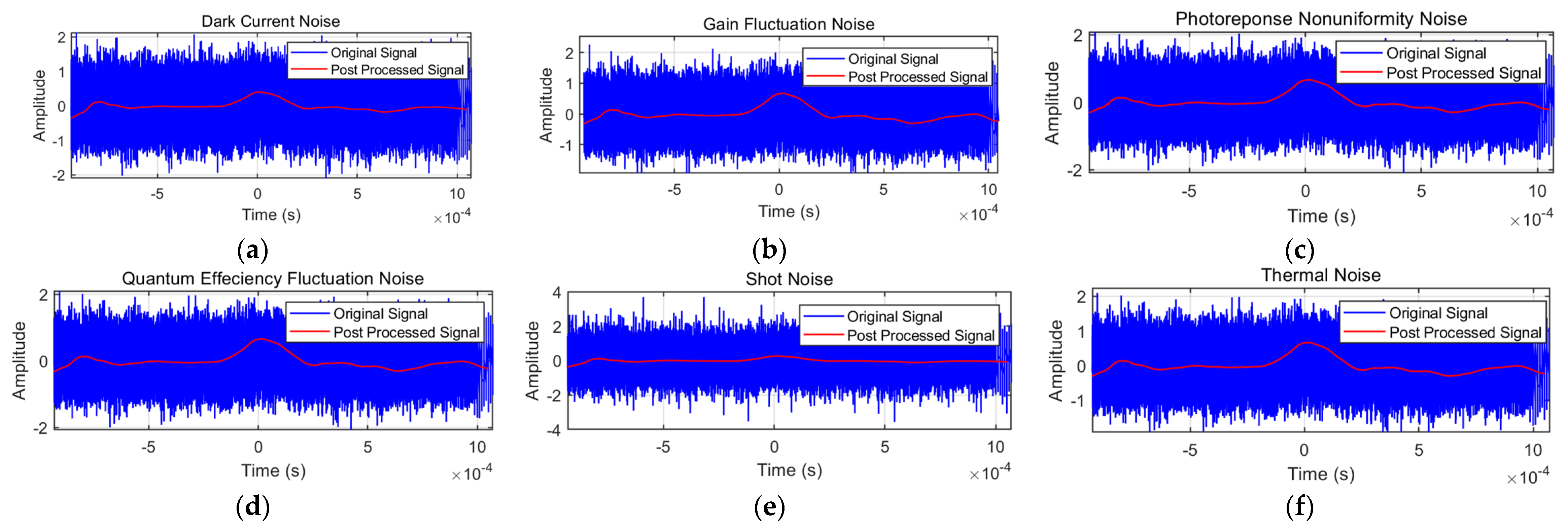
3.2.3. Processing Effects in Different Noise Environments
3.3. Algorithm Comparison Analysis
3.3.1. Different Module Contribution Analysis
3.3.2. Algorithm Stability Analysis
- Testing with Multiple Groups of Different Signal-to-Noise Ratio Data
- 2.
- Parameter Sensitivity Analysis Experiment
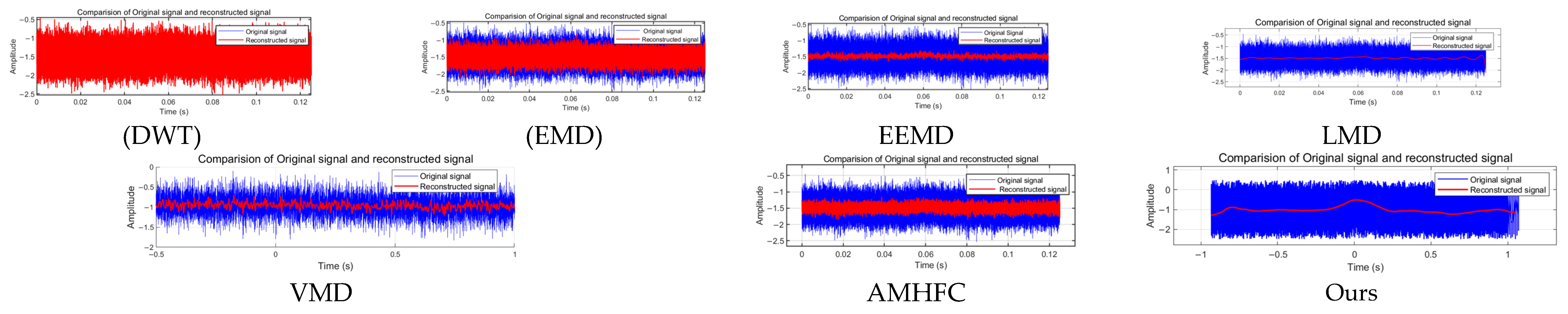
3.3.3. Comparison Between Different Algorithms
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Q.; Li, J.; He, Q. Photoelectric Measurement and Sensing: New Technology and Applications. Sensors 2023, 23, 7. [Google Scholar] [CrossRef]
- Galbács, G. A Critical Review of Recent Progress in Analytical Laser-Induced Breakdown Spectroscopy. Anal. Bioanal. Chem. 2015, 407, 7537–7562. [Google Scholar] [CrossRef]
- Fu, M.; Li, C.; Zhu, G.; Shi, H.; Chen, F. A High Precision Time Grating Displacement Sensor Based on Temporal and Spatial Modulation of Light-Field. Sensors 2020, 20, 921. [Google Scholar] [CrossRef]
- Fu, Y.; Shang, Y.; Hu, W.; Li, B.; Yu, Q.; Yu, Q. Non-Contact Optical Dynamic Measurements at Different Ranges: A Review. Acta Mech. Sin. 2021, 37, 537–553. [Google Scholar] [CrossRef]
- Yang, J.; Dong, T.; Chen, D.; Ni, J.; Kai, B. Measurement Method for Fragment Velocity Based on Active Screen Array in Static Detonation Test. Infrared Laser Eng. 2020, 49, 113003. [Google Scholar]
- Dang, H. Active Canopy Target Sensitivity Adjustment Technology. Master’s Dissertation, Xi’an University of Technology, Xi’an, China, 2024. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Dong, T.; Yang, S.; Zhang, H. Research on the Measurement Method for a Six-Light Curtain Canopy Standing Target Based on Dual-N Type. Opt. Technol. 2024, 50, 188–193. [Google Scholar] [CrossRef]
- Li, H. Multi-Target Space Position Identification and Matching Algorithm in Multi-Screen Intersection Measurement System Using Information Constraint Method. Measurement 2019, 145, 172–177. [Google Scholar] [CrossRef]
- Lee, D.; Han, K.; Huh, K. Collision Detection System Design Using a Multi-Layer Laser Scanner for Collision Mitigation. J. Automot. Eng. 2012, 226, 905–914. [Google Scholar] [CrossRef]
- Kubiak, P.; Siczek, K.; Dąbrowski, A.; Szosland, A. New high precision method for determining vehicle crash velocity based on measurements of body deformation. Int. J. Crashworthiness 2016, 21, 532–541. [Google Scholar] [CrossRef]
- Wang, F.; Tian, H.; Gao, Y.; Li, Z. Limit Detection Sensitivity Analysis and Maximum Detection Height Prediction for the Photoelectric Detection Target. Opt. Laser Eng. 2023, 164, 107530. [Google Scholar] [CrossRef]
- Yun, Y.; Hui, T. Analysis and Amendment on the Sensitivity of Large Target Area Light Screen. Infrared Laser Eng. 2018, 47, 0617004. [Google Scholar] [CrossRef]
- Wang, F.; Gao, Y.; Tian, H.; Li, B.; Guo, R. Denoising Method Based on EMD-CPSD for Low SNR Signals from Velocity Measuring Underwater Laser Light Screen. IEEE Trans. Instrum. Meas. 2024, 73, 7005811. [Google Scholar] [CrossRef]
- Lyon, D. The Discrete Fourier Transform, Part 4: Spectral Leakage. J. Object Technol. 2009, 8, 23–34. [Google Scholar] [CrossRef]
- Zemtsov, A. Multiscale Analysis of High Resolution Digital Elevation Models Using the Wavelet Transform. Sci. Vis. 2024, 16, 1–10. [Google Scholar] [CrossRef]
- Du, S.; Chen, S. Study on Optical Fiber Gas-Holdup Meter Signal Denoising Using Improved Threshold Wavelet Transform. IEEE Access 2023, 11, 18794–18804. [Google Scholar] [CrossRef]
- Islam, M.K.; Rastegarnia, A. Wavelet-Based Artifact Removal Algorithm for EEG Data by Optimizing Mother Wavelet and Threshold Parameters. In Proceedings of the 2020 Emerging Technology in Computing, Communication and Electronics (ETCCE), Online, 21–22 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Data Sci. Adapt. Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Yang, X.-M.; Yi, T.-H.; Qu, C.-X.; Li, H.-N.; Liu, H. Modal Identification of High-Speed Railway Bridges Through Free-Vibration Detection. J. Eng. Mech. 2020, 146, 04020107. [Google Scholar] [CrossRef]
- Zhou, S.; Yao, Y.; Luo, X.; Jiang, N.; Niu, S. Dynamic Response Evaluation for Single-Hole Bench Carbon Dioxide Blasting Based on the Novel SSA–VMD–PCC Method. Int. J. Geomech. 2023, 23, 04022248. [Google Scholar] [CrossRef]
- Li, C.-F.; Wang, Z.; Liu, X.-Y.; Yang, S.-H.; Xu, Z.; Fan, C.-Y. Anti-Scattering Signal Processing Method of VMD-ICA Based Underwater Lidar. Acta Phys. Sin. 2024, 73, 094203. [Google Scholar] [CrossRef]
- Deng, L.; Zhao, C.; Wang, X.; Wang, G.; Qiu, R. MRNet: Rolling Bearing Fault Diagnosis in Noisy Environment Based on Multi-Scale Residual Convolutional Network. Meas. Sci. Technol. 2024, 35, 126136. [Google Scholar] [CrossRef]
- Peng, L.; Fang, S.; Fan, Y.; Wang, M.; Zhang, Z. A Method of Noise Reduction for Radio Communication Signal Based on RaGAN. Sensors 2023, 23, 475. [Google Scholar] [CrossRef]
- Wu, J.; Yang, Y.; Lin, Z.; Lin, Y.; Wang, Y.; Zhang, W.; Ma, H. Weak Ultrasonic Guided Wave Signal Recognition Based on One-Dimensional Convolutional Neural Network Denoising Autoencoder and Its Application to Small Defect Detection in Pipelines. Measurement 2024, 242, 116234. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-Informed Machine Learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Sun, M.; Lan, L.; Zhu, C.-G.; Lei, F. Cubic spline interpolation with optimal end conditions. J. Comput. Appl. Math. 2023, 425, 115039. [Google Scholar] [CrossRef]
- Strang, G. Introduction to Applied Linear Algebra: Vectors, Matrices, and Least Squares. IEEE Control Syst. Mag. 2020, 40, 136. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef]
- Singh, P.; Joshi, S.D.; Patney, R.K.; Saha, K. The Fourier decomposition method for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 2017, 473, 20160871. [Google Scholar] [CrossRef]






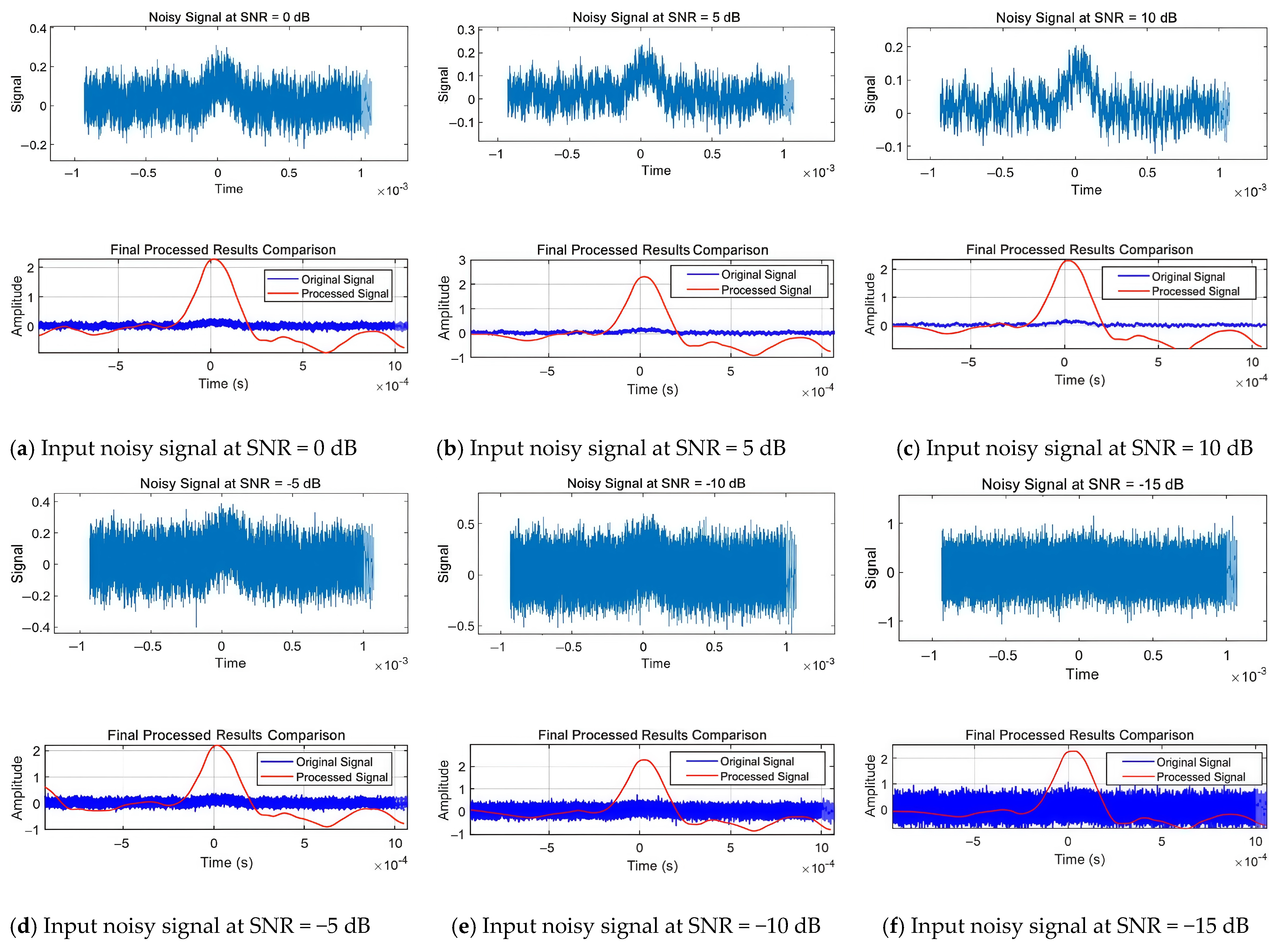
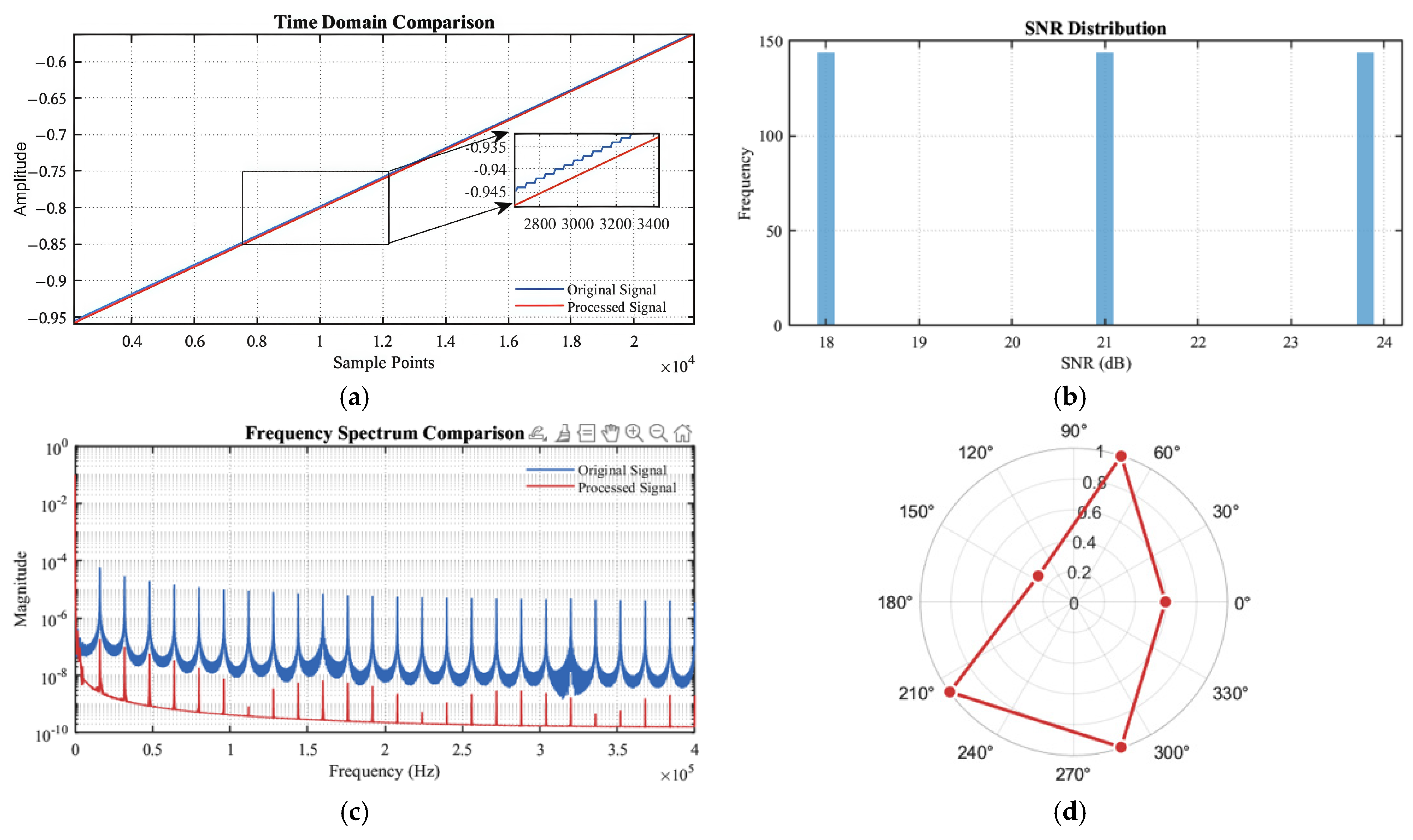

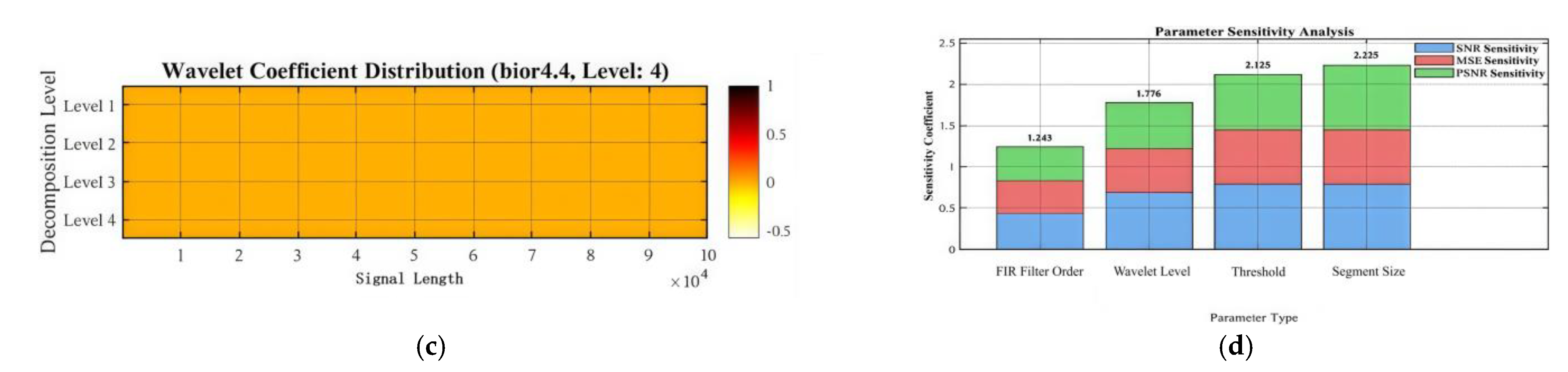
| Height | Signal-to-Noise Ratio of the Original Signal |
|---|---|
| 50 cm | 8 dB |
| 100 cm | 5 dB |
| 150 cm | 3 dB |
| Method | Correlation Coefficient | Mean Square Error | Signal-to-Noise Ratio (dB) |
|---|---|---|---|
| FIR Filtering | 0.4328 | 0.009996745 | 17.10 dB |
| Multi-stage Filtering | 0.9854 | 0.01331926 | 24.77 dB |
| Optimized Wavelet Transform | 0.9890 | 0.009579688 | 25.83 dB |
| Final Output | 0.9890 | 0.009579688 | 25.83 dB |
| Noise Type | Original Signal (SNR) | Processed Signal (SNR) | Signal-to-Noise Ratio Improvement |
|---|---|---|---|
| Dark Current Noise | −20 dB | 2.43 dB | 22.43 dB |
| Gain Fluctuation Noise | −20 dB | 4.88 dB | 24.88 dB |
| Photo-response Non-uniformity Noise | −20 dB | 4.088 dB | 24.08 dB |
| Quantum Efficiency Fluctuation Noise | −20 dB | 4.11 dB | 24.11 dB |
| Shot Noise | −20 dB | 1.19 dB | 21.19 dB |
| Thermal Noise | −20 dB | 4.67 dB | 24.67 dB |
| Method | Input SNR (dB) | Output SNR (dB) | Improvement Factor (dB) |
|---|---|---|---|
| FIR Filtering | −20 dB | 17.10 dB | 37.10 dB |
| Multi-stage Filtering | 17.10 dB | 24.77 dB | 7.67 dB |
| Optimized Wavelet Transform | 24.77 dB | 25.83 dB | 1.6 dB |
| Final Output | 25.83 dB | ||
| Case | Original (dB) | Processed (dB) | Changed (dB) | Coefficient of Variation | Autocorrelation Function |
|---|---|---|---|---|---|
| Case 1 | 0 dB | 26.82 dB | 26.82 dB | 1.5070 | 0.9812 |
| Case 2 | 5 dB | 28.23 dB | 23.23 dB | 1.5061 | 0.9818 |
| Case 3 | 10 dB | 28.05 dB | 17.05 dB | 1.5117 | 0.9817 |
| Case 4 | −5 dB | 28.06 dB | 33.06 dB | 1.4337 | 0.9773 |
| Case 5 | −10 dB | 28.60 dB | 38.60 dB | 1.4980 | 0.9808 |
| Case 6 | −15 dB | 30.36 dB | 45.36 dB | 1.4950 | 0.9823 |
| Method | Signal-to-Noise Ratio of Original Signal | Signal-to-Noise Ratio of Processed Signal | Signal-to-Noise Ratio Improvement (dB) | Correlation Coefficient |
|---|---|---|---|---|
| DWT [30] | −20 dB | −15 dB | 5 dB | 0.175 |
| EMD [18] | −20 dB | 2.85 dB | 22.85 dB | 0.815 |
| EEMD [19] | −20 dB | −8.3768 dB | 11.6232 dB | 0.195 |
| LMD [31] | −20 dB | 6.53 dB | 26.53 dB | 0.901 |
| VMD [20] | −20 dB | 0.01 dB | 20.01 dB | 0.301 |
| AMHFC [32] | −20 dB | −0.06 dB | 19.94 dB | 0.765 |
| Ours | −20 dB | 25 dB | 45 dB | 0.981 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Tian, H.; Wang, F.; Ni, J.; Chen, R. Low Signal-to-Noise Ratio Optoelectronic Signal Reconstruction Based on Zero-Phase Multi-Stage Collaborative Filtering. Sensors 2025, 25, 2758. https://doi.org/10.3390/s25092758
Yang X, Tian H, Wang F, Ni J, Chen R. Low Signal-to-Noise Ratio Optoelectronic Signal Reconstruction Based on Zero-Phase Multi-Stage Collaborative Filtering. Sensors. 2025; 25(9):2758. https://doi.org/10.3390/s25092758
Chicago/Turabian StyleYang, Xuzhao, Hui Tian, Fan Wang, Jinping Ni, and Rui Chen. 2025. "Low Signal-to-Noise Ratio Optoelectronic Signal Reconstruction Based on Zero-Phase Multi-Stage Collaborative Filtering" Sensors 25, no. 9: 2758. https://doi.org/10.3390/s25092758
APA StyleYang, X., Tian, H., Wang, F., Ni, J., & Chen, R. (2025). Low Signal-to-Noise Ratio Optoelectronic Signal Reconstruction Based on Zero-Phase Multi-Stage Collaborative Filtering. Sensors, 25(9), 2758. https://doi.org/10.3390/s25092758






