High-Precision Pose Measurement of Containers on the Transfer Platform of the Dual-Trolley Quayside Container Crane Based on Machine Vision
Abstract
1. Introduction
- To address the limitations of low efficiency and unstable accuracy in traditional manual operations for field engineering applications, a machine vision-based high-precision pose-measurement system for containers on the dual-trolley quayside container crane-transfer platform is proposed;
- To mitigate interference from complex illumination and meteorological interference in port environments on operational site images, an adaptive image-enhancement preprocessing algorithm is designed to strengthen image features;
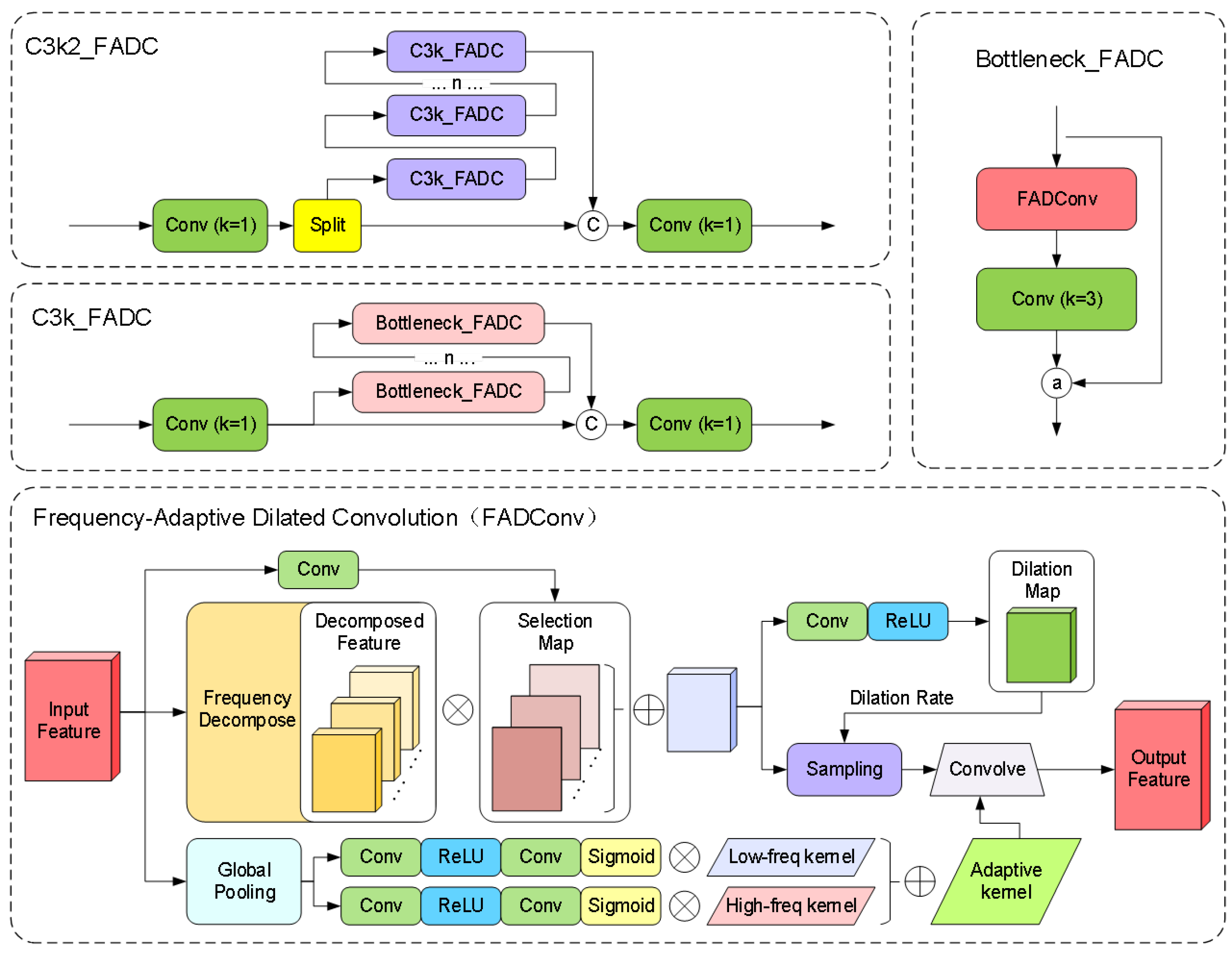
- To resolve the challenge of large-scale variations in lockhole keypoints on container tops caused by perspective transformation in operational scenarios, a multi-scale adaptive frequency object-detection framework is developed based on the YOLO11 architecture, enabling robust target recognition and keypoint detection;
- To overcome the low precision of traditional pose-estimation algorithms, an improved EPnP optimization method is proposed to achieve high-accuracy measurement of 3D container positions and orientations.
2. Related Work
3. Three-Dimensional Positioning and Pose-Measurement System
3.1. Hardware System
3.2. Algorithm Design
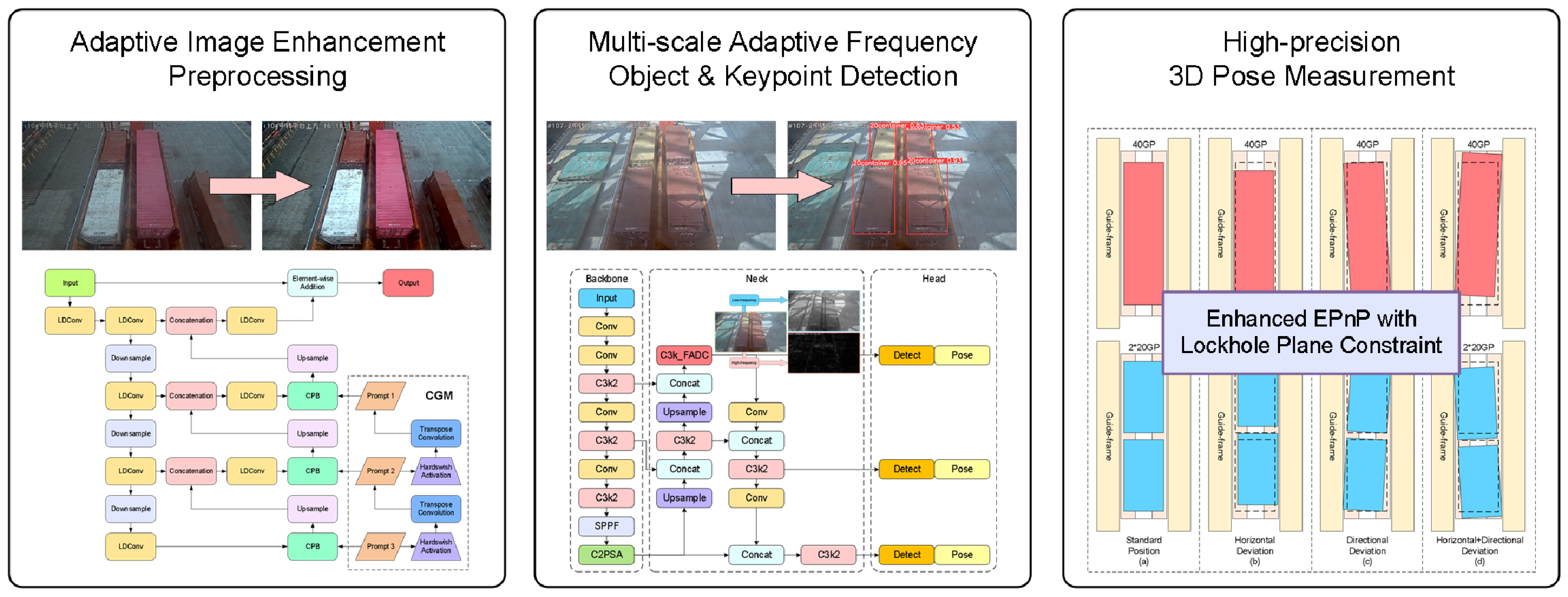
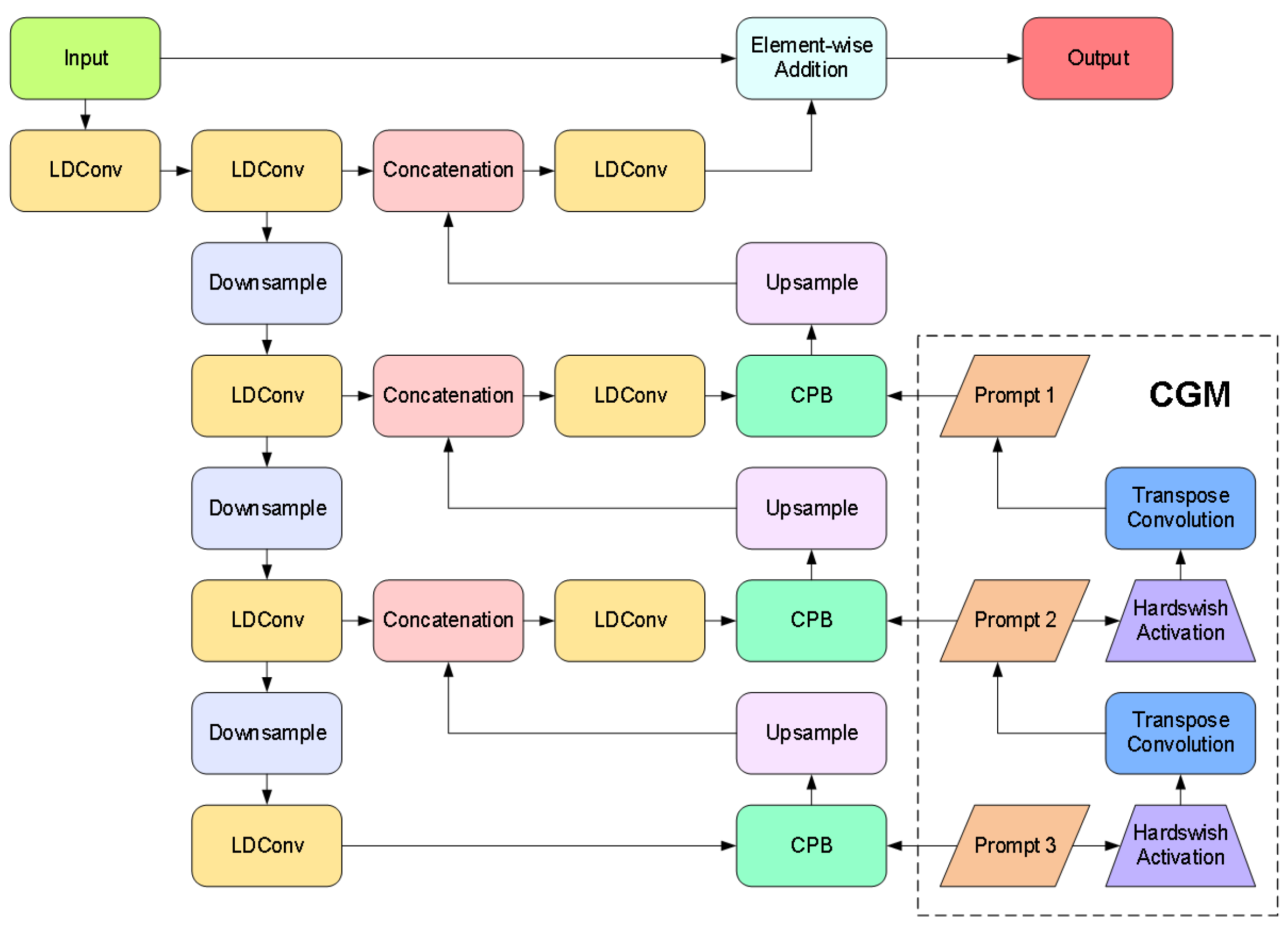
3.2.1. Adaptive Enhancement Image Feature Preprocessing Method
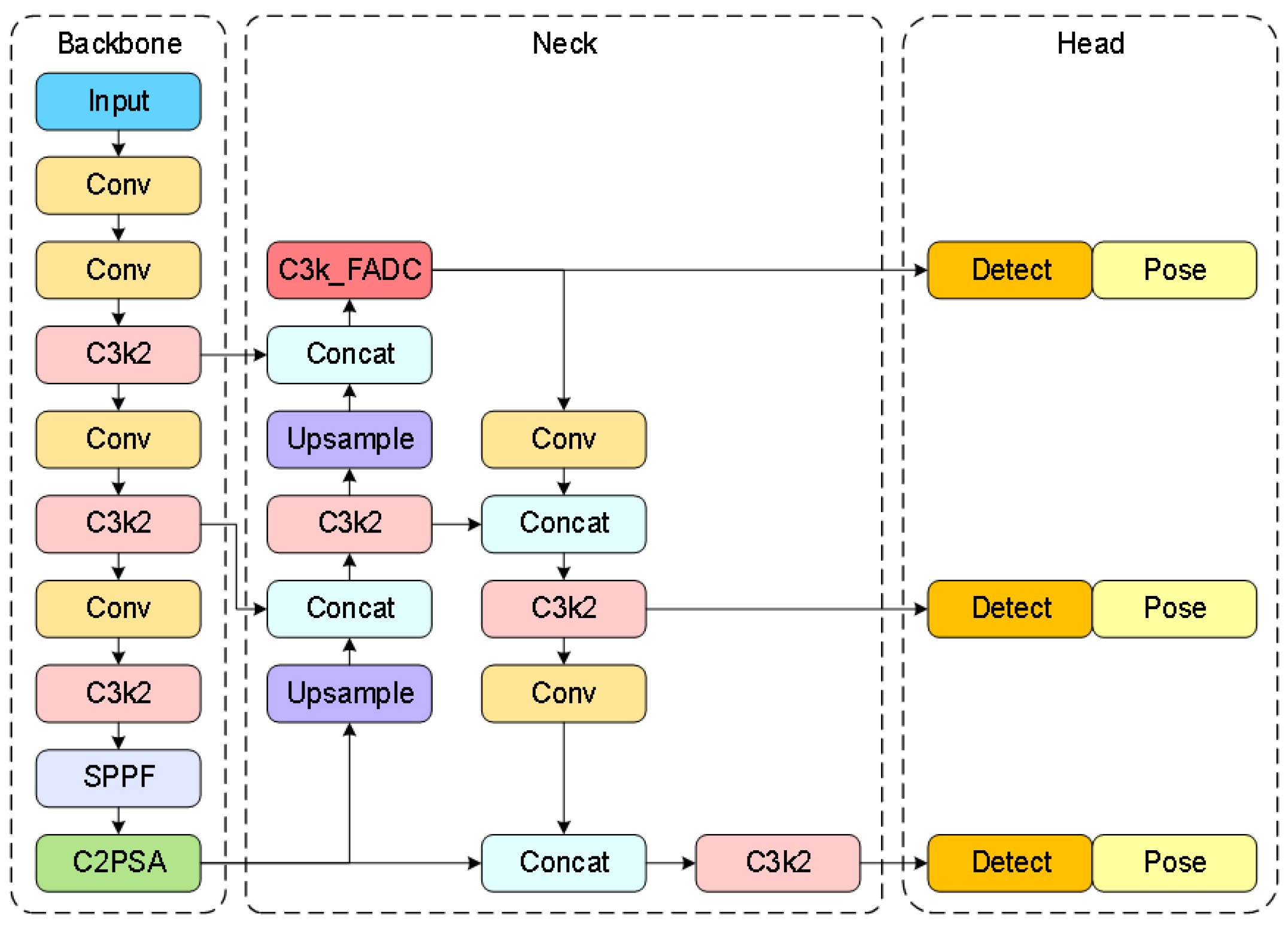
3.2.2. Multi-Scale Adaptive Frequency Object Recognition and Keypoint-Detection Method
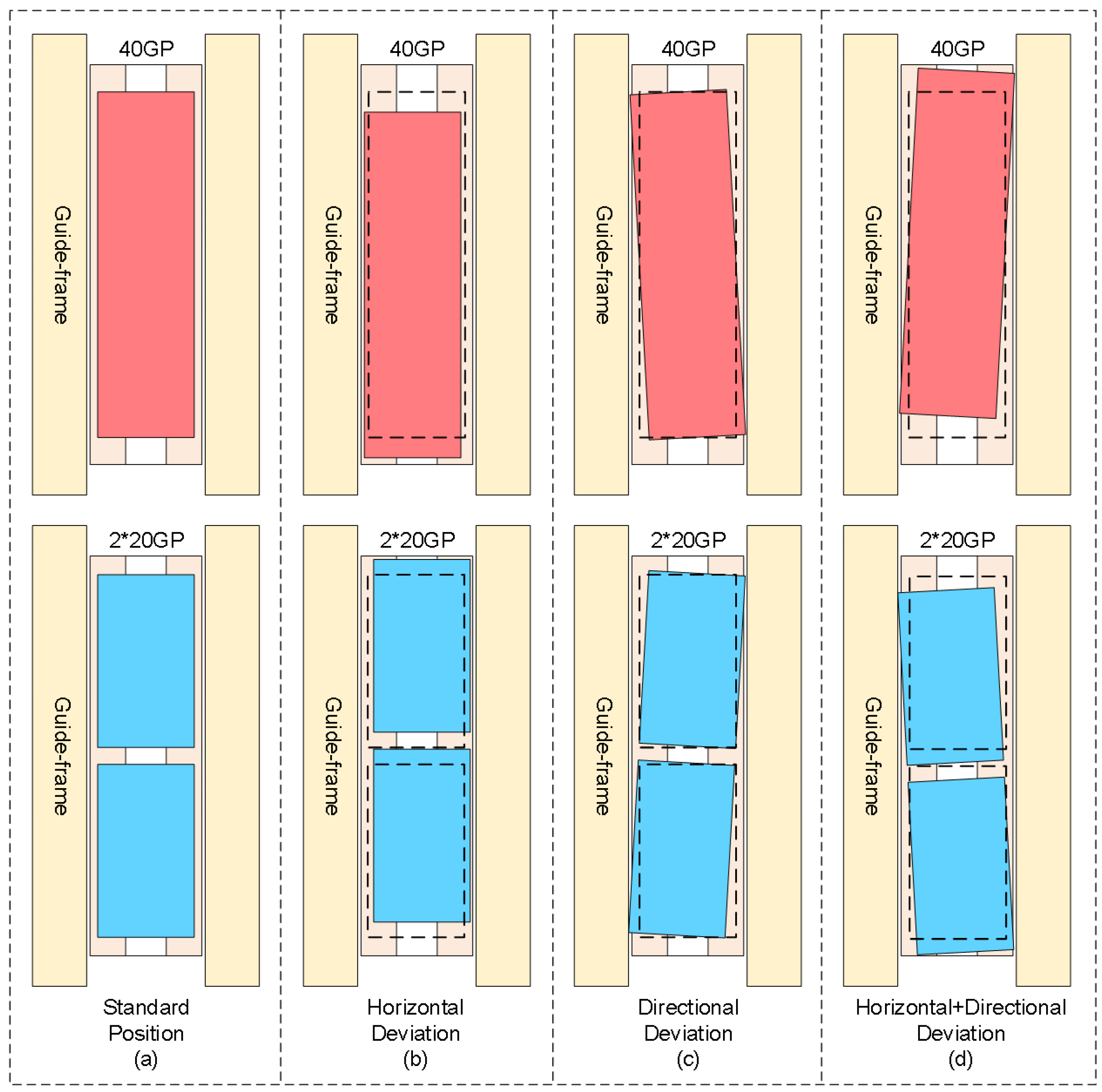
3.2.3. Three-Dimensional Position and Pose-Measurement Method for Containers
- Step 1: 2D–3D Lockhole Keypoint Coordinate Conversion.
- Control Point Initialization: Select four non-coplanar control points, typically choosing the centroid of the 3D point set and principal component directions;
- Weight Coefficient Calculation: Solve for using the least squares method to minimize the residual error in Equation (18);
- Camera Coordinate System Control Point Solution: Construct an overdetermined system of equations using Equation (19) and solve it via SVD;
- Extrinsic Parameter Recovery: Align control points in the world coordinate system with those in the camera coordinate system, minimizing registration errors as shown in Equation (20).
- Step 2: Container Pose Calculation.
4. Experiments
4.1. Experimental Setup
4.1.1. Experimental Environment
4.1.2. Datasets and Evaluation Metrics
4.2. Experimental Results
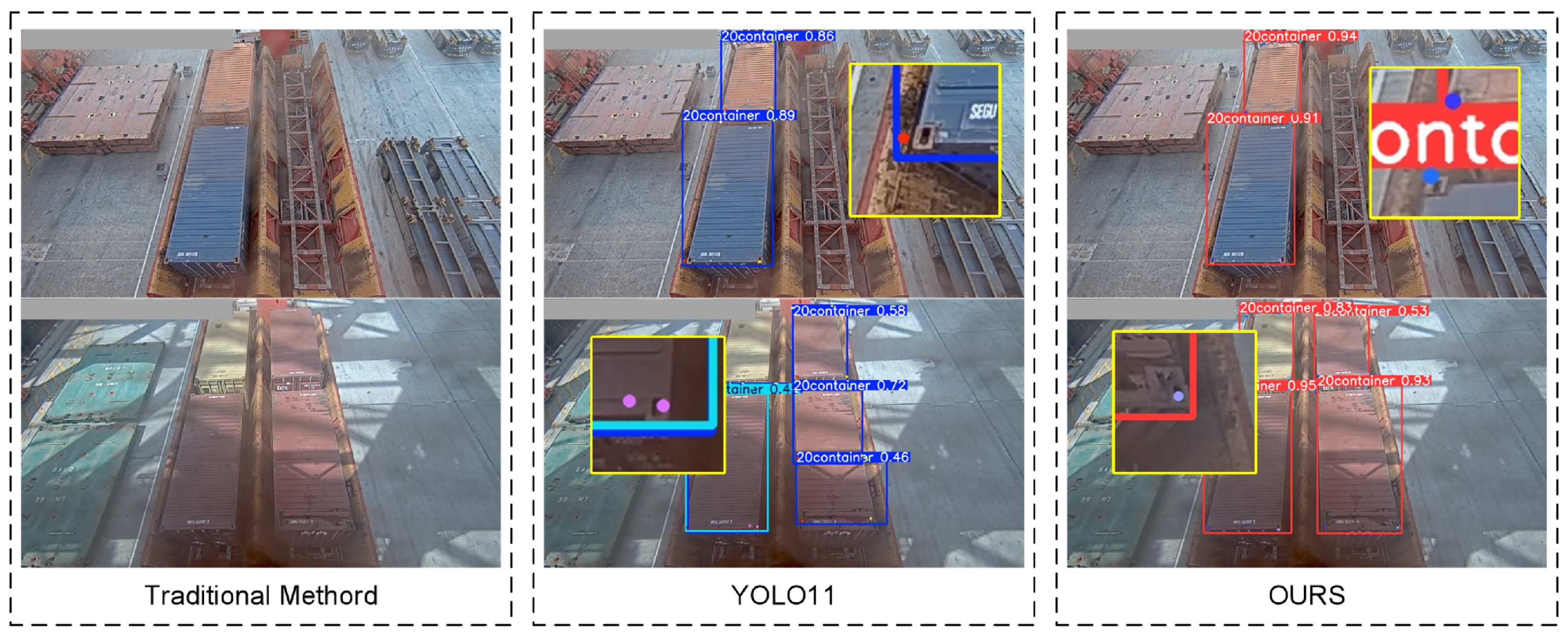
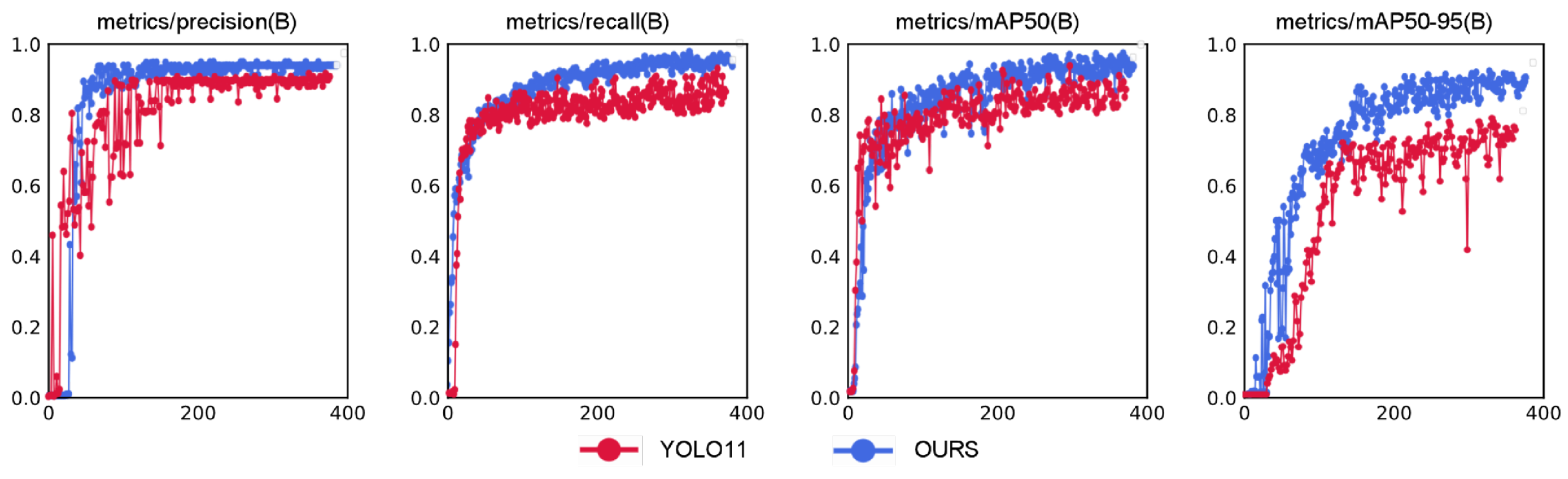
4.2.1. Model Accuracy Testing
4.2.2. The Detection Accuracy of Container Horizontal Deviation
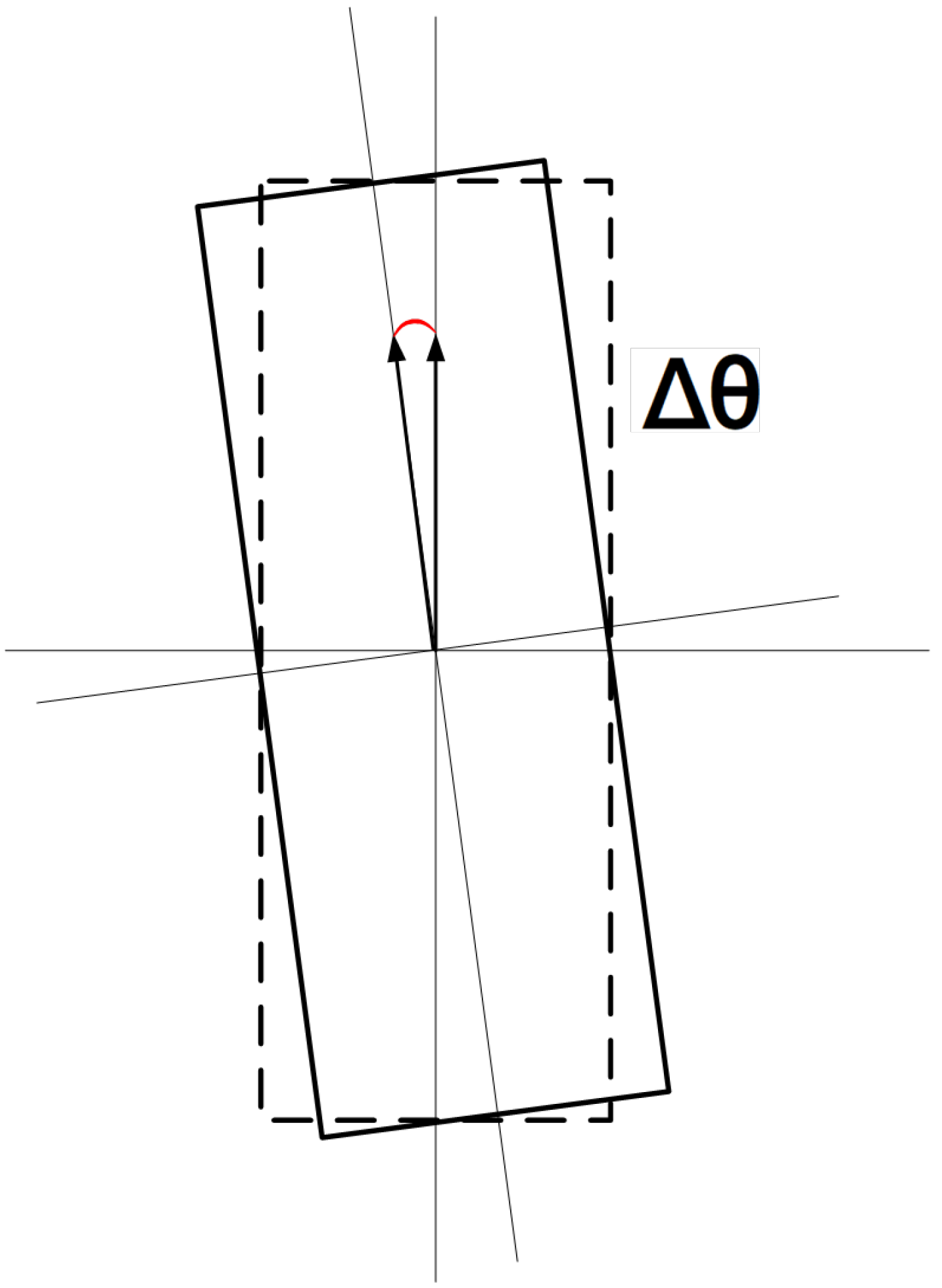
4.2.3. The Detection Accuracy of Container Rotational Deviation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, Y.; Man, X.; Wang, J.; Zhang, Y.; Mi, C. Truck Lifting Accident Detection Method Based on Improved PointNet++ for Container Terminals. J. Mar. Sci. Eng. 2025, 13, 256. [Google Scholar] [CrossRef]
- Jiang, Z. Frame Definition, Pose Initialization, and Real-Time Localization in a Non-Stationary Reference Frame with LiDAR and IMU: Application in Cooperative Transloading Tasks. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 2022. [Google Scholar]
- Shen, Z.; Wang, J.; Zhang, Y.; Zheng, L.; Mi, C.; Shen, Y. Identification and Positioning Method of Bulk Cargo Terminal Unloading Hopper Based on Monocular Vision Three-Dimensional Measurement. J. Mar. Sci. Eng. 2024, 12, 1282. [Google Scholar] [CrossRef]
- Kuo, S.Y.; Lin, P.C.; Huang, X.R.; Huang, G.Z.; Chen, L.B. Cad-Transformer: A CNN–Transformer Hybrid Framework for Automatic Appearance Defect Classification of Shipping Containers. IEEE Trans. Instrum. Meas. 2025, 74, 1–21. [Google Scholar] [CrossRef]
- Ji, Z.; Zhao, K.; Liu, Z.; Hu, H.; Sun, Z.; Lian, S. A Novel Vision-Based Truck-Lifting Accident Detection Method for Truck-Lifting Prevention System in Container Terminal. IEEE Access 2024, 12, 42401–42410. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, H.; Yi, X.; Ma, J. CRetinex: A progressive color-shift aware Retinex model for low-light image enhancement. Int. J. Comput. Vis. 2024, 132, 3610–3632. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, M.; Jonathan, Q.; Shen, W. A real-time anchor-free defect detector with global and local feature enhancement for surface defect detection. Expert Syst. Appl. 2024, 246, 123199. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, J.; Zhang, S.; Xu, N. Marine object detection in forward-looking sonar images via semantic-spatial feature enhancement. Front. Mar. Sci. 2025, 12, 1539210. [Google Scholar] [CrossRef]
- Nou, S.; Lee, J.S.; Ohyama, N.; Obi, T. Human pose feature enhancement for human anomaly detection and tracking. Int. J. Inf. Technol. 2025, 17, 1311–1320. [Google Scholar] [CrossRef]
- Li, L.; Xu, W.; Gao, Y.; Lu, Y.; Yang, D.; Liu, R.W.; Zhang, R. Attention-oriented residual block for real-time low-light image enhancement in smart ports. Comput. Electr. Eng. 2024, 120, 109634. [Google Scholar] [CrossRef]
- Lin, Z.; Dong, C.; Wan, Y. Research on Intelligent Recognition Algorithm of Container Numbers in Ports Based on Deep Learning. In Proceedings of the International Conference on Intelligent Computing, Tianjin, China, 5–8 August 2024; pp. 184–196. [Google Scholar]
- Bandong, S.; Nazaruddin, Y.Y.; Joelianto, E. Container detection system using CNN based object detectors. In Proceedings of the 2021 International Conference on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, 25–27 August 2021; pp. 106–111. [Google Scholar]
- Jiang, P.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. A Review of Yolo algorithm developments. Procedia Comput. Sci. 2022, 199, 1066–1073. [Google Scholar] [CrossRef]
- Wu, G.; Wu, Q. Enhancing Steel Surface Defect Detection: A Hyper-YOLO Approach with Ghost Modules and Hyper FPN. IAENG Int. J. Comput. Sci. 2024, 9, 1321–1330. [Google Scholar]
- Zhou, R.; Gu, M.; Hong, Z.; Pan, H.; Zhang, Y.; Han, Y.; Wang, J.; Yang, S. SIDE-YOLO: A Highly Adaptable Deep Learning Model for Ship Detection and Recognition in Multisource Remote Sensing Imagery. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1–5. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, Z.; Zhang, Z. Enhancing Image Perception Quality: Exploring Loss Function Variants in SRCNN. In Proceedings of the 2024 7th International Conference on Computer Information Science and Artificial Intelligence, Shaoxing, China, 13–15 September 2024; pp. 352–356. [Google Scholar]
- Qian, L.; Zheng, Y.; Cao, J.; Ma, Y.; Zhang, Y.; Liu, X. Lightweight ship target detection algorithm based on improved YOLOv5s. J. Real-Time Image Process. 2024, 21, 3. [Google Scholar] [CrossRef]
- Cao, J.; Li, Y.; Sun, M.; Chen, Y.; Lischinski, D.; Cohen-Or, D.; Chen, B.; Tu, C. Do-conv: Depthwise over-parameterized convolutional layer. IEEE Trans. Image Process. 2022, 31, 3726–3736. [Google Scholar] [CrossRef] [PubMed]
- Ren, C.; Wang, A.; Yang, C.; Wu, J.; Wang, M. Frequency Domain-Based Cross-Layer Feature Aggregation Network for Camouflaged Object Detection. IEEE Signal Process. Lett. 2025. [Google Scholar] [CrossRef]
- Weng, W.; Wei, M.; Ren, J.; Shen, F. Enhancing Aerial Object Detection with Selective Frequency Interaction Network. IEEE Trans. Artif. Intell. 2024, 5, 6109–6120. [Google Scholar] [CrossRef]
- Chen, L.; Gu, L.; Zheng, D.; Fu, Y. Frequency-adaptive dilated convolution for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 22–24 June 2024; pp. 3414–3425. [Google Scholar]
- Wang, B.; Bai, A.; Ma, F.; Ji, P. A 3D object localization method based on EPNP and dual-view images. In Proceedings of the 2024 IEEE 7th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 15–17 March 2024; Volume 7, pp. 1349–1353. [Google Scholar]
- Xie, X.; Zou, D. Depth-Based Efficient PnP: A Rapid and Accurate Method for Camera Pose Estimation. IEEE Robot. Autom. Lett. 2024, 9, 9287–9294. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Liu, Y.; Peng, X. CPA-Enhancer: Chain-of-Thought Prompted Adaptive Enhancer for Downstream Vision Tasks Under Unknown Degradations. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Suzhou, China, 23–25 May 2025; pp. 1–5. [Google Scholar]
- Alhassan, A.M.; Zainon, W.M.N.W. Brain tumor classification in magnetic resonance image using hard swish-based RELU activation function-convolutional neural network. Neural Comput. Appl. 2021, 33, 9075–9087. [Google Scholar] [CrossRef]
- Zhang, X.; Song, Y.; Song, T.; Yang, D.; Ye, Y.; Zhou, J.; Zhang, L. LDConv: Linear deformable convolution for improving convolutional neural networks. Image Vis. Comput. 2024, 149, 105190. [Google Scholar] [CrossRef]








| Hardware/Software | Configuration Parameters |
|---|---|
| CPU | Intel(R) Xeon(R) CPU E5-2690 |
| GPU | NVIDIA GeForce RTX 3090 |
| Memory | 64 GB |
| Operating System | Ubuntu 20.04 |
| Programming Language | Python = 3.10 |
| Deep Learning Framework | PyTorch = 2.0 |
| Methods | P (%) | R (%) | mAP@0.5 (%) | mAP@0.5:0.95 (%) |
|---|---|---|---|---|
| Traditional | 24.1 | 12.6 | / | / |
| HRNet | 90.3 | 88.6 | 92.1 | 88.1 |
| YOLO11 | 89.7 | 88.3 | 90.4 | 80.9 |
| OURS | 93.4 | 92.5 | 95.1 | 89.6 |
| Methods | Mean Absolute Deviation, MAD | MAD-P (m) | Average Operation Time (s) | |
|---|---|---|---|---|
| (m) | (m) | |||
| Manual operation | 0.013 | 0.016 | 0.023 | 9.36 |
| Ours | 0.012 | 0.018 | 0.024 | 8.68 |
| Methods | MAE- (°) | Average Operation Time (s) |
|---|---|---|
| Manual Operation | 0.15 | 9.86 |
| OURS | 0.11 | 8.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; He, M.; Zhang, Y.; Zhang, Z.; Postolache, O.; Mi, C. High-Precision Pose Measurement of Containers on the Transfer Platform of the Dual-Trolley Quayside Container Crane Based on Machine Vision. Sensors 2025, 25, 2760. https://doi.org/10.3390/s25092760
Wang J, He M, Zhang Y, Zhang Z, Postolache O, Mi C. High-Precision Pose Measurement of Containers on the Transfer Platform of the Dual-Trolley Quayside Container Crane Based on Machine Vision. Sensors. 2025; 25(9):2760. https://doi.org/10.3390/s25092760
Chicago/Turabian StyleWang, Jiaqi, Mengjie He, Yujie Zhang, Zhiwei Zhang, Octavian Postolache, and Chao Mi. 2025. "High-Precision Pose Measurement of Containers on the Transfer Platform of the Dual-Trolley Quayside Container Crane Based on Machine Vision" Sensors 25, no. 9: 2760. https://doi.org/10.3390/s25092760
APA StyleWang, J., He, M., Zhang, Y., Zhang, Z., Postolache, O., & Mi, C. (2025). High-Precision Pose Measurement of Containers on the Transfer Platform of the Dual-Trolley Quayside Container Crane Based on Machine Vision. Sensors, 25(9), 2760. https://doi.org/10.3390/s25092760








