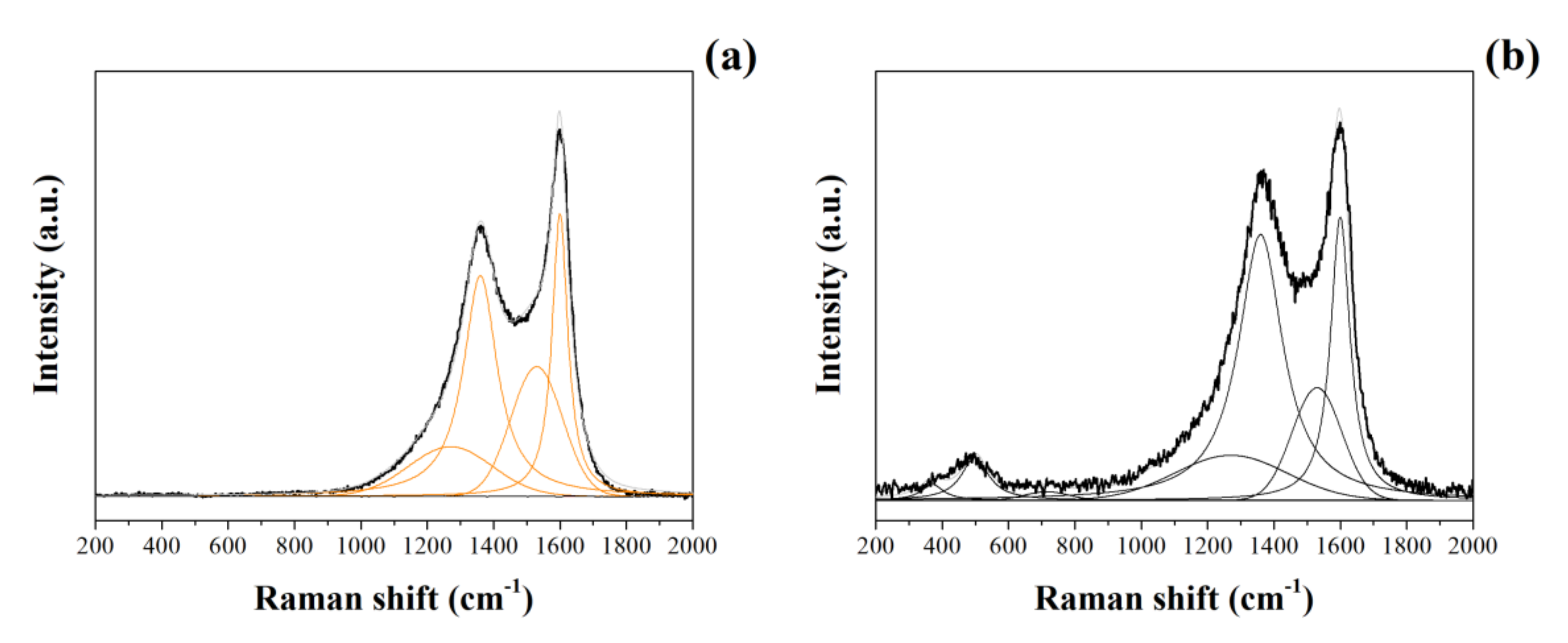
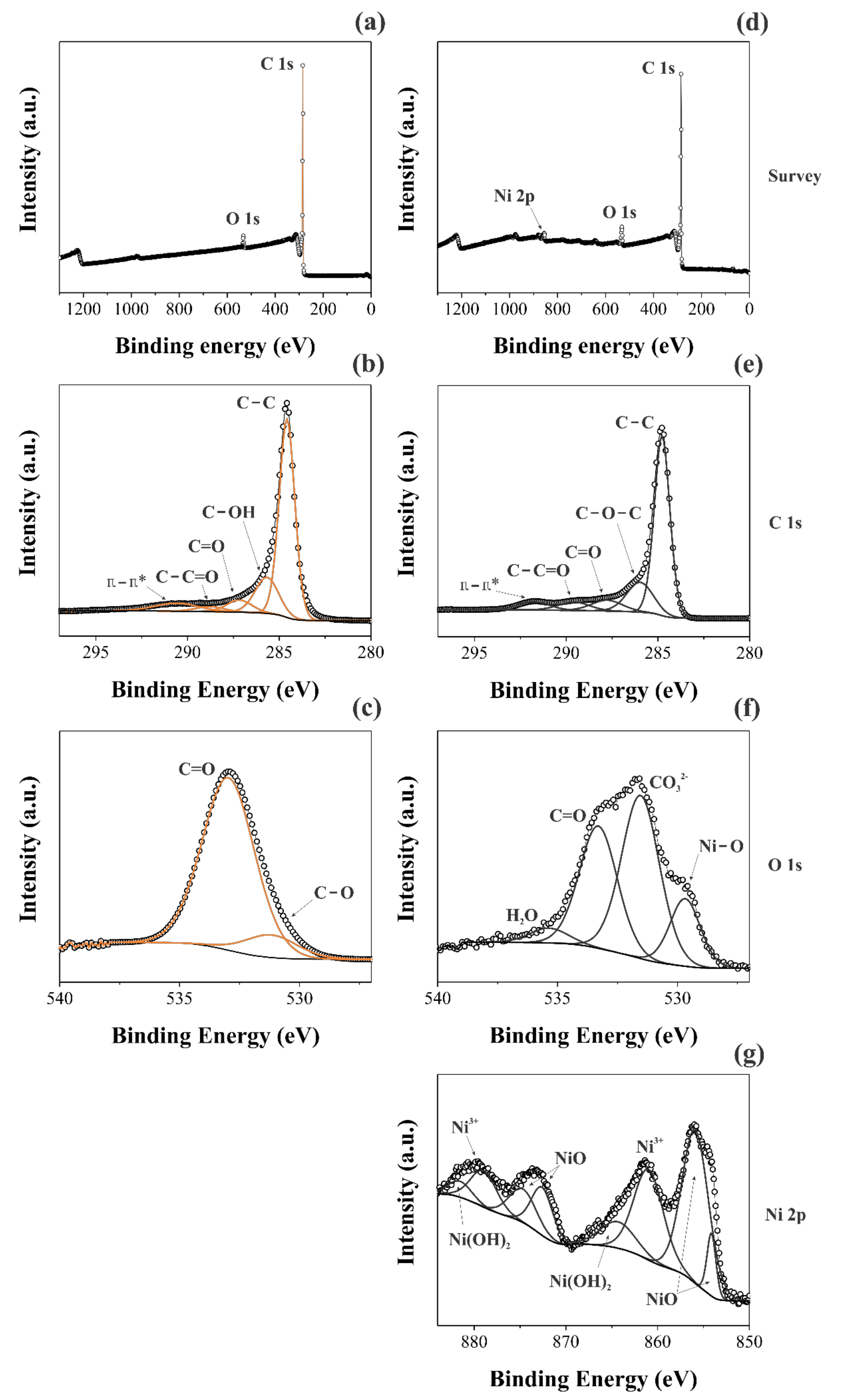
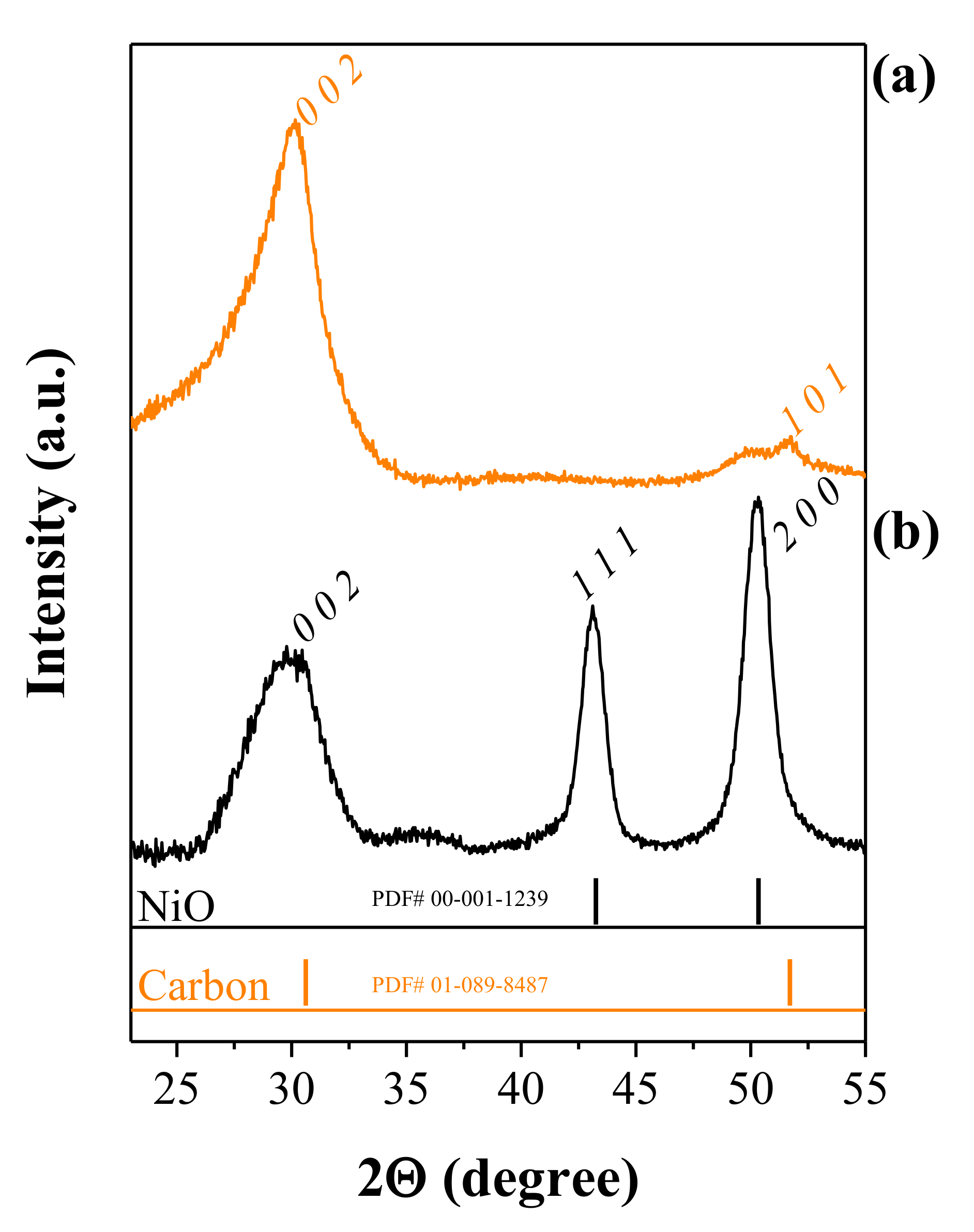
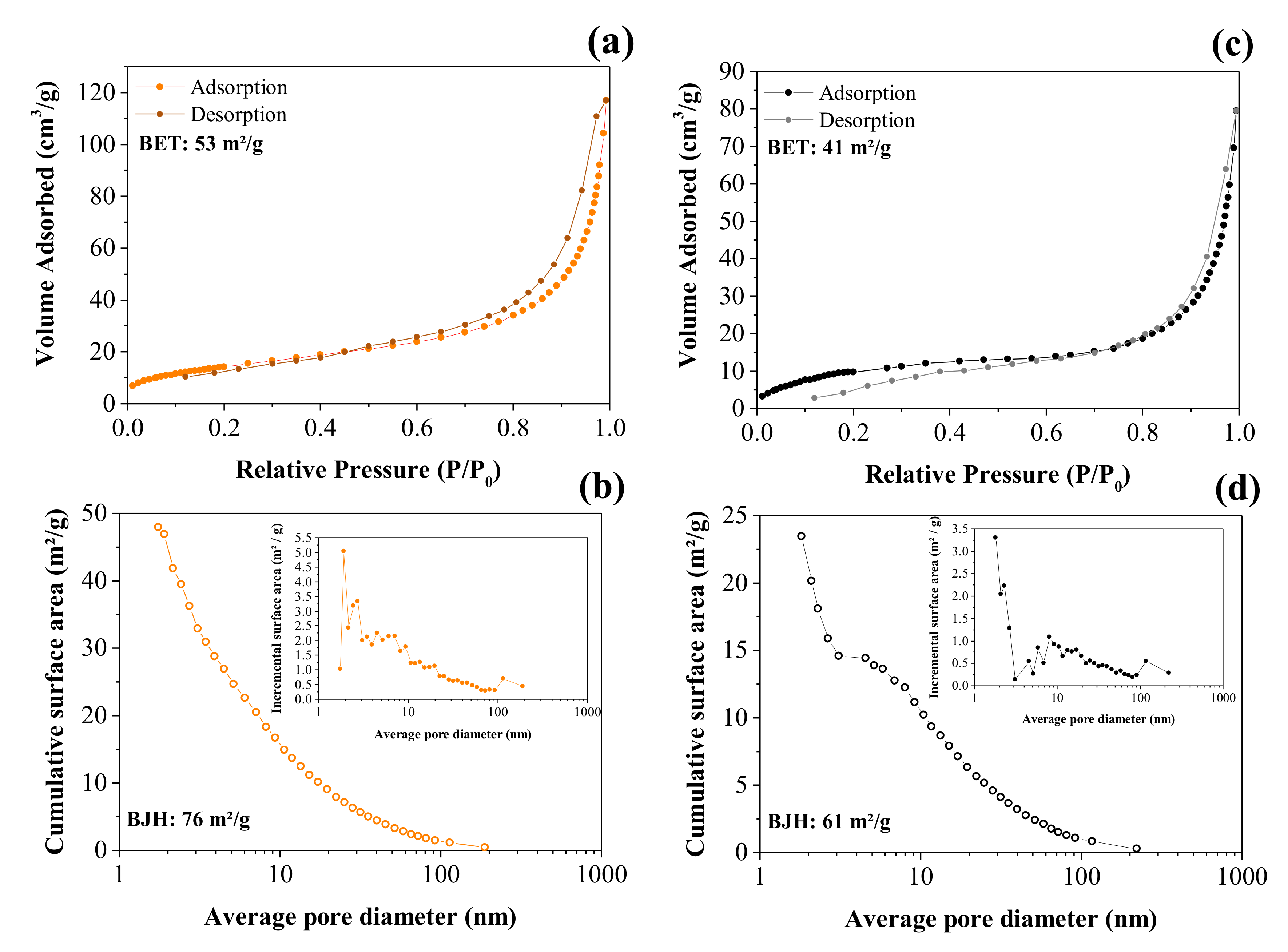
As already emphasized, our intention with this work is to obtain electrochemical information concerning the fundamental events during the charge storage process, i.e., charge transport anomalies involving the ionic and/or electronic charge carriers, which are affected by the disordered electrode materials used in EDLC and PC symmetric devices. However, to provide further information about the synthesized model materials, we present in this section an ex situ characterization.
3.2. Frequency Domain Analysis Using the EIS Technique: Identification of Charge Transport Anomalies during the Charge Storage Process in EDLC and PC Devices
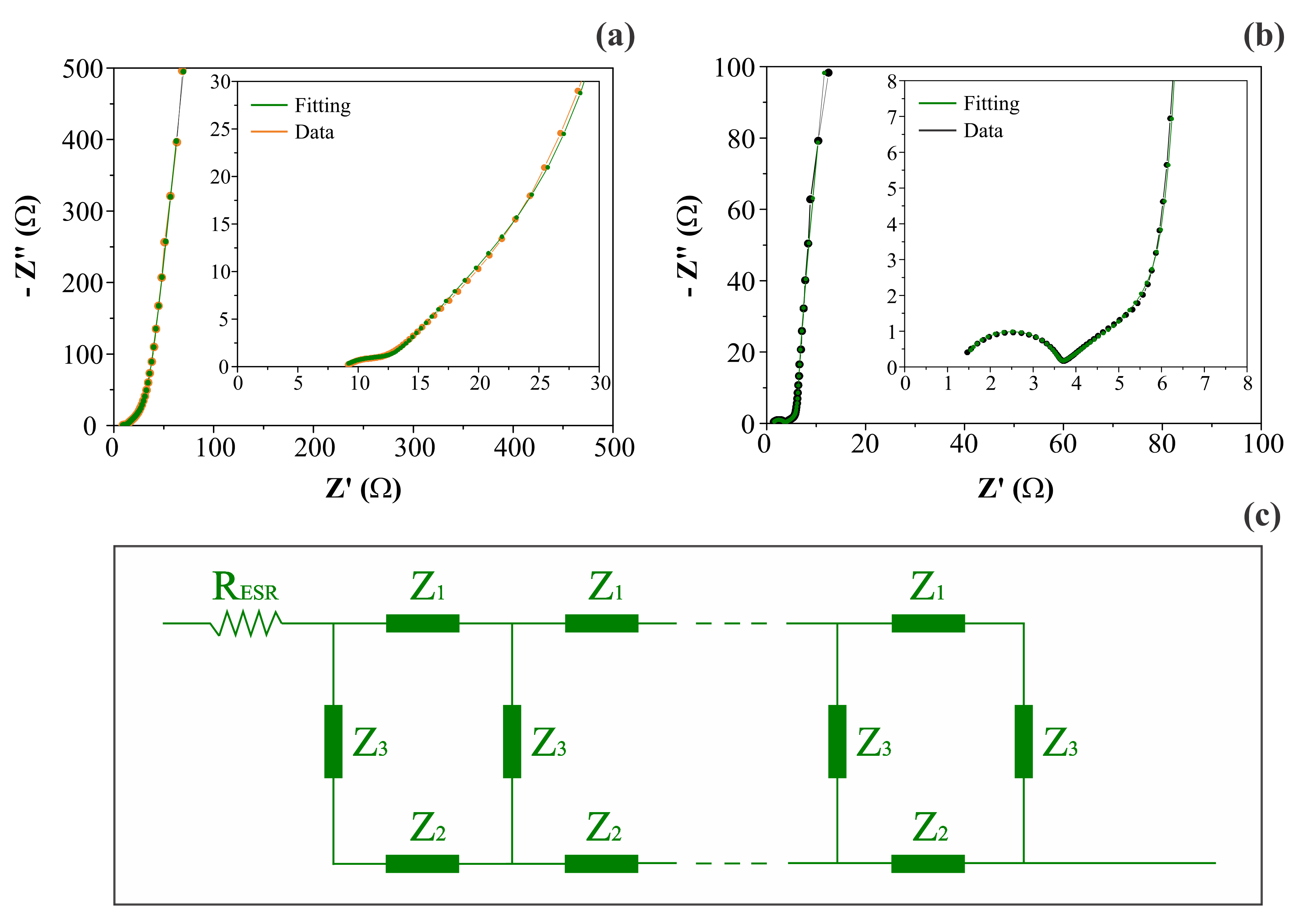
Figure 6 shows the complex plane (Nyquist) plots obtained for different symmetric coin cells containing the (a) CNF or (b) NiO@CNF electrodes, and the (c) generic double-channel transmission line model, where each impedance
Z is composed of a circuit containing an ohmic resistor (
R) in parallel to a constant phase element (CPE) representing the different dispersive effects. As can be seen, the impedance response was characterized by the following characteristics: (i) the presence of a resistive/capacitive arc in the high-frequency range; (ii) the occurrence of an inclined line with a phase angle close to −45° at medium frequencies, and (iii) the presence of an almost vertical straight line in the low-frequency range with a phase angle close to −90°. According to [
19], this type of impedance behavior, in the absence of irreversible Faradaic reactions (e.g., water splitting), is in agreement with the theoretical predictions of the porous electrode model, with the additional inclusion of the anomalous transport phenomenon for the ionic and/or electronic charge carriers. The anomalous transport effects occur from the medium- to the high-frequency interval of the impedance spectrum [
21].
More specifically, when the intermixed solid (
Z1) and liquid (
Z2) phases have a similar
dc resistance, the influence of the disordered solid phase on the electronic transport commonly appears as an arc in the high-frequency region of the impedance spectrum (see
Figure 6a,b). However, it is worth mentioning that the
interfacial (parallel) impedance (
Z3), including the electrical double-layer capacitance and pseudocapacitive effects, can also affect this region of the spectrum.
Inspired by the classical solid-state physics studies regarding the anomalous charge transport in disordered solids, Bisquert et al. [
21] proposed a robust generic impedance model for the study of different types of electrochemical systems with disorder/dispersive characteristics (e.g., a power law behavior or dispersive effects). In addition, Bisquert [
40] also discussed some particular cases of great interest for studying the different electrochemical systems used in technological applications. The total impedance (
Ztotal) for the porous or mixed-phase electrodes, considering the presence of anomalous transport and the additional influence of the uncompensated ohmic resistance (
RESR) intrinsic to the supercapacitors, is given by the following transfer function [
21]:
where:
The parameter L is the length of the intermixed (porous) phase, and is commonly unknown. From the point of view of the macro aspects of the impedance model (see further discussion in this section), the particular L-value is irrelevant for most applications. However, to obtain internal consistency between the unities of the transverse and parallel impedances, the apparent length of the porous electrode layer is given in the current work by the equation L = m/ρA, where m is the mass of the active layer, ρ is the apparent density of the electrode layer, and A is the geometric surface area of the porous electrode.
The individual (macroscopic) parameters measured are
R1 =
Lr1 (e.g., the total
dc electrolyte resistance inside the irregular ionic channels),
Q1 =
q1/
L (e.g., the information about the anomalous ionic transport mechanism or the transversal electrolyte capacitive-like effects),
R2 =
Lr2 (e.g., the total
dc electrode resistance),
Q2 =
q2/
L (e.g., the anomalous electronic transport in the electrode material or the transverse electrode capacitance), and
Q3 =
q3L (e.g., the constant phase element coefficient (
Qedl*), which is representative of the nonideal overall electrical double layer, including pseudocapacitance). As emphasized by Bisquert et al. [
21], impedances
Z1 and
Z2 represent “single transport mechanisms” rather than a conventional association of resistive and capacitive elements used in purely electrostatic processes.
In light of the theoretical analysis proposed by Paasch et al. [
19], the impedance model represented by Equation (1) agrees with the effective macro homogeneous description of two closely mixed phases. The latter is more appropriate for practical applications than the traditional view, where the porous electrode model is derived based on the presence of a perfect cylinder geometry whose pore length is longer than its diameter. As it is a common practice in EIS studies to facilitate the numerical analysis of the experimental findings, the transfer function described by Equation (1) can be represented by the equivalent double-channel transmission line shown in
Figure 6c. In this model,
Z1 and
Z2 are impedances per unit length (Ω m
−1) transverse to the macroscopic outer surfaces, while
Z3 is the impedance length (Ω m) parallel to the macroscopic surfaces. The impedance
Z3 represents the capacitance or pseudocapacitance of the electrode/solution interface, i.e.,
Z3 = 1/
Q3(
jω)
β. For convenience, the transverse and parallel impedances are represented using gravimetric quantities (e.g.,
Z1/Ω g
−1,
Z2/Ω g
−1, and
Z3/Ω g), since, as discussed above,
L ∝
m.
The anomalous charge transport across narrow pores filled with the electrolyte can be understood considering the impedances
Z1 and/or
Z2 must be frequency-dependent, exhibiting a power law behavior (e.g.,
n < 1 and/or
s < 1; see Equations (3) and (4)). These particular impedances must be lower at high frequencies than at lower frequencies due to the effect of narrow ‘throats’ and bottleneck structures that restrict the long-range (e.g., low-frequency) ionic motion, as well as the presence of disordered structures in the solid phase, which affects the electronic transport [
21]. In general, the dispersive effects commonly found for semiconductors and conducting polymers and represented by the power law expressions (see Equations (3) and (4)) due to the anomalous charge transport in disordered phases being associated with discrete transitions between localized states that originated from the different types of structural disorder/defects present in porous electrode materials, which can be characterized by a characteristic time constant or relaxation time (
τc) [
41].
To overcome the difficulties involving the specification of a particular conduction mechanism, Bisquert et al. [
21] considered the problem of
anomalous charge transport using the concept of a model-independent macroscopic phenomenological theory based on a generalized constitutive equation and the general Einstein relationship for diffusional processes. As a result, different types of electrode materials that exhibit dispersive effects for charge transport can be studied using the proposed model. In this sense, the porous electrodes operate by simultaneous transport of electronic and ionic species occurring in the solid and liquid phases, respectively, to attain the principle of local electroneutrality. In this scenario, the solid phase provides a continuous path for the transport of electrons, but the dimensions of the structural elements in the disordered solid are quite small, especially in the presence of nano-sized domains. Accordingly, the electrolyte penetrates the accessible void regions present in the solid phase, resulting in very narrow liquid channels that exhibit a high degree of tortuosity. As a result, the electrode system is characterized by two closely mixed phases with a possible degree of disorder for the electronic and ionic charge carriers [
21].
The results of the CNLS simulation are summarized in
Table 2. As can be seen, the decoration of the CNFs with NiO caused strong changes in the electrochemical characteristics of the composite electrode. The major impedance parameters accounting for the performance of supercapacitors are
RESR and
Qedl. As seen, the
RESR value decreased after the decoration process, which is very good for the overall performance of the coin cell.
In principle, these findings indicate that the spontaneous hydration of the nickel oxide (e.g., NiO + H2O → Ni(OH)2) promoted an increase of the wettability of the inner surface regions of the porous electrode, thus increasing the overall cell conductivity. As seen, the apparent (fractal) electrical double-layer capacitance verified for the carbon-based scaffold or the apparent (fractal) pseudocapacitance observed for the decorated electrode was characterized by a dispersive exponent very close to 1 (e.g., β ≥ 0.95). This implies with great accuracy that Q ≈ C. It was verified that the decoration process using NiO strongly increased the coin cell charge storage characteristics from 2.62 to ≈ 536 F g−1 (since β ≈ 1), promoting an enormous improvement in the device’s performance. These findings explicitly reveal the paramount importance of the reversible solid-state redox reactions (RSR) to the overall charge storage process.
Considering the lower specific surface area exhibited by the composite material compared to the carbon-based scaffold, one can propose that the main contribution to the overall specific capacitance is a bulk-like or near-surface pseudocapacitance instead of the purely surface electrostatic process. We can argue that the strong electrochemical activity exhibited by Ni(OH)
2 for the charge storage process is due to the presence of RSR involving the Ni
2+/Ni
3+ redox couple [
42]. According to the literature, the redox reaction involving Ni(OH)
2 is a solid-to-solid transformation [
43]. We present the well-known Bode’s reaction scheme to represent the electrochemical behavior of Ni(OH)
2 during the charging–discharging process [
44]:
In short, the α ↔ γ and β ↔ β pathways, involving the solid-state redox transitions of the type Ni2+/Ni3+, are of interest to the reversible charging–discharging process in supercapacitors. The α → β phase change only occurs under potentially extended cycling, while the γ → β transformation occurs at the expense of excessive charge insertion.
For convenience, the gradual changes in the Ni(OH)
2 material occurring during proton intercalation/deintercalation can be simplified as follows [
45]:
where it is commonly assumed that the
β ↔
β pathway of the Bode’s scheme is dominant. It is worth mentioning that, due to the nature of amphoteric oxide, the issue of whether the species that diffuses through the Ni(OH)
2 structure is H
+ and/or OH
− remains open to discussion [
46].
Another possible origin for the pseudocapacitive behavior involving Ni(OH)
2 might be the intercalation/deintercalation of Li
+ ions into the hydrated oxide structure. According to [
45], the intercalation/deintercalation of Li
+ in Ni(OH)
2 is more probable in a concentrated LiOH aqueous solution or in rigorously anhydrous electrolytes (e.g., LiClO
4 + PC (propylene carbonate)). According to Faria et al. [
47], who proposed the occurrence of an exchange reaction, when different cations are present in the solution the proton intercalation can govern the overall charging–discharging processes comprising a mixed intercalation process, involving to a minor extent the intercalation/deintercalation of species like Li
+. Thus, it is plausible to consider for the hydrated oxide the following parallel process involving a substitutive solid-state redox reaction:
Therefore, it is prudent to consider for aqueous solutions that the overall pseudocapacitive process is a combined process given by the above solid-state reactions (Equations (7) and (8)) [
46].
The other set of impedance parameters presented in
Table 2 involves the ionic and electronic transport characteristics in the disordered phases. The ionic resistance inside the irregular pores decreased about 5-fold in the presence of Ni(OH)
2, while the exponent (
n) representing the anomaly degree increased from 0.42 to 0.92, i.e., the anomalous ionic transport practically disappeared for the composite electrode. In addition, we found for the decorated electrode that
Rionic(CFs) >
Rionic(NiO@CNFs). In principle, these findings suggest the occurrence of a Grotthuss-like mechanism for protons and/or Li
+ species inside the hydrated (gel layer) structure that formed during hydration of the nickel oxide. As a result, there is the formation of more regular paths for the ionic transport during the charge–discharge events and, therefore, the overall ionic transport in both liquid and solid (gel layer) phases behaves similarly to a normal (Fickian) process. On the contrary, for the carbon-based electrode, the transport of protons and/or Li
+ species is abruptly interrupted at the blocked electrode/solution interface, resulting in a severe anomaly during the fast charge–discharge process. Also, the more disordered structure of the carbon material creates zig-zag paths that decrease the mean free paths in narrow channels, thus reducing the overall ionic conductivity.
According to [
48], the diffusion coefficients for protons (
DH+) in the bulk liquid phase and the hydrated nickel oxide (
DH+(NiO)) are 9.32 × 10
−5 cm
2 s
−1 and ≈3 × 10
−10 cm
2 s
−1, respectively. Therefore, at least in principle, the Faradaic intercalation reaction during the charge storage process can be controlled by the slower ionic transport on the solid phase, which is sometimes indirectly verified in several
battery-like systems by the irreversible peaked shape voltammograms obtained at low scan rates (e.g.,
ν ≤ 10 mV s
−1) and/or the pronounced voltage plateau verified in the GCD curves [
49]. It was verified in the current work that
n(NiO) = 0.92 for ionic transport in the hydrated composite electrode and, therefore, we can consider that the overall proton diffusion in the two closely mixed phases is practically a nondispersive (Fickian) event. Thus, in the presence of a concentrated supporting electrolyte to sustain the migration current, there is the general phenomenological relationship
J =
D(Δ
CH+/Δ
x) for Nernst’s layer, where Δ
CH+/Δ
x is the concentration gradient driving the flow (
J), and
D/Δ
x =
kmt is the diffusion mass transport coefficient. In addition, from the continuity condition, we know that the three different coupled flows involved in the Faradaic (pseudocapacitive) process must be equal (e.g.,
J(e−) =
J(H+) =
JH+(NiO)). Therefore, considering that
DH+ >>
DH+(NiO), we propose that
k(mt)-H+(NiO) is not so different from
k(mt)-(H+), i.e., as already mentioned, the composite electrode material can provide many alternative routes for the ionic and electronic charges, thus resulting in short-range paths (Δ
x) for proton transport. As a result, the flow of ionic charge considerably increases in the hydrated oxide structure. The electrochemical system behaves like a real capacitive system instead of a battery-like one.
Sharma et al. [
50] recently reported on tuning the nanoparticle interfacial properties and stability of the core shell structure in Zn-doped NiMoO
4@AWO
4 electrodes. They considered Zn-doped nickel molybdate (NiMoO
4) (ZNM) as a core crystal structure and AWO
4 (A = Co or Mg) as a shell surface. They verified the ability to tune the core shell nanocomposites with surface reconstruction as a source for surface energy (de)stabilization. It was verified that the performance of the core shell is significantly affected by the chosen intrinsic properties of metal oxides with high performance compared to a single-component system in supercapacitors. The constructed asymmetric device (e.g., Zn-doped NiMoO
4@CoWO
4 (ZNM@CW)||activated carbon) exhibited superior pseudocapacitance, delivering a high areal capacitance of 892 mF cm
−2 at 2 mA cm
−2 and excellent cycling stability (i.e., 96% capacitance retention after 1000 charge–discharge cycles). Sharma et al. [
50] presented theoretical and experimental insights into the extent of the surface reconstruction to explain the storage properties in SCs.
The diffuse or drift effects in a disordered solid phase containing many traps are correlated with the number of electrons effectively contributing to the charge flux, which in turn depends on the frequency. Thus, the presence of dispersive (anomalous) effects can be identified through the dispersive exponent (
s) in Equation (4) [
51]. Using the Nernst–Einstein relationship, we can verify that, for most crystalline electronic conductors, the diffusion coefficient for the electrons (
De) is in the range of 7 to 241 cm
2 s
−1 [
52,
53]. However, in some cases involving disordered electronic materials where
s << 1, the
De values can be drastically reduced by up to two orders of magnitude due to the pronounced multiple trapping events caused by the structural inhomogeneities present in the solid phase. On the contrary, we observed a nearly 2-fold improvement in the electronic transport process after the electrode decoration with NiO. Since
s ≥ 0.98, we verified that the anomalous transport in the solid electrode structure is practically absent for the different materials. These findings indicate that, in the nano-sized domains of the electrode material, the electronic transport behaves like a normal one. A comparison of the experimental findings revealed that
Rionic/
Relectronic = 16. This small discrepancy in the resistance values is responsible for the presence of a well-defined straight line in the complex plane plot (see
Figure 6b) in the medium-frequency range with a phase angle close to −45°, as is theoretically predicted when
Z1 ≈
Z2 [
21]. By contrast, when this resistance ratio is very high (e.g.,
Rionic/
Relectronic > 100), the transmission line behavior is dictated only by the high impedance channel, i.e., the double-channel transmission line is converted to a single-channel one, and the complex plane plot exhibits a different profile to that shown in
Figure 6b.
The overall DC resistance (e.g., the purely resistive impedance) incurred by the normal and/or anomalous transports of the electronic and ionic charge carriers in the two channels of the transmission line representation can be determined from the low-frequency limit (
ω → 0) of Equation (1) (the physical model) [
54]:
Thus, the impedance of the transmission line is characterized by two ohmic resistances in parallel. It is predicted that the almost vertical capacitive straight line verified at very low frequencies for blocked electrodes, as is the case with supercapacitors, can be displaced more or less to the right-hand side of the complex plane plot, depending on the magnitude of the ohmic resistances imposed by the liquid and solid phases in intimate contact. Obviously, if R1 >> R2, Zd.c. ≅ R2. On the other hand, Zd.c. ≅ R1. These conditions imply that a single ohmic resistor describes the overall DC resistance. However, this is not the case in the present study since we verified that R1 ≈ R2. We found that the Zd.c. values for the CNF and NiO@CNF electrodes were 203 Ω g−1 and 88 Ω g−1, respectively. These findings reveal that the dissipative effects caused by ohmic losses are lower for the decorated electrode.
The crossover frequencies (
ωc) between DC and AC regimes for the transverse (e.g.,
Z1 and
Z2) impedances of the two closely mixed phases are as follows [
53]:
Thus, considering the relationship between the time constant (e.g.,
τc(1) = (
RQ)
1/n and
τc(2) = (
RQ)
1/s), and the characteristic frequency (
fc) given by
fc = 1/
τc, one can evaluate these quantities for the ionic and electronic transport phenomena using Equations (10) and (11), respectively, as shown in
Table 3.
The analysis of the data in
Table 3 revealed two distinct scenarios for the different electrode materials used in the symmetric coin cells. In the case of the CNF electrodes, the time constants (
τc) were not so different for the distinct charge transport in the ionic (
τc(1) = 1.25 s) and electronic (
τc(2) = 0.67 s) phases. The very close characteristic frequencies of 0.81 s
−1 and 1.50 s
−1 revealed that the transition between DC and AC regimes for the ionic and electronic phases is coupled and occurs in the low to medium frequency range of the impedance spectrum. Therefore, the formation of a well-defined semicircle at the high frequencies characterized by a given time constant was not observed (see
Figure 6a inset). For comparison, using a multiscale impedance model to study different supercapacitors using carbon-based porous electrodes, Huang et al. [
14] recently reported
τc(1) values in the range of 0.16 s to 2.35 s for their different electrodes. However, due to the limitations of the model, they did not evaluate the
τc(2) values and the eventual presence of anomalous transport.
The analysis of the other case comprising the NiO@CNF composite electrodes revealed very different time constants of
τc(1) = 2.70 × 10
−4 s and
τc(2) = 2.06 s for the ionic and electronic charge transports, respectively. Thus, we obtained different characteristic (crossover) frequencies of 3.71 × 10
3 s
−1 and 0.48 s
−1 representing the transition regions in the complex plane plot for the ionic and electronic transports, respectively. As a result, three different regions can be clearly identified in the impedance spectrum (see
Figure 6b): (i) the well-defined semicircle at high frequencies; (ii) the false Warburg-like straight line localized in the medium–low-frequency region, and (iii) the capacitive/pseudocapacitive straight line at very low frequencies. It is worth noting that the physicochemical origin of the high-frequency semicircle in the case of porous blocked electrodes is not due to a Faradaic (charge transfer) reaction. On the contrary, this behavior, which is predicted by the theory represented by Equation (1), is due to a combination of two factors: (i) the penetration depth dependency of the sinusoidal perturbation on applied frequency, and (ii) the presence of an “abnormal charge transport” phenomenon involving the electronic and/or ionic charge carriers in disordered media, i.e., the different phases being in intimate contact along the porous electrode surface. Unfortunately, this vital aspect, which has been known about for a long time, is ignored in most literature reports dealing with SCs. Commonly, authors not acquainted with the theoretical aspects of EIS misuse equivalent circuit analogs without a physicochemical meaning.
In fact, with rare exceptions, most of the circuit analogs used in EIS studies are merely statistical devices used as part of a trial and error method to obtain a good simulation of the impedance data using the different analog circuits present in commercial software packages. The impedance data are often simulated with good statistics. However, as expected, this nonphysical approach fails to provide a physicochemical meaning to the used circuit’s parameters. For more details, please see the excellent books by Barsoukov and Macdonald [
54], Orazem and Tribollet [
55], and Lasia [
18], which constitute a trustworthy source of knowledge about the impedance method of analysis. Unfortunately, as can be seen in several papers, the current literature using the EIS technique for dealing with energy storage devices is full of fundamental errors that are propagated in several important articles published by different research groups.
A possible explanation for the large difference in the time constants verified for the electron transport in the different electrode materials (e.g.,
τc(carbon material) = 1.25 s and
τc(composite) = 2.70 × 10
−4 s) is the pronounced occurrence of the RSR involving the Ni
2+/Ni
3+ redox couple, i.e., due to the Faradaic nature of the charge storage process, a great fraction of the transported electrons taking part in the RSR process is subjected to an activation barrier, involving the presence of entropic (dissipative) effects, as predicted by the transition state theory (TST) [
56]. As a result, the overall flux of electrons measured in the impedance experiments is partially suppressed by an energetic barrier in the case of the composite electrode, thus decreasing the time constant.
In general, the above discussion involving the EIS technique conveys the importance of using relevant physicochemical models represented by a transfer function (or the equivalent transmission line representation) for the detailed analysis of the significant events occurring during the charge storage process in SCs. Therefore, it becomes evident that the use of equivalent circuit analogs, commonly derived from modified versions of the well-known Randles–Ershler circuit, which was further improved by Grahame and Sluyters with the concept of Faradaic impedance for the study of different electrochemical reactions on the mercury electrode, must be used with great caution to avoid speculative discussions involving solid electrodes used in different energy storage devices that exhibit different dispersive effects.
3.3. CV and GCD Analyses
Obviously, there are several important parameters determined using EIS that are not available from the CV and GCD experiments. However, to verify the internal consistency of the specific capacitance experimental findings obtained using different electrochemical techniques, we also conducted studies using the CV and the GCD techniques. As will be seen, good agreement was found since the CV and GCD profiles are representative of true supercapacitors instead of undesirable battery-like systems. Also, the specific capacitance values determined from the EIS and GCD findings are similar.
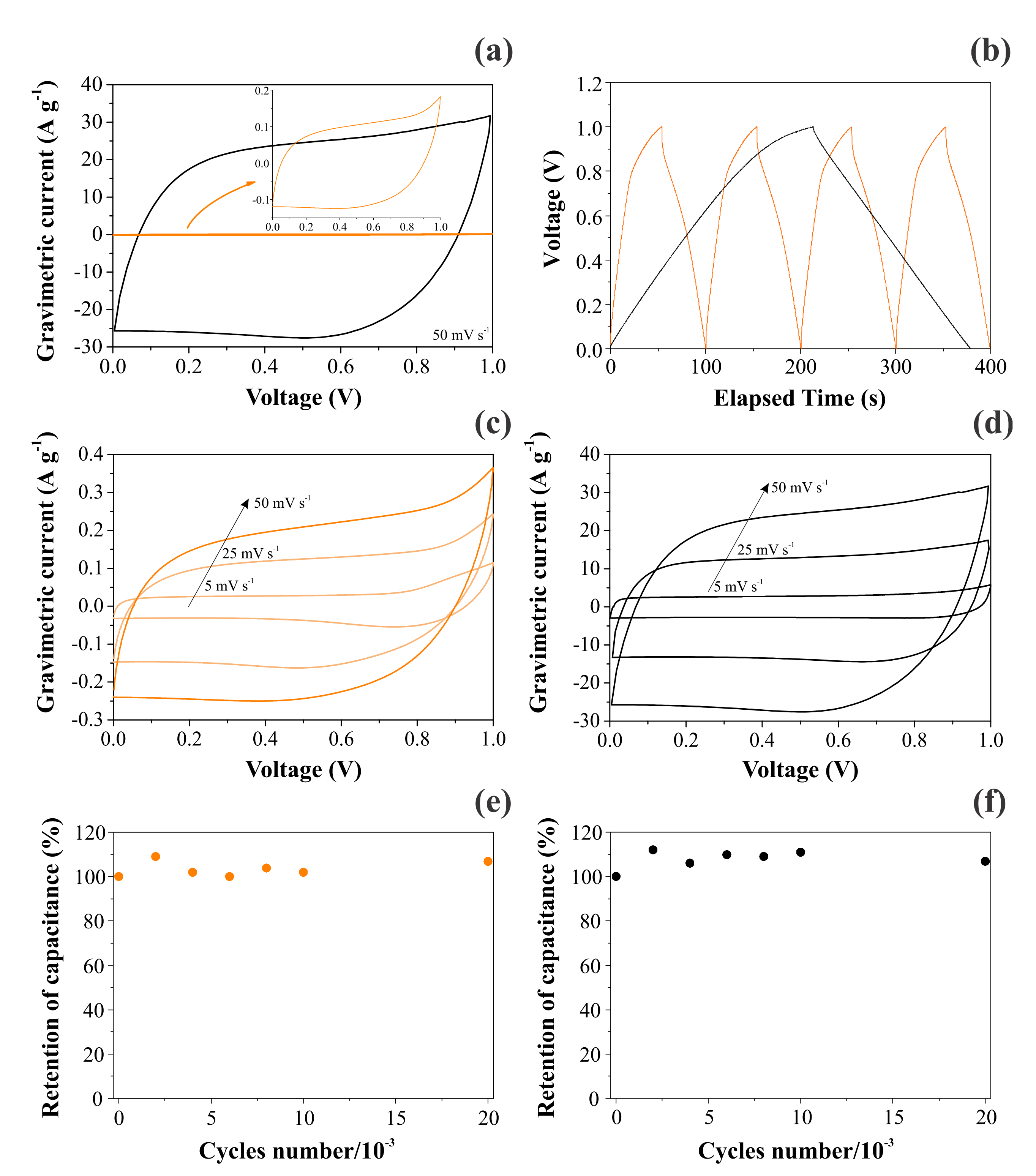
Figure 7 contrasts the CV and GCD findings obtained for CNFs and NiO@CNFs in two distinct symmetric coin cells filled with a 1.0 M Li
2SO
4 aqueous solution. As seen in
Figure 7a, we obtained a capacitive/pseudocapacitive voltage window of 1.0 V for both cells. Two important features ensured that our coin cells behaved as true supercapacitors: (i) the voltammetric curves were almost rectangular, with a “mirror-like” shape even at 50 mV s
−1 (e.g., the absence of the peaked-shape voltammograms characteristic of “battery-like” systems), and (ii) the GCD profiles were almost triangular (e.g., the absence of the voltage plateau verified for “battery-like” systems). In addition, the retention of capacitance was excellent even after 30,000 cycles (see
Figure 7e,f). The small oscillations verified for the capacitance values can be ascribed to the progressive activation of the inner surface regions by deeper penetration of the electrolyte ions [
36]. In any case, the coin cell maintained high capacitance retention (e.g., >95%) during the long-term charge–discharge experiments, which is typical for well-behaved supercapacitors. These important findings revealed that the solid-state redox process involving the nickel species in the hydrated oxide (e.g., gel layer structure) is highly reversible.
A comparison of the VCs in
Figure 7a,c,d revealed an enormous increase in the specific voltammetric current for the composite containing Ni(OH)
2. For the applied scan rates of 50, 25, and 5 mV s
−1, the specific capacitances obtained for CNF electrodes were 4.2, 5.0, and 5.6 F g
−1, respectively. At the same time, the corresponding values for the NiO@CNF electrodes were 500, 520, and 620 F g
−1, respectively. These findings are similar to those for Ni-based oxide electrode materials used in SCs [
1,
8,
9,
10,
11,
12]. As previously verified by Fantini and Gorenstein [
57], the CV profiles for nickel hydroxide thin films are practically identical in neutral and alkaline solutions. Therefore, the absence in the present study of the pronounced peaks/bands commonly verified for battery-like Ni(OH)
2 composite materials in alkaline solutions can be understood considering the occurrence of a strong synergism in the composite, i.e., the pseudocapacitive process was spread over the entire voltage window where the electrolyte is stable due to the presence of a uniform distribution in the porous electrode structure of reactive sites with different activation energies for the charge transfer reaction [
3,
28,
33]. As a result, the electrochemical response is quite similar to that commonly verified for EDLCs. These are very important findings since, in most studies, the authors are interested in fabricating a composite material that exhibits the intrinsic characteristics of well-behaved supercapacitors. This featureless voltammetric profile verified for a hydrated transition metal oxide (TMO) is not new. For example, similar findings are commonly verified for the well-known RuO
2⋅xH
2O system in acidic and neutral solutions [
58]. In addition, in the case of two-electrode cells, the faradaic current is distributed on a more flattened pattern in the voltammetric curves since the voltage for the working electrode (anode) is not measured against a true reference electrode having a potential benchmark that is constant during the experiments.
The analysis of
Figure 7b evidenced a huge increase in the discharge time when Ni(OH)
2 was incorporated in the carbon-based scaffold. As a result, the specific capacitance was strongly increased.
Table 4 gathers the specific capacitances determined using the GCD findings for the different electrodes and normalizing factors. As seen, the overall specific capacitance for the two-electrode (coin cell) case is in good agreement with that verified in the EIS study (see
Table 2). We chose to use the specific capacitance values corresponding to the individual (single) electrodes (e.g., the specific capacitances obtained in three-electrode cells) in addition to the two-electrode case obtained for the symmetric coin cell.
Obviously, the specific pseudocapacitance values of practical importance are those referring to the two-electrode case, as in the current EIS study. However, to facilitate a comparison with the literature regarding the use of traditional three-electrode cells, we calculated the capacitances obtained from GCDs for the individual electrodes. In this sense, using the experimental masses of 12.3 mg (CNFs) and 12.6 mg (composite), we verified a very small specific capacitance of 16 F g
−1 for CNFs. On the contrary, we verified an enormous specific pseudocapacitance of 2548 F g
−1 for NiO/Ni(OH)
2 that is very close to the predicted theoretical value of ~2600 F g
−1 [
59]. The maximum specific energy and power obtained for the NiO@CNF composite electrodes were 88.47 Wh kg
−1 and 20,833 W kg
−1, respectively. The maximum specific energy and power obtained for the CNF electrodes were 0.56 Wh kg
−1 and 96.78 W kg
−1, respectively. These GCD findings were obtained at 1 mA.
It is worth mentioning that it is not correct to normalize the capacitance using very small electrode masses for extrapolation purposes since the electrochemical data probably would not scale up with the larger masses used in practical electrodes [
60]. Moreover, we would like to emphasize that, in several studies, the pseudocapacitance values reported for single- and two-electrode cases are illusory (incorrect), i.e., different battery-like electrochemical systems were erroneously characterized as true pseudocapacitors. As recently discussed by some of the present authors [
1], this important issue arises from the incorrect distinction between the
capacity (Ah g
−1) and
capacitance (F g
−1) concepts [
61].