Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review
Abstract
:1. Introduction
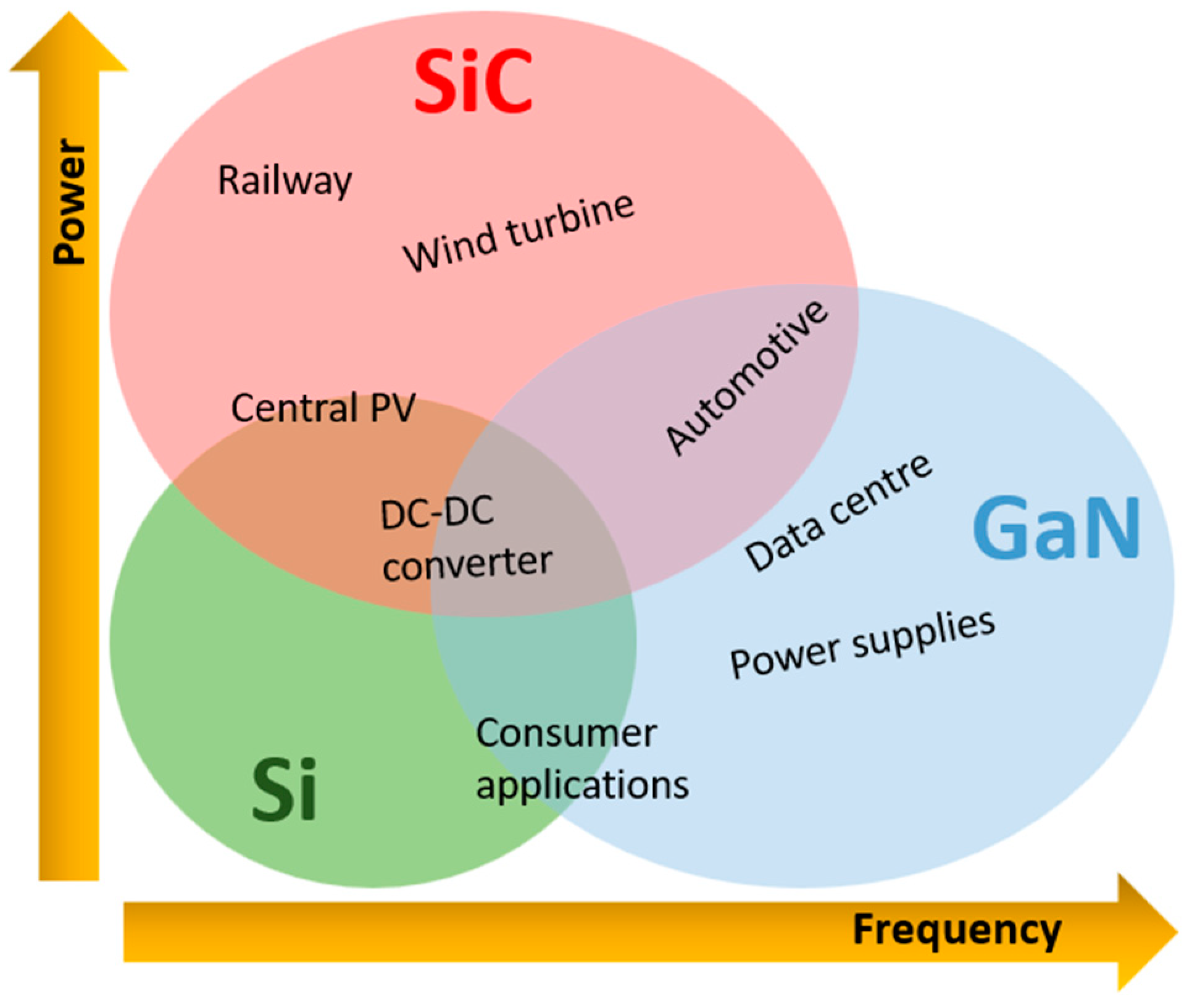
2. Comparison between MOSFET and GaN HEMT
- Output characteristic;
- Transfer characteristic;
- Threshold voltage;
- Conduction resistance;
- Third quadrant and reverse recovery current;
- Parasitic capacitances.
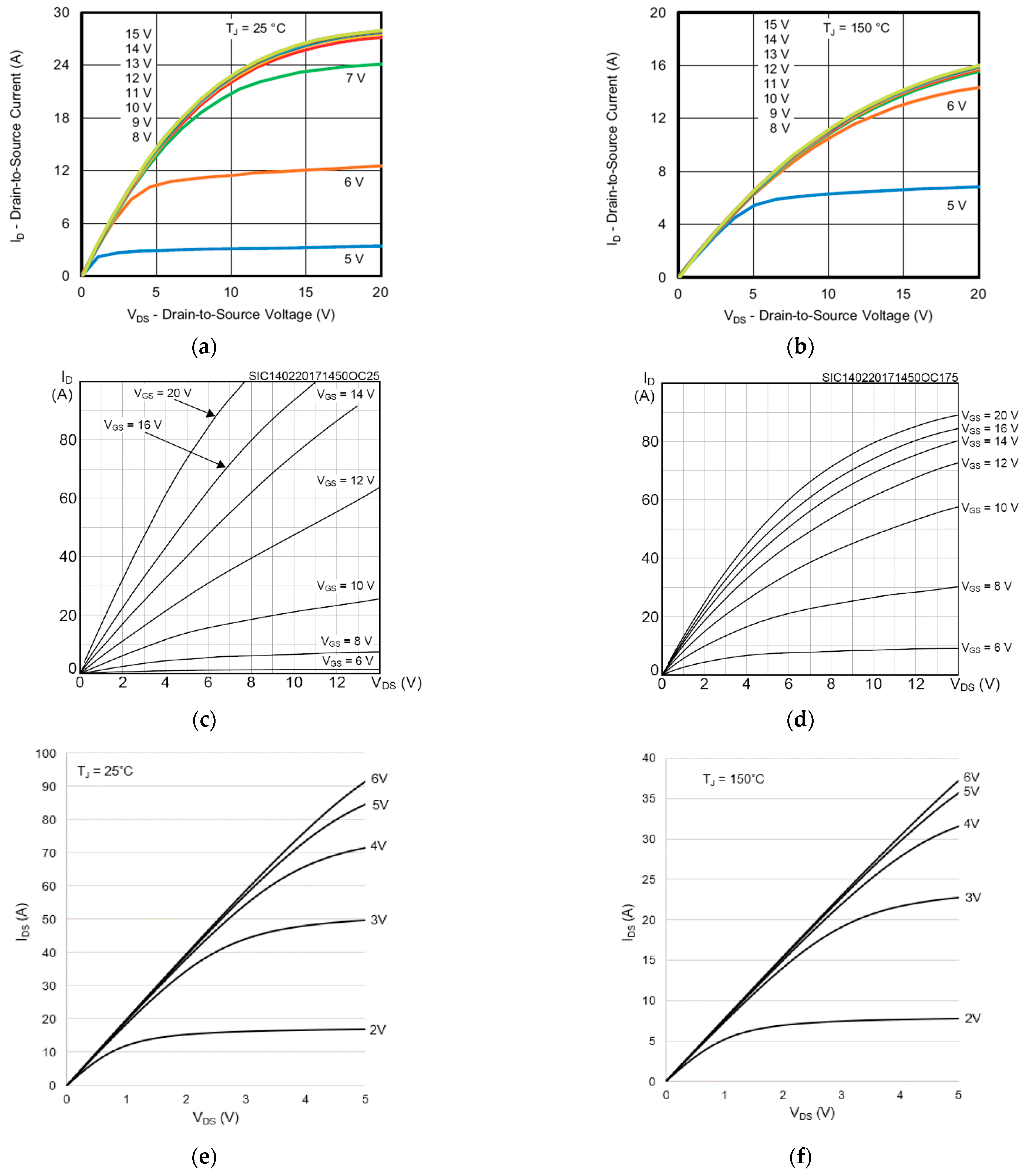
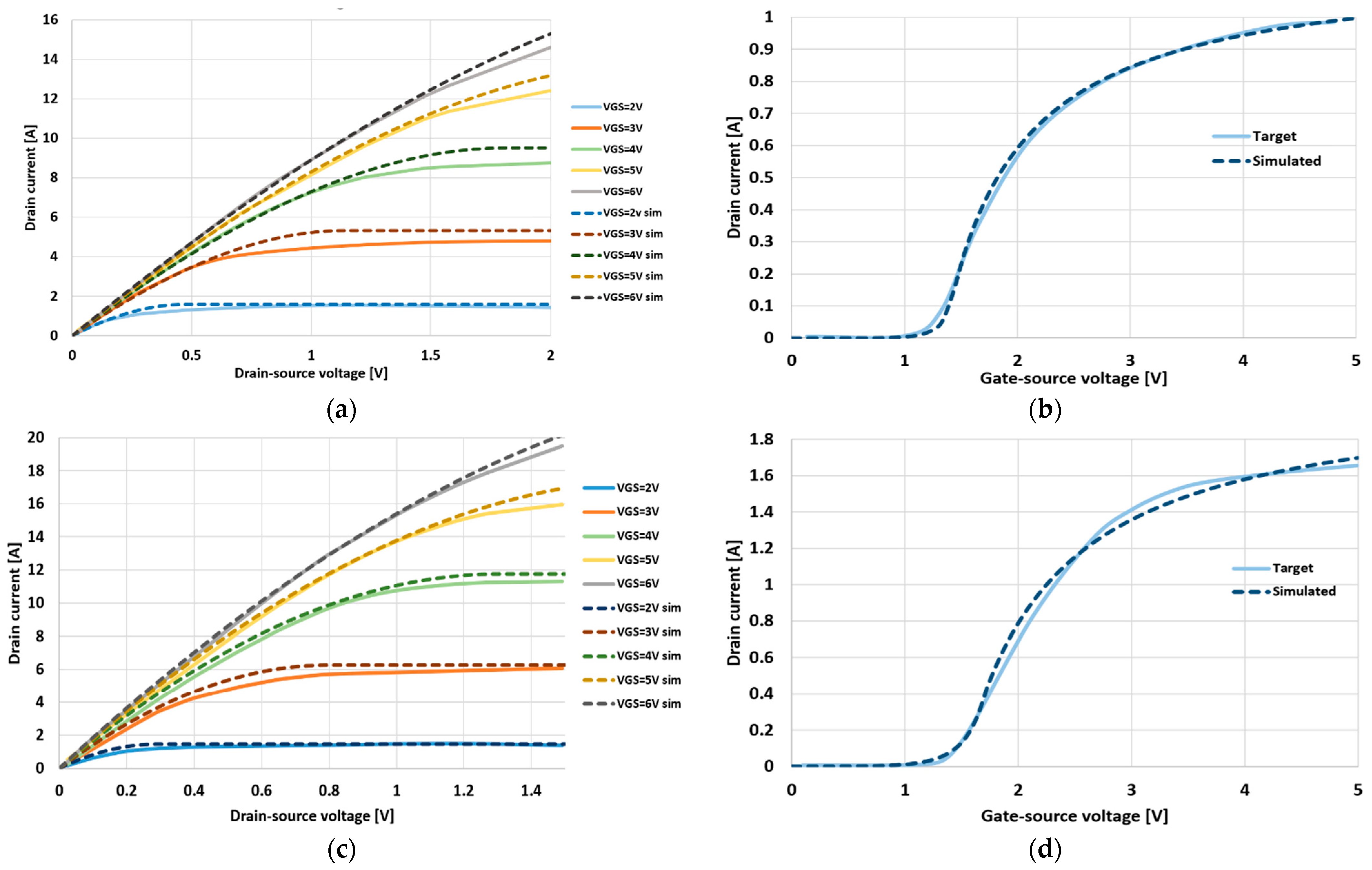
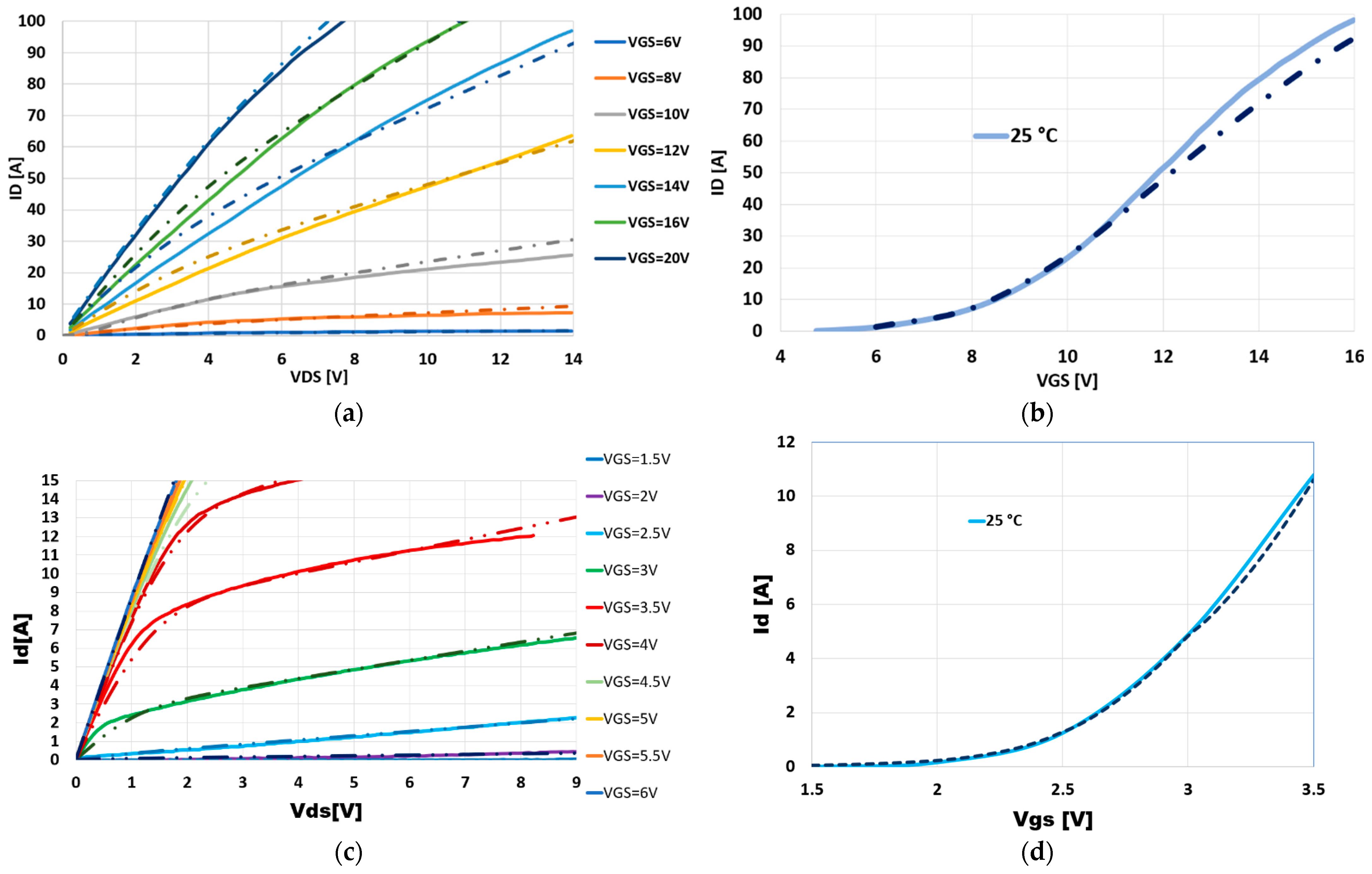
2.1. Output Characteristic
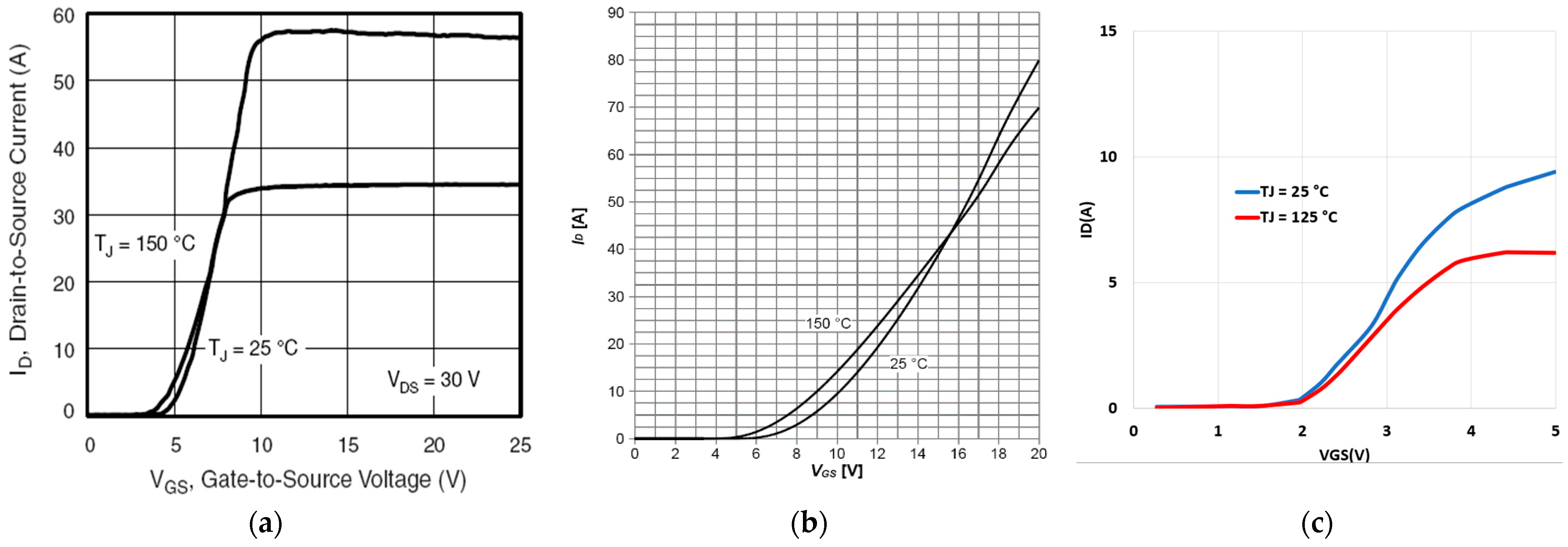
2.2. Transfer Characteristic
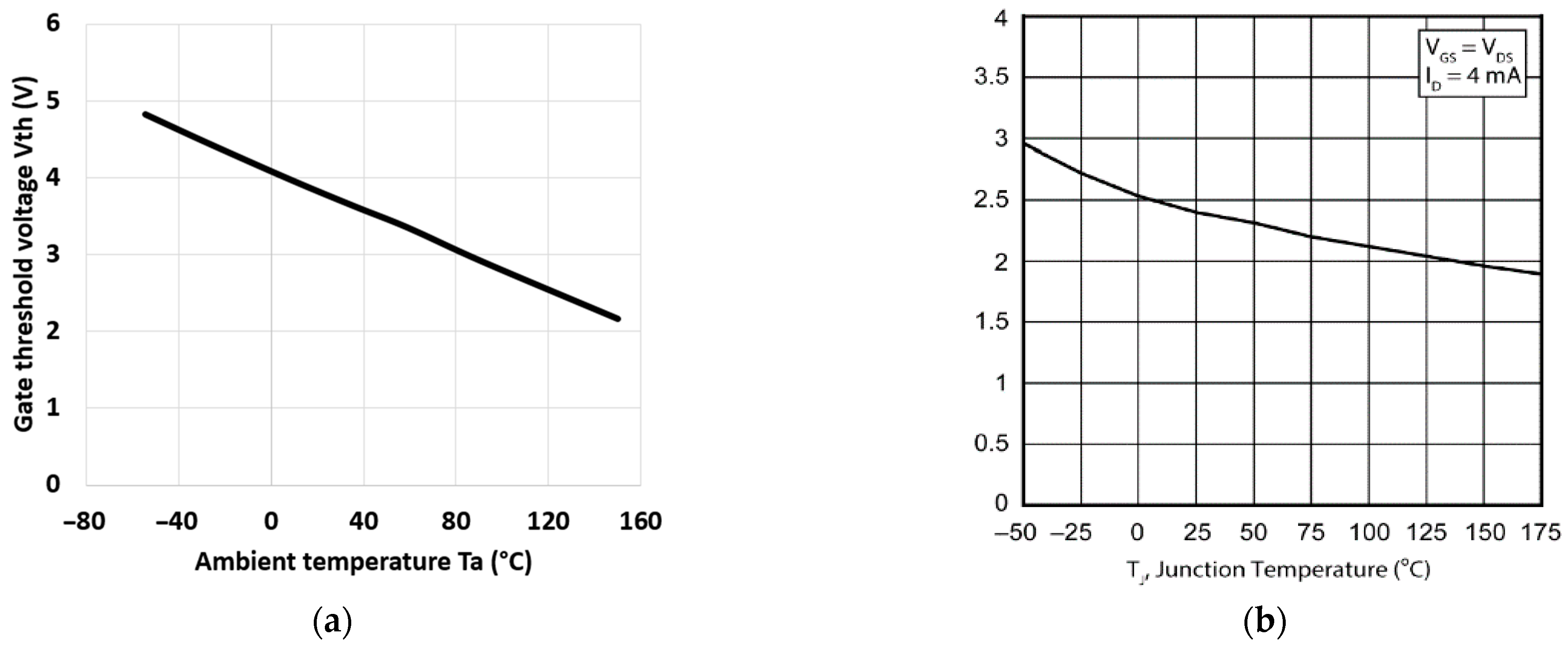
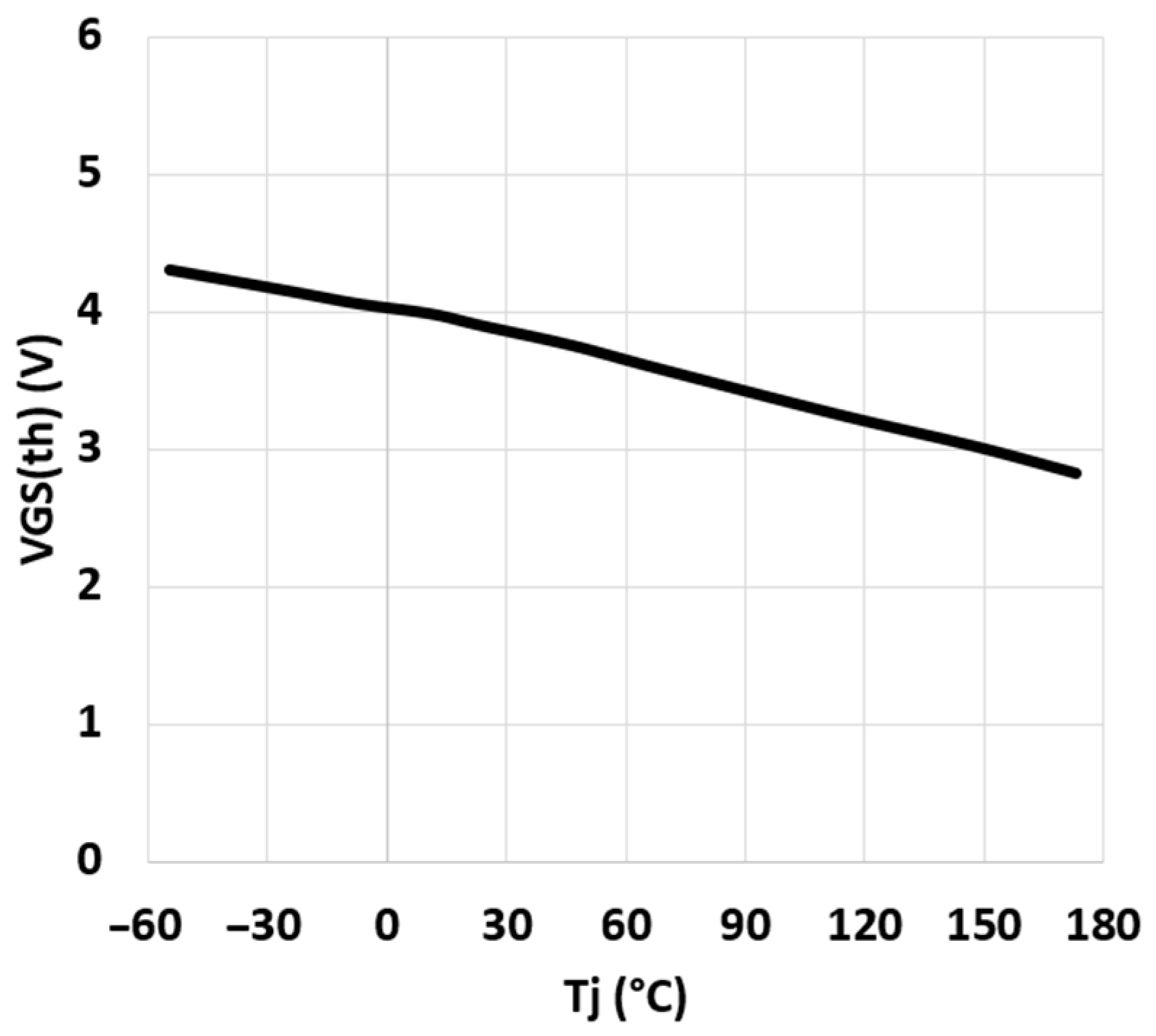
2.3. Threshold Voltage Characteristic
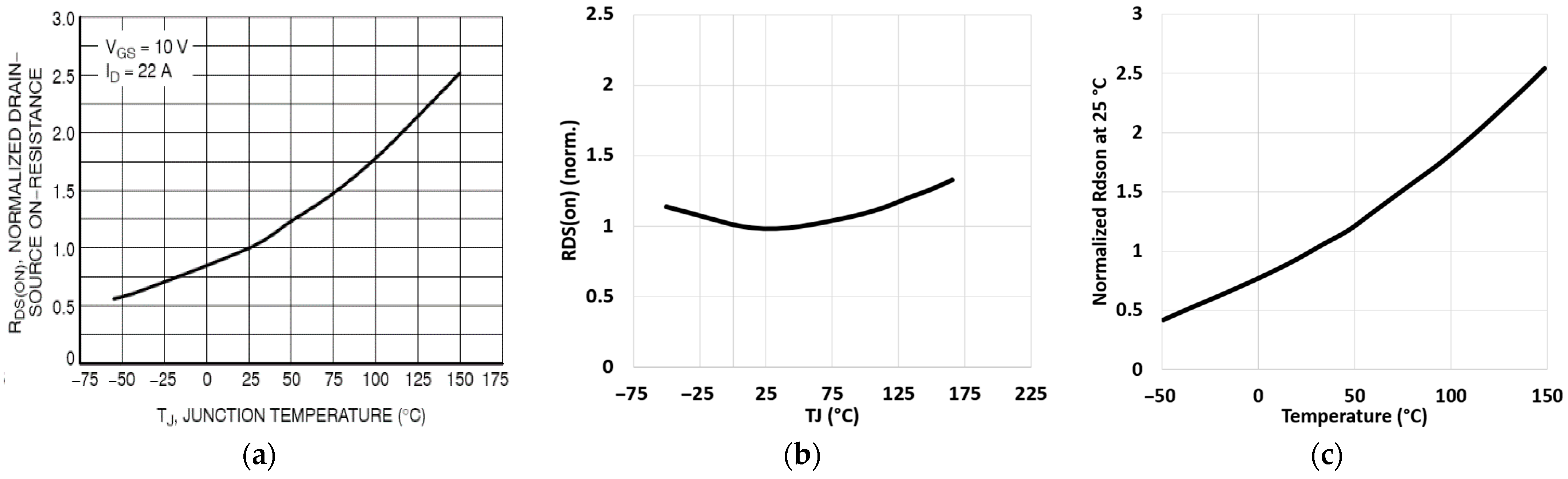
2.4. Static On-Resistance (RDS,on) Characteristic
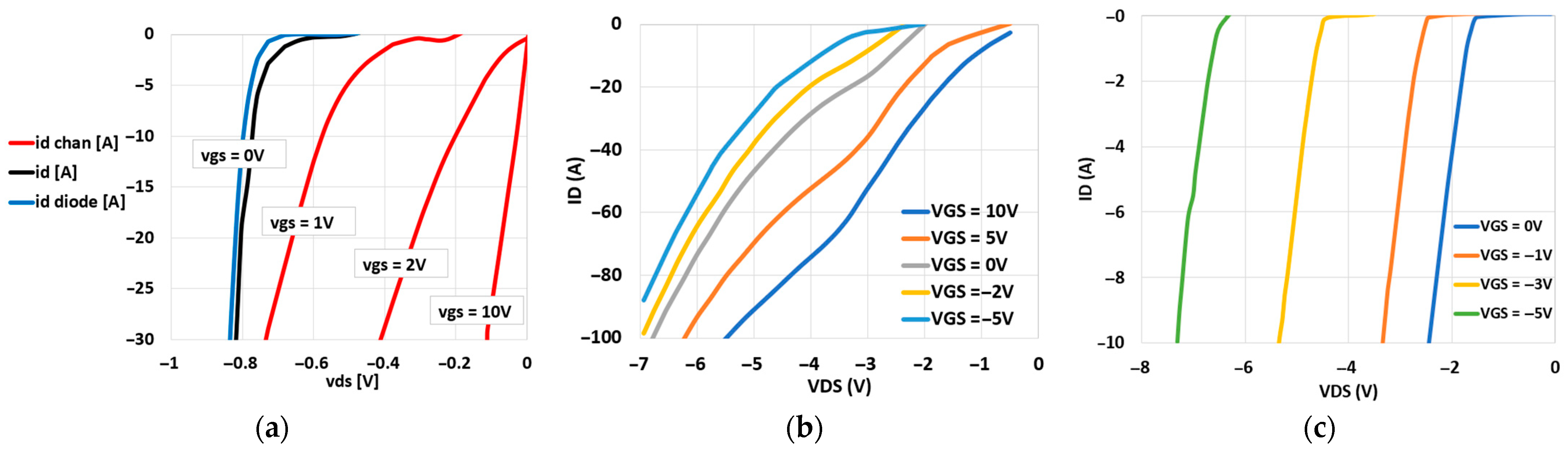
2.5. Third Quadrant and Reverse Recovery Current Characteristics
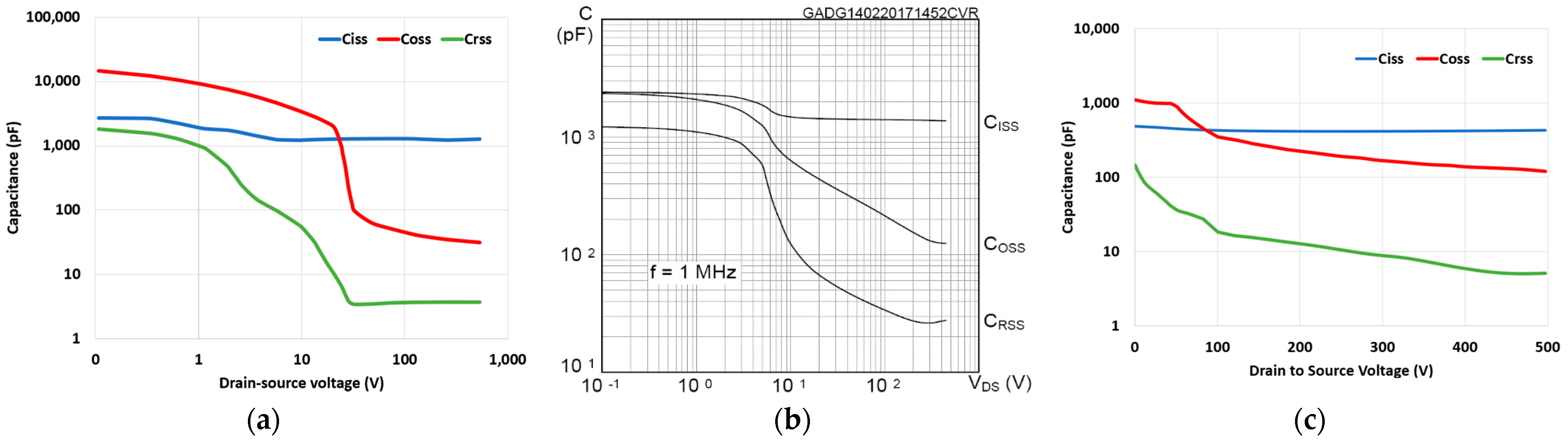
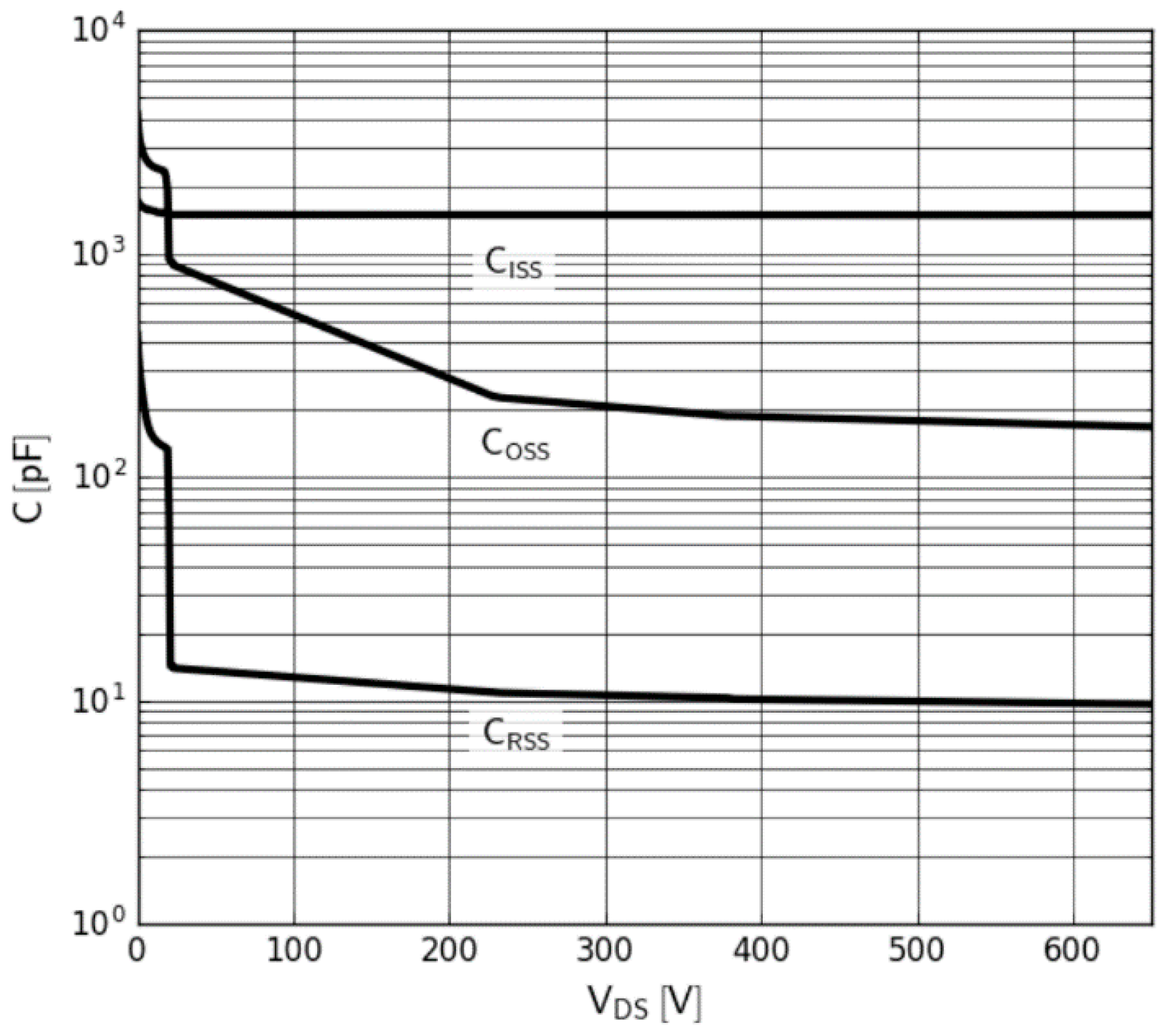
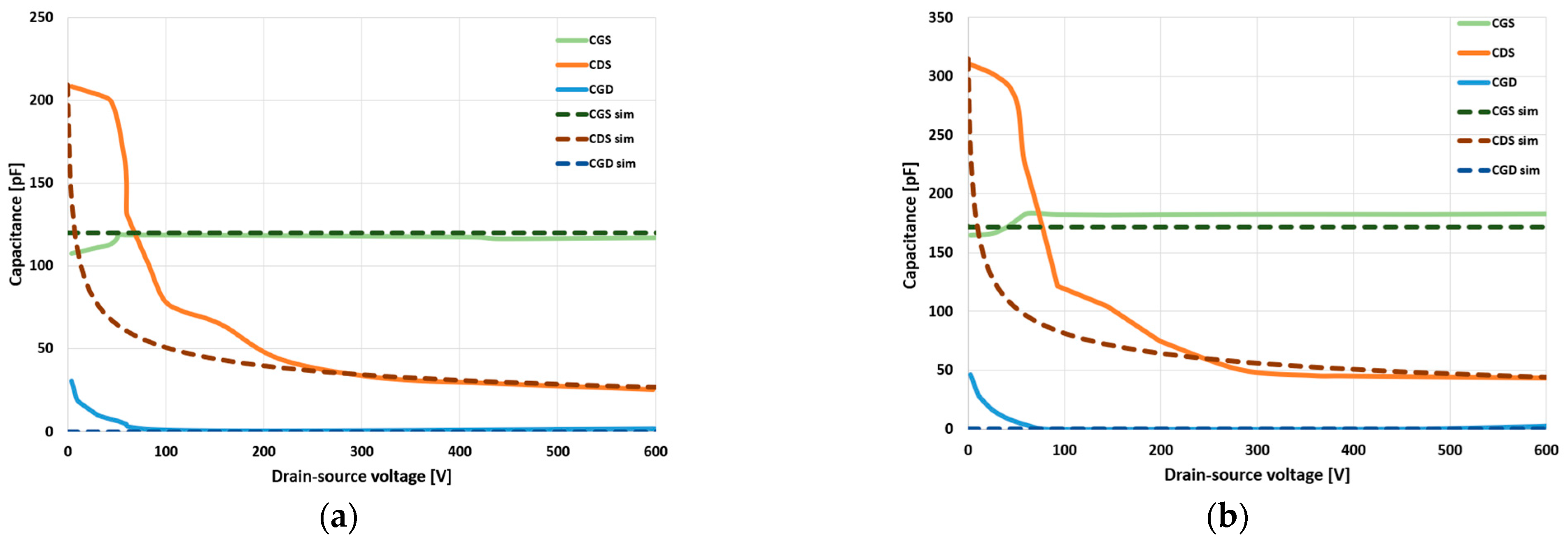
2.6. Capacitance Characteristic
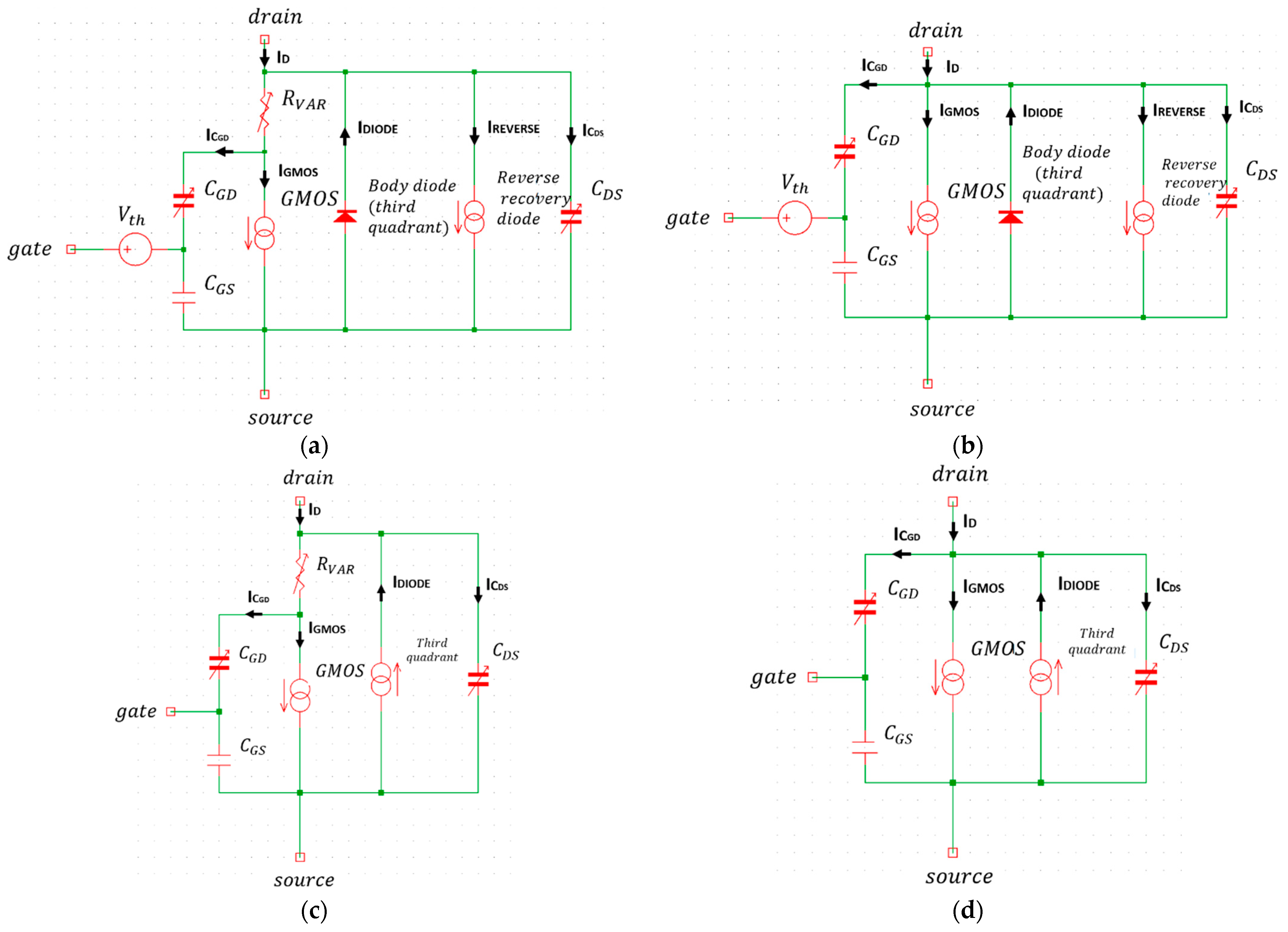
3. Circuit Model
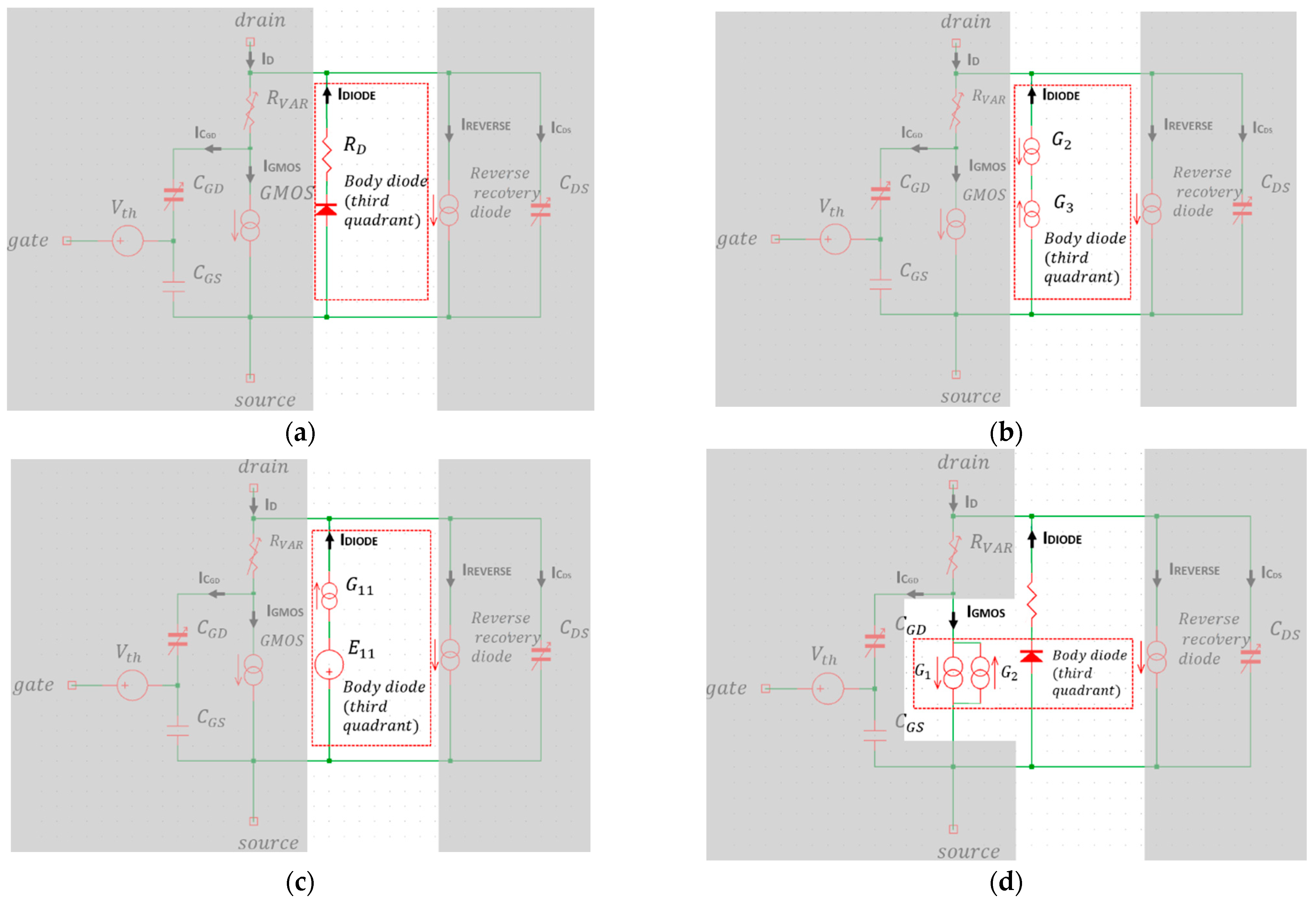
3.1. GMOS
3.2. Vth-Threshold Voltage
3.3. RVAR
3.4. Third Quadrant Conduction
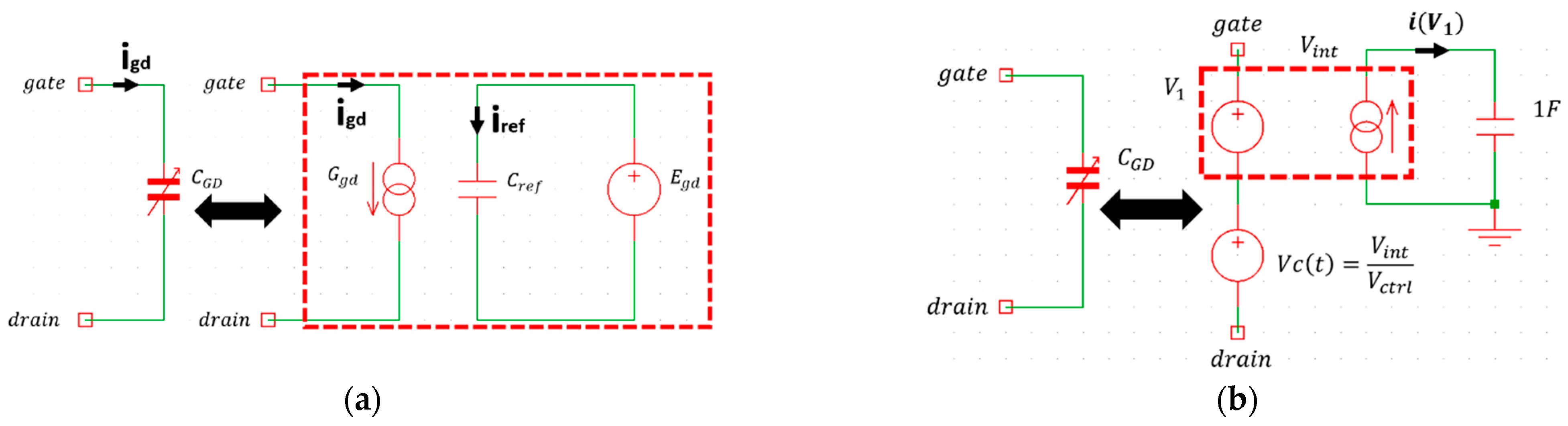
3.5. Parasitic Capacitances
3.6. Summary Table
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviation
| WGB | Wide bandgap |
| Si | Silicon |
| SiC | Silicon carbide |
| GaN | Gallium nitride |
| MOSFET | Metal oxide semiconductor field effect transistor |
| HEMT | High-electron-mobility transistor |
| CAD | Computer-aided design |
| TCAD | Technology computer-aided design |
| ID | Drain current |
| VDS | Drain-source voltage |
| VGS | Gate-source voltage |
| VGD | Gate-drain voltage |
| VSD | Source-drain voltage |
| IGMOS | GMOS current |
| IGMOS,25 | GMOS current at 25 °C |
| VGMOS | GMOS voltage |
| Idiode | Diode current |
| Vdiode | Diode voltage |
| Rdiode | Parasitic resistance diode |
| Rdiode,25 | Parasitic resistance diode at 25 °C |
| RVAR,25 | Typical RDS,on value at 25 °C |
| VTH | Threshold voltage |
| VTH,25 | Threshold voltage at 25 °C |
| T25, Tj | Room, junction temperature |
| IS,25 | Saturation current |
| CDS | Drain-source capacitance |
| CGS | Gate-source capacitance |
| CDG | Drain-gate capacitance |
| CISS | Input small signal capacitance |
| COSS | Output small signal capacitance |
| CRSS | Reverse small signal capacitance |
| q | Electron charge |
| k | Boltzmann’s constant |
| N | Emission coefficient |
| VEG | Bandgap voltage |
| Mobility modulation constant | |
| W | Channel width |
| L | Channel length |
| Rs | Source resistance |
| Rd | Drain resistance |
| Surface potential in strong inversion | |
| Body-effect parameter | |
| λ | Channel modulation |
| Ks | Sub-threshold slope |
| Transconductance coefficient | |
| ϕt | Thermal voltage |
| M | P-n gradient factor |
| Vbi | Built-in junction potential |
| CGD(0) | Zero-bias gate-drain capacitance |
| CDS(0) | Zero-bias drain-source capacitance |
References
- Lee, I.-O.; Kim, J.; Lee, W. A High-Efficient Low-Cost Converter for Capacitive Wireless Power Transfer Systems. Energies 2017, 10, 1437. [Google Scholar] [CrossRef] [Green Version]
- Pham, C.; Kerekes, T.; Teodorescu, R. High efficient bidirectional battery converter for residential PV systems. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 890–894. [Google Scholar]
- Lee, S.-H.; Cho, Y.-W.; Cha, W.-J.; Kim, K.-T.; Kwon, B.-H. High efficient series resonant converter using direct power conversion. IET Power Electron. 2014, 7, 3045–3051. [Google Scholar] [CrossRef]
- Zhang, Z.; Tu, H.; She, X.; Sadilek, T.; Ramabhadran, R.; Hu, H.; Earls, W. High-Efficiency Silicon Carbide-Based Buck-Boost Converter in an Energy Storage System: Minimizing Complexity and Maximizing Efficiency. IEEE Ind. Appl. Mag. 2021, 27, 51–62. [Google Scholar] [CrossRef]
- Shi, C.; Wang, H.; Dusmez, S.; Khaligh, A. A SiC-Based High-Efficiency Isolated Onboard PEV Charger with Ultrawide DC-Link Voltage Range. IEEE Trans. Ind. Appl. 2017, 53, 501–511. [Google Scholar] [CrossRef]
- Ramachandran, R.; Nymand, M. Experimental Demonstration of a 98.8% Efficient Isolated DC–DC GaN Converter. IEEE Trans. Ind. Electron. 2017, 64, 9104–9113. [Google Scholar] [CrossRef]
- Lee, W.; Han, D.; Morris, C.T.; Sarlioglu, B. High-Frequency GaN HEMTs Based Point-of-Load Synchronous Buck Converter with Zero-Voltage Switching. J. Power Electron. 2017, 17, 601–609. [Google Scholar] [CrossRef]
- Kasper, M.; Deboy, G. GaN HEMTs Enabling Ultra-Compact and Highly Efficient 3 kW 12 V Server Power Supplies. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Hayashi, Y. Approach for highly efficient and ultra compact converters in next generation 380 V DC distribution system. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3803–3810. [Google Scholar]
- Gutierrez, A.; Marcault, E.; Alonso, C.; Tremouilles, D. Experimental comparison of discrete cascode gan-gan and single e-gan in high-frequency power converter. In Proceedings of the PCIM Europe Conference Proceedings, 1, Nuremburg, Germany, 7–8 July 2020; pp. 1655–1661. [Google Scholar]
- Delaine, J.; Jeannin, P.; Frey, D.; Guepratte, K. High frequency DC-DC converter using GaN device. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1754–1761. [Google Scholar]
- Foti, S.; De Caro, S.; Scelba, G.; Scimone, T.; Testa, A.; Cacciato, M.; Scarcella, G. An Optimal Current Control Strategy for Asymmetrical Hybrid Multilevel Inverters. IEEE Trans. Ind. Appl. 2018, 54, 4425–4436. [Google Scholar] [CrossRef]
- Faraci, G.; Grasso, C.; Schembra, G. Fog in the Clouds: UAVs to Provide Edge Computing to IoT Devices. ACM Trans. Internet Technol. 2020, 20, 1–26. [Google Scholar] [CrossRef]
- Klein, K.; Hoene, E.; Lang, K.-D. Packages for fast switching HV GaN power devices. In Proceedings of the PCIM Europe Conference Proceedings, Nuremberg, Germany, 20–22 May 2014; pp. 594–601. [Google Scholar]
- Wang, Z.; Honea, J.; Shi, Y.; Li, H. Investigation of driver circuits for GaN HEMTs in leaded packages. In Proceedings of the 2014 IEEE Workshop on Wide Bandgap Power Devices and Applications, Knoxville, TN, USA, 13–15 October 2014; pp. 81–87. [Google Scholar]
- Pace, L.; Idir, N.; Duquesne, T.; De Jaeger, J.-C. Parasitic Loop Inductances Reduction in the PCB Layout in GaN-Based Power Converters Using S-Parameters and EM Simulations. Energies 2021, 14, 1495. [Google Scholar] [CrossRef]
- Efthymiou, L.; Camuso, G.; Longobardi, G.; Chien, T.; Chen, M.; Udrea, F. On the Source of Oscillatory Behaviour during Switching of Power Enhancement Mode GaN HEMTs. Energies 2017, 10, 407. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Y.; Tang, Q.; Wang, L. Analysis of oscillation in bridge structure based on GaN devices and ferrite bead suppression method. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 391–398. [Google Scholar]
- Li, R.; Zhu, Q.; Xie, M. A New Analytical Model for Predicting dv/dt-Induced Low-Side MOSFET False Turn-ON in Synchronous Buck Converters. IEEE Trans. Power Electron. 2019, 34, 5500–5512. [Google Scholar] [CrossRef]
- Chen, J.; Luo, Q.; Huang, J.; He, Q.; Sun, P.; Du, X. Analysis and Design of an RC Snubber Circuit to Suppress False Triggering Oscillation for GaN Devices in Half-Bridge Circuits. IEEE Trans. Power Electron. 2020, 35, 2690–2704. [Google Scholar] [CrossRef]
- Dymond, H.C.P.; Liu, D.; Wang, J.; Dalton, J.J.O.; McNeill, N.; Pamunuwa, D.; Hollis, S.J.; Stark, B.H. Reduction of oscillations in a GaN bridge leg using active gate driving with sub-ns resolution, arbitrary gate-resistance patterns. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Versèle, C.; Deblecker, O.; Lobry, J. A computer-aided design tool dedicated to isolated DC-DC converters based on multiobjective optimization using genetic algorithms. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 583–603. [Google Scholar] [CrossRef]
- Yu, R.; Ho, G.K.Y.; Pong, B.M.H.; Ling, B.W.; Lam, J. Computer-Aided Design and Optimization of High-Efficiency LLC Series Resonant Converter. IEEE Trans. Power Electron. 2012, 27, 3243–3256. [Google Scholar] [CrossRef] [Green Version]
- Ventura, C.; Tina, G.M.; Gagliano, A.; Aneli, S. Enhanced models for the evaluation of electrical efficiency of PV/T modules. Sol. Energy 2021, 224, 531–544. [Google Scholar] [CrossRef]
- Pagano, R.; Abedinpour, S.; Raciti, A.; Musumeci, S. Modeling of planar coils for wireless power transfer systems including substrate effects. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1129–1136. [Google Scholar]
- DeMan, H.J.; Mertens, R. SITCAP—A simulator of bipolar transistors for computer-aided circuit analysis programs. In Proceedings of the International Solid-State Circuits Conference (ISSCC), Technical Digest, Philadelphia, PA, USA, 14–16 February 1973; pp. 104–105. [Google Scholar]
- Lee, J.-H.; Lee, H.-J. Circuit model parameter generation with TCAD simulation. In Proceedings of the International Conference on Solid-State and Integrated Circuits Technology Proceedings, ICSICT, 2, Beijing, China, 18–21 October 2004; pp. 1084–1087. [Google Scholar]
- Kloes, A. Multiscale Simulation: Can Compact Models be More Than a One-Way Bridge between TCAD and Circuit Simulation? In Proceedings of the 2021 IEEE Latin America Electron Devices Conference (LAEDC), Mexico, Mexico, 19–21 April 2021; pp. 1–4. [Google Scholar]
- Wang, J.; Zhao, T.; Li, J.; Huang, A.Q.; Callanan, R.; Husna, F.; Agarwal, A. Characterization, Modeling, and Application of 10-kV SiC MOSFET. IEEE Trans. Electron Devices 2008, 55, 1798–1806. [Google Scholar] [CrossRef]
- Purschel, M. PSpice simulation of the power stage for DC brush motors using state of the art power MOSFETs. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1567–1572. [Google Scholar]
- Xiao, Y.; Victory, J.; Pearson, S.; Sarkar, T.; Challa, A.; Dagan, M.; Collanton, P.; Andreev, C. Corner and Statistical SPICE Model Generation for Shielded-Gate Trench Power MOSFETs Based on Backward Propagation of Variance. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 17–21 March 2019; pp. 508–515. [Google Scholar]
- Raciti, A.; Rizzo, S.A.; Susinni, G. Parametric PSpice Circuit of Energy Saving Lamp Emulating Current Waveform. Appl. Sci. 2019, 9, 152. [Google Scholar] [CrossRef] [Green Version]
- Mudholkar, M.; Ahmed, S.; Ericson, M.N.; Frank, S.S.; Britton, C.L.; Mantooth, H.A. Datasheet driven silicon carbide power MOSFET model. IEEE Trans. Power Electron. 2014, 29, 2220–2228. [Google Scholar] [CrossRef]
- Rizzo, S.A.; Salerno, N.; Raciti, A.; Bazzano, G.; Raffa, A.; Veneziano, P. Parameters optimization of a behavioural SPICE model of an automotive grade SiC MOSFET using Particle Swarm Optimization algorithm. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 381–386. [Google Scholar]
- Datasheet Vishay SiHA15N80AEF. Available online: https://www.vishay.com/docs/92411/siha15n80aef.pdf (accessed on 18 March 2022).
- Datasheet STMicroelectronics SCTL35N65G2V. Available online: https://www.st.com/resource/en/datasheet/sctl35n65g2v.pdf (accessed on 18 March 2022).
- Datasheet GaNSystem GS66508B. Available online: https://gansystems.com/wp-content/uploads/2020/04/GS66508B-DS-Rev-200402.pdf (accessed on 18 March 2022).
- Datasheet Vishay SiNB22N65E. Available online: https://www.vishay.com/docs/91538/sihb22n65e.pdf (accessed on 18 March 2022).
- Datasheet Infineon IMZA65R107M1H. Available online: https://www.infineon.com/dgdl/Infineon-IMZA65R107M1H-DataSheet-v02_00-EN.pdf?fileId=5546d4626f229553016f859930890460 (accessed on 18 March 2022).
- Datasheet GANPOWER GPI65008DF56. Available online: http://iganpower.com/wp-content/uploads/2020/08/GPI65008DF56_V2.0.pdf (accessed on 18 March 2022).
- Practical Considerations of Trench MOSFET Stability When Operating in Linear Mode. Available online: https://www.onsemi.com/pub/collateral/an-4161.pdf (accessed on 18 November 2021).
- Sedra, A.S.; Smith, K.C. Microelectronic Circuits; Holt, Rinehart and Winston: New York, NY, USA, 1982. [Google Scholar]
- Wang, G.; Mookken, J.; Rice, J.; Schupbach, M. Dynamic and static behavior of packaged silicon carbide MOSFETs in paralleled applications. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1478–1483. [Google Scholar] [CrossRef]
- Datasheet Toshiba TK22V65X5. Available online: https://toshiba.semicon-storage.com/info/docget.jsp?did=54459&prodName=TK22V65X5 (accessed on 18 March 2022).
- Datasheet Microsemi MSC015SMA070B. Available online: https://www.microsemi.com/document-portal/doc_download/1244454-msc015sma070b-datasheet (accessed on 18 March 2022).
- Datasheet Nexperia GAN041-650WSB. Available online: https://assets.nexperia.com/documents/data-sheet/GAN041-650WSB.pdf (accessed on 18 March 2022).
- Datasheet Onsemi NTB1070N65S3. Available online: https://www.onsemi.cn/pdf/datasheet/ntbl070n65s3-d.pdf (accessed on 18 March 2022).
- Datasheet GaNSystem GS-065-004-1-L-DS. Available online: https://gansystems.com/wp-content/uploads/2021/04/GS-065-004-1-L-DS-Rev-210322.pdf (accessed on 18 March 2022).
- Callanan, R.; Rice, J.; Palmour, J. Third quadrant behavior of SiC MOSFETs. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1250–1253. [Google Scholar] [CrossRef]
- Elferich, R.; Lopez, T. Impact of gate voltage bias on reverse recovery losses of power MOSFETs. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, 2006. APEC’06, Dallas, TX, USA, 19–23 March 2006; p. 6. [Google Scholar] [CrossRef]
- Datasheet STMicroelectronics SCTH35N65G2V. Available online: https://www.st.com/resource/en/datasheet/scth35n65g2v-7.pdf (accessed on 18 March 2022).
- Datasheet Infineon IGO60R070D1. Available online: https://www.infineon.com/dgdl/Infineon-IGO60R070D1-DataSheet-v02_11-EN.pdf?fileId=5546d46265f064ff016685f053216514 (accessed on 18 March 2022).
- Sørensen, C.; Fogsgaard, M.L.; Christiansen, M.N.; Graungaard, M.K.; Nørgaard, J.B.; Uhrenfeldt, C.; Trintis, I. Conduction, reverse conduction and switching characteristics of GaN E-HEMT. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Reiner, R.; Waltereit, P.; Weiss, B.; Quay, R.; Ambacher, O. Investigation of GaN-HEMTs in Reverse Conduction. In Proceedings of the PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 16–18 May 2017; pp. 1–8. [Google Scholar]
- Datasheet Toshiba TK14G65W. Available online: https://toshiba.semicon-storage.com/info/docget.jsp?did=14506&prodName=TK14G65W (accessed on 18 March 2022).
- Datasheet GANPOWER GPI65060DFN. Available online: http://iganpower.com/wp-content/uploads/2019/11/GPI65060DFN.pdf (accessed on 18 March 2022).
- Datasheet Transphormusa TP65H035WS. Available online: https://www.transphormusa.com/en/document/datasheet-tp65h035ws-650v-gan-fet/ (accessed on 18 March 2022).
- Stefanskyi, A.; Starzak, Ł.; Napieralski, A. Review of commercial SiC MOSFET models: Topologies and equations. In Proceedings of the 2017 MIXDES-24th International Conference Mixed Design of Integrated Circuits and Systems, Bydgoszcz, Poland, 22–24 June 2017; pp. 484–487. [Google Scholar] [CrossRef]
- Shichman, H.; Hodges, D.A. Modeling and simulation of insulated-gate field-effect transistor switching circuits. IEEE J. Solid-State Circuits 1968, 3, 285–289. [Google Scholar] [CrossRef] [Green Version]
- Pspice A/D Reference Guide, version 16.5; Cadence Design System: Portland, OR, USA, 2011.
- Shah, K.; Shenai, K. Simple and Accurate Circuit Simulation Model for Gallium Nitride Power Transistors. IEEE Trans. Electron Devices 2012, 59, 2735–2741. [Google Scholar] [CrossRef]
- Jadli, U.; Mohd-Yasin, F.; Moghadam, H.A.; Pande, P.; Chaturvedi, M.; Dimitrijev, S. Modeling Power GaN-HEMTs Using Standard MOSFET Equations and Parameters in SPICE. Electronics 2021, 10, 130. [Google Scholar] [CrossRef]
- Datasheet GaNSystem GS66504B. Available online: https://gansystems.com/wp-content/uploads/2020/04/GS66504B-DS-Rev-200402.pdf (accessed on 21 March 2022).
- Datasheet GaNSystem GS66506T. Available online: https://gansystems.com/wp-content/uploads/2020/04/GS66506T-DS-Rev-200402.pdf (accessed on 21 March 2022).
- Stefanskyi, A.; Starzak, Ł.; Napieralski, A. Review of commercial SiC MOSFET models: Validity and accuracy. In Proceedings of the 2017 MIXDES-24th International Conference Mixed Design of Integrated Circuits and Systems, Bydgoszcz, Poland, 22–24 June 2017; pp. 488–493. [Google Scholar] [CrossRef]
- Yang, P.; Ming, W.; Liang, J. A Step-by-step Modelling Approach for SiC Half-bridge Modules Considering Temperature Characteristics. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 2827–2834. [Google Scholar] [CrossRef]
- Lima, A.A.; Torres, L.M.; Cheralathan, M.; Blawid, S. A modified Shichman-Hodges model for OTFTs usable in the Quite Universal Circuit Simulator. ICCEEg 2016, 1, 44–48. [Google Scholar]
- Enz, C.C.; Krummenacher, F.; Vittoz, E.A. (1995) An Analytical MOS Transistor Model Valid in All Regions of Operation and Dedicated to Low-Voltage and Low-Current Applications. Analog. Integr. Circuits Signal Processing 1995, 8, 83–114. [Google Scholar] [CrossRef]
- Pushpakaran, B.N.; Bayne, S.B.; Wang, G.; Mookken, J. Fast and accurate electro-thermal behavioral model of a commercial SiC 1200V, 80 mΩ power MOSFET. In Proceedings of the 2015 IEEE Pulsed Power Conference (PPC), Austin, TX, USA, 31 May–4 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Angelov, I.; Zirath, H.; Rosman, N. A new empirical nonlinear model for HEMT and MESFET devices. IEEE Trans. Microw. Theory Tech. 1992, 40, 2258–2266. [Google Scholar] [CrossRef] [Green Version]
- Hsu, F.-J.; Hung, C.-C.; Chu, K.-T.; Lee, L.-S.; Lee, C.-Y. A Dynamic Switching Response Improved SPICE Model for SiC MOSFET with Non-linear Parasitic Capacitance. In Proceedings of the 2020 IEEE Workshop on Wide Bandgap Power Devices and Applications in Asia (WiPDA Asia), Suita, Japan, 23–25 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Hsu, F.J.; Yen, C.T.; Hung, C.C.; Lee, C.Y.; Lee, L.S.; Chu, K.T.; Li, Y.F. High accuracy large-signal SPICE model for silicon carbide MOSFET. In Proceedings of the 2018 IEEE 30th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Chicago, IL, USA, 13–17 May 2018; pp. 403–406. [Google Scholar] [CrossRef]
- Sakairi, H.; Yanagi, T.; Otake, H.; Kuroda, N.; Tanigawa, H. Measurement Methodology for Accurate Modeling of SiC MOSFET Switching Behavior Over Wide Voltage and Current Ranges. IEEE Trans. Power Electron. 2018, 33, 7314–7325. [Google Scholar] [CrossRef]
- Curtice, W.R.; Ettenberg, M. A Nonlinear GaAs FET Model for Use in the Design of Output Circuits for Power Amplifiers. IEEE Trans. Microw. Theory Tech. 1985, 33, 1383–1394. [Google Scholar] [CrossRef]
- Endruschat, A.; Novak, C.; Gerstner, H.; Heckel, T.; Joffe, C.; März, M. A Universal SPICE Field-Effect Transistor Model Applied on SiC and GaN Transistors. IEEE Trans. Power Electron. 2019, 34, 9131–9145. [Google Scholar] [CrossRef]
- Stefanskyi, A.; Starzak, L.; Napieralski, A. Universal Behavioural Model for SiC Power MOSFETs under Forward Bias. In Proceedings of the 2018 25th International Conference Mixed Design of Integrated Circuits and System (MIXDES), Gdynia, Poland, 21–23 June 2018; pp. 343–348. [Google Scholar] [CrossRef]
- Mukunoki, Y.; Konno, K.; Matsuo, T.; Horiguchi, T.; Nishizawa, A.; Kuzumoto, M.; Hagiwara, M.; Akagi, H. An Improved Compact Model for a Silicon-Carbide MOSFET and Its Application to Accurate Circuit Simulation. IEEE Trans. Power Electron. 2018, 33, 9834–9842. [Google Scholar] [CrossRef]
- Bottaro, E.; del Pizzo, A.; di Noia, L.P.; Nardo, D.; Rizzo, S.A.; Scuto, A. High Frequency Model of a SiC based DC-DC converter for on Board Electric Systems. In Proceedings of the 2021 AEIT International Conference on Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Torino, Italy, 17–19 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Bottaro, E.; Cacciato, M.; Raffa, A.; Rizzo, S.A.; Salerno, N.; Veneziano, P.P. Development of a SPICE modelling strategy for power devices in GaN technology. In Proceedings of the IECON 2021-47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Li, H.; Zhao, X.; Sun, K.; Zhao, Z.; Cao, G.; Zheng, T.Q. A Non-Segmented PSpice Model of SiC mosfet With Temperature-Dependent Parameters. IEEE Trans. Power Electron. 2019, 34, 4603–4612. [Google Scholar] [CrossRef]
- Sun, K.; Wu, H.; Lu, J.; Xing, Y.; Huang, L. Improved Modeling of Medium Voltage SiC MOSFET Within Wide Temperature Range. IEEE Trans. Power Electron. 2014, 29, 2229–2237. [Google Scholar] [CrossRef]
- Pratap, R.; Singh, R.K.; Agarwal, V. SPICE model development for SiC power MOSFET. In Proceedings of the 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; pp. 1–5. [Google Scholar] [CrossRef]
- D’Alessandro, V.; Magnani, A.; Riccio, M.; Breglio, G.; Irace, A.; Rinaldi, N.; Castellazzi, A. SPICE modeling and dynamic electrothermal simulation of SiC power MOSFETs. In Proceedings of the 2014 IEEE 26th International Symposium on Power Semiconductor Devices & IC’s (ISPSD), Waikoloa, HI, USA, 15–19 June 2014; pp. 285–288. [Google Scholar] [CrossRef]
- Xu, Y.; Ho, C.N.M.; Ghosh, A.; Muthumuni, D. A Datasheet-Based Behavioral Model of SiC MOSFET for Power Loss Prediction in Electromagnetic Transient Simulation. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 521–526. [Google Scholar] [CrossRef]
- Yeo, H.L.; Tseng, K.J. Modelling technique utilizing modified sigmoid functions for describing power transistor device capacitances applied on GaN HEMT and silicon MOSFET. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3107–3114. [Google Scholar] [CrossRef]
- Datasheet Infineon IPP60R099C6. Available online: https://www.infineon.com/dgdl/Infineon-IPP60R099C6-DS-v02_03-EN.pdf?fileId=db3a30432313ff5e012394c84a4c068e (accessed on 21 March 2022).
- Datasheet EPC EPC2021. Available online: https://epc-co.com/epc/Portals/0/epc/documents/datasheets/EPC2001_datasheet.pdf (accessed on 21 March 2022).
- Duan, Z.; Fan, T.; Wen, X.; Zhang, D. Improved SiC Power MOSFET Model Considering Nonlinear Junction Capacitances. IEEE Trans. Power Electron. 2018, 33, 2509–2517. [Google Scholar] [CrossRef]
- Alhoussein, A.; Alawieh, H.; Riah, Z.; Azzouz, Y. A New SiC Power MOSFET Model with a Parameter Optimization Procedure. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.11. [Google Scholar] [CrossRef]
- Bargieł, K.; Bisewski, D.; Zarębski, J. Modelling of Dynamic Properties of Silicon Carbide Junction Field-Effect Transistors (JFETs). Energies 2020, 13, 187. [Google Scholar] [CrossRef] [Green Version]
- Riccio, M.; d’Alessandro, V.; Romano, G.; Maresca, L.; Breglio, G.; Irace, A. A Temperature-Dependent SPICE Model of SiC Power MOSFETs for Within and Out-of-SOA Simulations. IEEE Trans. Power Electron. 2018, 33, 8020–8029. [Google Scholar] [CrossRef]
- Sochor, P.; Huerner, A.; Elpelt, R. A Fast and Accurate SiC MOSFET Compact Model for Virtual Prototyping of Power Electronic Circuits. In Proceedings of the PCIM Europe 2019; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 7–9 May 2019; pp. 1–8. [Google Scholar]

| Model | GMOS | VTH | RVAR | Third Quadrant | Capacitance |
|---|---|---|---|---|---|
| [58] | ● | - | x | ● | ✓ |
| [62] | ✓ | - | - | - | ● |
| [66] | ● | - | - | ✓ | ● |
| [67] | ✓ | - | - | - | - |
| [69] | ● | - | - | ● | ✓ |
| [71] | ✓ | - | - | - | - |
| [72] | ✓ | - | ● | - | ● |
| [73] | ✓ | - | - | - | - |
| [75] | ✓ | - | - | - | - |
| [76] | ● | - | - | - | - |
| [77] | ✓ | - | - | - | - |
| [78] | ✓ | - | - | - | - |
| [80] | ● | - | - | ● | - |
| [81] | ✓ | x | x | - | - |
| [82] | ✓ | x | - | - | - |
| [83] | - | x | x | - | - |
| [84] | - | - | ✓ | - | - |
| [85] | - | - | - | ✓ | ✓ |
| [88] | - | - | - | - | ● |
| [89] | - | - | - | - | ● |
| [90] | - | - | - | - | ✓ |
| [91] | - | - | - | - | ✓ |
| [92] | - | - | - | - | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bottaro, E.; Rizzo, S.A.; Salerno, N. Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review. Energies 2022, 15, 3415. https://doi.org/10.3390/en15093415
Bottaro E, Rizzo SA, Salerno N. Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review. Energies. 2022; 15(9):3415. https://doi.org/10.3390/en15093415
Chicago/Turabian StyleBottaro, Enrico, Santi Agatino Rizzo, and Nunzio Salerno. 2022. "Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review" Energies 15, no. 9: 3415. https://doi.org/10.3390/en15093415
APA StyleBottaro, E., Rizzo, S. A., & Salerno, N. (2022). Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review. Energies, 15(9), 3415. https://doi.org/10.3390/en15093415