Competition of Magnetic Anisotropies in Permalloy Antidot Lattices
Abstract
:1. Introduction
2. Materials and Methods
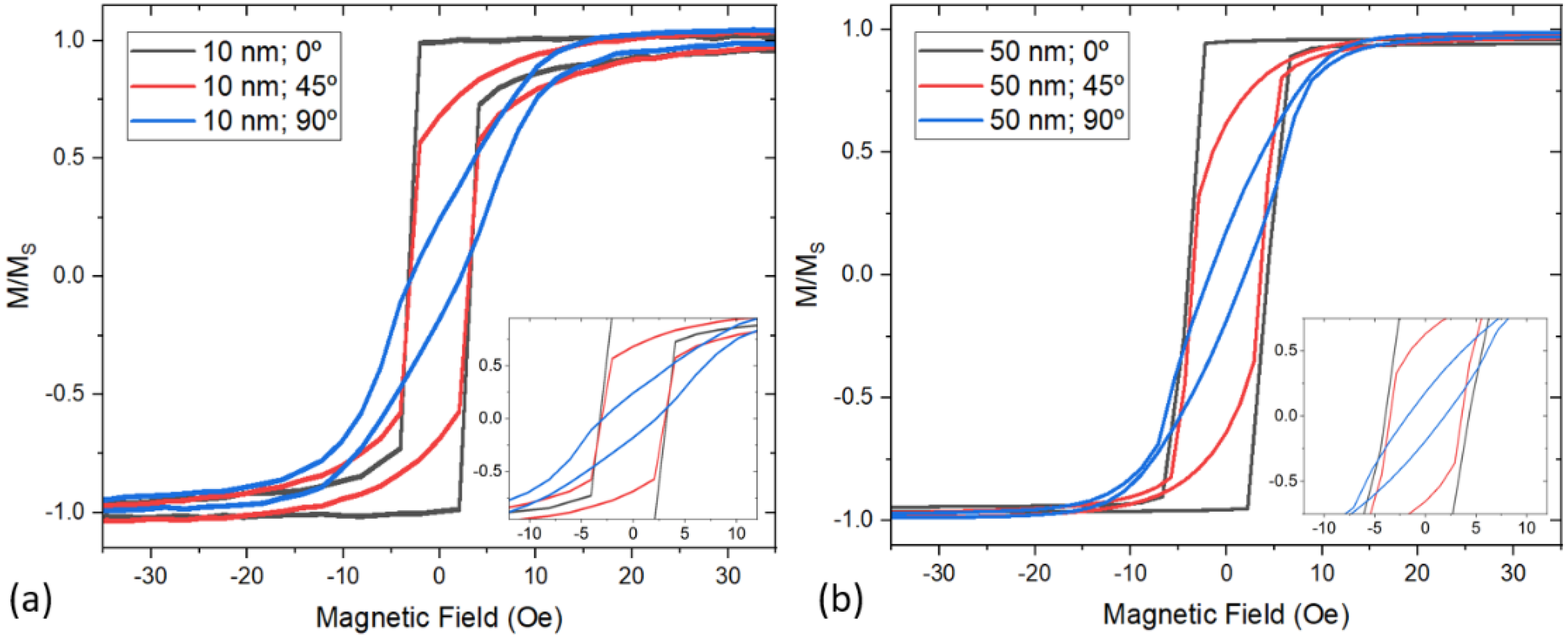
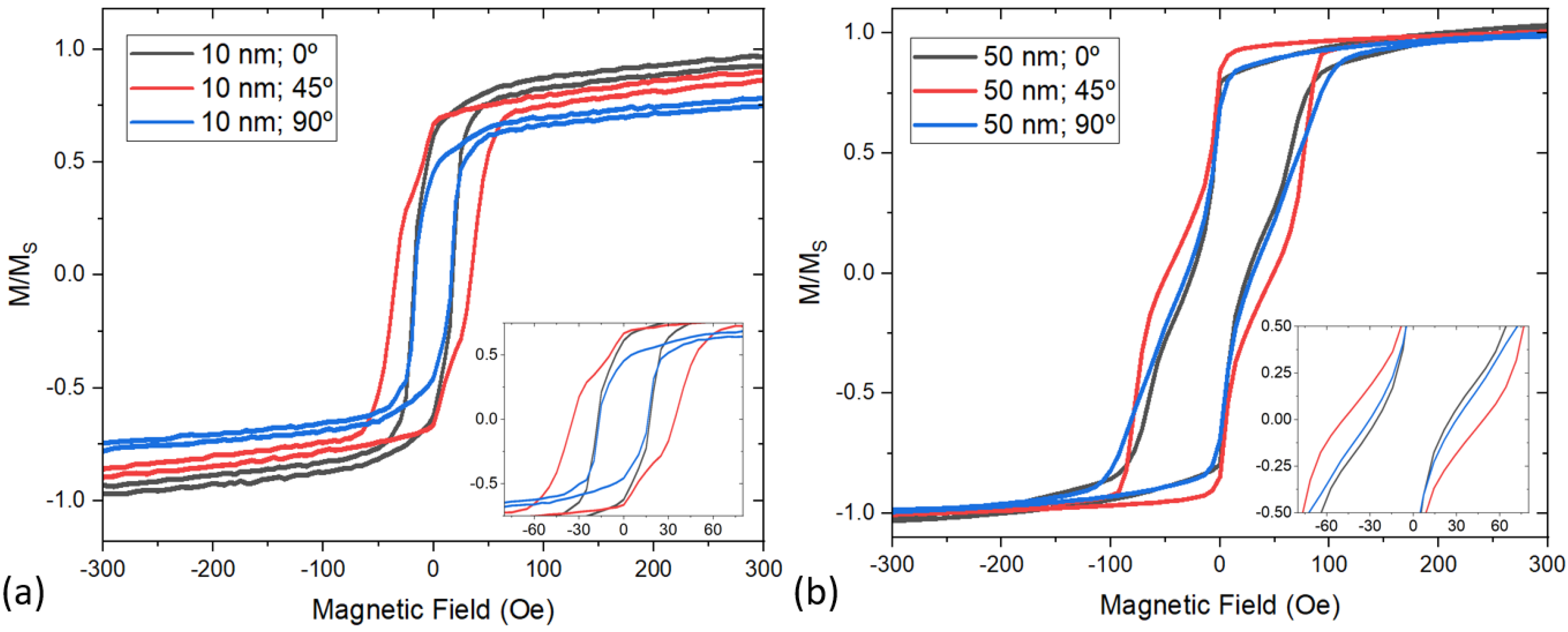
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, Z.; Zhang, Z.; Wu, W.; Ji, X.; Sun, S.; Jiang, Y.; Tan, C.C.; Yang, L.; Chong, C.T.; Qiu, C.W.; et al. Floating solid-state thin films with dynamic structural colour. Nat. Nanotechnol. 2021, 16, 795–801. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wei, C.; Feng, Y.; Cao, H.; Li, W.; Cao, Y.; Guan, B.O.; Tsukamoto, A.; Kirilyuk, A.; Kimel, A.V.; et al. Dual-shot dynamics and ultimate frequency of all-optical magnetic recording on GdFeCo. Light Sci. Appl. 2021, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Komlev, A.S.; Karpenkov, D.Y.; Kiselev, D.A.; Ilina, T.S.; Chirkova, A.; Gimaev, R.R.; Usami, T.; Taniyama, T.; Zverev, V.I.; Perov, N.S. Ferromagnetic phase nucleation and its growth evolution in FeRh thin films. J. Alloys Compd. 2021, 874, 159924. [Google Scholar] [CrossRef]
- Alexandrakis, V.; Rodríguez-Aseguinolaza, I.; Anastasakos-Paraskevopoulos, D.; Barandiarán, J.M.; Chernenko, V.; Porro, J.M. Spontaneous Zero-Field Cooling Exchange Bias in Ni-Co-Mn-Sn Metamagnetic Heusler Sputtered Film. Nanomaterials 2021, 11, 2188. [Google Scholar] [CrossRef] [PubMed]
- Chumak, O.M.; Pacewicz, A.; Lynnyk, A.; Salski, B.; Yamamoto, T.; Seki, T.; Domagala, J.Z.; Głowiński, H.; Takanashi, K.; Baczewski, L.T.; et al. Magnetoelastic interactions and magnetic damping in Co2Fe0.4Mn0.6Si and Co2FeGa0.5Ge0.5 Heusler alloys thin films for spintronic applications. Sci. Rep. 2021, 11, 7608. [Google Scholar] [CrossRef]
- Wu, H.; Chen, A.; Zhang, P.; He, H.; Nance, J.; Guo, C.; Sasaki, J.; Shirokura, T.; Hai, P.N.; Fang, B.; et al. Magnetic memory driven by topological insulators. Nat. Commun. 2021, 12, 6251. [Google Scholar] [CrossRef] [PubMed]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Porro, J.M.; Morley, S.A.; Venero, D.A.; Macêdo, R.; Rosamond, M.C.; Linfield, E.H.; Stamps, R.L.; Marrows, C.H.; Langridge, S. Magnetization dynamics of weakly interacting sub-100 nm square artificial spin ices. Sci. Rep. 2019, 9, 19967. [Google Scholar] [CrossRef]
- Morley, S.A.; Porro, J.M.; Hrabec, A.; Rosamond, M.C.; Venero, D.A.; Linfield, E.H.; Burnell, G.; Im, M.Y.; Fischer, P.; Langridge, S.; et al. Thermally and field-driven mobility of emergent magnetic charges in square artificial spin ice. Sci. Rep. 2019, 9, 15989. [Google Scholar] [CrossRef] [Green Version]
- Porro, J.M.; Berger, A.; Grimsditch, M.; Metlushko, V.; Ilic, B.; Vavassori, P. Effect of spatially asymmetric dipolar interactions in the magnetization reversal of closely spaced ferromagnetic nanoisland arrays. J. Appl. Phys. 2012, 111, 07B913. [Google Scholar] [CrossRef]
- Wang, T.Y.; Han, H.S.; Su, C.; Li, Q.; Yang, M.; Chao, W.; Zhang, X.; Hwang, C.; Zettl, A.; Im, M.Y.; et al. Magnetic anisotropy in permalloy antidot square lattice. J. Magn. Magn. Mater. 2022, 544, 168680. [Google Scholar] [CrossRef]
- Kaidatzis, A.; del Real, R.P.; Alvaro, R.; Niarchos, D.; Vázquez, M.; García-Martín, J.M. Nanopatterned hard/soft bilayer magnetic antidot arrays with long-range periodicity. J. Magn. Magn. Mater. 2020, 498, 166142. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Martínez-Goyeneche, L.; Álvarez-Alonso, P.; Fernández, A. Enhancement the perpendicular magnetic anisotropy of nanopatterned hard/soft bilayer magnetic antidot arrays for spintronic application. Nanotechnology 2020, 31, 485708. [Google Scholar] [CrossRef] [PubMed]
- Heyderman, L.J.; Nolting, F.; Backes, D.; Czekaj, S.; Lopez-Diaz, L.; Kläui, M.; Rüdiger, U.; Vaz, C.A.F.; Bland, J.A.C.; Matelon, R.J.; et al. Magnetization reversal in cobalt antidot arrays. Phys. Rev. B-Condens. Matter Mater. Phys. 2006, 73, 214429. [Google Scholar] [CrossRef] [Green Version]
- Tse, D.H.Y.; Steinmuller, S.J.; Trypiniotis, T.; Anderson, D.; Jones, G.A.C.; Bland, J.A.C.; Barnes, C.H.W. Static and dynamic magnetic properties of Ni80 Fe20 square antidot arrays. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 79, 054426. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.T.; Shams, N.N.; Lai, C.H.; Fidler, J.; Suess, D. Co/Pt perpendicular antidot arrays with engineered feature size and magnetic properties fabricated on anodic aluminum oxide templates. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 81, 014418. [Google Scholar] [CrossRef]
- Liu, X.M.; Ding, J.; Adeyeye, A.O. Magnetization dynamics and reversal mechanism of Fe filled Ni80Fe20 antidot nanostructures. Appl. Phys. Lett. 2012, 100, 242411. [Google Scholar] [CrossRef]
- Krupinski, M.; Sobieszczyk, P.; Zieliński, P.; Marszałek, M. Magnetic reversal in perpendicularly magnetized antidot arrays with intrinsic and extrinsic defects. Sci. Rep. 2019, 9, 13276. [Google Scholar] [CrossRef] [Green Version]
- Salaheldeen, M.; Méndez, M.; Vega, V.; Fernández, A.; Prida, V.M. Tuning Nanohole Sizes in Ni Hexagonal Antidot Arrays: Large Perpendicular Magnetic Anisotropy for Spintronic Applications. ACS Appl. Nano Mater. 2019, 2, 1866–1875. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Vega, V.; Ibabe, A.; Jaafar, M.; Asenjo, A.; Fernandez, A.; Prida, V.M. Tailoring of perpendicular magnetic anisotropy in Dy13Fe87 thin films with hexagonal antidot lattice nanostructure. Nanomaterials 2018, 8, 227. [Google Scholar] [CrossRef] [Green Version]
- Béron, F.; Kaidatzis, A.; Velo, M.F.; Arzuza, L.C.C.; Palmero, E.M.; del Real, R.P.; Niarchos, D.; Pirota, K.R.; García-Martín, J.M. Nanometer Scale Hard/Soft Bilayer Magnetic Antidots. Nanoscale Res. Lett. 2016, 11, 86. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Challab, N.; Faurie, D.; Haboussi, M.; Adeyeye, A.O.; Zighem, F. Differentiated Strain-Control of Localized Magnetic Modes in Antidot Arrays. ACS Appl. Mater. Interfaces 2021, 13, 29906–29915. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Mondal, S.; Zelent, M.; Szwierz, R.; Pal, S.; Hellwig, O.; Krawczyk, M.; Barman, A. Edge localization of spin waves in antidot multilayers with perpendicular magnetic anisotropy. Phys. Rev. B 2020, 101, 014403. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, S.; Barman, S.; Otani, Y.C.; Barman, A. Controlled evolution of spin waves in unconventional defective honeycomb antidot lattices. J. Magn. Magn. Mater. 2019, 489, 165408. [Google Scholar] [CrossRef]
- Kuanr, B.K.; Veerakumar, V.; Camley, R.E.; Celinski, Z. Permalloy (NiFe) nanometer square-antidot arrays: Dynamic modes and use as a monolithic microwave band-pass filter. J. Magn. Magn. Mater. 2019, 484, 272–278. [Google Scholar] [CrossRef]
- Gubbiotti, G.; Montoncello, F.; Tacchi, S.; Madami, M.; Carlotti, G.; Giovannini, L.; Ding, J.; Adeyeye, A.O. Angle-resolved spin wave band diagrams of square antidot lattices studied by Brillouin light scattering. Appl. Phys. Lett. 2015, 106, 262406. [Google Scholar] [CrossRef]
- Kumar, D.; Sabareesan, P.; Wang, W.; Fangohr, H.; Barman, A. Effect of hole shape on spin-wave band structure in one-dimensional magnonic antidot waveguide. J. Appl. Phys. 2013, 114, 023910. [Google Scholar] [CrossRef] [Green Version]
- Mandal, R.; Saha, S.; Kumar, D.; Barman, S.; Pal, S.; Das, K.; Raychaudhuri, A.K.; Fukuma, Y.; Otani, Y.; Barman, A. Optically induced tunable magnetization dynamics in nanoscale Co antidot lattices. ACS Nano 2012, 6, 3397–3403. [Google Scholar] [CrossRef]
- Ding, J.; Tripathy, D.; Adeyeye, A.O. Dynamic response of antidot nanostructures with alternating hole diameters. EPL 2012, 98, 16004. [Google Scholar] [CrossRef]
- Duerr, G.; Madami, M.; Neusser, S.; Tacchi, S.; Gubbiotti, G.; Carlotti, G.; Grundler, D. Spatial control of spin-wave modes in Ni80Fe20 antidot lattices by embedded Co nanodisks. Appl. Phys. Lett. 2011, 99, 202502. [Google Scholar] [CrossRef] [Green Version]
- Ulrichs, H.; Lenk, B.; Münzenberg, M. Magnonic spin-wave modes in CoFeB antidot lattices. Appl. Phys. Lett. 2010, 97, 092506. [Google Scholar] [CrossRef] [Green Version]
- Neusser, S.; Botters, B.; Becherer, M.; Schmitt-Landsiedel, D.; Grundler, D. Spin-wave localization between nearest and next-nearest neighboring holes in an antidot lattice. Appl. Phys. Lett. 2008, 93, 122501. [Google Scholar] [CrossRef]
- Martyshkin, A.A.; Odintsov, S.A.; Gubanova, Y.A.; Beginin, E.N.; Sheshukova, S.E.; Nikitov, S.A.; Sadovnikov, A.V. Controlled Spin-Wave Transport in a Magnon-Crystal Structure with a One-Dimensional Array of Holes. JETP Lett. 2019, 110, 533–539. [Google Scholar] [CrossRef]
- Feilhauer, J.; Saha, S.; Tobik, J.; Zelent, M.; Heyderman, L.J.; Mruczkiewicz, M. Controlled motion of skyrmions in a magnetic antidot lattice. Phys. Rev. B 2020, 102, 184425. [Google Scholar] [CrossRef]
- Abbas, S.K.; Saleem, M.; Naseem, S.; Riaz, S.; Atiq, S. Synthesis of Ni80Fe20 permalloy antidots for high storage ferroelectric memories. Mater. Lett. 2020, 271, 127852. [Google Scholar] [CrossRef]
- Silva, A.S.; Hierro-Rodriguez, A.; Bunyaev, S.A.; Kakazei, G.N.; Dobrovolskiy, O.V.; Redondo, C.; Morales, R.; Crespo, H.; Navas, D. Magnetic properties of permalloy antidot array fabricated by interference lithography. AIP Adv. 2019, 9, 035136. [Google Scholar] [CrossRef] [Green Version]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef] [Green Version]
- Abo, G.S.; Hong, Y.K.; Park, J.; Lee, J.; Lee, W.; Choi, B.C. Definition of magnetic exchange length. IEEE Trans. Magn. 2013, 49, 4937–4939. [Google Scholar] [CrossRef]
- Rodriguez, A.; Echeverría, M.; Ellman, M.; Perez, N.; Verevkin, Y.K.; Peng, C.S.; Berthou, T.; Wang, Z.; Ayerdi, I.; Savall, J.; et al. Laser interference lithography for nanoscale structuring of materials: From laboratory to industry. Microelectron. Eng. 2009, 86, 937–940. [Google Scholar] [CrossRef]
- Goto, M.; Tange, H.; Kamimori, T. Thickness dependence of field induced uniaxial anisotropy in 80-permalloy films. J. Magn. Magn. Mater. 1986, 62, 251–255. [Google Scholar] [CrossRef]
- Tannous, C.; Gieraltowski, J. The Stoner-Wohlfarth model of ferromagnetism. Eur. J. Phys. 2008, 29, 475. [Google Scholar] [CrossRef]
- Wang, C.C.; Adeyeye, A.O.; Singh, N. Magnetic antidot nanostructures: Effect of lattice geometry. Nanotechnology 2006, 17, 1629–1636. [Google Scholar] [CrossRef] [PubMed]
- Saavedra, E.; Corona, R.M.; Vidal-Silva, N.; Palma, J.L.; Altbir, D.; Escrig, J. Dynamic and static properties of stadium-shaped antidot arrays. Sci. Rep. 2020, 10, 20024. [Google Scholar] [CrossRef] [PubMed]
- Tripathy, D.; Vavassori, P.; Porro, J.M.; Adeyeye, A.O.; Singh, N. Magnetization reversal and anisotropic magnetoresistance behavior in bicomponent antidot nanostructures. Appl. Phys. Lett. 2010, 97, 42512. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porro, J.M.; Villar, A.; Redondo, C.; Río-López, N.A.; Lasheras, A.; Salazar, D.; Morales, R.; Fernández-Martín, E. Competition of Magnetic Anisotropies in Permalloy Antidot Lattices. Magnetochemistry 2022, 8, 55. https://doi.org/10.3390/magnetochemistry8050055
Porro JM, Villar A, Redondo C, Río-López NA, Lasheras A, Salazar D, Morales R, Fernández-Martín E. Competition of Magnetic Anisotropies in Permalloy Antidot Lattices. Magnetochemistry. 2022; 8(5):55. https://doi.org/10.3390/magnetochemistry8050055
Chicago/Turabian StylePorro, Jose M., Aritz Villar, Carolina Redondo, Natalia A. Río-López, Andoni Lasheras, Daniel Salazar, Rafael Morales, and Eduardo Fernández-Martín. 2022. "Competition of Magnetic Anisotropies in Permalloy Antidot Lattices" Magnetochemistry 8, no. 5: 55. https://doi.org/10.3390/magnetochemistry8050055








