A molecular structure [
1] is a graph whose edges correspond to the bonds and vertices of the atoms. Such invariants and indices in graphs have gained increasing interest over time, since they allow scientists to make new classifications for the graphs being studied. One of its many examples is the
or quantitative structure–property relationship (see, for example [
2,
3,
4,
5]) levels of the alkanes (see [
6,
7]). This index was named after him as the Wiener index. Since the introduction of the Wiener index, around 200 other indices have been defined and studied, such as those presented by Wazzan et al. (see, for example, [
8,
9,
10]), Gutman (see, for example, [
11,
12]), and Çevik (see, for example, [
13,
14]). Some of these indices have been used indirectly or directly in the applications of chemistry, physics, or pharmacology. Since indices have been found to have many applications, many graph theorist still aim to find similar indices and their applications in graph theory. Among the successful attempts are the Sombor
and Omega indices
(see [
15,
16]) in which the coinvestigator has partaken in these graph invariants studies. Wazzan et al. in [
17] introduced two novel topological indices named the first and second locating indices, and in [
18] multiplicative locating indices are calculated for families of graphs. In addition, the
of hexane and its isomers is investigated by the locating indices. We show that locating indices have positive correlation with at least one property, have structural interpretation, preferably contradistinguish. They can also be generalizable to more advanced analogues, be elementary, not be established based on properties, not be trivially related to other descriptors, be possible to compute effectively, and be based on organizable structure. These reasons motivated us to introduce new versions of these indices, we called them first and second Hyper locating indices, Randić locating index and Sombor locating index. In 2013, Shirdel et al. [
19] introduced a new distance-based group of Zagreb indices named Hyper–Zagreb indices, as
and
The Randić index of a graph
introduced by Randić [
20] is the most important and widely applied, it is defined as
The Sombor index of a graph
, which is a novel vertex-degree-based molecular structure descriptor proposed by Gutman [
21] is defined as
We keep in mind the definition of first and second locating indices given in [
17], in order to grasp the importance of this paper. Since this paper is a continuation of our work in [
17,
22], let us recall the basic facts regarding these indices: let
be a connected graph with the vertex set
with at least two edges a
locating function of
denoted by
is a function
where
A is the set of all non-negative integers such that
, where
is the distance between the vertices
and
in
. The vector
is called the
locating vector corresponding to the vertex
, where
is the dot product of the vectors
and
and
is the sum of vectors
and
in the integers space
such that
is adjacent to
. For any vector
the magnitude of
is
In this paper we consider a connected graph
with an edge set
[has at least two edges] and vertex set
we introduce the following locating indices:
The topological indices with a high positive correlation factor play a crucial role in quantitative structure–property relationships
and quantitative structure–activity relationships
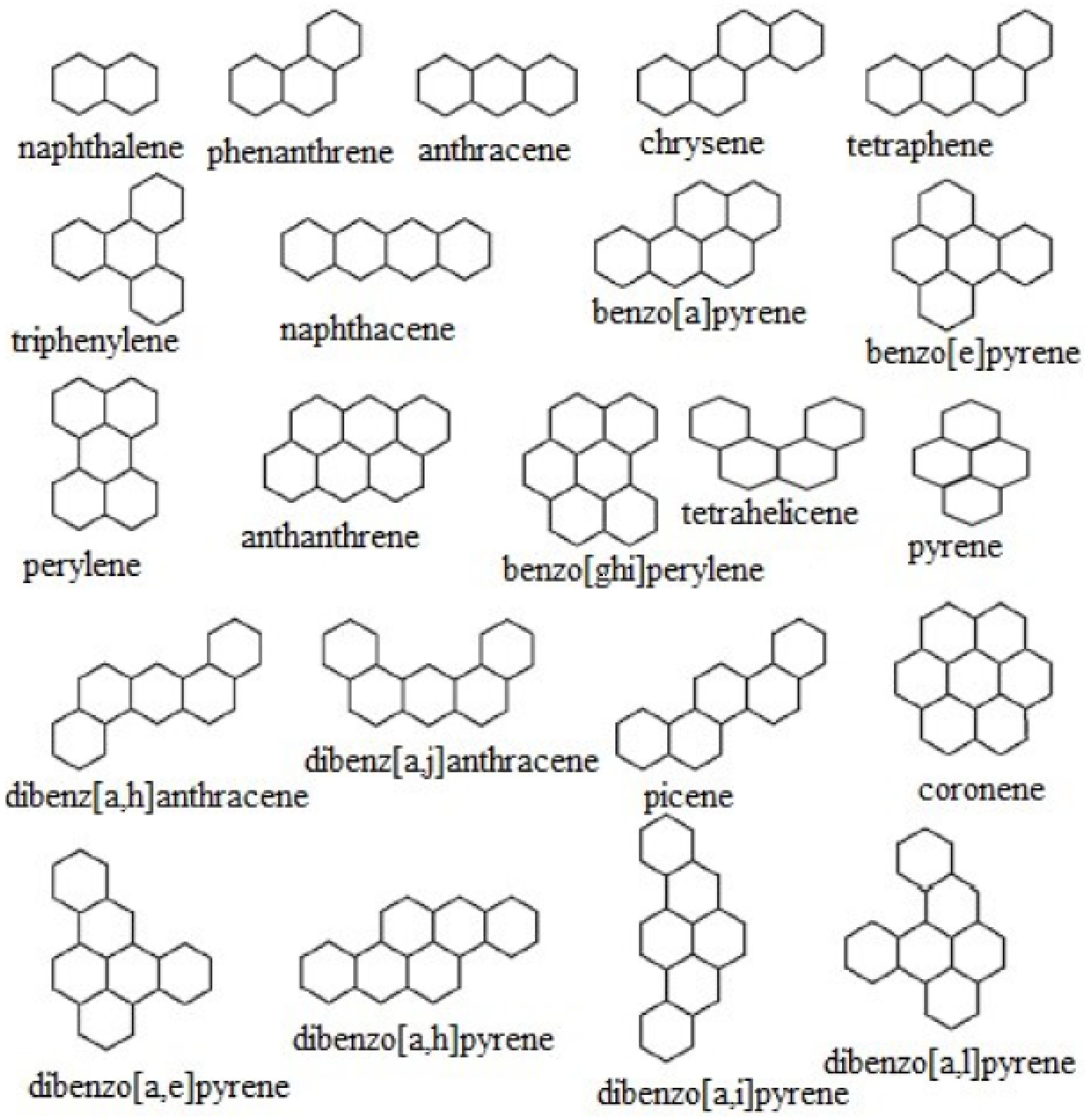
analysis. In order to predict the validity of these new versions of locating indices we consider one branch of Benzene which is the polycyclic aromatic hydrocarbons. For the two other kinds the linear and branched hydrocarbons, whose properties can also be described by these kind of indices, according to the result obtained in this report, we can predict the validities of the new version of locating indices in the other two kind of hydrocarbons. Hence, we leave this investigation for future work. Benzene (
is an organic chemical compound composed of six carbon atoms joined in a planar ring with one hydrogen atom attached to each ring. Benzene is classified as a hydrocarbon because it contains only hydrogen and carbon atoms. Benzene is a natural ingredient of crude oil and is one of the basic petrochemicals. It is described as an aromatic hydrocarbon due to the cyclic connected pi bonds between the carbon atoms. The abbreviation of it is
. Benzene is a colorless and highly flammable liquid. It is used as a precursor to the synthesis of more complex chemical structure, such as cumene and ethylbenzene. The toxicity of benzene limits its use in consumer items despite its popularity as a major industrial chemical [
23].
To test the predictive ability of these new indices, we discuss the linear regression analysis of 11 benzenoid hydrocarbons, which are used many times to approach the efficiency of any topological descriptor in quantitative structure property relationships. We inspect the following physicochemical properties: boiling point , molar entropy acentric factor , octanol–water partition coefficient complexity , and Kovats retention index