Computer Optimization of Biodegradable Nanoparticles Fabricated by Dispersion Polymerization
Abstract
:1. Introduction
2. Materials and Methods

| Standard Order | Run Order | A: Crosslinking Agent (mmol) | B: Initiator System (mmol) | C: Stabilizer (PEG-MMA) (mmol) | D: Macromonomer (mmol) | Response 1 (Particle Size: nm) | Response 2 (Percent Yield %) |
|---|---|---|---|---|---|---|---|
| 9 | 1 | 0.048 | 0.359 | 0.304 | 0.289 | 297.6 | 56.87 |
| 8 | 2 | 0.056 | 0.285 | 0.215 | 0.445 | 306.6 | 28.99 |
| 1 | 3 | 0.087 | 0.377 | 0.091 | 0.445 | 261.5 | 62.39 |
| 5 | 4 | 0.018 | 0.565 | 0.214 | 0.204 | 270.6 | 35.26 |
| 19 | 5 | 0.087 | 0.377 | 0.091 | 0.445 | 268.1 | 58.82 |
| 12 | 6 | 0.042 | 0.452 | 0.259 | 0.247 | 286.4 | 31.88 |
| 20 | 7 | 0.018 | 0.565 | 0.214 | 0.204 | 295.8 | 61.08 |
| 17 | 8 | 0.087 | 0.183 | 0.304 | 0.426 | 326.4 | 31.13 |
| 14 | 9 | 0.018 | 0.312 | 0.304 | 0.367 | 290.3 | 41.19 |
| 15 | 10 | 0.053 | 0.415 | 0.148 | 0.384 | 322.3 | 45.15 |
| 3 | 11 | 0.055 | 0.625 | 0.115 | 0.204 | 293.1 | 47.87 |
| 4 | 12 | 0.087 | 0.183 | 0.304 | 0.426 | 322.9 | 34.18 |
| 13 | 13 | 0.036 | 0.522 | 0.163 | 0.279 | 320.7 | 43.08 |
| 2 | 14 | 0.018 | 0.446 | 0.091 | 0.445 | 313.1 | 24.43 |
| 11 | 15 | 0.087 | 0.500 | 0.091 | 0.321 | 273.3 | 43.32 |
| 16 | 16 | 0.018 | 0.446 | 0.091 | 0.445 | 293.8 | 35.08 |
| 18 | 17 | 0.055 | 0.625 | 0.115 | 0.204 | 305.9 | 39.22 |
| 6 | 18 | 0.018 | 0.234 | 0.304 | 0.445 | 320.9 | 35.98 |
| 7 | 19 | 0.018 | 0.625 | 0.091 | 0.265 | 295.6 | 44.71 |
| 10 | 20 | 0.087 | 0.394 | 0.198 | 0.321 | 314.9 | 37.59 |
| Standard Order | Run Order | A: Crosslinking Agent (mmol) | B: Initiator System (mmol) | C: Stabilizer (PEG-MMA) (mmol) | D: Macromonomer (mmol) | Response 1 (Particle Size: nm) | Response 2 (Negative Zeta Potential: mV) |
|---|---|---|---|---|---|---|---|
| 9 | 1 | 0.018 | 0.358 | 0.422 | 0.203 | 691.5 | 14.1 |
| 11 | 2 | 0.038 | 0.298 | 0.449 | 0.215 | 131.4 | 36 |
| 20 | 3 | 0.021 | 0.480 | 0.255 | 0.244 | 675.9 | 20.5 |
| 19 | 4 | 0.027 | 0.332 | 0.401 | 0.240 | 378.3 | 31.1 |
| 25 | 5 | 0.027 | 0.411 | 0.311 | 0.251 | 328.3 | 15.3 |
| 2 | 6 | 0.016 | 0.499 | 0.305 | 0.180 | 653 | 29.7 |
| 6 | 7 | 0.033 | 0.379 | 0.397 | 0.191 | 148.4 | 31.7 |
| 17 | 8 | 0.034 | 0.502 | 0.237 | 0.227 | 228 | 28.2 |
| 5 | 9 | 0.024 | 0.512 | 0.279 | 0.185 | 235.6 | 27.4 |
| 7 | 10 | 0.034 | 0.438 | 0.334 | 0.194 | 130.8 | 22 |
| 18 | 11 | 0.034 | 0.502 | 0.237 | 0.227 | 224 | 27.7 |
| 14 | 12 | 0.019 | 0.475 | 0.287 | 0.219 | 749 | 23.1 |
| 21 | 13 | 0.038 | 0.407 | 0.308 | 0.247 | 181.3 | 15.5 |
| 27 | 14 | 0.045 | 0.356 | 0.342 | 0.257 | 130.8 | 36.6 |
| 29 | 15 | 0.023 | 0.364 | 0.350 | 0.263 | 687 | 20 |
| 10 | 16 | 0.018 | 0.566 | 0.213 | 0.204 | 635.5 | 21.4 |
| 28 | 17 | 0.022 | 0.451 | 0.269 | 0.258 | 603.6 | 29.2 |
| 23 | 18 | 0.032 | 0.345 | 0.373 | 0.249 | 255.1 | 25 |
| 8 | 19 | 0.035 | 0.556 | 0.209 | 0.201 | 131.6 | 0.05 |
| 30 | 20 | 0.037 | 0.389 | 0.293 | 0.281 | 241 | 0.04 |
| 24 | 21 | 0.027 | 0.411 | 0.311 | 0.251 | 372.3 | 17.4 |
| 1 | 22 | 0.024 | 0.462 | 0.347 | 0.167 | 242.7 | 32.4 |
| 26 | 23 | 0.044 | 0.442 | 0.262 | 0.252 | 152.6 | −0.11 |
| 13 | 24 | 0.019 | 0.475 | 0.287 | 0.219 | 550.5 | 0.07 |
| 4 | 25 | 0.024 | 0.512 | 0.279 | 0.185 | 224 | 35.8 |
| 12 | 26 | 0.024 | 0.366 | 0.392 | 0.218 | 390.7 | 33.9 |
| 16 | 27 | 0.020 | 0.388 | 0.368 | 0.224 | 703 | 0.04 |
| 22 | 28 | 0.038 | 0.407 | 0.308 | 0.247 | 263.1 | 0.04 |
| 15 | 29 | 0.019 | 0.304 | 0.457 | 0.220 | 788.6 | 0.01 |
| 3 | 30 | 0.021 | 0.410 | 0.384 | 0.185 | 325.1 | −0.08 |
3. Results
3.1. Data Analysis, Generation of Scheffe Polynomials from Data Analysis
Followed by Optimization
3.2. Poly-l-Lactide-Based Nanoparticles
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 6011.26 | 7 | 858.75 | 6.83 | 0.0020 | s |
| Linear mixture | 1431.12 | 3 | 477.04 | 3.79 | 0.0401 | s |
| AB | 693.79 | 1 | 693.79 | 5.52 | 0.0368 | s |
| AC | 2723.37 | 1 | 2723.37 | 21.65 | 0.0006 | s |
| BC | 694.88 | 1 | 694.88 | 5.52 | 0.0367 | s |
| CD | 1247.85 | 1 | 1247.85 | 9.92 | 0.0084 | s |
| Residual | 1509.25 | 12 | 125.77 | |||
| Lack of Fit | 895.66 | 7 | 127.95 | 1.04 | 0.4994 | ns |
| Pure Error | 613.59 | 5 | 122.72 | |||
| Cor Total | 7520.52 | 19 |


| Source | Sum of Squares | df | Mean Square | F-Value | p-Value (Prob > F) | |
|---|---|---|---|---|---|---|
| Model | 1163.07 | 5 | 232.61 | 2.98 | 0.0488 | s |
| Linear Mixture | 326.63 | 3 | 108.88 | 1.40 | 0.2854 | ns |
| AB | 508.70 | 1 | 508.70 | 6.52 | 0.0230 | s |
| AD | 822.41 | 1 | 822.41 | 10.54 | 0.0059 | s |
| Residual | 1092.30 | 14 | 78.02 | |||
| Lack of Fit | 653.82 | 9 | 72.65 | 0.83 | 0.6211 | ns |
| Pure Error | 438.48 | 5 | 87.70 | |||
| Cor Total | 2255.38 | 19 |


3.3. Poly-ɛ-Caprolactone-Based Nanoparticles
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value (Prob > F) | |
|---|---|---|---|---|---|---|
| Model | 1.98 | 4 | 0.49 | 126.80 | <0.0001 | s |
| Linear Mixture | 1.92 | 3 | 0.64 | 163.82 | <0.0001 | s |
| A2 | 0.061 | 1 | 0.061 | 15.71 | 0.0005 | s |
| Residual | 0.098 | 25 | 3.904e-003 | |||
| Lack of Fit | 0.074 | 20 | 3.691e-003 | 0.78 | 0.6921 | ns |
| Pure Error | 0.024 | 5 | 4.756e-003 | |||
| Cor Total | 2.08 | 29 |


| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value (Prob > F) | |
|---|---|---|---|---|---|---|
| Model | 43.01 | 4 | 10.75 | 2.87 | 0.0437 | s |
| Linear Mixture | 4.58 | 3 | 1.53 | 0.41 | 0.7487 | ns |
| AC | 38.43 | 1 | 38.43 | 10.27 | 0.0037 | s |
| Residual | 93.56 | 25 | 3.74 | |||
| Lack of Fit | 77.93 | 20 | 3.90 | 1.25 | 0.4389 | ns |
| Pure Error | 15.63 | 5 | 3.13 | |||
| Cor Total | 136.57 | 29 |


4. Discussion
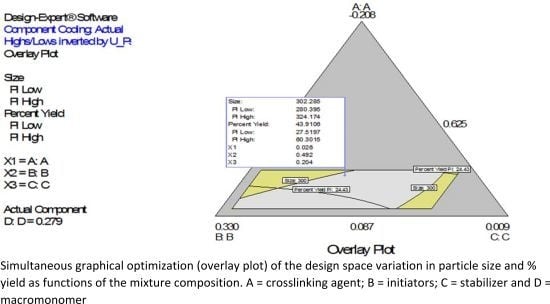
4.1. Simultaneous Numerical and Graphical Optimizations of Nanoparticle Size and Percent Yield for Poly-l-Lactide-Based Nanoparticles

4.2. Simultaneous Numerical and Graphical Optimizations of Nanoparticle Size and Zeta Potential for Poly-Ɛ-Caprolactone-Based Nanoparticles

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akala, E.O. Strategies for transmembrane passage of polymer-based nanostructures. In Polymer-Based Nanostructures: Medical Applications; Pavel, B., Harry, K., O’Brien, P., Harold, C., Eds.; Royal Society of Chemistry: Cambridge, UK, 2010; pp. 16–80. [Google Scholar]
- Akala, E.O.; Okunola, O. Novel stealth degradable nanoparticles prepared by dispersion polymerization for the delivery of bioactive agents Part I. Pharm. Ind. 2013, 75, 1191–1196. [Google Scholar]
- Ferrari, M. Cancer nanotechnology: Opportunities and challenges. Nat. Rev. Cancer 2005, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Shadabul, H.; Shadab, M.M.; Intekhab, A.; Jasjeet, K.S.; Javed, A. Nanostructure-based drug delivery systems for brain targeting. Drug Dev. Ind. Pharm. 2012, 38, 387–391. [Google Scholar]
- Hillareau, H.; Couvreur, P. Polymeric nanoparticles as drug carriers. In Polymers in Drug Delivery; Uchegbu, I.F., Schatzlein, A.G., Eds.; CRC (Taylor and Francis Group): Boca Raton, FL, USA, 2006; pp. 101–110. [Google Scholar]
- Kelkar, S.S.; Reineke, T.M. Theranostics: Combining imaging and therapy. Bioconjug. Chem. 2011, 22, 1879–1903. [Google Scholar] [CrossRef] [PubMed]
- Ogunwuyi, O.; Adesina, S.; Akala, E.O. d-Optimal mixture experimental design for stealth biodegradable crosslinked docetaxel-loaded poly-caprolactone nanoparticles manufactured by dispersion polymerization. Pharmazie 2015, 70, 165–176. [Google Scholar] [PubMed]
- Adesina, S.K.; Holly, A.; Kramer-Marek, G.; Capala, J.; Akala, E.O. Polylactide-based paclitaxel-loaded nanoparticles fabricated by dispersion polymerization: characterization, evaluation in cancer cell lines, and preliminary biodistribution studies. J. Pharm. Sci. 2014, 103, 2546–2555. [Google Scholar] [CrossRef] [PubMed]
- Bolshakov, O.I.; Akala, E.O. MS-monitored conjugation of poly(ethyleneglycol) monomethacrylate to RGD peptides. J. Appl. Polym. Sci. 2014, 131, 40385–40395. [Google Scholar]
- Adesina, S.K.; Wight, S.A.; Akala, E.O. Optimization of the fabrication of novel stealth PLA-based nanoparticles by dispersion polymerization using d-optimal mixture design. Drug Dev. Ind. Pharm. 2014, 40, 1547–1556. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.X. Pharmaceutical quality by design: Product and process development, understanding, and control. Pharm. Res. 2008, 10, 781–791. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.X.; Amidon, G.; Khan, M.A.; Hoag, S.W.; Polli, J.; Raju, G.K.; Woodcock, J. Understanding pharmaceutical quality by design. AAPS J. 2014, 16, 771–783. [Google Scholar] [CrossRef] [PubMed]
- Rajin, M.; Bono, A.; Mun, H.C. Optimisation of natural ingredient based lipstick formulation by using mixture design. J. Appl. Sci. 2007, 7, 2099–2103. [Google Scholar]
- Shastri, P.N.; Ubale, R.V.; D’Souza, M.J. Implementation of mixture design for formulation of albumin containing enteric-coated spray-dried microparticles. Drug Dev. Ind. Pharm. 2013, 39, 164–175. [Google Scholar] [CrossRef] [PubMed]
- Cornell, J.A. Experiments with Mixtures, 3rd ed.; John, A., Cornell, J., Eds.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Lewis, G.A.; Chariot, M. Non classical experimental designs in pharmaceutical formulation. Drug Dev. Ind. Pharm. 1991, 17, 1551–1570. [Google Scholar] [CrossRef]
- Ulas, A.K. A note on model selection in mixture experiments. J. Math. Stat. 2007, 3, 93–99. [Google Scholar]
- Cafaggi, S.; Leardi, R.; Parodi, B.; Caviglioli, G.; Bignardi, G. An example of application of a mixture design with constraints to a pharmaceutical formulation. Chemom. Intell. Lab. Syst. 2003, 65, 139–147. [Google Scholar] [CrossRef]
- Jin, C.; Wu, H.; Liu, J.; Bai, L.; Guo, G. The effect of paclitaxel-loaded nanoparticles with radiation on hypoxic MCF-7 cells. J. Clin. Pharm. Ther. 2007, 32, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Xin, H.; Chen, L.; Gu, J.; Ren, X.; Wei, Z.; Luo, J.; Chen, Y.; Jiang, X.; Sha, X.; Fang, X. Enhanced anti-glioblastoma efficacy by PTX-loaded PEGylated poly(ɛ-caprolactone) nanoparticles: In vitro and in vivo evaluation. Int. J. Pharm. 2010, 402, 238–247. [Google Scholar] [CrossRef] [PubMed]
- Hongliang, X.; Liangcen, C.; Gu, G.; Xiaoqing, R.; Zhang, W.; Jieqi, L.; Yanzuo, C.; Xinyi, J.; Xianyi, S.; Xiaoling, F. Enhanced antiglioblastoma efficacy by PTX-loaded PEGylated poly(ɛ-caprolactone) nanoparticles: In vitro and in vivo evaluation. Int. J. Pharm. 2010, 402, 238–247. [Google Scholar]
- Li, S.; Huang, L. Pharmacokinetics and biodistribution of nanoparticles. Mol. Pharm. 2008, 5, 496–504. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akala, E.O.; Adesina, S.; Ogunwuyi, O. Computer Optimization of Biodegradable Nanoparticles Fabricated by Dispersion Polymerization. Int. J. Environ. Res. Public Health 2016, 13, 47. https://doi.org/10.3390/ijerph13010047
Akala EO, Adesina S, Ogunwuyi O. Computer Optimization of Biodegradable Nanoparticles Fabricated by Dispersion Polymerization. International Journal of Environmental Research and Public Health. 2016; 13(1):47. https://doi.org/10.3390/ijerph13010047
Chicago/Turabian StyleAkala, Emmanuel O., Simeon Adesina, and Oluwaseun Ogunwuyi. 2016. "Computer Optimization of Biodegradable Nanoparticles Fabricated by Dispersion Polymerization" International Journal of Environmental Research and Public Health 13, no. 1: 47. https://doi.org/10.3390/ijerph13010047
APA StyleAkala, E. O., Adesina, S., & Ogunwuyi, O. (2016). Computer Optimization of Biodegradable Nanoparticles Fabricated by Dispersion Polymerization. International Journal of Environmental Research and Public Health, 13(1), 47. https://doi.org/10.3390/ijerph13010047