Spatiotemporal Associations between PM2.5 and SO2 as well as NO2 in China from 2015 to 2018
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
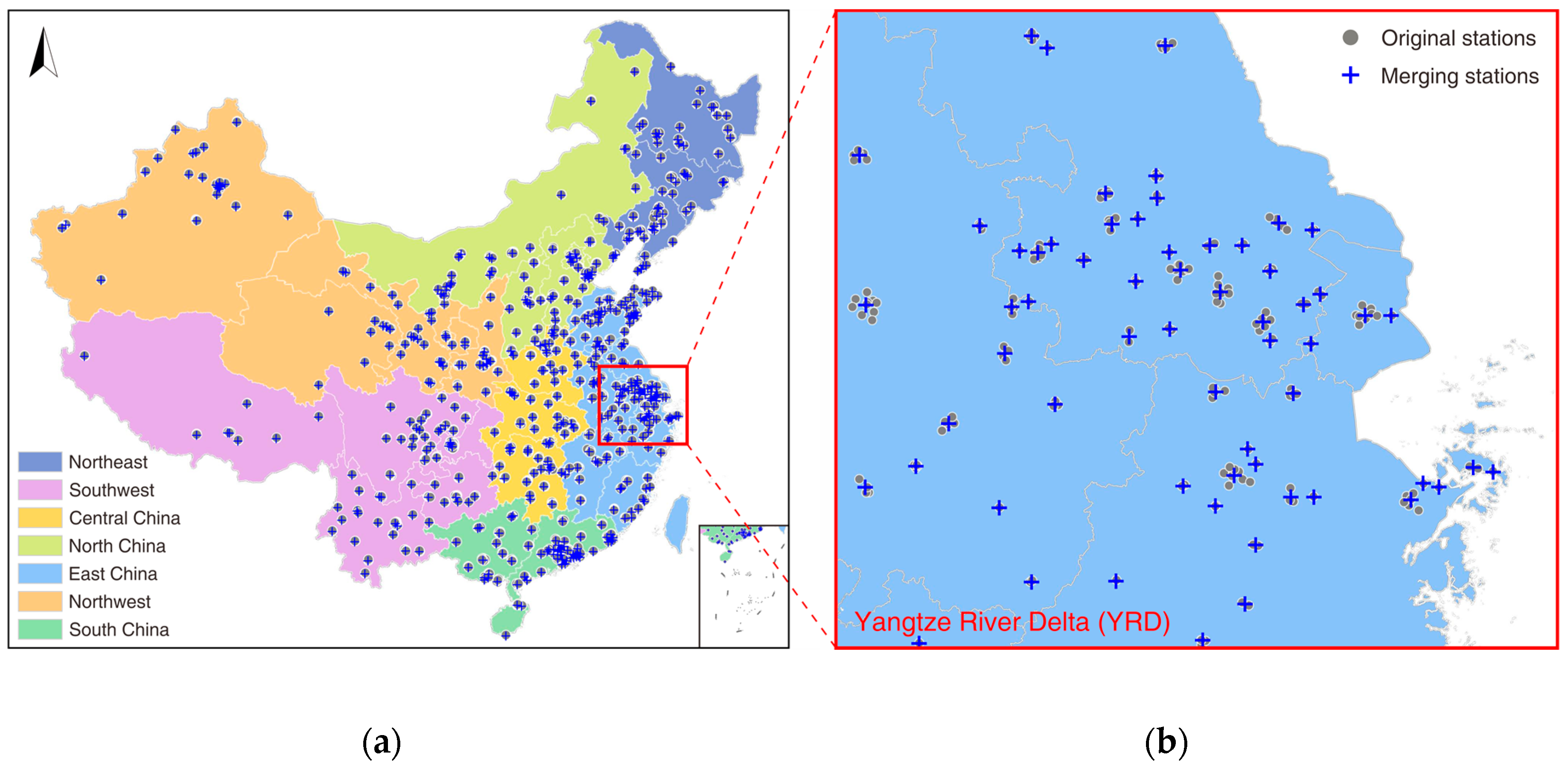
2.1.1. In Situ Air Quality Records
2.1.2. Quality Control and Data Integration
2.2. Methods
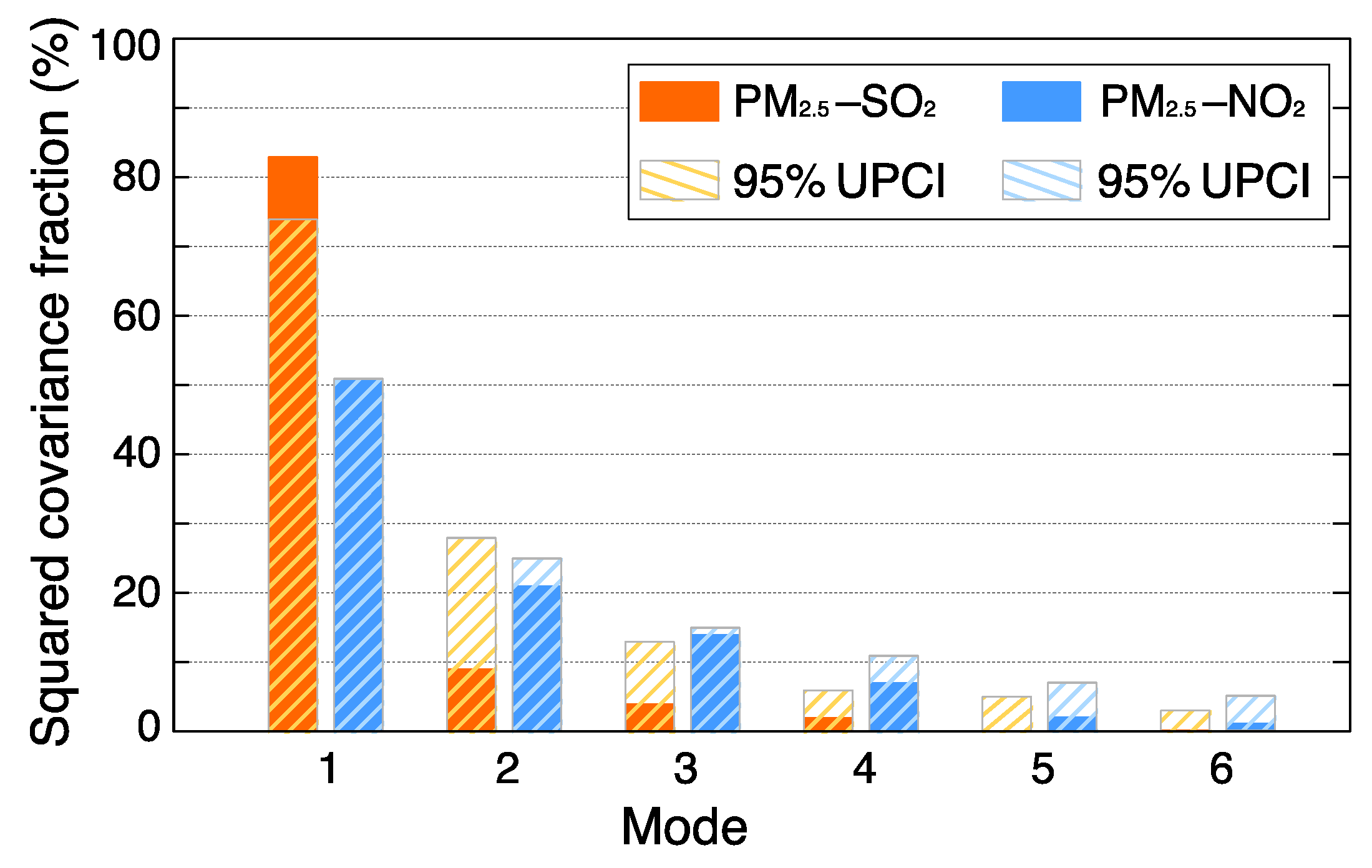
2.2.1. MCA Method
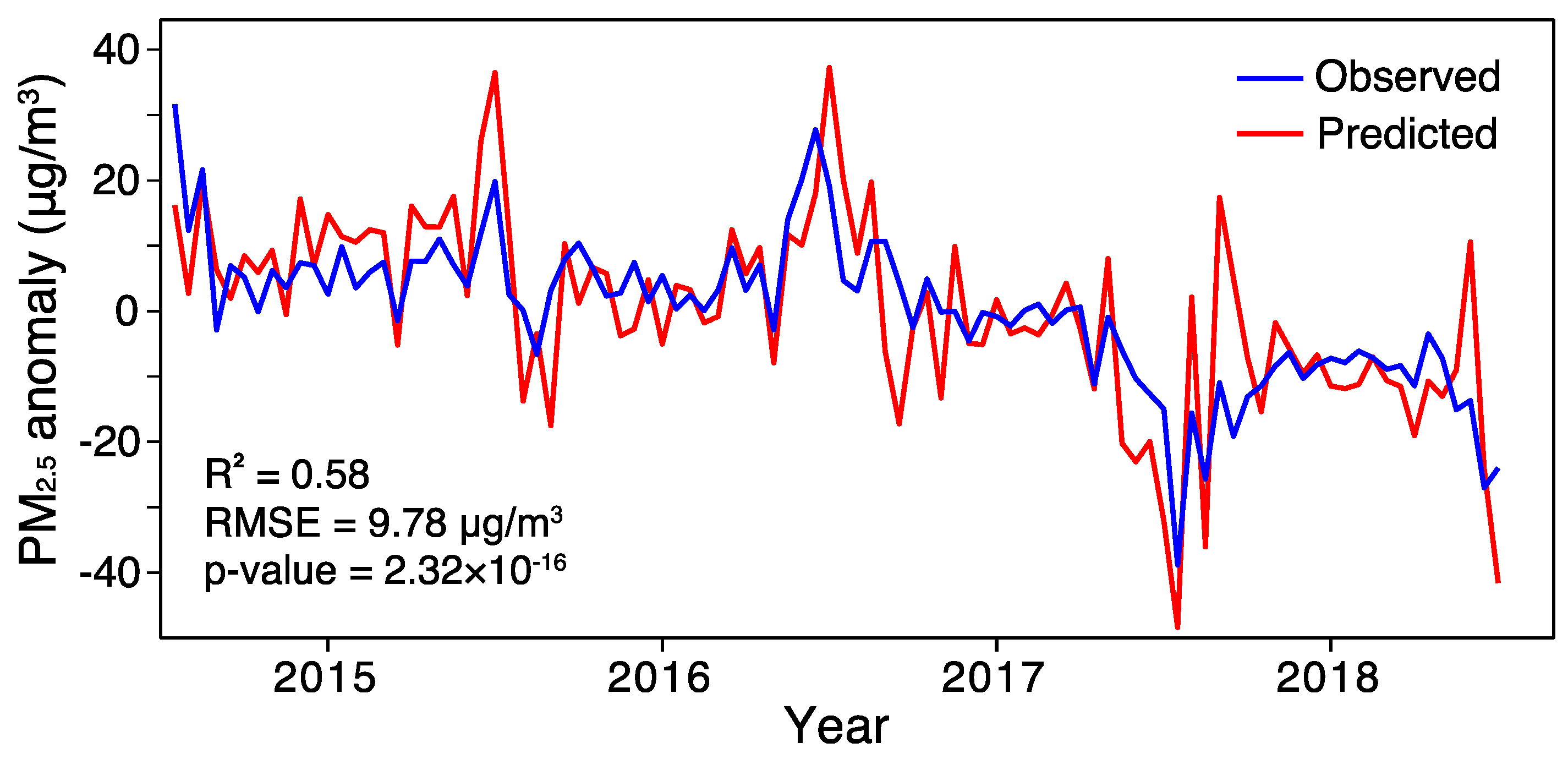
2.2.2. Quantifying the Relative Contribution of NO2 and SO2 to PM2.5 Variations
3. Results and Discussion
3.1. Linear Trends for PM2.5 and SO2 as well as NO2
3.2. Spatiotemporal Coupled Patterns between PM2.5 and SO2 as well as NO2
3.3. Relative Contributions of SO2 and NO2 to PM2.5 Variations in Northern China
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bai, K.; Ma, M.; Chang, N.-B.; Gao, W. Spatiotemporal trend analysis for fine particulate matter concentrations in China using high-resolution satellite-derived and ground-measured PM2.5 data. J. Environ. Manag. 2019, 233, 530–542. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Wang, Y.; Zhao, B.; Wang, S.; Chang, X.; Hao, J. The impact of the “Air Pollution Prevention and Control Action Plan” on PM2.5 concentrations in Jing–Jin–Ji region during 2012–2020. Sci. Total Environ. 2017, 580, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Xue, T.; Zhang, Q.; Geng, G.; Tong, D.; Li, X.; He, K. Air quality improvements and health benefits from China’s clean air action since 2013. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Xie, Y.; Zhao, B.; Zhang, L.; Luo, R. Spatiotemporal variations of PM2.5 and PM10 concentrations between 31 Chinese cities and their relationships with SO2, NO2, CO and O3. Particuology 2015, 20, 141–149. [Google Scholar] [CrossRef]
- Huang, X.H.H.; Bian, Q.; Ng, W.M.; Louie, P.K.K.; Yu, J.Z. Characterization of PM2.5 Major Components and Source Investigation in Suburban Hong Kong: A One Year Monitoring Study. Aerosol Air Qual. Res. 2014, 14, 237–250. [Google Scholar] [CrossRef]
- Xue, J.; Yuan, Z.; Griffith, S.M.; Yu, X.; Lau, A.K.H.; Yu, J.Z. Sulfate Formation Enhanced by a Cocktail of High NOx, SO2, Particulate Matter, and Droplet pH during Haze-Fog Events in Megacities in China: An Observation-Based Modeling Investigation. Environ. Sci. Technol. 2016, 50, 7325–7334. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.-F.; Ma, Z.-Y.; Ha, X.-Z. Spatial-temporal patterns of PM2.5 concentrations for 338 Chinese cities. Sci. Total Environ. 2018, 631–632, 524–533. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-based spatiotemporal trends in PM2.5 concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef]
- Mi, K.; Zhuang, R.; Zhang, Z.; Gao, J.; Pei, Q. Spatiotemporal characteristics of PM2.5 and its associated gas pollutants, a case in China. Sustain. Cities Soc. 2019, 45, 287–295. [Google Scholar] [CrossRef]
- Si, Y.; Yu, C.; Zhang, L.; Zhu, W.; Cai, K.; Cheng, L.; Chen, L.; Li, S. Assessment of satellite-estimated near-surface sulfate and nitrate concentrations and their precursor emissions over China from 2006 to 2014. Sci. Total Environ. 2019, 669, 362–376. [Google Scholar] [CrossRef]
- Li, K.; Jacob, D.J.; Liao, H.; Shen, L.; Zhang, Q.; Bates, K.H. Anthropogenic drivers of 2013–2017 trends in summer surface ozone in China. Proc. Natl. Acad. Sci. 2019, 116, 422–427. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Xu, J.; Xu, C.; Lu, D.; Ye, C.; Wang, Z.; Bai, L. Quantifying the influence of natural and socioeconomic factors and their interactive impact on PM2.5 pollution in China. Environ. Pollut. 2018, 241, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T.; Shen, H.; Zhang, L. The relationships between PM2.5 and aerosol optical depth (AOD) in mainland China: About and behind the spatio-temporal variations. Environ. Pollut. 2019, 248, 526–535. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, X.; Wang, Y. Relatively weak meteorological feedback effect on PM2.5 mass change in Winter 2017/18 in the Beijing area: Observational evidence and machine-learning estimations. Sci. Total Environ. 2019, 664, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Behera, S.N.; Sharma, M. Degradation of SO2, NO2 and NH3 leading to formation of secondary inorganic aerosols: An environmental chamber study. Atmos. Environ. 2011, 45, 4015–4024. [Google Scholar] [CrossRef]
- Hsu, Y.-M.; Clair, T.A. Measurement of fine particulate matter water-soluble inorganic species and precursor gases in the Alberta Oil Sands Region using an improved semicontinuous monitor. J. Air Waste Manag. Assoc. 2015, 65, 423–435. [Google Scholar] [CrossRef] [PubMed]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An Intercomparison of Methods for Finding Coupled Patterns in Climate Data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef] [Green Version]
- Wallace, J.M.; Smith, C.; Bretherton, C.S. Singular Value Decomposition of Wintertime Sea Surface Temperature and 500-mb Height Anomalies. J. Clim. 1992, 5, 561–576. [Google Scholar] [CrossRef]
- Bai, K.; Chang, N.-B.; Gao, W. Quantification of relative contribution of Antarctic ozone depletion to increased austral extratropical precipitation during 1979–2013. J. Geophys. Res. Atmos. 2016, 121, 1459–1474. [Google Scholar] [CrossRef]
- Ding, Q.; Steig, E.J.; Battisti, D.S.; Küttel, M. Winter warming in West Antarctica caused by central tropical Pacific warming. Nat. Geosci. 2011, 4, 398–403. [Google Scholar] [CrossRef] [Green Version]
- Casey, K.S. Sea surface temperature and sea surface height variability in the North Pacific Ocean from 1993 to 1999. J. Geophys. Res. 2002, 107, 3099. [Google Scholar] [CrossRef]
- Wu, Q. Observed impact of subtropical-midlatitude South Atlantic SST anomalies on the atmospheric circulation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Hu, Q. On the Uniqueness of the Singular Value Decomposition in Meteorological Applications. J. Clim. 1997, 10, 1762–1766. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; Uvo, C.B.; Ambrizzi, T. Exploring the impacts of the tropical Pacific SST on the precipitation patterns over South America during ENSO periods. Theor. Appl. Climatol. 2002, 71, 185–197. [Google Scholar] [CrossRef]
- Qiao, S.; Gong, Z.; Feng, G.; Qian, Z. Relationship between cold winters over Northern Asia and the subsequent hot summers over mid-lower reaches of the Yangtze River valley under global warming. Atmos. Sci. Lett. 2015, 16, 479–484. [Google Scholar] [CrossRef]
- Renwick, J.A.; Wallace, J.M. Predictable Anomaly Patterns and the Forecast Skill of Northern Hemisphere Wintertime 500-mb Height Fields. Mon. Weather Rev. 1995, 123, 2114–2131. [Google Scholar] [CrossRef] [Green Version]
- Frankignoul, C.; Chouaib, N.; Liu, Z. Estimating the Observed Atmospheric Response to SST Anomalies: Maximum Covariance Analysis, Generalized Equilibrium Feedback Assessment, and Maximum Response Estimation. J. Clim. 2011, 24, 2523–2539. [Google Scholar] [CrossRef] [Green Version]
- Brien, R.M.O. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 637–690. [Google Scholar] [CrossRef]
- Grömping, U. Relative Importance for Linear Regression in R: The Package relaimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Froyd, K.D.; Roberts, J.M.; Veres, P.R.; Hayes, P.L.; Jimenez, J.L.; Nenes, A.; Weber, R.J. Fine Particle pH and Gas-Particle Phase Partitioning of Inorganic Species in Pasadena, California, during the 2010 CalNex Campaign. Atmos. Chem. Phys. 2017, 17, 5703–5719. [Google Scholar] [CrossRef]
- Vasilakos, P.; Russell, A.; Weber, R.; Nenes, A. Understanding Nitrate Formation in A World with Less Sulfate. Atmos. Chem. Phys. 2018, 18, 12765–12775. [Google Scholar] [CrossRef]
- Dawson, J.P.; Adams, P.J.; Pandis, S.N. Sensitivity of PM2.5 to Climate in the Eastern US: A Modeling Case Study. Atmos. Chem. Phys. 2007, 7, 4295–4309. [Google Scholar] [CrossRef]
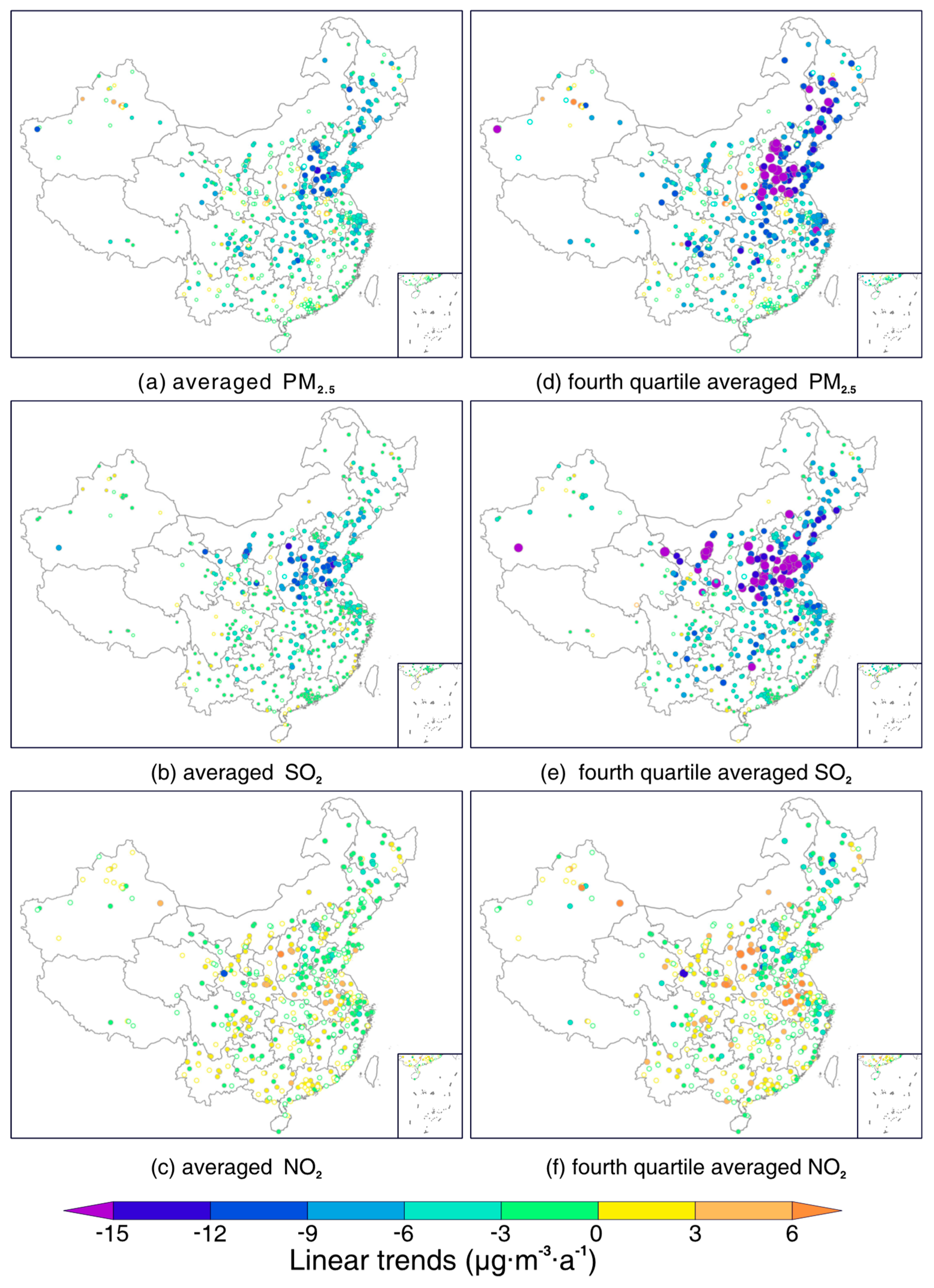


| Divisions. | Averaged PM2.5 (Fourth Quartile Averaged) | Averaged SO2 (Fourth Quartile Averaged) | Averaged NO2 (Fourth Quartile Averaged) |
|---|---|---|---|
| Northeast (53) | −4.55 ± 2.02 (−8.86 ± 4.85) | −3.23 ± 1.06 (−6.21 ± 1.99) | −1.19 ± 0.77 (−1.72 ± 1.35) |
| North China (55) | −4.15 ± 2.48 (−8.47 ± 5.14) | −4.92 ± 1.69 (−9.35 ± 3.13) | −0.13 ± 1.07 (−0.01 ± 1.72) |
| Central China (56) | −4.81 ± 2.24 (−7.61 ± 3.96) | −4.07 ± 0.98 (−7.74 ± 1.71) | −0.45 ± 0.91 (−0.39 ± 1.50) |
| East China (139) | −3.69 ± 1.75 (−6.73 ± 3.27) | −3.78 ± 0.83 (−7.31 ± 1.52) | −0.41 ± 1.00 (−0.28 ± 1.72) |
| South China (64) | −1.07 ± 1.32 (−2.06 ± 2.28) | −0.84 ± 0.46 (−1.87 ± 0.87) | 0.26 ± 0.82 (0.53 ± 1.46) |
| Northwest (73) | −1.47 ± 2.28 (−3.05 ± 4.54) | −2.37 ± 1.13 (−5.45 ± 2.24) | 0.33 ± 0.95 (0.75 ± 1.53) |
| Southwest (59) | −2.19 ± 1.33 (−3.42 ± 2.20) | −1.40 ± 0.59 (−3.10 ± 1.08) | 0.24 ± 0.70 (0.48 ± 1.17) |
| Regressor | Regression Coefficient | p-Value | LMG | L-SPR | F-SPR |
|---|---|---|---|---|---|
| SO2_PC1 (58.26%) | 8.48 | 1.64 | 0.31 | 0.10 | 0.53 |
| SO2_PC2 (24.30%) | 1.41 | 0.41 | 0.02 | 3.18 | 0.03 |
| NO2_PC1 (30.70%) | 3.33 | 0.04 | 0.21 | 0.02 | 0.42 |
| NO2_PC2 (24.07%) | 0.20 | 0.92 | 0.03 | 4.72 | 0.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Bai, K. Spatiotemporal Associations between PM2.5 and SO2 as well as NO2 in China from 2015 to 2018. Int. J. Environ. Res. Public Health 2019, 16, 2352. https://doi.org/10.3390/ijerph16132352
Li K, Bai K. Spatiotemporal Associations between PM2.5 and SO2 as well as NO2 in China from 2015 to 2018. International Journal of Environmental Research and Public Health. 2019; 16(13):2352. https://doi.org/10.3390/ijerph16132352
Chicago/Turabian StyleLi, Ke, and Kaixu Bai. 2019. "Spatiotemporal Associations between PM2.5 and SO2 as well as NO2 in China from 2015 to 2018" International Journal of Environmental Research and Public Health 16, no. 13: 2352. https://doi.org/10.3390/ijerph16132352
APA StyleLi, K., & Bai, K. (2019). Spatiotemporal Associations between PM2.5 and SO2 as well as NO2 in China from 2015 to 2018. International Journal of Environmental Research and Public Health, 16(13), 2352. https://doi.org/10.3390/ijerph16132352





