Evidence of Adaptation to Increasing Temperatures
Abstract
:1. Introduction
2. Materials and Methods
3. Results
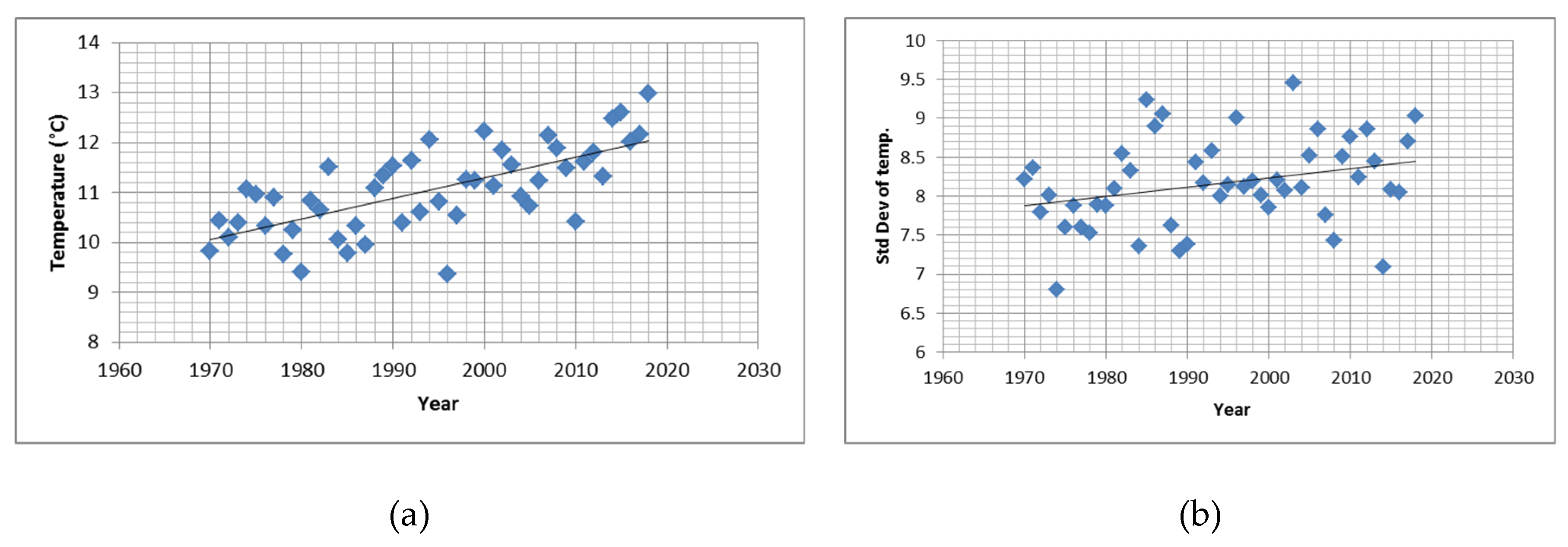
3.1. Descriptive Data
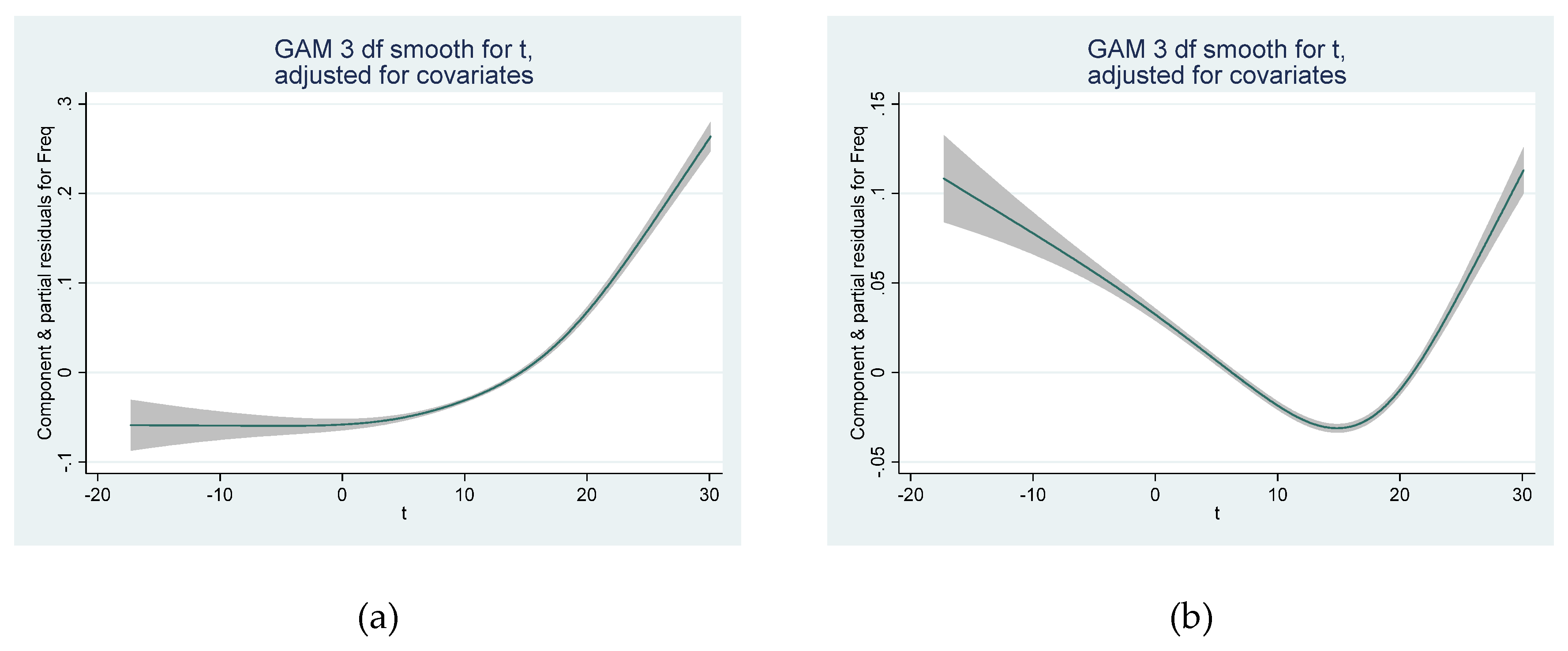
3.2. GAM Model
3.3. Parametric Models
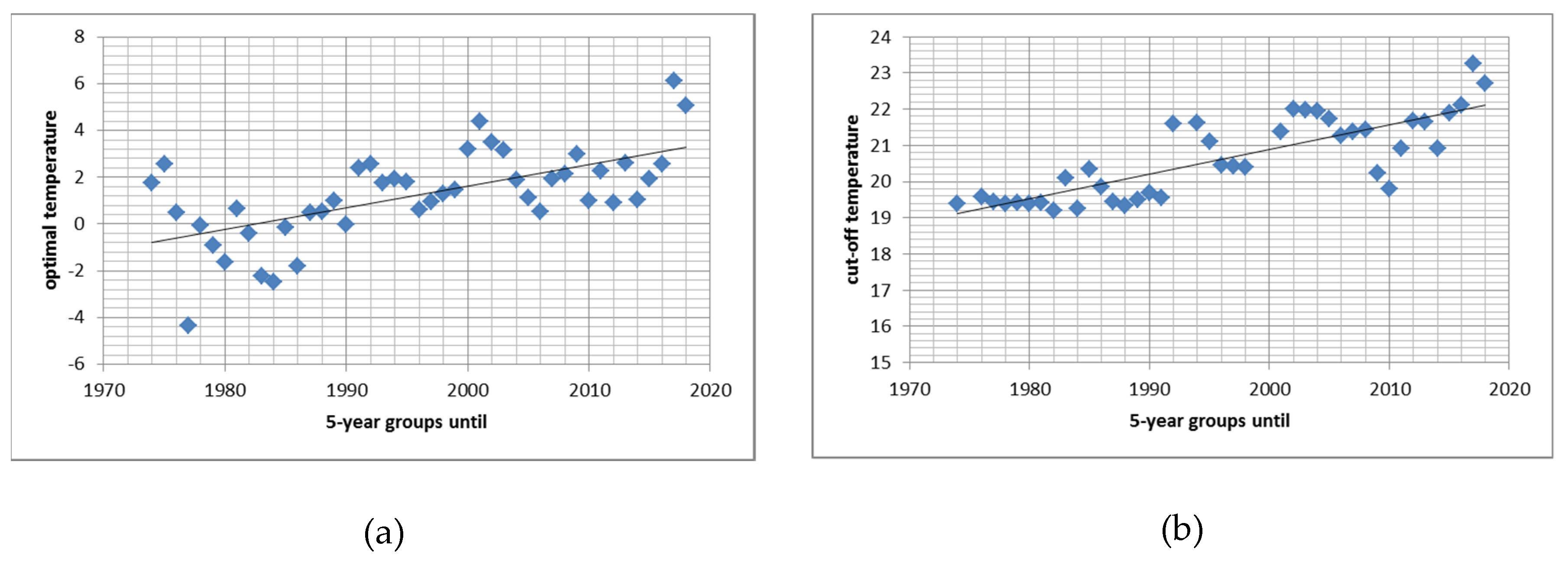
3.4. Time Trends in Optimal and in Threshold Temperature
3.5. Age Risk Groups for High Temperature
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Åström, D.O.; Veber, T.; Martinsone, Ž.; Kaļužnaja, D.; Indermitte, E.; Oudin, A.; Orru, H. Mortality related to cold temperatures in two capitals of the Baltics: Tallinn and Riga. Medicina 2019, 55, 429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Díaz, J.; Carmona, R.; Mirón, I.J.; Luna, M.Y.; Linares, C. Time trends in the impact attributable to cold days in Spain: Incidence of local factors. Sci. Total Environ. 2019, 655, 305–312. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Gasparrini, A.; Armstrong, B.G.; Tawatsupa, B.; Tobias, A.; Lavigne, E.; Coelho, M.d.S.Z.S.; Pan, X.; Kim, H.; Hashizume, M.; et al. Heat wave and mortality: A multicountry, multicommunity study. Environ. Health Perspect. 2017, 125, 087006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Achebak, H.; Devolder, D.; Ballester, J. Trends in temperature-related age-specific and sex-specific mortality from cardiovascular diseases in Spain: A national time-series analysis. Lancet Planet. Health 2019, 3, 297–306. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Xu, Z.; Bambrick, H.; Su, H.; Tong, S.; Hu, W. Impacts of heat, cold, and temperature variability on mortality in Australia, 2000–2009. Sci. Total Environ. 2019, 651, 2558–2565. [Google Scholar] [CrossRef] [PubMed]
- Curriero, F.; Heiner, K.; Samet, J.; Zeger, S.; Strug, L.; Patz, J. Temperature and mortality in 11 cities of the Eastern United States. Am. J. Epidemiol. 2002, 155, 80–87. [Google Scholar] [CrossRef]
- Baccini, M.; Biggeri, A.; Accetta, G.; Kosatsky, T.; Katsouyanni, K.; Analitis, A.; Anderson, H.; Bisanti, L.; D’Ippoliti, D.; Danova, J.; et al. Heat effects on mortality in 15 European cities. Epidemiology 2008, 19, 711–719. [Google Scholar] [CrossRef]
- Andry, O.; Bintanja, R.; Hazeleger, W. Time-dependent variations in the Arctic’s surface albedo feedback and the link to seasonality in sea ice. J. Clim. 2017, 30, 393–410. [Google Scholar] [CrossRef]
- APCC. Österreichischer Sachstandsbericht Klimawandel 2014 (AAR14); Austrian Panel on Climate Change (APCC), Verlag der Österreichischen Akademie der Wissenschaften: Vienna, Austria, 2014; ISBN 978-3-7001-7699-2. [Google Scholar]
- Neuberger, M.; Rabczenko, D.; Moshammer, H. Extended effects of air pollution on cardiopulmonary mortality in Vienna. Atmos. Environ. 2007, 41, 8549–8556. [Google Scholar] [CrossRef]
- Neuberger, M.; Moshammer, H.; Rabczenko, D. Acute and subacute effects of urban air pollution on cardiopulmonary emergencies and mortality: Time series studies in Austrian cities. Int. J. Environ. Res. Public Health 2013, 10, 4728–4751. [Google Scholar] [CrossRef]
- Moshammer, H.; Hutter, H.-P.; Kundi, M. Which metric of ambient ozone to predict daily mortality? Atmos. Environ. 2013, 65, 171–176. [Google Scholar] [CrossRef]
- Moshammer, H. Time-series on mortality related to air pollution in Vienna: A sensitivity analysis. Epidemiology 2009, 20, 15. [Google Scholar] [CrossRef]
- Ban, J.; Xu, D.; He, M.Z.; Sun, Q.; Chen, C.; Wang, W.; Zhu, P.; Li, T. The effect of high temperature on cause-specific mortality: A multi-county analysis in China. Environ. Int. 2017, 106, 19–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- STATA SE Vers. 13.1; StataCorp: College Station, TX, USA, 2013.
- Sheridan, S.C.; Lee, C.C.; Allen, M.J. The Mortality Response to Absolute and Relative Temperature Extremes. Int. J. Environ. Res. Public Health 2019, 16, 1493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akaike, H. Information theory as an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory; Petrov, B.N., Csaksi, F., Eds.; Akademiai Kiado: Budapest, Hungary, 1973. [Google Scholar]
- Moshammer, H.; Hutter, H.-P.; Frank, A.; Gerersdorfer, T.; Hlava, A.; Sprinzl, G. StartClim2005.A1a: Impacts of temperature on mortality and morbidity in Vienna. In Final Report StartClim2005: Climate Change and Health; Kromp-Kolb, H., Schwarzl, I., Eds.; University of Natural Resources and Applied Life Sciences: Vienna, Austria, 2006. [Google Scholar]
- Hutter, H.-P.; Moshammer, H.; Wallner, P.; Leitner, B.; Kundi, M. Heatwaves in Vienna: Effects on mortality. Wien. Klin. Wochenschr. 2007, 119, 223–227. [Google Scholar] [CrossRef]
- Gerersdorfer, T.; Frank, A.; Formayer, H.; Haas, P.; Moshammer, H.; Leitner, B. StartClim2005.A1b: Nocturnal cooling under a changing climate. In Final Report StartClim2005: Climate Change and Health; Kromp-Kolb, H., Schwarzl, I., Eds.; University of Natural Resources and Applied Life Sciences: Vienna, Austria, 2006. [Google Scholar]
- Kysely, J. Mortality and displaced mortality during heat waves in the Czech Republic. Int. J. Biometeorol. 2004, 49, 91–97. [Google Scholar] [CrossRef]
- Rocklöv, J.; Forsberg, B. The effect of temperature on mortality in Stockholm 1998–2003: A study of lag structures and heatwave effects. Scand. J. Public Health 2008, 36, 516–523. [Google Scholar] [CrossRef]
- Gasparrini, A.; Armstrong, B.; Kenward, M.G. Distributed lag non-linear models. Stat. Med. 2010, 29, 2224–2234. [Google Scholar] [CrossRef] [Green Version]
- Moshammer, H.; Hutter, H.-P.; Neuberger, M. Polynomial distributed lag models of short-term air pollution effects on lung function. Epidemiology 2006, 176, 261. [Google Scholar] [CrossRef]
- Moshammer, H.; Hutter, H.-P.; Wallner, P. Modeling the time course of temperature effects on daily mortality. Epidemiology 2006, 176, 125. [Google Scholar] [CrossRef]
- Goldberg, M.S.; Gasparrini, A.; Armstrong, B.; Valois, M.F. The short-term influence of temperature on daily mortality in the temperate climate of Montreal, Canada. Environ. Res. 2011, 111, 853–860. [Google Scholar] [CrossRef] [PubMed]
- Petkova, E.; Bader, D.; Anderson, G.; Horton, R.; Knowlton, K.; Kinney, P. Heat-related mortality in a warming climate: Projections for 12 U.S. cities. Int. J. Environ. Res. Public Health 2014, 11, 11371–11383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiao, Z.; Guo, Y.; Yu, W.; Tong, S. Assessment of Short- and Long-Term Mortality Displacement in Heat-Related Deaths in Brisbane, Australia, 1996–2004. Environ. Health Perspect. 2015, 123, 766–772. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocklöv, J.; Forsberg, B.; Meister, K. Winter mortality modifies the heat-mortality association the following summer. Eur. Respir. J. 2009, 33, 245–251. [Google Scholar] [CrossRef]
- Ebi, K.L.; Boyer, C.; Bowen, K.J.; Frumkin, H.; Hess, J. Monitoring and evaluation indicators for climate change-related health impacts, risks, adaptation, and Resilience. Int. J. Environ. Res. Public Health 2018, 15, 1943. [Google Scholar] [CrossRef] [Green Version]
- Scortichini, M.; De Sario, M.; De’Donato, F.K.; Davoli, M.; Michelozzi, P.; Stafoggia, M. Short-term effects of heat on mortality and effect modification by air pollution in 25 Italian cities. Int. J. Environ. Res. Public Health 2018, 15, 1771. [Google Scholar] [CrossRef] [Green Version]


| Model 1 | Coefficient | p-Value | R2 = 0.26 | AIC = 125,306.1 |
| sine | 0.025 | <0.001 | ||
| cosine | 0.074 | <0.001 | ||
| Year | −0.014 | <0.001 | ||
| Tue-Sun1 | −0.041; 0.004 | <0.001; 0.89 | ||
| Temp | −0.0015 | <0.001 | ||
| Temp-squared | 0.0005 | <0.001 | ||
| Rel. Humidity | 0.0001 | 0.138 | ||
| 28-day temp. | −0.010 | <0.001 | ||
| Constant | 32.04 | <0.001 | ||
| Model 2 | Coefficient | p-Value | R2 = 0.26 | AIC = 125,238.9 |
| sine | 0.042 | <0.001 | ||
| cosine | 0.089 | <0.001 | ||
| Year | −0.018 | <0.001 | ||
| Tue-Sun1 | −0.040; 0.004 | <0.001; 0.88 | ||
| Temp | −0.0001 | 0.882 | ||
| Temp-squared | 0.0004 | <0.001 | ||
| Rel. Humidity | 0.0002 | 0.066 | ||
| 14-day temp. | −0.0097 | <0.001 | ||
| Constant | 32.18 | <0.001 | ||
| Model 3 | Coefficient | p-Value | R2 = 0.26 | AIC = 125,643 |
| sine | 0.069 | <0.001 | ||
| cosine | 0.150 | <0.001 | ||
| Year | −0.014 | <0.001 | ||
| Tue-Sun 1 | −0.041; 0.004 | <0.001; 0.90 | ||
| Temp | −0.0038 | <0.001 | ||
| Temp-squared | 0.0005 | <0.001 | ||
| Rel. Humidity | 0.0002 | 0.017 | ||
| Constant | 32.61 | <0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weitensfelder, L.; Moshammer, H. Evidence of Adaptation to Increasing Temperatures. Int. J. Environ. Res. Public Health 2020, 17, 97. https://doi.org/10.3390/ijerph17010097
Weitensfelder L, Moshammer H. Evidence of Adaptation to Increasing Temperatures. International Journal of Environmental Research and Public Health. 2020; 17(1):97. https://doi.org/10.3390/ijerph17010097
Chicago/Turabian StyleWeitensfelder, Lisbeth, and Hanns Moshammer. 2020. "Evidence of Adaptation to Increasing Temperatures" International Journal of Environmental Research and Public Health 17, no. 1: 97. https://doi.org/10.3390/ijerph17010097
APA StyleWeitensfelder, L., & Moshammer, H. (2020). Evidence of Adaptation to Increasing Temperatures. International Journal of Environmental Research and Public Health, 17(1), 97. https://doi.org/10.3390/ijerph17010097






