Simulation-Optimization for Conjunctive Water Resources Management and Optimal Crop Planning in Kushabhadra-Bhargavi River Delta of Eastern India
Abstract
1. Introduction
2. Methodology
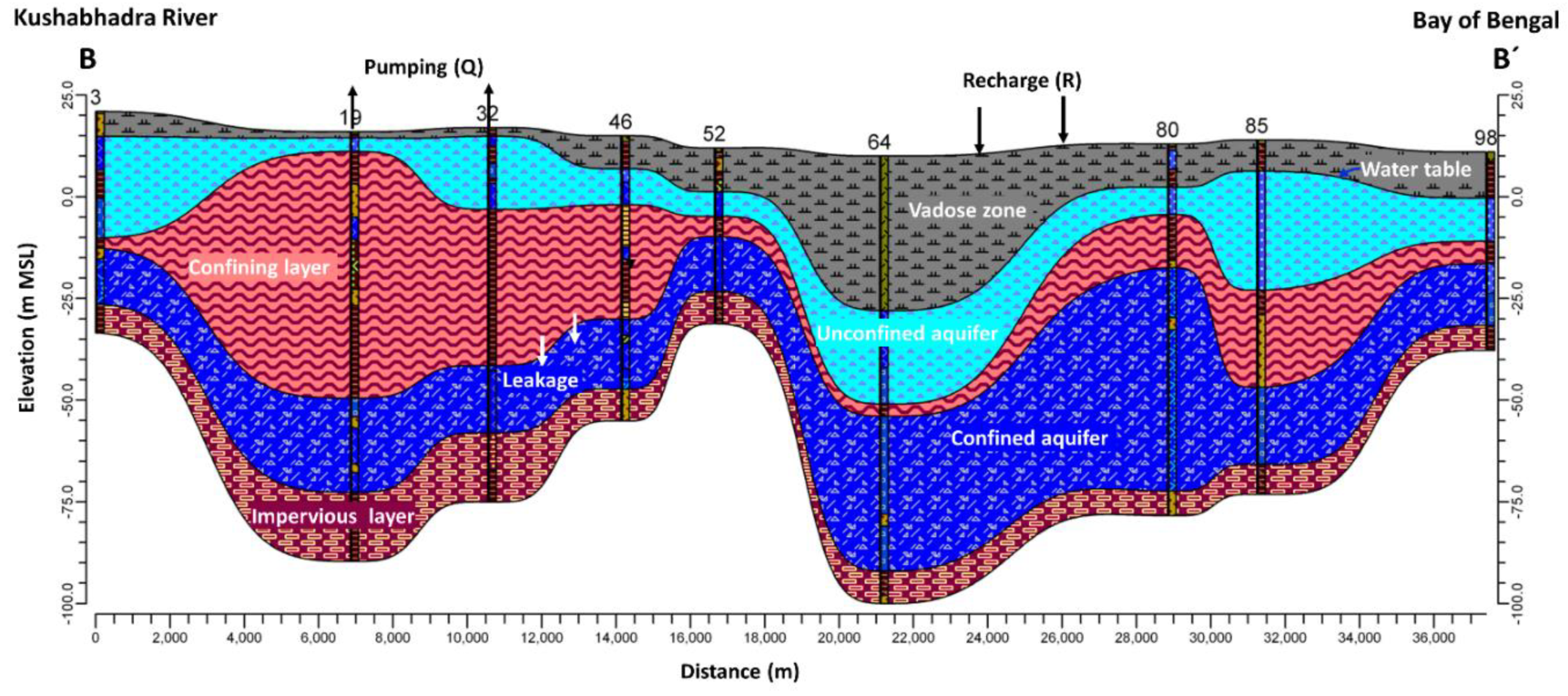
2.1. Study Area and Hydro-Climatic Settings
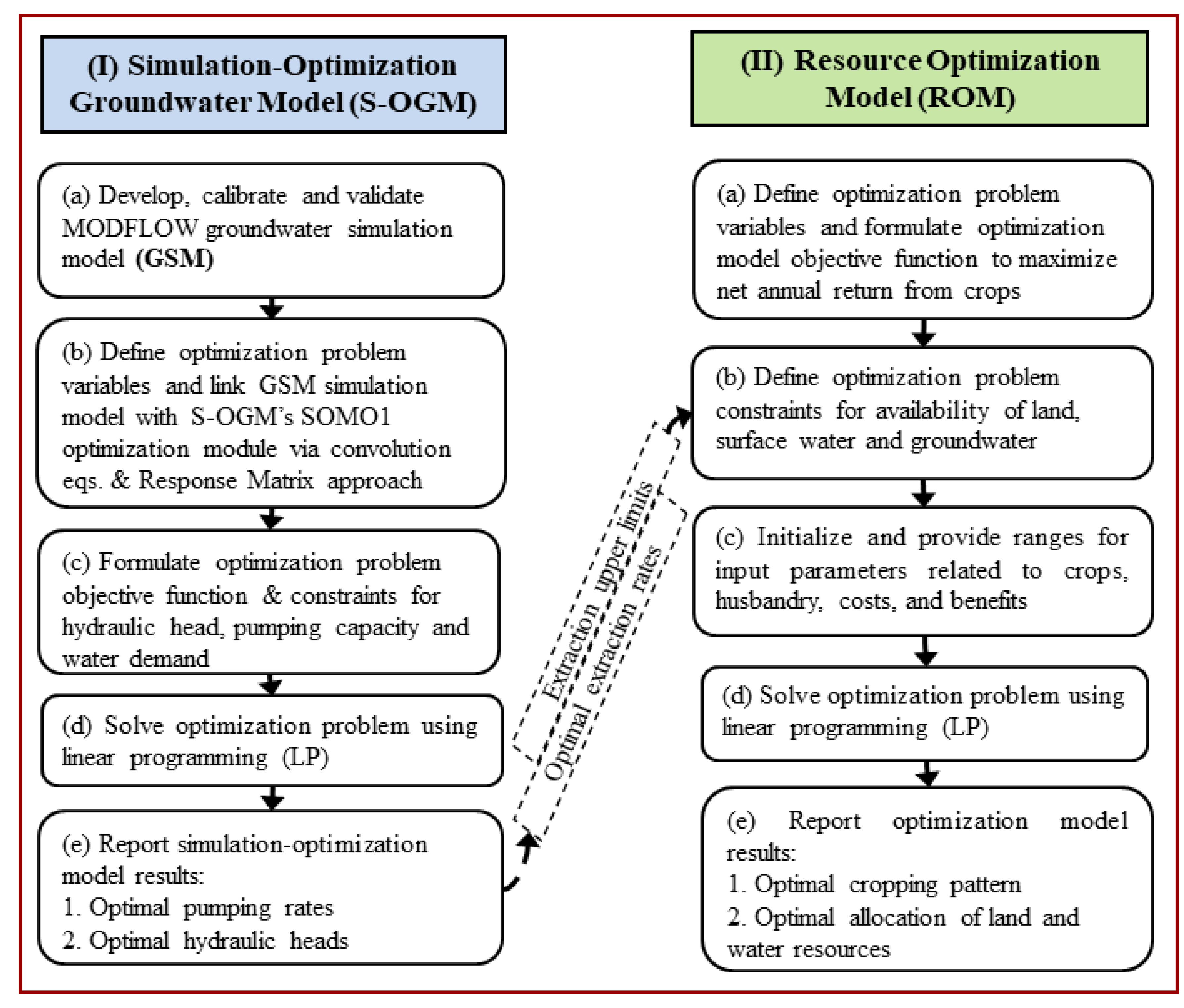
2.2. Integrated Simulation-Optimization Framework
2.2.1. Overview
2.2.2. Groundwater Simulation Model (GSM)
2.2.3. Simulation-Optimization Groundwater Model (S-OGM)
2.2.3.1. Response Matrix Approach
2.2.3.2. Formulation of Simulation-Optimization Groundwater Model (S-OGM)
2.2.4. Formulation of Resource Optimization Model (ROM)
3. Results and Discussion
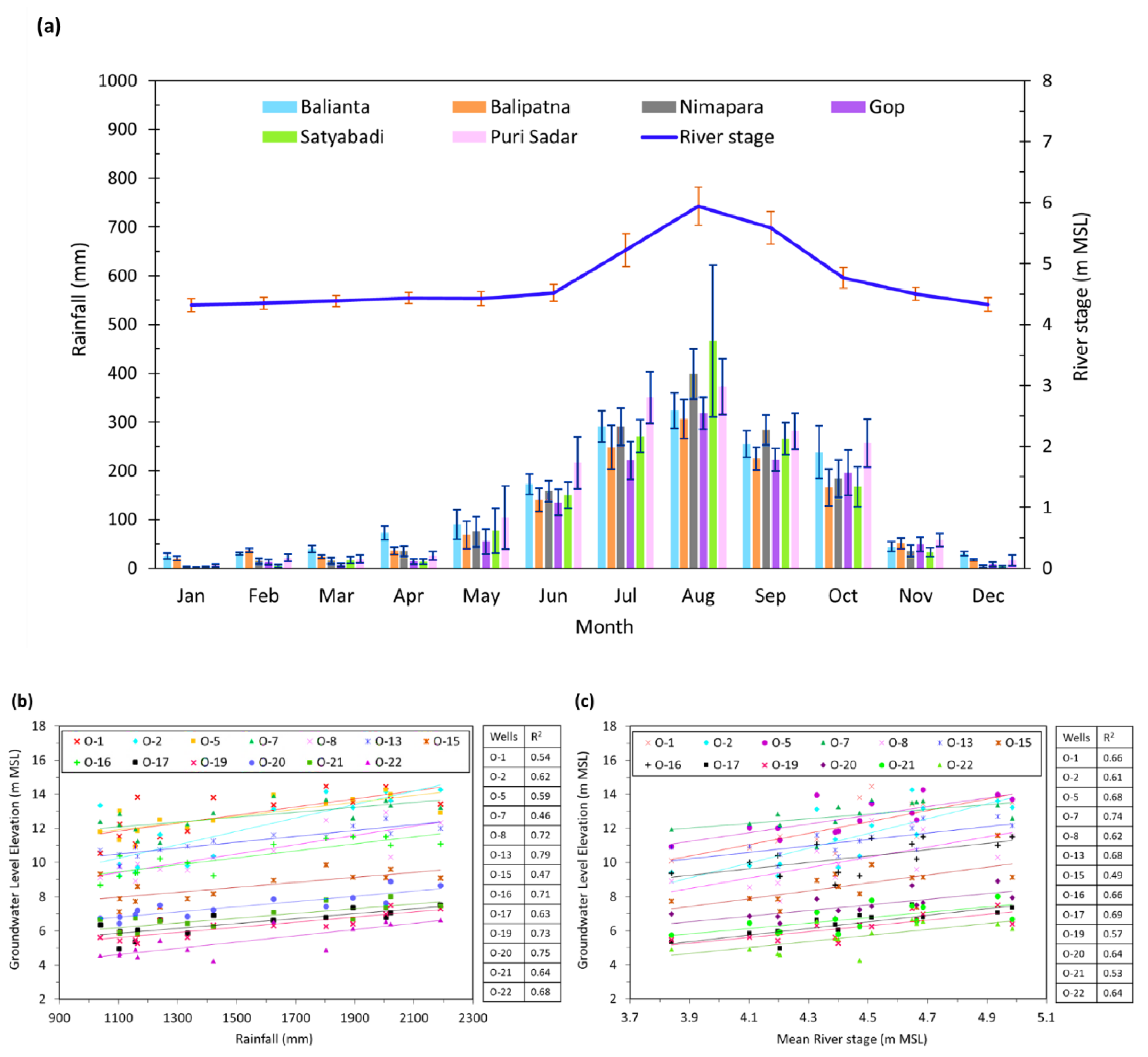
3.1. Relations between Rainfall, River Stage, and Groundwater Levels
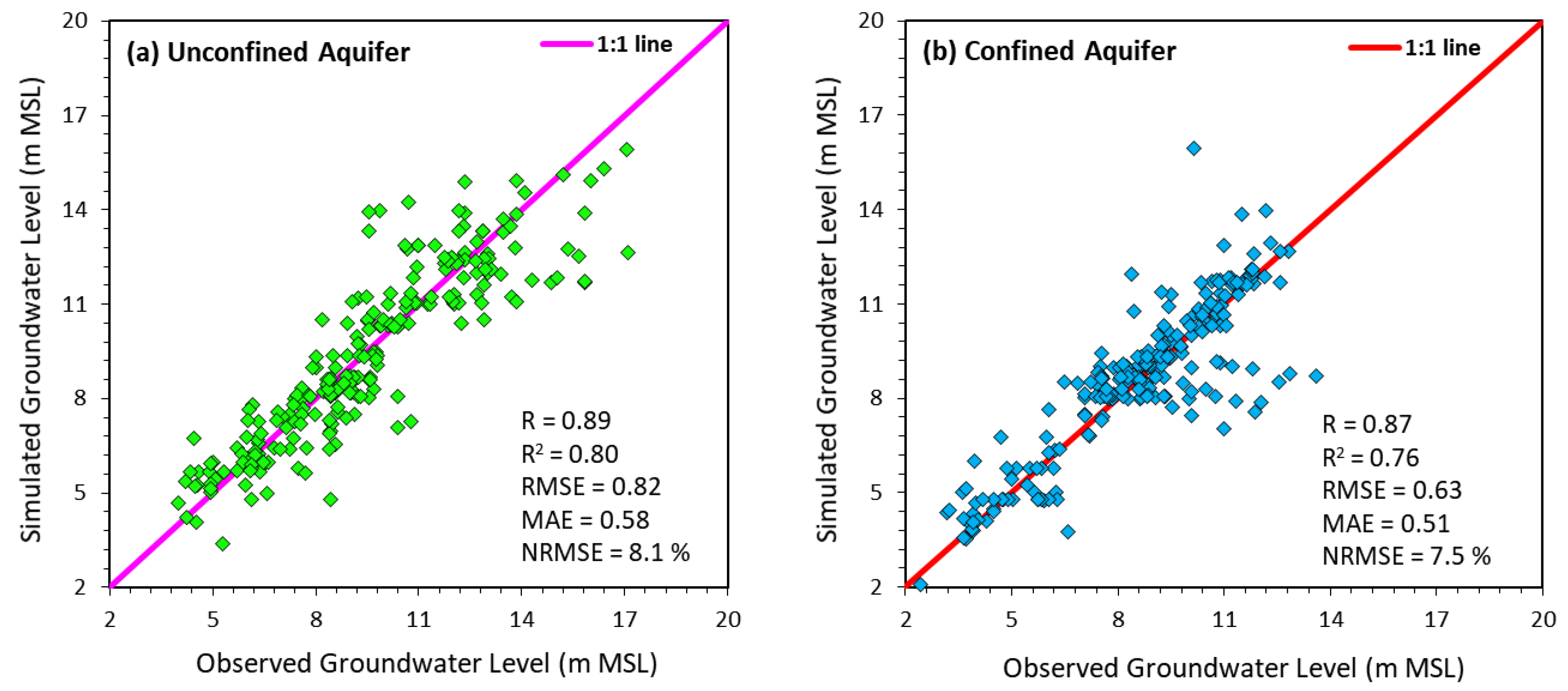
3.2. Groundwater-Flow Simulation Results Computed by MODFLOW-2005
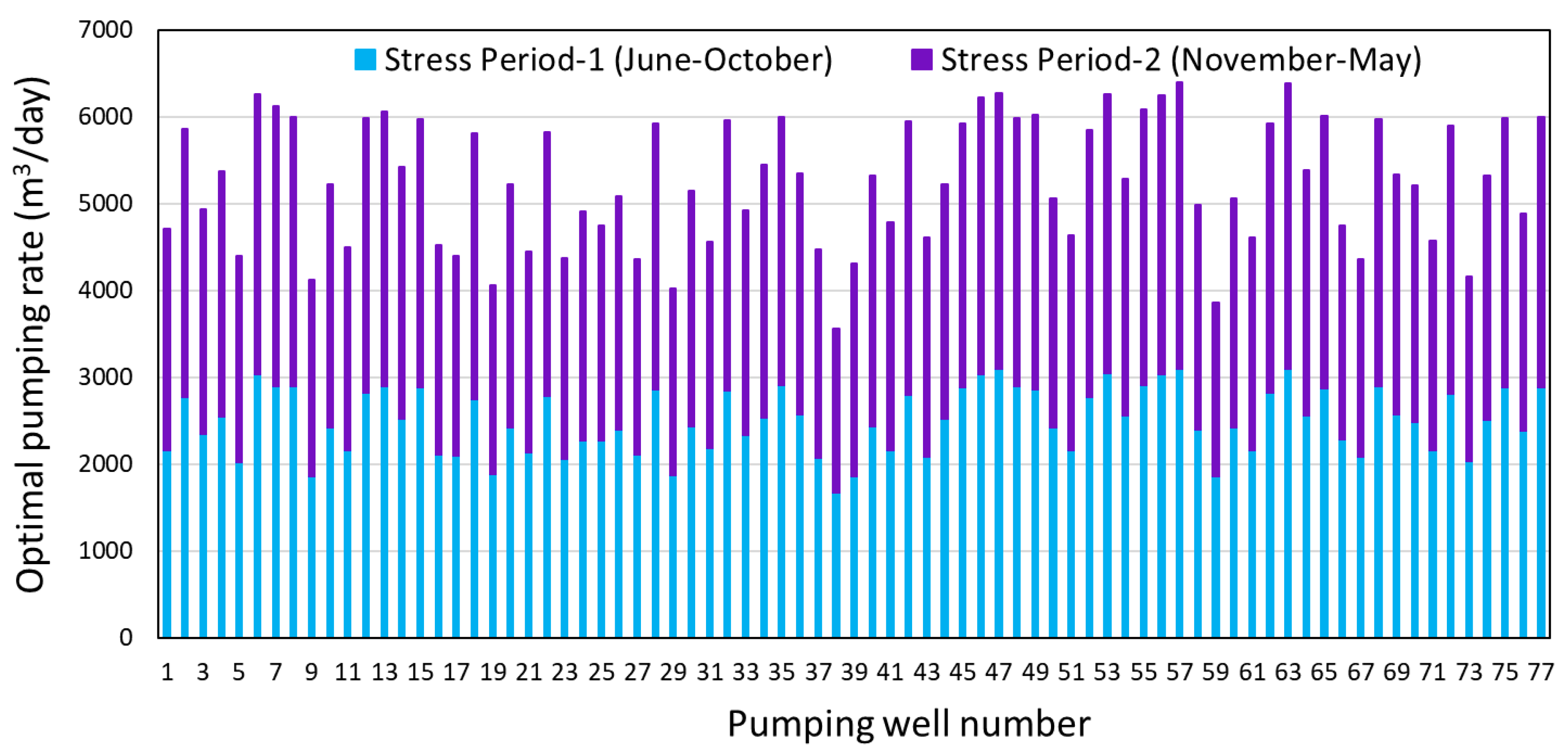
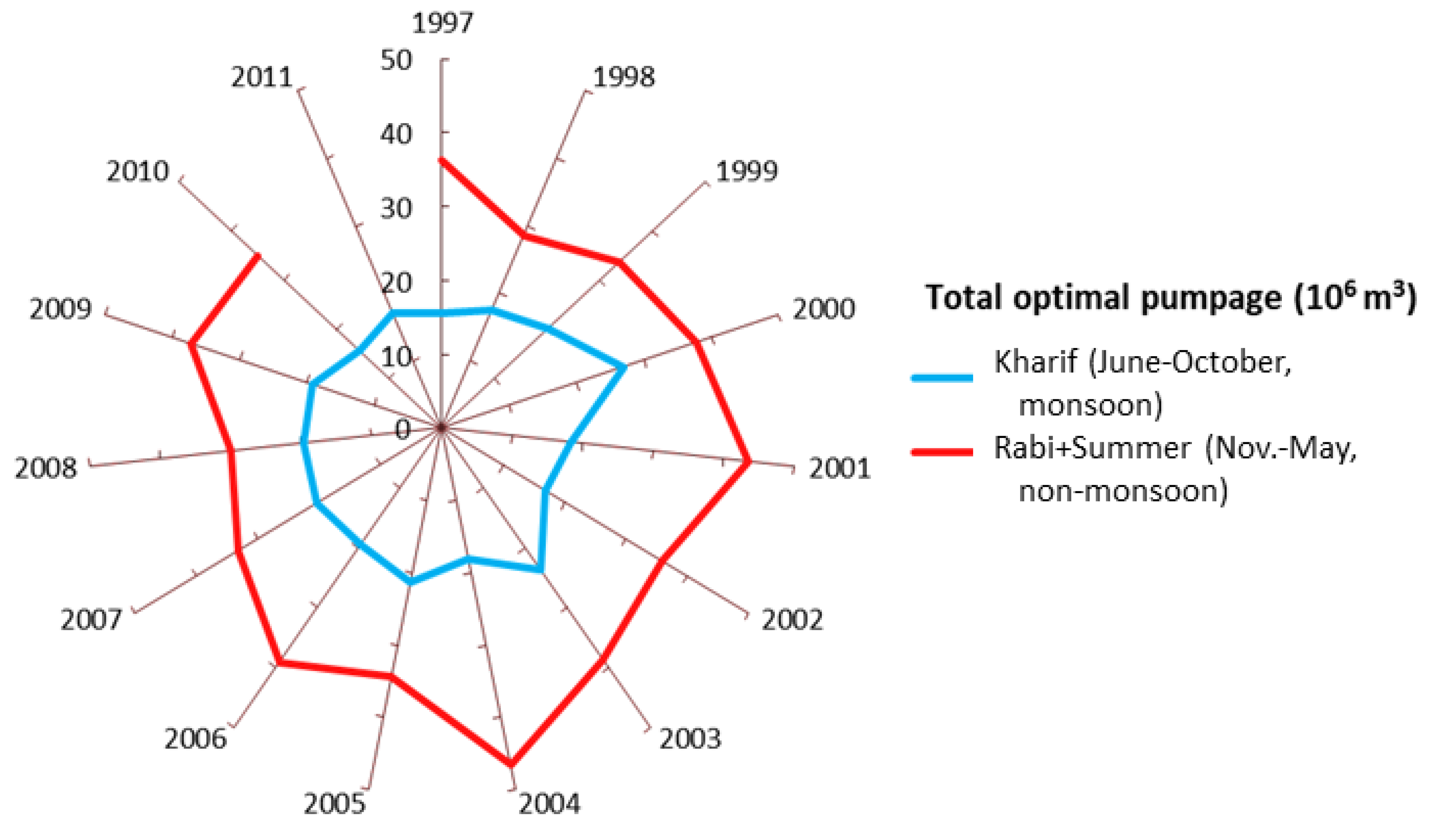
3.3. Maximum Groundwater Abstraction Strategy Computed by S-OGM
3.4. Optimal Plan for Land and Water Resources Computed by ROM
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haddeland, I.; Heinke, J.; Biemans, H.; Eisner, S.; Flörke, M.; Hanasaki, N.; Konzmann, M.; Ludwig, F.; Masaki, Y.; Schewe, J.; et al. Global water resources affected by human interventions and climate change. Proc. Natl. Acad. Sci. USA 2013, 111, 3251–3256. [Google Scholar] [CrossRef]
- Conway, D.; Van Garderen, E.A.; Deryng, D.; Dorling, S.; Krüger, T.; Landman, W.; Lankford, B.; Lebek, K.; Osborn, T.J.; Ringler, C.; et al. Climate and southern Africa’s water–energy–food nexus. Nat. Clim. Chang. 2015, 5, 837–846. [Google Scholar] [CrossRef]
- Weitz, N.; Strambo, C.; Kemp-Benedict, E.; Nilsson, M. Closing the governance gaps in the water-energy-food nexus: Insights from integrative governance. Glob. Environ. Chang. 2017, 45, 165–173. [Google Scholar] [CrossRef]
- Bovolo, C.I.; Parkin, G.; Sophocleous, M. Groundwater resources, climate and vulnerability. Environ. Res. Lett. 2009, 4, 035001. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Miller, K.A.; Belton, V. Water resource management and climate change adaptation: A holistic and multiple criteria perspective. Mitig. Adapt. Strat. Glob. Chang. 2014, 19, 289–308. [Google Scholar] [CrossRef]
- Henriksen, H.J.; Troldborg, L.; Nyegaard, P.; Sonnenborg, T.O.; Refsgaard, J.C.; Madsen, B. Methodology for construction, calibration and validation of a national hydrological model for Denmark. J. Hydrol. 2003, 280, 52–71. [Google Scholar] [CrossRef]
- Konikow, L.F.; Bredehoeft, J.D. Ground-water models cannot be validated. Adv. Water Resour. 1992, 15, 75–83. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. On the statistical forecasting of groundwater levels in unconfined aquifer systems. Environ. Earth Sci. 2014, 73, 3119–3136. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Theodossiou, N. Application of non-linear simulation and optimisation models in groundwater aquifer management. Water Resour. Manag. 2004, 18, 125–141. [Google Scholar] [CrossRef]
- Yeh, W.W.-G. Optimal management of flow in groundwater systems. Eos 2000, 81, 315. [Google Scholar] [CrossRef]
- Peralta, R.C.; Kalwij, I.M. Groundwater Optimization Handbook: Flow, Contaminant Transport and Conjunctive Management; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Heydari, F.; Saghafian, B.; Delavar, M. Coupled quantity-quality simulation-optimization model for conjunctive surface-groundwater use. Water Resour. Manag. 2016, 30, 4381–4397. [Google Scholar] [CrossRef]
- Mani, A.; Tsai, F.T.-C.; Kao, S.-C.; Naz, B.S.; Ashfaq, M.; Rastogi, D. Conjunctive management of surface and groundwater resources under projected future climate change scenarios. J. Hydrol. 2016, 540, 397–411. [Google Scholar] [CrossRef]
- Peralta, R.C.; Forghani, A.; Fayad, H. Multiobjective genetic algorithm conjunctive use optimization for production, cost, and energy with dynamic return flow. J. Hydrol. 2014, 511, 776–785. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, X.; Huang, Q.; Huo, Z.; Huang, G. Optimizing regional irrigation water use by integrating a two-level optimization model and an agro-hydrological model. Agric. Water Manag. 2016, 178, 76–88. [Google Scholar] [CrossRef]
- Nguyen, D.C.H.; Ascough, J.C.; Maier, H.R.; Dandy, G.; Andales, A.A. Optimization of irrigation scheduling using ant colony algorithms and an advanced cropping system model. Environ. Model. Softw. 2017, 97, 32–45. [Google Scholar] [CrossRef]
- Fazlali, A.; Shourian, M. A demand management based crop and irrigation planning using the simulation-optimization approach. Water Resour. Manag. 2017, 32, 67–81. [Google Scholar] [CrossRef]
- Garg, N.; Dadhich, S.M. Integrated non-linear model for optimal cropping pattern and irrigation scheduling under deficit irrigation. Agric. Water Manag. 2014, 140, 1–13. [Google Scholar] [CrossRef]
- Hussain, M.S.; Javadi, A.A.; Asr, A.A.; Farmani, R. A surrogate model for simulation–optimization of aquifer systems subjected to seawater intrusion. J. Hydrol. 2015, 523, 542–554. [Google Scholar] [CrossRef]
- Renau-Pruñonosa, A.; Morell, I.; Pulido-Velazquez, D. A methodology to analyze and assess pumping management strategies in coastal aquifers to avoid degradation due to seawater intrusion problems. Water Resour. Manag. 2016, 30, 4823–4837. [Google Scholar] [CrossRef]
- Christelis, V.; Mantoglou, A. Pumping optimization of coastal aquifers assisted by adaptive metamodelling methods and radial basis functions. Water Resour. Manag. 2016, 30, 5845–5859. [Google Scholar] [CrossRef]
- Sedki, A.; Driss, O. Simulation-optimization modeling for sustainable groundwater development: A Moroccan coastal aquifer case study. Water Resour. Manag. 2011, 25, 2855–2875. [Google Scholar] [CrossRef]
- Timani, B.; Peralta, R. Aggregated surrogate simulator for groundwater-surface water management via simulation-optimization modeling: Theory, development and tests. Environ. Model. Softw. 2017, 96, 210–231. [Google Scholar] [CrossRef]
- Forni, L.; Medellín-Azuara, J.; Tansey, M.; Young, C.; Purkey, D.; Howitt, R. Integrating complex economic and hydrologic planning models: An application for drought under climate change analysis. Water Resour. Econ. 2016, 16, 15–27. [Google Scholar] [CrossRef]
- Feng, D.; Zheng, Y.; Mao, Y.; Zhang, A.; Wu, B.; Li, J.; Tian, Y.; Wu, X. An integrated hydrological modeling approach for detection and attribution of climatic and human impacts on coastal water resources. J. Hydrol. 2018, 557, 305–320. [Google Scholar] [CrossRef]
- Skardi, M.J.E.; Afshar, A.; Saadatpour, M.; Solis, S.S. Hybrid ACO–ANN-based multi-objective simulation–optimization model for pollutant load control at basin scale. Environ. Model. Assess. 2014, 20, 29–39. [Google Scholar] [CrossRef]
- Ebrahim, G.Y.; Jonoski, A.; Al-Maktoumi, A.; Ahmed, M.; Mynett, A. Simulation-optimization approach for evaluating the feasibility of managed aquifer recharge in the Samail Lower Catchment, Oman. J. Water Resour. Plan. Manag. 2016, 142, 05015007. [Google Scholar] [CrossRef]
- Gharbi, A.; Peralta, R.C. Integrated embedding optimization applied to Salt Lake valley aquifers. Water Resour. Res. 1994, 30, 817–832. [Google Scholar] [CrossRef]
- Peralta, R.C.; Azarmnia, H.; Takahashi, S. Embedding and response matrix techniques for maximizing steady-state ground-water extraction: Computational comparison. Ground Water 1991, 29, 357–364. [Google Scholar] [CrossRef]
- Peralta, R.C.; Cantiller, R.R.A.; Terry, J.E. Optimal large-scale conjunctive water-use planning case study. J. Water Resour. Plan. Manag. 1995, 121, 471–478. [Google Scholar] [CrossRef]
- Peralta, R.C.; Kalwij, I.M.; Wu, S.; Aly, A.H. (Systems Simulation/Optimization Laboratory), SOMOS User’s Manual; SS/OL, Department of Biological and Irrigation Engineering, Utah State University: Logan, UT, USA, 2008. [Google Scholar]
- Ayvaz, M.T. Application of Harmony Search algorithm to the solution of groundwater management models. Adv. Water Resour. 2009, 32, 916–924. [Google Scholar] [CrossRef]
- Wu, B.; Zheng, Y.; Wu, X.; Tian, Y.; Han, F.; Liu, J.; Zheng, C. Optimizing water resources management in large river basins with integrated surface water-groundwater modeling: A surrogate-based approach. Water Resour. Res. 2015, 51, 2153–2173. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Wu, B.; Tian, Y.; Han, F.; Zheng, C. Optimizing conjunctive use of surface water and groundwater for irrigation to address human-nature water conflicts: A surrogate modeling approach. Agric. Water Manag. 2016, 163, 380–392. [Google Scholar] [CrossRef]
- Yeh, W.W. Review: Optimization methods for groundwater modeling and management. Hydrogeol. J. 2015, 23, 1051–1065. [Google Scholar] [CrossRef]
- Yeh, W.W. Systems analysis in ground-water planning and management. J. Water Resour. Plan. Manag. 1992, 118, 224–237. [Google Scholar] [CrossRef]
- Ahlfeld, D.P.; Mulvey, J.M.; Pinder, G.F.; Wood, E.F. Contaminated groundwater remediation design using simulation, optimization, and sensitivity theory: 1. Model development. Water Resour. Res. 1988, 24, 431–441. [Google Scholar] [CrossRef]
- Gorelick, S.M. A review of distributed parameter groundwater management modeling methods. Water Resour. Res. 1983, 19, 305–319. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, C. Groundwater management optimization using genetic algorithms and simulated annealing: Formulation and comparison. J. Am. Water Resour. Assoc. 1998, 34, 519–530. [Google Scholar] [CrossRef]
- Dogrul, E.C.; Kadir, T.; Brush, C.; Chung, F.I. Linking groundwater simulation and reservoir system analysis models: The case for California’s Central Valley. Environ. Model. Softw. 2016, 77, 168–182. [Google Scholar] [CrossRef]
- Timani, B.; Peralta, R. Multi-model groundwater-management optimization: Reconciling disparate conceptual models. Hydrogeol. J. 2015, 23, 1067–1087. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, P.; Chenglong, Z.; Ping, G. A generalized fuzzy credibility-constrained linear fractional programming approach for optimal irrigation water allocation under uncertainty. J. Hydrol. 2017, 553, 735–749. [Google Scholar] [CrossRef]
- An-Vo, D.-A.; Mushtaq, S.; Nguyen-Ky, T.; Bundschuh, J.; Tran-Cong, T.; Maraseni, T.N.; Reardon-Smith, K. Nonlinear optimization using production functions to estimate economic benefit of conjunctive water use for multicrop production. Water Resour. Manag. 2015, 29, 2153–2170. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Ma, M.; Liu, X. An intuitionistic fuzzy multi-objective non-linear programming model for sustainable irrigation water allocation under the combination of dry and wet conditions. J. Hydrol. 2017, 555, 80–94. [Google Scholar] [CrossRef]
- Macian-Sorribes, H.; Tilmant, A.; Pulido-Velazquez, M. Improving operating policies of large-scale surface-groundwater systems through stochastic programming. Water Resour. Res. 2017, 53, 1407–1423. [Google Scholar] [CrossRef]
- Zekri, S.; Triki, C.; Al-Maktoumi, A.; Bazargan-Lari, M.R. An optimization-simulation approach for groundwater abstraction under recharge uncertainty. Water Resour. Manag. 2015, 29, 3681–3695. [Google Scholar] [CrossRef]
- Ahmad, I.; Zhang, F.; Liu, J.; Anjum, M.N.; Zaman, M.; Tayyab, M.; Waseem, M.; Farid, H.U. A linear bi-level multi-objective program for optimal allocation of water resources. PLoS ONE 2018, 13, e0192294. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Ren, C. Water resources management models based on two-level linear fractional programming method under uncertainty. J. Water Resour. Plan. Manag. 2015, 141, 9. [Google Scholar] [CrossRef]
- Nicklow, J.W.; Reed, P.M.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the art for genetic algorithms and beyond in water resources planning and management. J. Water Resour. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, J.; Yang, Y.; Qian, J.; Wu, J. Multi-objective optimization of long-term groundwater monitoring network design using a probabilistic Pareto genetic algorithm under uncertainty. J. Hydrol. 2016, 534, 352–363. [Google Scholar] [CrossRef]
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.; Cunha, M.C.; Dandy, G.; Gibbs, M.; Keedwell, E.; Marchi, A.; et al. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Model. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef]
- Fowe, T.; Nouiri, I.; Ibrahim, B.; Karambiri, H.; Paturel, J.E. OPTIWAM: An intelligent tool for optimizing irrigation water management in coupled reservoir–groundwater systems. Water Resour. Manag. 2015, 29, 3841–3861. [Google Scholar] [CrossRef]
- Jha, M.K.; Sahoo, S. Efficacy of neural network and genetic algorithm techniques in simulating spatio-temporal fluctuations of groundwater. Hydrol. Process. 2014, 29, 671–691. [Google Scholar] [CrossRef]
- Perea, R.G.; Poyato, E.C.; Montesinos, P.; Díaz, J.A.R. Optimization of irrigation scheduling using soil water balance and genetic algorithms. Water Resour. Manag. 2016, 30, 2815–2830. [Google Scholar] [CrossRef]
- Yang, C.-C.; Chang, L.-C.; Chen, C.-S.; Yeh, M.-S. Multi-objective planning for conjunctive use of surface and subsurface water using genetic algorithm and dynamic programming. Water Resour. Manag. 2008, 23, 417–437. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; U.S. Geological Survey Techniques and Methods 6-A16; US Department of the Interior: Reston, VA, USA, 2005.
- Sahoo, S.; Jha, M.K.; Kumar, N.; Chowdary, V.M. Evaluation of GIS-based multicriteria decision analysis and probabilistic modeling for exploring groundwater prospects. Environ. Earth Sci. 2015, 74, 2223–2246. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Numerical groundwater-flow modeling to evaluate potential effects of pumping and recharge: Implications for sustainable groundwater management in the Mahanadi delta region, India. Hydrogeol. J. 2017, 25, 2489–2511. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Pattern recognition in lithology classification: Modeling using neural networks, self-organizing maps and genetic algorithms. Hydrogeol. J. 2016, 25, 311–330. [Google Scholar] [CrossRef]
- Sahoo, S. Assessment of Groundwater Resources and Simulation-Optimization Modeling in Deltaic Aquifer Systems. Ph.D. Thesis, Indian Institute of Technology Kharagpur, Kharagpur, India, 2015. [Google Scholar]
- Illangasekare, T.; Morel-Seytoux, H.J. Stream-aquifer influence coefficients as tools for simulation and management. Water Resour. Res. 1982, 18, 168–176. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J. A simple case of conjunctive surface-ground-water management. Ground Water 1975, 13, 506–515. [Google Scholar] [CrossRef]
- Waner, S.; Costenable, S. Finite Mathematics and Applied Calculus, 7th ed.; Cengage Learning: Boston, MA, USA, 2018. [Google Scholar]
- GAMS. GAMS User’s Guide; GAMS Development Corporation: Washington, DC, USA, 2020. [Google Scholar]
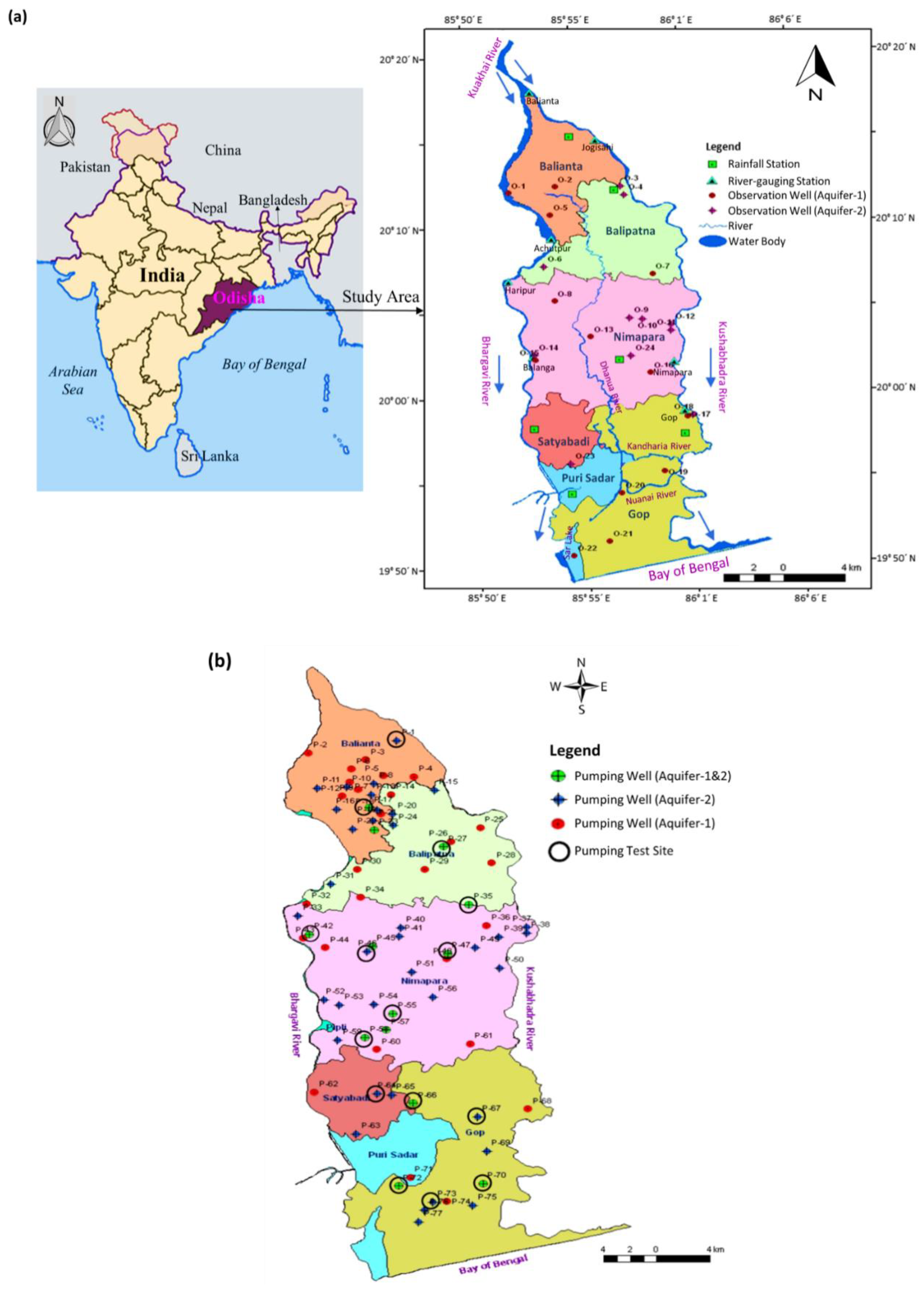

| Crop Growing Season (Period) | Type of Crop | Area Covered (ha) | Gross Irrigation Requirement (m) | |
|---|---|---|---|---|
| Kharif Season (mid-June to October-end) | Paddy | 22,893.37 | 0.36 | |
| Vegetables | 4973.34 | 0.48 | ||
| Rabi Season (November to February-end) | Cereals | Paddy | 2919.8 | 1.44 |
| Wheat | 28.34 | 0.456 | ||
| Maize | 16.34 | 0.66 | ||
| Pulses | Green Gram | 5870.1 | 0.18 | |
| Black Gram | 7773.6 | 0.18 | ||
| Horse Gram | 640.2 | 0.3 | ||
| Gram | 52.69 | 0.3 | ||
| Cow Peas | 45.6 | 0.384 | ||
| Oilseeds | Groundnut | 1788.4 | 0.42 | |
| Sesamum | 396.34 | 0.24 | ||
| Mustard | 631.34 | 0.42 | ||
| Sunflower | 177.52 | 0.36 | ||
| Linseed | 105.6 | 0.24 | ||
| Vegetables | Potato | 658.94 | 0.48 | |
| Onion | 115.36 | 0.72 | ||
| Tomato | 267.7 | 0.48 | ||
| Other Vegetables | 1812.3 | 0.42 | ||
| Spices | Chilli | 247.3 | 0.312 | |
| Garlic | 71.08 | 0.54 | ||
| Coriander | 274.23 | 0.36 | ||
| Sugarcane | 376.9 | 2.04 | ||
| Summer Season (March to mid-June) | Sesamum | 41.23 | 0.24 | |
| Okra | 85.7 | 0.48 | ||
| Cucumber | 94.5 | 0.36 | ||
| Watermelon | 95.6 | 0.54 | ||
| Head Control Location | Aquifer Layer | Row | Column | Optimal Head (Stress Period-1) | Optimal Head (Stress Period-2) |
|---|---|---|---|---|---|
| 1 | Aquifer-1 | 17 | 13 | 12.78 | 12.3 |
| 2 | Aquifer-2 | 42 | 44 | 12.57 | 12.25 |
| 3 | Aquifer-2 | 44 | 51 | 10.26 | 9.87 |
| 4 | Aquifer-2 | 43 | 51 | 12.15 | 11.78 |
| 5 | Aquifer-1 | 45 | 31 | 12.14 | 11.67 |
| 6 | Aquifer-2 | 49 | 17 | 6.25 | 5.87 |
| 7 | Aquifer-1 | 50 | 17 | 12.01 | 11.78 |
| 8 | Aquifer-1 | 53 | 45 | 8.15 | 8.02 |
| 9 | Aquifer-1 | 58 | 54 | 9.68 | 9.23 |
| 10 | Aquifer-2 | 58 | 55 | 10.8 | 8.55 |
| 11 | Aquifer-1 | 65 | 48 | 8.18 | 7.45 |
| 12 | Aquifer-1 | 16 | 24 | 8.45 | 7.56 |
| 13 | Aquifer-1 | 68 | 40 | 11.15 | 10.8 |
| 14 | Aquifer-1 | 79 | 33 | 11.25 | 10.5 |
| 15 | Aquifer-1 | 81 | 24 | 8.09 | 7.6 |
| 16 | Aquifer-2 | 64 | 24 | 9.45 | 8.65 |
| 17 | Aquifer-2 | 50 | 41 | 4.41 | 4.2 |
| 18 | Aquifer-2 | 17 | 40 | 5.06 | 4.5 |
| 19 | Aquifer-2 | 19 | 41 | 6.43 | 5.87 |
| 20 | Aquifer-1 | 23 | 23 | 7.53 | 6.45 |
| 21 | Aquifer-2 | 32 | 20 | 5.03 | 4.5 |
| 22 | Aquifer-1 | 33 | 47 | 4.17 | 4.05 |
| 23 | Aquifer-1 | 37 | 23 | 5.08 | 4.6 |
| 24 | Aquifer-2 | 41 | 41 | 8.45 | 7.65 |
| Season | Crop | Optimally Allocated Area (ha) | Gross Irrigation Requirement (106 m3) | Annual Income (107 Rs.) | |||
|---|---|---|---|---|---|---|---|
| High Land | Medium Land | Lowland | Total | ||||
| Kharif | Rice | 11,231.52 | 11,167.37 | 14,031.2 | 36,430.09 | 131.15 | 92.90 |
| Vegetables | 2933 | 5590 | 8523 | 40.91 | 71.93 | ||
| Rabi | Rice | 896 | 7590.8 | 3916 | 12,402.8 | 178.60 | 17.36 |
| Wheat | - | 36.04 | - | 36.04 | 0.16 | 0.03 | |
| Maize | - | 24.54 | - | 24.54 | 0.16 | 0.02 | |
| Green Gram | 1785.1 | - | - | 1785.1 | 3.21 | 1.68 | |
| Black Gram | 4663.6 | - | - | 4663.6 | 8.39 | 6.72 | |
| Horse Gram | 485.2 | - | - | 485.2 | 1.46 | 0.03 | |
| Gram | 72.69 | - | 72.69 | 0.22 | 0.09 | ||
| Cow Peas | - | 68.6 | - | 68.6 | 0.26 | 0.06 | |
| Groundnut | 794.4 | - | - | 794.4 | 3.34 | 1.15 | |
| Sesamum | - | - | 195 | 195 | 0.47 | 0.08 | |
| Mustard | - | - | 405 | 405 | 1.70 | 0.04 | |
| Sunflower | 192.2 | - | - | 192.2 | 0.69 | 0.50 | |
| Linseed | - | - | 105.6 | 105.6 | 0.25 | 0.01 | |
| Potato | - | 1258.94 | 781.84 | 2040.78 | 9.80 | 8.12 | |
| Onion | - | 514.36 | 175.36 | 689.72 | 4.97 | 4.16 | |
| Tomato | - | 187.7 | 477.7 | 665.4 | 3.19 | 5.29 | |
| Other Veg | - | 6571.5 | 10,976.3 | 17,547.8 | 73.70 | 147.75 | |
| Chilli | 282.3 | - | 297.3 | 579.6 | 1.81 | 1.94 | |
| Garlic | - | 95.08 | - | 95.08 | 0.51 | 0.58 | |
| Corriander | 304.23 | - | - | 304.23 | 1.10 | 0.63 | |
| Sugarcane | - | 798.9 | - | 798.9 | 16.30 | 1.95 | |
| Summer | Sesamum | - | - | 78.7 | 78.7 | 0.19 | 0.05 |
| Okra | - | - | 258.5 | 258.5 | 1.24 | 0.22 | |
| Cucumber | - | - | 387.5 | 387.5 | 1.40 | 1.05 | |
| Water melon | - | - | 445.5 | 445.5 | 2.41 | 1.78 | |
| Total | 487.58 | 366.13 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jha, M.K.; Peralta, R.C.; Sahoo, S. Simulation-Optimization for Conjunctive Water Resources Management and Optimal Crop Planning in Kushabhadra-Bhargavi River Delta of Eastern India. Int. J. Environ. Res. Public Health 2020, 17, 3521. https://doi.org/10.3390/ijerph17103521
Jha MK, Peralta RC, Sahoo S. Simulation-Optimization for Conjunctive Water Resources Management and Optimal Crop Planning in Kushabhadra-Bhargavi River Delta of Eastern India. International Journal of Environmental Research and Public Health. 2020; 17(10):3521. https://doi.org/10.3390/ijerph17103521
Chicago/Turabian StyleJha, Madan K., Richard C. Peralta, and Sasmita Sahoo. 2020. "Simulation-Optimization for Conjunctive Water Resources Management and Optimal Crop Planning in Kushabhadra-Bhargavi River Delta of Eastern India" International Journal of Environmental Research and Public Health 17, no. 10: 3521. https://doi.org/10.3390/ijerph17103521
APA StyleJha, M. K., Peralta, R. C., & Sahoo, S. (2020). Simulation-Optimization for Conjunctive Water Resources Management and Optimal Crop Planning in Kushabhadra-Bhargavi River Delta of Eastern India. International Journal of Environmental Research and Public Health, 17(10), 3521. https://doi.org/10.3390/ijerph17103521






