Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Formulating the SEIRD Model
- N was the total population given by the sum of each state;
- βcom, βhos, and βicu were the transmission rates in the three infectious categories;
- σ was the infection rate (i.e., the inverse of the incubation period) assumed to be the same for each infectious category;
- υcom, υhos, and υicu were the probabilities that each exposed individual progressed to Icom, Ihos or Iicu;
- γ was the removing rate (i.e., assumed to be the inverse of the infectious period between onset of symptoms and recovering/death);
- μcom, μhos, and μicu were the probabilities of dying among infectious individuals.
2.2. Fitting the Model to the Reported Number of ICU Patients and Deaths
- Iicu−obs and Iicu−est were the number of observed and estimated ICU patients at each time (t) from 24 February to 17 March. Thus, in the baseline scenario, nicu was set to 23 (i.e., the number of days between start and end dates of the model fitting on ICU patients);
- Dobs and Dest were the number of observed and estimated deaths at each time (t) from 24 February to 24 March. Thus, in the baseline scenario, ndeaths was set to 30 (i.e., the number of days between start and end dates of the model fitting on deaths).
2.3. Modeling the SARS-CoV-2 Transmission after the Adoption of Control Measures
2.4. Sensitivity Analysis
3. Results
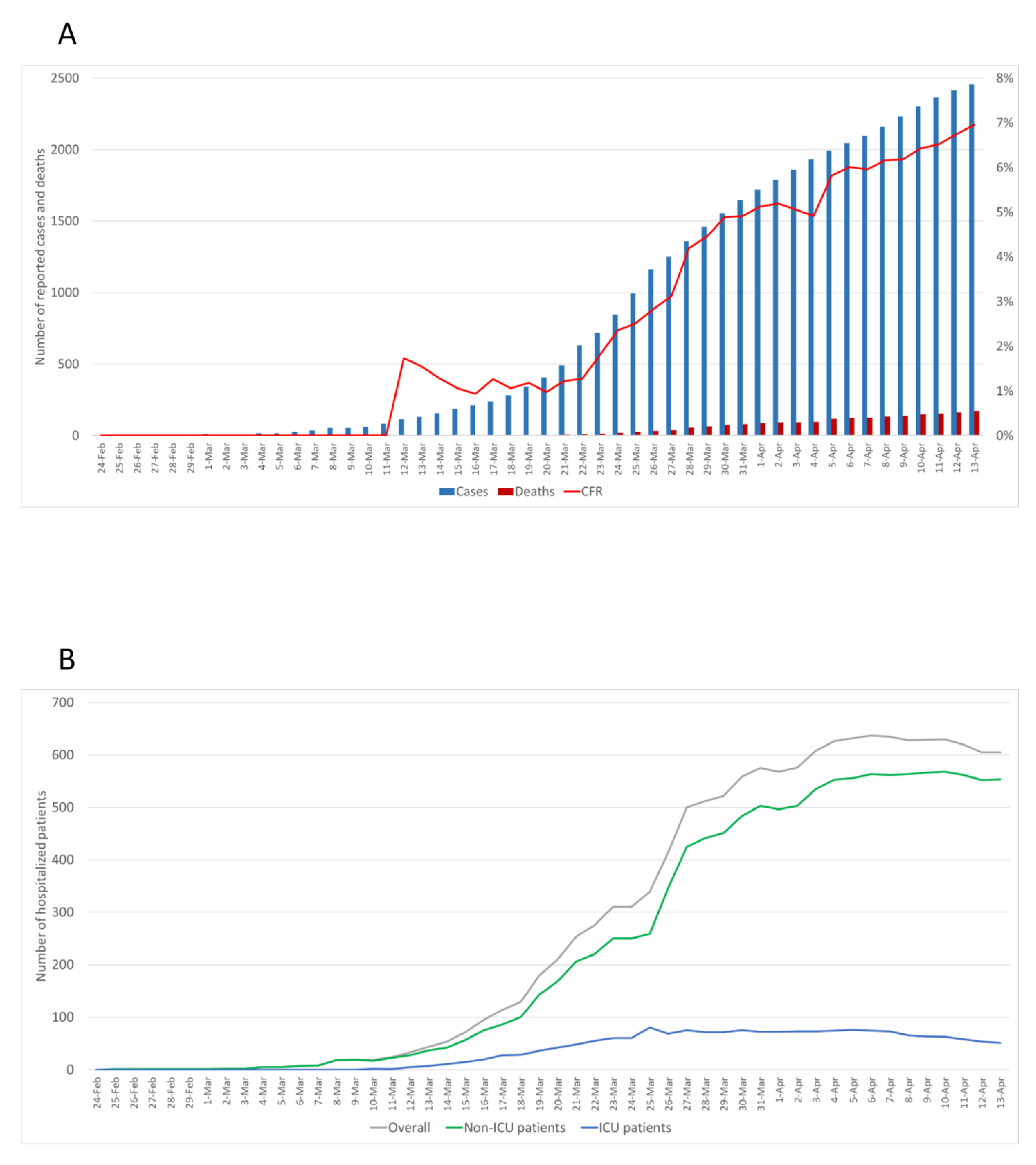
3.1. Description of Reported Data
3.2. The Epidemic Curve Prior to Restrictions
3.3. The Effect of Control Measures on Transmission Rates
3.4. Sensitivity Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Italian Ministry of Health. Covid-19: Situation Report Update at 14 April 18:00. Available online: http://opendatadpc.maps.arcgis.com/apps/opsdashboard/index.html#/b0c68bce2cce478eaac82fe38d4138b1 (accessed on 14 April 2020).
- World Health Organization. Health-Topics: Coronavirus. Available online: https://www.who.int/health-topics/coronavirus#tab=tab_1 (accessed on 30 May 2020).
- Italian Ministry of Health. Novel Coronavirus. Available online: http://www.salute.gov.it/portale/nuovocoronavirus/homeNuovoCoronavirus.jsp?lingua=english (accessed on 30 May 2020).
- Signorelli, C.; Scognamiglio, T.; Odone, A. COVID-19 in Italy: Impact of containment measures and prevalence estimates of infection in the general population. Acta Biomed. 2020, 91, 175–179. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science 2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Wang, Z.; Dong, Y.; Chang, R.; Xu, C.; Yu, X.; Zhang, S.; Tsamlag, L.; Shang, M.; Huang, J.; et al. Phase-adjusted estimation of the number of coronavirus disease 2019 cases in Wuhan, China. Cell Discov. 2020, 6, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maugeri, A.; Barchitta, M.; Battiato, S.; Agodi, A. Estimation of unreported novel coronavirus (SARS-CoV-2) infections from reported deaths: A susceptible exposed infectious recovered dead model. J. Clin. Med. 2020, 9, 1350. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M.; Donnelly, C.A.; Fraser, C.; Blake, I.M.; Cori, A.; Dorigatti, I.; Ferguson, N.M.; Garske, T.; Mills, H.L.; Riley, S.; et al. Potential biases in estimating absolute and relative case-fatality risks during outbreaks. PLoS Negl. Trop. Dis. 2015, 9, e0003846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gill, P.E.; Murray, W.; Saunders, M.A. Large-scale SQP Methods and their Application in Trajectory Optimization. In Computational Optimal Control; Bulirsch, R., Kraft, D., Eds.; Birkhäuser Basel: Basel, Switzerland, 1994; pp. 29–42. [Google Scholar]
- Zhu, H.; Li, Y.; Jin, X.; Huang, J.; Liu, X.; Qian, Y.; Tan, J. Transmission dynamics and control methodology of COVID-19: A modeling study. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Grasselli, G.; Zangrillo, A.; Zanella, A.; Antonelli, M.; Cabrini, L.; Castelli, A.; Cereda, D.; Coluccello, A.; Foti, G.; Fumagalli, R.; et al. Baseline characteristics and outcomes of 1591 patients infected with SARS-CoV-2 admitted to ICUs of the Lombardy Region, Italy. JAMA 2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, N.; Zhou, M.; Dong, X.; Qu, J.; Gong, F.; Han, Y.; Qiu, Y.; Wang, J.; Liu, Y.; Wei, Y.; et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet 2020, 395, 507–513. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Lu, Q.; Liu, M.; Wang, Y.; Zhang, A.; Jalali, N.; Dean, N.; Longini, I.; Halloran, M.; Xu, B.; et al. Epidemiological and clinical features of the 2019 novel coronavirus outbreak in China. medRxiv 2020, 02. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Imperial College COVID-19 Response Team. Estimating the Number of Infections and the Impact of Non-Pharmaceutical Interventions on COVID-19 in 11 European Countries; Imperial College London: London, UK, 2020. [Google Scholar]
- Tuite, A.R.; Ng, V.; Rees, E.; Fisman, D. Estimation of COVID-19 outbreak size in Italy. Lancet Infect Dis. 2020. [Google Scholar] [CrossRef] [Green Version]
- Onder, G.; Rezza, G.; Brusaferro, S. Case-Fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. JAMA 2020. [Google Scholar] [CrossRef] [PubMed]
- Scafetta, N. Distribution of the SARS-CoV-2 pandemic and its monthly forecast based on seasonal climate patterns. Int. J. Environ. Res. Public Health 2020, 17, 3493. [Google Scholar] [CrossRef] [PubMed]
- Torri, E.; Sbrogiò, L.G.; Rosa, E.D.; Cinquetti, S.; Francia, F.; Ferro, A. Italian public health response to the COVID-19 pandemic: Case report from the field, insights and challenges for the department of prevention. Int. J. Environ. Res. Public Health 2020, 17, 3666. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Sun, J.; Nie, S.; Li, H.; Kong, Y.; Liang, M.; Hou, J.; Huang, X.; Li, D.; Ma, T.; et al. Seroprevalence of immunoglobulin M and G antibodies against SARS-CoV-2 in China. Nat. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.G.; Klepac, P.; Liu, Y.; Prem, K.; Jit, M.; Eggo, R.M. CMMID COVID-19 working group. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med. 2020. [Google Scholar] [CrossRef]



| Initial Model Parameters | Definition | Assumption or Constraints |
|---|---|---|
| Starting date a | The first of the modeling | 20 February 2020 |
| Nb | Total population | 5,000,000 |
| S | Susceptible individuals | 4,999,999 |
| E | Exposed individuals | 0 |
| Icom | Non-hospitalized patients | 1 |
| Ihos | Patients hospitalized in non-intensive care wards | 0 |
| Iicu | Patients hospitalized in ICU | 0 |
| R | Recovered | 0 |
| D | Deaths | 0 |
| βcom | Transmission rates in the three infectious categories | 0.1 ≤ βcom ≤ 2 |
| βhos | 0.1 ≤ βhos ≤ 2 | |
| βicu | 0.1 ≤ βicu ≤ 2 | |
| σc | Infection rate | 0.19 |
| υcomd | Probabilities of progressing to Icom, Ihos or Iicu | 0.1 ≤ υcom < 1 |
| υhosd | 0.1 ≤ υhos < 0.25 | |
| υicud | 0.1 ≤ υicu < υhos | |
| γe | Removing rate | 0.08 |
| μcom | Probabilities of dying among Icom, Ihos or Iicu | 0 ≤ μcom < μhos |
| μhos | μcom < μhos < μicu | |
| μicu | μhos < μicu ≤ 1 |
| SEIRD Parameters | Definition | Estimated Values (95%CI) |
|---|---|---|
| βcom | Transmission rate | 0.99 (0.96–1.04) |
| βhos | 0.37 (0.32–0.43) | |
| βicu | 0.28 (0.24–0.33) | |
| υcom | Probability of progression to Icom, Ihos, or Iicu | 0.76 (0.70–0.82) |
| υhos | 0.19 (0.15–0.23) | |
| υicu | 0.05 (0.03–0.07) | |
| μcom | Probability of dying | 0.01 (0.00–0.02) |
| μhos | 0.07 (0.04–0.10) | |
| μicu | 0.26 (0.20–0.30) |
| Control Measures | Transmission Rates | Estimated Values (95%CI) |
|---|---|---|
| First set of restrictions adopted on $$$10 March 2020 | βcom | 0.67 (0.57–0.76) |
| βhos | 0.34 (0.33–0.35) | |
| βicu | 0.25 (0.23–0.27) | |
| Second set of restrictions adopted on 23 March 2020 | βcom | 0.20 (0.11–0.30) |
| βhos | 0.28 (0.25–0.31) | |
| βicu | 0.22 (0.20–0.25) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maugeri, A.; Barchitta, M.; Battiato, S.; Agodi, A. Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy. Int. J. Environ. Res. Public Health 2020, 17, 4964. https://doi.org/10.3390/ijerph17144964
Maugeri A, Barchitta M, Battiato S, Agodi A. Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy. International Journal of Environmental Research and Public Health. 2020; 17(14):4964. https://doi.org/10.3390/ijerph17144964
Chicago/Turabian StyleMaugeri, Andrea, Martina Barchitta, Sebastiano Battiato, and Antonella Agodi. 2020. "Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy" International Journal of Environmental Research and Public Health 17, no. 14: 4964. https://doi.org/10.3390/ijerph17144964
APA StyleMaugeri, A., Barchitta, M., Battiato, S., & Agodi, A. (2020). Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy. International Journal of Environmental Research and Public Health, 17(14), 4964. https://doi.org/10.3390/ijerph17144964








