Response of a Coastal Groundwater System to Natural and Anthropogenic Factors: Case Study on East Coast of Laizhou Bay, China
Abstract
1. Introduction
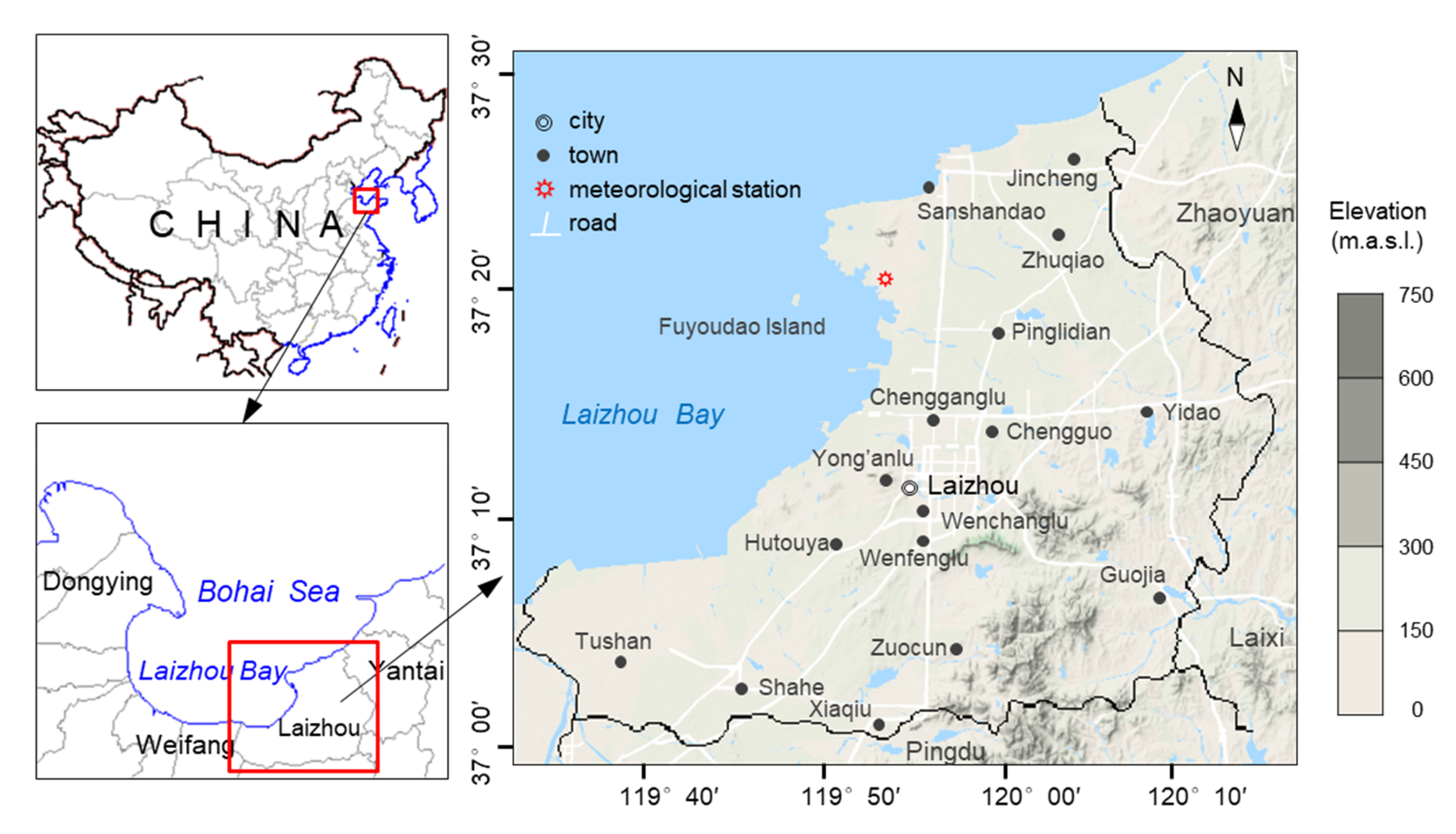
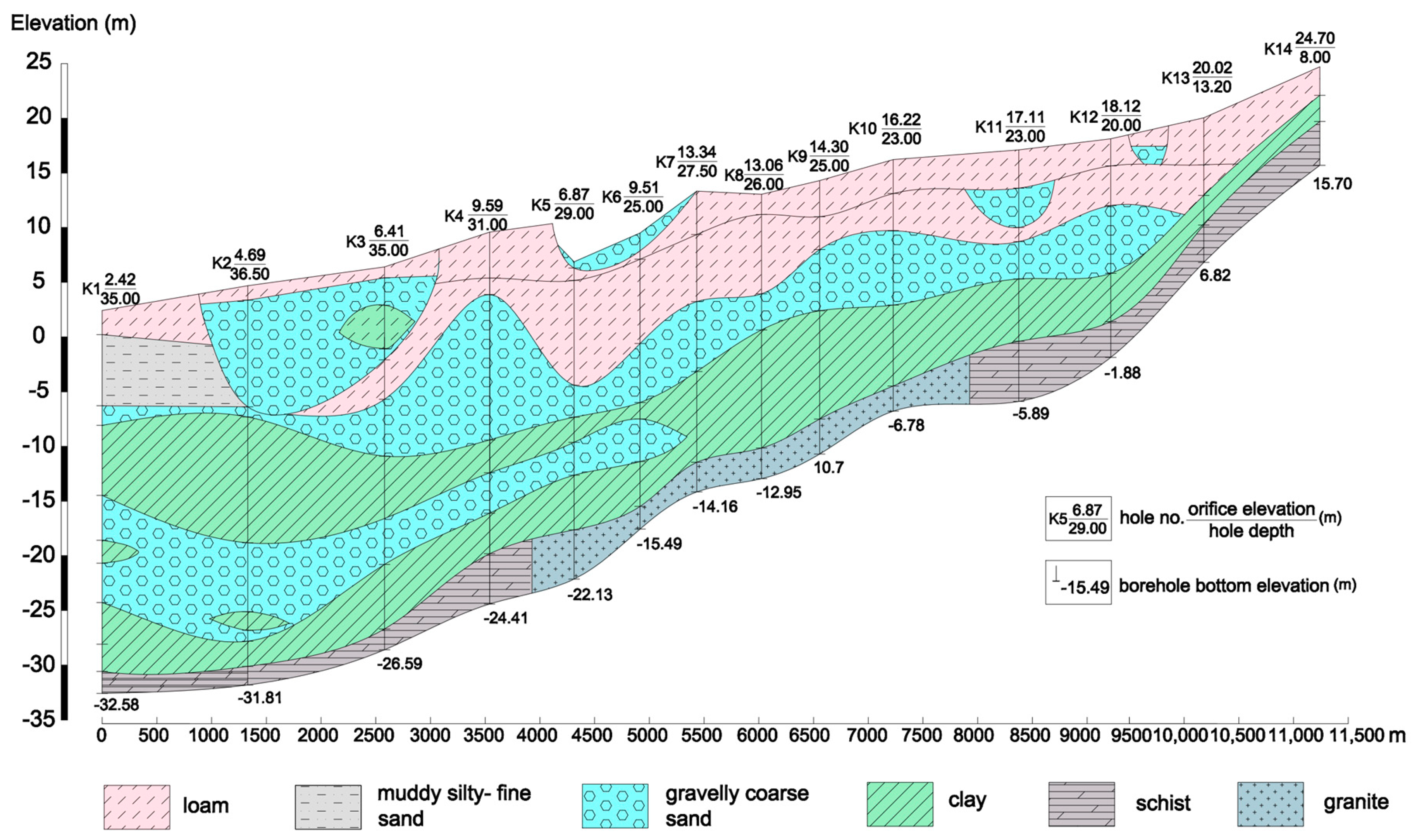
2. Overview of the Study Area
3. Materials and Methods
3.1. Water Sample Collection and Analysis
3.2. BP-ANN Model
3.2.1. Basic Theory and Algorithm
3.2.2. Determination of Input and Output Factors
3.3. Sensitivity Analysis
3.4. Hydrochemical Diagrams and ion Ratio Coefficients
3.5. Fuzzy Clustering
4. Results
4.1. BP-ANN Model for Groundwater Level Dynamics and Factor Sensitivity Analysis
4.2. Preprocessing of Training Samples
4.3. Model Construction and Training
4.4. Sensitivity Analysis
4.5. Groundwater Hydrochemical Characteristics
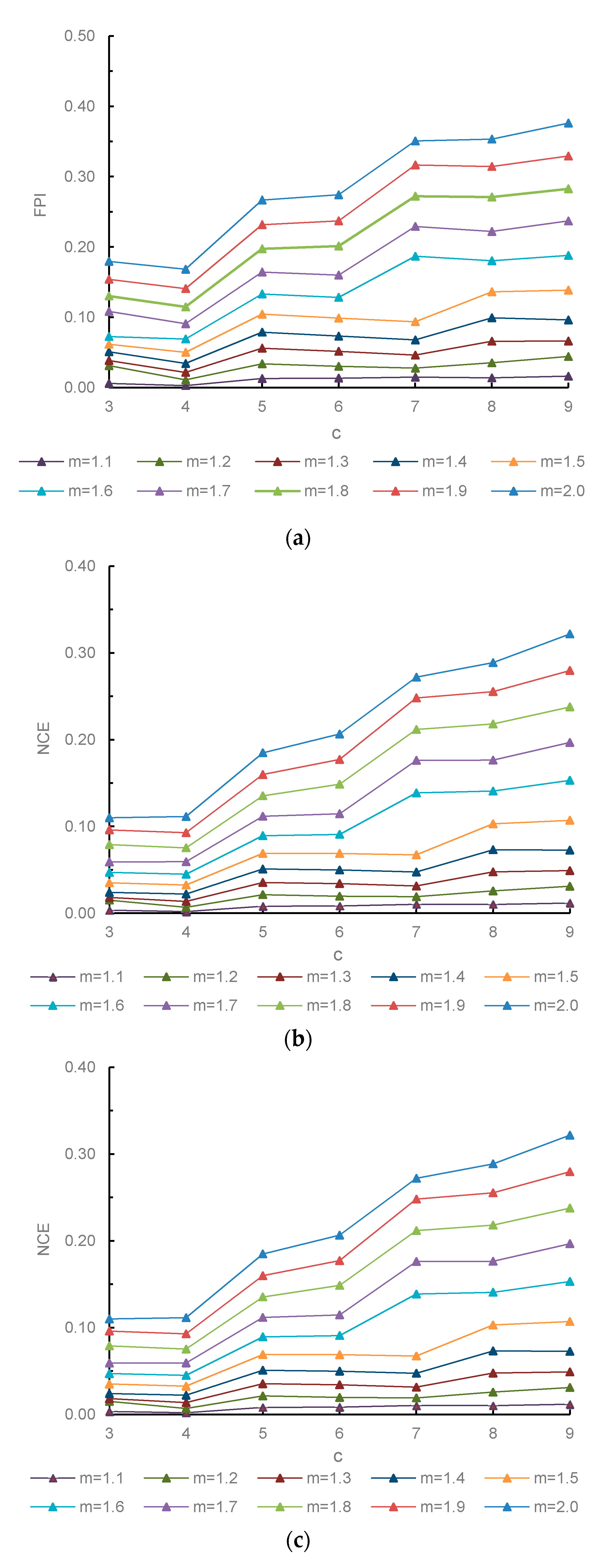
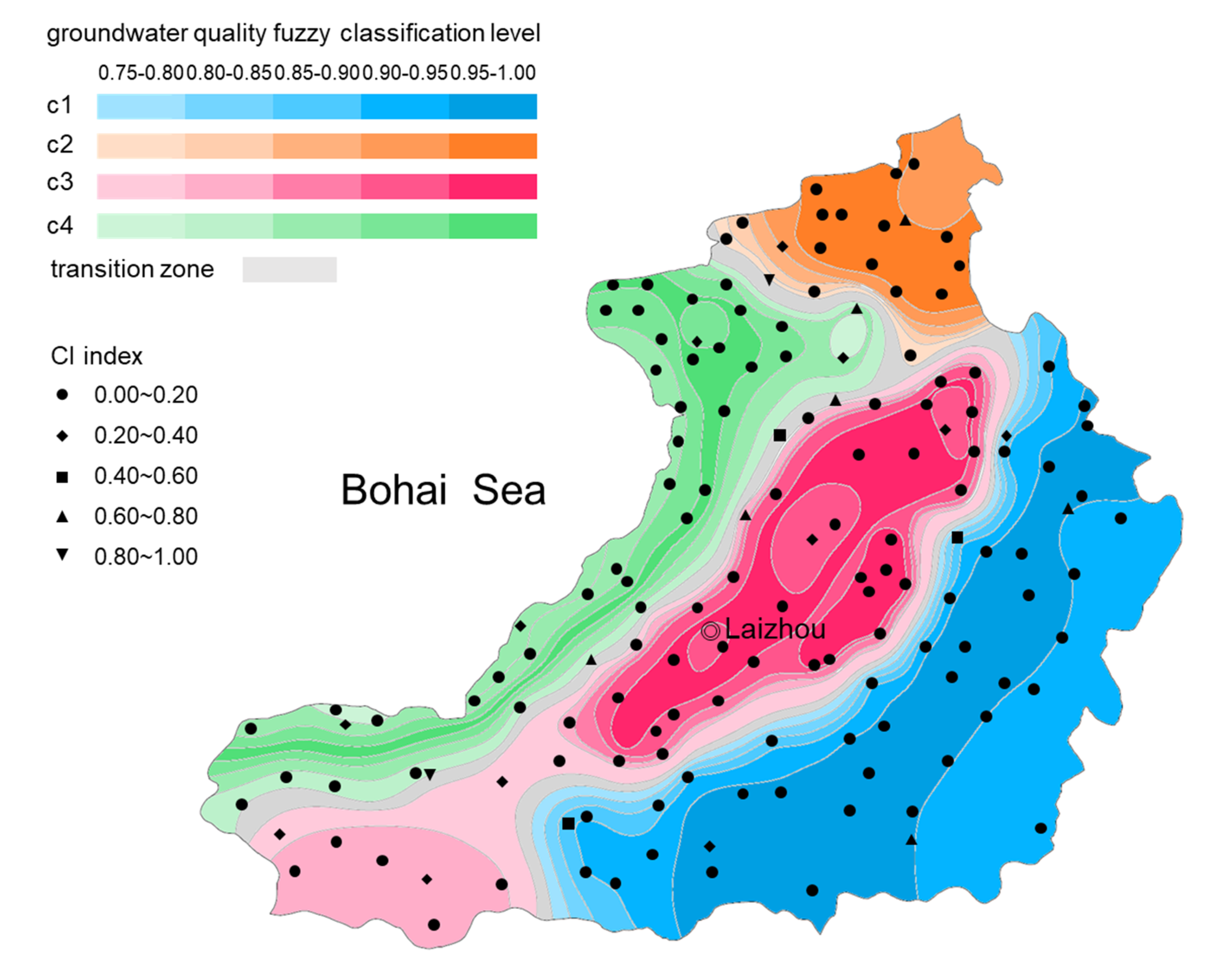
4.6. Groundwater Quality Classification Based on Fuzzy Clustering
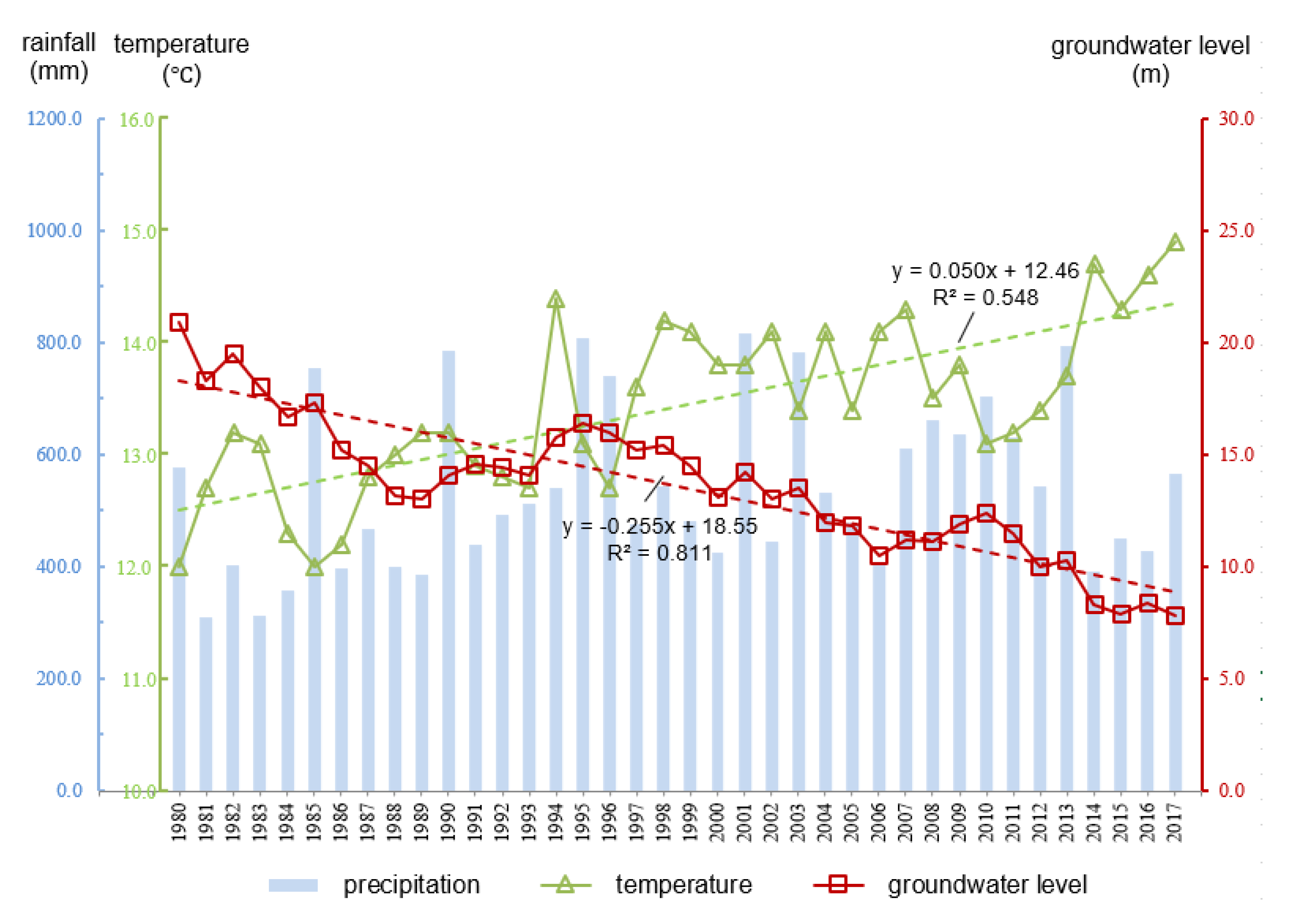
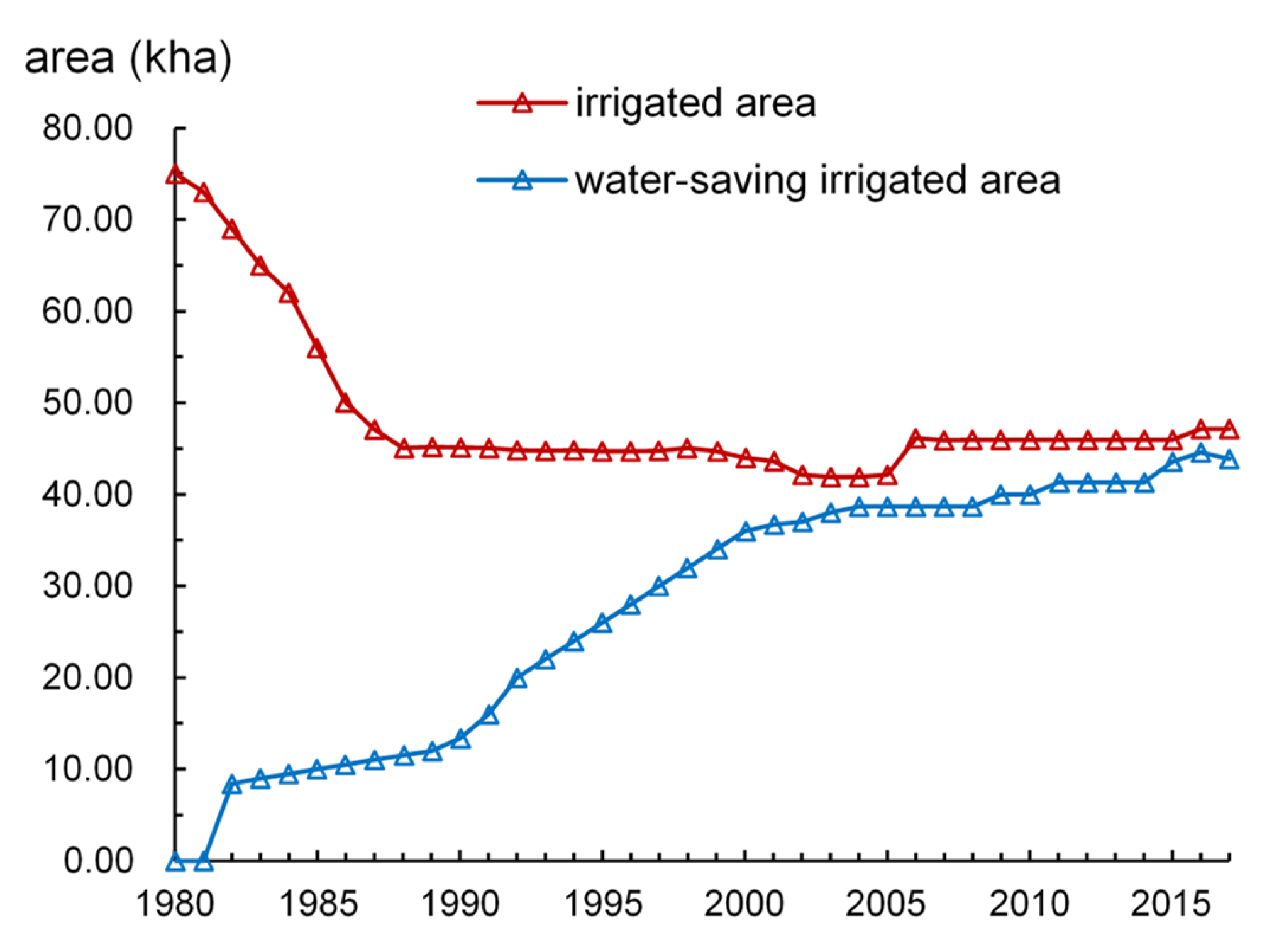
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferguson, G.; Gleeson, T. Vulnerability of coastal aquifers to groundwater use and climate change. Nat. Clim. Chang. 2012, 2, 342–345. [Google Scholar] [CrossRef]
- Michael, H.A.; Russoniello, C.; Byron, L.A. Global assessment of vulnerability to sea-level rise in topography-limited and recharge-limited coastal groundwater systems. Water Resour. Res. 2013, 49, 2228–2240. [Google Scholar] [CrossRef]
- Michael, H.A.; Post, V.E.A.; Wilson, A.M.; Werner, A. Science, society, and the coastal groundwater squeeze. Water Resour. Res. 2017, 53, 2610–2617. [Google Scholar] [CrossRef]
- Kammoun, S.; Re, V.; Trabelsi, R.; Zouari, K.; Daniele, S. Assessing seasonal variations and aquifer vulnerability in coastal aquifers of semi-arid regions using a multi-tracer isotopic approach: The case of Grombalia (Tunisia). Hydrogeol. J. 2018, 26, 2575–2594. [Google Scholar] [CrossRef]
- Re, V.; Faye, S.C.; Faye, A.; Faye, S.; Gaye, C.B.; Sacchi, E.; Zuppi, G.M. Water quality decline in coastal aquifers under anthropic pressure: The case of a suburban area of Dakar (Senegal). Environ. Monit. Assess. 2010, 172, 605–622. [Google Scholar] [CrossRef]
- Sbarbati, C.; Colombani, N.; Mastrocicco, M.; Aravena, R.; Petitta, M. Performance of different assessment methods to evaluate contaminant sources and fate in a coastal aquifer. Environ. Sci. Pollut. Res. 2015, 22, 15536–15548. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.H.; Wu, Q.; Mou, X.L.; Lai, Y.J. Potential Impacts of Climate Change on the Water Quality of Different Water Bodies. J. Environ. Inform. 2015, 25, 85–98. [Google Scholar] [CrossRef]
- Delinom, R.M.; Assegaf, A.; Abidin, H.Z.; Taniguchi, M.; Suherman, D.; Lubis, R.F.; Yulianto, E. The contribution of human activities to subsurface environment degradation in Greater Jakarta Area, Indonesia. Sci. Total. Environ. 2009, 407, 3129–3141. [Google Scholar] [CrossRef]
- Huang, G.; Sun, J.; Zhang, Y.; Chen, Z.; Liu, F. Impact of anthropogenic and natural processes on the evolution of groundwater chemistry in a rapidly urbanized coastal area, South China. Sci. Total. Environ. 2013, 463, 209–221. [Google Scholar] [CrossRef]
- Medici, G.; West, L.J.; Chapman, P.J.; Banwart, S.A. Prediction of contaminant transport in fractured carbonate aquifer types: A case study of the Permian Magnesian Limestone Group (NE England, UK). Environ. Sci. Pollut. Res. 2019, 26, 24863–24884. [Google Scholar] [CrossRef]
- Sekovski, I.; Newton, A.; Dennison, W.C. Megacities in the coastal zone: Using a driver-pressure-state-impact-response framework to address complex environmental problems. Estuarine, Coast. Shelf Sci. 2012, 96, 48–59. [Google Scholar] [CrossRef]
- Taniguchi, M. Groundwater and Subsurface Environments: Human Impacts in Asian Coastal Cities; Springer Science & Business Media: Berlin, Germany, 2011; ISBN 978-4-431-53904-9. [Google Scholar]
- Holman, I. Climate change impacts on groundwater recharge- uncertainty, shortcomings, and the way forward? Hydrogeol. J. 2005, 14, 637–647. [Google Scholar] [CrossRef]
- Lv, C.; Ling, M.; Wu, Z.; Gu, P.; Guo, X.; Di, D. Analysis of groundwater variation in the Jinci Spring area, Shanxi Province (China), under the influence of human activity. Environ. Geochem. Heal. 2018, 41, 921–928. [Google Scholar] [CrossRef]
- Chen, H.R.; Gao, Z.Y.; Wang, S.L.; Hu, Y.Q. Modeling on impacts of climate change and human activities variability on the shallow groundwater level using Modflow. J. Hydraul. Eng. 2012, 43, 344–353, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Wang, J.Z.; Zhang, G.H.; Nie, Z.L.; Yan, M.J.; Wang, Y. Disturbing Degree of Mankind Activities to Groundwater in the Hutuo River Valley Area. Bull. Soil Water Conserv. 2010, 30, 65–69, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Feng, S.Y.; Huo, Z.L.; Kang, S.J.; Chen, S.J. ANN model for simulating dynamic variation of groundwater under the condition of natural-human activity in arid-inland area. J. Hydraul. Eng. 2007, 38, 873–878, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Liu, J.; Yang, P.N.; Kan, J.; Gao, Y.Y. Dynamic Trend and Driving Factors of Groundwater in Shawan Irrigated District under Changing Environment. Water Saving Irrigation 2019, 3, 53–58, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Cheng, D.H.; Chen, H.H.; He, J.T.; Lin, J.; Yang, D.G.; Yu, H. A study of indicators of anthropogenic influence and water-rock interaction in groundwater system in the urban region of Beijing. Hydrogeol. Eng. Geol. 2007, 35, 37–42, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Zhao, W.; Lin, J.; Wang, S.-F.; Liu, J.-L.; Chen, Z.-R.; Kou, W.-J. Influence of human activities on groundwater environment based on coefficient variation method. Huan Jing Ke Xue 2013, 34, 1277–1283. [Google Scholar]
- Liu, L.; Zhou, X.; Ye, Y.H. Screening of characteristic indexes for shallow groundwater influenced by human activities using multivariate statistics. East China Geol. 2014, 35, 305–310, (In Chinese with English abstract). [Google Scholar]
- Peng, C.; He, J.T.; Liao, L.; Zhang, Z.G. Research on the influence degree of human activities on groundwater quality by the method of geochemistry: A case study from Liujiang Basin. Earth Sci. Front. 2017, 24, 321–331, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Zhang, X.-W.; He, J.-T.; Peng, C.; Zhang, C.-Y.; Ni, Z.-H. Comparison of Identification Methods of Main Component Hydrochemical Anomalies in Groundwater: A Case Study of Liujiang Basin. Huan Jing Ke Xue 2017, 38, 3225–3234. [Google Scholar] [PubMed]
- Güler, C.; Kurt, M.A.; Alpaslan, M.; Akbulut, C. Assessment of the impact of anthropogenic activities on the groundwater hydrology and chemistry in Tarsus coastal plain (Mersin, SE Turkey) using fuzzy clustering, multivariate statistics and GIS techniques. J. Hydrol. 2012, 414, 435–451. [Google Scholar] [CrossRef]
- Brink, C.V.D.; Frapporti, G.; Griffioen, J.; Zaadnoordijk, W. Statistical analysis of anthropogenic versus geochemical-controlled differences in groundwater composition in The Netherlands. J. Hydrol. 2007, 336, 470–480. [Google Scholar] [CrossRef]
- Re, V.; Sacchi, E.; Mas-Pla, J.; Menció, A.; El Amrani, N. Identifying the effects of human pressure on groundwater quality to support water management strategies in coastal regions: A multi-tracer and statistical approach (Bou-Areg region, Morocco). Sci. Total. Environ. 2014, 500, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Merchán, D.; Auqué, L.; Acero, P.; Gimeno, M.J.; Causapé, J. Geochemical processes controlling water salinization in an irrigated basin in Spain: Identification of natural and anthropogenic influence. Sci. Total. Environ. 2015, 502, 330–343. [Google Scholar] [CrossRef]
- Hecht, N.R. Kolmogorov’s Mapping Neural Network Existence Theorem. In Proceedings of the International Conference on Neural Networks, New York, NY, USA, 21 June 1987; IEEE Press: New York, NY, USA, 1987; Volume 3, pp. 11–13. [Google Scholar]
- Ju, Q.; Yu, Z.; Hao, Z.; Ou, G.; Zhao, J.; Liu, D. Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model. Neurocomputing 2009, 72, 2873–2883. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP Neural Network Algorithm in Traditional Hydrological Model for Flood Forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Huang, L.M.; Ren, S.M.; Yang, P.L.; Shui, P.; Cao, J.W.; Zhou, R. Soil moisture forecast BP-ANN model and simulation based on sensitivity analysis. J. China Agric. Univ. 2013, 18, 166–172. [Google Scholar]
- Liu, G.D.; Ding, J. Discussion on problems of BP neural networks applied to hydrological prediction. J. Hydraul. Eng. 1999, 1, 65–70. [Google Scholar] [CrossRef]
- Li, Z. Overview of groundwater extraction calculation methods. Haihe Water Resour. 2014, 1, 34–36. (In Chinese) [Google Scholar] [CrossRef]
- Deng, J.L. Grey System Theory and Method; Huazhong University of Science and Technology: Wuhan, China, 2005; ISBN 7-5609-3436-6. [Google Scholar]
- Lakshmanan, E.; Kannan, R.; Kumar, M.S. Major ion chemistry and identification of hydrogeochemical processes of ground water in a part of Kancheepuram district, Tamil Nadu, India. Environ. Geosci. 2003, 10, 157–166. [Google Scholar] [CrossRef]
- Global chemical weathering of surficial rocks estimated from river dissolved loads. Deep. Sea Res. Part B. Oceanogr. Lit. Rev. 1987, 34, 1041. [CrossRef]
- Sachse, A.; Jakobs, L.; Kolditz, O. (Eds.) Hydrogeology. In OpenGeoSys Tutorial; Springer: Cham, Switzerland, 2015; pp. 13–17. [Google Scholar]
- Mayo, A.L.; Loucks, M.D. Solute and isotopic geochemistry and ground water flow in the central Wasatch Range, Utah. J. Hydrol. 1995, 172, 31–59. [Google Scholar] [CrossRef]
- Jalali, M. Chemical characteristics of groundwater in parts of mountainous region, Alvand, Hamadan, Iran. Environ. Earth Sci. 2006, 51, 433–446. [Google Scholar] [CrossRef]
- Rouabhia, A.; Larbi, D.; Rihab, H.; Fethi, B.; Chemseddine, F.; Azzedine, H. Geochemical characterization of groundwater from shallow aquifer surrounding Fetzara Lake N. E. Algeria. Arab. J. Geosci. 2010, 5, 1–13. [Google Scholar] [CrossRef]
- Cerling, T.E.; Pederson, B.L.; Von Damm, K.L. Sodium-calcium ion exchange in the weathering of shales: Implications for global weathering budgets. Geol. 1989, 17, 552. [Google Scholar] [CrossRef]
- Schoeller, H. Qualitative Evaluation of Groundwater Resources. In Methods and Qualitative Evaluation of Groundwater Resources, In Methods and Techniques of Groundwater Investigation and Development; Water Resources Series No. 33; UNESCO: Paris, France, 1967; pp. 44–52. [Google Scholar]
- Schoeller, H. Geochemistry of groundwater. In Groundwater Studies—An International Guide for Research and Practice; UNESCO: Paris, France, 1977; pp. 1–18. [Google Scholar]
- Chang, N.-B.; Chen, H.; Ning, S. Identification of river water quality using the Fuzzy Synthetic Evaluation approach. J. Environ. Manag. 2001, 63, 293–305. [Google Scholar] [CrossRef]
- Chen, Q.; Mynett, A.E. Integration of data mining techniques and heuristic knowledge in fuzzy logic modelling of eutrophication in Taihu Lake. Ecol. Model. 2003, 162, 55–67. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Li, F.; Li, H. Delineation of site-specific management zones using fuzzy clustering analysis in a coastal saline land. Comput. Electron. Agric. 2007, 56, 174–186. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Soil Pattern Recognition with Fuzzy-c-means: Application to Classification and Soil-Landform Interrelationships. Soil Sci. Soc. Am. J. 1992, 56, 505–516. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science and Business Media LLC: Basel, Switzerland, 1981; ISBN 978–1–4757–0452–5. [Google Scholar]
- McBratney, A.B.; Moore, A. Application of fuzzy sets to climatic classification. Agric. For. Meteorol. 1985, 35, 165–185. [Google Scholar] [CrossRef]
- Lark, R.M.; Stafford, J.V. Classification as a first step in the interpretation of temporal and spatial variation of crop yield. Ann. Appl. Boil. 1997, 130, 111–121. [Google Scholar] [CrossRef]
- Burrough, P.; Van Gaans, P.; Hootsmans, R. Continuous classification in soil survey: Spatial correlation, confusion and boundaries. Geoderma 1997, 77, 115–135. [Google Scholar] [CrossRef]
- Du, S.; Su, X.; Zhang, W. Effective storage rates analysis of groundwater reservoir with surplus local and transferred water used in Shijiazhuang City, China. Water Environ. J. 2012, 27, 157–169. [Google Scholar] [CrossRef]
- Li, W.L.; Liu, C.Y.; Tang, H.Y. Groundwater Reservoir Design Theory and Engineering Practices; Yellow River Water Conservancy Press: Zhengzhou, China, 2012; ISBN 978-7-5509-0283-1. (In Chinese) [Google Scholar]
- Sun, Y.; Xu, S.G.; Kang, P.P.; Fu, Y.Z.; Wang, T.X. Impacts of Artificial Underground Reservoir on Groundwater Environment in the Reservoir and Downstream Area. Int. J. Environ. Res. Public Heal. 2019, 16, 1921. [Google Scholar] [CrossRef]
- Xu, W.D.; Li, W.T. Current Situation of Agricultural Water Resources in Laizhou and Development Strategies. Shandong Water Conserv. 1999, 2–3, 26. (In Chinese) [Google Scholar]
- Gibbs, R.J. Mechanisms Controlling World Water Chemistry. Science 1970, 170, 1088–1090. [Google Scholar] [CrossRef]
- Kang, P.; Xu, S. The impact of mariculture on nutrient dynamics and identification of the nitrate sources in coastal waters. Environ. Sci. Pollut. Res. 2015, 23, 1300–1311. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Bian, J.M.; Gao, Y. Analysis of Variation Regulation and Influence Factors of Groundwater Dynamic in Daan City. Hubei Agric. Sci. 2015, 54, 3379–3383, (In Chinese with English abstract). [Google Scholar]
- Kumar, M.; Ramanathan, A.; Rao, M.S.; Kumar, B. Identification and evaluation of hydrogeochemical processes in the groundwater environment of Delhi, India. Environ. Earth Sci. 2006, 50, 1025–1039. [Google Scholar] [CrossRef]




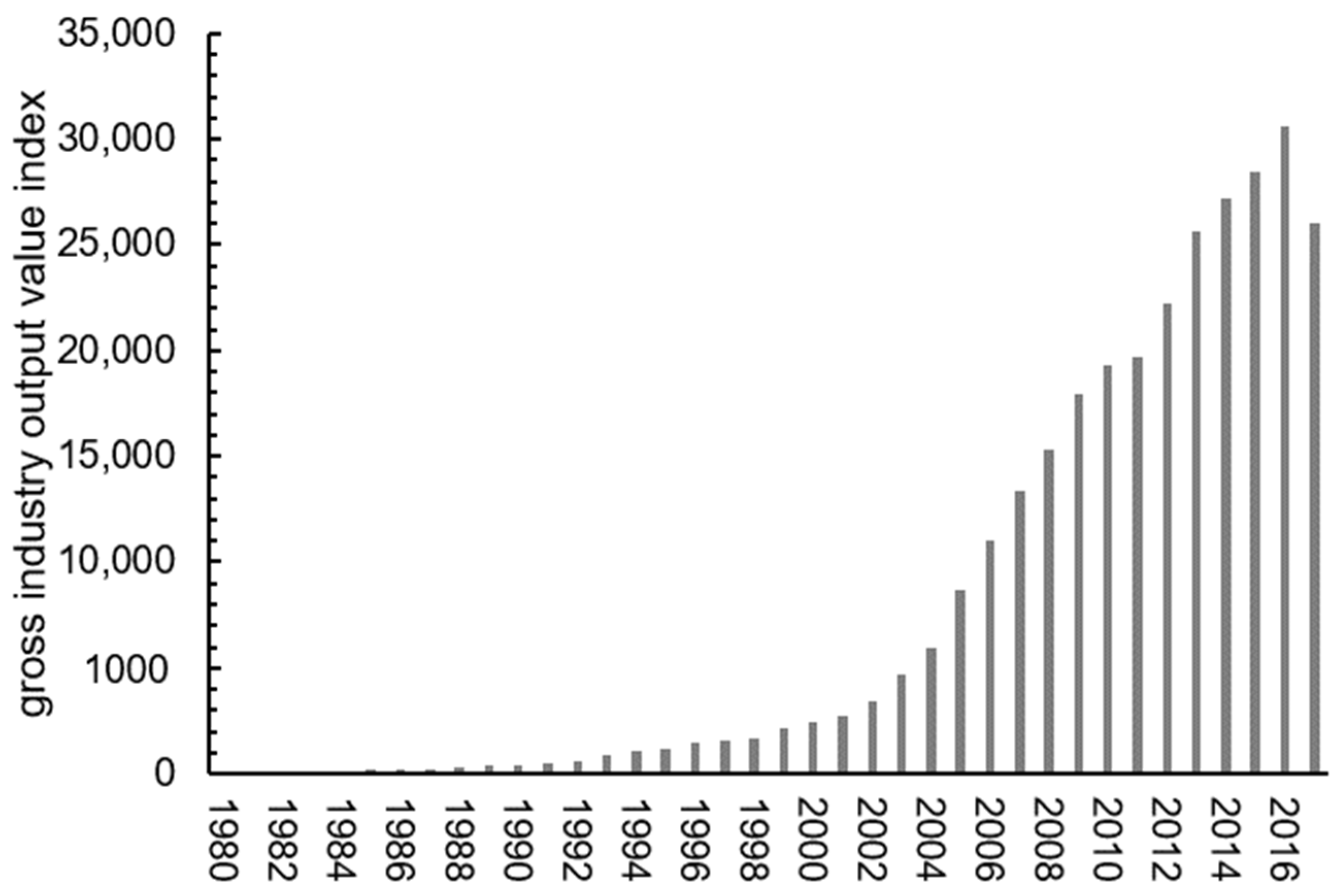

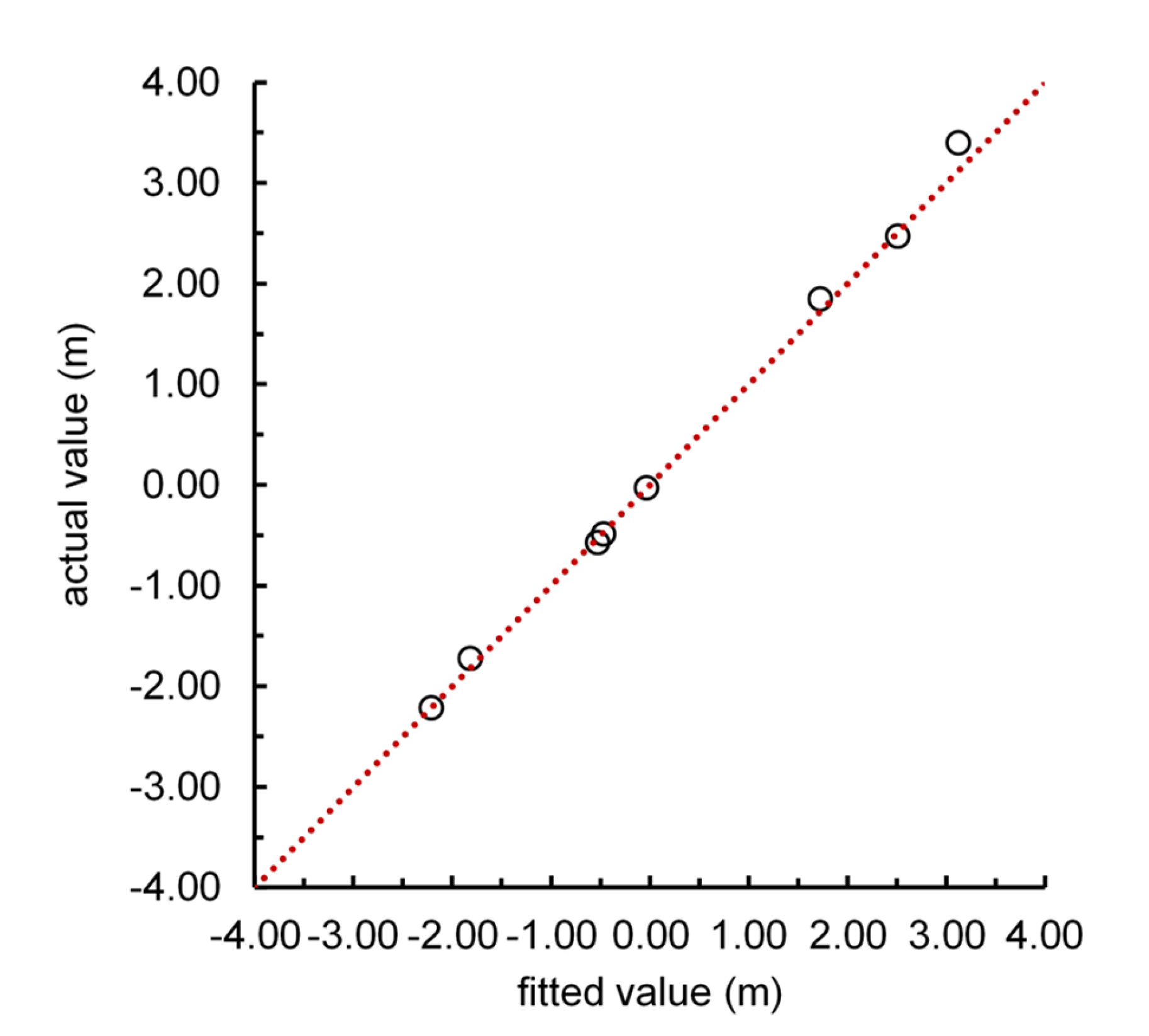

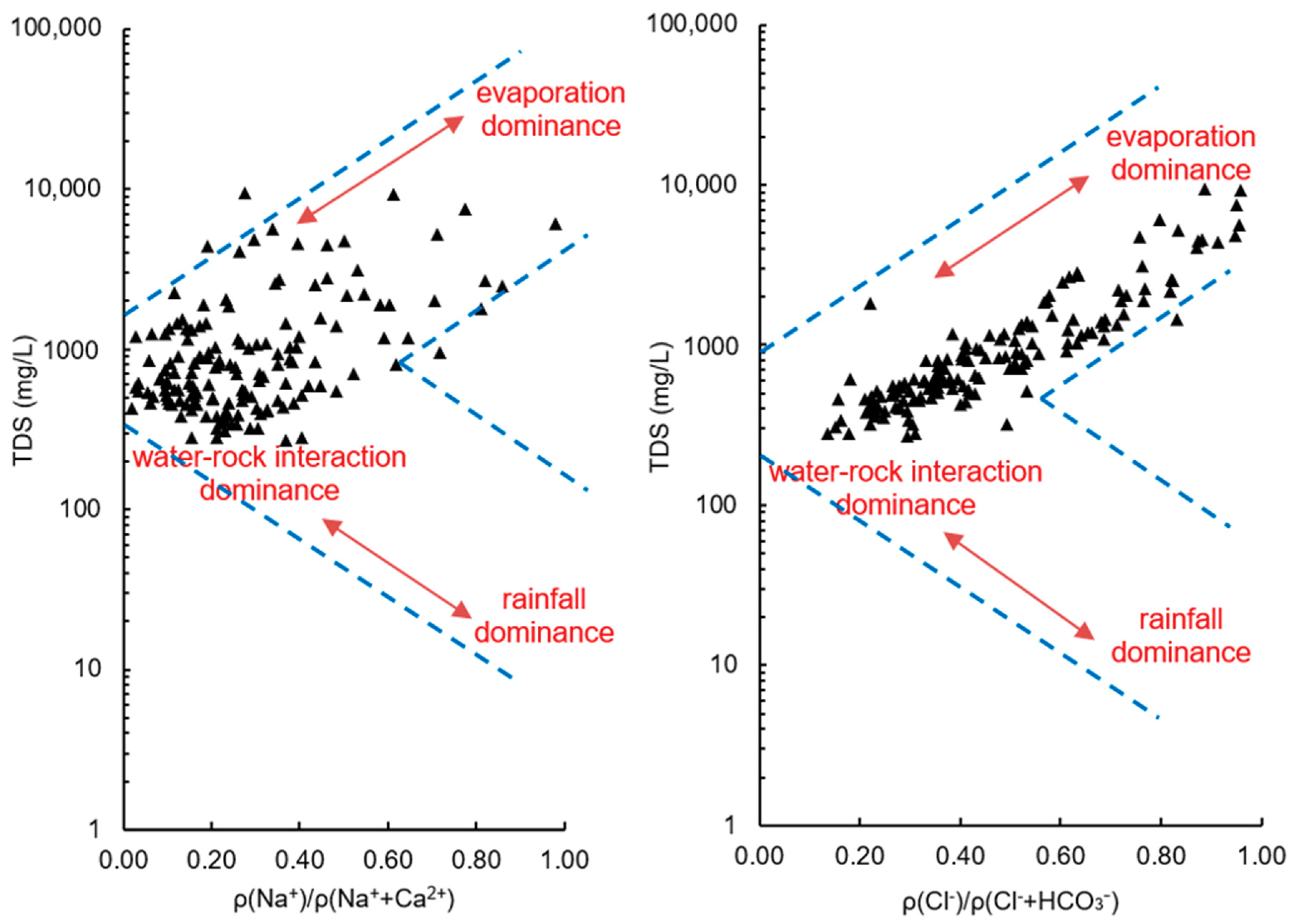
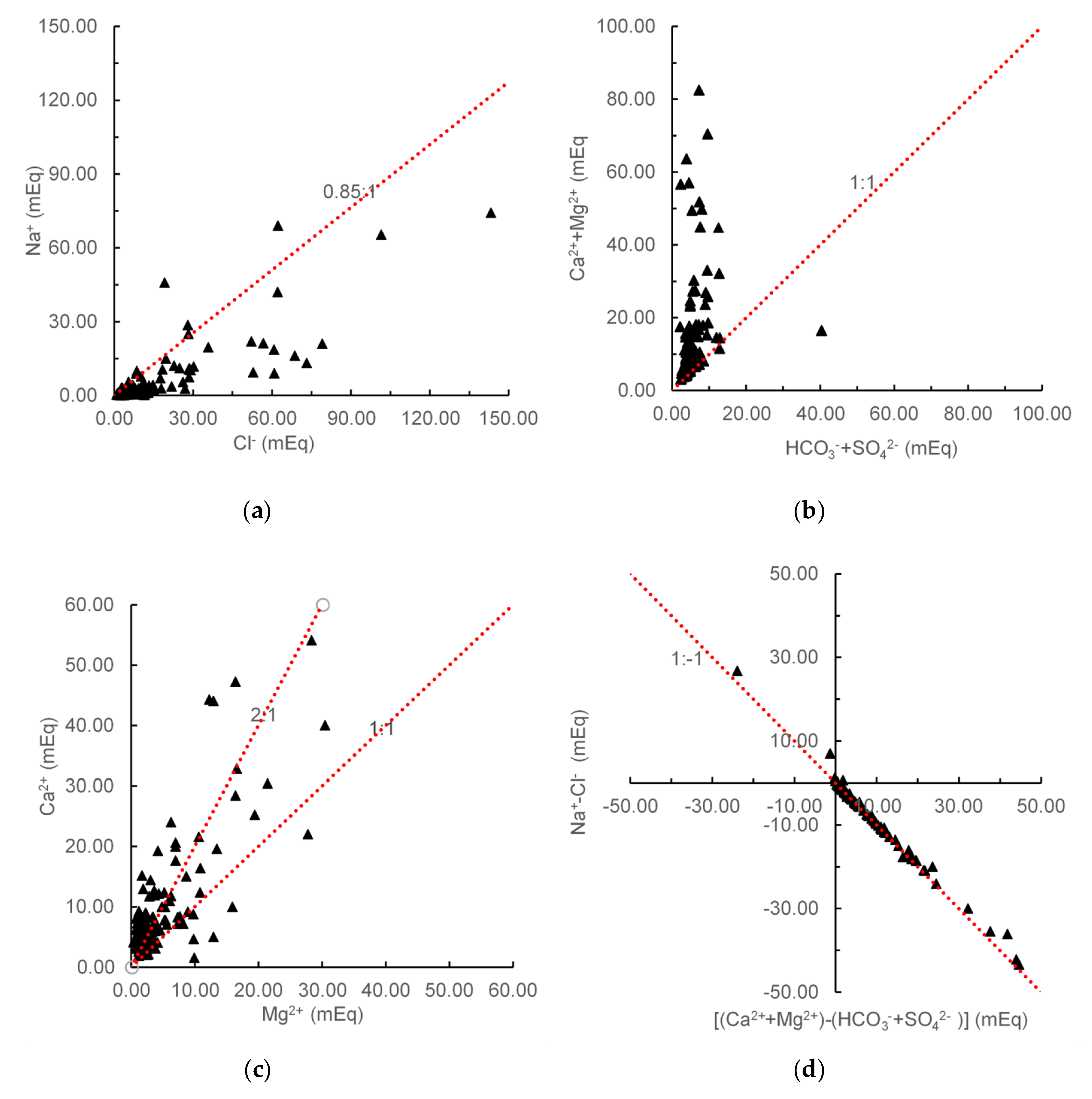

| Influencing Factors | Full Factor Model | Annual Precipitation (×1) | Average Temperature (×2) | Irrigated Area (×3) | Water-Saving Irrigated Area (×4) | Sown Area of High-Water-Consumption Crops (×5) | Gross Industrial Output Value Index (×6) | Reservoir Water Supply (×7) |
|---|---|---|---|---|---|---|---|---|
| mean absolute deviation | 0.069 | 0.414 | 0.113 | 0.532 | 0.438 | 0.187 | 0.261 | 0.093 |
| mean absolute value of relative error | 3.82 | 16.58 | 7.15 | 26.45 | 20.66 | 10.32 | 14.22 | 5.22 |
| R | / | 4.34 | 1.87 | 6.92 | 5.41 | 2.70 | 3.72 | 1.37 |
| sensitivity ranking | / | 3 | 6 | 1 | 2 | 5 | 4 | 7 |
| Influencing Factors | Annual Precipitation (×1) | Average Temperature (×2) | Irrigated Area (×3) | Water-Saving Irrigated Area (×4) | Sown Area of High-Water-Consumption Crops (×5) | Gross Industrial Output Value Index (×6) | Reservoir Water Supply (×7) |
|---|---|---|---|---|---|---|---|
| grey rational grade | 0.802 | 0.683 | 0.903 | 0.847 | 0.732 | 0.766 | 0.701 |
| sensitivity ranking | 3 | 7 | 1 | 2 | 5 | 4 | 6 |
| Statistic Values | Na++K+ | Ca2+ | Mg2+ | Cl− | + | TDS | pH | |
|---|---|---|---|---|---|---|---|---|
| (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (g/L) | ||
| minimum value | 1.57 | 32.06 | 3.89 | 32.08 | 2.94 | 123.83 | 8.61 | 6.13 |
| maximum value | 1708.79 | 1082.16 | 364.8 | 5078.16 | 237.6 | 2395.47 | 229.93 | 8.16 |
| average | 124.59 | 175.89 | 52 | 455.42 | 30.09 | 281.07 | 36.6 | 7.73 |
| coefficient of variation | 2.12 | 1.01 | 1.22 | 1.58 | 1.39 | 0.7 | 1.2 | 0.03 |
| Correlation Coefficients | Na++K+ | Ca2+ | Mg2+ | Cl− | + | TDS | |
|---|---|---|---|---|---|---|---|
| Na++K+ | 1.000 | 0.515 | 0.693 | 0.829 | 0.747 | 0.425 | 0.801 |
| Ca2+ | 1.0000 | 0.791 | 0.876 | 0.590 | 0.065 | 0.848 | |
| Mg2+ | 1.000 | 0.910 | 0.860 | 0.144 | 0.928 | ||
| Cl− | 1.000 | 0.790 | 0.122 | 0.969 | |||
| 1.000 | 0.256 | 0.843 | |||||
| + | 1.000 | 0.165 | |||||
| TDS | 1.000 |
| Cluster Center | Number of Samples | Characteristic Values | Na++K+ | Ca2+ | Mg2+ | Cl− | + | TDS | pH | CODMn | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (g/L) | (mg/L) | ||||
| c1 | 47 | cluster center | 30.75 | 138.42 | 24.39 | 121.24 | 13.28 | 257.68 | 0.59 | 7.78 | 0.85 |
| average | 29.71 | 100.77 | 22.73 | 133.41 | 11.78 | 248.77 | 0.6 | 7.82 | 0.94 | ||
| c2 | 16 | cluster center | 74.92 | 190.5 | 43.66 | 367.7 | 40.08 | 294.12 | 1.01 | 6.83 | 2.52 |
| average | 81.26 | 172.53 | 40.25 | 360.55 | 46.76 | 271 | 0.97 | 6.72 | 2.33 | ||
| c3 | 48 | cluster center | 156.67 | 220.02 | 80.15 | 597.63 | 38.46 | 266.32 | 1.36 | 7.51 | 3.65 |
| average | 176.34 | 216.86 | 67.96 | 631.07 | 40.08 | 298.68 | 1.67 | 7.7 | 3.7 | ||
| c4 | 33 | cluster center | 312.05 | 328.79 | 87.62 | 1224.59 | 88.61 | 294.39 | 2.4 | 7.42 | 1.33 |
| average | 362.6 | 301.41 | 105.27 | 1166.16 | 137.91 | 325.44 | 2.45 | 7.35 | 1.34 | ||
| Number of Samples | Total Coliforms | Volatile Phenol | Cyanide | Cr6+ | Pb | Zn | |||||
| (mg/L) | (mg/L) | (mg/L) | (/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | |||
| c1 | 47 | cluster center | 1.96 | 0.01 | 0.02 | 0.99 | 0.001 | 0.008 | 0.008 | 0.002 | 1.26 |
| average | 2.06 | 0.01 | 0.02 | 1.22 | 0.001 | 0.006 | 0.011 | 0.002 | 1.13 | ||
| c2 | 16 | cluster center | 3.56 | 0.03 | 0.11 | 1.16 | 0.009 | 0.082 | 0.081 | 0.099 | 2.24 |
| average | 3.42 | 0.02 | 0.08 | 1.17 | 0.008 | 0.071 | 0.09 | 0.087 | 2.54 | ||
| c3 | 48 | cluster center | 5.04 | 0.03 | 0.07 | 2.42 | 0.002 | 0.04 | 0.031 | 0.052 | 1.9 |
| average | 5.27 | 0.03 | 0.09 | 3.01 | 0.002 | 0.049 | 0.037 | 0.048 | 1.75 | ||
| c4 | 33 | cluster center | 2.58 | 0.05 | 0.15 | 1.52 | 0.003 | 0.033 | 0.022 | 0.033 | 1.63 |
| average | 3.41 | 0.07 | 0.17 | 1.38 | 0.002 | 0.025 | 0.026 | 0.029 | 1.78 |
| No. | Factory | Sewage Treatment and Discharge | CODMn | Cr6+ | Pb | Cyanide | Volatile Phenol | pH | ||
|---|---|---|---|---|---|---|---|---|---|---|
| (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | ||||
| 1 | food factory | discharged directly into the ground | 152.75 | 2.36 | 96.32 | 0.02 | 0.003 | 0.013 | 0.016 | 7.84 |
| 2 | brickworks | discharged into river after simple treatment such as neutralization | 186.2 | 4.55 | 158.67 | 0.017 | 0.012 | 0.034 | 0.037 | 7.05 |
| 3 | electroplating factory | discharged into river after simple treatment such as neutralization and chemical precipitation | 60.58 | 5.02 | 132.41 | 0.044 | 0.007 | 0.021 | 0.022 | 6.56 |
| 4 | paper mill | discharged into river after simple treatment such as neutralization | 34.01 | 15.89 | 141.6 | 0.035 | 0.019 | 0.082 | 0.025 | 6.81 |
| average | 108.39 | 6.96 | 0.038 | 0.025 | 132.25 | 0.046 | 0.01 | 7.07 | ||
| No. | Location | TN | pH | |||
|---|---|---|---|---|---|---|
| (mg/L) | (mg/L) | (mg/L) | (mg/L) | |||
| 1 | open-air sea cucumber pond | 0.036 | 0.002 | 0.122 | 0.856 | 8.02 |
| 2 | open-air shrimp pond | 0.515 | 0.003 | 0.169 | 0.929 | 7.91 |
| 3 | turbot pond in greenhouse | 0.424 | 0.004 | 0.069 | 0.957 | 7.41 |
| 4 | drainage ditch of open-sea cucumber pond | 0.225 | 0.003 | 0.28 | 0.931 | 7.75 |
| 5 | wastewater drainage of sea cucumber pond in greenhouse | 0.31 | 0.003 | 0.393 | 1.664 | 7.86 |
| 6 | drainage ditch of open-air shrimp pond | 0.138 | 0.051 | 0.307 | 1.21 | 7.81 |
| 7 | drainage ditch of pond in greenhouse | 0.624 | 0.028 | 0.729 | 1.444 | 7.22 |
| 8 | offshore water | 0.013 | 0.005 | 0.062 | 0.457 | 7.15 |
| 9 | offshore water | 0.029 | 0.004 | 0.058 | 0.335 | 7.42 |
| 10 | offshore water | 0.021 | 0.004 | 0.046 | 0.461 | 7.33 |
| average | 0.234 | 0.011 | 0.224 | 0.924 | 7.59 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Xu, S.; Wang, Q.; Hu, S.; Qin, G.; Yu, H. Response of a Coastal Groundwater System to Natural and Anthropogenic Factors: Case Study on East Coast of Laizhou Bay, China. Int. J. Environ. Res. Public Health 2020, 17, 5204. https://doi.org/10.3390/ijerph17145204
Sun Y, Xu S, Wang Q, Hu S, Qin G, Yu H. Response of a Coastal Groundwater System to Natural and Anthropogenic Factors: Case Study on East Coast of Laizhou Bay, China. International Journal of Environmental Research and Public Health. 2020; 17(14):5204. https://doi.org/10.3390/ijerph17145204
Chicago/Turabian StyleSun, Ya, Shiguo Xu, Qin Wang, Suduan Hu, Guoshuai Qin, and Huijuan Yu. 2020. "Response of a Coastal Groundwater System to Natural and Anthropogenic Factors: Case Study on East Coast of Laizhou Bay, China" International Journal of Environmental Research and Public Health 17, no. 14: 5204. https://doi.org/10.3390/ijerph17145204
APA StyleSun, Y., Xu, S., Wang, Q., Hu, S., Qin, G., & Yu, H. (2020). Response of a Coastal Groundwater System to Natural and Anthropogenic Factors: Case Study on East Coast of Laizhou Bay, China. International Journal of Environmental Research and Public Health, 17(14), 5204. https://doi.org/10.3390/ijerph17145204





