Greenhouse Gas Emission Efficiencies of World Countries
Abstract
:1. Introduction
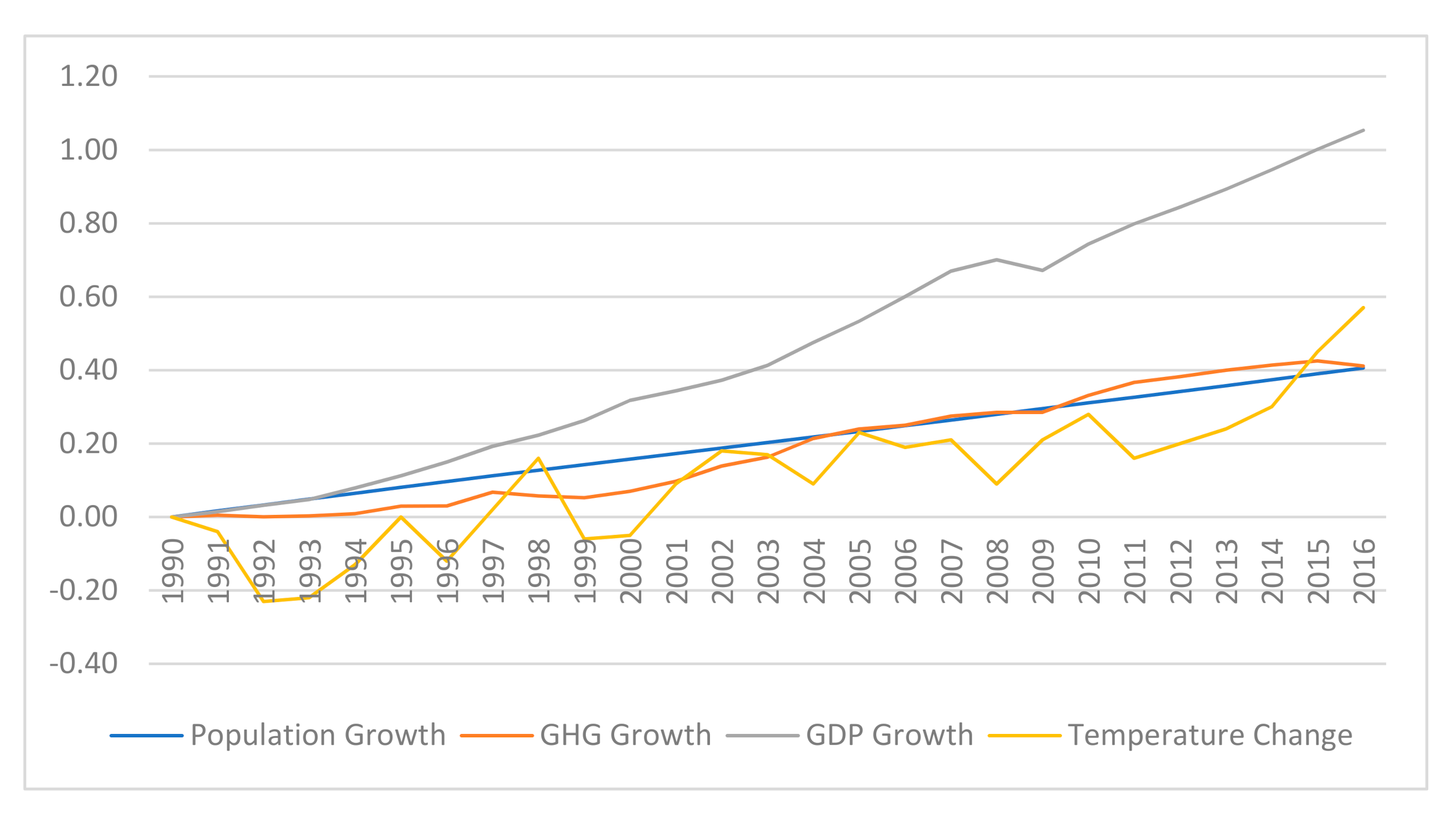
2. Changes in Temperature, CO2 Equivalent Emission, Population, and Real GDP
3. Materials and Methods
3.1. Data
3.2. Econometric Model
3.3. Empirical Model
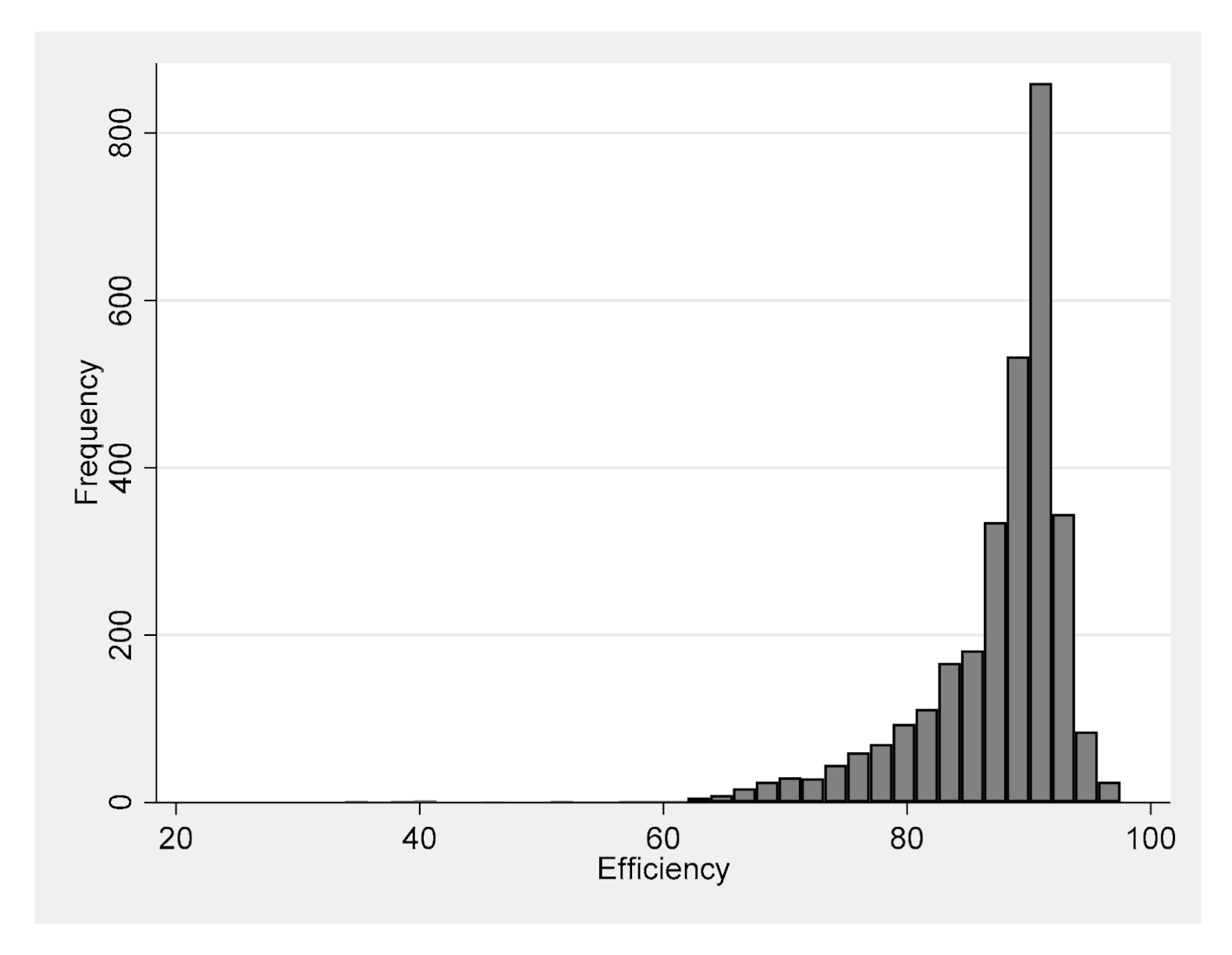
4. Results
5. Discussion
6. Conclusions
Funding
Conflicts of Interest
References
- Emrouznejad, A.; Yang, G.-L.; Amin, G.R. A novel inverse DEA model with application to allocate the CO2 emissions quota to different regions in Chinese manufacturing industries. J. Oper. Res. Soc. 2019, 70, 1079–1090. [Google Scholar] [CrossRef] [Green Version]
- Molinos-Senante, M.; Hernandez-Sancho, F.; Mocholi-Arce, M.; Sala-Garrido, R. Economic and environmental performance of wastewater treatment plants: Potential reductions in greenhouse gases emissions. Resour. Energy Econ. 2014, 38, 125–140. [Google Scholar] [CrossRef]
- Mukherjee, K. Measuring energy efficiency in the context of an emerging economy: The case of Indian manufacturing. Eur. J. Oper. Res. 2010, 201, 933–941. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Wang, D. Sustainability development for supply chain management in U.S. petroleum industry by DEA environmental assessment. Energy Econ. 2014, 46, 360–374. [Google Scholar] [CrossRef]
- Vlontzos, G.; Niavis, S.; Manos, B. A DEA approach for estimating the agricultural and environmental efficiency of EU countries. Renew. Sustain. Energy Rev. 2014, 40, 91–96. [Google Scholar] [CrossRef]
- Wegener, M.; Amin, G.R. Minimizing greenhouse gas emissions using inverse DEA with an application in oil and gas. Expert Syst. Appl. 2019, 122, 369–375. [Google Scholar] [CrossRef]
- Chung, Y.; Färe, R.; Grosskopf, S. Productivity and undesirable outputs: A directional distance function approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Färe, R.; Grosskopf, S.; Hernandez-Sancho, F. Environmental performance: An index number approach. Resour. Energy Econ. 2004, 26, 343–352. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lovell, C.A.K.; Pasurka, C. Multilateral productivity comparisons when some outputs are undesirable: A nonparametric approach. Rev. Econ. Stat. 1989, 71, 90–98. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Noh, D.-W.; Weber, W. Characteristics of a polluting technology: Theory and practice. J. Econom. 2005, 126, 469–492. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Tyteca, D. An activity analysis model of the environment performance of firms: Application to fossil-fuel-fired electric utilities. Ecol. Econ. 1996, 18, 161–175. [Google Scholar] [CrossRef]
- Fernández, C.; Koop, G.; Steel, M.F.J. Multiple-output production with undesirable outputs: An application to nitrogen surplus in agriculture. J. Am. Stat. Assoc. 2002, 97, 432–442. [Google Scholar] [CrossRef] [Green Version]
- Fernández, C.; Koop, G.; Steel, M.F.J. Alternative efficiency measures for multiple-output production. J. Econom. 2005, 126, 411–444. [Google Scholar] [CrossRef] [Green Version]
- Førsund, F. Good modelling of bad outputs: Pollution and multiple-output production. Int. Rev. Environ. Resour. Econ. 2009, 3, 1–38. [Google Scholar] [CrossRef]
- Herrala, R.; Goel, R.K. Global CO2 efficiency: Country-wise estimates using a stochastic cost frontier. Energy Policy 2012, 45, 762–770. [Google Scholar] [CrossRef]
- Jin, T.; Kim, J. A comparative study of energy and carbon efficiency for emerging countries using panel stochastic frontier analysis. Sci. Rep. 2019, 9, 6647. [Google Scholar] [CrossRef]
- Murty, S.; Russell, R.R.; Levkoff, S.B. On modeling pollution-generating technologies. J. Environ. Econ. Manag. 2012, 64, 117–135. [Google Scholar] [CrossRef] [Green Version]
- Robaina-Alves, M.M.; Moutinho, V.; Macedo, P. A new frontier approach to model the eco-efficiency in European countries. J. Clean. Prod. 2015, 103, 562–573. [Google Scholar] [CrossRef] [Green Version]
- Tyteca, D. On the measurement of the environmental performance of firms- a literature review and a productive efficiency perspective. J. Environ. Manag. 1996, 46, 281–308. [Google Scholar] [CrossRef]
- Tyteca, D. Linear programming models for the measurement of environmental performance of firms: Concepts and empirical results. J. Product. Anal. 1997, 8, 175–189. [Google Scholar] [CrossRef]
- Valadkhani, A.; Roshdi, I.; Smyth, R.L. A multiplicative environmental DEA approach to measure efficiency changes in the world’s major polluters. Energy Econ. 2016, 54, 363–375. [Google Scholar] [CrossRef]
- Zhou, P.; Poh, K.L.; Ang, B.W. A non-radial DEA approach to measuring environmental performance. Eur. J. Oper. Res. 2007, 178, 1–9. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. Slacks-based efficiency measures for modelling environmental performance. Ecol. Econ. 2006, 60, 111–118. [Google Scholar] [CrossRef]
- Zofio, J.L.; Prieto, A.M. Environmental efficiency and regulatory standards: The case of CO2 emissions from OECD industries. Resour. Energy Econ. 2001, 23, 63–83. [Google Scholar] [CrossRef]
- Dakpo, K.H.; Jeanneaux, P.; Latruffe, L. Modelling polluting-generating technologies in performance benchmarking: Recent developments, limits and future prospects in the nonparametric framework. Eur. J. Oper. Res. 2016, 250, 347–359. [Google Scholar] [CrossRef]
- Aigner, D.J.; Lovell, C.A.K.; Schmidt, P. Formulation and estimation of stochastic frontier production functions. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; van den Broeck, J. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 1977, 2, 435–444. [Google Scholar] [CrossRef]
- Jondrow, J.; Lovell, C.A.K.; Materov, I.S.; Schmidt, P. On the estimation of technical inefficiency in the stochastic frontier production function model. J. Econom. 1982, 19, 233–238. [Google Scholar] [CrossRef] [Green Version]
- Ahn, S.C.; Good, D.H.; Sickles, R.C. Estimation of long-run inefficiency levels: A dynamic frontier approach. Econom. Rev. 2000, 19, 461–492. [Google Scholar] [CrossRef] [Green Version]
- Assaf, A.G.; Gillen, D.; Tsionas, E.G. Understanding relative efficiency among airports: A general dynamic model for distinguishing technical and allocative efficiency. Transp. Res. Part. B 2014, 70, 18–34. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data with application to paddy farmers in India. J. Product. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Desli, E.; Ray, S.C.; Kumbhakar, S.C. A dynamic stochastic frontier production model with time-varying efficiency. Appl. Econ. Lett. 2003, 10, 623–626. [Google Scholar] [CrossRef] [Green Version]
- Duygun, M.; Kutlu, L.; and Sickles, R.C. Measuring Productivity and Efficiency: A Kalman Filter Approach. J. Product. Anal. 2016, 46, 155–167. [Google Scholar] [CrossRef]
- Huang, T.H.; Chen, Y.H. A study on long-run inefficiency levels of a panel dynamic cost frontier under the framework of forward-looking rational expectations. J. Bank. Financ. 2009, 33, 842–849. [Google Scholar] [CrossRef]
- Tsionas, E.G. Inference in dynamic stochastic frontier models. J. Appl. Econom. 2006, 21, 669–676. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lovell, C.A.K. Stochastic Frontier Analysis; Cambridge University Press: Cambridge, UK, 2003; ISBN 13: 978-0521481847. [Google Scholar]
- Greene, W.H. Fixed and random effects in stochastic frontier models. J. Product. Anal. 2005, 23, 7–32. [Google Scholar] [CrossRef] [Green Version]
- Greene, W.H. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econom. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Kutlu, L.; Tran, K.C.; Tsionas, M.G. A Time-Varying True Individual Effects Model with Endogenous Regressors. J. Econom. 2019, 211, 539–559. [Google Scholar] [CrossRef] [Green Version]
- Kutlu, L.; Tran, K.C.; Tsionas, M.G. Unknown Latent Structure and Inefficiency in Panel Stochastic Frontier Models. J. Product. Anal. 2020, 54, 75–86. [Google Scholar] [CrossRef]
- Wang, H.J.; Ho, C.W. Estimating fixed-effect panel stochastic frontier models by model transformation. J. Econom. 2010, 157, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Kutlu, L.; Tran, K.C. Heterogeneity and Endogeneity in Panel Stochastic Frontier Models. In Panel Data Econometrics: Theory, 1st ed.; Tsionas, M.G., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 131–146. [Google Scholar] [CrossRef]
- Kutlu, L.; McCarthy, P. US Airport Governance and Efficiency. Transp. Res. Part. E 2016, 89, 117–132. [Google Scholar] [CrossRef] [Green Version]
- Caruso, G.; Colantonio, E.; Gattone, S.A. Relationships between Renewable Energy Consumption, Social Factors, and Health: A Panel Vector Auto Regression Analysis of a Cluster of 12 EU Countries. Sustainability 2020, 12, 2915. [Google Scholar] [CrossRef] [Green Version]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. Future Trajectories of Renewable Energy Consumption in the European Union. Resources 2018, 7, 10. [Google Scholar] [CrossRef] [Green Version]
| Variable | Unit | Mean | Std. Dev. | 5th Perc. | Median | 95th Perc. |
|---|---|---|---|---|---|---|
| GHG | Million tonnes | 315.86 | 903.79 | 7.31 | 69.02 | 1266.66 |
| GDP | Billion dollars | 578.10 | 1611.86 | 11.08 | 110.66 | 2397.32 |
| L | Million | 22.09 | 77.10 | 0.49 | 4.79 | 67.37 |
| K | Billion dollars | 1264.48 | 3544.88 | 19.69 | 195.31 | 5692.87 |
| E | Million kg oil equivalent | 85.42 | 271.69 | 1.69 | 15.89 | 305.71 |
| POP | Million | 48.70 | 154.07 | 1.11 | 10.55 | 148.52 |
| # of Obs. | 3048 |
| Model 1 | Model 2 | Model 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ln(GHG/GDP) | Coeff. | S.E. | Coeff. | S.E. | Coeff. | S.E. | |||
| ln(L) | 0.0315 | 0.1039 | 0.0353 | 0.1050 | 0.0293 | 0.1063 | |||
| ln(K) | −0.1436 | 0.0302 | *** | –0.1439 | 0.0301 | *** | –0.1440 | 0.0302 | *** |
| ln(E) | 0.3628 | 0.0324 | *** | 0.3642 | 0.0325 | *** | 0.3634 | 0.0325 | *** |
| T | −0.0191 | 0.0014 | *** | –0.0259 | 0.0013 | *** | –0.0264 | 0.0016 | *** |
| 0.5 × ln(L)2 | −0.1485 | 0.0404 | *** | –0.1547 | 0.0407 | *** | –0.1549 | 0.0408 | *** |
| 0.5 × ln(K)2 | 0.0893 | 0.0278 | *** | 0.0967 | 0.0274 | *** | 0.0970 | 0.0274 | *** |
| 0.5 × ln(E)2 | −0.1413 | 0.0452 | ** | –0.1422 | 0.0451 | ** | –0.1424 | 0.0453 | *** |
| 0.5 × T2 | −0.0019 | 0.0002 | *** | –0.0022 | 0.0002 | *** | –0.0023 | 0.0003 | *** |
| ln(L) × ln(K) | 0.0133 | 0.0187 | 0.0143 | 0.0186 | 0.0146 | 0.0187 | |||
| ln(L) × ln(E) | 0.1898 | 0.0302 | *** | 0.2006 | 0.0305 | *** | 0.2014 | 0.0307 | *** |
| ln(L) × T | −0.0061 | 0.0011 | *** | –0.0060 | 0.0011 | *** | –0.0060 | 0.0011 | *** |
| ln(K) × ln(E) | −0.0423 | 0.0312 | –0.0535 | 0.0308 | –0.0542 | 0.0308 | |||
| ln(K) × T | 0.0045 | 0.0010 | *** | 0.0041 | 0.0010 | *** | 0.0041 | 0.0010 | *** |
| ln(E) × T | −0.0007 | 0.0012 | –0.0002 | 0.0012 | –0.0002 | 0.0012 | |||
| ln(POP) | −0.0377 | 0.1204 | –0.0319 | 0.1214 | –0.0227 | 0.1234 | |||
| σv | |||||||||
| Constant | −3.4049 | 0.0412 | *** | –3.4925 | 0.0662 | *** | –3.5034 | 0.0803 | *** |
| σu | |||||||||
| T | −0.2251 | 0.0277 | *** | - | - | - | - | - | - |
| D1998_2007 | − | - | - | - | - | - | –1.3956 | 0.1948 | *** |
| D2008_2012 | − | - | - | - | - | - | –1.2147 | 0.3915 | ** |
| D1998_2012 | − | - | - | –1.3935 | 0.1931 | *** | - | - | - |
| D2013_2015 | − | - | - | –0.5455 | 0.2335 | * | –0.4154 | 0.3355 | |
| Constant | −4.5389 | 0.2840 | *** | –2.6561 | 0.1588 | *** | –2.6648 | 0.1606 | *** |
| Ave. Efficiency | 90.19 | 87.41 | 87.23 | ||||||
| Log-likelihood | 495.9877 | 489.8614 | 490.0955 | ||||||
| COUNTRY | 1990–1997 | 1998–2007 | 2008–2012 | 2013–2015 | 1990–2015 | COUNTRY | 1990–1997 | 1998–2007 | 2008–2012 | 2013–2015 | 1990–2015 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Albania | 80.42 | 90.84 | 91.48 | 87.26 | 87.34 | Lithuania | 74.60 | 91.02 | 91.89 | 90.00 | 85.86 |
| Algeria | 88.24 | 90.99 | 88.05 | 79.67 | 88.62 | Luxembourg | 74.57 | 91.57 | 90.28 | 89.54 | 85.86 |
| Angola | 73.29 | 88.76 | 93.79 | 93.16 | 85.17 | Malaysia | 68.62 | 86.09 | 94.00 | 95.65 | 82.85 |
| Argentina | 86.81 | 90.12 | 89.54 | 86.13 | 88.62 | Malta | 84.81 | 91.53 | 88.49 | 83.99 | 88.17 |
| Armenia | 66.70 | 91.76 | 91.86 | 87.49 | 83.42 | Mauritius | 90.87 | 90.04 | 86.85 | 78.33 | 88.73 |
| Australia | 84.05 | 90.17 | 90.68 | 89.78 | 88.34 | Mexico | 88.11 | 91.32 | 87.47 | 81.38 | 88.44 |
| Austria | 86.69 | 90.86 | 89.26 | 84.18 | 88.50 | Moldova | 81.73 | 90.16 | 91.29 | 89.75 | 87.65 |
| Azerbaijan | 79.66 | 87.99 | 92.41 | 88.22 | 86.23 | Mongolia | 77.37 | 89.08 | 92.78 | 93.57 | 86.43 |
| Bahrain | 88.21 | 90.83 | 88.48 | 80.12 | 88.67 | Morocco | 90.02 | 90.79 | 85.86 | 77.79 | 88.52 |
| Bangladesh | 80.54 | 90.81 | 91.45 | 88.99 | 87.50 | Mozambique | 77.78 | 91.17 | 91.64 | 86.23 | 86.58 |
| Belarus | 71.78 | 91.11 | 92.22 | 82.26 | 84.44 | Myanmar | 72.96 | 90.40 | 92.47 | 91.18 | 85.29 |
| Belgium | 81.77 | 90.86 | 91.17 | 87.74 | 87.76 | Namibia | 82.73 | 91.18 | 89.00 | 89.21 | 88.10 |
| Benin | 78.75 | 91.12 | 91.14 | 88.37 | 86.95 | Nepal | 77.73 | 89.64 | 92.86 | 89.46 | 86.46 |
| Bolivia | 83.06 | 90.90 | 89.24 | 89.50 | 87.95 | Netherlands | 80.06 | 91.58 | 90.76 | 85.48 | 87.18 |
| Botswana | 73.28 | 85.12 | 94.75 | 91.03 | 83.73 | New Zealand | 86.93 | 90.85 | 89.22 | 83.76 | 88.51 |
| Brazil | 80.33 | 88.85 | 93.07 | 91.92 | 87.21 | Nicaragua | 77.38 | 88.39 | 89.86 | 95.77 | 85.75 |
| Bulgaria | 85.20 | 91.29 | 88.96 | 84.47 | 88.33 | Niger | - | 91.82 | 88.08 | 84.41 | 89.59 |
| Cambodia | 83.08 | 89.82 | 91.49 | 90.42 | 89.29 | Nigeria | 69.50 | 90.17 | 93.22 | 90.93 | 84.23 |
| Cameroon | 87.59 | 90.81 | 87.37 | 81.83 | 88.38 | North Macedonia | 88.32 | 90.09 | 89.32 | 84.64 | 88.93 |
| Canada | 87.43 | 90.35 | 89.93 | 83.97 | 88.63 | Norway | 76.27 | 90.97 | 91.53 | 88.51 | 86.27 |
| China | 80.99 | 90.80 | 91.16 | 89.60 | 87.63 | Oman | 92.26 | 90.15 | 81.54 | 65.56 | 87.13 |
| Colombia | 84.07 | 88.41 | 90.91 | 94.01 | 87.97 | Pakistan | 88.37 | 91.17 | 87.46 | 78.71 | 88.53 |
| Congo, Dem. Rep. | 89.76 | 87.94 | 89.48 | 90.08 | 89.00 | Panama | 80.37 | 90.65 | 91.56 | 89.68 | 87.46 |
| Congo, Rep. | 80.92 | 89.72 | 89.61 | 89.49 | 86.87 | Paraguay | 89.70 | 91.02 | 84.08 | 76.27 | 88.03 |
| Costa Rica | 38.17 | 85.65 | 94.28 | 95.74 | 72.99 | Peru | 86.35 | 90.50 | 89.38 | 87.88 | 88.74 |
| Cote d’Ivoire | 82.56 | 89.33 | 87.28 | 86.59 | 86.53 | Philippines | 88.06 | 88.86 | 88.40 | 92.09 | 88.77 |
| Croatia | 89.85 | 91.19 | 84.33 | 70.55 | 87.74 | Poland | 75.08 | 90.97 | 92.31 | 86.79 | 85.86 |
| Cyprus | 84.78 | 91.20 | 89.92 | 82.82 | 88.22 | Portugal | 88.29 | 90.71 | 89.19 | 80.23 | 88.47 |
| Czech Republic | 82.38 | 90.90 | 90.78 | 87.96 | 87.92 | Qatar | 83.60 | 90.05 | 91.57 | 89.14 | 88.22 |
| Denmark | 80.19 | 90.99 | 90.87 | 89.44 | 87.46 | Russian Federation | 84.58 | 90.19 | 90.89 | 86.75 | 88.26 |
| Dominican Republic | 91.46 | 89.50 | 86.13 | 78.45 | 88.57 | Saudi Arabia | 90.28 | 90.84 | 85.55 | 76.93 | 88.49 |
| Ecuador | 83.19 | 90.92 | 90.48 | 88.00 | 88.13 | Senegal | 85.66 | 90.72 | 90.31 | 84.27 | 88.50 |
| Egypt, Arab Rep. | 87.70 | 90.93 | 88.74 | 80.50 | 88.62 | Singapore | 77.05 | 90.19 | 92.55 | 90.89 | 86.51 |
| El Salvador | 88.27 | 91.29 | 86.88 | 79.05 | 88.46 | Slovak Republic | 73.19 | 90.87 | 92.25 | 90.34 | 85.63 |
| Estonia | 80.36 | 91.52 | 89.62 | 82.16 | 86.64 | Slovenia | 81.60 | 91.98 | 88.36 | 83.27 | 87.09 |
| Ethiopia | 83.51 | 89.96 | 91.31 | 89.84 | 88.15 | South Africa | 88.24 | 91.10 | 87.69 | 79.08 | 88.54 |
| Finland | 86.35 | 91.35 | 88.44 | 76.24 | 87.51 | Spain | 87.74 | 90.47 | 89.68 | 83.97 | 88.73 |
| France | 81.65 | 91.10 | 90.54 | 87.98 | 87.72 | Sri Lanka | 70.06 | 91.32 | 92.32 | 90.55 | 84.66 |
| Georgia | 73.17 | 91.74 | 90.73 | 81.95 | 84.81 | Sudan | 91.13 | 89.75 | 85.74 | 81.75 | 88.75 |
| Germany | 84.62 | 91.35 | 89.68 | 83.93 | 88.10 | Suriname | - | 90.20 | 90.23 | 84.16 | 89.40 |
| Ghana | 82.74 | 85.14 | 93.61 | 87.15 | 86.23 | Sweden | 68.31 | 90.94 | 82.60 | 76.70 | 80.73 |
| Greece | 86.73 | 91.42 | 88.85 | 79.33 | 88.09 | Switzerland | 84.76 | 90.91 | 90.24 | 86.05 | 88.33 |
| Guatemala | 84.50 | 90.26 | 90.40 | 90.13 | 88.44 | Syrian Arab Republic | 85.66 | 91.73 | 88.73 | 69.47 | 87.41 |
| Haiti | 91.80 | 89.75 | 84.94 | 73.43 | 88.14 | Tajikistan | 83.48 | 90.28 | 89.98 | 85.70 | 87.68 |
| Honduras | 77.65 | 90.85 | 91.81 | 88.06 | 86.60 | Tanzania | 74.48 | 90.12 | 92.68 | 92.76 | 85.84 |
| Hungary | 83.88 | 90.96 | 90.47 | 86.29 | 88.15 | Thailand | 86.33 | 90.95 | 89.36 | 83.11 | 88.53 |
| Iceland | 80.54 | 90.85 | 91.18 | 88.87 | 87.51 | Togo | 87.84 | 90.96 | 87.61 | 81.48 | 88.53 |
| India | 79.91 | 91.03 | 91.29 | 88.40 | 87.31 | Trinidad and Tobago | 78.53 | 92.07 | 89.77 | 83.48 | 86.59 |
| Indonesia | 82.66 | 90.40 | 90.53 | 86.97 | 87.67 | Tunisia | 85.57 | 90.99 | 89.88 | 83.68 | 88.45 |
| Iran, Islamic Rep. | 89.39 | 91.04 | 86.95 | 73.24 | 88.27 | Turkey | 86.67 | 91.01 | 89.14 | 84.15 | 88.53 |
| Iraq | 64.08 | 92.91 | 90.16 | 82.14 | 82.27 | Ukraine | 85.46 | 90.13 | 90.45 | 83.36 | 88.16 |
| Ireland | 71.29 | 91.30 | 91.93 | 89.15 | 85.02 | United Arab Emirates | 82.70 | 91.41 | 89.98 | 84.85 | 87.81 |
| Israel | 86.92 | 90.84 | 89.19 | 84.93 | 88.64 | United Kingdom | 80.09 | 91.20 | 90.82 | 88.39 | 87.38 |
| Italy | 88.12 | 90.94 | 88.42 | 82.22 | 88.58 | United States | 83.79 | 91.37 | 90.03 | 84.49 | 87.99 |
| Japan | 89.37 | 91.33 | 87.04 | 71.36 | 87.60 | Uruguay | 94.83 | 82.96 | 78.80 | 63.24 | 84.35 |
| Jordan | 77.58 | 91.71 | 91.21 | 83.44 | 86.43 | Uzbekistan | 85.92 | 89.38 | 91.29 | 91.11 | 88.70 |
| Kazakhstan | 76.82 | 91.61 | 90.67 | 87.81 | 86.38 | Venezuela, RB | 83.73 | 89.44 | 91.97 | 84.63 | 87.86 |
| Korea, Rep. | 84.68 | 91.42 | 89.53 | 83.75 | 88.10 | Vietnam | 94.28 | 86.79 | 79.41 | 69.37 | 87.03 |
| Kuwait | 81.23 | 91.41 | 88.07 | 79.28 | 87.23 | Yemen, Rep. | 89.17 | 91.42 | 84.41 | 69.58 | 88.30 |
| Kyrgyz Republic | 89.16 | 89.87 | 76.44 | 81.51 | 86.29 | Zambia | 74.39 | 89.78 | 93.54 | 93.34 | 85.58 |
| Lebanon | 89.42 | 89.80 | 89.09 | 80.77 | 88.82 | Zimbabwe | 91.75 | 87.99 | 85.68 | 87.70 | 88.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutlu, L. Greenhouse Gas Emission Efficiencies of World Countries. Int. J. Environ. Res. Public Health 2020, 17, 8771. https://doi.org/10.3390/ijerph17238771
Kutlu L. Greenhouse Gas Emission Efficiencies of World Countries. International Journal of Environmental Research and Public Health. 2020; 17(23):8771. https://doi.org/10.3390/ijerph17238771
Chicago/Turabian StyleKutlu, Levent. 2020. "Greenhouse Gas Emission Efficiencies of World Countries" International Journal of Environmental Research and Public Health 17, no. 23: 8771. https://doi.org/10.3390/ijerph17238771
APA StyleKutlu, L. (2020). Greenhouse Gas Emission Efficiencies of World Countries. International Journal of Environmental Research and Public Health, 17(23), 8771. https://doi.org/10.3390/ijerph17238771





