Effects of a Wireless Charging System Built for An Electric Kick Scooter on Human Biological Tissue
Abstract
:1. Introduction
2. Theoretical Background
2.1. Specific Absorption Rate (SAR)
2.2. Bio-Heat Transfer
2.3. Relation between SAR and Bio-Heat Transfer
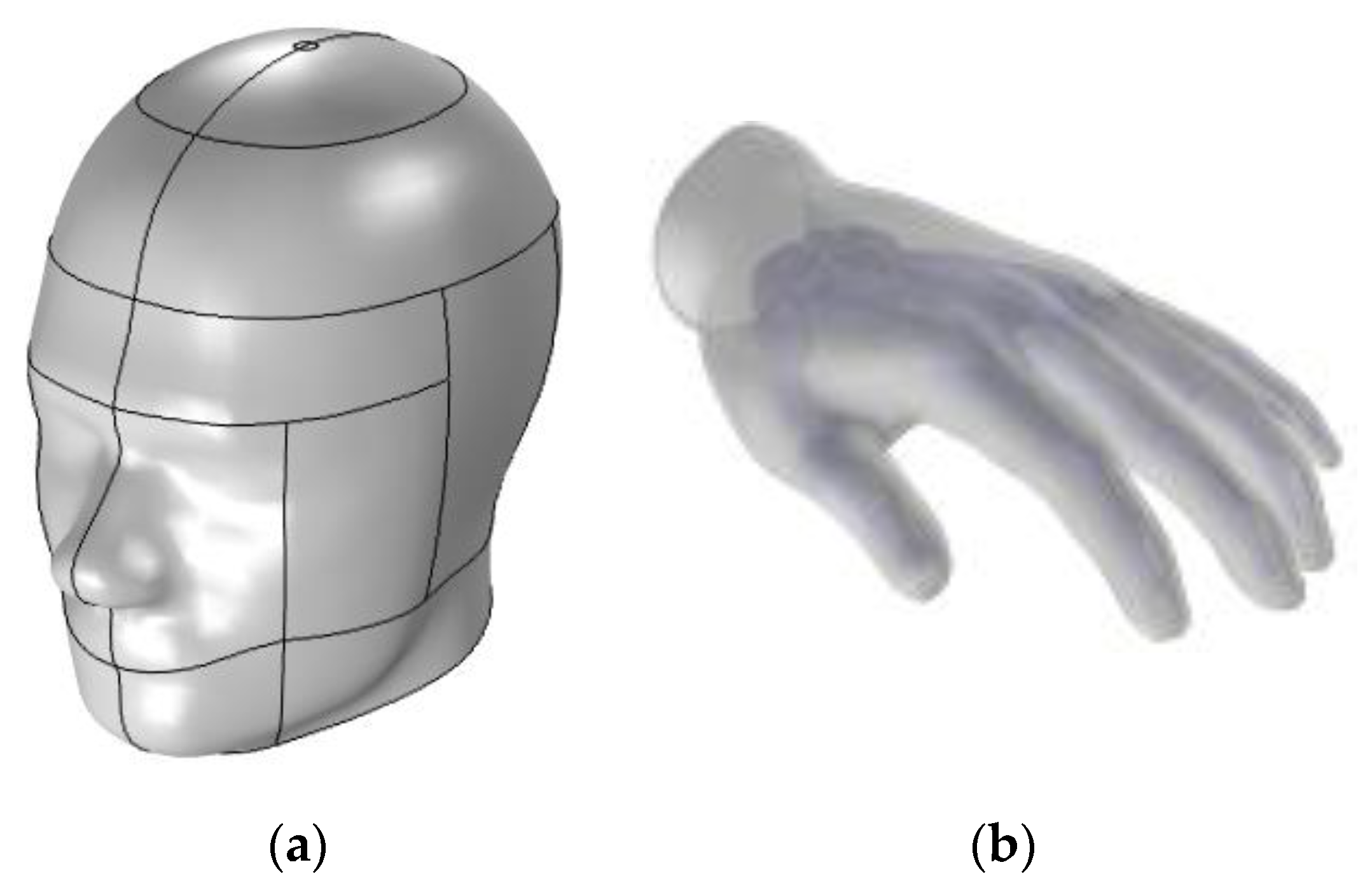
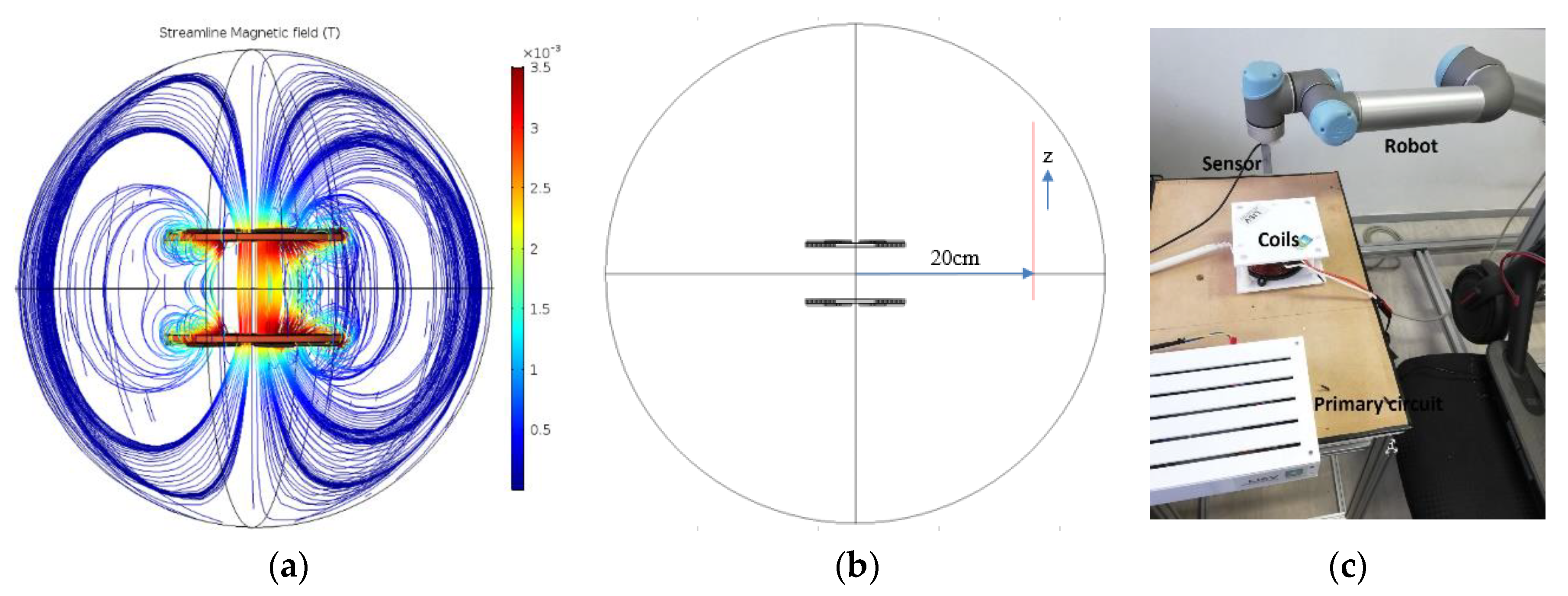
3. COMSOL Model
4. Calculated Results and Discussion
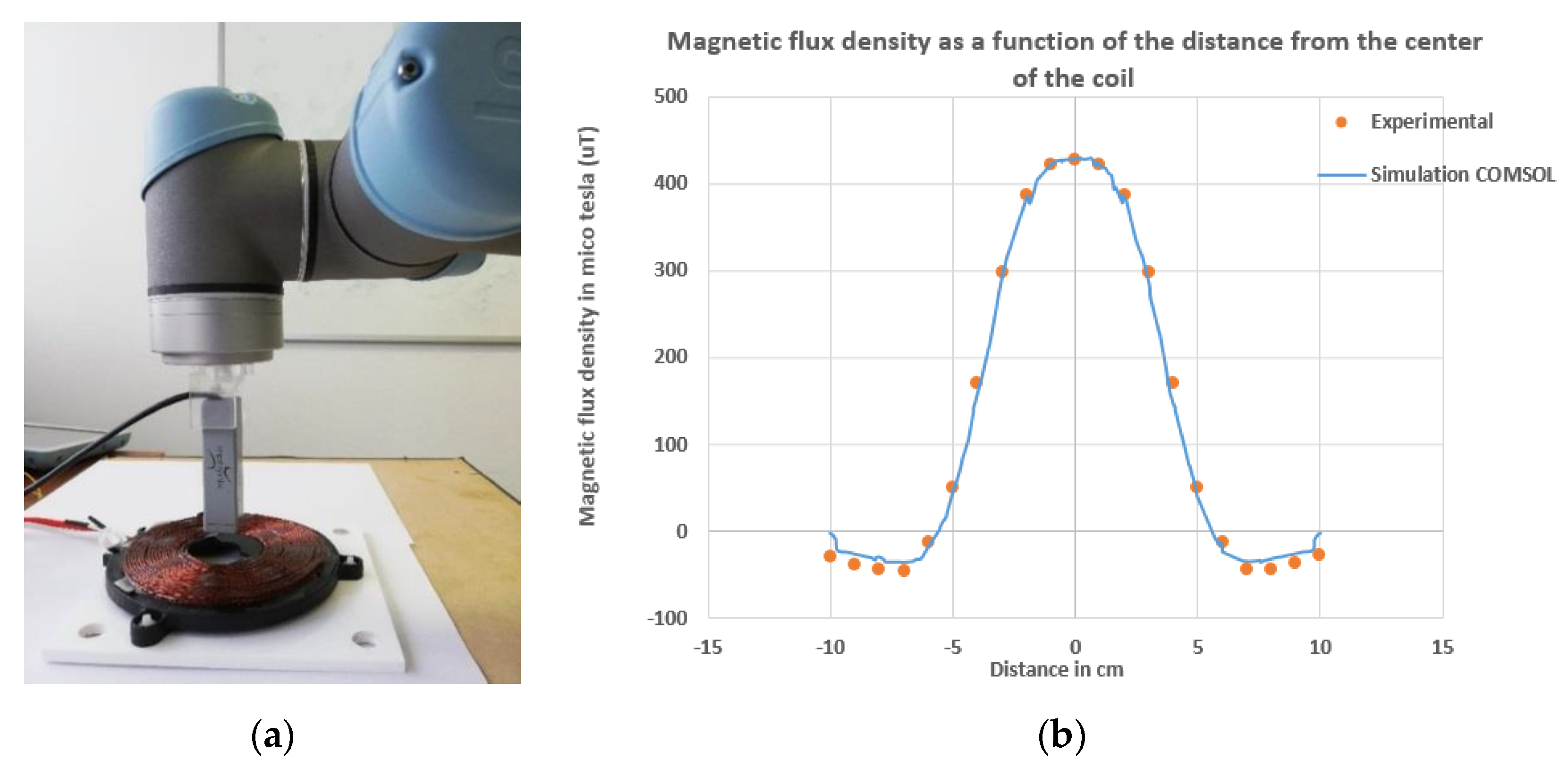
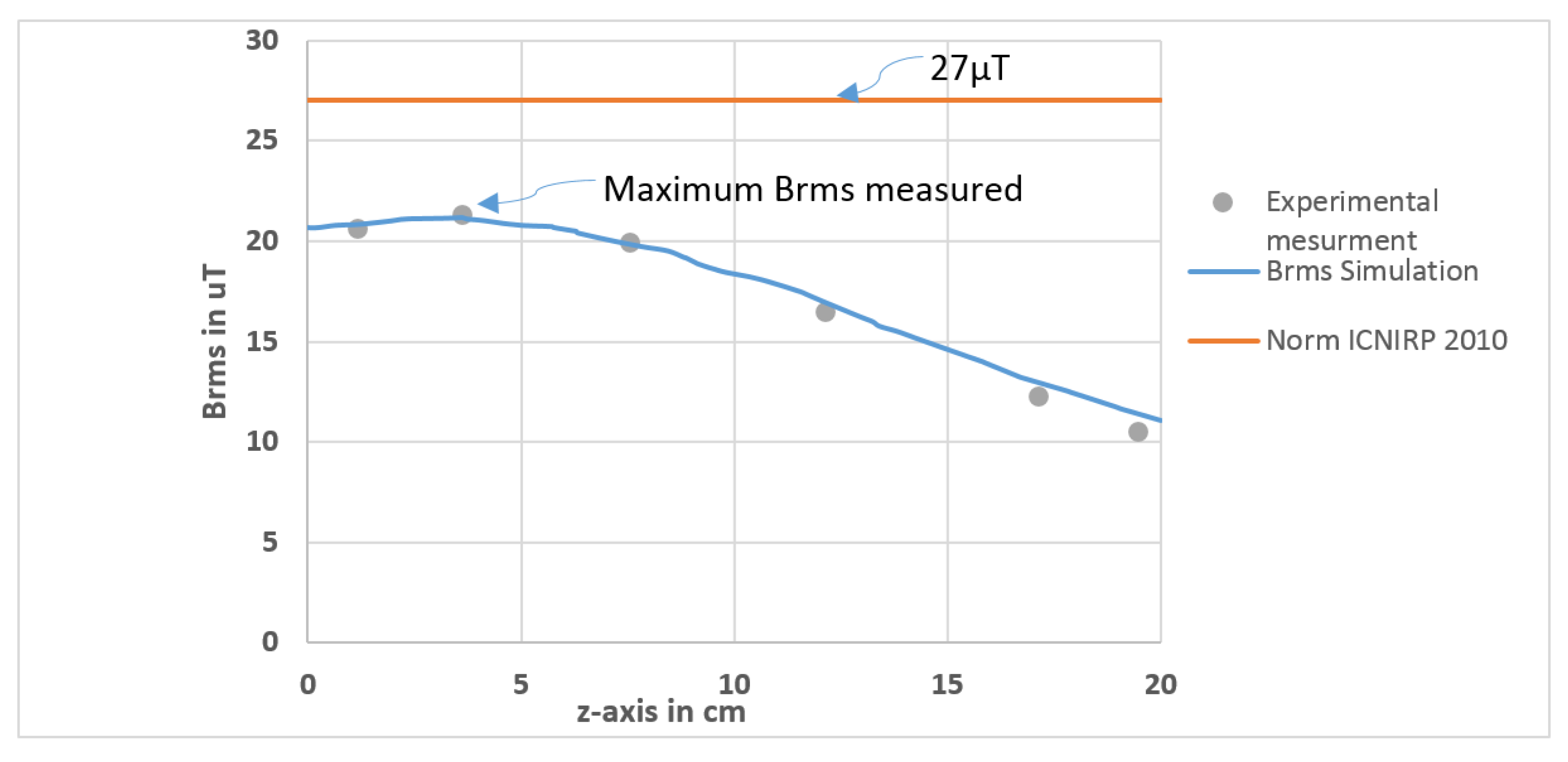
4.1. Magnetic Flux Density and Induced Current
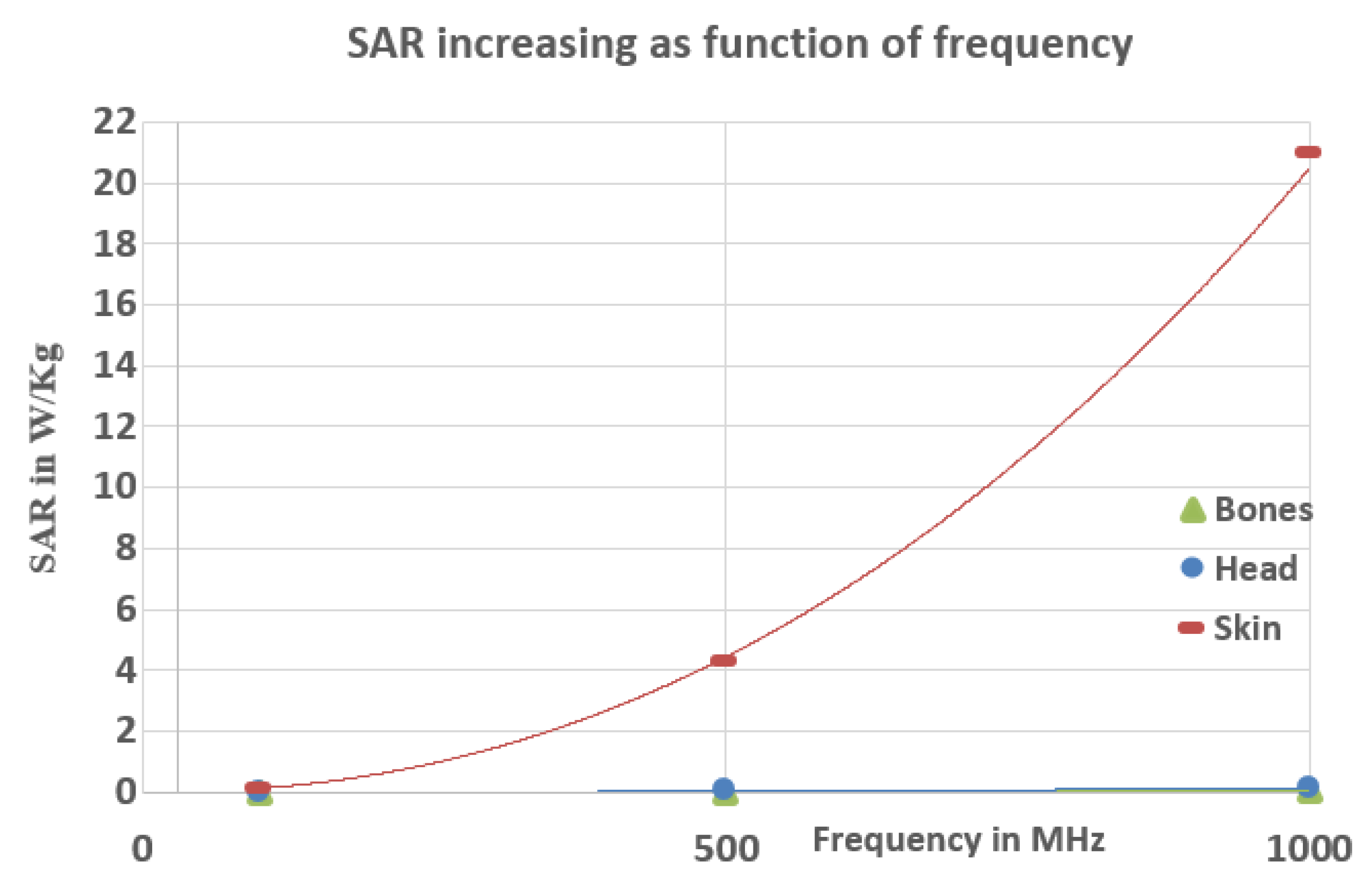
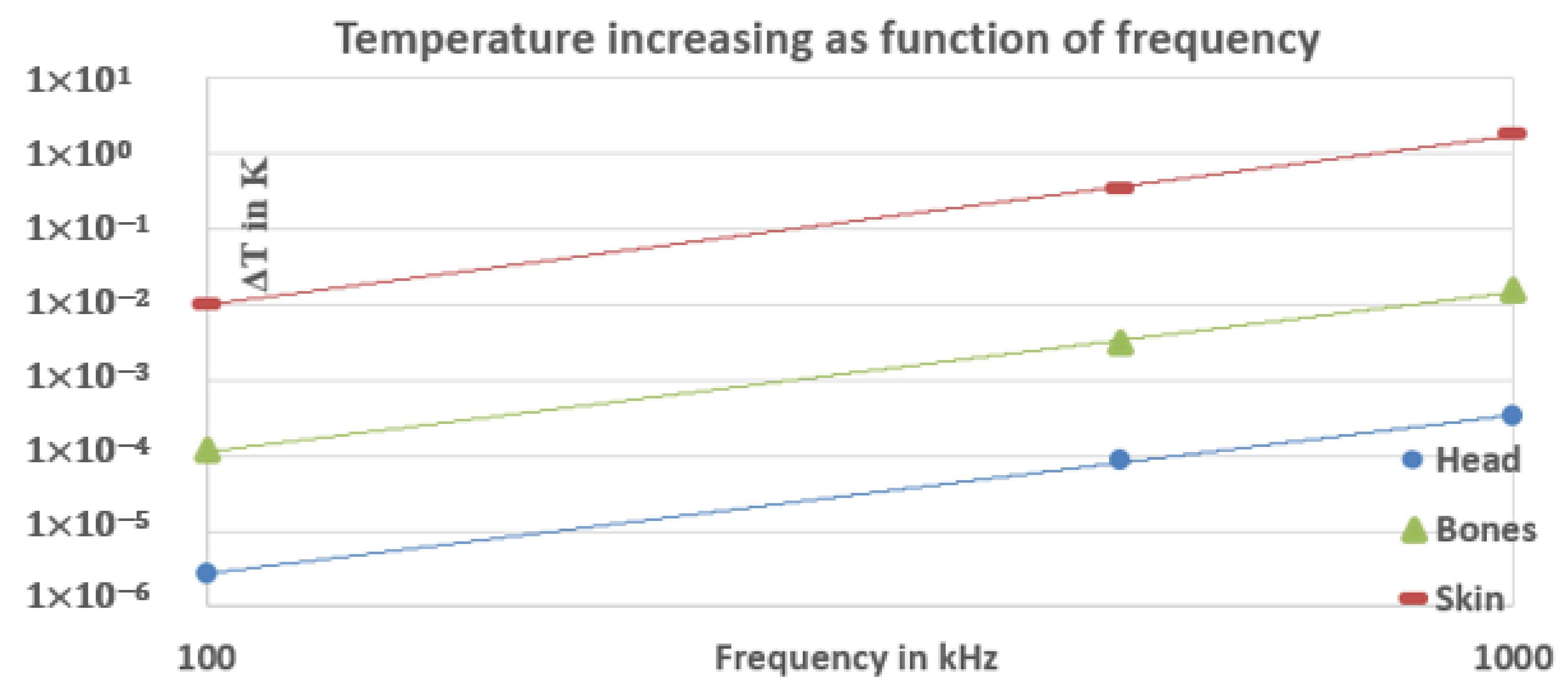
4.2. SAR and Heat Transfer
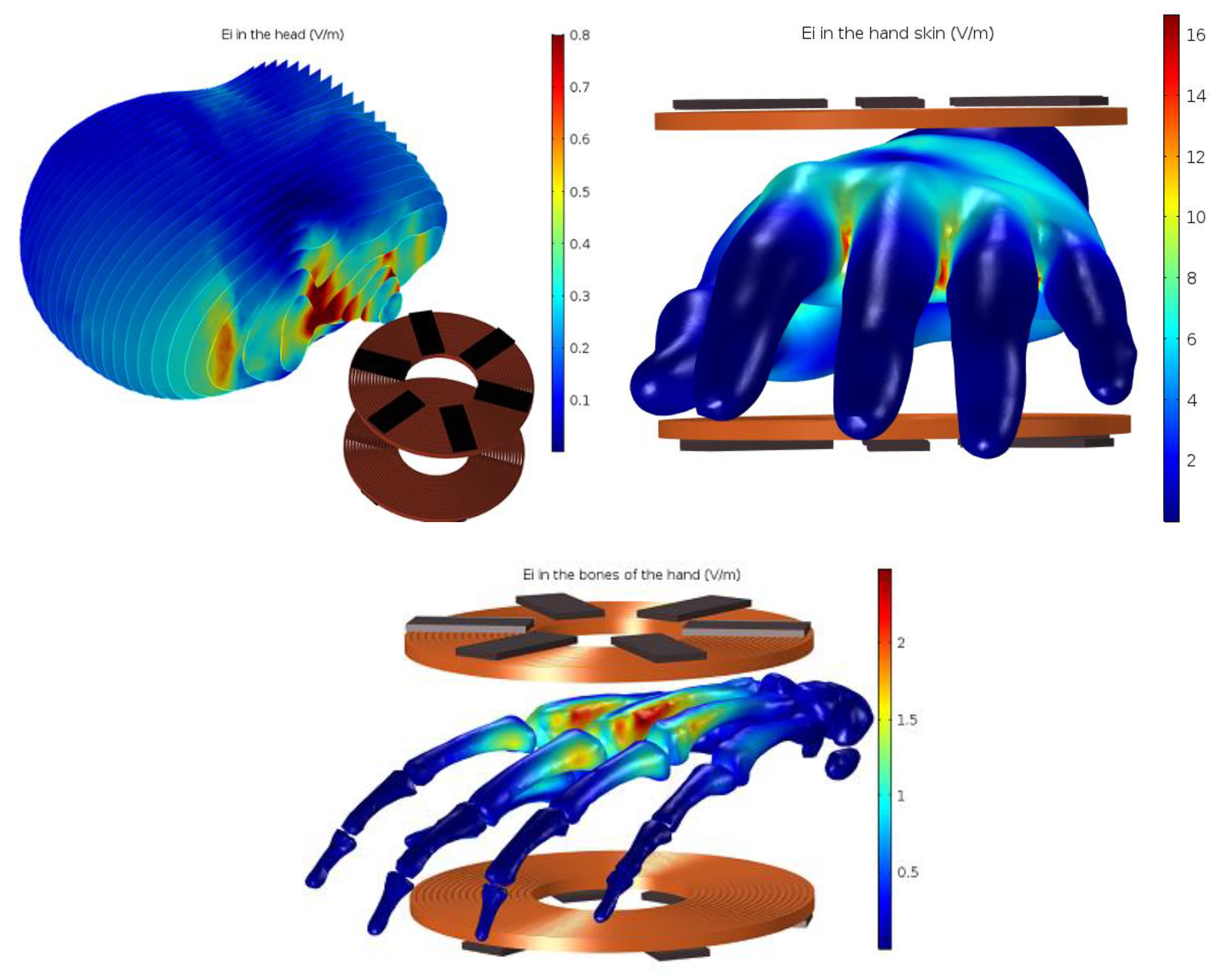
4.2.1. and Heat Transfer at 100 kHz
4.2.2. Evolution of and Temperature
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (1 Hz to 100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar]
- Non-Binding Guide to Good Practice for Implementing Directive 2013/35/EU Electromagnetic Fields; Publication Office of the European Union: Luxembourg, 2015; Practical Guide; Volume 1.
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric, magnetic and electromagnetic field (100 kHz TO 300 GHz). Health Phys. 2009, 97, 257–258. [Google Scholar] [CrossRef] [PubMed]
- IEEE. Recommended Practice for Measurements and Computations of Electric, Magnetic and Electromagnetic Fields with Respect to Human Exposure to Such Fields, 0 Hz to 100 kHz, IEEE Std C95.3.1-2010; The Institute of Electrical and Electronics Engineers: New York, NY, USA, 2010. [Google Scholar]
- IEEE. IEEE Standard for Safety Levels with Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 3 kHz to 300 GHz, IEEE Std C95.1™-2005; The Institute of Electrical and Electronics Engineers: New York, NY, USA, 2006. [Google Scholar]
- World Health Organization. Department of protection of the human environment. Establishing a dialogue on risks from electromagnetic fields. In Radiation and Environmental Health; World Health Organization: Geneva, Switzerland, 2002. [Google Scholar]
- World Health Organization. Non-ionizing radiation, part 2: Radiofrequency electromagnetic fields. In IARC Monographs; World Health Organization: Geneva, Switzerland, 2013; Volume 102. [Google Scholar]
- Chan, K.H.; Hattori, J.; Laakso, I.; Hirata, A.; Taki, M. Computational dosimetry for grounded and ungrounded human models due to contact current. Phys. Med. Biol. 2013, 58, 5153. [Google Scholar] [CrossRef] [PubMed]
- De Santis, V.; Chen, X.L.; Laakso, I.; Hirata, A. An equivalent skin conductivity model for low-frequency magnetic field dosimetry. Biomed. Phys. Eng. Express 2015, 1, 15201. [Google Scholar] [CrossRef]
- Hirata, A.; Yamazaki, K.; Hamada, S.; Kamimura, Y.; Tarao, H.; Wake, K.; Suzuki, Y.; Hayashi, N.; Fujiwara, O. Intercomparison of induced fields in Japanese male model for ELF magnetic field exposures: Effect of different computational methods and codes. Radiat. Prot. Dosim. 2010, 138, 237–244. [Google Scholar] [CrossRef] [PubMed]
- Dimbylow, P. Development of the female voxel phantom, NAOMI, and its application to calculations of induced current densities and electric fields from applied low frequency magnetic and electric fields. Phys. Med. Biol. 2005, 50, 1047. [Google Scholar] [CrossRef]
- Laakso, I.; Hirata, A. Reducing the staircasing error in computational dosimetry of low-frequency electromagnetic fields. Phys. Med. Biol. 2012, 57, N25–N34. [Google Scholar] [CrossRef]
- Neufeld, E.; Iacono, M.I.; Akinnagbe, E.; Wolf, J.; Oikonomidis, I.V.; Sharma, D.; Wilm, B.; Wyss, M.; Jakab, A.; Cohen, E. Computational platform combining detailed and precise functionalized anatomical phantoms with EM-Neuron interaction modeling. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar]
- Bakker, J.F.; Paulides, M.M.; Neufeld, E.; Christ, A.; Chen, X.L.; Kuster, N.; van Rhoon, G.C. Children and adults exposed to low-frequency magneticfields at the ICNIRP reference levels: Theoretical assessment of the induced electric fields. Phys. Med. Biol. 2012, 57, 1815. [Google Scholar] [CrossRef]
- Poljak, D.; Cvetkovi´c, M.; Bottauscio, O.; Hirata, A.; Laakso, I.; Neufeld, E.; Reboux, S.; Warren, C.; Giannopolous, A.; Costen, F. On the use of conformal models and methods in dosimetry for nonuniform field exposure. IEEE Trans. Electromagn. Compat. 2017, 60, 328–337. [Google Scholar] [CrossRef]
- Lin, J.C. Electromagnetic fields in biological systems. In IARC Monographs, 1st ed.; CRC Press: London, UK, 2011. [Google Scholar]
- Poljak, D. Numerical Methods and Advanced Simulation in Biomechanics and Biological Process; Academic Press: Cambridge, MA, USA, 2018; Chapter 7; pp. 119–143. [Google Scholar]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Modifed pennes’ equation modelling bio-heat transfer inliving tissues: Analytical and numerical analysis. Nat. Sci. 2010, 2, 1375–1385. [Google Scholar]
- Ji, X.; Zheng, J.; Yang, R.; Kainz, W.; Chen, J. Evaluations of the MRI RF-induced heating for helical stents under a 1.5T MRI system. IEEE Trans. Electromagn. Compat. 2019, 61, 57–64. [Google Scholar] [CrossRef]
- Wen, F.; Huang, X.L. Human exposure to electromagnetic fields from parallel wireless power transfer systems. Int. J. Environ. Res. Public Health 2017, 14, 157. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, J.D.; Bernard, T.E.; Dukes-Dobos, F.N. Evaluation and Control of Hot Working Environments: Part I—Guidelines for the Practitioner. Int. J. Ind. Ergon. 2000, 1, 329–336. [Google Scholar] [CrossRef]
- Ahmadikia, H.; Moradi, A.; Fazlali, R.; Parsa, A.B. Analytical solution of non-fourier and fourier bioheat transfer analysis during laser irradiation of skin tissue. J. Mech. Sci. Technol. 2012, 26, 1937–1947. [Google Scholar] [CrossRef]
- Marinova, I.; Mateev, V. Electromagnetic field modeling in human tissue. Int. J. Biomed. Biol. Eng. 2010, 4. [Google Scholar] [CrossRef]
- Ding, P.; Bernard, L.; Pichon, L.; Razek, A. Evaluation of electromagnetic fields in human body exposed to wireless inductive charging system. IEEE Trans. Magn. 2014, 50. [Google Scholar] [CrossRef]
- Mohammad, M.; Wodajo, E.T.; Choi, S.; Elbuluk, M. Modeling and design of passive shield to limit EMF emission and to minimize shield loss in unipolar wireless charging system for EV. IEEE Trans. Power Electron. 2019, 34, 12235–12245. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Kang, J.; Wang, Y. Electromagnetic safety evaluation and protection methods for a wireless charging system in an electric vehicle. IEEE Trans. Electromagn. Compat. 2019, 61, 1913–1925. [Google Scholar] [CrossRef]
- Touazi, A.; Dergham, I.; Alayli, Y.; Chassagne, L.; Linares, J. COMSOL simulation of an attenuated magnetic field through a metallic plate. J. Phys. Conf. Ser. 2018, 1141, 12156. [Google Scholar] [CrossRef]
- Anele, A.O.; Hamam, Y.; Alayli, Y.; Djouani, K. Computation of the mutual inductance between circular filaments with coil misalignment. In Proceedings of the IEEE Africon, Pointe-Aux-Piments, Mauritius, 9–12 September 2013. [Google Scholar]
- Anele, A.; Hamam, Y.; Chassagne, L.; Linares, J.; Alayli, Y.; Djouani, K. Computation and experimental measurements of the magnetic fields between filamentary circular coils. Int. J. Phys. Chem. 2015, 1, 5–13. [Google Scholar]
- Lee, A.; Hong, S.; Choi, H. Is the SAM phantom conservative for SAR evaluation of all phone designs? ETRI J. 2019, 41, 337–347. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: II. Measurements in the frequency range 10Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues; Version 4.0. 2018. Available online: www.itis.ethz.ch/database (accessed on 16 March 2020).
- Lifesciencedb, BodyParts3D, Anatomography. Available online: https://lifesciencedb.jp/bp3d/ (accessed on 10 January 2020).
- Schmid, G.; Cecil, S.; Uberbacher, R. The role of skin conductivity in a low frequency exposure assessment for peripheral nerve tissue according to the ICNIRP 2010 guidelines. Phys. Med. Biol. 2013, 58, 4703–4716. [Google Scholar] [CrossRef] [PubMed]
- Wake, K.; Sasaki, K.; Watanabe, S. Conductivities of epidermis, dermis, and subcutaneous tissue at intermediate frequencies. Phys. Med. Biol. 2016, 61, 4376–4389. [Google Scholar] [CrossRef] [PubMed]
- Oltulu, P.; Ince, B.; Kokbudak, N.; Findik, S.; Kilinc, F. Measurement of epidermis, dermis, and total skin thicknesses from six different body regions with a new ethical histometric technique. Turk. J. Plast. Surg. 2018, 26, 56–61. [Google Scholar] [CrossRef]
- Federal Communications Commission. FCC-11-125; Federal Communications Commission: Washington, DC, USA, 2011; p. 20554.


| Symbol | Quantity | Unit |
|---|---|---|
| Magnetic flux density | T | |
| Current density | A/m2 | |
| Electrical field strength | V/m | |
| permeability | H/m | |
| conductivity | S/m | |
| Mass density | kg/m3 | |
| Heat capacity | J/(kg·K) | |
| Thermal conductivity | W/(m·K) | |
| Relative permeability | ||
| Relative Permittivity | ||
| Arterial temperature | K | |
| heat capacity of blood | J/(kg·K) | |
| blood perfusion rate | kg/(s·m3) | |
| Metabolic heat | W/m3 |
| Tissues | σ | ρ | ||
|---|---|---|---|---|
| Skin (30 kHz) | 1 | 1.13 × | 0.095 | 1090 |
| Bones of arms (30 kHz) | 1 | 308 | 2.06 × | 1920 |
| Skin (100 kHz) | 1 | 1.12 × | 0.1 | 1090 |
| Bones of arms (100 kHz) | 1 | 228 | 2.08 × | 1920 |
| Frequency 30 kHz | |
|---|---|
| All tissues of head and body (ICNIRP 2010) | 4.05 V/m |
| Entire body(European commission) | 8.06 V/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dergham, I.; Alayli, Y.; Imad, R.; Hamam, Y. Effects of a Wireless Charging System Built for An Electric Kick Scooter on Human Biological Tissue. Int. J. Environ. Res. Public Health 2020, 17, 2662. https://doi.org/10.3390/ijerph17082662
Dergham I, Alayli Y, Imad R, Hamam Y. Effects of a Wireless Charging System Built for An Electric Kick Scooter on Human Biological Tissue. International Journal of Environmental Research and Public Health. 2020; 17(8):2662. https://doi.org/10.3390/ijerph17082662
Chicago/Turabian StyleDergham, Ibrahim, Yasser Alayli, Rodrigue Imad, and Yskandar Hamam. 2020. "Effects of a Wireless Charging System Built for An Electric Kick Scooter on Human Biological Tissue" International Journal of Environmental Research and Public Health 17, no. 8: 2662. https://doi.org/10.3390/ijerph17082662
APA StyleDergham, I., Alayli, Y., Imad, R., & Hamam, Y. (2020). Effects of a Wireless Charging System Built for An Electric Kick Scooter on Human Biological Tissue. International Journal of Environmental Research and Public Health, 17(8), 2662. https://doi.org/10.3390/ijerph17082662






