Study of Sorption Kinetics and Sorption–Desorption Models to Assess the Transport Mechanisms of 2,4-Dichlorophenoxyacetic Acid on Volcanic Soils
Abstract
1. Introduction
2. Materials and Methods
2.1. Soil Samples
2.2. Analytical methods
2.3. Chemicals
2.4. Sorption Kinetic Experiments, Sorption–Desorption Experiments and Models
2.4.1. Kinetic Sorption Experiments
2.4.2. Sorption–Desorption Experiments
2.5. Sample preparation for the Raman and SERS Measurements
2.6. Statistical Analysis
3. Results and Discussion
3.1. Physiochemical Properties of VADS
3.2. Sorption Kinetics
Pseudo-First-Order () and Pseudo-Second-Order () Models
3.3. Solute Transport Mechanism
3.3.1. Elovich Model
3.3.2. Intraparticle Diffusion () Model
3.3.3. Boyd Model
3.3.4. Two-Site Non-Equilibrium () Model
3.4. Sorption Models
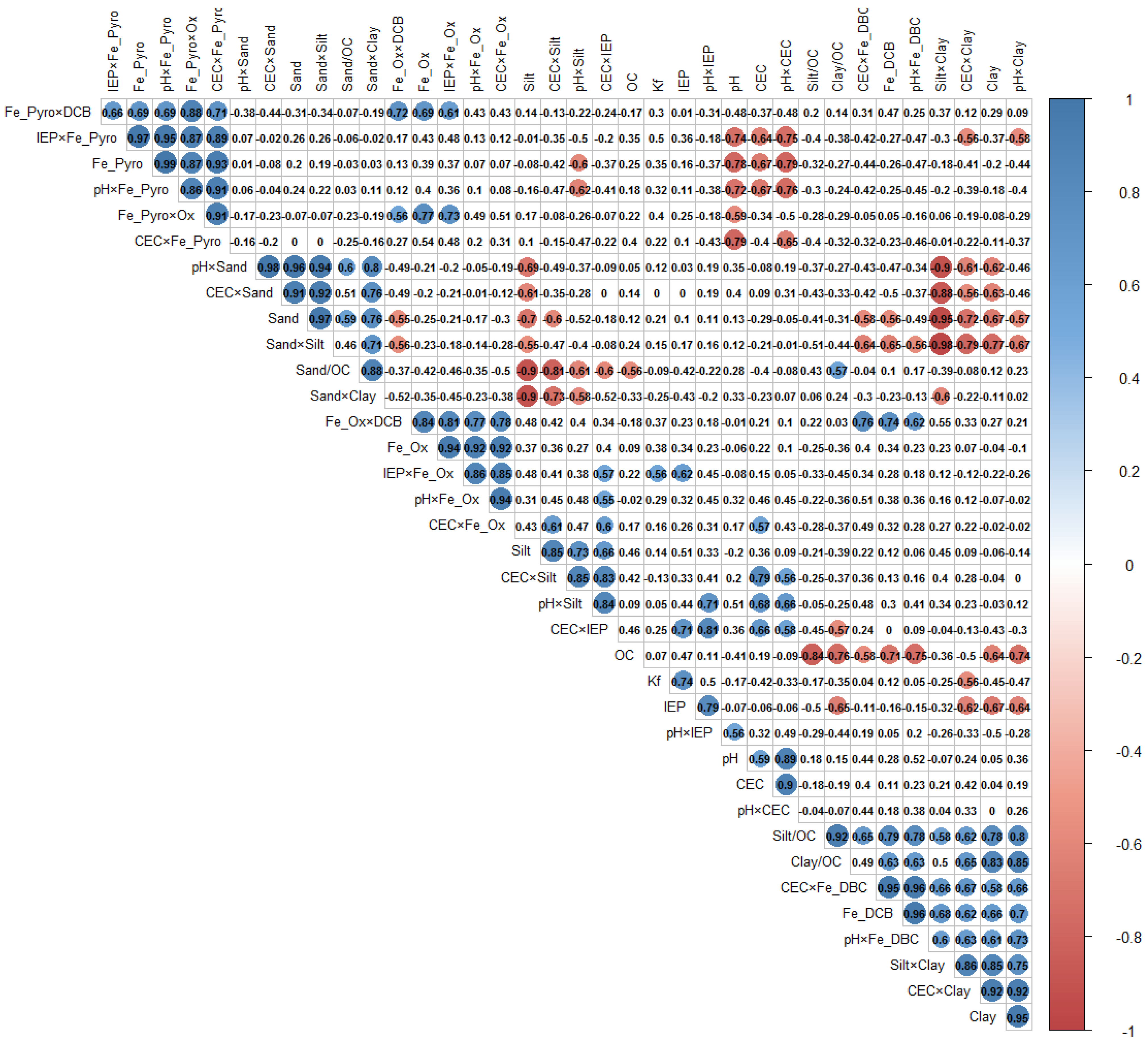
3.5. Exploratory MLR Model of 2,4-D Sorption
3.6. Spectroscopic Analysis
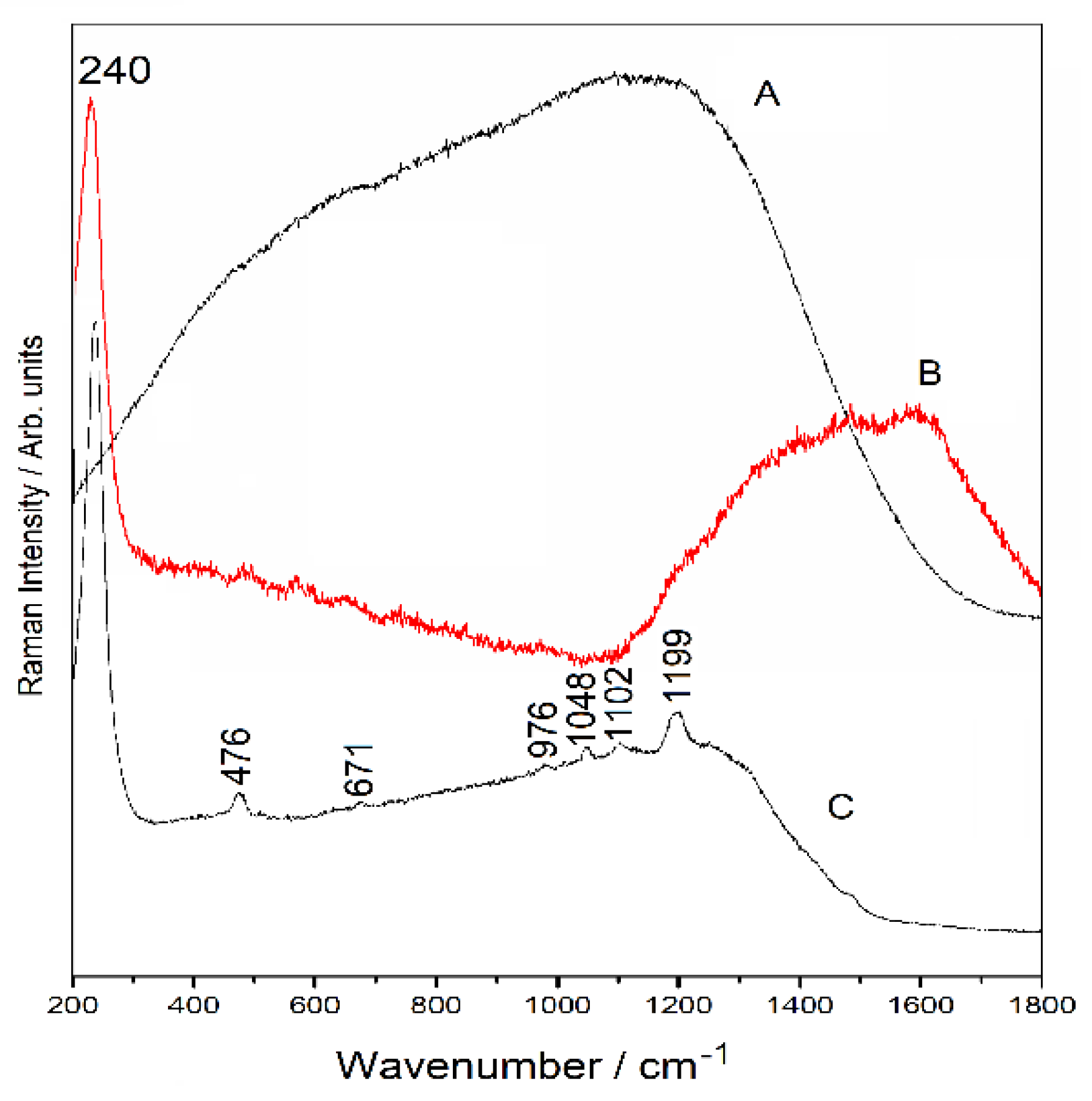
3.6.1. Raman Spectra
3.6.2. SERS Spectra
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caceres-Jensen, L.; Rodríguez-Becerra, J.; Sierra-Rosales, P.; Escudey, M.; Valdebenito, J.; Neira-Albornoz, A.; Dominguez-Vera, V.; Villagra, C.A. Electrochemical method to study the environmental behavior of Glyphosate on volcanic soils: Proposal of adsorption-desorption and transport mechanisms. J. Hazard. Mater. 2019, 379, 120746. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Garg, N.; Joshi, H.; Sharma, M. Persistence and mobility of 2,4-D in unsaturated soil zone under winter wheat crop in sub-tropical region of India. Agric. Ecosyst. Environ. 2012, 146, 60–72. [Google Scholar] [CrossRef]
- Werner, D.; Garratt, J.A.; Pigott, G. Sorption of 2,4-D and other phenoxy herbicides to soil, organic matter, and minerals. J. Soils Sediments 2012, 13, 129–139. [Google Scholar] [CrossRef]
- Ololade, I.A.; Alomaja, F.; Oladoja, N.A.; Ololade, O.O.; Oloye, F.F. Kinetics and isotherm analysis of 2,4-dichlorophenoxyl acetic acid adsorption onto soil components under oxic and anoxic conditions. J. Environ. Sci. Health Part B 2015, 50, 492–503. [Google Scholar] [CrossRef]
- Johnson, W.G.; Lavy, T.L.; Gbur, E.E. Sorption, Mobility and Degradation of Triclopyr and 2,4-D on Four Soils. Weed Sci. 1995, 43, 678–684. [Google Scholar] [CrossRef]
- Brusseau, M.L.; Famisan, G.B.; Artiola, J.F.; Janick, F.A.; Ian, L.P.; Mark, L.B. Chemical Contaminants. In Environmental Monitoring and Characterization; Academic Press: Burlington, VT, USA, 2004; pp. 299–312. [Google Scholar]
- Dahlgren, R.A.; Saigusa, M.; Ugolini, F.C.; Donald, L.S. The Nature, Properties and Management of Volcanic Soils. In Advances in Agronomy; Academic Press: Cambridge, MA, USA, 2004; Volume 82, pp. 113–182. [Google Scholar]
- Shoji, S.; Takahashi, T. Environmental and agricultural significance of volcanic ash soils. Glob. Environ. Res. 2002, 6, 113–135. [Google Scholar]
- Nanzyo, M.; Shoji, S.; Dahlgren, R. Physical Characteristics of Volcanic Ash Soils. In Developments in Soil Science; Shoji, S., Nanzyo, M., Dahlgren, R., Eds.; Elsevier: Amsterdam, The Netherlands, 1993; Chapter 7; pp. 189–207. [Google Scholar]
- Shoji, S.; Nanzyo, M.; Dahlgren, R. Productivity and Utilization of Volcanic Ash Soils. In Developments in Soil Science; Shoji, S., Nanzyo, M., Dahlgren, R., Eds.; Elsevier: Amsterdam, The Netherlands, 1993; Chapter 8; pp. 209–251. [Google Scholar]
- Ugolini, F.C.; Dahlgren, R.A. Soil development in volcanic ash. Glob. Environ. Res. 2002, 6, 69–81. [Google Scholar]
- Caceres-Jensen, L.; Rodriguez-Becerra, J.; Escudey, M. Impact of Physical/Chemical Properties of Volcanic Ash-Derived Soils on Mechanisms Involved during Sorption of Ionisable and Non-Ionisable Herbicides. In Advanced Sorption Process Applications; Edebali, D.S., Ed.; IntechOpen: London, UK, 2018; pp. 95–149. [Google Scholar] [CrossRef]
- Shinohara, H. Volcanic gases emitted during mild Strombolian activity of Villarrica volcano, Chile. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Vergara, M.; López-Escobar, L.; Palma, J.; Hickey-Vargas, R.; Roeschmann, C. Late tertiary volcanic episodes in the area of the city of Santiago de Chile: New geochronological and geochemical data. J. S. Am. Earth Sci. 2004, 17, 227–238. [Google Scholar] [CrossRef]
- Stern, C.R. Active Andean volcanism: Its geologic and tectonic setting. Revista Geológica Chile 2004, 31, 161–206. [Google Scholar] [CrossRef]
- Rivera, A.; Bown, F.; Carrión, D.; Zenteno, P. Glacier responses to recent volcanic activity in Southern Chile. Environ. Res. Lett. 2012, 7, 014036. [Google Scholar] [CrossRef]
- Lira, J.R.; Juica, W.G.; Thomas, C.V.; Canales, K.R.; Monetta, M.V.T.; Soto, R.T.; López, E.L.; Cornejo, I.F.; Moraga, P.R.; Meneses, F.I. Declaración de Ventas de Plaguicidas; Servicio Agrícola y Ganadero, División de Protección Agrícola, Subdepartamento de Plaguicidas y Fertilizantes: Santiago, Chile, 2006. [Google Scholar]
- Borggaard, O.K.; Gimsing, A.L. Fate of glyphosate in soil and the possibility of leaching to ground and surface waters: A review. Pest Manag. Sci. 2008, 64, 441–456. [Google Scholar] [CrossRef]
- Borie, G.; Peirano, P.; Zunino, H.; Aguilera, S.M. N-pool in volcanic ash-derived soils in Chile and its changes in deforested sites. Soil Biol. Biochem. 2002, 34, 1201–1206. [Google Scholar] [CrossRef]
- Matus, F.; Garrido, E.; Sepúlveda, N.; Cárcamo, I.; Panichini, M.; Zagal, E. Relationship between extractable Al and organic C in volcanic soils of Chile. Geoderma 2008, 148, 180–188. [Google Scholar] [CrossRef]
- Caceres-Jensen, L.; Neira-Albornoz, A.; Escudey, M. Herbicides Mechanisms Involved in the Sorption Kinetic of Ionisable and Non Ionisable Herbicides: Impact of Physical/Chemical Properties of Soils and Experimental Conditions. In Kinetic Modeling for Environmental Systems; Rahman, R.O.A., Ed.; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Caceres-Jensen, L.; Escudey, M.; Fuentes, E.; Báez, M.E. Modeling the sorption kinetic of metsulfuron-methyl on Andisols and Ultisols volcanic ash-derived soils: Kinetics parameters and solute transport mechanisms. J. Hazard. Mater. 2010, 179, 795–803. [Google Scholar] [CrossRef]
- Caceres-Jensen, L.; Rodriguez-Becerra, J.; Escudey, M.; Joo-Nagata, J.; Villagra, C.A.; Dominguez-Vera, V.; Neira-Albornoz, A.; Cornejo-Huentemilla, M. Nicosulfuron sorption kinetics and sorption/desorption on volcanic ash-derived soils: Proposal of sorption and transport mechanisms. J. Hazard. Mater. 2020, 385, 121576. [Google Scholar] [CrossRef]
- Brusseau, M.; Rao, P. The influence of sorbate-organic matter interactions on sorption nonequilibrium. Chemosphere 1989, 18, 1691–1706. [Google Scholar] [CrossRef]
- Allison, L.E. Organic Carbon. In Methods of Soil Analysis; American Society of Agronomy: Madison, WI, USA, 1965; pp. 1367–1396. [Google Scholar]
- Blake, G.R. Particle Density. In Methods of Soil Analysis; Black, C.A., Ed.; American Society of Agronomy: Madison, WI, USA, 1965; Volume 9, pp. 371–373. [Google Scholar]
- Pizarro, C.; Escudey, M.; Fabris, J.D. Influence of Organic Matter on the Iron Oxide Mineralogy of Volcanic Soils. Hyperfine Interact. 2003, 148, 53–59. [Google Scholar] [CrossRef]
- Garrido, C.; Weiss-Lopez, B.E.; Vallette, M.M.C. Surface-enhanced Raman scattering activity of negatively charged bio-analytes from a modified silver colloid. Spectrosc. Lett. 2015, 49, 11–18. [Google Scholar] [CrossRef]
- Hiradate, S.; Furubayashi, A.; Uchida, N.; Fujii, Y. Adsorption of 2,4-Dichlorophenoxyacetic Acid by an Andosol. J. Environ. Qual. 2007, 36, 101–109. [Google Scholar] [CrossRef]
- Hyun, S.; Lee, L.S. Quantifying the Contribution of Different Sorption Mechanisms for 2,4-Dichlorophenoxyacetic Acid Sorption by Several Variable-Charge Soils. Environ. Sci. Technol. 2005, 39, 2522–2528. [Google Scholar] [CrossRef]
- Garrido, C.; Aguayo, T.; Clavijo, E.; Gómez-Jeria, J.S.; Campos-Vallette, M.M. The effect of the pH on the interaction of L-arginine with colloidal silver nanoparticles. A Raman and SERS study. J. Raman Spectrosc. 2013, 44, 1105–1110. [Google Scholar] [CrossRef]
- Cáceres-Jensen, L.; Rodríguez-Becerra, J.; Parra-Rivero, J.; Escudey, M.; Barrientos, L.; Castro-Castillo, V. Sorption kinetics of diuron on volcanic ash derived soils. J. Hazard. Mater. 2013, 261, 602–613. [Google Scholar] [CrossRef]
- Azizian, S. Kinetic models of sorption: A theoretical analysis. J. Colloid Interface Sci. 2004, 276, 47–52. [Google Scholar] [CrossRef]
- Önal, Y. Kinetics of adsorption of dyes from aqueous solution using activated carbon prepared from waste apricot. J. Hazard. Mater. 2006, 137, 1719–1728. [Google Scholar] [CrossRef]
- Wankasi, D.; Jnr, M.H.; Spiff, A.I. Sorption kinetics of Pb2+ and Cu2+ ions from aqueous solution by Nipah palm (Nypa fruticans Wurmb) shoot biomass. Electron. J. Biotechnol. 2006, 9, 587–592. [Google Scholar] [CrossRef]
- Kumar, K.V.; Ramamurthi, V.; Sivanesan, S. Modeling the mechanism involved during the sorption of methylene blue onto fly ash. J. Colloid Interface Sci. 2005, 284, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Hameed, B.; El-Khaiary, M. Equilibrium, kinetics and mechanism of malachite green adsorption on activated carbon prepared from bamboo by K2CO3 activation and subsequent gasification with CO2. J. Hazard. Mater. 2008, 157, 344–351. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, B.; Cabrita, I.; Mestre, A.; Parra, J.; Pires, J.; Carvalho, A.; Ania, C. Surface heterogeneity effects of activated carbons on the kinetics of paracetamol removal from aqueous solution. Appl. Surf. Sci. 2010, 256, 5171–5175. [Google Scholar] [CrossRef]
- Ho, Y. Review of second-order models for adsorption systems. J. Hazard. Mater. 2006, 136, 681–689. [Google Scholar] [CrossRef]
- Fernández-Bayo, J.D.; Nogales, R.; Romero, E. Evaluation of the Sorption Process for Imidacloprid and Diuron in Eight Agricultural Soils from Southern Europe Using Various Kinetic Models. J. Agric. Food Chem. 2008, 56, 5266–5272. [Google Scholar] [CrossRef]
- Rudzinski, W.; Panczyk, T. Kinetics of Isothermal Adsorption on Energetically Heterogeneous Solid Surfaces: A New Theoretical Description Based on the Statistical Rate Theory of Interfacial Transport. J. Phys. Chem. B 2000, 104, 9149–9162. [Google Scholar] [CrossRef]
- Wu, F.-C.; Tseng, R.-L.; Juang, R.-S. Characteristics of Elovich equation used for the analysis of adsorption kinetics in dye-chitosan systems. Chem. Eng. J. 2009, 150, 366–373. [Google Scholar] [CrossRef]
- Wu, F.-C.; Tseng, R.-L.; Juang, R.-S. Initial behavior of intraparticle diffusion model used in the description of adsorption kinetics. Chem. Eng. J. 2009, 153, 1–8. [Google Scholar] [CrossRef]
- Inoue, M.H.; Oliveira, R.S.; Regitano, J.B.; Tormena, C.A.; Constantin, J.; Tornisielo, V.L. Sorption Kinetics of Atrazine and Diuron in Soils from Southern Brazil. J. Environ. Sci. Health Part B 2004, 39, 589–601. [Google Scholar] [CrossRef]
- Nkedi-Kizza, P.; Shinde, D.; Savabi, M.R.; Ouyang, Y.; Nieves, L. Sorption Kinetics and Equilibria of Organic Pesticides in Carbonatic Soils from South Florida. J. Environ. Qual. 2006, 35, 268–276. [Google Scholar] [CrossRef]
- Appel, J. Freundlich’s adsorption isotherm. Surf. Sci. 1973, 39, 237–244. [Google Scholar] [CrossRef]
- Sparks, D.L. Sorption Phenomena on Soils. In Environmental Soil Chemistry, 2nd ed.; Academic Press: Burlington, VT, USA, 2003; pp. 133–186. [Google Scholar]
- Maqueda, C.; Undabeytia, T.; Villaverde, J.; Morillo, E. Behaviour of glyphosate in a reservoir and the surrounding agricultural soils. Sci. Total. Environ. 2017, 593–594, 787–795. [Google Scholar] [CrossRef]
- Okada, E.; Costa, J.L.; Bedmar, F. Adsorption and mobility of glyphosate in different soils under no-till and conventional tillage. Geoderma 2016, 263, 78–85. [Google Scholar] [CrossRef]
- Ioannou, Z.; Simitzis, J. Adsorption kinetics of phenol and 3-nitrophenol from aqueous solutions on conventional and novel carbons. J. Hazard. Mater. 2009, 171, 954–964. [Google Scholar] [CrossRef]
- Tan, K.; Hameed, B. Insight into the adsorption kinetics models for the removal of contaminants from aqueous solutions. J. Taiwan Inst. Chem. Eng. 2017, 74, 25–48. [Google Scholar] [CrossRef]
- Beltran, J.; Gerritse, R.G.; Hernandez, F. Effect of flow rate on the adsorption and desorption of glyphosate, simazine and atrazine in columns of sandy soils. Eur. J. Soil Sci. 1998, 49, 149–156. [Google Scholar] [CrossRef]
- Paz-Y-Miño, C.; Sanchez, M.-E.; Arévalo, M.; Muñoz, M.J.; Witte, T.; De-La-Carrera, G.O.; Leone, P.E. Evaluation of DNA damage in an Ecuadorian population exposed to glyphosate. Genet. Mol. Biol. 2007, 30, 456–460. [Google Scholar] [CrossRef]
- West, S.L.; White, G.N.; Deng, Y.; McInnes, K.J.; Juo, A.S.R.; Dixon, J.B. Kaolinite, Halloysite, and Iron Oxide Influence on Physical Behavior of Formulated Soils. Soil Sci. Soc. Am. J. 2004, 68, 1452–1460. [Google Scholar] [CrossRef]
- Vereecken, H. Mobility and leaching of glyphosate: A review. Pest. Manag. Sci. 2005, 61, 1139–1151. [Google Scholar] [CrossRef]
- Mella, A.; Kühne, A. Mapas Geológicos y Carta de Suelos, Mapa de Ubicación de los Suelos Derivados de Materiales Vocánicos, 1: 1.000. 000. In Suelos Volcánicos de Chile; Instituto de Investigaciones Agropecuarias (INIA): Santiago, Chile, 1985. [Google Scholar]
- Kosmulski, M. pH-dependent surface charging and points of zero charge. IV. Update and new approach. J. Colloid Interface Sci. 2009, 337, 439–448. [Google Scholar] [CrossRef]
- Cáceres-Jensen, L.; Gan, J.; Báez, M.; Fuentes, R.; Escudey, M. Adsorption of Glyphosate on Variable-Charge, Volcanic Ash-Derived Soils. J. Environ. Qual. 2009, 38, 1449–1457. [Google Scholar] [CrossRef]
- Spadotto, C.A.; Hornsby, A.G. Soil sorption of acidic pesticides: Modeling pH effects. J. Environ. Qual. 2003, 32, 949–956. [Google Scholar] [CrossRef]
- Villaverde, J.; Kah, M.; Brown, C.D. Adsorption and degradation of four acidic herbicides in soils from southern Spain. Pest. Manag. Sci. 2008, 64, 703–710. [Google Scholar] [CrossRef]
- Magga, Z.; Tzovolou, D.N.; Theodoropoulou, M.A.; Tsakiroglou, C.D. Combining experimental techniques with non-linear numerical models to assess the sorption of pesticides on soils. J. Contam. Hydrol. 2012, 129–130, 62–69. [Google Scholar] [CrossRef]
- Wang, P.; Keller, A.A. Sorption and desorption of atrazine and diuron onto water dispersible soil primary size fractions. Water Res. 2009, 43, 1448–1456. [Google Scholar] [CrossRef] [PubMed]
- Villaverde, J.; Van Beinum, W.; Beulke, S.; Brown, C.D. The Kinetics of Sorption by Retarded Diffusion into Soil Aggregate Pores. Environ. Sci. Technol. 2009, 43, 8227–8232. [Google Scholar] [CrossRef] [PubMed]
- Brusseau, M.L. Factors influencing the transport and fate of contaminants in the subsurface. J. Hazard. Mater. 1992, 32, 137–143. [Google Scholar] [CrossRef]
- Cáceres, L.; Fuentes, R.; Escudey, M.; Fuentes, E.; Báez, M.E. Metsulfuron-methyl Sorption/Desorption Behavior on Volcanic Ash-Derived Soils. Effect of Phosphate and pH. J. Agric. Food Chem. 2010, 58, 6864–6869. [Google Scholar] [CrossRef]
- Hyun, S.; Lee, L.S. Factors Controlling Sorption of Prosulfuron by Variable-Charge Soils and Model Sorbents. J. Environ. Qual. 2004, 33, 1354–1361. [Google Scholar] [CrossRef]
- Alister, C.; Araya, M.; Cordova, A.; Saavedra, J.; Kogan, M. Humic Substances and their Relation to Pesticide Sorption in Eight Volcanic Soils. Planta Daninha 2020, 38, 38. [Google Scholar] [CrossRef]
- Worrall, F.; Parker, A.; Rae, J.E.; Johnson, A.C. A Study of Suspended and Colloidal Matter in the Leachate from Lysimeters and its Role in Pesticide Transport. J. Environ. Qual. 1999, 28, 595–604. [Google Scholar] [CrossRef]
 ). (a) Hyperbolic; (b) Pseudo-second-order (); (c) Elovich; (d) Intraparticle Diffusion (); (e) Boyd, and (f) Two-Site Non-Equilibrium () models. Symbols represent the experimental data, and lines represent the theoretical curves described by each model.
). (a) Hyperbolic; (b) Pseudo-second-order (); (c) Elovich; (d) Intraparticle Diffusion (); (e) Boyd, and (f) Two-Site Non-Equilibrium () models. Symbols represent the experimental data, and lines represent the theoretical curves described by each model.
 ). (a) Hyperbolic; (b) Pseudo-second-order (); (c) Elovich; (d) Intraparticle Diffusion (); (e) Boyd, and (f) Two-Site Non-Equilibrium () models. Symbols represent the experimental data, and lines represent the theoretical curves described by each model.
). (a) Hyperbolic; (b) Pseudo-second-order (); (c) Elovich; (d) Intraparticle Diffusion (); (e) Boyd, and (f) Two-Site Non-Equilibrium () models. Symbols represent the experimental data, and lines represent the theoretical curves described by each model.
| Soil | Classification | Location |
|---|---|---|
| COLL | Fine, Mesic, Xeric, Paleumult | 36°58′ S; 72°09′ W |
| MET | Fine, Mesic, Paleumult | 38°34′ S; 72°22′ W |
| FRE | Medial, Mesic, Xeric, Placandept | 38°57′ S; 72°36′ W |
| STB | Ashy, Medial, Mesic, Typic, Dystrandept | 36°50′ S; 71°55′ W |
| OSN | Medial, Mesic, Typic, Dystrandept | 40°32′ S; 73°05′ W |
| DIG | Medial, Thermic, Typic, Dytrandept | 36°53′ S; 72°10′ W |
| TCO | Medial, Mesic, Entic Dystrandep | 38°6′ S; 72°36′ W |
| RAL | Mesic, Umbric, Vitrandept | 41°32′ S; 73°05′ W |
| NBR | Ashy, Mesic, Hydric, Dystrandept | 41°19′ S; 73°06′ W |
| FRU | Medial, Isomesic, Typic, Placandept | 41°06′ S; 73°07′ W |
| Pesticide Name (CAS RN) | Molar Mass (g mol−1) | Use and APPR 1 (g ha−1) | 2 | 3 | 4 (mg L−1) | DT50 5 (days) | |||
|---|---|---|---|---|---|---|---|---|---|
| 2,4-D (94-75-7) | 221.04 | Post-emergence herbicide and selective mode of action. The APPR of 2,4-D is very low (280–2300) for weed control in corn. | 2.97 | 0.027 in alkaline condition, 29.23 in acidic condition | 300 at = 1 and >20,000 at = 5 (20 °C) | 10–24 | |||
| HPLC Analysis | |||||||||
| HPLC mobile phase | Flow rate (mL min−1) | Injection volume (µL) | Wavelength (nm) | Temp (°C) | Column | Detection limit (mg L−1) | |||
| 65:35 (v/v) = AcN:water at 2.8 | 1 | 25 | 224 | 35 °C | MultiHigh 100 RP C18 (150 mm × 4.6 mm ID, 5µm). | 0.009 | |||
| Equation | Equation Number | Parameters | Theoretical and Empirical Description |
|---|---|---|---|
| Adsorbed quantity: | (1) | : Adsorbed quantity (μg g−1) at any soil-solution contact time (min) for kinetic sorption experiments; : Initial concentration of 2,4-D in solution; : Equilibrium concentration of 2,4-D in solution; : Solution/soil ratio. | The adsorbed quantity is obtained from a mass balance between initial and equilibrium concentration of 2,4-D in solution. This equation is valid when degradation and precipitation are negligible during the sorption process. |
| Sorption kinetic models | |||
| Pseudo-first-order () model [32]: | (2) | : is the maximum sorbed amount (µg g−1). : Rate constant (min−1). | This equation fits better at high values. The is a combination of sorption and desorption rate constants [33]. Its magnitude is influenced by experimental conditions ( and temperature) and particle size (small particle size imply large values of ). |
| Pseudo-second-order () model [33,34,35,36,37,38,39]: | (3) | : Rate constant (g μg−1 min−1). Derived parameters from Equation (3): : Initial sorption rate (g μg−1 min−1), ; : Half-life time (min), . | Better fits at low values [33]. The is a complex function of with a time scale factor that decreases when increases. Additionally, this model assumes sorption capacity to be proportional to the number of active sites occupied on the soil [40]. |
| Solute transport mechanism | |||
| Elovich model [34,41]: | : Initial sorption rate (μg g−1 min−1); : Number of sites available for the sorption (g μg −1), related to the extent of surface coverage and activation energy for chemisorption; : Approaching equilibrium factor. When , the curve rises slowly (Zone I), in the range , the curve rises moderately (Zone II); in the range , the curve rises rapidly (Zone III); and when the curve reaches equilibrium instantly (Zone IV). : Longest time in the sorption process ( at equilibrium); : Solid-phase concentration at (); (1/β): rate constant during the slow phase of the reaction. | Describe second order kinetics only for systems with a heterogeneous adsorbing surface. The deviations of the Elovich model at high surface coverage could result in this model neglecting simultaneously occurring desorption. At low surface coverage, this equation might be applied only in cases of strongly heterogeneous surfaces. | |
| (4) | |||
| Dimensionless Elovich model [42]: | |||
| (5) | |||
| Intraparticle Diffusion (IPD) model [34,36]: | : Rate constant of step (μg g−1 min1/2); : Thickness of the boundary layer in step (μg g−1); : Initial sorption factor in step (if , the applicability of dimensionless IPD model is limited to only one step). The initial sorption can be weak (zone I, ), medium (zone II, ), strong (zone III, ) or complete (zone IV, ) regarding the equilibrium sorption. | is proportional to the boundary layer thickness representing the initial sorption on external sites [44]. When , is the most critical rate process controlling sorption; , is not the only rate-controlling step. Thus, the first step must be attributed to the across the boundary layer controlled by liquid film diffusion. The positive intercepts result from the greater boundary layer effect indicating rapid sorption on adsorbents with a wide distribution of pore sizes [43]. | |
| (6) | |||
| Dimensionless Intraparticle Diffusion () model [43]: | |||
| (7) | |||
| Boyd model: | : Empirical constant related with the effective diffusion coefficient () and the effective particle size () for the sorption process. | If the plot of Equation (9) is linear with , the rate of mass transfer is controlled by pore diffusion. If the plot is non-linear or linear but , the film diffusion or chemisorption controls the sorption rate [32]. | |
| (8) | |||
| (9) | |||
| Two-Site Non-Equilibrium (TSNE) model [45]: | (10) | : Solute concentration at any time (μg mL−1); : Initial added solute concentration (μg mL−1); Retardation factor, proportional to the sorption strength; : Fraction of retardation for Type 1 sites (where sorption is assumed to be instantaneous); : First-order desorption rate constant for desorption from the Type 2 sites (where sorption is considered time-dependent) (h−1). Derived parameters from Equation (10): : Linear sorption partition coefficient at equilibrium (mL μg−1); ; : Fraction of the total sorption in the Type 1 sites when the system is in equilibrium, ; : Rate constant for EMT, calculated from the slope of linearisation in the plot of vs. time at initial time intervals. | The sorption parameters and are inversely related for neutral organic chemicals in soils and sediments [45]. The is considered as a parameter that indiscriminately combines several processes, such as intra- diffusion and delayed that control of sorbate into the complex. |
| Sorption–desorption process | |||
| Sorbed and desorbed fraction: | : Sorbed fraction (%); : Desorbed fraction (%); and : 2,4-D adsorbed in equilibrium (μg g−1) for sorption and desorption batch experiments, respectively. | The sorbed fraction can be calculated by means of the model if different steps are present during the sorption process. | |
| (11) | |||
| (12) | |||
| Linear model: | (13) | : Linear soil-solution distribution coefficient. Derived parameters from Equation (13): : distribution coefficient from . | The linear model is useful to describe sorption when the process is independent of the solute concentration. |
| Freundlich model for sorption: | : Freundlich constant;: Freundlich sorption coefficient. Derived parameters from Equation (14): : distribution coefficient from ; ; : Hysteresis coefficient for sorption loop; . | The Freundlich model assumes a heterogeneous surface [46]. The single term implies that the energy of sorption on a homogeneous surface is independent of surface coverage [47]. In this sense, the energy of binding is the same for the adsorptive sites, and interactions between adsorbed atoms do not exist [46]. The coefficient is related to the surface heterogeneity and the diversity of the energies associates with the sorption reaction [48]. If , the sorption process shows cooperative sorption; If , Freundlich model is equivalent to Linear model indicating low heterogeneity among the sites of the sorbent [48]; If , the relative sorption decreases when the concentration increases. This is characteristic of an L-type sorption isotherm and suggests that specific sites approached saturation as herbicide concentration increased [5], indicating that the sorption firstly occurred on higher energy sites of sorption, followed by low energy sites [49]. A value of close to 1 means that hysteresis is absent, while a value of < 1 indicates that hysteresis takes place. | |
| (14) | |||
| Freundlich model for desorption: | |||
| (15) | |||
| Soils | COLL | MET | FRE | STB | OSN | DIG | TCO | RAL | NBR | FRU |
|---|---|---|---|---|---|---|---|---|---|---|
| Physicochemical Properties | ||||||||||
| (%) | 1.5 | 2.3 | 4.5 | 5.1 | 5.1 | 5.8 | 6.4 | 6.9 | 9.5 | 11.0 |
| 5.2 | 4.7 | 4.4 | 5.7 | 4.6 | 6.2 | 5.4 | 4.4 | 4.1 | 4.1 | |
| 8.7 | 9.3 | 7.1 | 10.3 | 9.8 | 11.8 | 12.1 | 7.1 | 10.3 | 9.5 | |
| (%) | 13.7 | 8.0 | 21.3 | 7.2 | 10.1 | 35.5 | 16.1 | 47.3 | 6.2 | 16.3 |
| (%) | 40.7 | 56.7 | 54.2 | 66.5 | 50.9 | 45.1 | 58.2 | 38.5 | 66.2 | 63.9 |
| (%) | 45.7 | 35.3 | 24.5 | 26.3 | 39.1 | 19.4 | 25.7 | 12.9 | 27.6 | 19.7 |
| (%) | 0.7 | 0.8 | 2.2 | 0.3 | 1.4 | 0.4 | 0.7 | 1.8 | 1.8 | 1.0 |
| (%) | 0.9 | 1.8 | 2.5 | 1.9 | 2.0 | 1.9 | 2.2 | 1.4 | 3.3 | 0.6 |
| (%) | 6.2 | 7.1 | 4.3 | 5.3 | 3.0 | 3.5 | 3.9 | 1.4 | 5.1 | 0.6 |
| 2.0 | 2.5 | 3.1 | 3.8 | 2.1 | 2.6 | 2.9 | 3.3 | 3.3 | 2.9 | |
| Mineral | ||||||||||
| Allophane | +++++ | +++++ | +++++ | +++++ | +++++ | +++++ | +++++ | +++++ | ||
| α-Cristobalite | + | + | + | ++ | + | + | + | |||
| Chlorite–AL | + | ++ | ||||||||
| Feldspars | + | + | + | |||||||
| Ferrihydrite | + | + | + | + | ||||||
| Gibbsite | ++ | + | ++ | ++ | ||||||
| Goethite | + | |||||||||
| Halloysite | + | +++++ | ++ | +++ | ++ | + | ||||
| Kaolinite | +++++ | |||||||||
| Montmorillonite | + | |||||||||
| Organo-allophanic | ++ | + | ++ | + | ++ | ++ | + | |||
| Plagioclase | + | ++ | ++ | + | ||||||
| Quartz | + | + | ||||||||
| Vermiculite | + | ++ | + | + | ++ | |||||
| Parameters | COLL | MET | FRE | STB | OSN | DIG | TCO | RAL | NBR | FRU |
|---|---|---|---|---|---|---|---|---|---|---|
| (exp.) | 9.0 | 9.5 | 12.0 | 15.7 | 13.5 | 8.1 | 13.2 | 24.5 | 38.9 | 14.9 |
| Pseudo-second order | ||||||||||
| (μg g−1) a | 9.3 | 8.9 | 12.1 | 15.8 | 14.0 | 9.9 | 13.5 | 24.9 | 39.7 | 14.9 |
| (g μg −1 min−1) a | 1 × 10−2 | 2 × 10−2 | 2 × 10−2 | 2 × 10−2 | 1 × 10−2 | 9 × 10−3 | 1 × 10−2 | 9 × 10−3 | 8 × 10−3 | 5 × 10−2 |
| 0.9992 | 0.9993 | 0.9997 | 0.9997 | 0.9992 | 0.9997 | 0.9996 | 0.9992 | 0.9999 | 1.0000 | |
| (g μg −1 min−1) a | 1.2 | 1.4 | 3.6 | 5.8 | 2.4 | 0.9 | 2.6 | 5.6 | 13.3 | 11.6 |
| (min) a | 7.7 | 6.4 | 3.3 | 2.7 | 5.7 | 11.5 | 5.1 | 4.5 | 3.0 | 1.3 |
| Parameters | COLL | MET | FRE | STB | OSN | DIG | TCO | RAL | NBR | FRU |
|---|---|---|---|---|---|---|---|---|---|---|
| (exp.) | 2.4 | 2.9 | 4.3 | 6.9 | 5.4 | 2.3 | 5.1 | 10.8 | 50.4 | 4.7 |
| Elovich | ||||||||||
| (μg g−1 min−1) | 12.0 ± 0.2 a | 32.5 ± 0.2 | (1.0 ± 0.3)103 | (2.0 ± 0.4)104 | 52.8 ± 0.3 | 2.6 ± 0.4 | (2.0 ± 0.0)102 | (1.0 ± 0.1)104 | (3.0 ± 2.3)102 | (2.0 ± 0.2)109 |
| (g μg−1) | 0.8 ± 0.1 | 1.0 ± 0.1 | 1.0 ± 0.1 | 0.9 ± 0.1 | 0.6 ± 0.1 | 0.6 ± 0.1 | 0.7 ± 0.0 | 0.6 ± 0.1 | 0.2 ± 0.6 | 1.8 ± 0.1 |
| 0.9724 | 0.9794 | 0.9239 | 0.9016 | 0.9652 | 0.9505 | 0.9652 | 0.9890 | 0.7961 | 0.8956 | |
| Intraparticle Diffusion | ||||||||||
| (μg g−1) | 0.7 ± 0.0 | 0.6 ± 0.0 | 0.8 ± 0.0 | 1.0 ± 0.0 | 0.8 ± 0.0 | 1.4 ± 0.1 | 0.7 ± 0.0 | 1.0 ± 0.0 | 4.8 ± 0.6 | 0.5 ± 0.0 |
| (μg g−1) | 3.2 ± 0.4 | 3.8 ± 0.3 | 6.5 ± 0.2 | 9.4 ± 0.3 | 6.6 ± 0.2 | 0.0 ± 0.4 | 7.3 ± 0.2 | 16.4 ± 0.1 | 12.3 ± 2.3 | 11.7 ± 0.2 |
| 0.9360 | 0.9796 | 0.9968 | 0.9828 | 0.9780 | 0.9824 | 0.9862 | 0.9954 | 0.9323 | 0.9675 | |
| (μg g−1) | 0.2 ± 0.0 | 0.1 ± 0.0 | 0.1 ± 0.0 | 0.1 ± 0.0 | 0.1 ± 0.0 | 0.2 ± 0.0 | 0.1 ± 0.0 | 0.4 ± 0.0 | 0.2 ± 0.0 | 0.1 ± 0.0 |
| (μg g−1) | 6.7 ± 0.1 | 6.8 ± 0.1 | 10.5 ± 0.1 | 14.1 ± 0.0 | 12.0 ± 0.4 | 6.2 ± 0.1 | 11.5 ± 0.2 | 19.4 ± 0.2 | 36.4 ± 0.1 | 14.1 ± 0.0 |
| 0.9400 | 0.9788 | 0.8878 | 0.9553 | 0.6203 | 0.9649 | 0.9254 | 0.9630 | 0.9324 | 0.9905 | |
| Boyd | ||||||||||
| −0.2 ± 0.2 | −0.6 ± 0.5 | 1.0 ± 0.1 | 1.0 ± 0.2 | 0.1 ± 0.2 | 0.0 ± 0.1 | −0.0 ± 0.2 | 0.5 ± 0.2 | 1.3 ± 0.2 | 1.8 ± 0.1 | |
| (min−1) | 0.04 ± 0.00 | 0.05 ± 0.00 | 0.02 ± 0.00 | 0.03 ± 0.00 | 0.04 ± 0.00 | 0.03 ± 0.00 | 0.04 ± 0.00 | 0.03 ± 0.00 | 0.02 ± 0.00 | 0.02 ± 0.00 |
| 0.9498 | 0.8102 | 0.9333 | 0.9005 | 0.9742 | 0.9699 | 0.9411 | 0.9278 | 0.8289 | 0.9366 | |
| Two Site Non-Equilibrium | ||||||||||
| (mL g−1) | 2.2 ± 0.0 | 2.2 ± 0.0 | 3.7 ± 0.0 | 5.6 ± 0.0 | 5.0 ± 0.0 | 2.0 ± 0.0 | 4.6 ± 0.0 | 6.0 ± 0.0 | 24.3 ± 0.2 | 2.8 ± 0.0 |
| 0.4 ± 0.0 | 0.4 ± 0.0 | 0.5 ± 0.0 | 0.5 ± 0.0 | 0.4 ± 0.0 | 0.1 ± 0.0 | 0.5 ± 0.0 | 0.6 ± 0.00 | 0.1 ± 0.0 | 0.7 ± 0.0 | |
| (h−1) | 1.9 ± 0.3 | 1.9 ± 0.2 | 3.2 ± 0.5 | 3.2 ± 0.5 | 1.3 ± 0.3 | 2.3 ± 0.0 | 1.4 ± 0.1 | 1.0 ± 0.1 | 1.5 ± 0.4 | 4.2 ± 0.5 |
| 0.9712 | 0.9857 | 0.9713 | 0.9715 | 0.9887 | 0.9840 | 0.9948 | 0.9879 | 0.9939 | 0.9774 | |
| (h−1) | 0.1 ± 0.1 | 0.1 ± 0.0 | 0.2 ± 0.0 | 0.3 ± 0.0 | 0.2 ± 0.0 | 0.3 ± 0.0 | 0.2 ± 0.0 | 0.1 ± 0.0 | 0.6 ± 0.0 | 0.1 ± 0.0 |
| 0.8269 | 0.8868 | 0.9691 | 0.9378 | 0.9257 | 0.9371 | 0.9518 | 0.9126 | 0.8597 | 0.9116 | |
| Parameters | COLL | MET | FRE | STB | OSN | DIG | TCO | RAL | NBR | FRU |
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | 53 | 56 | 52 | 54 | 54 | 56 | 70 | 59 | 69 | 71 |
| (%) | 34 | 43 | 54 | 60 | 47 | 8 | 54 | 55 | 31 | 79 |
| (%) | 66 | 57 | 47 | 41 | 53 | 92 | 46 | 45 | 69 | 22 |
| Linear | ||||||||||
| (mL g−1) | 2.4 + 0.0 | 0.4 + 0.1 | 4.0 + 0.2 | 5.2 + 0.4 | 5.3 + 0.1 | 2.4 + 0.1 | 7.8 + 0.3 | 9.1 + 0.4 | 48.8 + 1.5 | 5.6 + 0.1 |
| 0.9982 | 0.8777 | 0.9753 | 0.9653 | 0.9961 | 0.9908 | 0.9899 | 0.9886 | 0.9925 | 0.9964 | |
| 160 | 19 | 89 | 103 | 105 | 42 | 122 | 132 | 514 | 51 | |
| Freundlich | ||||||||||
| (µg1−1/n mL1/ng−1) | 2.6 + 0.1 | 16.2 + 0.2 | 18.6 + 0.4 | 23.4 + 0.7 | 4.3 + 0.3 | 10.6 + 0.3 | 1.1 + 0.1 | 24.1 + 0.6 | 20.2 + 0.8 | 5.3 + 0.4 |
| 1.0 + 0.0 | 0.2 + 0.0 | 0.5 + 0.0 | 0.5 + 0.0 | 1.1 + 0.0 | 0.6 + 0.0 | 1.7 + 0.0 | 0.7 + 0.0 | 1.5 + 0.0 | 1.0 + 0.0 | |
| 0.9981 | 0.9908 | 0.9981 | 0.9961 | 0.9971 | 0.9982 | 0.9983 | 0.9987 | 0.9983 | 0.9967 | |
| 175 | 704 | 412 | 460 | 84 | 183 | 17 | 350 | 212 | 48 | |
| Desorption | ||||||||||
| (µg1−1/n mL1/ng−1) | 17.3 + 0.2 | 21.6 + 0.1 | 33.4 + 0.4 | 51.0 + 0.5 | 19.1 + 0.6 | 16.3 + 0.2 | 23.3 + 0.4 | 1.0 + 1.1 | 104.4 + 1.5 | 46.7 + 0.4 |
| 0.3 + 0.0 | 0.1 + 0.0 | 0.3 + 0.0 | 0.2 + 0.0 | 0.5 + 0.0 | 0.4 + 0.0 | 0.5 + 0.0 | 0.4 + 0.0 | 0.4 + 0.0 | 0.2 + 0.0 | |
| 0.9983 | 0.9901 | 0.9971 | 0.9921 | 0.9933 | 0.9987 | 0.9975 | 0.9932 | 0.9923 | 0.9963 | |
| % des (%) | 86 | 92 | 80 | 83 | 75 | 83 | 74 | 72 | 41 | 85 |
| Hysteresis | ||||||||||
| 0.3 | 0.4 | 0.5 | 0.4 | 0.5 | 0.7 | 0.3 | 0.6 | 0.3 | 0.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cáceres-Jensen, L.; Rodríguez-Becerra, J.; Garrido, C.; Escudey, M.; Barrientos, L.; Parra-Rivero, J.; Domínguez-Vera, V.; Loch-Arellano, B. Study of Sorption Kinetics and Sorption–Desorption Models to Assess the Transport Mechanisms of 2,4-Dichlorophenoxyacetic Acid on Volcanic Soils. Int. J. Environ. Res. Public Health 2021, 18, 6264. https://doi.org/10.3390/ijerph18126264
Cáceres-Jensen L, Rodríguez-Becerra J, Garrido C, Escudey M, Barrientos L, Parra-Rivero J, Domínguez-Vera V, Loch-Arellano B. Study of Sorption Kinetics and Sorption–Desorption Models to Assess the Transport Mechanisms of 2,4-Dichlorophenoxyacetic Acid on Volcanic Soils. International Journal of Environmental Research and Public Health. 2021; 18(12):6264. https://doi.org/10.3390/ijerph18126264
Chicago/Turabian StyleCáceres-Jensen, Lizethly, Jorge Rodríguez-Becerra, Carlos Garrido, Mauricio Escudey, Lorena Barrientos, Jocelyn Parra-Rivero, Valentina Domínguez-Vera, and Bruno Loch-Arellano. 2021. "Study of Sorption Kinetics and Sorption–Desorption Models to Assess the Transport Mechanisms of 2,4-Dichlorophenoxyacetic Acid on Volcanic Soils" International Journal of Environmental Research and Public Health 18, no. 12: 6264. https://doi.org/10.3390/ijerph18126264
APA StyleCáceres-Jensen, L., Rodríguez-Becerra, J., Garrido, C., Escudey, M., Barrientos, L., Parra-Rivero, J., Domínguez-Vera, V., & Loch-Arellano, B. (2021). Study of Sorption Kinetics and Sorption–Desorption Models to Assess the Transport Mechanisms of 2,4-Dichlorophenoxyacetic Acid on Volcanic Soils. International Journal of Environmental Research and Public Health, 18(12), 6264. https://doi.org/10.3390/ijerph18126264








