Implications of Nonstationary Effect on Geographically Weighted Total Least Squares Regression for PM2.5 Estimation
Abstract
:1. Introduction
2. Methods and Data
2.1. Ordinary Least Squares Regression
2.2. Geographically Weighted Regression
2.3. GWTLSR
2.4. Comparison of Regression Models
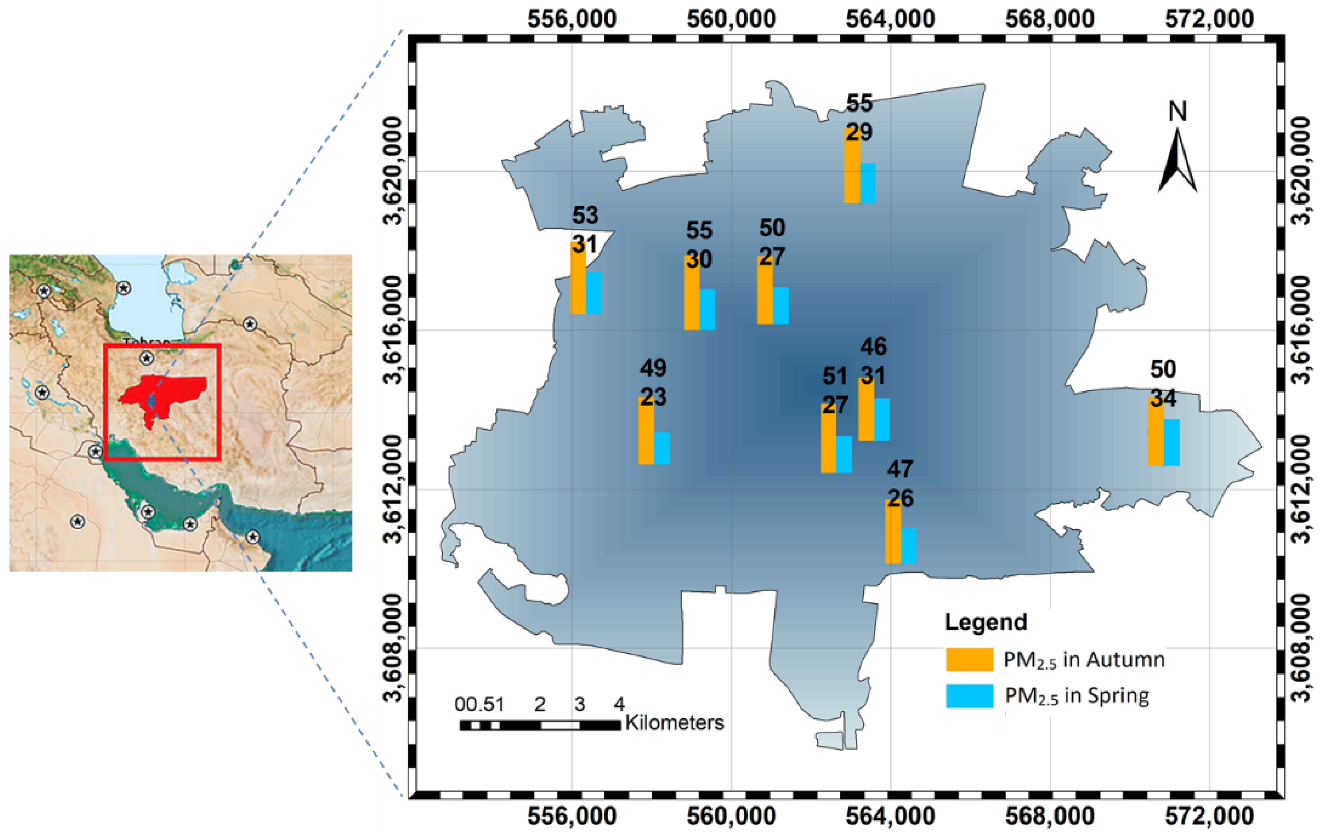
2.5. Study Area and Data Preparation
- The meteorological parameters included temperature, humidity, precipitation, pressure, and wind speed measured by the Isfahan Weather Forecast Organization at the synoptic stations. The measurements were taken in three-hour intervals during the spring and autumn from 2017 to 2019. The daily average of the measured value was considered to be an independent variable at each station.
- The traffic data obtained from the Isfahan Municipality included traffic volume from a four-stage transportation model. First, the hourly traffic counts were determined for sample days during the spring and autumn from 2017 to 2019. Second, they were extracted in buffers around the monitoring stations of 150, 300, 600, and 1200 m radius. Finally, the buffers with the highest correlation were eventually kept in the model.
- The land use data were derived from a 2019 map (scale = 1:2000). The original land use classes were reclassified into residential and non-residential classes. Subsequently, buffers of 100, 200, and 500 m radius were used to estimate the relevant independent variables.
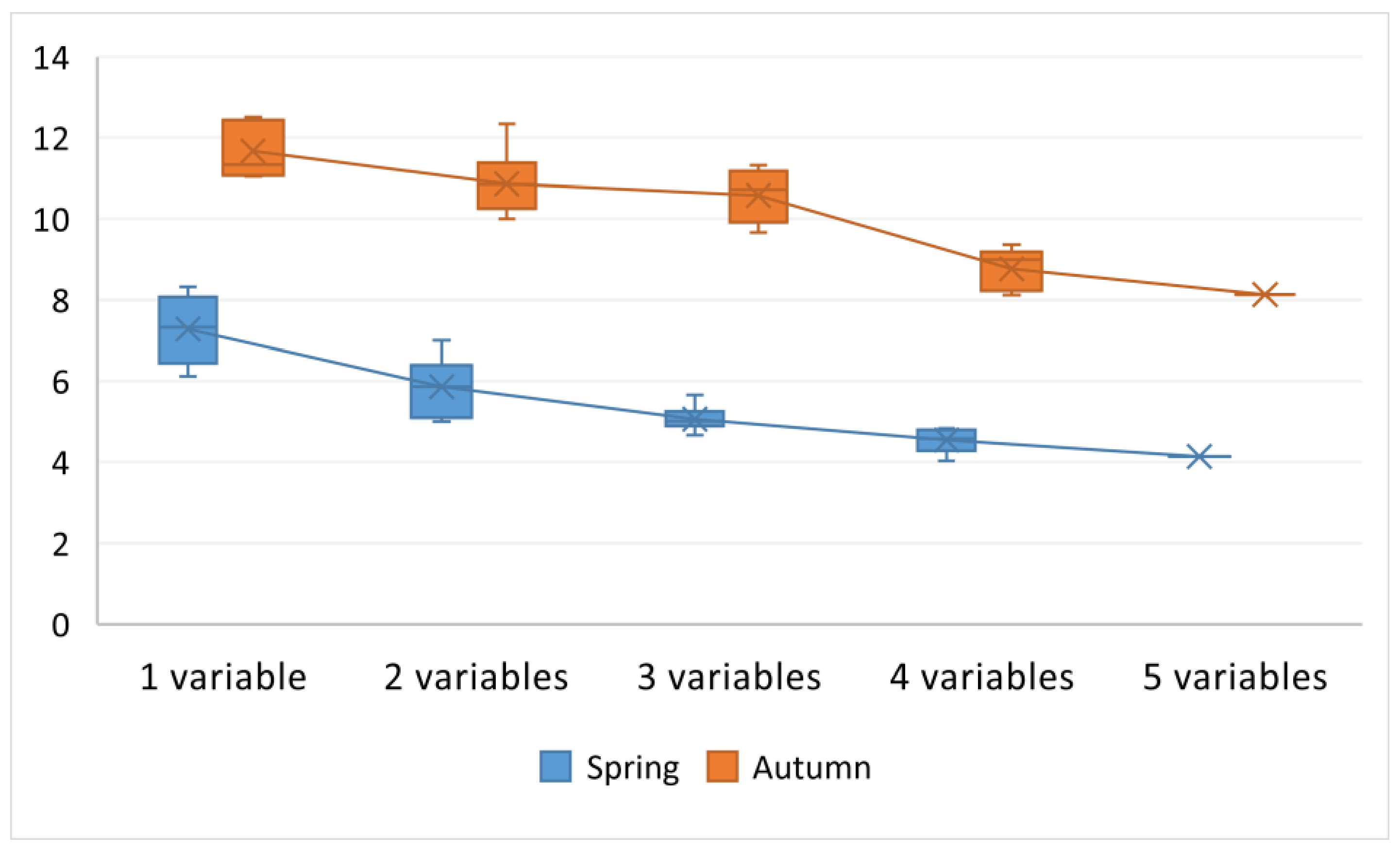
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ganivet, E. Growth in human population and consumption both need to be addressed to reach an ecologically sustainable future. Environ. Dev. Sustain. 2019, 22, 4979–4998. [Google Scholar] [CrossRef]
- Riley, W.J.; Matson, P.A. Nloss: A mechanistic model of denitrified N2O and N2 evolution from soil. Soil Sci. 2000, 165, 237–249. [Google Scholar] [CrossRef]
- Chen, J.; Hoek, G. Long-term exposure to PM and all-cause and cause-specific mortality: A systematic review and meta-analysis. Environ. Int. 2020, 143, 105974. [Google Scholar] [CrossRef] [PubMed]
- Dockery, D.W.; Pope, C.A.; Xu, X.; Spengler, J.D.; Ware, J.H.; Fay, M.E.; Ferris, B.G.; Speizer, F.E. An Association between Air Pollution and Mortality in Six U.S. Cities. N. Engl. J. Med. 1993, 329, 1753–1759. [Google Scholar] [CrossRef] [Green Version]
- Cohen, A.J.; Anderson, H.R.; Ostro, B.; Pandey, K.D.; Krzyzanowski, M.; Künzli, N.; Gutschmidt, K.; Pope, A.; Romieu, I.; Samet, J.M.; et al. The Global Burden of Disease Due to Outdoor Air Pollution. J. Toxicol. Environ. Health Part A 2005, 68, 1301–1307. [Google Scholar] [CrossRef]
- Balakrishnan, K.; Dey, S.; Gupta, T.; Dhaliwal, R.S.; Brauer, M.; Cohen, A.J.; Stanaway, J.; Beig, G.; Joshi, T.K.; Aggarwal, A.N.; et al. The impact of air pollution on deaths, disease burden, and life expectancy across the states of India: The Global Burden of Disease Study 2017. Lancet Planet. Health 2019, 3, e26–e39. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Geng, G.; Zhang, Q.; Davis, S.J.; Li, X.; Liu, Y.; Peng, L.; Li, M.; Zheng, B.; Huo, H.; et al. Inequality of household consumption and air pollution-related deaths in China. Nat. Commun. 2019, 10, 4337. [Google Scholar] [CrossRef] [Green Version]
- Alfaro-Moreno, E.; Martínez, L.; García-Cuellar, C.; Bonner, J.C.; Murray, J.C.; Rosas, I.; Rosales, S.P.D.; Osornio-Vargas, A.R. Biologic effects induced in vitro by PM10 from three different zones of Mexico City. Environ. Health Perspect. 2002, 110, 715–720. [Google Scholar] [CrossRef]
- Miller, M.R.; Newby, E.D. Air pollution and cardiovascular disease: Car sick. Cardiovasc. Res. 2019, 116, 279–294. [Google Scholar] [CrossRef]
- Osornio-Vargas, A.R.; Bonner, J.C.; Alfaro-Moreno, E.; Martínez, L.; García-Cuellar, C.; Rosales, S.P.-D.-L.; Miranda, J.; Rosas, I. Proinflammatory and cytotoxic effects of Mexico City air pollution particulate matter in vitro are dependent on particle size and composition. Environ. Health Perspect. 2003, 111, 1289–1293. [Google Scholar] [CrossRef] [Green Version]
- WHO. 2016. Available online: https://www.who.int/gho/phe/outdoor_air_pollution/burden_text/en/ (accessed on 13 November 2019).
- Brehmer, C.; Norris, C.; Barkjohn, K.K.; Bergin, M.H.; Zhang, J.; Cui, X.; Teng, Y.; Zhang, Y.; Black, M.; Li, Z.; et al. The impact of household air cleaners on the oxidative potential of PM2.5 and the role of metals and sources associated with indoor and outdoor exposure. Environ. Res. 2020, 181, 108919. [Google Scholar] [CrossRef]
- Geiser, M.; Kreyling, W.G. Deposition and biokinetics of inhaled nanoparticles. Part. Fibre Toxicol. 2010, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Möller, W.; Felten, K.; Sommerer, K.; Scheuch, G.; Meyer, G.; Meyer, P.; Häussinger, K.; Kreyling, W.G. Deposition, Retention, and Translocation of Ultrafine Particles from the Central Airways and Lung Periphery. Am. J. Respir. Crit. Care Med. 2008, 177, 426–432. [Google Scholar] [CrossRef]
- Askariyeh, M.H.; Zietsman, J.; Autenrieth, R. Traffic contribution to PM2.5 increment in the near-road environment. Atmos. Environ. 2020, 224, 117113. [Google Scholar] [CrossRef]
- Morawska, L.; Wang, H.; Ristovski, Z.; Jayaratne, E.R.; Johnson, G.; Cheung, H.C.; Ling, X.; He, C. JEM Spotlight: Environmental monitoring of airborne nanoparticles. J. Environ. Monit. 2009, 11, 1758–1773. [Google Scholar] [CrossRef] [Green Version]
- Saremi, P. The Role of Traffic Culture Making in Air Pollution Reduction in Metropolitans of Developing Countries. Int. J. Transp. Eng. Traffic Syst. 2020, 6, 42–54. [Google Scholar]
- Hoek, G.; Beelen, R.; de Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Jerrett, M.; Arain, M.A.; Kanaroglou, P.; Beckerman, B.; Potoglou, D.; Sahsuvaroglu, T.; Morrison, J.; Giovis, C. A review and evaluation of intraurban air pollution exposure models. J. Expo. Sci. Environ. Epidemiology 2005, 15, 185–204. [Google Scholar] [CrossRef]
- Miller, K.A.; Siscovick, D.S.; Sheppard, L.; Shepherd, K.; Sullivan, J.H.; Anderson, G.L.; Kaufman, J.D. Long-Term Exposure to Air Pollution and Incidence of Cardiovascular Events in Women. N. Engl. J. Med. 2007, 356, 447–458. [Google Scholar] [CrossRef]
- Adams, M.D.; Massey, F.; Chastko, K.; Cupini, C. Spatial modelling of particulate matter air pollution sensor measurements collected by community scientists while cycling, land use regression with spatial cross-validation, and applications of machine learning for data correction. Atmos. Environ. 2020, 230, 117479. [Google Scholar] [CrossRef]
- Morley, D.W.; Gulliver, J. A land use regression variable generation, modelling and prediction tool for air pollution exposure assessment. Environ. Model. Softw. 2018, 105, 17–23. [Google Scholar] [CrossRef]
- Yu, X.; Ivey, C.; Huang, Z.; Gurram, S.; Sivaraman, V.; Shen, H.; Eluru, N.; Hasan, S.; Henneman, L.; Shi, G.; et al. Quantifying the impact of daily mobility on errors in air pollution exposure estimation using mobile phone location data. Environ. Int. 2020, 141, 105772. [Google Scholar] [CrossRef] [PubMed]
- Briggs, D.J.; Collins, S.; Elliott, P.; Fischer, P.; Kingham, S.; Lebret, E.; Pryl, K.; Van Reeuwijk, H.; Smallbone, K.; Van Der Veen, A. Mapping urban air pollution using GIS: A regression-based approach. Int. J. Geogr. Inf. Sci. 1997, 11, 699–718. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Yuval; Broday, D.M. Re-framing the Gaussian dispersion model as a nonlinear regression scheme for retrospective air quality assessment at a high spatial and temporal resolution. Environ. Model. Softw. 2020, 125, 104620. [Google Scholar] [CrossRef]
- Jerrett, M.; Arain, M.A.; Kanaroglou, P.; Beckerman, B.; Crouse, D.; Gilbert, N.; Brook, J.R.; Finkelstein, N.; Finkelstein, M.M. Modeling the Intraurban Variability of Ambient Traffic Pollution in Toronto, Canada. J. Toxicol. Environ. Health Part A 2007, 70, 200–212. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Zou, L.; Xia, J.; Pang, W. Spatial imputation for air pollutants data sets via low rank matrix completion algorithm. Environ. Int. 2020, 139, 105713. [Google Scholar] [CrossRef]
- Marshall, J.D.; Nethery, E.; Brauer, M. Within-urban variability in ambient air pollution: Comparison of estimation methods. Atmospheric Environ. 2008, 42, 1359–1369. [Google Scholar] [CrossRef]
- Ainslie, B.; Steyn, D.; Su, J.; Buzzelli, M.; Brauer, M.; Larson, T.; Rucker, M. A source area model incorporating simplified atmospheric dispersion and advection at fine scale for population air pollutant exposure assessment. Atmospheric Environ. 2008, 42, 2394–2404. [Google Scholar] [CrossRef]
- Janssen, N.A.; van Vliet, P.H.; Aarts, F.; Harssema, H.; Brunekreef, B. Assessment of exposure to traffic related air pollution of children attending schools near motorways. Atmospheric Environ. 2001, 35, 3875–3884. [Google Scholar] [CrossRef]
- Just, A.C.; Wright, R.O.; Schwartz, J.; Coull, B.A.; Baccarelli, A.A.; Tellez-Rojo, M.M.; Moody, E.; Wang, Y.; Lyapustin, A.; Kloog, I. Using high-resolution satellite aerosol optical depth to estimate daily PM2.5 geographical distribution in Mexico City. Environ. Sci. Technol. 2015, 49, 8576–8584. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Li, X.; Chen, Z.; Zeng, G.; Leon, T.; Liang, J.; Huang, G.; Gao, Z.; Jiao, S.; He, X.; et al. Land use regression models coupled with meteorology to model spatial and temporal variability of NO2 and PM10 in Changsha, China. Atmos. Environ. 2015, 116, 272–280. [Google Scholar] [CrossRef]
- Basu, B.; Alam, S.; Ghosh, B.; Gill, L.; McNabola, A. Augmenting limited background monitoring data for improved performance in land use regression modelling: Using support vector regression and mobile monitoring. Atmospheric Environ. 2019, 201, 310–322. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.; Brunsdon, C. Measuring Spatial Variations in Relationships with Geographically Weighted Regression. In Recent Developments in Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 1997; pp. 60–82. [Google Scholar]
- Son, Y.; Osornio-Vargas, Á.R.; O’Neill, M.S.; Hystad, P.; Texcalac-Sangrador, J.L.; Ohman-Strickland, P.; Meng, Q.; Schwander, S. Land use regression models to assess air pollution exposure in Mexico City using finer spatial and temporal input parameters. Sci. Total. Environ. 2018, 639, 40–48. [Google Scholar] [CrossRef]
- Song, W.; Jia, H.; Li, Z.; Wang, C. Detecting urban land-use configuration effects on NO2 and NO variations using geographically weighted land use regression. Atmos. Environ. 2019, 197, 166–176. [Google Scholar] [CrossRef]
- Mikhail, M.E.; Ackermann, F.E. Observations and Least Squares; University Press of America: Lanham, MD, USA, 1982. [Google Scholar]
- Xiao, L.; Lang, Y.; Christakos, G. High-resolution spatiotemporal mapping of PM2.5 concentrations at Mainland China using a combined BME-GWR technique. Atmos. Environ. 2018, 173, 295–305. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Yu, X.; Wang, Y.; Niu, R.; Hu, Y. A Combination of Geographically Weighted Regression, Particle Swarm Optimization and Support Vector Machine for Landslide Susceptibility Mapping: A Case Study at Wanzhou in the Three Gorges Area, China. Int. J. Environ. Res. Public Health 2016, 13, 487. [Google Scholar] [CrossRef] [Green Version]
- Markovsky, I.; Rastello, M.L.; Premoli, A.; Kukush, A.; Van Huffel, S. The element-wise weighted total least-squares problem. Comput. Stat. Data Anal. 2006, 50, 181–209. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.; Jazaeri, S. Weighted total least squares formulated by standard least squares theory. J. Géod. Sci. 2012, 2, 113–124. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-Euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Kang, D.; Eder, B.K.; Stein, A.F.; Grell, G.A.; Peckham, S.E.; McHenry, J. The New England Air Quality Forecasting Pilot Program: Development of an Evaluation Protocol and Performance Benchmark. J. Air Waste Manag. Assoc. 2005, 55, 1782–1796. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z.; Hu, C.; Wang, C. Improving the North American multi-model ensemble (NMME) precipitation forecasts at local areas using wavelet and machine learning. Clim. Dyn. 2019, 53, 601–615. [Google Scholar] [CrossRef]
- Zarrabi, A.; Mohammadi, J.; Abdollahi, A. Evaluation of mobile and stationary sources of Isfahan air pollution. Geography 2010, 26, 151–164. [Google Scholar]
- Tashayo, B.; Alimohammadi, A. Modeling urban air pollution with optimized hierarchical fuzzy inference system. Environ. Sci. Pollut. Res. 2016, 23, 19417–19431. [Google Scholar] [CrossRef]
- Tashayo, B.; Alimohammadi, A.; Sharif, M. A Hybrid Fuzzy Inference System Based on Dispersion Model for Quantitative Environmental Health Impact Assessment of Urban Transportation Planning. Sustainability 2017, 9, 134. [Google Scholar] [CrossRef] [Green Version]





| Season | Variables | p-Value | VIF |
|---|---|---|---|
| Spring | Temperature | 1.28 | |
| Pressure | |||
| Traffic | 1.04 | ||
| Residential land use | 1.004 | ||
| Non-residential land use | 1.012 | ||
| Autumn | Temperature | 1.007 | |
| Pressure | |||
| Traffic | 1.06 | ||
| Residential land use | 1.04 | ||
| Non-residential land use | 1.01 |
| Season | Model | |||||
|---|---|---|---|---|---|---|
| Spring | OLS | 5.19 | 4.96 | 4.43 | 4.15 | 777.8 |
| GWR | 5.02 | 4.66 | 4.11 | 3.85 | 607.9 | |
| GWTLSR | 4.26 | 3.83 | 3.55 | 3.14 | 574.5 | |
| Autumn | OLS | 8.66 | 8.36 | 6.81 | 6.55 | 909.2 |
| GWR | 8.40 | 8.04 | 6.62 | 6.42 | 715.2 | |
| GWTLSR | 7.12 | 4.34 | 5.26 | 3.51 | 596.5 |
| Season | Model | Moran’s I | z-Score | p-Value | Pattern |
|---|---|---|---|---|---|
| Spring | OLS | 0.19 | 2.03 | 0.04 | Clustered |
| GWR | −0.17 | −0.35 | 0.72 | Almost random | |
| GWTLSR | −0.10 | 0.13 | 0.89 | Random | |
| Autumn | OLS | 0.17 | 2.05 | 0.03 | Clustered |
| GWR | −0.18 | −0.41 | 0.68 | Almost random | |
| GWTLSR | −0.12 | −0.02 | 0.98 | Random |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokhtari, A.; Tashayo, B.; Deilami, K. Implications of Nonstationary Effect on Geographically Weighted Total Least Squares Regression for PM2.5 Estimation. Int. J. Environ. Res. Public Health 2021, 18, 7115. https://doi.org/10.3390/ijerph18137115
Mokhtari A, Tashayo B, Deilami K. Implications of Nonstationary Effect on Geographically Weighted Total Least Squares Regression for PM2.5 Estimation. International Journal of Environmental Research and Public Health. 2021; 18(13):7115. https://doi.org/10.3390/ijerph18137115
Chicago/Turabian StyleMokhtari, Arezoo, Behnam Tashayo, and Kaveh Deilami. 2021. "Implications of Nonstationary Effect on Geographically Weighted Total Least Squares Regression for PM2.5 Estimation" International Journal of Environmental Research and Public Health 18, no. 13: 7115. https://doi.org/10.3390/ijerph18137115
APA StyleMokhtari, A., Tashayo, B., & Deilami, K. (2021). Implications of Nonstationary Effect on Geographically Weighted Total Least Squares Regression for PM2.5 Estimation. International Journal of Environmental Research and Public Health, 18(13), 7115. https://doi.org/10.3390/ijerph18137115






