Development of Machine Learning Models for Prediction of Osteoporosis from Clinical Health Examination Data
Abstract
:1. Introduction
2. Materials and Methods
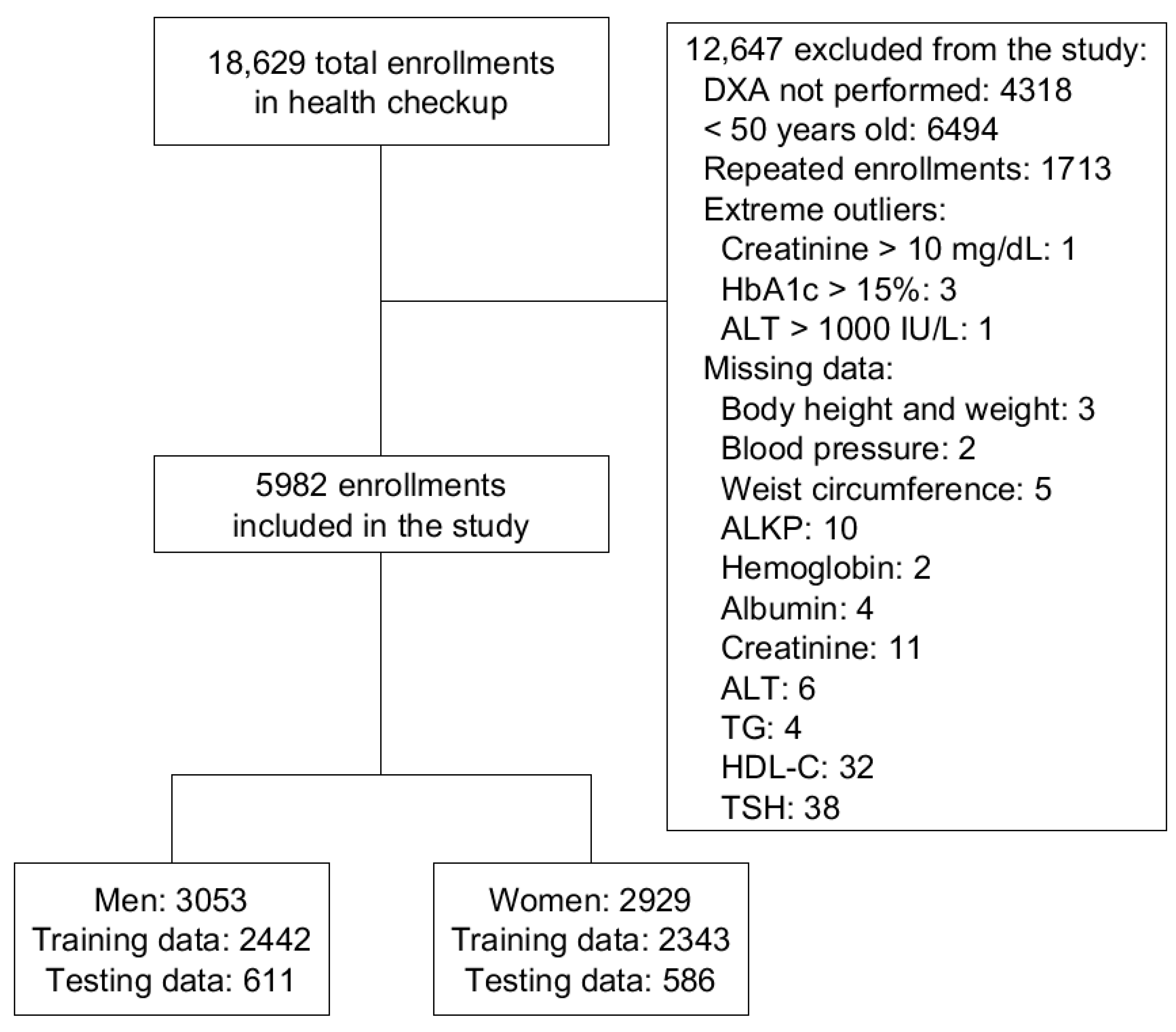
2.1. Data Acquirement
2.2. Feature Selection and Data Preprocessing
2.3. Machine Learning Model Development
2.4. Statistical Analysis
3. Results
3.1. Demographic Information of the Study Population
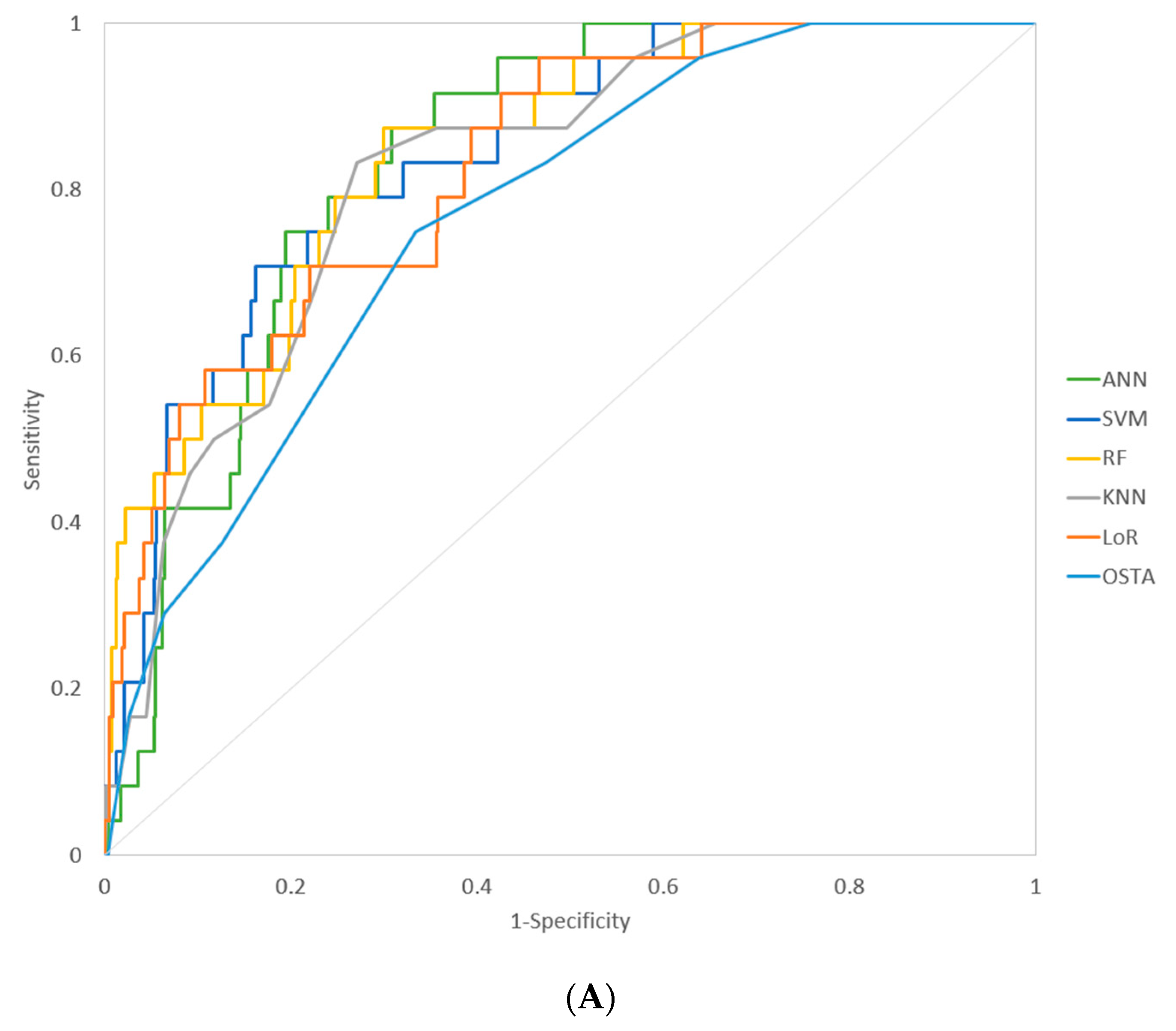
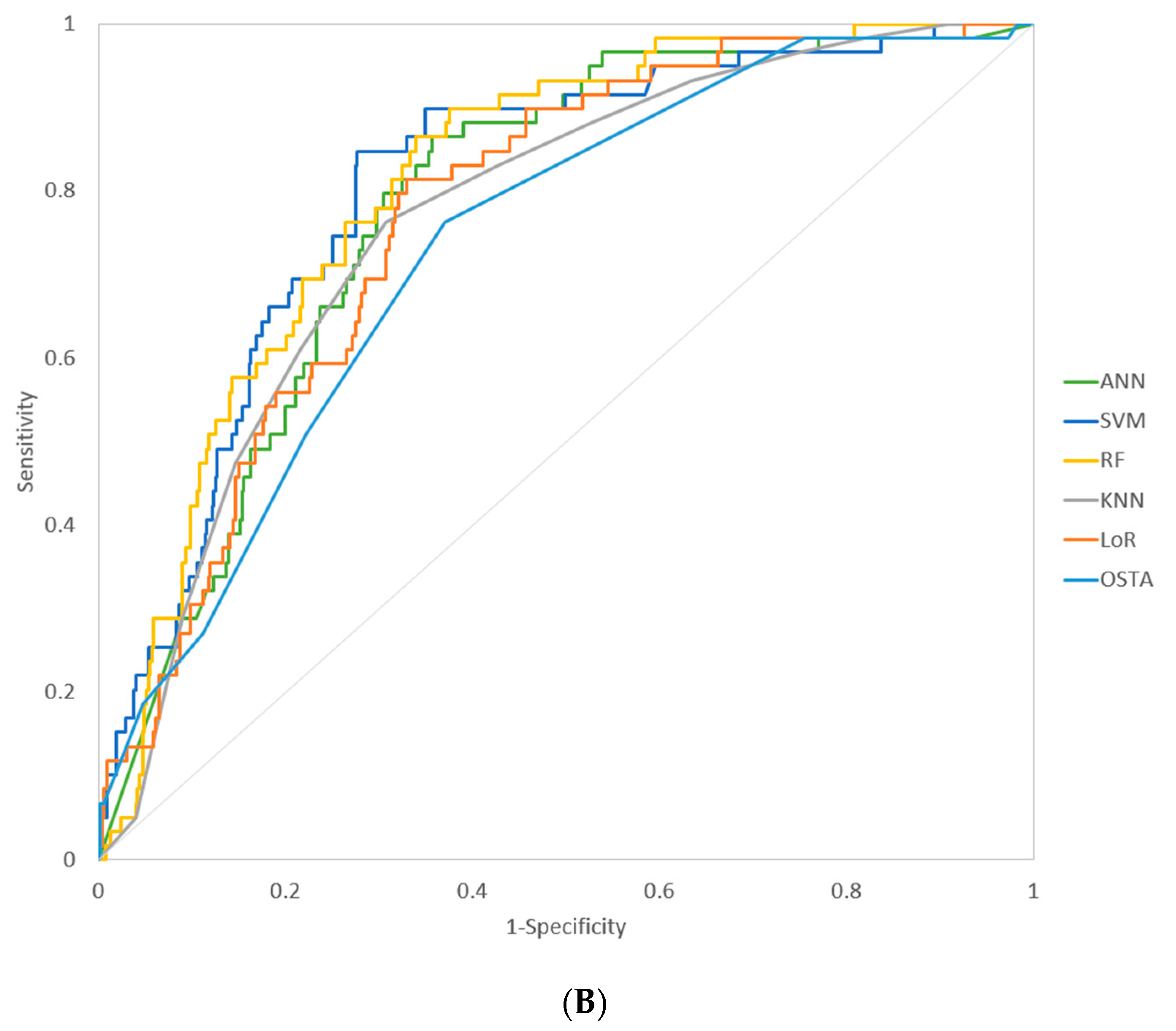
3.2. Model Performance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, F.-P.; Huang, T.-S.; Fu, T.-S.; Sun, C.-C.; Chao, A.-S.; Tsai, T.-L. Secular trends in incidence of osteoporosis in Taiwan: A nationwide population-based study. Biomed. J. 2018, 41, 314–320. [Google Scholar] [CrossRef] [PubMed]
- Lupsa, B.C.; Insogna, K. Bone Health and Osteoporosis. Endocrinol. Metab. Clin. N. Am. 2015, 44, 517–530. [Google Scholar] [CrossRef] [PubMed]
- Raichandani, K.; Agarwal, S.; Jain, H.; Bharwani, N. Mortality profile after 2 years of hip fractures in elderly patients treated with early surgery. J. Clin. Orthop. Trauma 2021, 18, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Curtis, E.; Moon, R.J.; Harvey, N.; Cooper, C. The impact of fragility fracture and approaches to osteoporosis risk assessment worldwide. Bone 2017, 104, 29–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Looker, A.C.; Melton, L.J., 3rd; Harris, T.B.; Borrud, L.G.; Shepherd, J.A. Prevalence and trends in low femur bone density among older US adults: NHANES 2005-2006 compared with NHANES III. J. Bone Miner Res. 2010, 25, 64–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, C.B.; Dagar, M. Osteoporosis in Older Adults. Med. Clin. N. Am. 2020, 104, 873–884. [Google Scholar] [CrossRef] [PubMed]
- Yusuf, A.A.; Cummings, S.R.; Watts, N.B.; Feudjo, M.T.; Sprafka, J.M.; Zhou, J.; Cooper, C. Real-world effectiveness of osteoporosis therapies for fracture reduction in post-menopausal women. Arch. Osteoporos. 2018, 13, 33. [Google Scholar] [CrossRef] [Green Version]
- Camacho, P.M.; Petak, S.M.; Binkley, N.; Diab, D.L.; Eldeiry, L.S.; Farooki, A.; Harris, S.T.; Hurley, D.L.; Kelly, J.; Lewiecki, E.M.; et al. American Association of Clinical Endocrinologists/American College of Endocrinology Clinical Practice Guidelines for The Diagnosis and Treatment of Postmenopausal Osteoporosis-2020 Update. Endocr. Pract. 2020, 26 (Suppl. 1), 1–46. [Google Scholar] [CrossRef] [PubMed]
- Choksi, P.; Jepsen, K.J.; Clines, G.A. The challenges of diagnosing osteoporosis and the limitations of currently available tools. Clin. Diabetes Endocrinol. 2018, 4, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Casella, M.; Becciolini, A.; Di Donato, E.; Basaglia, M.; Zardo, M.; Lucchini, G.; Riva, M.; Ariani, A.; Magalini, F. Internal medicine inpatients’ prevalence of misdiagnosed severe osteoporosis. Osteoporos. Int. 2021, 1–4. [Google Scholar] [CrossRef]
- Bijelic, R.; Milicevic, S.; Balaban, J. Risk Factors for Osteoporosis in Postmenopausal Women. Med. Arch. 2017, 71, 25–28. [Google Scholar] [CrossRef] [Green Version]
- Kelsey, J.L. Risk factors for osteoporosis and associated fractures. Public Health Rep. 1989, 104, 14–20. [Google Scholar] [PubMed]
- Delitala, A.P.; Scuteri, A.; Doria, C. Thyroid Hormone Diseases and Osteoporosis. J. Clin. Med. 2020, 9, 1034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Compston, J.E.; McClung, M.R.; Leslie, W.D. Osteoporosis. Lancet 2019, 393, 364–376. [Google Scholar] [CrossRef]
- NIH Consensus Development Panel on Osteoporosis Prevention, Diagnosis, and Therapy. Osteoporosis prevention, diagnosis, and therapy. JAMA 2001, 285, 785–795. [Google Scholar] [CrossRef]
- Ilić, K.; Obradović, N.; Vujasinović-Stupar, N. The relationship among hypertension, antihypertensive medications, and osteoporosis: A narrative review. Calcif. Tissue Int. 2013, 92, 217–227. [Google Scholar] [CrossRef]
- Kanazawa, I. Interaction between bone and glucose metabolism. Endocr. J. 2017, 64, 1043–1053. [Google Scholar] [CrossRef] [Green Version]
- Pan, M.-L.; Chen, L.-R.; Tsao, H.-M.; Chen, K.-H. Iron Deficiency Anemia as a Risk Factor for Osteoporosis in Taiwan: A Nationwide Population-Based Study. Nutrients 2017, 9, 616. [Google Scholar] [CrossRef]
- Aspray, T.J.; Hill, T.R. Osteoporosis and the Ageing Skeleton. Prokaryotic Cytoskelet. 2019, 91, 453–476. [Google Scholar] [CrossRef]
- Koh, L.K.H.; Ben Sedrine, W.; Torralba, T.P.; Kung, A.; Fujiwara, S.; Chan, S.P.; Huang, Q.R.; Rajatanavin, R.; Tsai, K.-S.; Park, H.M.; et al. A Simple Tool to Identify Asian Women at Increased Risk of Osteoporosis. Osteoporos. Int. 2001, 12, 699–705. [Google Scholar] [CrossRef]
- Ho-Pham, L.T.; Doan, M.C.; Van, L.H.; Nguyen, T.V. Development of a model for identification of individuals with high risk of osteoporosis. Arch. Osteoporos. 2020, 15, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Deo, R.C. Machine Learning in Medicine. Circulation 2015, 132, 1920–1930. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benke, K.; Benke, G. Artificial Intelligence and Big Data in Public Health. Int. J. Environ. Res. Public Health 2018, 15, 2796. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kruse, C.; Eiken, P.; Vestergaard, P. Machine Learning Principles Can Improve Hip Fracture Prediction. Calcif. Tissue Int. 2017, 100, 348–360. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.J.; Lee, J.-H.; Han, S.-S.; Kim, Y.H.; Jeong, H.-G.; Choi, Y.J.; Park, W. Strut analysis for osteoporosis detection model using dental panoramic radiography. Dentomaxillofacial Radiol. 2017, 46, 20170006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shim, J.-G.; Kim, D.W.; Ryu, K.-H.; Cho, E.-A.; Ahn, J.-H.; Kim, J.-I.; Lee, S.H. Application of machine learning approaches for osteoporosis risk prediction in postmenopausal women. Arch. Osteoporos. 2020, 15, 1–9. [Google Scholar] [CrossRef]
- Kim, S.K.; Yoo, T.K.; Oh, E.; Kim, D.W. Osteoporosis risk prediction using machine learning and conventional methods. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), Osaka, Japan, 3–7 July 2013; Volume 2013, pp. 188–191. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, E. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ying, X. An Overview of Overfitting and Its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Li, D.-L.; Shen, F.; Yin, Y.; Peng, J.-X.; Chen, P.-Y. Weighted Youden index and its two-independent-sample comparison based on weighted sensitivity and specificity. Chin. Med. J. 2013, 126, 1150–1154. [Google Scholar]
- Rücker, G.; Schumacher, M. Summary ROC curve based on a weighted Youden index for selecting an optimal cutpoint in meta-analysis of diagnostic accuracy. Stat. Med. 2010, 29, 3069–3078. [Google Scholar] [CrossRef]
- Meng, J.; Sun, N.; Chen, Y.; Li, Z.; Cui, X.; Fan, J.; Cao, H.; Zheng, W.; Jin, Q.; Jiang, L.; et al. Artificial neural network optimizes self-examination of osteoporosis risk in women. J. Int. Med. Res. 2019, 47, 3088–3098. [Google Scholar] [CrossRef] [PubMed]
- Rinonapoli, G.; Ruggiero, C.; Meccariello, L.; Bisaccia, M.; Ceccarini, P.; Caraffa, A. Osteoporosis in Men: A Review of an Underestimated Bone Condition. Int. J. Mol. Sci. 2021, 22, 2105. [Google Scholar] [CrossRef] [PubMed]
- Metz, C.E. Basic principles of ROC analysis. Semin. Nucl. Med. 1978, 8, 283–298. [Google Scholar] [CrossRef]
- Schisterman, E.; Faraggi, D.; Reiser, B.; Hu, J. Youden Index and the optimal threshold for markers with mass at zero. Stat. Med. 2008, 27, 297–315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subramaniam, S.; Ima-Nirwana, S.; Chin, K.Y. Performance of Osteoporosis Self-Assessment Tool (OST) in Predicting Osteoporosis-A Review. Int. J. Environ. Res. Public Health 2018, 15, 1445. [Google Scholar] [CrossRef] [Green Version]
| Hyperparameter | Examined Range * | Selected Hyperparameter for the Men Model | Selected Hyperparameter for the Women Model |
|---|---|---|---|
| ANN | |||
| Number of hidden layers | 1–2 | 2 | 2 |
| Number of nodes | 4–20 in each hidden layer | 9 in hidden layer 1, 4 in hidden layer 2 | 13 in hidden layer 1, 7 in hidden layer 2 |
| Learning rate | 0.01–0.0001 | 0.001 | 0.001 |
| Dropout rate | 0–60% | 40% | 40% |
| SVM | |||
| Kernel type | linear, polynomial, or radial basis function | radial basis function | radial basis function |
| Regularization parameter C | 2−2–29 | 25 | 24 |
| Kernel coefficient gamma | 2−9–22 | 2−3 | 2−1 |
| Degree for Polynomial Function | 1–4 | - | - |
| RF | |||
| Number of trees | 100–1000 | 300 | 600 |
| Number of features to consider | 3–11 | 8 | 10 |
| Maximum depth of the tree | 3–11 | 8 | 10 |
| KNN | |||
| Number of neighbors | 1–30 | 28 | 13 |
| Leaf size | 1–49 | 15 | 3 |
| Power parameter p | Manhattan distance or Euclidean distance | Manhattan distance | Euclidean distance |
| Characteristic | Total (n = 5982) | Men (n = 3053) | Women (n = 2929) | p-Value * |
|---|---|---|---|---|
| Age (years) | 59.3 ± 7.0 | 59.3 ± 7.0 | 59.3 ± 7.0 | 0.9650 |
| Body height (cm) | 161.8 ± 8.4 | 167.7 ± 6.2 | 155.7 ± 5.5 | <0.0001 |
| Body weight (kg) | 63.5 ± 11.7 | 69.8 ± 10.2 | 56.9 ± 9.2 | <0.0001 |
| Waist circumference (cm) | 83.9 ± 9.8 | 87.8 ± 8.4 | 79.9 ± 9.5 | <0.0001 |
| History of smoking (n, %) | 1255 (21.0) | 1133 (37.1) | 122 (4.2) | <0.0001 |
| History of alcohol drinking (n, %) | 484 (8.1) | 414 (13.6) | 70 (2.4) | <0.0001 |
| Diabetes mellitus (n, %) | 1075 (18.0) | 618 (20.2) | 457 (15.6) | <0.0001 |
| Hypertension (n, %) | 2226 (37.2) | 1250 (40.9) | 976 (33.3) | <0.0001 |
| Albumin (g/dL) | 4.50 ± 0.30 | 4.52 ± 0.27 | 4.45 ± 0.26 | <0.0001 |
| Hemoglobin (g/dL) | 14.1 ± 1.4 | 15.0 ± 1.2 | 13.2 ± 1.1 | <0.0001 |
| ALT (IU/L) | 27.5 ± 18.6 | 30.5 ± 20.0 | 24.4 ± 16.6 | <0.0001 |
| Creatinine (mg/dL) | 0.89 ± 0.27 | 1.03 ± 0.26 | 0.75 ± 0.21 | <0.0001 |
| TG (mg/dL) | 133.1 ± 84.8 | 147.2 ± 95.2 | 118.4 ± 69.1 | <0.0001 |
| HDL-C (mg/dL) | 55.1 ± 16.4 | 48.76 ± 13.54 | 61.78 ± 1.57 | <0.0001 |
| ALK-P (IU/L) | 67.9 ± 19.9 | 66.0 ± 18.4 | 69.9 ± 21.2 | <0.0001 |
| TSH (uIU/mL) | 2.32 ± 2.34 | 2.18 ± 2.15 | 2.47 ± 2.52 | <0.0001 |
| Menopause (n, %) | 2448 (83.6) | |||
| History of HRT (n, %) | 283 (9.7) | |||
| Parity (n) | 2.4 ± 1.4 | |||
| Categories of bone density result | <0.0001 | |||
| Normal (n, %) | 3058 (51.1) | 1802 (59.0) | 1256 (42.9) | |
| Osteopenia (n, %) | 2503 (41.8) | 1134 (37.1) | 1369 (46.7) | |
| Osteoprosis (n, %) | 421 (7.0) | 117 (3.8) | 304 (10.4) |
| Feature | Normal Bone Density (n = 3058, 51.1%) | Decreased Bone Density * (n = 2924, 48.9%) | p-Value ** |
|---|---|---|---|
| Age (years) | 57.6 ± 6.1 | 61.1 ± 7.3 | <0.0001 |
| Body height (cm) | 163.9 ± 8.0 | 159.6 ± 8.1 | <0.0001 |
| Body weight (kg) | 67.1 ± 11.5 | 59.8 ± 10.6 | <0.0001 |
| Waist circumference (cm) | 85.7 ± 9.5 | 82.1 ± 9.6 | <0.0001 |
| History of smoking (n, %) | 739 (24.2) | 516 (17.7) | <0.0001 |
| History of alcohol drinking (n, %) | 291 (9.5) | 193 (6.6) | <0.0001 |
| Diabetes mellitus (n, %) | 550 (18.0) | 525 (18.0) | 0.9753 |
| Hypertension (n, %) | 1151 (37.6) | 1075 (36.8) | 0.4844 |
| Albumin (g/dL) | 4.49 ± 0.26 | 4.47 ± 0.28 | 0.0289 |
| Hemoglobin (g/dL) | 14.3 ± 1.5 | 13.9 ± 1.4 | <0.0001 |
| ALT (IU/L) | 28.9 ± 19.4 | 26.0 ± 17.7 | <0.0001 |
| Creatinine (mg/dL) | 0.92 ± 0.26 | 0.86 ± 0.28 | <0.0001 |
| TG (mg/dL) | 138.2 ± 84.3 | 127.8 ± 85.0 | <0.0001 |
| HDL-C (mg/dL) | 52.9 ± 15.6 | 57.5 ± 16.9 | <0.0001 |
| ALK-P (IU/L) | 64.9 ± 17.9 | 71.1 ± 21.5 | <0.0001 |
| TSH (uIU/mL) | 2.32 ± 2.05 | 2.32 ± 2.63 | 0.9480 |
| Abnormal TSH level (<0.01 or ≥4.5 uIU/mL) (n, %) | 222 (7.3) | 253 (8.7) | 0.0464 |
| Menopause (n, %) | 937 (74.6) | 1511 (90.3) | <0.0001 |
| History of HRT (n, %) | 127 (10.1) | 156 (9.3) | 0.4756 |
| Parity | 2.24 ± 1.25 | 2.60 ± 1.55 | <0.0001 |
| Model | AUROC (95% CI) | Sensitivity * | Specificity * | p-Value ** (Compare with OSTA) |
|---|---|---|---|---|
| Men | ||||
| ANN | 0.837 (0.805–0.865) | 0.917 | 0.646 | 0.0151 |
| SVM | 0.840 (0.809–0.868) | 0.917 | 0.547 | 0.0061 |
| RF | 0.843 (0.812–0.871) | 0.875 | 0.700 | 0.0321 |
| KNN | 0.821 (0.788–0.851) | 0.833 | 0.729 | 0.1087 |
| LoR | 0.827 (0.794–0.856) | 0.958 | 0.533 | 0.0421 |
| OSTA *** | 0.766 (0.730–0.799) | 0.958 | 0.361 | |
| Women | ||||
| ANN | 0.781 (0.745–0.814) | 0.864 | 0.643 | 0.0258 |
| SVM | 0.807 (0.773–0.838) | 0.898 | 0.651 | 0.0136 |
| RF | 0.811 (0.777–0.842) | 0.898 | 0.624 | 0.0006 |
| KNN | 0.767 (0.731–0.801) | 0.762 | 0.692 | 0.3563 |
| LoR | 0.772 (0.732–0.806) | 0.814 | 0.670 | 0.0808 |
| OSTA*** | 0.734 (0.697–0.770) | 0.763 | 0.630 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou Yang, W.-Y.; Lai, C.-C.; Tsou, M.-T.; Hwang, L.-C. Development of Machine Learning Models for Prediction of Osteoporosis from Clinical Health Examination Data. Int. J. Environ. Res. Public Health 2021, 18, 7635. https://doi.org/10.3390/ijerph18147635
Ou Yang W-Y, Lai C-C, Tsou M-T, Hwang L-C. Development of Machine Learning Models for Prediction of Osteoporosis from Clinical Health Examination Data. International Journal of Environmental Research and Public Health. 2021; 18(14):7635. https://doi.org/10.3390/ijerph18147635
Chicago/Turabian StyleOu Yang, Wen-Yu, Cheng-Chien Lai, Meng-Ting Tsou, and Lee-Ching Hwang. 2021. "Development of Machine Learning Models for Prediction of Osteoporosis from Clinical Health Examination Data" International Journal of Environmental Research and Public Health 18, no. 14: 7635. https://doi.org/10.3390/ijerph18147635
APA StyleOu Yang, W.-Y., Lai, C.-C., Tsou, M.-T., & Hwang, L.-C. (2021). Development of Machine Learning Models for Prediction of Osteoporosis from Clinical Health Examination Data. International Journal of Environmental Research and Public Health, 18(14), 7635. https://doi.org/10.3390/ijerph18147635






