Safety Issues in Buckling of Steel Structures by Improving Accuracy of Historical Methods
Abstract
:1. Introduction
- Maximum critical load which depletes the column.
- Undetermined coefficient, with units of force over length.
- Cross-sectional area of the column.
- Length of the column.
- C Material dependent coefficient and cross section, in units of force multiplied by length squared.
- E
- Modulus of longitudinal elasticity of the column’s material. The Young’s Modulus.
- I
- Moment of inertia with respect to the axis buckling takes place.
- Lk
- Buckling length of the column. In the case of pinned–pinned bar, it corresponds to the geometrical length, precisely because it is a pinned–pinned column.
- σcrit
- Maximum critical compression stress that triggers the buckling of the column.
- λk
- Mechanical slenderness of the column.
2. Development of Steel Construction: 19th, and Beginnings of the 20th, Century
- Po
- Fracture/buckling load, in kp.
- d
- Outer diameter of the column, in cm.
- L
- Length of the column, in dm.
- K
- Coefficient of values 10,320 for a fixed bar, 5954 for fixed–pinned, and 2977 for pinned–pinned.
- P0
- Maximum fracture load which the column can withstand.
- α
- Coefficient that depends on the boundary conditions, 1 for a fixed member, 4/7 for a fixed–pinned member, and 2/7 for a pinned–pinned member.
- R′
- Simple compressive fracture stress of the material the column is made of.
- w
- Cross-sectional area.
- L
- Member length.
- d
- Outer diameter of the column.
- L
- Member length.
- kz
- Radius of gyration of the section with respect to the buckling axis.
- σmax
- Steel yield stress (fy).
- σc
- Maximum compression stress which depletes the column.
- e
- Load eccentricity caused by the flexural momentum acting on the section, measured in relation to the section’s center of gravity.
- c
- Section’s center of gravity distance with respect to the most compressed fiber, for symmetric sections c = h/2 (half the section’s edge).
- E
- Longitudinal elasticity modulus of the column’s material. The Young’s Modulus.
- r
- Radius of gyration of the section with respect to the buckling axis.
- L
- Buckling length of the member.
3. The First Construction Standards, the Second Half of the 20th Century
- P*
- Maximum design load the column can withstand.
- ω
- Nondimensional buckling coefficient greater than or equal to the unit, a function of the type of steel, yield stress, and mechanical slenderness of the member.
- A
- Gross cross-sectional area.
- σadm
- Tolerable steel strength equal to its yield stress.
- λk
- Mechanical slenderness of the column.
- E
- Modulus of longitudinal elasticity of the material the column is made of. The Young’s modulus.
- a, b
- Nondimensional auxiliary coefficients.
- ω
- Nondimensional buckling coefficient greater than or equal to the unit, a function of the type of steel, yield stress, and mechanical slenderness of the member.
4. Operative Standards, Current Situation
- Nb,Rd
- Design buckling resistance of a compression member.
- NEd
- Design value of the compression force.
- χ
- Buckling coefficient less than or equal to the unit, a function of the imperfection factor and of the member’s reduced slenderness.
- A
- Gross cross-sectional area.
- fyd
- Design yield stress.
- χ
- Nondimensional buckling coefficient less than or equal to the unit, a function of the member’s imperfection factor and reduced slenderness.
- λ
- Member’s reduced slenderness with respect to the selected axis. It should be less than or equal to 3.
- α
- Imperfection factor, dependent on the type of cross section and buckling axis.
- I
- Cross-sectional inertia dependent on the selected axis.
- A
- Gross cross-sectional area.
- Lk
- Buckling length of the column.
- fy
- Yield stress of steel.
- E
- Modulus of elasticity of steel.
- Fe
- Elastic buckling stress through an elastic buckling analysis .
- Fy
- Specified minimum yield stress of the type of steel being used.
- r
- Radius of gyration.
- Lc
- Effective length of the member for buckling about the minor axis.
- N
- Axial compression in the calculated portion of the member.
- N’Ex
- Parameter, N’Ex = π2EA/(1.1 λx2).
- φx
- Stability factor of axial compression members buckling in the plane of bending.
- Mx
- Maximum moment in the calculated portion of the member.
- W1x
- Gross section modulus referred to the more compressed fiber in the plane of bending.
- Βmx
- Factor of equivalent moment, taken between 0.65–1.00.
- f
- Yield stress.
5. Numerical Simulation
5.1. Geometry
5.2. Finite Element Model Description
5.3. Results
6. Conclusions
- Buckling is a transcendent phenomenon for the safety of building and bridge structures. Buckling problems must be considered in the design, calculation, and construction phase of the structures.
- Euler’s equation [7] has been applied in structural mechanics for almost 300 years with barely any modification. The fact that it is still being applied today makes it the most long-lived equation in structural engineering.
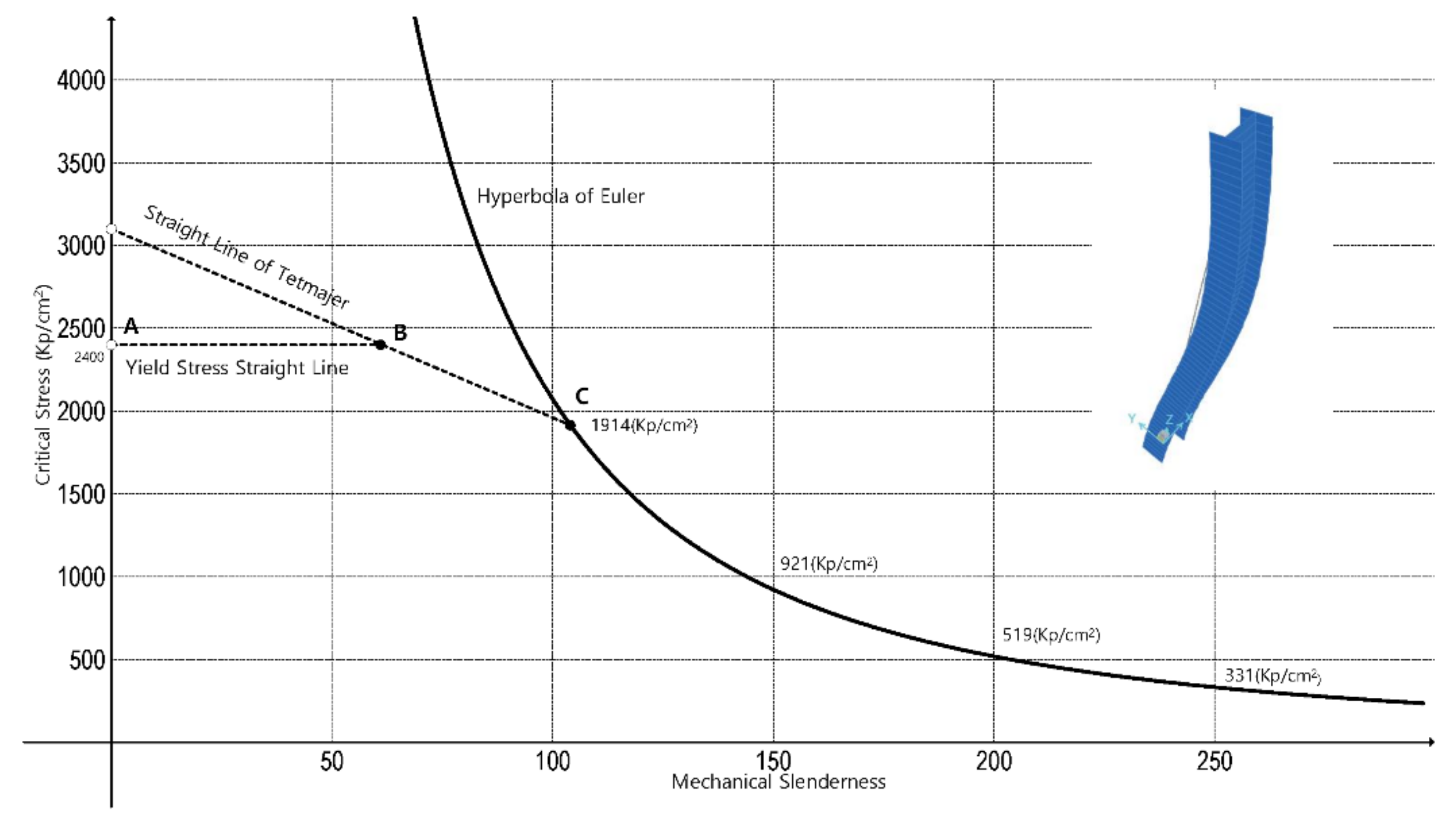
- Every model predicts that for mechanical slenderness of approximately 20, the member will not undergo the process of buckling.
- The secant method formula yield values very much in line with those proposed by the standards.
- Rankine’s [9] and AISC [10] models yield values in line with those much more elaborated coming afterwards for mechanical slenderness of less than 100. Specifically, Rankine’s equation, even though old, is in tune with all the mechanical slenderness values predicted by much more sophisticated modern models.
- Older models, such as Barré–Marvá’s [8], yield more conservative values, somehow far from today’s actual values but quite acceptable nonetheless. The reason could well reside in the fact that those values were to be applied to cast iron columns that exhibited less slenderness than those used later.
- According to the performed numerical simulations, older models, such as Euler [7], Tetmajer [12], Rankine [9], and AISC [10], tend to slightly overestimate the critical buckling stress for high slenderness ratios from around 100 (except Euler, which considerably overestimates the critical stress for low and mid-slenderness ratios because it does not consider the nonlinear behavior of the steel when the yielding takes place). Besides, the Tetmajer [12] model also overestimates critical buckling stress for low slendernesses below approximately 30.
- The order of the theoretical curves, considering their degree of overestimation of the critical buckling stress, is (1) Euler [7], (2) Tetmajer [12], (3) Rankine [9], (4) Timoshenko’s secant [11], (5) Barré–Marvá [8]. From a design point of view, Timoshenko’s secant [11] and Barré–Marvá [8] curves are on the safe side for any value of mechanical slenderness according to the finite element model results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sibly, P.G.; Bouch, T.; Walker, A.C.; Cooper, T.; Stephenson, R.; Moisseiff, L.S. Structural accidents and their causes. Proc. Inst. Civ. Eng. 1977, 62, 191–208. [Google Scholar]
- Augenti, N.; Parisi, F. Buckling analysis of a long-span roof structure collapsed during construction. J. Perform. Constr. Facil. 2013, 77, 77–88. [Google Scholar] [CrossRef]
- Al-Marwaee, M. Structural failure of buildings: Issues and challenges. Sci. World J. 2017, 66, 97–108. [Google Scholar]
- Timoshenko, S.P. History of Strength of Materials; McGraw-Hill: New York, NY, USA, 1953; ISBN 9780070647251. [Google Scholar]
- Galilei, G. Diálogos Acerca de dos Nuevas Ciencias; Losada: Ciudad de Buenos Aires, Argentina, 2004; ISBN 9789500392136. [Google Scholar]
- Van Musschenbroek, P. Physicæ Experimentales, et Geometricæ, de Magnete, Tuborum Capillarium Vitreorumque Speculorum Attractione, Magnitudine Térrea, Cohaerentia Corporum Firmorum. Dissertationes, ut et Ephemerides Meteorologicae Ultrajectinae; Trattner, J.T., Ed.; apud Samuelem Luchtmans: Lugduni Batavorum, The Netherlands, 1756. [Google Scholar]
- Euler, L. Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes; Nabu Press: Charleston, SC, USA, 2011; ISBN 9781271750634. [Google Scholar]
- Marvá Mayer, J. Mecánica Aplicada a las Construcciones; Palacios, J., Ed.; Imprenta y Litografía de Julián Palacios: Madrid, Spain, 1916. [Google Scholar]
- Rankine, W.J.M. A Manual of Civil Engineering; Griffin and Company: London, UK, 1876. [Google Scholar]
- American Institute of Steel Construction Standard. Specification for Structural Steel for Buildings; American Institute of Steel Construction Standard: Chicago, CA, USA, 2016. [Google Scholar]
- Timoshenko, S. Strength of Materials, 2nd ed.; Nostrand, V., Ed.; Springer: New York, NY, USA, 1940. [Google Scholar]
- Von Tetmajer, L. Die Gesetze der Knickungs und der Zusammengesetzten Druckfestigkeit der Technisch Wichtigsten Baustoffe; Kessinger Publishing, LLC: Whitefish, MT, USA, 2010; ISBN 9781161096316. [Google Scholar]
- Von Karman, T. Untersuchungen uber die Knickfestigkeit, Mitteilungen uber Forschungsarbeiten auf dem Gebiete des Ingenieurwensen; Springer: Berlin/Heidelberg, Germany, 1910. [Google Scholar]
- Southwell, R.V. On the General Theory of Elastic Stability. Phil. Trans. Roy. Soc. Lond. 1914, 213, 187–244. [Google Scholar]
- Bleich, F. Theorie und Berechnung der Eiseren Brucken; Springer: Berlin/Heidelberg, Germany, 1924. [Google Scholar]
- Lundquist, E.E. Local Instability of Symmetrical Rectangular Tubes under Axial Compression; National Advisory Committee for Aeronautics: Langley Field, VA, USA, 1939; Volume 686, pp. 1–25.
- Kappus, R. Twisting Failure of Centrally Loaded Open Section Columns in the Elastic Range; US Government Publishing: Washington, DC, USA, 1938.
- Goodier, J.N. The Buckling of Compressed Bars by Torsion and Flexure; Brown University: New York, NY, USA, 1941. [Google Scholar]
- Shanley, F.R. The Column Paradox. J. Aeronaut. Sci. 1946, 13, 678. [Google Scholar] [CrossRef]
- Shanley, F.R. Inelastic Column Theory. J. Aeronaut. Sci. 1947, 14, 261–268. [Google Scholar] [CrossRef]
- Codes, G. DIN 4114-1:1952-07 Steel Structures Stability (Buckling Overturnung Bulging), Method of Calculation, Regulations; German Institute for Standardisation: Berlin, Germany, 1952. [Google Scholar]
- Dutheil, J. Théorie de l’inestabilité par divergence d’équilibre. In Proceedings of the Association Internationale des Pont et Charpentes, London, UK, 25 August–5 September 1952; Congrès, I.V., Ed.; e-periodica: Zurich, Switzerland, 2021. [Google Scholar]
- Instituto Eduardo Torroja. Instrucción Para Estructuras de Acero; EM-6; Instituto Eduardo Torroja: Madrid, Spain, 1969. [Google Scholar]
- Ministerio de Obras Públicas y Urbanismo. Norma Básica de la Edificación. Cálculo de Las Estructuras de Acero Laminado en Edificación; NBE-MV 103; Dirección General Para la Vivienda y Arquitectura, Ministerio de Obras Públicas y Urbanismo: Madrid, Spain, 1972.
- Ministerio de Fomento. Norma Básica de la Edificación. Estructuras de Acero en Edificación; NBE EA-95; Ministerio de Fomento: Madrid, Spain, 1995.
- Ministerio de Vivienda. Código Técnico de la Edificación; Documento Básico. Seguridad Estructural. Acero CTE DB-SE-A; Ministerio de Vivienda: Madrid, Spain, 2006.
- European Recommendations for Steel Construction. Manual on Stability of Steel Structures. In European Convention for Constructional Steelwork (ECCS); European Convention for Constructional Steelwork: Brussels, Belgium, 1976. [Google Scholar]
- Ministerio de Fomento. EAE: Instrucción de Acero Estructural; Ministerio de Fomento: Madrid, Spain, 2012; ISBN 978-84-498-0912-5.
- Ministerio de Transportes Movilidad y Agenda Urbana. Código Estructural; Ministerio de Transportes Movilidad y Agenda Urbana: Madrid, Spain, 2021.
- European Commission of Standardization. Eurocode 3: Design of steel structures—Part 1-1: General Rules and Rules for Buildings; European Commission of Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the Peoples’s Republic of China. Code for Design of Steel Structures. Department of Standard and Norms; GB 50017; Ministry of Housing and Urban-Rural Development of the Peoples’s Republic of China: Beijing, China, 2003.
- Moen, C.D.; Schafer, B.W. Elastic buckling of cold-formed steel columns and beams with holes. Eng. Struct. 2009, 31, 2812–2824. [Google Scholar] [CrossRef]
- Musa, I.A. Buckling of plates including effect of shear deformations: A hyperelastic formulation. Struct. Eng. Mech. 2016, 57, 1107–1124. [Google Scholar] [CrossRef]
- Wang, J.; Afshan, S.; Schillo, N.; Theofanous, M.; Feldmann, M.; Gardner, L. Material properties and compressive local buckling response of high strength steel square and rectangular hollow sections. Eng. Struct. 2017, 130, 297–315. [Google Scholar] [CrossRef] [Green Version]
- Le, T.; Bradford, M.A.; Liu, X.; Valipour, H.R. Buckling of welded high-strength steel I-beams. J. Constr. Steel Res. 2020, 168, 105938. [Google Scholar] [CrossRef]
- Huang, Z.; Li, D.; Uy, B.; Thai, H.T.; Hou, C. Local and post-local buckling of fabricated high-strength steel and composite columns. J. Constr. Steel Res. 2019, 154, 235–249. [Google Scholar] [CrossRef]
- Martínez, A.; Miguel, V.; Coello, J.; Manjabacas, M.C. Determining stress distribution by tension and by compression applied to steel: Special analysis for TRIP steel sheets. Mater. Des. 2017, 125, 11–25. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Wu, Q.; Yu, J.; Frank Chen, Y.; Lu, G.-B. Experimental and analytical studies on elastic-plastic local buckling behavior of steel material under complex cyclic loading paths. Constr. Build. Mater. 2018, 181, 495–509. [Google Scholar] [CrossRef]
- Singh, T.G.; Chan, T.M. Effect of access openings on the buckling performance of square hollow section module stub columns. J. Constr. Steel Res. 2021, 177, 106438. [Google Scholar] [CrossRef]
- Chen, Y.; Shu, G.; Zheng, B.; Lu, R. Overall buckling behaviour of welded π-shaped compression columns. J. Constr. Steel Res. 2020, 165, 105891. [Google Scholar] [CrossRef]
- Tian, W.; Hao, J.; Zhong, W. Buckling of stepped columns considering the interaction effect among columns. J. Constr. Steel Res. 2021, 177, 106416. [Google Scholar] [CrossRef]
- Mirtaheri, M.; Sehat, S.; Nazeryan, M. Improving the behavior of buckling restrained braces through obtaining optimum steel core length. Struct. Eng. Mech. 2018, 65, 401. [Google Scholar] [CrossRef]
- Bourada, M.; Bouadi, A.; Bousahla, A.A.; Senouci, A.; Bourada, F.; Tounsi, A.; Mahmoud, S.R. Buckling behavior of rectangular plates under uniaxial and biaxial compression. Struct. Eng. Mech. 2019, 70, 113. [Google Scholar] [CrossRef]
- ABAQUS Inc. In Simulia Abaqus Unified FEA (Software); ABAQUS Inc.: Palo Alto, CA, USA.
- Pereiro-Barceló, J.; Bonet, J.L. Ni-Ti SMA bars behaviour under compression. Constr. Build. Mater. 2017, 155, 348–362. [Google Scholar] [CrossRef] [Green Version]










| Profile | h (mm) | b (mm) | r (mm) | tw (mm) | tf (mm) | Area (mm2) | Y Axis Inertia—Iy (mm4) | Z Axis Inertia—Iz (mm4) |
|---|---|---|---|---|---|---|---|---|
| HEB-200 | 200 | 200 | 18 | 9 | 15 | 78.1 | 5696 | 2003 |
| UPE-200 | 200 | 80 | 13 | 6 | 11 | 29 | 1910 | 187 |
| Two-welded UPE-200 | 200 | 160 | 13 | 9 | 11 | 58 | 3820 | 2090 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pomares, J.C.; Pereiro-Barceló, J.; González, A.; Aguilar, R. Safety Issues in Buckling of Steel Structures by Improving Accuracy of Historical Methods. Int. J. Environ. Res. Public Health 2021, 18, 12253. https://doi.org/10.3390/ijerph182212253
Pomares JC, Pereiro-Barceló J, González A, Aguilar R. Safety Issues in Buckling of Steel Structures by Improving Accuracy of Historical Methods. International Journal of Environmental Research and Public Health. 2021; 18(22):12253. https://doi.org/10.3390/ijerph182212253
Chicago/Turabian StylePomares, Juan Carlos, Javier Pereiro-Barceló, Antonio González, and Rafael Aguilar. 2021. "Safety Issues in Buckling of Steel Structures by Improving Accuracy of Historical Methods" International Journal of Environmental Research and Public Health 18, no. 22: 12253. https://doi.org/10.3390/ijerph182212253
APA StylePomares, J. C., Pereiro-Barceló, J., González, A., & Aguilar, R. (2021). Safety Issues in Buckling of Steel Structures by Improving Accuracy of Historical Methods. International Journal of Environmental Research and Public Health, 18(22), 12253. https://doi.org/10.3390/ijerph182212253







