Predicting and Interpreting Spatial Accidents through MDLSTM
Abstract
:1. Introduction
2. Literature Review
2.1. Spatial Analysis of Traffic Accidents
2.2. Influencing Factors of Traffic Accidents
3. Materials and Methods
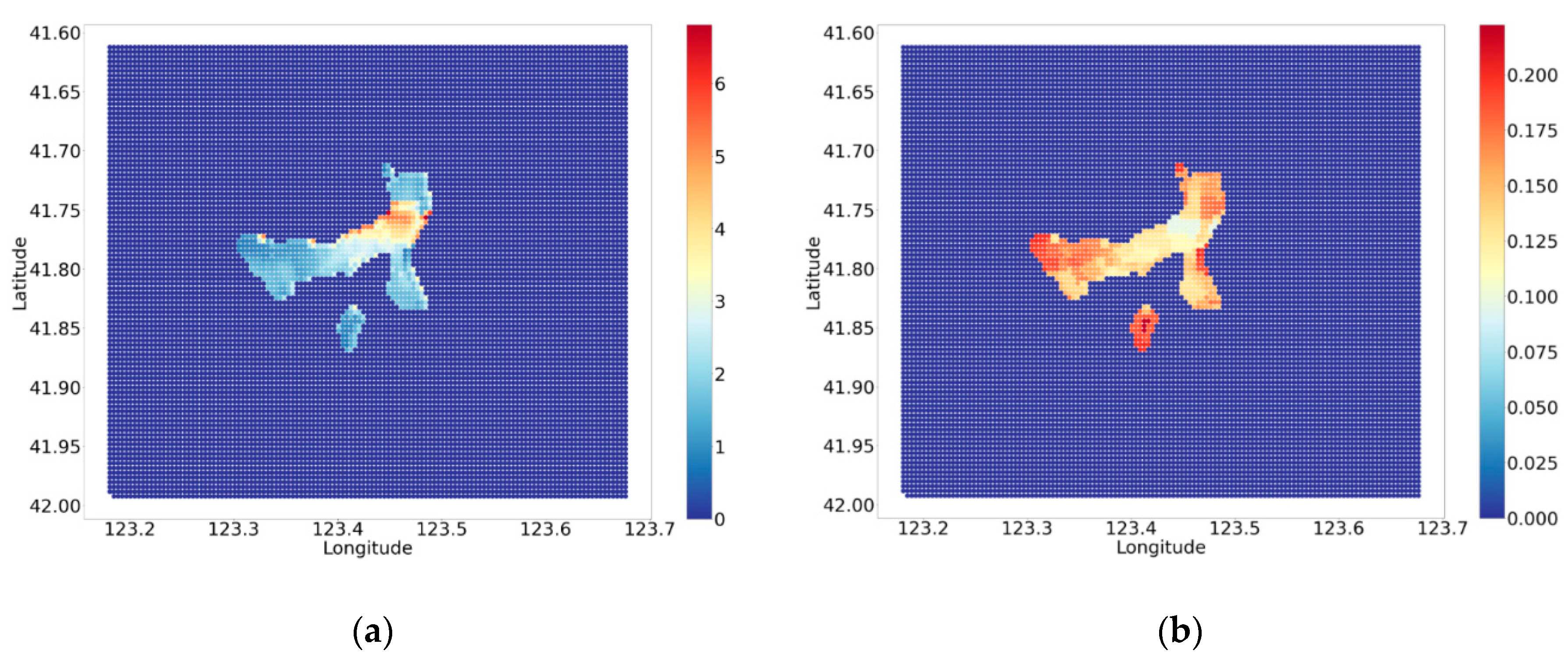
3.1. Data
3.1.1. Data Sources
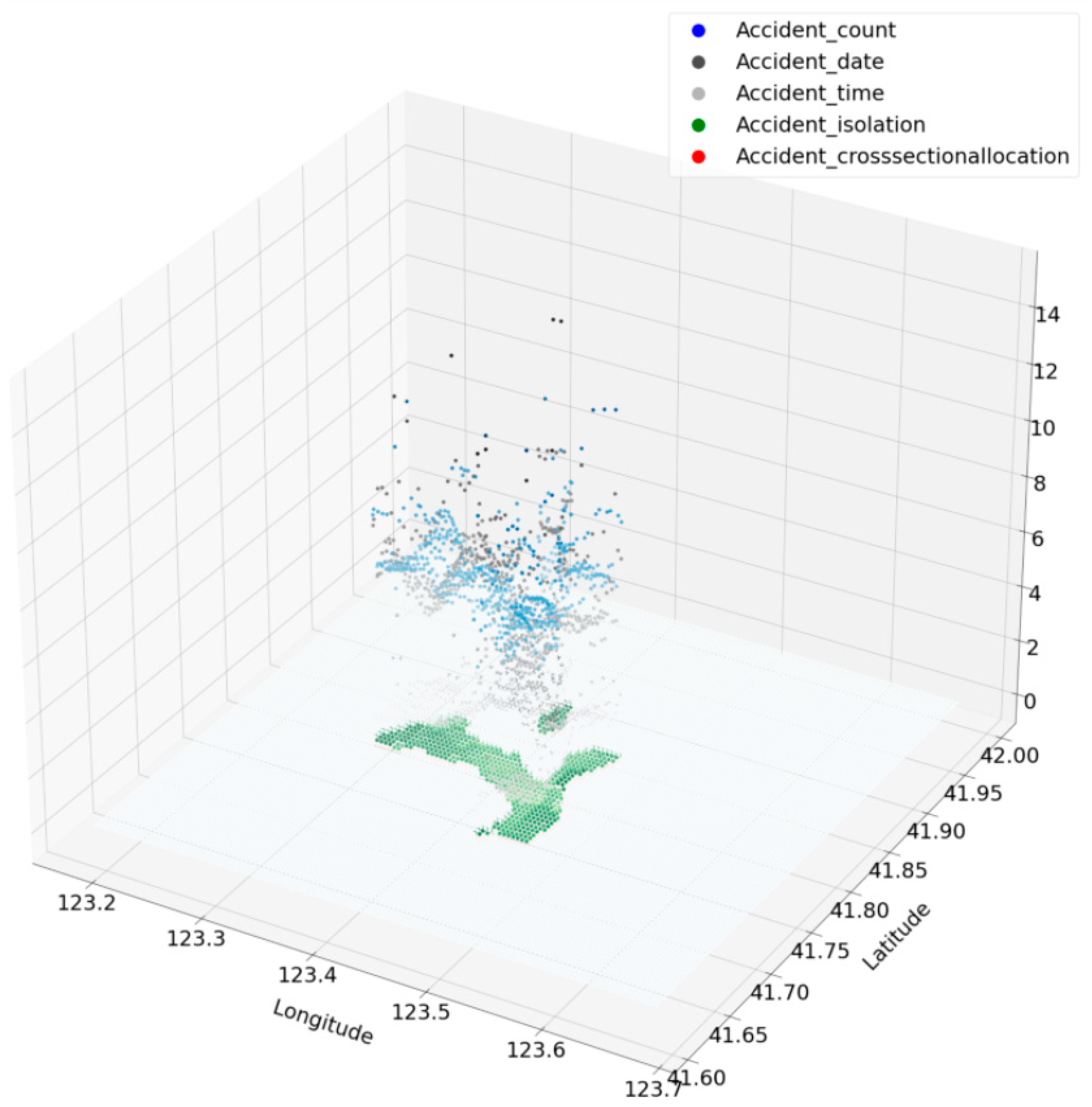
3.1.2. Distribution of Accidents Characteristics
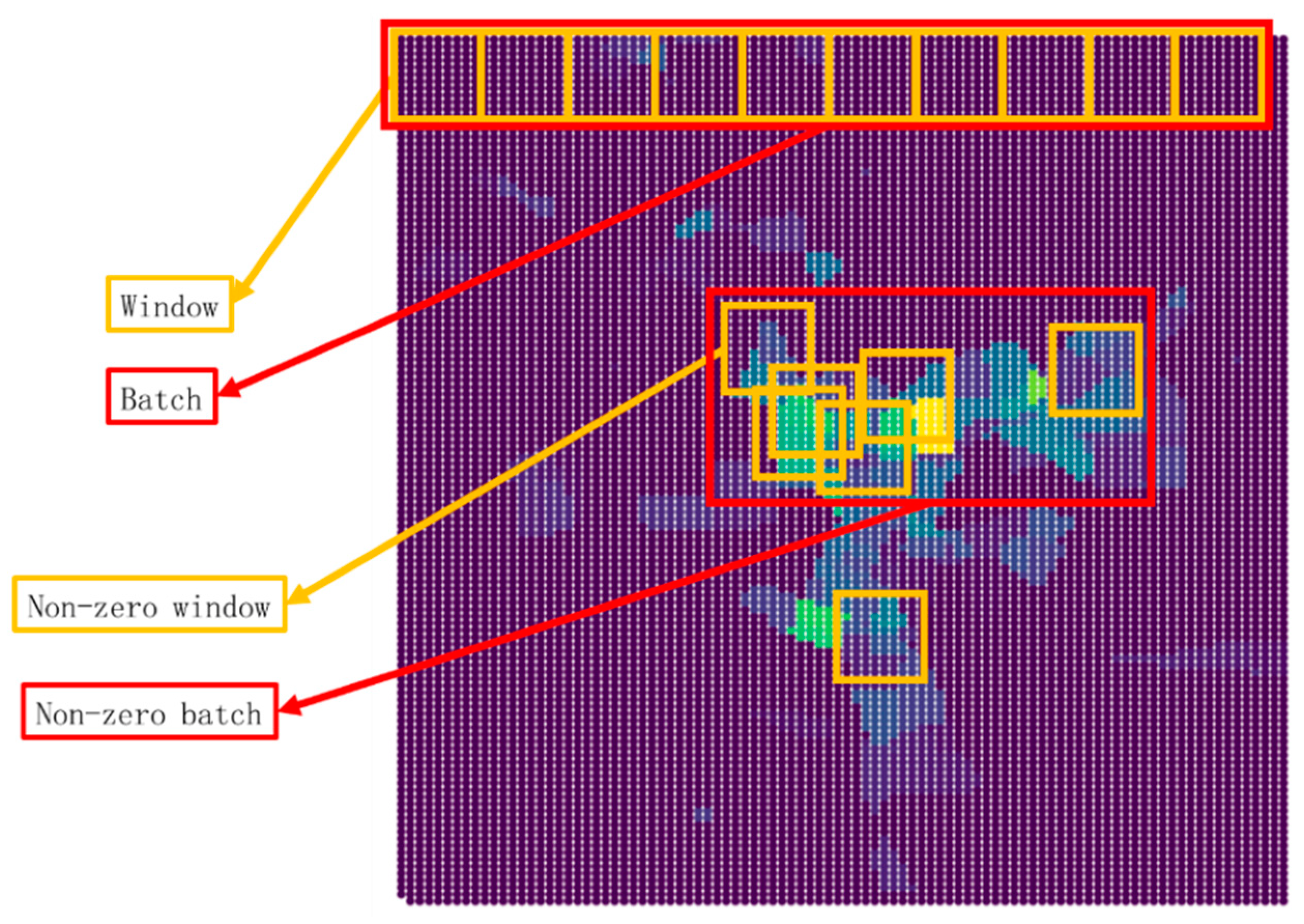
3.1.3. Rasterization
3.2. Validation of the Spatial Autocorrelation
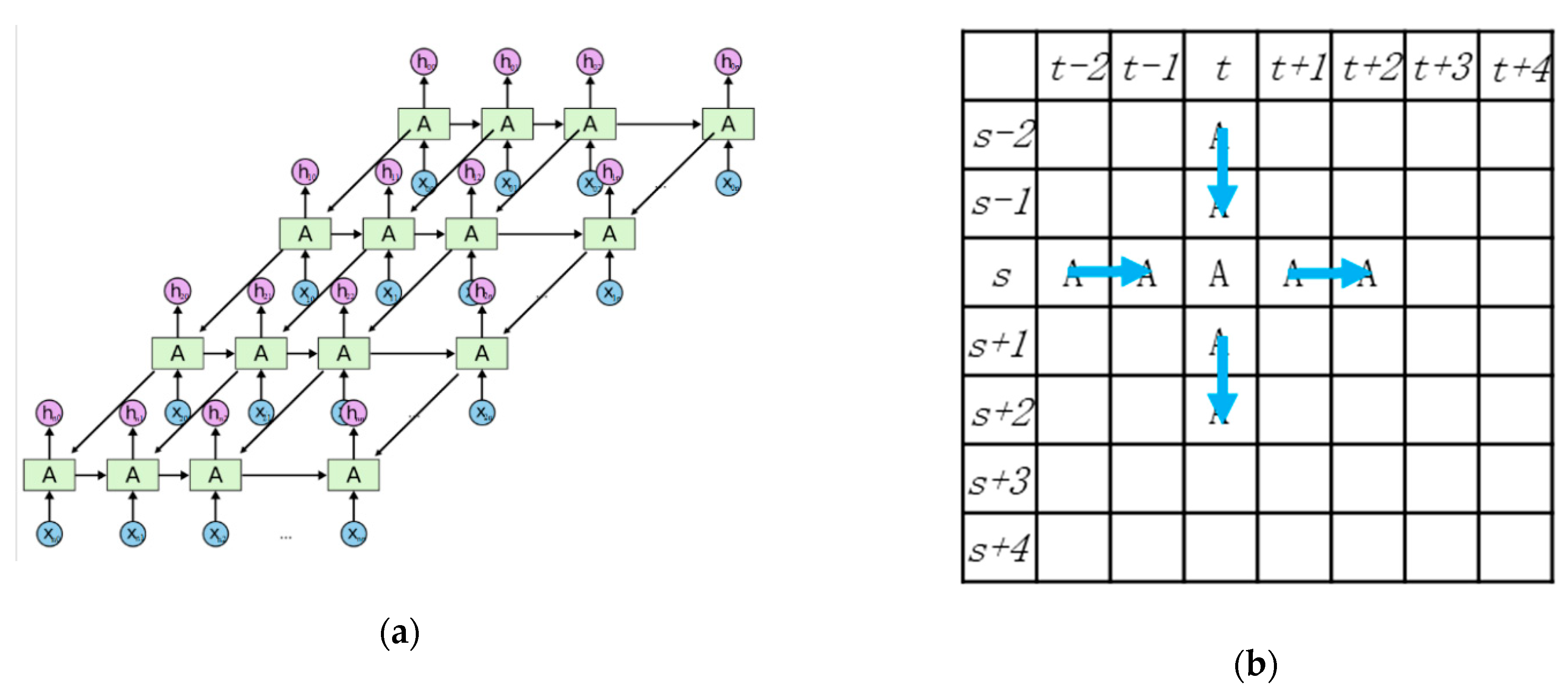
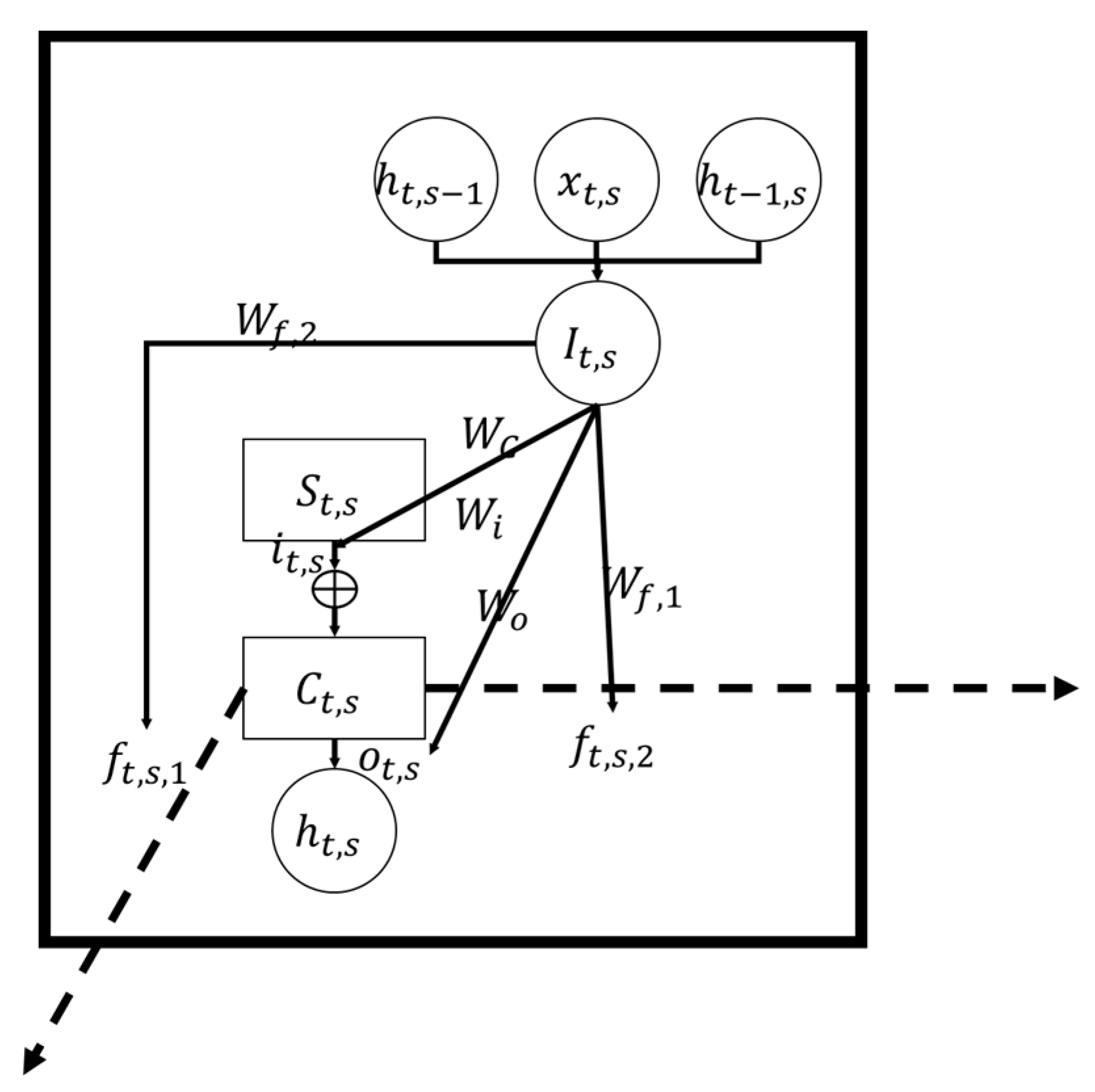
3.3. MDLSTM Model
4. Discussion
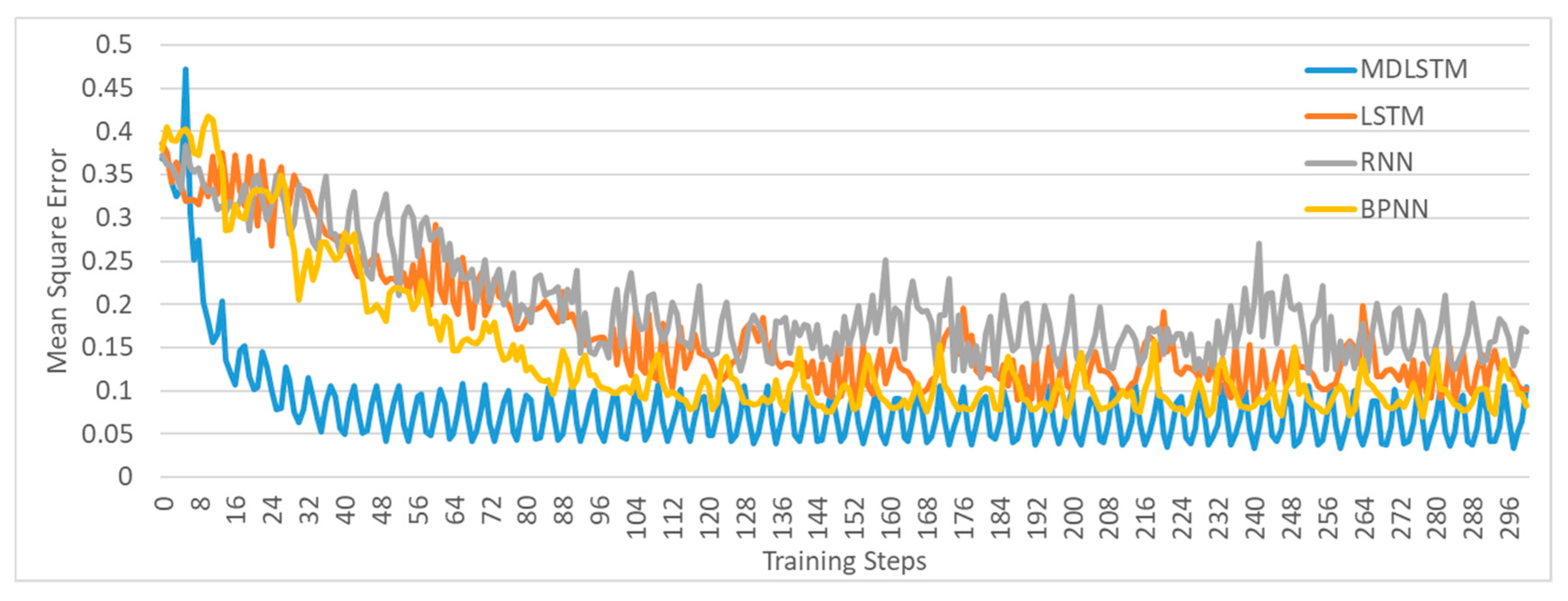
4.1. Validation of the MDLSTM Model
4.2. Characteristics of Traffic Accident Potential
4.3. The Impact of Land Use Properties and Spatial Effect on the Traffic Accident
4.4. General Rules Based on the Interpretation of the Weight Matrix
4.4.1. Relationship between Land Use Properties and Accident Potential
4.4.2. Accident Potential Based on the Local One
4.4.3. Accident Potential Transfer from the Neighboring Grid Cells and
4.4.4. Proportion of Accident Potential That Leads to an Accident
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Road Traffic Injuries. Available online: https://www.who.int/health-topics/road-safety#tab=tab_1 (accessed on 29 December 2020).
- Ziakopoulos, A.; Yannis, G. A review of spatial approaches in road safety. Accid. Anal. Prev. 2019, 135, 105323. [Google Scholar] [CrossRef]
- Imprialou, M.I.; Quddus, M.; Pitfield, D.E.; Lord, D. Re-visiting crash–speed relationships: A new perspective in crash modelling. Accid. Anal. Prev. 2016, 86, 173–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erdogan, S. Explorative spatial analysis of traffic accident statistics and road mortality among the provinces of Turkey. J. Saf. Res. 2009, 40, 341–351. [Google Scholar] [CrossRef]
- Jonathan, A.V.; Wu, K.F.K.; Donnell, E.T. A multivariate spatial crash frequency model for identifying sites with promise based on crash types. Donnell Accid. Anal. Prev. 2016, 87, 8–16. [Google Scholar] [CrossRef]
- Dong, N.; Huang, H.; Lee, J.; Gao, M.; Abdel-Aty, M. Macroscopic hotspots identification: A Bayesian spatio-temporal interaction approach. Accid. Anal. Prev. 2016, 92, 256–264. [Google Scholar] [CrossRef]
- Liu, J.; Khattak, A.J.; Wali, B. Do safety performance functions used for predicting crash frequency vary across space? Applying geographically weighted regressions to account for spatial heterogeneity. Accid. Anal. Prev. 2017, 109, 132–142. [Google Scholar] [CrossRef] [PubMed]
- Dereli, M.A.; Erdogan, S. A new model for determining the traffic accident black spots using GIS-aided spatial statistical methods. Transp. Res. Part A Policy Pract. 2017, 103, 106–117. [Google Scholar] [CrossRef]
- Wang, J.; Huang, H. Road network safety evaluation using Bayesian hierarchical joint model. Accid. Anal. Prev. 2016, 90, 152–158. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Abdel-Aty, M.; Hu, J.; Lee, J. Investigating macro-level hotzone identification and variable importance using big data: A random forest models approach. Neuro-Comput. 2016, 181, 53–63. [Google Scholar] [CrossRef]
- Xie, Z.; Yan, J. Detecting traffic accident clusters with network kernel density estimation and local spatial statistics: An integrated approach. J. Transp. Geogr. 2013, 31, 64–71. [Google Scholar] [CrossRef]
- Levine, N.; Kim, K.E.; Nitz, L.H. Spatial Analysis of Honolulu Motor Vehicle Crashes: Ⅰ. Spatial Patterns. Accid. Anal. Prev. 1995, 27, 663–674. [Google Scholar] [CrossRef]
- Levine, N.; Kim, K.E.; Nitz, L.H. Spatial Analysis of Honolulu Motor Vehicle Crashes: Ⅱ. Zonal Generators. Accid. Anal. Prev. 1995, 27, 675–685. [Google Scholar] [CrossRef]
- Quddus, M.A. Modelling Area-wide Count Outcomes with Spatial Correlation and Heterogeneity: An Analysis of London Crash Data. Accid. Anal. Prev. 2008, 40, 1486–1497. [Google Scholar] [CrossRef] [Green Version]
- Lord, D.; Persaud, B.N. Estimating the Safety Performance of Urban Road Transportation Networks. Accid. Anal. Prev. 2004, 36, 609–620. [Google Scholar] [CrossRef]
- Lovegrove, G.R.; Sayed, T. Macro-level Collision Prediction Models for Evaluating Neighborhood Traffic Safety. Can. J. Civ. Eng. 2006, 33, 609–621. [Google Scholar] [CrossRef]
- Al-Bdairi, N.; Hernandez, S. Comparison of contributing factors for injury severity of large truck drivers in run-off-road (ROR) crashes on rural and urban roadways: Accounting for unobserved heterogeneity. Int. J. Transp. Sci. Technol. 2020, 9, 116–127. [Google Scholar] [CrossRef]
- Ahmed, M.; Franke, R.; Ksaibati, K.; Shinstine, D. Effects of truck traffic on crash injury severity on rural highways in Wyoming using Bayesian binary logit models. Accid. Anal. Prev. 2018, 117, 106–113. [Google Scholar] [CrossRef]
- Wang, Y.; Prato, C. Determinants of injury severity for truck crashes on mountain expressways in China: A case-study with a partial proportional odds model. Saf. Sci. 2019, 117, 100–107. [Google Scholar] [CrossRef]
- Osman, M.; Paleti, R.; Mishra, S. Analysis of passenger-car crash injury severity in different work zone configurations. Accid. Anal. Prev. 2018, 111, 161–172. [Google Scholar] [CrossRef]
- Liu, P.; Fan, W. Exploring injury severity in head-on crashes using latent class clustering analysis and mixed logit model: A case study of North Carolina. Accid. Anal. Prev. 2020, 135, 105388. [Google Scholar] [CrossRef]
- Kelley, M.E.; Talton, J.W.; Aa, W.; Usoro, A.O.; Barnard, E.R.; Miller, A.N. Associations between upper extremity injury patterns in side impact motor vehicle collisions with occupant and crash characteristics. Accid. Anal. Prev. 2019, 122, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.; Gill, G.; Sakrani, T.; Dasu, M.; Zhou, J. Predicting motorcycle crash injury severity using weather data and alternative Bayesian multivariate crash frequency models. Accid. Anal. Prev. 2017, 108, 172–180. [Google Scholar] [CrossRef] [PubMed]
- Theofilatos, A.; Yannis, G. Factors Affecting Accident Severity Inside and Outside Urban Areas in Greece. Traffic Inj. Prev. 2012, 13, 458–467. [Google Scholar] [CrossRef]
- Sze, N.; Wong, S. Diagnostic analysis of the logistic model for pedestrian injury severity in traffic crashes. Accid. Anal. Prev. 2007, 39, 1267–1278. [Google Scholar] [CrossRef]
- Liu, X.; Long, Y. Automated identification and characterization of parcels (AICP) with OpenStreetMap and Points of Interest. Environ. Plan. B 2015, 43, 498–510. [Google Scholar]
- Yue, Y.; Zhuang, Y.; Yeh, A.G.O.; Xie, J.Y.; Li, Q.Q. Measurements of POI-based mixed use and their relationships with neighborhood vibrancy. Int. J. Geogr. Inf. Syst. 2017, 31, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Erdogan, S.; Yilmaz, I.; Baybura, T.; Gullu, M. Geographical information systems aided traffic accident analysis system case study: City of Afyonkarahisar. Accid. Anal. Prev. 2008, 40, 174–181. [Google Scholar] [CrossRef]
- Schlgl, M. A multivariate analysis of environmental effects on road accident occurrence using a balanced bagging approach. Accident. Anal. Prev. 2019, 136, 105–398. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Fernandez, S.; Schmidhuber, J. Multi-dimensional recurrent neural networks. In Proceedings of the International Conference on Artificial Neural Networks, London, UK, 9–13 September 2007. [Google Scholar]
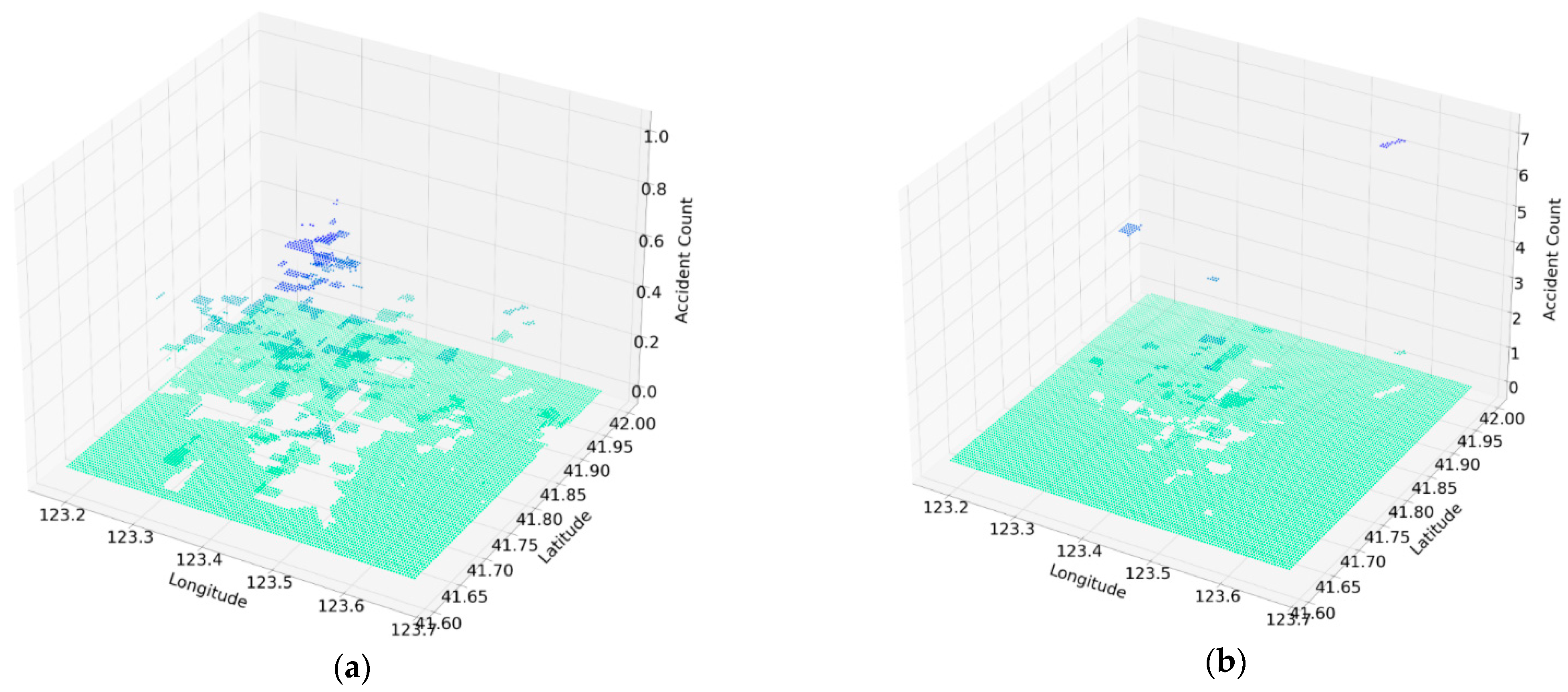
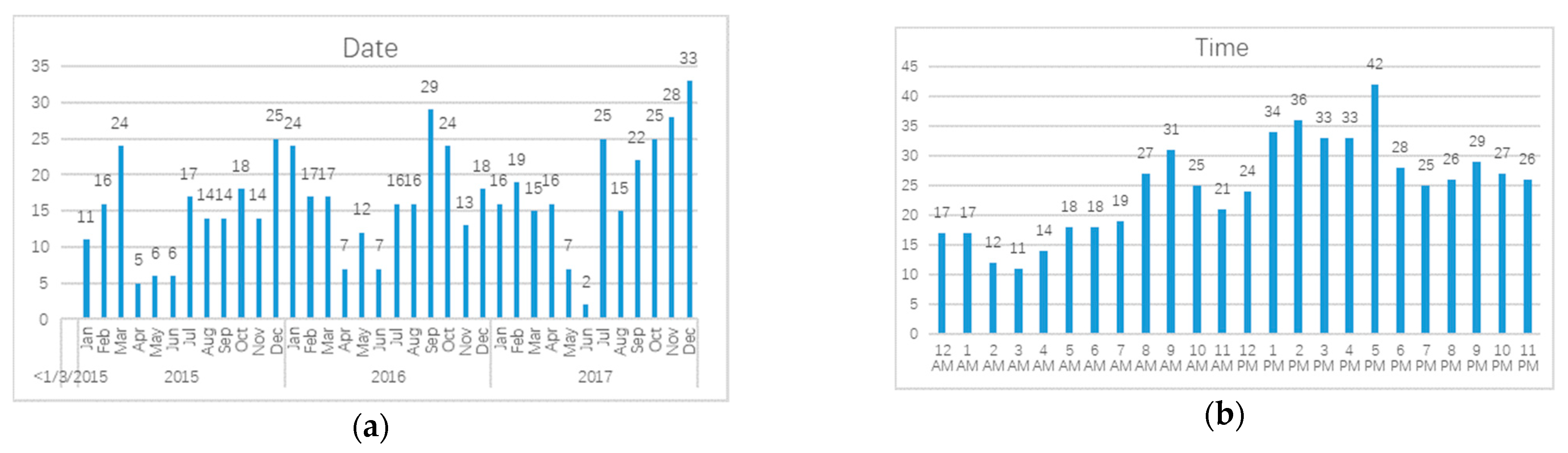
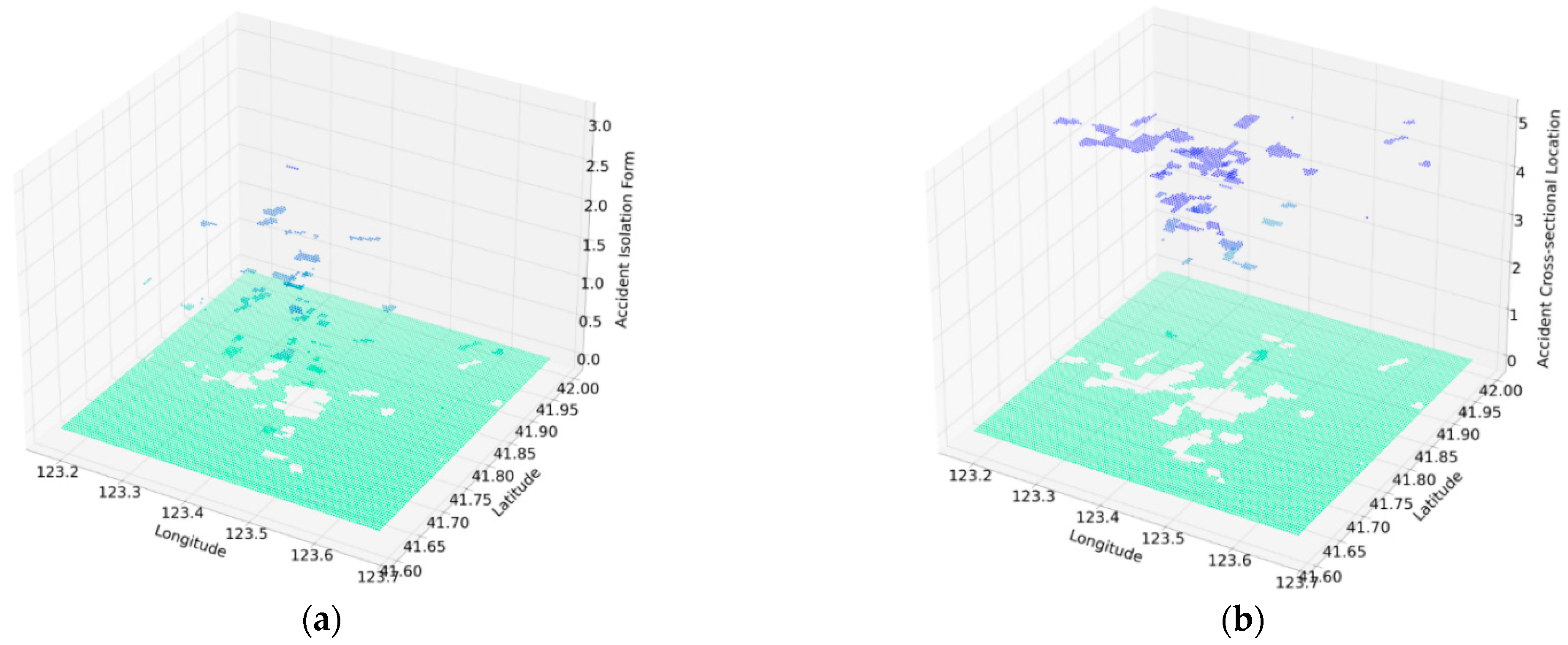




| Land Use Properties | Unit | Data Range | |||
|---|---|---|---|---|---|
| Minimum (Min) | Maximum (Max) | Mean | Standard Error (Std) | ||
| Plot ratio | - | 0 | 6.62 | 0.341 | 0.777 |
| Number of types of POIs * | - | 2.00 | 13.0 | 4.39 | 1.92 |
| Centrality | m (meter) | 4.49 × 103 | 3.37 × 104 | 1.31 × 104 | 5.60 × 103 |
| Distance to CBD * | m | 643 | 3.21 × 104 | 1.00 × 103 | 5.53 × 103 |
| Number of surrounding road sections | - | 0 | 221 | 34.1 | 34.1 |
| Congestion ratio | % | 0 | 0.486 | 0.00245 | 0.0227 |
| Traffic Accident Characteristics | Unit | Data Range | |||
|---|---|---|---|---|---|
| Min | Max | Mean | Std | ||
| Accident count | - | 0 | 45 | 11.4 | 9.39 |
| Accident date | d (day) | 0 | 183 | 117 | 52.2 |
| Accident time | s (second) | 300 | 8.62 × 104 | 4.54 × 104 | 2.33 |
| Accident isolation | - | 0 | 3 | 0.490 | 0.893 |
| Accident cross-sectional location | - | 0 | 5 | 4.60 | 0.957 |
| Global Moran’s I | 0.128 | |
| I | p-value | 1.76 × 10 − 10 |
| z-score | 6.38 | |
| Global Geary’s C | 0.868 | |
| C | p-value | 0.000171 |
| z-score | −3.58 | |
| Testing Indicator | MDLSTM | LSTM | RNN | BPNN |
|---|---|---|---|---|
| Mean squared error of the whole test dataset | 0.16 | 0.27 | 0.30 | 0.34 |
| Intermediate Variable | Accident Count | Accident Date | Accident Time | Accident Isolation | Accident Cross-Section Location |
|---|---|---|---|---|---|
| 0.30 | 0.77 | 0.41 | 0.29 | 0.23 | |
| 0.12 | −0.27 | 0.97 | 0.61 | 0.70 | |
| 0.74 | 0.65 | 0.26 | 0.59 | 0.66 | |
| 0.05 | 0.05 | 0.07 | 0.08 | 0.06 | |
| 0.60 | 0.56 | 0.62 | 0.45 | 0.47 |
| Key Features | Accident Count | Accident Date | Accident Time | Accident Isolation | Accident Cross-Section Location |
|---|---|---|---|---|---|
| Plot ratio | −0.39 | 0.13 | 0.09 | 0.00 | −0.49 |
| Number of types of POIs | −0.12 | 0.32 | 0.37 | 0.25 | −0.27 |
| Centrality | −0.12 | 0.22 | 0.32 | −0.28 | 0.04 |
| Distance to CBD | 0.41 | −0.24 | 0.30 | 0.19 | 0.49 |
| Number of surrounding road sections | −0.49 | 0.39 | 0.08 | 0.04 | −0.57 |
| Congestion ratio | 1.02 | 2.11 | −0.73 | 1.66 | 0.21 |
| Sum | 0.31 | 2.93 | 0.42 | 1.86 | −0.59 |
| Key Features | Accident Count | Accident Date | Accident Time | Accident Isolation | Accident Cross-Section Location |
|---|---|---|---|---|---|
| Plot ratio | 0.19 | 0.09 | −0.03 | 0.31 | 0.27 |
| Number of types of POIs | 0.00 | −0.27 | 0.01 | 0.07 | −0.99 |
| Centrality | 0.03 | 0.34 | 0.16 | −0.26 | 0.64 |
| Distance to CBD | 0.71 | −0.85 | 1.09 | −0.50 | 1.61 |
| Number of surrounding road sections | −0.01 | 0.13 | −0.03 | 0.13 | −0.23 |
| Congestion ratio | −1.34 | 3.24 | 0.62 | 1.15 | −2.05 |
| Sum | −0.43 | 2.69 | 1.82 | 0.89 | −0.74 |
| Key Features | Accident Count | Accident Date | Accident Time | Accident Isolation | Accident Cross-Section Location |
|---|---|---|---|---|---|
| Plot ratio | −0.43 | −0.26 | −0.35 | 0.90 | −0.05 |
| Number of types of POIs | 0.04 | 0.02 | 0.39 | 0.99 | −0.15 |
| Centrality | −0.87 | 0.72 | −0.18 | −1.35 | −0.48 |
| Distance to CBD | 0.22 | 0.13 | 0.01 | −0.95 | −0.36 |
| Number of surrounding road sections | 0.01 | 0.60 | 0.15 | −0.71 | 0.17 |
| Congestion ratio | −1.55 | −0.14 | −0.86 | 4.15 | −0.10 |
| Sum | −2.58 | 1.08 | −0.84 | 3.04 | −0.97 |
| Key Features | Accident Count | Accident Date | Accident Time | Accident Isolation | Accident Cross-Section Location |
|---|---|---|---|---|---|
| Plot ratio | 0.08 | 0.23 | 0.21 | −0.05 | −0.29 |
| Number of types of POIs | −0.13 | −0.01 | 0.16 | −0.15 | 0.13 |
| Centrality | −0.17 | 0.01 | −0.42 | 0.44 | −0.35 |
| Distance to CBD | 0.20 | 0.09 | −0.70 | −1.07 | 0.64 |
| Number of surrounding road sections | 0.39 | 0.03 | −0.38 | 0.15 | −0.47 |
| Congestion ratio | 0.27 | −0.29 | −0.42 | −0.26 | −0.16 |
| Sum | 0.64 | 0.06 | −1.55 | −0.94 | −0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, T.; Lu, H.; Wang, J.; Wang, K. Predicting and Interpreting Spatial Accidents through MDLSTM. Int. J. Environ. Res. Public Health 2021, 18, 1430. https://doi.org/10.3390/ijerph18041430
Xiao T, Lu H, Wang J, Wang K. Predicting and Interpreting Spatial Accidents through MDLSTM. International Journal of Environmental Research and Public Health. 2021; 18(4):1430. https://doi.org/10.3390/ijerph18041430
Chicago/Turabian StyleXiao, Tianzheng, Huapu Lu, Jianyu Wang, and Katrina Wang. 2021. "Predicting and Interpreting Spatial Accidents through MDLSTM" International Journal of Environmental Research and Public Health 18, no. 4: 1430. https://doi.org/10.3390/ijerph18041430
APA StyleXiao, T., Lu, H., Wang, J., & Wang, K. (2021). Predicting and Interpreting Spatial Accidents through MDLSTM. International Journal of Environmental Research and Public Health, 18(4), 1430. https://doi.org/10.3390/ijerph18041430






